Х 3 2 модуль: Mathway | Популярные задачи

2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от

x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

WSRD Модуль управления запуском Can-Am X3 | 2017-2022 QRSX+ Clutch — Whalen’s Speed ​​R&D

WSRD Can-Am X3 Launch Control Module | 2017-2022 QRSX+ Clutch — исследования и разработки Whalen’s Speed ​​| Уэлен Тюнинг перейти к содержанию

по WSRD

Исходная цена $384,00 — Изначальная цена $505,00

Первоначальная цена 384,00 долл. США

389,00 долл. США

$389.00 — $479.00

Текущая цена $389,00

| /

Модуль управления запуском WSRD (LCM) предназначен для того, чтобы машина могла иметь контролируемую постоянную скорость запуска путем отключения зажигания на желаемых оборотах, а также увеличения наддува за счет управления задержкой зажигания. Этот блок может быть добавлен к любой машине или к любой настройке и позволяет пользователю точно настроить скорость запуска и то, насколько агрессивной будет машина.

Операция управления запуском:

• WSRD LCM стандартно поставляются с задержкой операций
• Старые LCM поставлялись с трехсекундной задержкой между нажатием кнопки активации и фактической активацией LCM
• WSRD обновил это, чтобы теперь включать задержку в одну секунду с 1 февраля 2022 г.
• Для правильной работы нажмите кнопку мгновенного действия LCM, подождите одну секунду, а затем нажмите педаль газа для активации LCM

WSRD LCM имеет возможность замедления до 40*. Задержка зажигания позволяет больше нагревать выхлопные газы, что помогает скорости вращения вала турбины создавать больший наддув.

WSRD LCM будет отправлен с нашей стандартной настройкой 2200 об/мин с задержкой -30*. Мы также предлагаем настройку 2600 об/мин, которая может быть предварительно загружена. Это может быть изменено пользователем. С помощью нашего LCM Max Effort мы можем настроить и помочь пользователю с настройкой, а при использовании нашей настройки объединить как LCM, так и нашу настройку для достижения наилучших результатов.

• WSRD Стандартная настройка управления запуском 2200 об/мин
• Требуется синяя первичная пружина KWI (зацепление на 2500 об/мин), которая ранее использовалась в системах сцепления KWI AO (ВНИМАНИЕ: KWI теперь поставляет синюю/оранжевую первичную пружину со всеми системами сцепления, это НЕ поддерживает нашу конфигурацию управления запуском. 
• Системы сцепления других производителей поддерживают это с аналогичными зацепляющими пружинами
• WSRD Расширенная настройка управления запуском 2600 об/мин
• Требуется WSRD | KWI Pink Primary Spring (2900 RPM Engagement), которая указана выше как НОВАЯ доступная опция
.
• Системы сцепления других производителей поддерживают это с аналогичными зацепляющими пружинами
• WSRD Настройка управления запуском максимального усилия
• Перед покупкой проконсультируйтесь с Джоном
• Поддерживается сцеплением KWI Tapp Clutch и STM Powersports с высоким сцеплением

9.2 – Подкоренные выражения и рациональные показатели

Цели обучения

• (9.2.1) – Дать определение и определить подкоренное выражение
• (9.2.2) — Преобразование радикалов в выражения с рациональными показателями
• (9.2.3) — Преобразование выражений с рациональными показателями в их радикальные эквиваленты
• (9.2.4) – Рациональные показатели, числитель которых не равен единице
• (9.2.5) — Упрощение подкоренных выражений
  • Упрощение подкоренных выражений с помощью факторизации
  • Упростить подкоренные выражения с использованием рациональных показателей и законов показателей

Квадратные корни чаще всего записываются с использованием радикала, например, [латекс] \sqrt{4}[/латекс].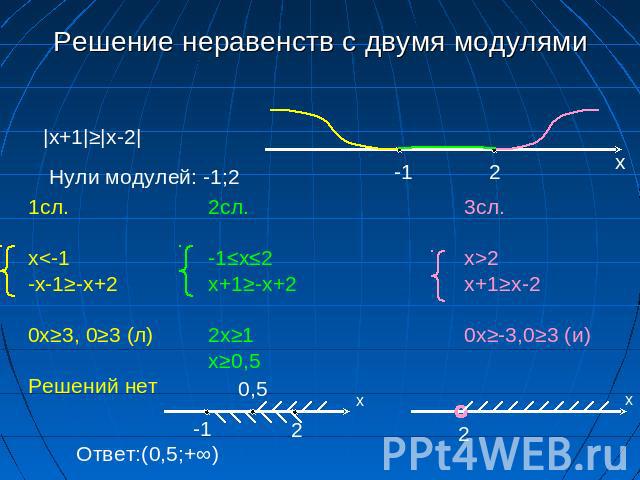

{4 }}y}[/латекс] 9{\tfrac{1}{2}}}[/латекс] 10

Давайте рассмотрим еще несколько примеров, но на этот раз с кубическими корнями. Помните, что кубирование числа возводит его в степень три. Обратите внимание, что в приведенных ниже примерах в знаменателе рационального показателя степени стоит число 3.

Радикальная форма	Форма экспонента	Основной корень
[латекс] \sqrt[3]{8}[/латекс] 98\hspace{-0.1in} \sqrt{\,\,\,}[/латекс]. Помните, что показатели степени относятся только к количеству непосредственно слева от них, если только не используется символ группировки. Приведенный ниже пример очень похож на предыдущий с одним важным отличием — здесь нет круглых скобок! Посмотрите, что происходит. Гибкость Мы можем записывать радикалы с рациональными показателями, и, как мы увидим, упрощая более сложные радикальные выражения, это может упростить задачу. Наличие различных способов выражения и записи алгебраических выражений позволяет нам иметь гибкость при их решении и упрощении. Это похоже на тезаурус, когда вы пишете, вы хотите иметь варианты для самовыражения! Пример Запишите [латекс] \sqrt[4]{81}[/латекс] как выражение с рациональным показателем степени. Показать решение Все числители дробных степеней в приведенных выше примерах равны 1. Вы можете использовать дробные степени, числители которых отличны от 1, для выражения корней, как показано ниже. 93}[/латекс] Показать решение В нашем последнем примере мы перепишем выражения с рациональными показателями как радикалы. Эта практика поможет нам, когда мы будем упрощать более сложные радикальные выражения, и когда мы научимся решать радикальные уравнения. Обычно легче упростить, когда мы используем рациональные показатели степени, но это упражнение предназначено для того, чтобы помочь вам понять, как числитель и знаменатель показателя степени являются показателем степени подкоренного и индексом подкоренного. 9{\ гидроразрыва {4} {7}} [/латекс] Показать ответ В следующем видео мы покажем больше примеров написания подкоренных выражений с рациональными показателями и выражений с рациональными показателями в качестве подкоренных выражений. Мы будем использовать это обозначение позже, поэтому вернитесь к практике, если вы забудете, как писать радикал с рациональным показателем. Основные выражения — это выражения, содержащие радикалы. Радикальные выражения бывают разных форм, от простых и знакомых, таких как [латекс] \sqrt{16}[/латекс], до довольно сложных, таких как [латекс] \sqrt[3]{250{{x}^{4 }}y}[/латекс]. 9{\frac{1}{2}}}[/latex] А поскольку вы знаете, что возведение числа в степень [latex] \frac{1}{2}[/latex] 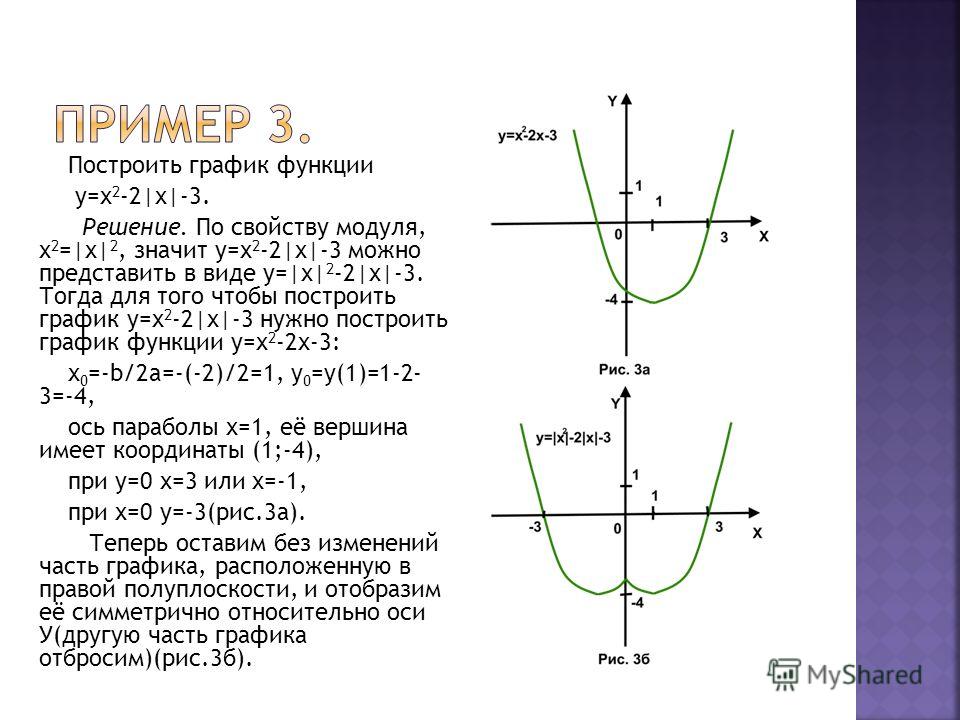равносильно возведению в квадрат корень этого числа, вы также можете записать его таким образом. [латекс] \sqrt{3x}=\sqrt{3}\cdot \sqrt{x}[/latex] Посмотрите на это — любое число под радикалом можно представить как произведение отдельных множителей , каждый под своим радикалом. Продукт, преобразованный в степенное правило или иногда называемый квадратный корень из правила продукта Для любых вещественных чисел [латекс]а[/латекс] и [латекс]b[/латекс], [латекс] \sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex]. Например: [латекс] \sqrt{100}=\sqrt{10}\cdot \sqrt{10}[/латекс] и [латекс] \sqrt{75}=\sqrt{25}\cdot \sqrt {3}[/latex] Это правило важно, потому что оно помогает вам думать об одном радикале как о произведении нескольких радикалов. Если вы можете идентифицировать правильные квадраты внутри радикала, как в случае [латекс] \sqrt{(2\cdot 2)(2\cdot 2)(3\cdot 3})[/latex], вы можете переписать выражение как произведение из нескольких идеальных квадратов: [латекс] \sqrt{{{2}^{2}}}\cdot \sqrt{{{2}^{2}}}\cdot \sqrt{{{3}^{2}} }[/латекс]. Квадратный корень из правила произведения поможет нам упростить несовершенные корни, как показано в следующем примере. Упрощение подкоренных выражений с помощью разложения на множители Пример Упрощение. [латекс] \sqrt{63}[/латекс] Показать решение Окончательный ответ [латекс] 3\sqrt{7}[/латекс] может показаться немного странным, но он в упрощенной форме. Вы можете прочитать это как «три радикальных семи» или «три умножить на квадратный корень из семи». В следующем видео показано больше примеров того, как упростить квадратные корни, которые не имеют идеальных квадратных корней. 9{2}}[/латекс] Радикальный Экспонента [латекс] \sqrt{9}[/латекс] [латекс]\влево|х\вправо|[/латекс] [латекс]−5[/латекс] 25 5 5 [латекс]−2[/латекс] 4 2 2 0 0 0 0 6 36 6 6 10 100 10 10 9{2}}}=4\left|xy\right|[/latex] Мы объединим это с квадратным корнем правила произведения в нашем следующем примере, чтобы упростить выражение с тремя переменными в подкоренной части. 2-6x+9}[/латекс]. Показать ответ В нашем следующем примере мы начнем с выражения, записанного с рациональным показателем. Вы увидите, что вы можете использовать аналогичный процесс — разложение членов на множители и сортировку по квадратам — для упрощения этого выражения. Вот еще один пример с идеальными квадратами. Упрощение кубических корней Мы можем использовать те же методы, которые мы использовали для упрощения квадратных корней, для упрощения корней более высокого порядка. Например, чтобы упростить кубический корень, цель состоит в том, чтобы найти множители под радикалом, которые являются идеальными кубами , чтобы вы могли извлечь их кубический корень. Нам больше не нужно беспокоиться о том, определили ли мы главный корень, поскольку теперь мы находим кубические корни. Сосредоточьтесь на поиске идентичных трио факторов по мере упрощения. 9{5}}}[/latex] Показать решение Помните, что из отрицательного выражения можно извлечь кубический корень. В следующем примере мы упростим кубический корень с отрицательным подкоренным числом. Вы также можете пропустить шаг разложения отрицательного числа на множители, когда освоитесь с определением кубов. В следующем видео мы покажем больше примеров упрощения кубических корней. Упрощение корней четвертой степени Теперь давайте перейдем к упрощению корней четвертой степени. Независимо от того, какой корень вы упрощаете, применяется одна и та же идея: найдите кубы для кубических корней, степени четырех для четвертых корней и т. д. Вспомните, что когда ваше упрощенное выражение содержит четный индексированный радикал и переменный множитель с нечетным показателем, вам нужно применить абсолютное значение. Упрощение подкоренных выражений с использованием рациональных показателей и законов показателей. Альтернативный метод факторизации – переписать выражение с рациональными показателями, а затем использовать правила показателей для упрощения. Вы можете обнаружить, что предпочитаете один метод другому. В любом случае приятно иметь варианты. Мы снова покажем последний пример, используя эту идею. В следующем видео мы покажем еще один пример того, как упростить корень четвертой и пятой степени. 9{4}}}}[/латекс] . В этом выражении две переменные, дробь и радикал. Давайте рассмотрим это шаг за шагом и посмотрим, может ли использование дробных показателей помочь нам упростить его. Мы начнем с упрощения знаменателя, так как именно здесь находится подкоренной знак. Напомним, что показатель степени в знаменателе или дроби можно переписать как отрицательный показатель степени. Ну, это заняло некоторое время, но вы сделали это. Вы применили свои знания о дробных показателях, отрицательных показателях и правилах показателей, чтобы упростить выражение. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт