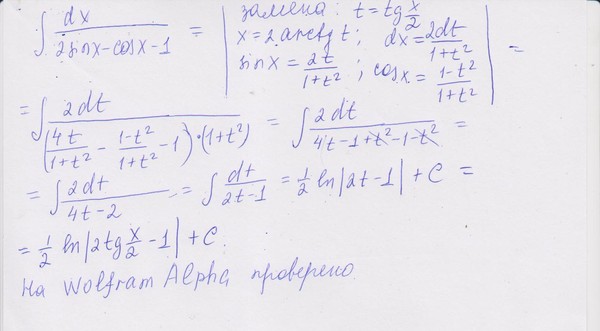Интеграл dx sinx cosx: Mathway | Популярные задачи

alexxlab / / Разное
2

3. Интегрирование тригонометрических функций.

1.Первообра́зная. Функция F(x) называется первообразной для функции ƒ(x) на некотором отрезке [a,b], если для всех из этого отрезка выполняется равенство:

F'(x)= ƒ(x).

Неопределенный интеграл и его свойства. Неопределённый интегра́л для функции — это совокупность всех первообразных данной функции.

Свойства неопределенного интеграла:

1.

2.

3.

4.  где u, v, w – некоторые функции от х.

6.     

1. ∫ xαdx = xα+1/ (α+1) + C

α ≠-1

10. = ln | x + | + C

2. = ln |x| + C

11.

= arctg( )+C

3. ∫ ex= ex + C

12. = ln | | + C

4. ∫ ax dx = ax/lna + C

13 = ln | | + C

5. ∫ sin(x)dx = — cos(x) + C

14. = ln |tg( )| + C

6. ∫ cos(x)dx = sin(x) + C

15. = ln |tg( )| + C

7. = tg(x) + C

16.∫ tg(x) dx = – ln |cos(x)| + C

8. = -ctg(x) + C

17.∫ ctg(x) dx = ln |sin(x)| + C

9. = arcsin ( )+ C

2.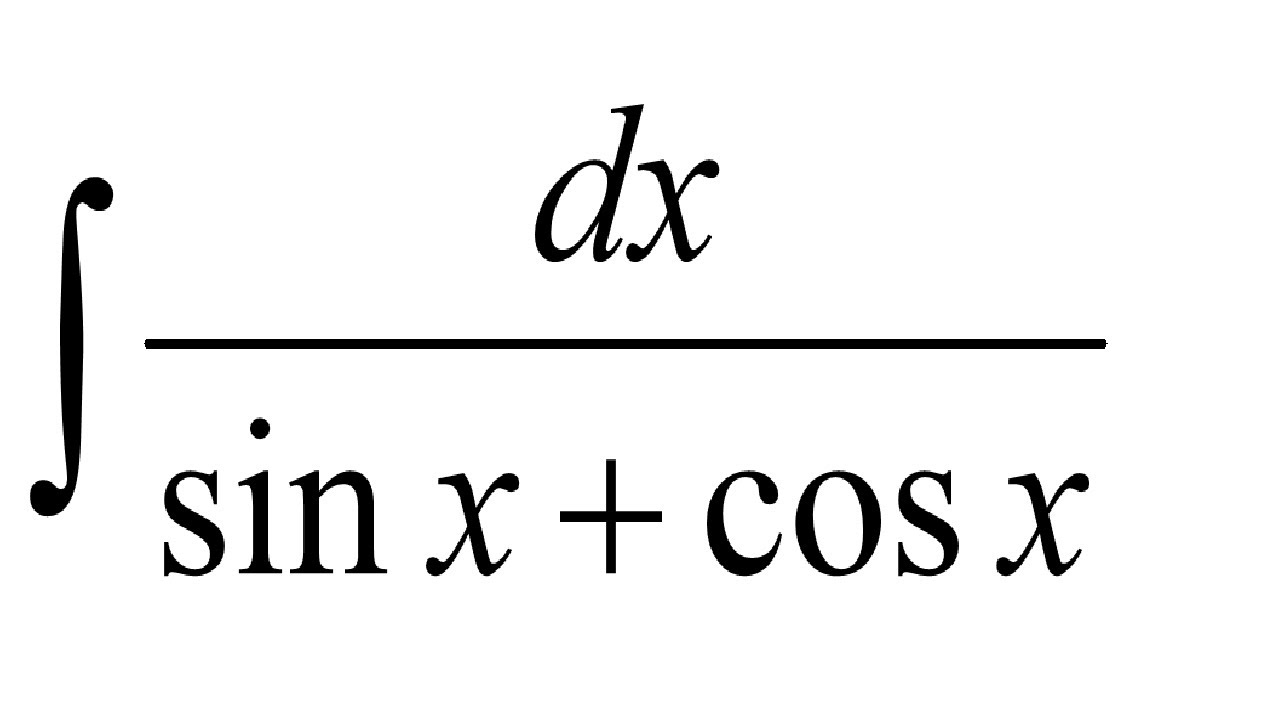 Понятие об основных методах интегрирования

а). Метод разложения.

Пусть f(x) = f1(x) + f2(x). Тогда на основании свойства 4

.

f1, f2 стараемся подобрать так, чтобы интегралы брались непосредственно.

б). Метод подстановки (введение новой переменной)

Так как неопределенный интеграл не зависит от выбора аргумента и, учитывая, что

dx = j/(t)dt,

получаем формулу замены переменной в неопределенном интеграле

.

То есть интеграл, стоящий в правой части, может оказаться проще интеграла в левой части.

в) Метод интегрирования по частям

Пусть u и v — непрерывно дифференцируемые функции от х.

d(u×v) = udv + vdu.

Отсюда udv=d(u×v)-vdu.

Интегрируя обе части этого уравнения, получим

.

Интегрирование рациональных дробей.

Нужно вычислить интеграл вида

, где Р(х) — целый многочлен; а,b,c — const, a ¹ 0.

Разделив Р(х) на знаменатель, получаем

.

Теперь все сводится к вычислению

.

Интегрирование тригонометрических функций.

I. Интеграл вида ∫R(sinx;cosx)dx, где R(sin(x), cos(x)) – это рациональная функция относительно sin(x) и cos(x) подстановкой tg(x/2) = t сводится к интегралу от рациональной функции относительно t.

Такая подстановка называется универсальной, т.е. она пригодна для вычислений интеграла sin(x) и cos(x).

II. Интеграл вида ∫(sinmx)*(cosnx)dx I случай. m и n – положительные, одно из них нечетное.

Пусть m=2p+1 , тогда ∫sin2p(x)cosn(x) sin(x)dx = – ∫(sin2x) p cosn(x) d(cos(x)) =

= – ∫(1 –cos2x) p cosn(x) d(cos(x)).

II.случай. m и n – целые, положительные, четные.

Пусть m=2p, n=2q, тогда

∫sinm(x)cosn(x)dx = ∫sin2p(x)cos2q(x)dx = ∫(sin2x) p(cos2x) qdx =((1-cos2x)/2)p*((1+cos2x)/2)q;

Возводя скобки в соответствующие степени и разбивая интеграл на сумму интегралов, в результате получаем интегралы либо типа а), либо типа б).

III.случай. m + n = –2k; tg(x)=t; ctg(x)=t;

Интегрирование иррациональных функций.

I. Интеграл вида R(X,((ax+b)/(cx+d))(1/n)), где R(X,((ax+b)/(cx+d))(1/n)) — рациональная функция относительно x и ((ax+b)/(cx+d))(1/n) , подстановкой (ax+b)/(cx+d)=tn сводится к интегралу от рациональной функции относительно t.

II. Интегралы от дифференцированных биномов (биномиальный дифференциал).

Определение : xm(a + bxn)P dx – называется дифференциальным биномом.

Академик Чебышев доказал, что ∫ xm

(a + bxn)P dx выражается через элементарные функции в трех случаях:

1) если P-целое, то следует сделать подстановку

(x)λ=t, где λ – общий знаменатель чисел m и n.

2)P – не целое, (m+1)/n — целое, тогда вводим a+bxn=ts, где s – знаменатель P.

3) P+(m+1)/n- целое, тогда замена такая:

ax–n + b = tS , где s – знаменатель P.

В остальных случаях интеграл не берется.

III. Тригонометрические подстановки.

R(X,(a2-x2)(1/2) ))

а) Интеграл вида ∫R(X,(a2-x2)(1/2) )dx

подстановкой x = a∙sin(t) сводится к интегралу от рациональной функции относительно sin(t) и cos(t).

б) интеграл вида ∫R(X,(a

2-x2)(1/2) )dx подстановкой x= a∙ sec(t) сводится к интегралу от рациональной функции относительно sin(t) и cos(t).

в) интеграл вида ∫R(X,(a2-x2)(1/2) )dx подстановкой x = a∙tg(t) сводится к интегралу от рациональной функции относительно sin(t) и cos(t).

4. Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которыхстремится к нулю: Где Формула Ньютона-Лейбница Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) — первообразная функции f (x) на [a, b], то

Замена переменной в определенном интеграле

Определенный интеграл по переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t):

Новые пределы интегрирования по переменной t определяются выражениями

где g -1 — обратная функция к g, т. е. t = g -1(x).

Интегрирование по частям для определенного интеграла

В этом случае формула интегрирования по частям имеет вид:

где означает разность значений произведения функций uv при x = b и x = a.

int(dx)/(sin x+cos x)

  • Курс
    • NCERT
      • Класс 12
      • Класс 11
      • Класс 10
      • Класс 9 90 008
      • Класс 8
      • Класс 7
      • Класс 6
    • IIT JEE
  • Exam
    • JEE MAINS
    • JEE ADVANCED
    • X BOARDS
    • XII BO ARDS
    • NEET
      • Neet Предыдущий год (по годам)
      • Физика Предыдущий год
      • Химия Предыдущий год
      • Биология Предыдущий год
      • Нет Все образцы работ
      • Образцы работ Биология
      • Образцы работ Физика
      • Образцы работ Химия
  • Скачать PDF-файлы
    • Класс 12
    • Класс 11
    • Класс 10
    • Класс 9
    • Класс 8
    • Класс 7
    • Класс 6
  • Экзаменационный уголок
  • Онлайн-класс
  • Викторина
  • Задать вопрос в Whatsapp
  • Поиск Doubtnut
  • Английский словарь
  • Toppers Talk
  • Блог
  • Скачать
  • Получить приложение Видео0123

    Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!

    Видео по теме

    sinxsin(cosx)dx

    127289095

    01:37

    ∫sinx+xcosxxsinxdx

    127289199

    03:04

    ∫sinxsin(cosx)dx

    172115799

    9 0122 03:08

    निम्नलिखित समाकलनों को ज्ञात कीजिए: 901 62 (i) ∫(cosx−sin)dx (ii ) ∫(sin4x−cos4x)dx (iii) ∫1+cosxsin2xdx 93 x dx

    412651376

    07:42

    ∫sinxsin(cosx)dx.

    412651378

    01:11

    ∫sin2x−cos2xsinxcosxdx=_____

    412652300

    03:36 9012 3

    РЕКЛАМА

    • Рекомендуемые вопросы

    • int(dx)/(sin x+cos x)

      04:51

    • Найдите следующие интегралы: (i) int(sinx+cosx)dx (ii) intcosecx(cos…

      02:28

    • int(sinx+xcos) х)/(хсинх )дх 9((1) / (2)) (x) / ((sin x + cos x) dx)

      05:25

    • int(sin x+cos x)/(sin x-cos x)dx

      01:09

    • int sin x sin ( cos x) dx

      02:05

    • int (sin x+ cos x)/( sin x — cos x)dx

      90 122 01:29

    1. Ask Unlimited Doubts
    2. Видеорешения на нескольких языках (включая хинди)
    3. Видеолекции экспертов
    4. Бесплатные PDF-файлы (документы за предыдущий год, книжные решения и многое другое)
    5. Посещайте специальные консультационные семинары для IIT-JEE, NEET и экзаменов совета директоров

    Doubtnut хочет отправлять вам уведомления. Разрешите получать регулярные обновления!

    Прослушивание…

    int(dx)/(sinx+cosx)=

    • Курс
      • NCERT
        • Класс 12
        • Класс 11
        • Класс 10
        • Класс 9
        • Класс 8
        • Класс 7
        • Класс 6
      • IIT JEE
    • Exam
      • JEE MAINS
      • JEE ADVANCED
      • X BOARDS
      • XII BOARDS
      • NEET
        • Neet Предыдущий год (по годам)
          • 9 0003 Физика Предыдущий год
        • Химия Предыдущий год
        • Биология Предыдущий год
        • Нет Все образцы Статьи
        • Образцы работ Биология
        • Образцы работ Физика
        • Образцы работ Химия
    • Скачать PDF’s
      • Класс 12
      • Класс 11
      • Класс 10
      • Класс 9
      • Класс 8
      • Класс 7
      • Класс 6
    • Экзаменационный уголок
    • Онлайн-класс
    • Викторина
    • Задать вопрос Whatsapp
    • Поиск Doubtnut
    • Английский словарь
    • Toppers Talk
    • Блог
      • 900 21
      • Скачать
      • Получить приложение

      Вопрос

      Обновлено: 26/04/2023

      ML KHANNA-ИНТЕГРАЦИЯ-САМООЦЕНКА TESET

      10 видео

      РЕКЛАМА 9012 3

      Текст Решение

      A

      logtan(π8+x2)

      B

      logtan(π8−x2)+c

      C

      1√2logtan(π8+x2)+c

      D

      ни один из этих

      Ответ

      90 122 Правильный ответ C

      Ab Padhai karo бина объявления ке

      Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

      Связанные видео

      Оценка: ∫sinx+cosxsinx-cosxdx

      8490643

      03:23

      ∫sinx(sinx-cosx) дх=?

      61751190

      02:15

      ∫dx(sinx+cosx)(2cosx+sinx)=

      95421799

      07:01

      ∫cosxsinx+cosxdx=

      121559717

      02:32

      ∫sinxsinx −cosxdx=

      121560011

      02:32

      ∫(sinx+cosx)dxsinx

      204364297

      01:18 9012 3

      ∫dxcosx-sinx=

      217285018

      02:58

      ∫sinxsinx-cosxdx=

      217285055

      03:54

      ∫cosxcosx-sinxdx=

      217285060

      03:41

      ∫cosxcosx-sinxdx का मान ज्ञात कीजिए ।

      226109004

      03:14

      ∫(sinx⋅cosx)dx

      280788769

      00:37

      সমাকলন করো :∫cosxsinx+cosxdx

      333025189

      04:45

      ∫sinx+cosxcosx−sinxdx

      352282733

      01:06

      int(sinx)/(sinx-cosx)dx=

      642977221

      03:38

      ∫cosx−2sinxsinx+cosxdx ज्ञात कीजिए |

      643553810

      04:24

      Вычислить: ∫cosxsinx+√sinxdx

      644031040

      03:23

      РЕКЛАМА

      • ML KHANNA-ИНТЕГРАЦИЯ-САМООЦЕНКА TESET

      • int(sinx)/(sin (x-альфа))dx =

        01:46

      • intqrt(1+sin((x)/(2)))dx= 9(9//2))dx равно для некоторых арби.

        No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *