Диаметр — что это такое
Обновлено 22 июля 2021 Просмотров: 44 965 Автор: Дмитрий ПетровЗдравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о том, что такое ДИАМЕТР. Это одно из базовых понятий в математике, которое начинают изучать еще в 3-м классе.
Но и повседневной жизни он встречается настолько часто, что знать его просто необходимо.
Диаметр — это…
Диаметр – это в первую очередь, хорда. Так называют отрезок (что это?) прямой, который соединяет две определенные точки. В нашем случае эти точки располагаются на максимально отдаленном друг от друга расстоянии на окружности, благодаря чему хорда проходит через ее центр.
В то же время диаметром еще называют и длину это самой хорды. Кстати, аналогичные определения применимы не только к окружностям, но и к другим геометрическим фигурам, таким как шар или сфера.
Графически это выглядит вот так:
Само слово «диаметр», как и многие термины в нашем языке, пришло из Древней Греции.
Ведь именно в этой стране жили прославленные математики, такие как Евклид, Пифагор, Архимед, Платон. Так вот, греческое слово можно перевести как «поперечник».
Интересно, что во многих современных языках есть также похожие слова. Например, на латыни это «diametrus». А в русском языке мы нередко употребляем слово «диаметральный».
Например, говорим «диаметральные взгляды» или «диаметральные точки зрения», подразумевая совершенно противоположное отношение к чему-либо. Ну, точно как противоположные точки на окружности, разделенные диаметром.
Обозначения и символ диаметра
Диаметр имеет несколько сокращенных обозначений.
Например, если речь идет о математике, то в ней чаще всего употребляется латинская буква «D». Причем допускается как прописное написание этой буквы, так и строчное – «d». Второй вариант даже чаще встречается в задачках.
Например, это может выглядеть так:
d = 12 см или D = 12 см
А вот если говорить о бытовом понятии «диаметра», то тут уже чаще используется другой символ.
Это – перечеркнутая буква «О».
Именно такой знак вы наверняка увидите, когда речь идет о трубах, о размере сверла и так далее. И записываются они так:
Ø6, Ø8, Ø12, Ø15, Ø20, Ø100
По умолчанию считается, что подобные обозначения всегда считаются в миллиметрах.
Стоит сказать, что символа «Ø» нет на обычной раскладке клавиатуры. И чтобы напечатать его в тексте, нужно или открыть специальный раздел «дополнительные символы» в программе Word, или просто скопировать откуда-нибудь, а потом вставить.
Радиус и другие величины, связанные с диаметром
Главной величиной, которая неизменно связана с диаметром, является радиус.
Радиус – это расстояние от центра окружности до любой точки на дуге окружности. Соответственно, радиусом также называют и длину этого отрезка.
Радиус обозначается буквой «R» или «r». И он всегда равен половине диаметра. В математике это уравнение записывают как:
D = 2R или R = D/2
Еще одна важная величина – длина окружности.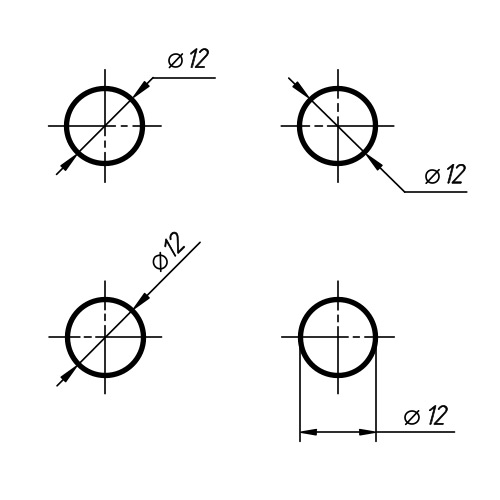
Это расстояние всей дуги окружности. Оно обозначается буквой «С». Чтобы рассчитать ее, нужно пользоваться простой формулой:
С = 2πR или С = πD
Где «π», как многие знают, это математическая константа. И считать ее принято как 3,14, хотя после запятой там бесконечное количество знаков.
И наконец, еще одна величина – площадь окружности (круга). Это размер всего, что находится внутри ее границ. Обозначается она буквой «S». И чтобы ее вычислить, опять же надо воспользоваться определенной формулой:
S=πR²
Соответственно, эти формулы можно и перевернуть. То есть, зная длину или площадь окружности, всегда можно высчитать ее диаметр.
Интересные факты о диаметре
Первое документальное упоминание слова «диаметр» в России относится к 1720 году.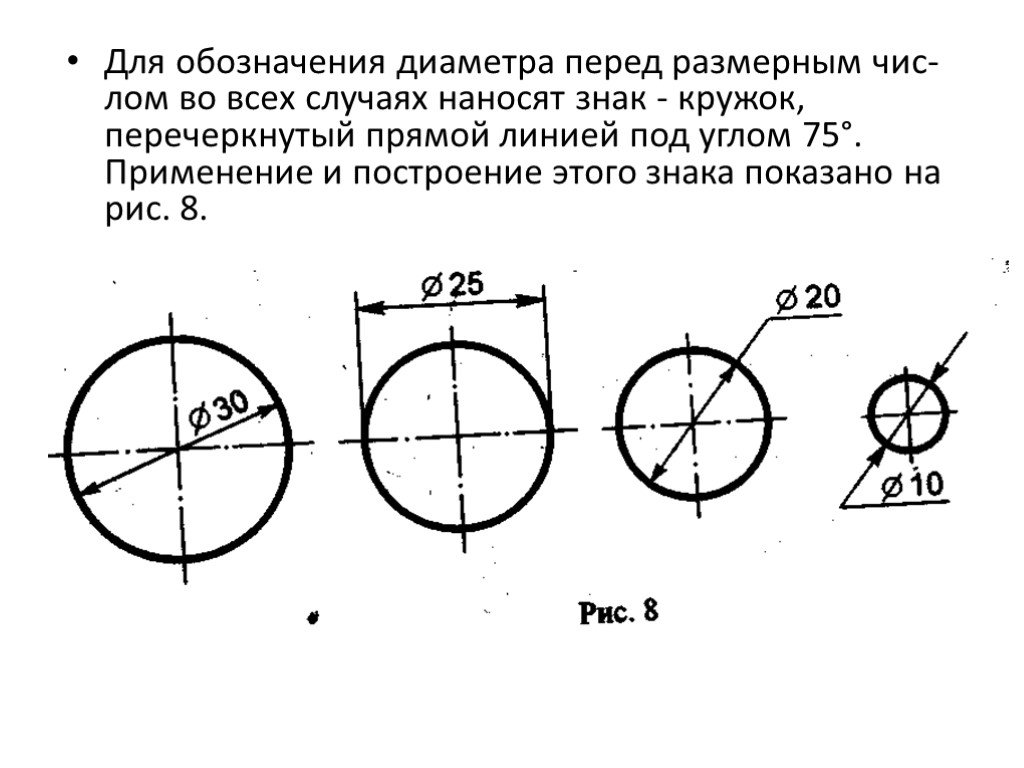
И записано оно было в морском уставе. Хотя это неудивительно, так как моряки просто обязаны были разбираться в подобных математических задачах.
Диаметр Земли составляет 12 543 километра. Это огромное расстояние. Но и оно кажется маленьким, если сравнить, например, с Солнцем. А у него диаметр составляет 1 390 000 километров, что в 109 раз больше земного.
Диаметр 10-копеечных монет в нашей стране не менялись на протяжении сотни лет. Он составляет 17,5 миллиметров. Таким он был еще при Николае II, таким же и в советское время, таким же остался и сейчас.
Вот и все, что мы хотели рассказать о таком понятии, как диаметр. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
- Математика
Обозначение диаметра, радиуса, квадрата, конусности, уклона и дуги
На
чертежах используются следующие знаки:
– диаметр, R –
радиус, – квадрат, – уклон, – конусность, –
дуга, относительные размеры которых по
отношению к цифрам показаны на рис.
2.11.
Диаметр. Цилиндрические поверхности обозначаются на чертежах знаком , который представляет собой окружность, пересеченную прямой линией. Высота и наклон прямой линии одинаковы с высотой и наклоном цифр размерного числа, а диаметр окружности равен 5/7 высоты цифр. Наносится знак диаметра над размерной линией перед размерным числом.
Обозначение диаметра цилиндрической поверхности рекомендуется наносить на том изображении, где ось ее проецируется в линию, т.е. между образующими (см. рис. 2.81). При этом размерную линию разрешается проводить с обрывом независимо от того, изображена ли окружность полностью или частично. Обрыв размерной линии производится дальше центра окружности. Размещение обозначения диаметра на окружности допускается (см. рис. 2.86).
Если деталь имеет несколько одинаковых цилиндрических отверстий, то размер дают один раз с указанием общего их числа (рис. 2.88).
Рис.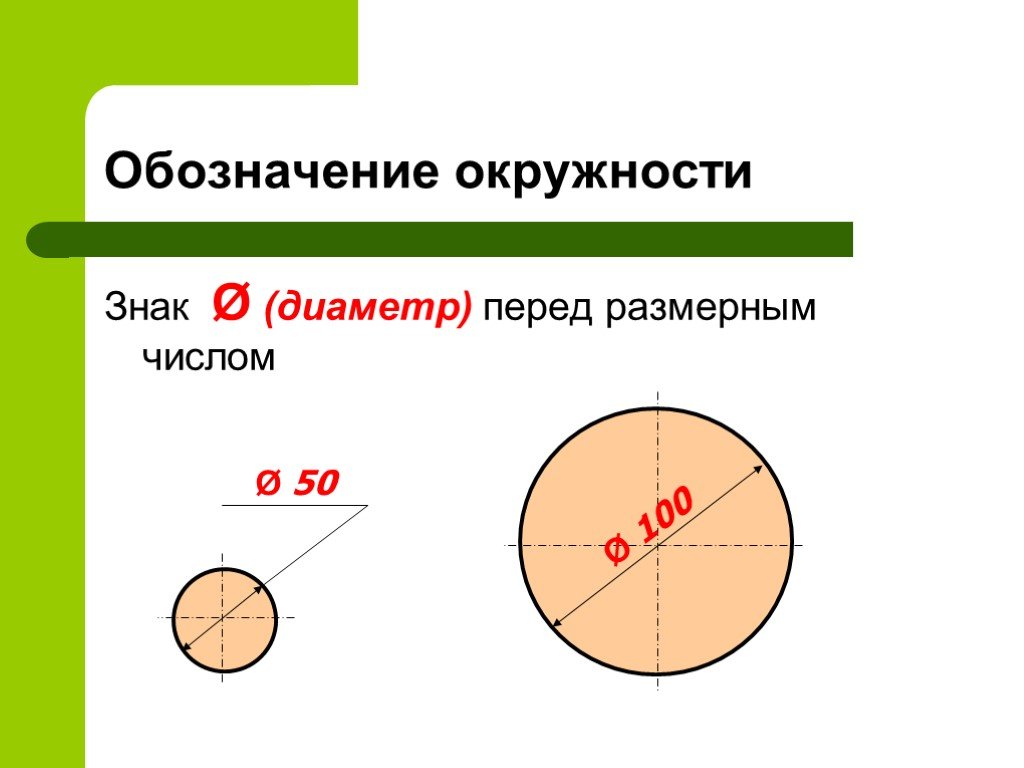
2.88
В таблице 2.6 приведен нормальный ряд чисел, установленный ГОСТ 6636–69* для использования при выборе размера диаметра.
Таблица 2.6
0,5 | 3 | 11 | 21 | 35 | 52 | 78 | 105 | 155 | 210 | 310 | 410 |
0,8 | 3,5 | 12 | 22 | 36 | 55 | 80 | 110 | 160 | 220 | 320 | 420 |
1 | 4 | 13 | 38 | 58 | 82 | 115 | 165 | 230 | 330 | 430 | |
1,2 | 4,5 | 14 | 24 | 40 | 60 | 85 | 120 | 170 | 240 | 340 | 440 |
1,5 | 5 | 15 | 25 | 42 | 62 | 88 | 125 | 175 | 250 | 350 | 450 |
1,8 | 6 | 16 | 26 | 44 | 65 | 90 | 130 | 180 | 260 | 360 | 460 |
2 | 7 | 17 | 28 | 45 | 68 | 92 | 135 | 185 | 270 | 370 | 470 |
2,2 | 8 | 18 | 30 | 46 | 70 | 95 | 140 | 190 | 280 | 380 | 480 |
2,5 | 9 | 19 | 32 | 48 | 72 | 98 | 145 | 195 | 290 | 390 | 490 |
2,8 | 10 | 20 | 34 | 50 | 75 | 100 | 150 | 200 | 300 | 500 |
Р
адиус.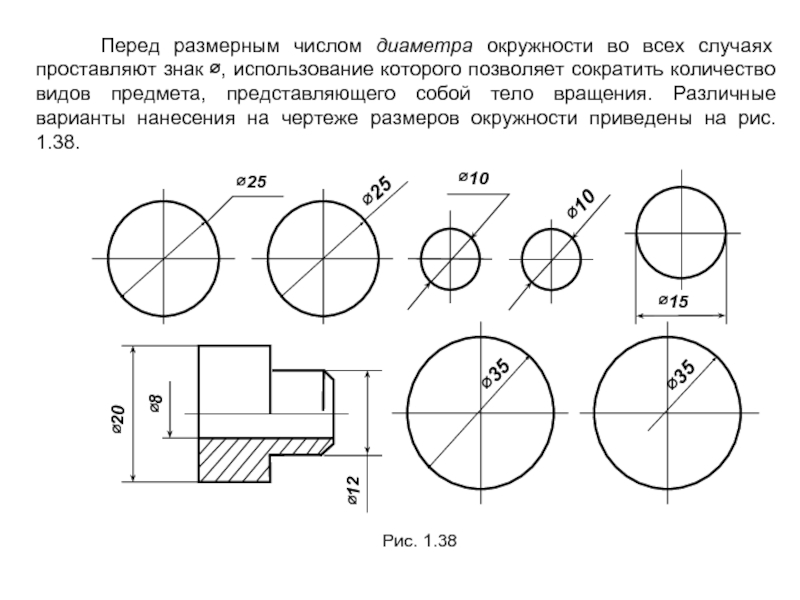
Перед размерным числом, определяющим
радиус, обязательно пишется прописная
латинская буква R (например, R25).
Высота этой буквы и высота размерного
числа должны быть одинаковыми.
На рис. 2.89 приведены примеры нанесения наружных дуг окружностей, а на рис. 2.90 – внутренних.
Размерная линия радиуса наносится на том изображении, где дуга проецируется в истинном виде. Из рис. 2.89 и рис. 2.90 следует, что размерная линия радиуса должна располагаться в направлении истинного радиуса и оканчиваться одной стрелкой, примыкающей к контурной (или выносной) линии.
Рис. 2.90
Нанесение размерных чисел при различных положениях размерных линий на чертеже определяется удобством чтения чертежа.
При проведении нескольких размерных линий радиусов из одного центра они не должны располагаться на одной прямой (рис. 2.91).
В
случае, если необходимо указать центр
дуги большого радиуса, допускается
приближать его, выполняя размерную
линию с изломом под углом 90° (рис.
2.92).
П ри необходимости положение центра дуги задается пересечением центровых или выносных линий (рис. 2.93).
Если на чертеже радиусы скруглений, сгибов и других подобных элементов одинаковы или какой-либо радиус является преобладающим, то вместо нанесения этих значений на изображение рекомендуется выносить их в технические требования в виде записей «Радиусы скруглений 4 мм»; «Внутренние радиусы сгибов 10 мм»; «Неуказанные радиусы 8 мм» и др.
Нормальные радиусы скруглений, установленные для использования ГОСТ 10948–64, приведены в таблице 2.7.
Таблица 2.7
Diameter — SAT Math
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
SAT Math Help » Геометрия » Плоская геометрия » Круги » Диаметр
Если площадь круга в четыре раза больше длины окружности того же круга, то каков диаметр круга?
Возможные ответы:
16
8
4
2
32
Правильный ответ: 9 0016
16
Объяснение:
Установите площадь круга, равную четырехкратной длине окружности πr 2 = 4(2 πr ).
Вычеркните оба символа π и по одному r с каждой стороны, и у вас останется r = 4(2), поэтому r = 8 и, следовательно, d = 16.
Сообщить об ошибке
Периметр круга равен 36 π. Каков диаметр круга?
Возможные ответы:
36
18
72
6
3
Правильный ответ:
36
Объяснение:
Периметр круга = 2 πr = πd
Следовательно, d = 36
Сообщить об ошибке
Если площадь круга, касающегося квадрата на рисунке выше, равна , каково ближайшее значение к площадь квадрата?
Возможные ответы:
Объяснение:
Получите радиус круга из площади.
Разделите квадрат на 4 треугольника, соединив противоположные углы. Эти треугольники будут иметь прямой угол в центре квадрата, образованный двумя радиусами круга, и двумя углами по 45 градусов в углах квадрата. Потому что у тебя 45-45-90 треугольник, вы можете вычислить стороны треугольников как , , и . Радиусы круга (от центра до углов квадрата) будут 9. Гипотенуза (сторона квадрата) должна быть .
Тогда площадь квадрата равна .
Сообщить об ошибке
Две стороны прямоугольного треугольника имеют соответственно 3 и 4 длины. Чему равна площадь окружности, описанной около треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы окружность содержала все 3 вершины, гипотенуза должна быть равна диаметру окружности. Гипотенуза и, следовательно, диаметр равны 5, так как это должен быть прямоугольный треугольник 3-4-5.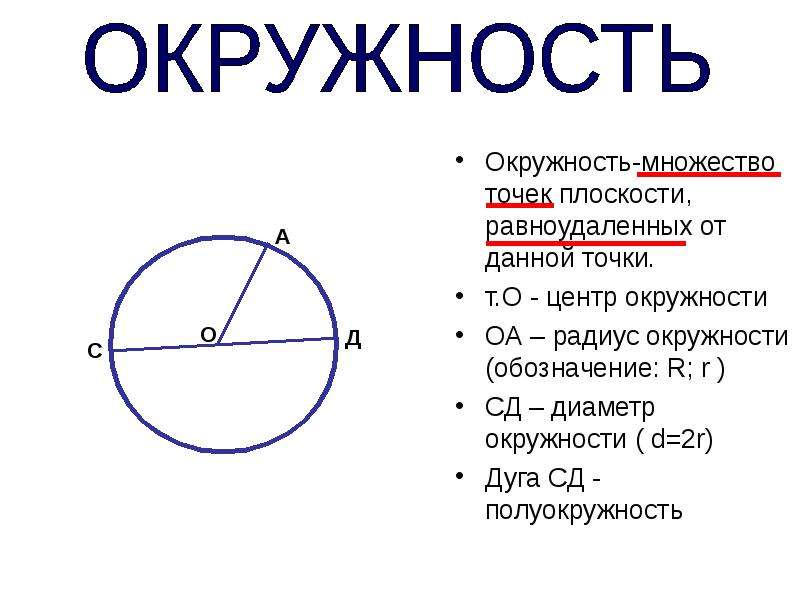
Уравнение площади круга: A = πr 2 .
Сообщить об ошибке
Длина окружности . Какой диаметр?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу длины окружности.
Подставить окружность.
Сообщить об ошибке
Найдите диаметр круга, площадь которого равна .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить, просто используйте формулу площади круга, чтобы найти радиус, а затем умножьте ее на 2, чтобы найти диаметр. Таким образом,
Сообщить об ошибке ответ:
Объяснение:
Чтобы решить, просто используйте формулу диаметра круга.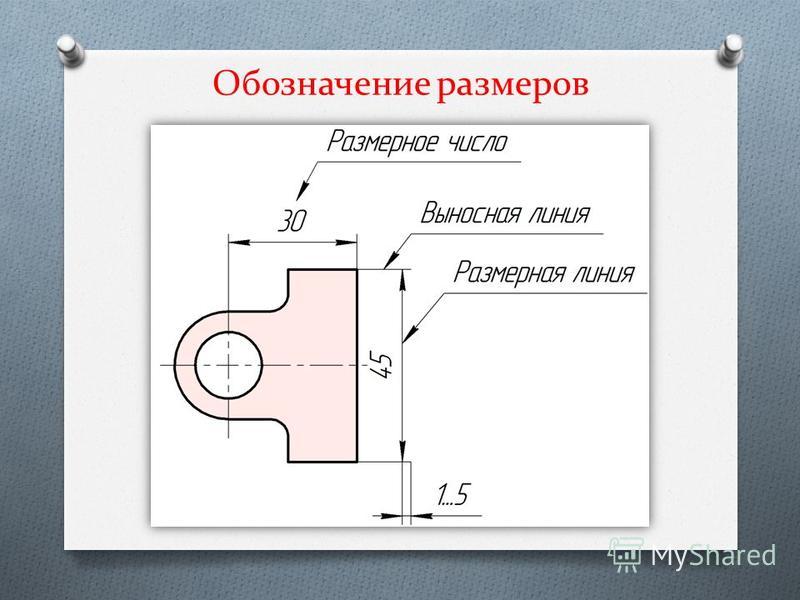
Таким образом,
Сообщить об ошибке
Найдите длину диаметра, если радиус равен 5.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить, просто используйте формулу диаметра круга
, где r равно 5. Таким образом,
Помните, что диаметр — это самое длинное расстояние через круг, а поскольку радиус равен 5 , вы можете просто удвоить это. Таким образом, ответ равен 10.
Сообщить об ошибке
Найдите диаметр круга, если радиус равен 6.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить, просто используйте формулу диаметра круга.
Помните, поскольку диаметр — это расстояние между двумя точками на противоположных сторонах круга, вы просто удваиваете радиус.
Пи не участвует в диаметре, только в окружности, площади и т. д.
Сообщить об ошибке
Длина окружности данного круга составляет половину его площади. Каков диаметр круга?
Возможные ответы:
Правильный ответ:
Объяснение:
Помните, что длина окружности определяется как , а площадь – как .
Если длина окружности этого круга составляет половину его площади, то можно сказать . Или, .
Мы можем решить это уравнение для r следующим образом:
Поскольку диаметр круга в два раза больше его радиуса, то диаметр этого круга равен 8.
Чтобы проверить ответ, подставьте r=4 в формулы длины окружности и площади. Вы увидите, что площадь этого круга и его длина окружности , что составляет ровно половину его площади.
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все математические ресурсы SAT
16 Диагностические тесты 660 практических тестов Вопрос дня Карточки Учитесь по концепции
Диаметр | Rhino 3-D моделирование
Диаметр | Трехмерное моделирование носорога| Панель инструментов | Меню |
|---|---|
Анализ | Анализ Диаметр |
Команда Диаметр сообщает диаметр кривой в указанной точке.
шагов
- точек на кривой.
Объектная привязка по центру игнорируется, если она включена.
| Параметры командной строки | |
|---|---|
Выберите кривую | Ограничить выбор указанной кривой. Нажмите, чтобы выбрать любую кривую. |
МаркДиаметр | Помещает точечный объект в оцененную точку на кривой и создает окружность кривизны через эту точку. |
Единицы | Установите единицы для отображения длины. Этот параметр доступен, только если объекты не выбраны. |
СубКрв | Введите subcrv, чтобы выбрать часть кривой в качестве входных данных. |
| Панель инструментов | Меню |
|---|---|
Анализ | Анализ Радиус |
Команда «Радиус» сообщает радиус кривой в указанной точке.
шагов
- точек на кривой.
Объектная привязка по центру игнорируется, если она включена.
| Параметры командной строки | |
|---|---|
Выберите кривую | Ограничить выбор указанной кривой. Нажмите, чтобы выбрать любую кривую. |
МаркРадиус | Помещает точечный объект в оцененную точку на кривой и создает окружность кривизны через эту точку. |
Единиц | Установите единицы для отображения длины. Этот параметр доступен, только если объекты не выбраны. |
СубКрв | Введите subcrv, чтобы выбрать часть кривой в качестве входных данных. |
Вложение команд «Длина», «Радиус» и «Расстояние»
Команды «Длина», «Радиус» и «Расстояние» можно вкладывать друг в друга. Это означает, что если Rhino запрашивает расстояние в команде, вы можете использовать эти команды для измерения другого объекта или расстояния, и полученное значение будет передано в команду, как если бы вы набрали число.
Пример использования смещения
- Запустите команду OffsetSrf.
- В ответ на запрос расстояния смещения введите Длина, Радиус или Расстояние и нажмите Enter.
