Обсудить на форуме Пройти тест Полный список курсов обучения Бесплатные видеоуроки Нужна информация! |
Таблица производных. Доказательство формул
Приведем сводную таблицу для удобства и наглядности при изучении темы.
Константа y=C (C)’=0 Степенная функция y=xp (xp)’=p·xp-1 | Показательная функция y=ax (ax)’=ax·ln a В частности, при a=e имеем y=ex (ex)’=ex |
Логарифмическая функция (logax)’=1x·ln a В частности, при a=e имеем y=ln x (ln x)’=1x | Тригонометрические функции (sin x)’=cos x(cos x)’=-sin x(tgx)’=1cos2x(ctgx)’=-1sin2x |
Обратные тригонометрические функции (arcsin x)’=11-x2(arccos x)’=-11-x2(arctg x)’=11+x2(arcctg x)’=-11+x2 | Гиперболические функции (shx)’=chx(chx)’=shx(thx)’=1ch3x(cthx)’=-1sh3x |
Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.
Производная постоянной
Доказательство 1Для того, чтобы вывести данную формулу, возьмем за основу определение производной функции в точке. Используем x0=x, где x принимает значение любого действительного числа, или, иначе говоря, x является любым числом из области определения функции f(x)=C. Составим запись предела отношения приращения функции к приращению аргумента при ∆x→0:
lim∆x→0∆f(x)∆x=lim∆x→0C-C∆x=lim∆x→00∆x=0
Обратите внимание, что под знак предела попадает выражение 0∆x. Оно не есть неопределенность «ноль делить на ноль», поскольку в числителе записана не бесконечно малая величина, а именно нуль. Иначе говоря, приращение постоянной функции всегда есть нуль.
Итак, производная постоянной функции f(x)=C равна нулю на всей области определения.
Пример 1Даны постоянные функции:
f1(x)=3,f2(x)=a, a∈R,f3(x)=4.13722,f4(x)=0,f5(x)=-87
Необходимо найти их производные.
Решение
Опишем заданные условия. В первой функции мы видим производную натурального числа 3. В следующем примере необходимо брать производную от а, где а — любое действительное число. Третий пример задает нам производную иррационального числа 4.13722, четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби -87.
В первой функции мы видим производную натурального числа 3. В следующем примере необходимо брать производную от а, где а — любое действительное число. Третий пример задает нам производную иррационального числа 4.13722, четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби -87.
Ответ: производные заданных функций есть нуль при любом действительном x (на всей области определения)
f1′(x)=(3)’=0,f2′(x)=(a)’=0, a∈R,f3′(x)=4.13722’=0,f4′(x)=0’=0,f5′(x)=-87’=0
Производная степенной функции
Переходим к степенной функции и формуле ее производной, имеющей вид: (xp)’=p·xp-1, где показатель степени p является любым действительным числом.
Доказательство 2Приведем доказательство формулы, когда показатель степени – натуральное число: p=1, 2, 3, …
Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:
(xp)’=lim∆x→0=∆(xp)∆x=lim∆x→0(x+∆x)p-xp∆x
Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:
(x+∆x)p-xp=Cp0+xp+Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+. ..++Cpp-1·x·(∆x)p-1+Cpp·(∆x)p-xp==Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p
..++Cpp-1·x·(∆x)p-1+Cpp·(∆x)p-xp==Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p
Таким образом:
(xp)’=lim∆x→0∆(xp)∆x=lim∆x→0(x+∆x)p-xp∆x==lim∆x→0(Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p)∆x==lim∆x→0(Cp1·xp-1+Cp2·xp-2·∆x+…+Cpp-1·x·(∆x)p-2+Cpp·(∆x)p-1)==Cp1·xp-1+0+0+…+0=p!1!·(p-1)!·xp-1=p·xp-1
Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.
Доказательство 3Чтобы привести доказательство для случая, когда p — любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.
Рассмотрим два случая: когда x положительны и когда x отрицательны.
Итак, x>0. Тогда: xp>0. Логарифмируем равенство y=xp по основанию e и применим свойство логарифма:
y=xpln y=ln xpln y=p·ln x
На данном этапе получили неявно заданную функцию. Определим ее производную:
Определим ее производную:
(ln y)’=(p·ln x)1y·y’=p·1x⇒y’=p·yx=p·xpx=p·xp-1
Теперь рассматриваем случай, когда x – отрицательное число.
Если показатель p есть четное число, то степенная функция определяется и при x<0, причем является четной: y(x)=-y((-x)p)’=-p·(-x)p-1·(-x)’==p·(-x)p-1=p·xp-1
Тогда xp<0 и возможно составить доказательство, используя логарифмическую производную.
Если p есть нечетное число, тогда степенная функция определена и при x<0, причем является нечетной: y(x)=-y(-x)=-(-x)p. Тогда xp<0, а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:
y'(x)=(-(-x)p)’=-((-x)p)’=-p·(-x)p-1·(-x)’==p·(-x)p-1=p·xp-1
Последний переход возможен в силу того, что если p — нечетное число, то p-1 либо четное число, либо нуль (при p=1), поэтому, при отрицательных x верно равенство (-x)p-1=xp-1.
Итак, мы доказали формулу производной степенной функции при любом действительном p.
Пример 2Даны функции:
f1(x)=1×23,f2(x)=x2-14,f3(x)=1xlog712
Определите их производные.
Решение
Часть заданных функций преобразуем в табличный вид y=xp, опираясь на свойства степени, а затем используем формулу:
f1(x)=1×23=x-23⇒f1′(x)=-23·x-23-1=-23·x-53f2′(x)=x2-14=2-14·x2-14-1=2-14·x2-54f3(x)=1xlog712=x-log712⇒f3′(x)=-log712·x-log712-1=-log712·x-log712-log77=-log712·x-log784
Производная показательной функции
Доказательство 4Выведем формулу производной, взяв за основу определение:
(ax)’=lim∆x→0ax+∆x-ax∆x=lim∆x→0ax(a∆x-1)∆x=ax·lim∆x→0a∆x-1∆x=00
Мы получили неопределенность. Чтобы раскрыть ее, запишем новую переменную z=a∆x-1 (z→0 при ∆x→0). В таком случае a∆x=z+1⇒∆x=loga(z+1)=ln(z+1)ln a. Для последнего перехода использована формула перехода к новому основанию логарифма.
Осуществим подстановку в исходный предел:
(ax)’=ax·lim∆x→0a∆x-1∆x=ax·ln a·lim∆x→011z·ln(z+1)==ax·ln a·lim∆x→01ln(z+1)1z=ax·ln a·1lnlim∆x→0(z+1)1z
Вспомним второй замечательный предел и тогда получим формулу производной показательной функции:
(ax)’=ax·ln a·1lnlimz→0(z+1)1z=ax·ln a·1ln e=ax·ln a
Пример 3Даны показательные функции:
f1(x)=23x,f2(x)=53x,f3(x)=1(e)x
Необходимо найти их производные.
Решение
Используем формулу производной показательной функции и свойства логарифма:
f1′(x)=23x’=23x·ln23=23x·(ln 2-ln 3)f2′(x)=53x’=53x·ln 513=13·53x·ln 5f3′(x)=1(e)x’=1ex’=1ex·ln1e=1ex·ln e-1=-1ex
Производная логарифмической функции
Доказательство 5Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значениях основания а логарифма. Опираясь на определение производной, получим:
(logax)’=lim∆x→0loga(x+∆x)-logax∆x=lim∆x→0logax+∆xx∆x==lim∆x→01∆x·loga1+∆xx=lim∆x→0loga1+∆xx1∆x==lim∆x→0loga1+∆xx1∆x·xx=lim∆x→01x·loga1+∆xxx∆x==1x·logalim∆x→01+∆xxx∆x=1x·logae=1x·ln eln a=1x·ln a
Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифма. Равенство lim∆x→01+∆xxx∆x=e является верным в соответствии со вторым замечательным пределом.
Пример 4Заданы логарифмические функции:
f1(x)=logln3 x,f2(x)=ln x
Необходимо вычислить их производные.
Решение
Применим выведенную формулу:
f1′(x)=(logln3 x)’=1x·ln(ln 3);f2′(x)=(ln x)’=1x·ln e=1x
Итак, производная натурального логарифма есть единица, деленная на x.
Производные тригонометрических функций
Доказательство 6Используем некоторые тригонометрические формулы и первый замечательный предел, чтобы вывести формулу производной тригонометрической функции.
Согласно определению производной функции синуса, получим:
(sin x)’=lim∆x→0sin (x+∆x)-sin x∆x
Формула разности синусов позволит нам произвести следующие действия:
(sin x)’=lim∆x→0sin (x+∆x)-sin x∆x==lim∆x→02·sin x+∆x-x2·cosx+∆x+x2∆x==lim∆x→0sin ∆x2·cosx+∆x2∆x2==cosx+02·lim∆x→0sin ∆x2∆x2
Наконец, используем первый замечательный предел:
sin’ x=cos x+02·lim∆x→0sin∆x2∆x2=cos x
Итак, производной функции sin x будет cos x.
Совершенно также докажем формулу производной косинуса:
cos’ x=lim∆x→0cos (x+∆x)-cos x∆x==lim∆x→0-2·sin x+∆x-x2·sinx+∆x+x2∆x==-lim∆x→0sin∆x2·sinx+∆x2∆x2==-sinx+02·lim∆x→0sin∆x2∆x2=-sin x
Т. е. производной функции cos x будет –sin x.
е. производной функции cos x будет –sin x.
Формулы производных тангенса и котангенса выведем на основе правил дифференцирования:
tg’x=sin xcos x’=sin’ x·cos x-sin x·cos’ xcos2 x==cos x·cos x-sin x·(-sin x)cos2 x=sin2 x+cos2 xcos2 x=1cos2 xctg’x=cos xsin x’=cos’x·sin x-cos x·sin’xsin2 x==-sin x·sin x-cos x·cos xsin2 x=-sin2 x+cos2 xsin2 x=-1sin2 x
Производные обратных тригонометрических функций
Раздел о производной обратных функций дает исчерпывающую информацию о доказательстве формул производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому дублировать материал здесь не будем.
Производные гиперболических функций
Доказательство 7Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:
sh’x=ex-e-x2’=12ex’-e-x’==12ex—e-x=ex+e-x2=chxch’x=ex+e-x2’=12ex’+e-x’==12ex+-e-x=ex-e-x2=shxth’x=shxchx’=sh’x·chx-shx·ch’xch3x=ch3x-sh3xch3x=1ch3xcth’x=chxshx’=ch’x·shx-chx·sh’xsh3x=sh3x-ch3xsh3x=-1sh3x
Рекомендуется выучить формулы из таблицы производных: они не столь сложны для запоминания, но экономят много времени, когда необходимо решать задачи дифференцирования.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Дифференциальное исчисление
Производные и выражения дифференцирования.

Рекламные ссылки
Дифференциальное исчисление — это раздел исчисления, изучающий скорость изменения величин.
| Expression | Derivatives | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| y = x n | dy/dx = n x n-1 | |||||||||
| y = a x n | dy/dx = a n x n-1 | |||||||||
| f(x) = a x n | f'(x) = a n x n-1 | |||||||||
| y = e x | dy/dx = e x | |||||||||
| y = e a x | dy/dx = a e х | |||||||||
| y = a x | dy/dx = a x ln(a) | |||||||||
| y = ln(x) | dy/dx = 1 / x | |||||||||
| y = sin (θ) | dy/dθ = cos (θ) | |||||||||
| y = cos (θ) | dy/dθ = -sin (θ) | dy/dθ = -sin (θ) | dy/dθ = -sin (θ)| dy/dθ = — | y = tan(Θ) | dy/dΘ = сек 2 (Θ) | | ||||
| y = cot (θ) | DY/Dθ = COSEC 2 (θ) | |||||||||
| y = sec (θ) | 4 DAH = Sec (θ) | 44 DAY/DY = Sec (θ) | 444444444 DAY/D (θ) | 44 DAY/DY = Sec (θ) 9244 DAY/DO).|||||||
| y = cosec(Θ) | dy/dΘ = — cot(Θ) cosec(Θ) = — cos(Θ) / sin 2 (Θ) | |||||||||
| y = sin -1 (x / a) | DY/ DX = 1/ (A 2 — x 2 ) 1/2 | |||||||||
| Y = COS -1 ( y = cos -1 (./ A = Cos -1 (./ A = COS -1 (. ( y = cos -1 ( y = cos -1 (. DX = — 1 / (A 2 — x 2 ) 1/2 | ||||||||||
| Y = TAN -1 (x / A) | 4 DY / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX. а 2 + х 2 ) | |||||||||
| у = кроватка -1 (х/а) | dy/dx = — a / (a 2 + x 2 ) | |||||||||
| y = sec -1 (x / a) /dy 9x | 0 ( (x 2 — A 2 ) 1/2 ) | |||||||||
| Y = COSEC -1 (x / A) | DY / DX / DX / DX = -а (x / a) | DY / DX = — A / A (x / A) | DY / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / DX / (x / A) | .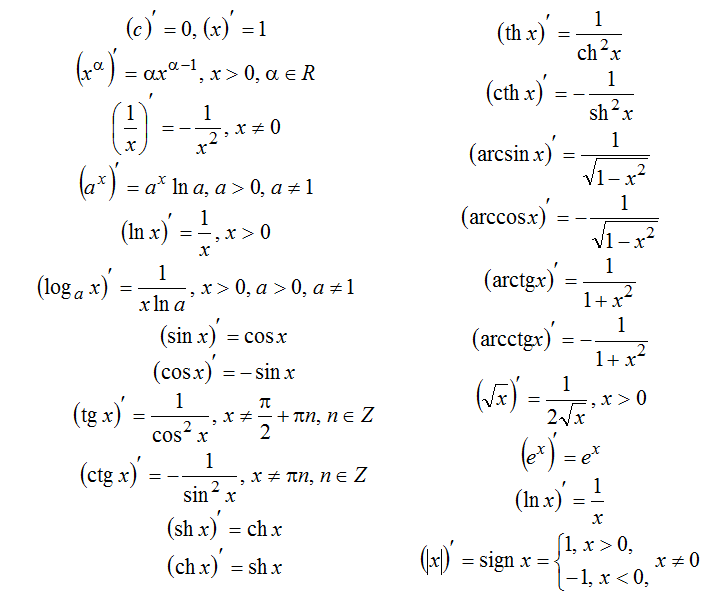 2 — a 2 ) 1/2 ) 2 — a 2 ) 1/2 ) |
Рекламные ссылки
Похожие темы
Связанные документы
Engineering ToolBox — Расширение SketchUp — 3D-моделирование онлайн!
Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т. д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, увлекательными и бесплатными программами SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!
Перевести
О Engineering ToolBox!
Мы не собираем информацию от наших пользователей. В нашем архиве сохраняются только электронные письма и ответы. Файлы cookie используются только в браузере для улучшения взаимодействия с пользователем.
Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложения на локальном компьютере.

 Нахождение дробной степени числа
Нахождение дробной степени числа Рiвнiсть векторiв
Рiвнiсть векторiв
 Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента. Именно такое значение и возвращает выражение x / |x| . Когда x < 0 оно равно (-1), а когда x > 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
Именно такое значение и возвращает выражение x / |x| . Когда x < 0 оно равно (-1), а когда x > 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.

 (Θ)
(Θ)