Умножение матриц с тремя строками и тремя столбцами: 13.1.3. Умножение матриц

13.1.3. Умножение матриц

1. Умножение матриц — это специфическая операция, со­ставляющая основу алгебры матриц. Строки и столбцы мат­риц можно рассматривать как векторы-строки и векторы-стол­бцы соответствующих размерностей: иными словами, любую матрицу можно интерпретировать как совокупность векторов-строк или векторов-столбцов.

Пусть даны матрица А размером Т Х п и матрица В разме­ром П х K. Будем рассматривать матрицу А как совокупность Т векторов-строк I размерности П каждый, а матрицу В — Как совокупность K векторов-столбцов J, каждый из которых содержит по П координат:

Векторы-строки матрицы А и векторы-столбцы матрицы В Показаны в записи этих матриц (13.3). Длина строки матри­цы А равна высоте столбца матрицы В, и потому скалярное произведение этих векторов имеет смысл.

Определение 3. Произведением матриц А и В называется матрица

С, элементы которой CIj равны скалярным произве­дениям векторов-строк I матрицы А на векторы-столбцы J Матрицы В:

Произведение матриц А и В — матрица С — имеет размер Т х K, поскольку длина П векторов-строк и векторов-столбцов исчезает при суммировании произведений координат этих век­торов в их скалярных произведениях, как показано в формулах (13. 4). Таким образом, для вычисления элементов первой строки матрицы С необходимо последовательно получить скаляр­ные произведения первой строки матрицы А на все столбцы матрицы В; вторая строка матрицы С получается как ска­лярные произведения второй вектор-строки матрицы А На все векторы-столбцы матрицы В и так далее. Для удобства за­поминания размера произведения матриц нужно перемножить отношения размеров матриц-сомножителей:, т. е. размер матрицы

С равен произведению оставшихся в отношении чисел: Т х K.

В операции умножения матриц есть характерная особен­ность: произведение матриц А и В имеет смысл, если число столбцов в А равно числу строк в В. Тогда если А и В — Прямоугольные матрицы, то произведение В и А уже не будет иметь смысла, так как в скалярных произведениях, формиру­ющих элементы соответствующей матрицы, должны участво­вать векторы с одинаковым числом координат.

Если матрицы А И В квадратные размером N х N, то име­ет смысл как произведение матриц АВ, так и произведение матриц BA, причем размер этих матриц такой же, как и у ис­ходных сомножителей. При этом в общем случае перемноже­ния матриц правило перестановочности не соблюдается, т. е. АВ ≠ ВА.

Рассмотрим примеры на умножение матриц.

Решение. Поскольку число столбцов матрицы А равно числу строк матрицы В, то произведение матриц АВ имеет смысл. По формулам (13.4) получаем в произведении матрицу размером 3 х 2:

Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.

Решение. Здесь мы найдем произведения данных матриц АВ и ВА:

Как видно из результата, матрица произведения зависит от по­рядка расположения матриц в произведении. В обоих случаях произведения матриц имеют тот же размер, что и у исходных сомножителей: 2 х 2.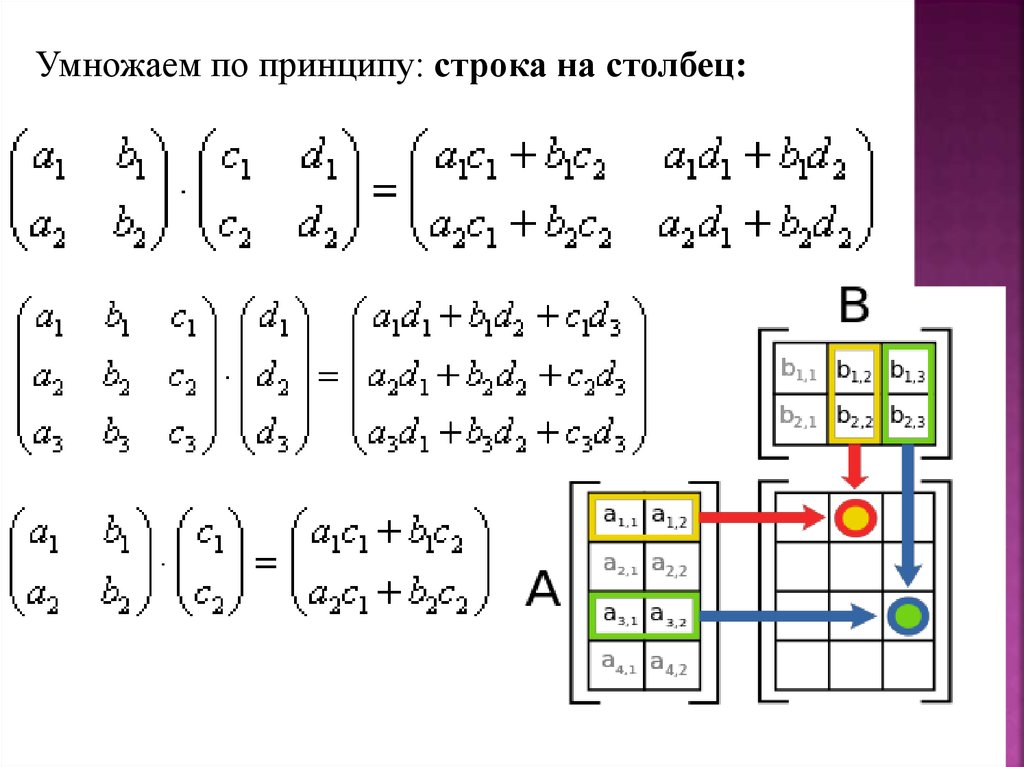

Решение. В данном случае матрица В представляет собой вектор-столбец, т. е. матрицу, у которой три строки и один столбец. Вообще, векторы — это частные случаи матриц: век­тор-строка длины

П представляет собой матрицу с одной стро­кой и П столбцами, а вектор-столбец высоты N — матрицу с N строками и одним столбцом. Размеры данных матриц соот­ветственно 2 х 3 и 3 х 1, так что произведение этих матриц определено. Имеем

В произведении получена матрица размером 2 х 1 или вектор-столбец высоты 2.

Решение. Путем последовательного умножения матриц находим

2. Свойства произведения матриц. Пусть А, В и С — мат­рицы соответствующих размеров (чтобы произведения матриц были определены), а α — действительное число. Тогда следу­ющие свойства произведения матриц имеют место:

1) (АВ)С = А(ВС),

2) (А + В)С = AC + ВС,

3) А(В + С) = АВ + АС,

4) α(АВ) = (αА)В = А(αВ).

В п. 1 этого раздела введено понятие единичной матрицы

Е. Нетрудно убедиться, что в алгебре матриц она играет роль единицы, т. е. можно отметить еще два свойства, связанные с умножением на эту матрицу слева и справа в случае квадрат­ных матриц:

5) АЕ = А,

6) ЕА = А.

Иными словами, произведение любой матрицы на единич­ную матрицу, если оно имеет смысл, не меняет исходную мат­рицу.

< Предыдущая		Следующая >

Умножение матриц: алгоритм, свойства произведения, примеры

Оглавление

Время чтения:  8 минут

743

Алгоритм умножения матриц в различных случаях

Умножаем данные в строке для первой матрицы на соответствующие данные в столбцах из второй матрицы.

• Перемножаем числовые значения первой строки на значения из первого столбца:

1. Производим умножение первого элемента первой строки на соответствующий элемент из первого столбца.
2. Находим произведение второго элемента первой строки и второго элемента, который берем из столбца №1.
3. Проделываем такие же действия со всеми элементами, до тех пор, пока не дойдем до конца первой строки матрицы.  
4. Вычисленные произведения необходимо сложить между собой.
5. Вычисленный результат будет равняться элементу для первой строки.

• Используя идентичный алгоритм, можно перемножить данные в первой строке из первой матрицы на данные всех последующих столбцов из второй матрицы. Вычисленные значения данных будет являться первой строкой матрицы, которую необходимо вычислить.

• Строка под номером два определяемой матрицы вычисляется также. Произведение числовых данных второй строки из первой матрицы на соответствующие данные для каждого столбца из второй матрицы. Окончательные данные фиксируются в составленную, новую матрицу, после окончания каждого определения суммы значений.
• Аналогичные действия нужно проводить с каждой строкой вычисляемой матрицы.  Вычисления проводятся до тех пор все строчки новой матрицы не будут заполнены значениями.

Правило умножения произведения двух и более матриц

Умножение двух матриц. Произведение матриц (С= А x В) —  является действием только для матриц А и В которые согласованы между собой. Для данных значений, число столбцов у матрицы А должно равняться количеству строк матрицы В:

\[C=A \cdot B\]

\[m \cdot n\] \[m \cdot p\] \[p \cdot n\]

Примеры решения:

Пример №1:

Необходимо выполнить умножение двух матриц:

\[A=a_{i j}\] у которой размеры \[m \times n\] 

\[B=b_{i j}\] у которой размеры \[p \times n\] 

Необходимо вычислить матрицу C.

Элементы \[C_{i j}\].

Для вычисления применим формулу:

\[c_{i j}=a_{i 1} \cdot b_{i 1}+a_{i 2} \cdot b_{i 2}+\ldots .+a_{i p} \cdot b_{p j}, \mathrm{i}=1, \ldots . \mathrm{m}, \mathrm{j}=, \ldots . . \mathrm{m}\].

Умножение трёх матриц

Чтобы вычислить произведение трех матриц применяют два способа.

1. Определить AB и умножить на значение С: (АВ)*С;
2. Находим произведение ВС, затем умножаем полученное значение на А.

Пример №2:

Выполним умножение матриц двумя способами.

Умножение матрицы на число

Произведение значение матрицы, равное числу A на некое значение К, будет выглядеть следующим образом.

\[B=A \cdot k\]

Размер будет таким же, как и в исходной матрице, который получен путем перемножения на заданное число все матричных элементов.

• \[1 \cdot A=A\]
• \[0 \cdot A=\] значение матрицы с нулевым результатом;
• \[k(A+B)=k A+k B\]
• \[(k+n) A=k A+n A\]
• \[(k \cdot n) \cdot A=k(n \cdot A)\]

Пример:

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Принцип умножения матрицы на вектор значения

Для определения значения произведения матрицы и вектора, нужно использовать правило, которое звучит как: “умножение строки на столбе”

• при умножении матрицы на векторный столбец, значение столбцов в любой матрице обязательно должно совпадать с количеством строк в вектор-столбце. {2} \cdot A=\left(\begin{array}{cc} 7 & 10 \\ 15 & 22 \end{array}\right) \cdot\left(\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right)=\left(\begin{array}{cc} 7+30 & 14+40 \\ 15+66 & 30+88 \end{array}\right)=\left(\begin{array}{cc} 37 & 54 \\ 81 & 118 \end{array}\right)\]

  Основные свойства и правила умножения матриц

  1. \[(A \times B) \times C=A(B C)-\] принцип сочетательного свойства при перемножении матричных значений.
  2. \[A(B+C)=A B+A C-\] распределительное сочетание и распределение при перемножении матриц.
  3. \[(A+B) C=A C+B C-\] аналогичные характерные действия, которые свойственны второму пункту.
  4. \[\lambda(A B)=(\lambda A) B\].

  Оценить статью (0 оценок):

  Поделиться

  3 способа понять умножение матриц | by Glenn Henshaw

  Развивайте свою интуицию в матричном умножении с нуля

  Photo by Markus Spiske на Unsplash

  Когда я впервые узнал о матричном умножении, я был удивлен тем, как трудно мне было развить интуицию в отношении этой операции. Обычное определение матричного умножения скрывает множество интересных фактов, которые легче распознать, если посмотреть с разных точек зрения. В этом посте я опишу умножение матриц с трех точек зрения: столбцы, строки и их комбинации. Я также расскажу о некоторых простых фактах, которые помогут проверить вашу интуицию. Мы надеемся, что после прочтения вы получите более глубокое представление об умножении матриц, строках и столбцах. Этот пост был вдохновлен курсом линейной алгебры, который вел великий Гилберт Странг (MIT) .

  В этом посте перечислены три способа интерпретации умножения матриц. Для каждой из этих интерпретаций мы обсудим следующее.

  1. Интерпретация: Что это значит?
  2. Почему это работает?: Как эта интерпретация возникает из определения умножения матриц?
  3. Проверьте свою интуицию: Список фактов, которые вы можете использовать, чтобы проверить свою интуицию для интерпретации, которую мы рассматриваем.

  Иногда я упоминаю понятия линейной комбинации , линейной зависимости, линейной независимости, скалярного произведения . Если вы хотите быстро освежить свою память по этим темам, посмотрите мою статью 3 основных понятия в линейной алгебре.

  Пример. Допустим, у нас есть три завсегдатая: Ларс, Фатима и Джорджия. На вечеринке Ларс купил 2 пива и 1 коктейль, Фатима купила 1 пиво и 2 коктейля, а у Джорджии было 4 пива и никаких коктейлей. Пиво стоит 7 долларов, а коктейли — 10 долларов. Мы можем смоделировать их расходы на ночь с помощью матричного умножения.

  Как были вычислены числа справа?

  Наша цель — понять свойства умножения матриц в более общем виде, поэтому в этом посте мы будем рассматривать произведение матрицы 3×3 A и матрицы 3×2 B 900 06 . Результатом будет матрица 3×2 C .

  Жак Филипп Мари Бине … признан первым, кто вывел правило умножения матриц в 1812 году. — Оливер Книлл

  Обычный способ определить умножение матриц — это суммирование или, более компактно, скалярное произведение строк A и столбцов B. Скалярное произведение строки 1 A и столбца 1 B даст первую запись C.

  В общем случае ij-я запись C представляет собой i-ю строку A , разделенную точками с j-м столбцом B .

  Пример. Найдите третью строку и второй столбец произведения C .

  Ответ: (1)(1)+(2)(2) +(3)(1) = 8. Попробуйте использовать определение, чтобы найти остальные элементы С .

  Интерпретация: Запись C является скалярным произведением строки A и столбца B . Нулевые записи в C соответствуют строке A и столбцу B , которые ортогональны (под прямым углом друг к другу).

  Проверьте свою интуицию: С этой точки зрения некоторые факты становятся яснее .

  • Количество столбцов A должно равняться количеству строк B . В противном случае суммы в определении не будут определены.
  • Произведение AB будет матрицей с тем же количеством столбцов, что и A , и тем же количеством строк, что и B.
  • Нулевая запись в 9 0042 C означает, что соответствует ряду A и столбец B ортогональны. Ортогональные векторы линейно независимы . Но не все пары линейно независимых векторов ортогональны.

  Первое, на что следует обратить внимание относительно AB = C , это то, что столбцы матрицы C связаны со столбцами матрицы A важным образом.

  Интерпретация Каждый из столбцов C является матрицей A умножить на столбец B. Результатом этого является то, что столбцы C являются линейными комбинациями столбцов A с весами, указанными столбцы B.

  Почему это работает? Чтобы понять, почему столбцы C являются линейными комбинациями столбцов A , давайте внимательно посмотрим, как мы вычисляем первый столбец C.

  Проверьте свою интуицию: С этой точки зрения некоторые факты становятся яснее .

  • Матрица, умноженная на вектор, Ax , представляет собой просто линейную комбинацию столбцов a с элементами x. Таким образом, столбцы A линейно независимы тогда и только тогда, когда уравнение Ax = 0 имеет только нулевое решение.
  • Мы можем просмотреть столбцы C как результат применения линейного преобразования, определенного B , к столбцам A .
  • Предположим, что столбцы A линейно независимы. Тогда, если C имеет столбец нулей, B также должен иметь столбец нулей.
  • Если столбцы C линейно зависимы и столбцы B линейно независимы, тогда столбцы A зависимы. Это следует из того, что если x является нетривиальным решением Cx = 0 , то Bx является нетривиальным решением 90 006 из Ах = 0.
  • Если уравнение Ax = b не имеет решения, то уравнение ABx = Cx = b не имеет решения. Ведь столбцы C — это просто комбинации столбцов A .
  • Пролет колонн C содержится в пролете колонн A . Следовательно, ранг(AB) ≤ ранг(A) .
  • Если B обратим с обратным B’ , то столбцы A и AB имеют такой же диапазон. Мы можем доказать это из предыдущего факта, ранг(AB) ≤ ранг(A) в сочетании с тем фактом, что ранг(A) = ранг(AI) = ранг(ABB’) ≤ ранг(AB).

  Итак, умножение матриц с точки зрения столбцов. Теперь перейдем к рядам?

  Интерпретация Строки C являются строками A , умноженными на матрицу B . Следовательно, строки C являются линейными комбинациями строк B с весами, указанными в строках A.

  Почему это работает? Чтобы понять, почему строки C являются линейными комбинациями строк B , давайте внимательно посмотрим, как мы вычисляем первую строку C , используя определение умножения матриц.

  Проверьте свою интуицию: Еще раз перечислим некоторые факты о строках, которые выводятся из этой интерпретации умножения матриц.

  • Для AB = C , если строки C линейно независимы, то строки B линейно независимы. Предупреждение: обратное не обязательно верно.
  • Если A имеет ряд нулей, то AB имеет ряд нулей.
  • Диапазон строк B содержит диапазон строк C .
  • Если Е — обратимая матрица n×n , а B — любая матрица n×m . Тогда EB имеет то же место в строке, что и E . В частности, элементарные операции со строками сохраняют пространство строк.

  Мы можем использовать интерпретацию строки и столбца, чтобы помочь набросать доказательство интересного результата о размерности пространства строки и пространства столбца m×n матрица. Размерность размаха столбцов матрицы называется ее рангом . Размер промежутка строк называется rowrank .

  Претензия: ранг и rowrank из m×n матрица 9004 3 C равны.

  Есть много m×r матриц A и r×n матрицы B такие, что C = AB. Выберите A и B так, чтобы r было минимальным. р колонны из А пролет колонны 9004 3 место с. р строк B охватывают пространство строк C. Поскольку мы выбрали r как наименьшее такое число, rank(C) = rowrank(C) = r.

  Утверждение: Если A и B являются квадратными матрицами и AB = I , то BA = I. Следовательно, B является обратный А.

  У нас есть АВ = I . Поэтому столбцы A линейно независимы. Следовательно, уравнение Ax = 0 имеет только тривиальное решение. умножьте первое уравнение справа на A , чтобы получить ABA = A . Тогда АВА-А = А(ВА-I)=0 . Следовательно, ВА = I .

  Наша последняя интерпретация дает нам способ разложить произведение двух матриц на сумму матриц.

  Интерпретация Матрица C представляет собой сумму матриц, состоящих из столбцов A , умноженных на строки B. Матрицы, составляющие сумму, имеют столбцы, скалярно кратные столбцу A.

  Почему это работает? Чтобы понять, почему это так, рассмотрим, что происходит, когда вы записываете матрицу A как сумму матриц и вычисляете AB путем распределения B .

  Проверь свою интуицию:

  • Каждая из матриц в слагаемом имеет одномерные столбцы.
  • Вы можете поменять местами два столбца A и получить тот же продукт AB , если вы поменяете местами соответствующие строки B .

  Мы говорили о трех разных способах понимания умножения матриц.

  1. Матрица, умноженная на столбцы
  2. Строки, умноженная на матрицы
  3. И столбцы, умноженные на строки

  Мы использовали эти различные интерпретации для обзора некоторых основных фактов о матричном умножении, независимости и интервале.

  Умножение матриц Обзор | Penji

  Обзор

  
  

  Матрицы — это способ группировки чисел, организованный в строки и столбцы. Матрицы часто используются как способ представления нескольких уравнений в более удобном для организации формате, однако для решения этих систем уравнений мы должны иметь возможность выполнять матричные операции, такие как умножение.
  

  Строки и столбцы

  
  

  Приведенная ниже матрица является примером матрицы [3×2]. Матрицы описываются в форме [RxC], где R представляет количество строк матрицы, а C представляет количество столбцов матрицы.
  

  Приведенная выше матрица имеет размер [3×2], так как в ней 3 строки и 2 столбца.
  

  Умножение на скаляр

  
  

  Любую матрицу можно умножить на так называемую скалярную величину. В этом случае скаляр представляет собой действительное число, умноженное на всю матрицу. Например:

  Умножение матриц

  
  

  Также можно перемножать две матрицы вместе, однако матрицы можно перемножать только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы. Если две матрицы соответствуют этому критерию, их можно перемножить. Результатом будет третья матрица с таким же количеством строк, как и в первой матрице, и таким же количеством столбцов, как во второй матрице.
  

  Пример

  
  

  Можно ли перемножать следующие матрицы? Каковы будут размеры ответа?

  1. [2×3] * [2×2]
  2. [3×2] * [2×2]
  3. [2*3] * [3*1]

  Ответ

  
  

  1. Мы не можем умножать эти матрицы, потому что матрица 1 имеет три столбца, а матрица 2 имеет только две строки.

  2. Мы можем перемножить эти матрицы, потому что матрица 1 имеет два столбца, а матрица 2 — 2 строки. Результирующая матрица будет иметь столько строк, сколько матрица 1, и столбцов, как матрица 2, поэтому она будет [3×2].

  3. Мы можем перемножить эти две матрицы, потому что матрица 1 имеет три столбца, а матрица 2 — три строки. Результатом будет [2×1].
  

  Примечание: Это упражнение должно было показать, что порядок имеет значение при умножении двух матриц. Попробуйте изменить порядок любого из приведенных выше примеров и посмотрите, изменится ли результат.

  Правила умножения матриц

  
  

  Как только мы узнали, можно ли перемножить две матрицы, пришло время выполнить это умножение. Умножение двух матриц также известно как «точечный продукт». Каждое число в матрице ответов является результатом умножения одной из строк матрицы 1 на один из столбцов матрицы 2.

  Чтобы найти первую строку, первый столбец матрицы ответов, умножьте первую строку матрицы 1 на первый столбец матрицы 2. Чтобы найти строку 1, второй столбец матрицы ответов, умножьте первую строку матрицы 1 на второй столбец матрицы 2. При умножении строки на столбец совпадающие термины умножаются и складываются.
  

  Пример: Найдите скалярное произведение двух матриц

  Матрица 1 состоит из двух столбцов, а матрица 2 состоит из двух строк, поэтому их можно перемножить. Ответ будет состоять из двух строк, поскольку в матрице 1 две строки и три столбца, поскольку в матрице 2 три столбца. Таким образом, ответ будет [2×3].

  Допустим, мы сначала хотим найти верхний левый угол матрицы ответов (отмечен X). Поскольку место, которое мы хотим найти, находится в строке 1 столбца 1, мы должны умножить строку 1 первой матрицы на столбец 1 второй матрицы. Строка и столбец, которые необходимо умножить, отмечены стрелками.

  При умножении строки и столбца мы умножаем первое число в строке на первое число в столбце, умножаем второе число в строке на второе число в столбце и складываем результат.

  No related posts.