Как вычисляется корень если дискриминант равен нулю. Как решать квадратные уравнения
», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.
Что называют квадратным уравнением
Важно!
Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.
Если максимальная степень, в которой стоит неизвестное — «2 », значит, перед вами квадратное уравнение.
Примеры квадратных уравнений
- 5x 2 − 14x + 17 = 0
- −x 2 + x + = 0
- x 2 + 0,25x = 0
- x 2 − 8 = 0
Важно! Общий вид квадратного уравнения выглядит так:
A x 2 + b x + c = 0
«a », «b » и «c » — заданные числа.
- «a » — первый или старший коэффициент;
- «b » — второй коэффициент;
- «c » — свободный член.
Чтобы найти «a
», «b
» и «c
»
нужно сравнить свое уравнение с общим видом квадратного уравнения
«ax 2 + bx + c = 0
».
Давайте потренируемся определять коэффициенты «a », «b » и «c » в квадратных уравнениях.
| Уравнение | Коэффициенты |
|---|---|
| |
| |
| |
| |
| x 2 − 8 = 0 |
|
Как решать квадратные уравнения
В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней .
Запомните!
Чтобы решить квадратное уравнение нужно:
- привести квадратное уравнение к общему виду «ax 2 + bx + c = 0 ». То есть в правой части должен остаться только «0 »;
- использовать формулу для корней:
Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения.
Решим квадратное уравнение.
X 2 − 3x − 4 = 0
Уравнение « x 2 − 3x − 4 = 0 » уже приведено к общему виду «ax 2 + bx + c = 0 » и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения .
Определим коэффициенты «a », «b » и «c » для этого уравнения.
x 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
С её помощью решается любое квадратное уравнение.
В формуле «x 1;2 =
» часто заменяют подкоренное выражение
«b 2 − 4ac
» на букву «D
» и называют
дискриминантом
. Более подробно понятие дискриминанта рассматривается в уроке
«Что такое дискриминант ».
Рассмотрим другой пример квадратного уравнения.
x 2 + 9 + x = 7x
В данном виде определить коэффициенты «a », «b » и «c » довольно сложно. Давайте вначале приведем уравнение к общему виду «ax 2 + bx + c = 0 ».
X 2 + 9 + x = 7x
x 2 + 9 + x − 7x = 0
x 2 + 9 − 6x = 0
x 2 − 6x + 9 = 0
Теперь можно использовать формулу для корней.
X 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
x =
x = 3
Ответ: x = 3
Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем оказывается отрицательное число.
Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.
О каких уравнениях пойдет речь?
На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.
Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка.
Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.
Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.
Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.
Способы решения уравнений второго порядка
Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:
- с помощью факторизации;
- используя формулу для полного квадрата;
- применяя график соответствующей квадратичной функции;
- используя уравнение дискриминанта.
Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.
Формула для получения корней уравнения
Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду.
То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).
Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.
В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).
В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.
Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.
Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»).
Для этого в него достаточно подставить коэффициенты b, c, и a.
Понятие о дискриминанте
В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.
Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:
- D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
- D=0: у уравнения всего один корень, и он является действительным числом.
Задача на определение дискриминанта
Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.
Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0.
Здесь a=-2, b=2, c=-11.
Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.
Пример неравенства через дискриминант
Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.
В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.
Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0.
В свою очередь, число -4 не удовлетворяет неравенству (-4Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.
Пример решения уравнения
Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.
В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.
Геометрическая задача
Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.
У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.
Геометрический смысл квадратного уравнения
Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х)
. Из этого следует, что есть три возможных случая:
1)
парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).
2) парабола имеет одну точку пересечения с осью Ох . Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).
3)
Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс.
Отсюда находим
Формула дискриминанта и корней квадратного уравнения
Дискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0 При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле
Теорема Виета
Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p
, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q
. Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а
отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета.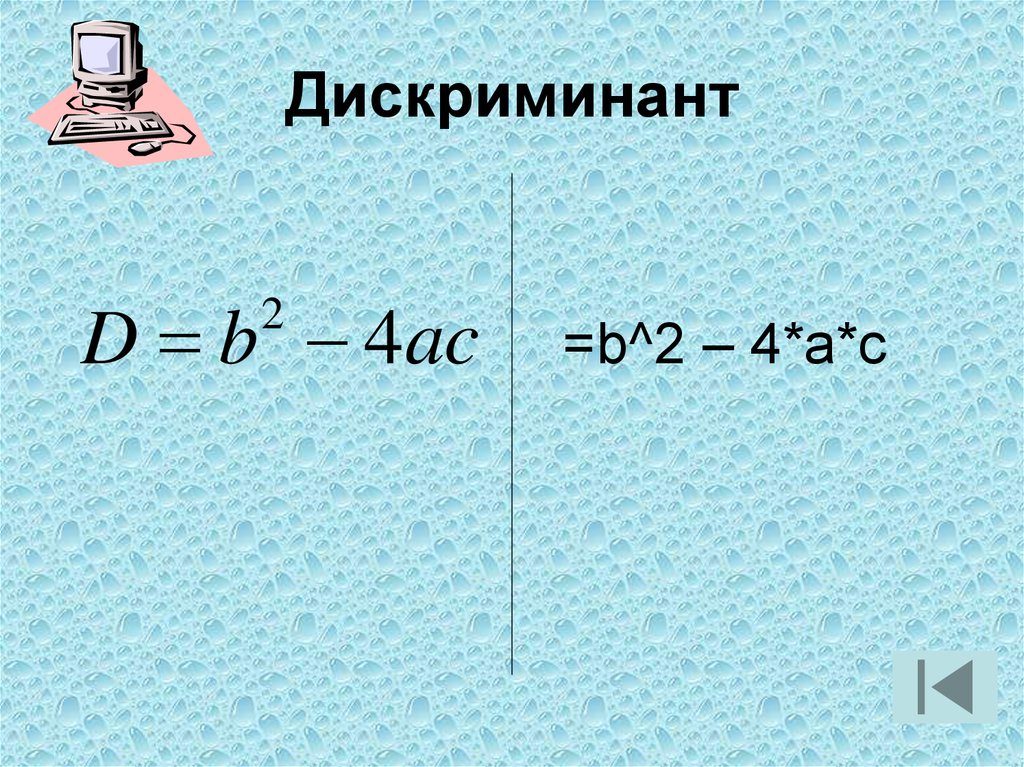
Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения
С второго условия получаем, что произведение должно быть равно -6
. Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2}
. С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равны
Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см 2 .
Решение:
Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х
– большую сторону, тогда 18-x
меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;
или
Найдем дискриминант уравнения
Вычисляем корни уравнения
Если х=11
,
то 18-х=7
,
наоборот тоже справедливо (если х=7
, то 21-х=9
).
Задача 6. Разложить квадратное 10x 2 -11x+3=0 уравнения на множители.
Решение:
Вычислим корни уравнения, для этого находим дискриминант
Подставляем найденное значение в формулу корней и вычисляем
Применяем формулу разложения квадратного уравнения по корнями
Раскрыв скобки получим тождество.
2+(2а+6)х-3а-9=0
имеет более одного корня?
Решение:
Рассмотрим сначала особые точки, ими будут значения а=0
и а=-3
. При а=0
уравнение упростится до вида 6х-9=0; х=3/2
и будет один корень. При а= -3
получим тождество 0=0
.
Вычислим дискриминант
и найдем значения а
при котором оно положительно
С первого условия получим а>3
. Для второго находим дискриминант и корни уравнения
Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0
получим 3>0
.
Итак, за пределами промежутка (-3;1/3)
функция отрицательная. Не стоит забывать о точке а=0
,
которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи
Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.
2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D)
:
D>0
– уравнение имеет 2
различных действительных корня;
D=0
— уравнение имеет 1
корень (2
совпадающих корня):
D Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.
.
Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле
Формулируется теорема не только для квадратных уравнений, но и для многочленов.
Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни
До 4
уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6,
следовательно корнями могут быть значения (1, 6)
и (2, 3)
или пары с противоположным знаком. Сумма корней равна 7
(коэффициент при переменной с противоположным знаком).
Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».
Давайте попробуем разобраться,
что описывает дискриминант?В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить.
Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0)
,
или парабола ветвями вниз (a
Вершина параболы лежит посередине между корнями
Физический смысл дискриминанта:
Если дискриминант больше нуля (D>0)
парабола имеет две точки пересечения с осью Ox
.
Если дискриминант равен нулю (D=0)
то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два.
Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Варенье из бузины: польза и вред
Узнать встретимся ли мы. Сонник дома солнца. Как правильно сформулировать вопрос в процессе гадания
Формула для нахождения дискриминанта — Dudom
Дискриминант квадратного уравнения – это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения.
Дискриминант обозначается латинской буквой D.
| Вид уравнения | Формула корней | Формула дискриминанта |
|---|---|---|
| ax 2 + bx + c = 0 | b 2 — 4ac | |
| ax 2 + 2kx + c = 0 | k 2 — ac | |
| x 2 + px + q = 0 | ||
| p 2 — 4q |
Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:
| Вид уравнения | Формула |
|---|---|
| ax 2 + bx + c = 0 | , где D = b 2 — 4ac |
| ax 2 + 2kx + c = 0 | , где D = k 2 — ac |
| x 2 + px + q = 0 | , где D = |
| , где D = p 2 — 4q |
Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:
- Если дискриминант больше нуля, то уравнение имеет два корня.
- Если дискриминант равен нулю, то уравнение имеет один корень.
- Если дискриминант меньше нуля, то уравнение не имеет корней.
Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:
так как она относится к формуле:
которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.
Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.
Пример 1. Решить уравнение:
Определим, чему равны коэффициенты:
D = b 2 — 4ac = (-4) 2 — 4 · 3 · 2 = 16 — 24 = -8, D 2 — 6x + 9 = 0
Определим, чему равны коэффициенты:
D = b 2 — 4ac = (-6) 2 — 4 · 1 · 9 = 36 — 36 = 0, D = 0
Уравнение имеет всего один корень:
Определим, чему равны коэффициенты:
D = b 2 — 4ac = (-4) 2 — 4 · 1 · (-5) = 16 + 20 = 36, D > 0
Мы уже разобрали, как решать квадратные уравнения.
Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.
Вернемся к нашей формуле для нахожденя корней квадратного уравнения.
x1;2 =
| −b ± √ b 2 − 4ac |
| 2a |
Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
x1;2 =
| −b ± √ D |
| 2a |
, где « D = b 2 − 4ac »
По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».
В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
I случай
D > 0
(дискриминант больше нуля)
D —> , где « D = b 2 − 4ac »
—> —> D = b 2 − 4ac
D = 5 2 − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| −5 ± √ 81 |
| 2 · 2 |
x1;2 =
| −5 ± 9 |
| 4 |
| −5 + 9 |
| 4 |
Ответ: x1 = 1; x2 = −3
Вывод: когда « D > 0 » в квадратном уравнении два корня .
II случай
D = 0
(дискриминант равен нулю)
16x 2 − 8x + 1 = 0
D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| 8 ± √ 0 |
| 32 |
x1;2 =
| 8 ± 0 |
| 32 |
x =
x =
Ответ: x =
Вывод: когда « D = 0 » в квадратном уравнении один корень .
III случай
D
(дискриминант меньше нуля)
D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| 8 ± √ −36 |
| 32 |
Ответ: нет действительных корней
Вывод: когда « D » в квадратном уравнении нет корней .
Решение квадратных уравнений.
Дискриминант. Формула дискриминанта. Теорема Виета.
Квадратным уравнением называется уравнение вида
,
a,b,c — постоянные (числовые) коэффициенты.
В общем случае решение квадратных уравнений сводится к нахождению дискриминанта:
| Формула дискриминанта: | . |
О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :
- D>0 — уравнение имеет 2 различных вещественных корня
- D=0 — уравнение имеет 2 совпадающих вещественных корня
- D 2 .
Раздел недели: Плоские фигуры. | ||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа. Поделиться:
| |||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||
Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Теорема Виета. Версия для печати.
Натуральных чисел от 1 до 30 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99.
В таблице ниже представлена связь между значением дискриминанта и решениями квадратного уравнения.
