Термин » корень » иногда называют «радикалом» — это тоже самое.
Извлечение корня — это арифметическая операция, обратная возведению в степень.
Степенью \(n\) числа \(a\) называют произведение \(n\) множителей, каждый из которых равен \(a\).
Если в радикальном выражении нет показателя, то показатель принимается равным \(2\), то есть пишут \( \sqrt{a} \), т.е. опускают показатель корня — и такое выражение называют квадратным корнем.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Марина Валериевна Петрова
Репетитор по математике
Стаж (лет)
Образование:
Курский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 1-4 классы и русскому языку 1-4 классы.
Математика — точная наука, которая развивает логическое мышление, учит думать и является основой для дальнейшего изучения школьных предметов в старшей школе.
Главное, чтобы ребенок перестал боятся задач, «трудных» уравнений и «длинных» примеров. Результат работы — мои ученики победители и призеры муниципальных и краевых олимпиад.
Сейчас работаю по программе «Школа России». Есть несколько выпусков по программе»ХХI век» и опыт работы по учебнику математики Л.Петерсон.
Юлия Евгеньевна Храбан
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов.
Дарья Андреевна Тюрина
Репетитор по математике
Стаж (лет)
Образование:
Южный федеральный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-7 классов.
Я люблю математику за то, что она развивает в нас упорство, смелость, находчивость и системность. Благодаря ей можно научиться видеть скрытые связи между, на первый взгляд, совершенно разными вещами, а также посмотреть на различные ситуации под самым неожиданным углом.
Каждый ребёнок по-своему уникален, поэтому в обучении просто необходим индивидуальный подход. Моя цель — не только помочь ребёнку понять эту увлекательную науку, но и дать возможность понять себя, свои слабые и сильные стороны через изучение математики.
Похожие статьи
- Касательная к окружности. Точка касания окружности
- Значение синуса, косинуса и тангенса 30°, 45° и 60°
- Факультет ПЭК (МГИМО): проходной балл, отзывы
- МИФИ: Информационная безопасность
- РУДН: факультет Строительства
- РУДН: Мировая Экономика (Факультет)
- Числа и вычисления.
База, ОГЭ - Новогодние блюда, которые подойдут детям и тем, кто на диете
База, ОГЭНажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Урок алгебры по теме «Двойной радикал». 8-й класс
Цели урока:
Учебная:
- Углубить знания учащихся по теме квадратные корни и обобщить учебный материал.
- Познакомить учащихся с понятием двойного радикала.
- Научить преобразовывать двойные радикалы выделением полного квадрата подкоренного выражения.
- Научить учащихся использовать формулу двойного радикала.
- Развивать умения и навыки работы с иррациональными выражениями.
Развивающая:
- Развитие внимания учащихся.
- Развитие умения добиваться результатов труда.
- Развитие интереса к изучению алгебры и навыков самостоятельной работы.
Воспитывающая:
- Воспитание чувства коллективизма.
- Формирование чувства ответственности за результат работы.
- Формирование у учащихся адекватной самооценки при выборе отметки за работу на уроке.
Оборудование: компьютер, проектор.
1 этап работы. Организационный момент.2 этап работы. Мотивация и выход на постановку проблемыДо восьмого класса мы осуществляли над числами пять арифметических действий: сложение, вычитание, умножение, деление и возведение в степень, причем при вычислениях, мы активно использовали различные свойства этих операций.
В курсе алгебры восьмого класса была введена новая операция – извлечение квадратного корня из неотрицательного числа. Выражения, содержащие операцию извлечения квадратного корня, называются иррациональными.
В большом толковом словаре можно найти следующее определение иррациональности:
С философской точки зрения иррациональность – недоступность разуму, то, что не может быть постигнуто разумом, что явно не подчиняется законам логики, и не может быть выражено в логических понятиях, что оценивается как «сверхразумное».
С математической точки зрения иррациональность – несоизмеримость с единицей; не является ни целой, ни дробной величиной.
Действительно ли понятие иррациональности – это что-то «уму не постижимое, несоизмеримое, немыслимое»?
На этот вопрос мы постараемся сегодня найти ответ.
3 этап работы. Повторение ранее изученного материала1) Свойства квадратного корня
Чтобы успешно выполнять преобразования выражений, содержащих операцию извлечения квадратного корня, нужно знать свойства этой операции.
Вспомним эти свойства:
1) Квадратный корень из произведения двух неотрицательных чисел равен произведению квадратных корней из этих чисел.
2) Если a≥0, b>0, то справедливо равенство
3) Если a≥0 и n – натуральное число, то
4) При любом a справедливо тождество
Если хорошо знать приёмы преобразования рациональных выражений, приёмы преобразования алгебраических дробей, усвоить определение понятия корня и свойства квадратного корня, уметь вносить множитель под знак квадратного корня, выносить множитель из – под знака квадратного корня, то можно выполнить преобразование любого выражения, содержащего операцию извлечения квадратного корня.
2) Способы преобразования радикалов
Кроме перечисленных теорем при преобразовании радикалов применяются некоторые специальные приёмы, тоже вытекающие из этих теорем, но требующие некоторого навыка.
Первый называется уничтожением иррациональности в знаменателе дроби. Если в знаменателе дроби имеется корень или несколько корней, то обращаться с такой дробью не совсем удобно. Смысл этого приёма заключается в том, что надо подобрать такой множитель, чтобы его произведение на знаменатель не содержало корней.
Второе интересное преобразование радикалов называется преобразованием двойного радикала .
4 этап работы. Ввести понятие двойного радикала и доказатьформулу сложного радикала.Выражения вида и называют двойными радикалами или сложными радикалами. Преобразовать двойной радикалэто значит избавиться от внешнего радикала.
Справедливы тождества
=
При каждое подкоренное выражение неотрицательно.
Докажем эти равенства(доказывает ученик):
Для этого возведём в квадрат обе части данных выражений, воспользовавшись при этом формулой квадрата суммы (разности) двух чисел и формулой разности квадратов.
Возведем в квадрат левую часть:
=
Возведем в квадрат правую часть:
= ∙ = = = = = = =
Заметим, что доказанное тождество позволяет существенно облегчить вычисления и преобразования, если выражение представляет полный квадрат.
5 этап работы. Рассмотрим способы преобразования двойного радикала.1 способ:
Можно выполнить алгебраические действия в некотором выражении, содержащем двойные радикалы.
Примеры:
= = = = = =
= = = = = =
= = = = = =
2 способ
Можно привести подкоренное выражение к полному квадрату.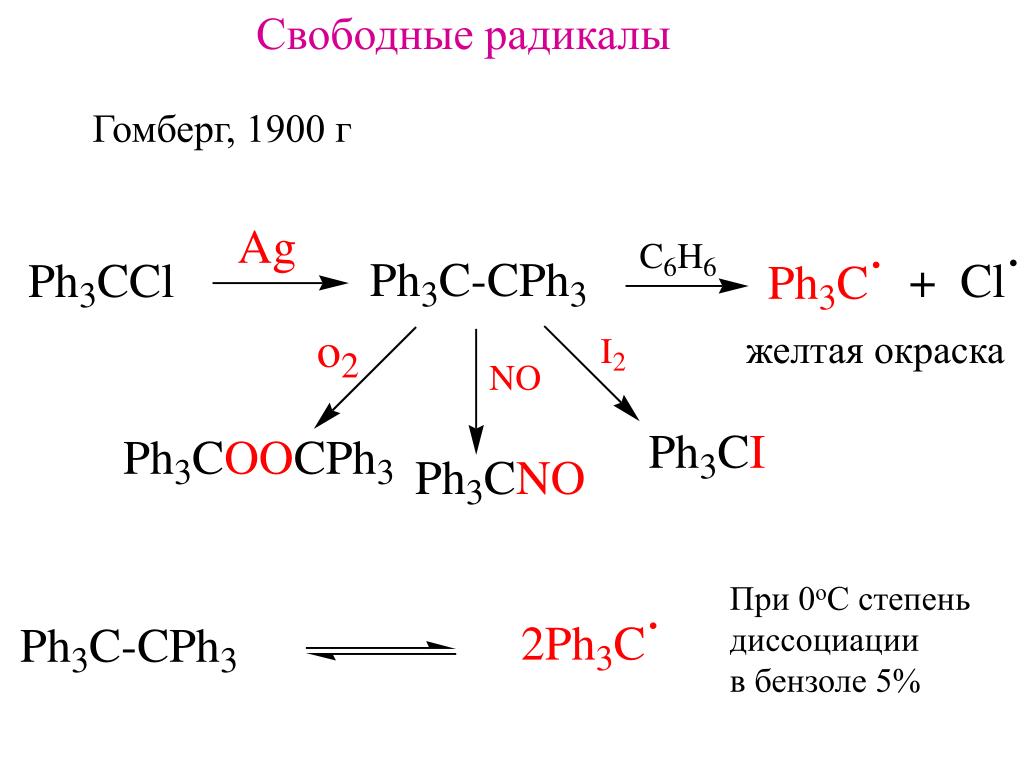
Примеры:
- = = = = =
- = = = = =
Таким образом, если подкоренное выражение представить в виде полного квадрата, то можно легко освободиться от внешнего радикала.
Попробуем решить
НЕ УДАЕТСЯ!!!
3 способ
В тех случаях, когда подкоренное выражение нелегко представить в виде полного квадрата, то можно использовать готовую формулу сложного радикала
=
Примеры:
- = = = = = = =
- = = = = = =
- = = = = = =
Закрепление изученного материала.Преобразуйте выражения, содержащие двойные радикалы:
Преобразовать двойные радикалы можно следующим образом:
- выполняя в выражении, содержащем двойные радикалы, алгебраические действия, применив свойства квадратных корней;
- приводя подкоренное выражение к полному квадрату;
- используя формулы сложного радикала.
Дома вы преобразуете двойные радикалы разными способами (раздать листы с заданиями).
Урок окончен. Спасибо за урок!
Иррациональность дроби — как правильно избавиться от знака корня в знаменателе? » Kupuk.net
Выполняя преобразование выражений с радикалами, важно знать, как заменить дробь или как избавиться от иррациональности в знаменателе.
Математическое правило, которое предполагает освобождение от радикала, основано на действиях с сопряженными выражениями. Для правильного выполнения действий с иррациональными дробями следует знать понятие рационального числа.
Определение иррациональности
Часто в задачах по математике можно встретить примеры, которые содержат иррациональность. Если условие направлено на избавление от нее, значит, нужно выполнить математические действия с рациональными числами. Иррациональны дроби, нижняя часть которых содержит подкоренное выражение.
Присутствие квадратного корня в математическом примере следует исключить, согласно правилу, требующему преобразования в рациональное число радикала. В результате действий он будет в числителе. Преобразованный пример, содержащий иррациональность, не теряет своего исходного значения.
Правила избавления от радикала
Придерживаясь общего правила замены подкоренной части тождественно равным выражением, можно освободиться от иррациональности в знаменателе дроби.
Достаточно выполнить несложное действие умножения дроби на выражение, которое содержит знак радикала и сопряжено с нижней частью. Полученная в результате дробь не должна содержать подкоренной части.
Общее правило позволяет извлечь из знаменателя квадратный корень. Аналогично можно решать примеры, вычисляя радикал любой степени. Облегчить задачу поможет специальный онлайн-калькулятор. Рациональное число достаточно представить в виде произведения АВ, если это значение не имеет знака радикала. При этом А и В сопряжены между собой.
Например, чтобы представить корень кубический из дроби с числами 1 и 3 в верхней и нижней части, нужно выполнить следующие действия:
Для решения подобных примеров иногда нужно домножить 2 члена дробного выражения на разность между корнями, когда делитель представлен в виде суммы.
Если он выражен как разность составляющих, то следует умножить дробь на радикал из суммы аналогичных чисел. В примерах, которые содержат радикалы, имеющие различные показатели, вначале избавляются от одного корня, а затем от другого.
Использование средств преобразования
Способ приведения иррационального примера к рациональному виду зависит от нижней части с радикалом. Он может включать несколько подкоренных выражений. Если решение алгебраической задачи требует уничтожить иррациональность, тогда нужно освободить выражение от иррациональности в знаменателе. Используемый способ зависит от вида выражения, представляющего собой дробь, нижняя часть которой имеет:
- сумму или разницу квадратных корней;
- радикал 2-й степени;
- разницу либо сумму радикалов 3-й степени;
- иррациональное значение в виде корня n-й степени.
В последнем случае необходимо для избавления знаменателя дроби от иррациональности подобрать множитель, позволяющий извлечь целый корень. Подкоренное выражение, представленное как число в k-й степени, нужно привести к рациональному виду. Учитывая, что n>k, число под корнем возводят в степень n-k. При этом обе дробные части умножают на сопряженное выражение.
Пользуясь правилом преобразования выражений с радикалом, следует помнить о том, что нужно обязательно получить рациональное число. Приводить к таком виду можно разные примеры с корнями. Искомое число дают 2 корня, взятые в виде суммы и разности при умножении на сопряженное выражение с противоположным знаком.
Результат можно представить аналогичным способом, если числитель и знаменатель содержат не 2 корня, а сумму или разность числа и радикала. Зная, как избавляться от иррациональности в знаменателе дроби, на его вид нужно обратить внимание в первую очередь. Это позволит правильно упростить выражение и убрать корень.
Более сложные примеры могут потребовать возведения в степень иррационального знаменателя дроби. Замену дроби с иррациональным числителем либо знаменателем производят на тождественное ей дробное выражение. Оно содержит рациональный числитель или знаменатель, а действие является уничтожением иррациональности.
Для избавления знаменателя дроби от подкоренной части применяют формулы сокращенного умножения, или ФСУ. Умножая разность корней на их сумму, можно получить разность квадратов радикалов, которая будет рациональным числом.
Решение радикальных уравнений — алгебра среднего уровня
Корни и радикалы
Цели обучения
К концу этого раздела вы сможете:
- Решать радикальные уравнения
- Решите радикальные уравнения с двумя радикалами
- Используйте радикалы в приложениях
Прежде чем начать, пройдите этот тест на готовность.
- Упрощение:
Если вы пропустили эту проблему, просмотрите (рисунок).
- Решить:
Если вы пропустили эту проблему, просмотрите (рисунок).
- Решить
Если вы пропустили эту проблему, просмотрите (рисунок).
Решение подкоренных уравнений
В этом разделе мы будем решать уравнения, в которых подкоренное выражение содержит переменную. Уравнение такого типа называется радикальным уравнением.
Подкоренное уравнение
Уравнение, в котором переменная стоит под корнем подкоренного выражения, называется радикальное уравнение .
Как обычно, при решении этих уравнений то, что мы делаем с одной частью уравнения, мы должны делать и с другой его частью. Как только мы изолируем радикал, наша стратегия будет состоять в том, чтобы возвести обе части уравнения в степень индекса. Это устранит радикал.
Решение радикального уравнения, содержащего четный индекс, путем возведения обеих частей в степень индекса может привести к алгебраическому решению, которое не будет решением исходного радикального уравнения.
Опять же, мы называем это посторонним решением, как мы это делали, когда решали рациональные уравнения.
В следующем примере мы увидим, как решить радикальное уравнение. Наша стратегия основана на возведении радикала с индексом n в степень n th . Это устранит радикал.
Как решить радикальное уравнение
Решить:
Решить:
Решить:
Решить радикальное уравнение с одним радикалом.
- Изолируйте радикал на одной стороне уравнения.
- Возведите обе части уравнения в степень индекса.
- Решите новое уравнение.
- Проверьте ответ в исходном уравнении.
Когда мы используем радикальный знак, он указывает на главный или положительный корень. Если уравнение имеет радикал с четным индексом, равным отрицательному числу, то это уравнение не будет иметь решения.
Решить:
The resulting equation is square root of the quantity 9 k minus 2 in parentheses plus 1 minus 1 equals 0 minus 1. Simplifying this we get square root of the quantity 9 k minus 2 in parentheses equals negative 1. Since the square root of a real number is always positive there is no solution to the equation.» data-label=»»>Поскольку квадратный корень равен отрицательному числу, уравнение не имеет решения.
Решите:
Решите:
Если одна сторона уравнения с квадратным корнем является двучленом, мы используем шаблон произведения биномиальных квадратов, когда возводим его в квадрат.
Биномиальные квадраты
Не забудьте средний член!
Решить:
Checking the answer p equals 1. Does the square root of the quantity 1 minus 1 in parentheses equal 1? The square root of zero plus 1 equals 1 so p equals 1 is a solution. Checking the answer p equals 2. Does the square root of the quantity 2 minus 1 in parentheses plus 1 equal 2. Since the square root of 1 plus 1 equals 2, p equals 2 is also a solution. The solutions are p equals 1 and p equals 2.» data-label=»»> правильно.
Затем решите новое уравнение.
Решить:
Решить:
Когда индекс радикала равен 3, мы кубируем обе стороны, чтобы удалить радикал.
Решить:
| Чтобы выделить радикал, вычтите 8 с обеих сторон. | |
Куб обеих частей уравнения. | |
| Упрощение. | |
| Решите уравнение. | |
| Проверьте ответ. | |
| Решение |
Решите:
Решите:
Иногда уравнение будет содержать рациональные показатели вместо радикала. Мы используем те же методы для решения уравнения, что и в случае, когда у нас есть радикал.
Возведем каждую часть уравнения в степень знаменателя рационального показателя. Так как у нас, например,
Вспомнить и
Решить:
| Чтобы выделить член с рациональным показателем, вычесть 3 с обеих сторон. | |
| Возведите каждую часть уравнения в четвертую степень. | |
| Упрощение. | |
| Решите уравнение. | |
| Проверьте ответ. | |
| Решение |
Решить:
Решить:
Иногда решение радикального уравнения приводит к двум алгебраическим решениям, но одно из них может быть посторонним решением!
Решить:
The resulting equation is square root of the quantity r plus 4 in parentheses equals r minus 2. Squaring both sides of the equation we get the square of the square root of the quantity r plus 4 in parentheses equals the square of the quantity r minus 2 in parentheses. Simplify using the binomial squares pattern on the right. The simplified equation is r plus 4 equals r squared minus 4 r plus 4. This is a quadratic equation, so get zero on one side. 0 equals r squared minus 5 r. Factor the right side. 0 equals r times the quantity r minus 5 in parentheses. Use the zero procuct property. 0 equals r and 0 equals r minus 5. Solving each equation we get r equals 0 and r equals 5. Checking the answer r equals 0. Does the square root of the quantity 0 plus 4 in parentheses minus 0 plus 2 equal 0? The square root of 4 plus 2 equals 0 so r equals 0 is a solution. Checking the answer r equals 5. Does the square root of the quantity 5 plus 4 in parentheses minus 5 plus 2 equal 0. Since the square root of 9 minus 3 equals 0, r equals 5 is also a solution.
The solutions are r equals 0 and r equals 5.» data-label=»»>одна сторона.
Решите:
Решите:
Когда перед радикалом стоит коэффициент, мы также должны возвести его в степень индекса.
Решить:
Square root of the quantity 3 x minus 5 in parentheses equals 4. Square both sides of the equation. The square of the square root of the quantity 3 x minus 5 in parentheses equals 4 squared. Simplify, then solve the new equation. 3 x minus 5 equals 16. 3 x equals 21. x equals 7. Check the answer x equals 7. Does 3 times the square root of the quantity 3 times 7 minus 5 in parentheses minus 8 equal 4? Simplifying the left side we get 3 times the square root of the quantity 21 minus 5 in parentheses minus 8 which equals 3 times the square root of 16 minus 8 which equals 3 times 4 minus 8 which equals 4. The solution is x equals 7.» data-label=»»>
Решить:
Решить:
Решение радикального уравнения с двумя радикалами
Если радикальное уравнение имеет два радикала, мы начинаем с выделения одного из них.
Часто проще всего сначала выделить более сложный радикал.
В следующем примере при выделении одного радикала также выделяется второй радикал.
Решить:
Решить:
Решить:
Иногда после возведения обеих частей уравнения в степень у нас все еще есть переменная внутри радикала. Когда это происходит, мы повторяем Шаг 1 и Шаг 2 нашей процедуры. Мы изолируем радикал и снова возводим обе части уравнения в степень индекса.
Как решить радикальное уравнение
Решить:
Решить:
Решить:
Здесь мы суммируем шаги. Мы скорректировали наши предыдущие шаги, чтобы включить в уравнение более одного радикала. Теперь эта процедура будет работать для любых радикальных уравнений.
Решите радикальное уравнение.
- Изолируйте один из радикальных членов на одной стороне уравнения.
- Возведите обе части уравнения в степень индекса.
- Есть еще радикалы?
Если да, повторите Шаг 1 и Шаг 2 еще раз.
Если нет, решите новое уравнение.
- Проверьте ответ в исходном уравнении.
Будьте осторожны при возведении в квадрат биномов в следующем примере. Запомните шаблон или
Решите:
Remember to square both the 6 and the square root of the quantity q minus 2. When squaring the right side use the formula the quantity a minus b in parentheses squared equals a squared minus 2 a b plus b squared. The resulting equation is 6 squared times the square of the square root of the quantity q minus 2 in parentheses equals the quantity 3 q in parentheses squared minus 2 times 3 q times 6 plus 6 squared. Simplifying we get 36 times the quantity q minus 2 in parentheses equals 9 q squared minus 36 q plus 36. Distributing we get 36 q minus 72 equals 9 q squared minus 36 q plus 36. It is a quadratic equation, so get zero on one side. 0 equals 9 q squared minus 72 q plus 108. Factor the right side to get 0 equals 9 times the quantity q minus 6 in parentheses times the quantity q minus 2 in parentheses. Use the zero product property to get the equations q minus 6 equals 0 and q minus 2 equals 0. Solving eah equation we get q equals 6 and q equals 2. The checks are left to you. The solutions are q equals 6 and q equals 2.
» data-label=»»>с обеих сторон.
мы должны повторить предыдущие шаги. Изолировать
радикал.
разделите обе части на 6. Не забудьте
квадратных и 6 и
одна сторона.
Решить:
Решить:
Использование радикалов в приложениях
По мере прохождения курсов в колледже вы столкнетесь с формулами, включающими радикалы, во многих дисциплинах.
Мы немного изменим нашу стратегию решения задач для приложений геометрии, чтобы получить план решения приложений с формулами из любой дисциплины.
Используйте стратегию решения проблем для приложений с формулами.
- Прочтите задачу и убедитесь, что все слова и идеи понятны. При необходимости нарисуйте рисунок и подпишите его с помощью данной информации.
- Определите , что мы ищем.
- Назовите то, что мы ищем, выбрав переменную для ее представления.
- Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените предоставленную информацию.
- Решите уравнение , используя хорошие методы алгебры.
- Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.
Одно из применений радикалов связано с влиянием гравитации на падающие предметы. Формула позволяет определить, через какое время упавший предмет ударится о землю.
Падающие предметы
На Земле, если предмет падает с высоты ч футов, время в секундах, необходимое для достижения земли, находится по формуле
. Например, если объект падает с высоты 64 фута, мы можем найти время, необходимое для достижения земли путем подстановки в формулу.
Извлеките квадратный корень из 64. | |
| Упростите дробь. |
Объекту, упавшему с высоты 64 фута, потребуется 2 секунды, чтобы достичь земли.
Марисса уронила солнцезащитные очки с моста на высоте 400 футов над рекой. Используйте формулу, чтобы найти, сколько секунд потребовалось солнцезащитным очкам, чтобы достичь реки.
So t equals 20 divided by 4. So t equals 5. Step 6 is to check the answer in the problem and make sure it makes sense. Does 5 equal the square root of 400 divided 4. Since 5 equals 20 divided by 4, the answer is a solution to the equation. Does 5 seconds seem like a reasonable length of time? Yes. Step 7 is to answer the question. It will take 5 seconds for the sunglasses to reach the river.» data-label=»»>, чтобы добраться до реки
соответствующая формула. Заменить в заданном
информация.
уверен, что это имеет смысл.
время?
Ответьте на вопрос.солнечные очки, чтобы добраться до реки.
Вертолет сбросил спасательный пакет с высоты 1296 футов. Используйте формулу, чтобы найти, сколько секунд потребовалось пакету, чтобы достичь земли.
9 секунд
Мойщик окон уронил швабру с платформы на высоте 196 футов над тротуаром Используйте формулу, чтобы найти, сколько секунд потребовалось швабре, чтобы добраться до тротуара.
секунды
Полицейские, расследующие автомобильные аварии, измеряют длину следов заноса на тротуаре. Затем они используют квадратный корень, чтобы определить скорость в милях в час, которую двигала машина перед тем, как затормозить.
Следы заноса и скорость автомобиля
Если длина следов заноса составляет d футов, то скорость s автомобиля до включения тормозов можно найти по формуле
После автомобильной аварии следы заноса для одного автомобиля измеряется 190 футов.
Используйте формулу, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.
The car was traveling approximately 67.5 mph before the brakes were applied.» data-label=»»>соответствующую формулу. Замена в
данная информация.
Решите уравнение. было 67,5 миль в час.
Следователь ДТП измерил следы заноса автомобиля. Длина следов заноса составляла 76 футов. Используйте формулу, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.
фута
Длина следов заноса автомобиля, попавшего в аварию, составляла 122 фута. Используйте формулу, чтобы найти скорость автомобиля до включения тормозов.
Округлите ответ до десятых.
фута
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения радикальных уравнений.
- Решение уравнения с одним радикалом
- Решение уравнений с радикалами и рациональными показателями
- Решение радикальных уравнений
- Решение радикальных уравнений
- Приложение для расчета радикальных уравнений
Ключевые понятия
Практика ведет к совершенству
Решение радикальных уравнений
В следующих упражнениях решите.
no solution
no solution
Решите радикальные уравнения с двумя радикалами
В следующих упражнениях решите.
Использование радикалов в приложениях
В следующих упражнениях решите. Округление до одного десятичного знака.
Ландшафтный дизайн Рид хочет иметь квадратный садовый участок на заднем дворе. У него достаточно компоста, чтобы покрыть площадь в 75 квадратных футов. Используйте формулу, чтобы найти длину каждой стороны его сада. Округлите ответ до ближайшей десятой доли фута.
футов
Ландшафтный дизайн Винс хочет сделать квадратный внутренний дворик в своем дворе. У него достаточно бетона, чтобы замостить площадь в 130 квадратных футов.
Используйте формулу, чтобы найти длину каждой стороны его внутреннего дворика. Округлите ответ до ближайшей десятой доли фута.
Гравитация Дельтапланер сбросил свой мобильный телефон с высоты 350 футов. Используйте формулу, чтобы найти, сколько секунд потребовалось, чтобы сотовый телефон коснулся земли.
секунды
Гравитация Строитель уронил молот во время строительства надземной части Гранд-Каньона на высоте 4000 футов над рекой Колорадо. Используйте формулу, чтобы найти, сколько секунд потребовалось молоту, чтобы достичь реки.
Расследование несчастного случая Длина следов заноса автомобиля, попавшего в аварию, составляет 216 футов. Используйте формулу, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.
72 фута
Расследование происшествий Исследователь происшествий измерил следы заноса одного из транспортных средств, попавших в аварию.
Длина следов заноса составляла 175 футов. Используйте формулу, чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.
Письменные упражнения
Объясните, почему уравнение вида не имеет решения.
Ответы будут разными.
ⓐ Решить уравнение
ⓑ Объясните, почему одно из найденных «решений» на самом деле не было решением уравнения.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ Изучив этот контрольный список, что вы сделаете, чтобы быть уверенным в достижении всех целей?
Глоссарий
- радикальное уравнение
- Уравнение, в котором переменная стоит под корнем подкоренного выражения, называется подкоренным уравнением.
Решение радикальных уравнений — ChiliMath
Поиск Чтобы научиться решать радикальные уравнения, требуется много практики и знакомство с различными типами задач.
В этом уроке цель состоит в том, чтобы показать вам подробные проработанные решения некоторых задач с разным уровнем сложности.
Что такое радикальное уравнение?
Уравнение, в котором переменная содержится внутри подкоренного символа или имеет рациональный показатель степени. В частности, мы будем иметь дело с квадратным корнем, который является следствием наличия показателя степени \Large{1 \over 2}.
Ключевые шаги:
1) Выделение подкоренного символа в одной части уравнения
2) Возведение в квадрат обеих частей уравнения для исключения подкоренного символа
3) Решение уравнения, которое получается после процесса возведения в квадрат
4) Сверьте свои ответы с исходным уравнением , чтобы избежать посторонних значений
Примеры решения радикальных уравнений
Пример 1 : Решите радикальное уравнение
Радикал сам по себе с одной стороны, так что все в порядке возвести в квадрат обе части уравнений, чтобы избавиться от радикального символа.
Затем выполните обычные действия по решению линейных уравнений.
Вы должны ВСЕГДА проверять свои ответы, чтобы убедиться, что они «действительно» являются решением. Некоторые ответы из ваших расчетов могут быть посторонними. Подставьте x = 16 обратно в исходное радикальное уравнение, чтобы увидеть, дает ли оно верное утверждение.
Да, проверяет, так что x = 16 — это решение.
Пример 2 : Решение радикального уравнения
Схема выглядит хорошо, потому что радикал снова изолирован с одной стороны. Так что я могу возвести в квадрат обе стороны, чтобы исключить этот символ квадратного корня. Будьте осторожны с правой частью при возведении в квадрат бинома (x−1). Вы должны правильно применять метод FOIL.
Переносим все члены в правую часть уравнения, а затем продолжаем выносить трехчлен на множители. Применяя свойство нулевого произведения, мы получаем значения x = 1 и x = 3 .
Внимание! Всегда проверяйте расчетные значения из исходного радикального уравнения, чтобы убедиться, что они являются верными ответами, а не посторонними или «ложными» ответами.
Выглядит хорошо для обоих наших найденных значений x после проверки, поэтому наши решения равны х = 1 и х = 3 .
Пример 3 : Решить подкоренное уравнение
Нам нужно признать, что подкоренной символ еще не изолирован с левой стороны. Это означает, что мы должны избавиться от этого -1 , прежде чем возводить в квадрат обе части уравнения. Простой шаг добавления обеих сторон на 1 должен решить эту проблему. После этого «новое» уравнение похоже на те, которые мы рассмотрели до сих пор.
Возможные решения: х = -2 и х = 5 . Обратите внимание, что я использую слово «возможный», потому что оно не является окончательным, пока мы не выполним процесс проверки наших значений по сравнению с исходным радикальным уравнением.
Так как мы приходим к ложному утверждению , когда x = -2, поэтому это значение x считается посторонним , поэтому мы игнорируем его! Остается один верный ответ: x = 5 .
Пример 4 : Решение радикального уравнения
Левая сторона выглядит немного беспорядочно, потому что там два радикальных символа. Но это не так уж и плохо! Всегда помните ключевые шаги, предложенные выше. Поскольку оба квадратных корня находятся на одной стороне, это означает, что он определенно готов для возведения в квадрат всего радикального уравнения.
Итак, для нашего первого шага возведем в квадрат обе стороны и посмотрим, что получится.
Для задач такого типа совершенно нормально видеть еще один радикальный символ после первого применения возведения в квадрат. Из этого следует хорошая новость: остался только один. С этого момента попытайтесь снова изолировать единственный радикал на левой стороне, что должно заставить нас переместить остальные на противоположную сторону.
Как видите, это упрощенное радикальное уравнение определенно знакомо . Приступайте к обычному способу решения и убедитесь, что вы всегда сверяете решенные значения x с исходным радикальным уравнением.
Я предоставляю вам проверить, действительно ли x = 4 является решением.
Пример 5 : Решение радикального уравнения
Эта задача очень похожа на пример 4. Единственное отличие состоит в том, что на этот раз оба радикала имеют биномиальные выражения. Подход также заключается в том, чтобы возвести в квадрат обе стороны, поскольку радикалы находятся на одной стороне, и упростить. Но нам нужно выполнить второе применение возведения в квадрат, чтобы полностью избавиться от символа квадратного корня.
Решение x = 2 . Вы можете проверить это, подставив значение обратно в исходное радикальное уравнение и убедиться, что оно дает верное утверждение.
Пример 6 : Решите радикальное уравнение
Похоже, что наш первый шаг — возвести в квадрат обе стороны и посмотреть, что получится потом.
Не забывайте комбинировать одинаковые члены каждый раз, когда возводите стороны в квадрат. Если случится так, что после первого применения процесса возведения в квадрат сгенерируется еще один подкоренной символ, то имеет смысл сделать это еще раз. Помните, наша цель — избавиться от радикальных символов, чтобы освободить переменную, которую мы пытаемся решить или изолировать.
Что ж, похоже, нам нужно снова возвести в квадрат обе стороны из-за нового сгенерированного радикала. Но прежде чем сделать это, мы должны изолировать радикал с одной стороны уравнения. Я оставлю квадратный корень слева, и это заставит меня сдвинуть все вправо.
Пока выглядит хорошо! Теперь пришло время снова свести обе стороны в квадрат, чтобы окончательно устранить радикал.
Будьте осторожны при возведении в квадрат левой части уравнения. Вы также должны возвести в квадрат , что −2 слева от радикала.
Теперь у нас есть квадратное уравнение в стандартной форме. Лучший способ найти x — использовать квадратичную формулу, где a = 7, b = 8 и c = −44.
Таким образом, возможные решения: x = 2 и x = {{ — 22} \over 7}.
Я оставлю вам проверить эти два значения «x» обратно в исходное радикальное уравнение. Я надеюсь, вы согласны с тем, что x = 2 — это единственное решение , а другое значение — постороннее решение, так что не обращайте на него внимания!
Пример 7 : Решение радикального уравнения
Есть два способа решить эту задачу. Я мог бы сразу возвести в квадрат обе стороны, чтобы избавиться от радикалов, или сначала умножить два радикала, а затем возвести в квадрат. Обе процедуры должны приводить к одинаковым ответам при правильном выполнении. Для этого я буду использовать второй подход.
Далее переместите все в левую часть и решите полученное квадратное уравнение. Вы можете использовать квадратичную формулу для ее решения, но, поскольку ее легко вычислить, я просто вынесу ее за скобки.
Возможные решения: x = {{ — 5} \over 2} и x = 3 .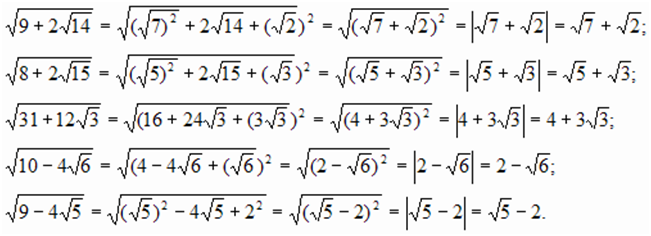
Я оставлю вам проверить ответы. Единственным ответом должно быть x = 3, что делает другой ответ лишним.
Вас также могут заинтересовать:
Упрощение подкоренных выражений
Сложение и вычитание подкоренных выражений
Умножение подкоренных выражений
Рационализация знаменателя
Алгебра — Уравнения с радикалами
Онлайн-заметки Пола
Главная
/
Алгебра
/
Решение уравнений и неравенств
/ Уравнения с радикалами
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-10: Уравнения с радикалами
Название этого раздела может ввести в заблуждение. Название, кажется, подразумевает, что мы будем рассматривать уравнения, в которых есть радикалы. Однако мы собираемся ограничиться уравнениями с квадратными корнями. Методы, которые мы собираемся применить здесь, можно использовать для решения уравнений с другими радикалами, однако работа обычно значительно сложнее, чем при работе с квадратными корнями. Поэтому в этом разделе мы будем работать только с квадратными корнями.
Прежде чем продолжить, следует также упомянуть, что в некоторых учебниках по алгебре вы найдете этот раздел с уравнениями, приводимыми к квадратичной форме.
Причина в том, что в большинстве случаев мы на самом деле приходим к решению квадратного уравнения. Однако подход существенно отличается, поэтому в этом курсе мы разделим две темы на разные разделы.
Обычно лучше всего посмотреть, как они работают, на примере.
Пример 1 Решить \(x = \sqrt {x + 6} \).
Показать решение
В этом уравнении основной проблемой является квадратный корень. Если бы этого не было, мы могли бы решить проблему. Весь процесс, который мы собираемся пройти здесь, настроен на устранение квадратного корня. Однако, как мы увидим, шаги, которые мы собираемся предпринять, на самом деле могут вызвать у нас проблемы. Итак, давайте посмотрим, как это все работает. 92} — x — 6 & = 0\\ \left( {x — 3} \right)\left( {x + 2} \right) & = 0\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0,25 дюйма}\hspace{0,25 дюйма}x = 3,\,\,\,x = — 2\end{align*}\]
После возведения в квадрат обеих частей мы видим, что мы получаем факторизуемое квадратное уравнение, которое дает нам два решения \(x = 3\) и \(x = — 2\).
Теперь, без всякой видимой причины, давайте сделаем то, чего мы фактически не делали со времен раздела о решении линейных уравнений. Давайте проверим наши ответы. Помните также, что нам нужно проверить ответы в исходном уравнении! Это очень важно. 9? \sqrt { — 2 + 6} \\ — 2 & \ne \sqrt 4 = 2\hspace{0,25 дюйма}\hspace{0,25 дюйма}{\mbox{НЕ ОК}}\end{align*}\]
У нас проблема. Напомним, что квадратные корни ВСЕГДА положительны, поэтому \(x = — 2\) не работает в исходном уравнении. Одна из возможностей здесь заключается в том, что мы где-то допустили ошибку. Однако мы можем вернуться и посмотреть, и мы быстро увидим, что не ошиблись.
Итак, в чем дело? Помните, что нашим первым шагом в процессе решения было возведение обеих сторон в квадрат. Заметьте, что если мы подставим \(x = — 2\) в квадратное уравнение, которое мы решили, оно на самом деле будет его решением. Когда мы возвели в квадрат обе части уравнения, мы фактически изменили уравнение и в процессе ввели решение, которое не является решением исходного уравнения.
При таких проблемах жизненно важно проверить свои решения, так как это часто случается. В этом случае мы берем только те значения, которые являются фактическими решениями исходного уравнения.
Итак, исходное уравнение имело единственное решение \(x = 3\).
Теперь, как показал этот пример, мы должны быть очень осторожны при решении этих уравнений. Когда мы решим квадратное уравнение, мы получим два решения, и возможно, что оба из них, одно из этих или ни одно из этих значений не являются решениями исходного уравнения. Единственный способ узнать это проверить свои решения!
Давайте поработаем еще с парой примеров, которые немного сложнее.
Пример 2. Решите каждое из следующих уравнений.
- \(у + \sqrt {у — 4} = 4\)
- \(1 = t + \sqrt {2t — 3} \)
- \(\sqrt {5z + 6} — 2 = z\)
Показать все решения Скрыть все решения
a \(y + \sqrt {y — 4} = 4\) Показать решение
В этом случае давайте заметим, что если мы просто возведем в квадрат обе стороны, у нас возникнут проблемы.
92}\]
с \(a = y\) и \(b = \sqrt {y — 4} \). Вы должны быть в состоянии сделать это, потому что, хотя это, возможно, не сработало здесь, нам понадобится такая работа в следующем наборе задач.
В чем проблема? Хорошо помните, что смысл возведения в квадрат обеих сторон в первой задаче заключался в том, чтобы исключить квадратный корень. Мы этого не сделали. В задаче по-прежнему есть квадратный корень, и мы сделали оставшуюся часть задачи еще более беспорядочной. 92} — 9y + 20\\ 0 & = \left( {y — 5} \right)\left( {y — 4} \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}y = 4 ,\,\,\,y = 5\end{align*}\]
Как и в первом примере, нам нужно убедиться и проверить оба этих решения. Опять же, убедитесь, что вы проверили исходное уравнение. Как только мы возведем в квадрат обе стороны, мы изменим задачу, и поэтому проверка здесь не принесет нам никакой пользы. На самом деле проверка там вполне может привести нас к неприятностям.
9? 4\\ 6 & \ne 4\hspace{0,25 дюйма}{\mbox{НЕ}}{\mbox{OK}}\end{align*}\] Итак, как и в первом примере, который мы рассмотрели, на самом деле существует единственное решение исходного уравнения \(y = 4\).
2} — z — 2\\ & 0 = \left( {z — 2 } \right)\left( {z + 1} \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,\,\,z = — 1,\,\,\, \,z = 2\конец{выравнивание*}\]
9? 2\\ 4 — 2 & = 2\hspace{0,25 дюйма}{\mbox{OK}}\end{align*}\]
Это тоже было решением.
Итак, в данном случае мы увидели пример, в котором оба возможных решения на самом деле также являются решениями исходного уравнения.
Итак, как мы видели в предыдущем наборе примеров, как только мы получим список возможных решений, от ни одного до всех, они могут быть решениями исходного уравнения. Не забывайте проверять свои ответы!
Хорошо, давайте поработаем над еще одним набором примеров, которые имеют дополнительную сложность. До сих пор все уравнения, которые мы рассматривали, содержали один квадратный корень. Однако в этих уравнениях может быть более одного квадратного корня. Следующий набор примеров предназначен для того, чтобы показать нам, как справляться с подобными проблемами.
Пример 3. Решите каждое из следующих уравнений.
- \(\sqrt {2x — 1} — \sqrt {x — 4} = 2\)
- \(\sqrt {t + 7} + 2 = \sqrt {3 — t} \)
Показать все решения Скрыть все решения
Показать обсуждение
В обоих из них есть два квадратных корня в задаче. Однако мы будем работать с ними в основном таким же образом. Первый шаг состоит в том, чтобы получить один из квадратных корней в одной части уравнения, а затем возвести в квадрат обе части. На этом этапе процесс отличается, поэтому мы увидим, как двигаться дальше, как только мы достигнем его в первом примере. 92}\\ 2x — 1 & = 4 + 4\sqrt {x — 4} + x — 4\\ 2x — 1 & = 4\sqrt {x — 4} + x\end{align*}\]
Итак, у нас все еще есть квадратный корень в задаче, но нам удалось исключить один из них. Не только это, но и то, что у нас осталось, идентично примерам, с которыми мы работали в первой части этого раздела.