Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||
| ||||||||||||
2-x-6=0
| ||||||||||||
10.13
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Помогите решить задачу 3 класса.
Вычисли и запиши ответ.Если разложить яблоки в ящики по 6 кг. в каждый,то потребуется 6 ящиков.Сколько ящиков по 9 кг потребуется для тех же яблок?Большое спасибо!
в 2 торговых центрах 270 магазинов.На каждом этаже из одинаковое количество.но в первом торговом центре на 3 этажа больше.Сколько магазинов на этаже?Сколько магазинов в каждом торговом центре?
Задача
длина беговой дорожки вокруг стадиона…
Задайте с помощью знаков модуля множество точек координатной оси:
Пользуйтесь нашим приложением
Also Read:
Derivative of root x
Integration of root(x )
Производная x root(x)
Распространяйте любовь
Вопрос Видео: Нахождение среднего значения корневой функции на заданном интервале
Стенограмма видео
Найдите среднее значение функции 𝑓 из 𝑥, равное квадратному корню из двух 𝑥 на замкнутом интервале от нуля до двух.
Вопрос дает нам функцию 𝑓 от 𝑥, которая является корнем два 𝑥. И хочет, чтобы мы нашли среднее значение этой функции на отрезке от нуля до двух. Начнем с того, что вспомним, что мы подразумеваем под средним значением функции на замкнутом интервале. Если функция 𝑓 непрерывна на отрезке от 𝑎 до 𝑏, то среднее значение этой функции на этом отрезке, 𝑓 среднее, равно единице, деленной на 𝑏 минус 𝑎, умноженный на интеграл от 𝑎 до 𝑏 от 𝑓 от 𝑥 по отношению к 𝑥. В нашем случае мы хотим, чтобы среднее значение функции 𝑓 из 𝑥 было равно корню два 𝑥 на замкнутом интервале от нуля до двух. Итак, мы хотим, чтобы наша функция 𝑓 из 𝑥 была корнем два 𝑥, 𝑎 равна нулю, а 𝑏 равна двум.
Сначала нам нужно проверить, что наша функция 𝑓 непрерывна на этом отрезке. Итак, мы знаем, что 𝑓 из 𝑥 непрерывно на всей своей области определения. Так, в частности, она непрерывна на отрезке от нуля до двух. Таким образом, это говорит нам, что мы можем использовать нашу формулу, чтобы найти среднее значение нашей функции на этом интервале.
𝑓 среднее равно единице, деленной на два минус нуль, умноженной на интеграл от нуля до двух от квадратного корня из двух 𝑥 по отношению к 𝑥. Но мы еще не можем вычислить наше подынтегральное выражение. Поэтому нам нужно переписать его, используя наши законы показателей. Во-первых, квадратный корень из двух 𝑥 равен корню, умноженному на два корня 𝑥. Далее мы перепишем корень 𝑥 как 𝑥 в половинной степени. Это позволит нам использовать правило мощности для интегрирования.
Таким образом, используя это, чтобы переписать наше подынтегральное выражение, мы имеем 𝑓среднее значение равно единице, деленной на два минус ноль, умноженное на интеграл от нуля до двух от корня, умноженный на 𝑥 в степени половины по отношению к 𝑥. И теперь мы можем интегрировать это, используя правило степени для дифференцирования. Напомним, это говорит нам, что для констант 𝑎 и 𝑛, где 𝑛 не равно отрицательной единице, интеграл от 𝑎𝑥 в 𝑛-й степени по 𝑥 равен 𝑎 умноженному на 𝑥 в степени 𝑛 плюс единица деленная на 𝑛 плюс один плюс 𝐶.
Мы добавляем единицу к нашему показателю 𝑥, а затем делим на этот новый показатель. В нашем случае показатель степени 𝑥 равен половине.
Теперь мы готовы упростить это выражение. Во-первых, мы упростим один на два минус ноль, чтобы получить половину. Далее мы оценим наш определенный интеграл, используя правило степени для интегрирования, где наше значение 𝑎 равно корню из двух, а наше значение 𝑛 равно половине. Таким образом, мы показали, что 𝑓среднее значение равно половине, умноженной на корень, умноженный на два, умноженный на 𝑥 в степени половина плюс один, деленный на половину плюс один, оцененный в пределах нашего интеграла, нуля и двух. И мы можем немного упростить это выражение, так как половина плюс один равно трем больше двух.
Теперь мы готовы найти значение 𝑓 в среднем. Нам просто нужно оценить это в пределах нашего интеграла. Вычисляя это в пределах нашего интеграла, мы получаем половину, умноженную на корень два раза два в степени три над двумя, деленную на три над двумя минус корень два раза ноль в степени три над двумя, деленное на три над двумя.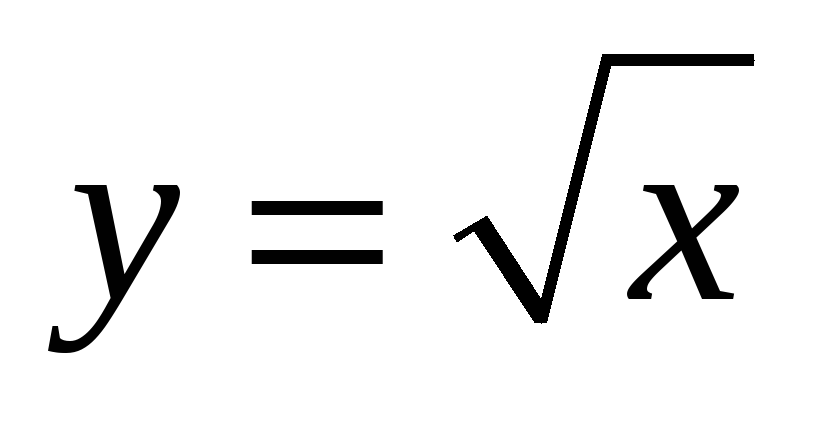
Итак, мы упростили наше выражение, чтобы показать, что 𝑓 среднее равно корню, умноженному на два в степени трех на два, деленной на три. И мы могли бы оставить наш ответ так. Однако мы упростим это дальше. По нашим законам показателей, два в степени трех над двумя равно двум в степени половины всего в кубе. Но тогда два в степени половины — это квадратный корень из двух. Таким образом, мы можем заменить два в степени трех над двумя в нашем числителе на квадратный корень из двух, возведенный в куб. Делая это, мы можем видеть, что наш числитель теперь равен корню, умноженному на два корня, умноженному на два в кубе. Итак, наш числитель — это корень два, умноженный на себя четыре раза. Это равно четырем. И это дает нам окончательный ответ.