Интегрирование по частям. Вторая часть.
Высшая математика » Неопределённые интегралы » Интегрирование по частям » Вторая часть.
Первая часть
Вторая часть
В этой части мы продолжим тему интегрирования по частям в неопределённом интеграле, начатую здесь. Вновь нам будут нужны таблица неопределенных интегралов и таблица производных. Перед прочтением данной страницы рекомендую ознакомиться с предыдущей частью, ибо там были даны полные пояснения к каждому примеру. Здесь же будут затронуты интегралы, которые не подпадают под стандартные правила, указаные в первой части, но, тем не менее, берутся с помощью интегрирования по частям. Мы будем использовать ту же формулу, что и ранее:
$$ \begin{equation} \int u \; dv=u\cdot v-\int v\; du \end{equation} $$
Также рассмотрим интегралы, при вычислении которых получается уравнение относительно исходного интеграла.
Пример №7
Найти $\int\cos\ln x\;dx$.
Решение
Метод решения данного примера аналогичен применённому в предыдущем примере №6:
$$ \int\cos\ln x\;dx=\left | \begin{aligned} & u=\cos\ln x; \; du=-\frac{\sin\ln x}{x}dx.\\ & dv=dx; \; v=x. \end{aligned} \right| =x\cdot \cos\ln x+\int x\cdot\frac{\sin\ln x}{x}dx=\\ =x\cdot \cos\ln x+\int \sin\ln x dx=\left | \begin{aligned} & u=\sin\ln x; \; du=\frac{\cos\ln x}{x}dx.\\ & dv=dx; \; v=x. \end{aligned} \right|=\\ =x\cdot \cos\ln x+x\cdot\sin\ln x-\int x\cdot\frac{\cos\ln{x}}{x}dx =x\cdot \cos\ln x+x\cdot\sin\ln x-\int \cos\ln x \;dx $$
Итак, мы получили уравнение с искомым интегралом:
$$ \int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x-\int \cos\ln x \;dx $$
Перенося $\int \cos\ln x \;dx$ из правой части в левую, будем иметь:
$$
2\int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x+2C.
$$
Деля обе части последнего равенства на $2$, получим:
$$ \int\cos\ln x\;dx=\frac{1}{2}x\cdot \cos\ln x+\frac{1}{2}x\cdot\sin\ln x+C=\frac{x}{2}\cdot (\cos\ln x+\sin\ln x)+C. $$
Ответ: $\int\cos\ln x\;dx=\frac{x}{2}\cdot (\cos\ln x+\sin\ln x)+C$.
Полагаю, что у читателя тут не обойдётся без вопроса, который я изложу ниже.
Вопрос №1
Постойте, тут что-то не сходится. Откуда вообще взялась константа $C$? У нас было равенство
$$ \int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x-\int \cos\ln x \;dx. $$
Если перенести $\int \cos\ln x \;dx$ в левую часть, то никакой константы не возникнет, а будет вот что:
$$ 2\int\cos\ln x\;dx=x\cdot \cos\ln x+x\cdot\sin\ln x. $$
Тут вообще нет константы! Как же она возникла в изложенном выше решении?
Ответ
Для того, чтобы разобраться с «внезапно возникшей» контантой, нужно вспомнить, что такое неопределённый интеграл.
3{x}}+\frac{3\tg{x}}{8\cos{x}}+\frac{3}{8}\ln\left|\tg\left(\frac{\pi}{4}+\frac{x}{2}\right)\right|+C
$$
Ответ:
Первая часть
Вторая часть
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | интеграл от cos(2x) относительно x | ||
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Интеграл от 2sinx — формула, доказательство, примеры
Интеграл от 2sinx равен -2cosx + C.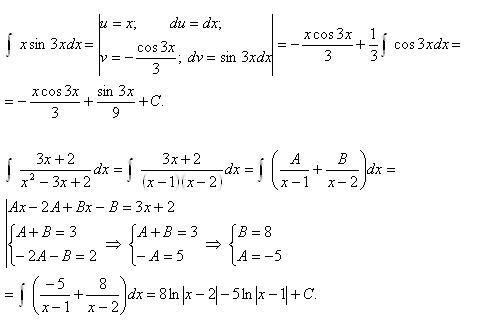
В этой статье мы вычислим интеграл от 2sinx и выведем его формулу. Мы также оценим определенную интеграцию 2sinx с различными ограничениями и рассмотрим несколько решенных примеров, основанных на аналогичной концепции, для лучшего понимания.
| 1. | Что такое интеграл от 2sinx? |
| 2. | Интеграл 2sinx Formula |
| 3. | Определенная интеграция 2sinx |
| 4. | Часто задаваемые вопросы по интегралу 2sinx |
Что такое интеграл от 2sinx?
Интеграл от 2sinx можно вычислить, используя формулу для интеграла от sinx, которая определяется как ∫sin x dx = -cos x + C, где C — постоянная интегрирования.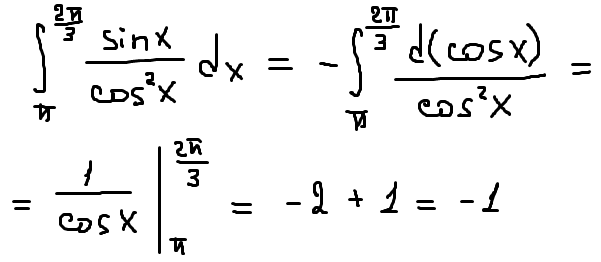
Теперь, чтобы найти интегрирование 2sinx, мы используем эту формулу и математически запишем интеграл от 2sinx как ∫2sinx dx = -2cosx + C, где C — константа интегрирования. Давайте теперь рассмотрим формулу для того же самого в следующем разделе.
Интеграл формулы 2sinx
Поскольку мы знаем, что ∫sin x dx = -cos x + C, поэтому формула для интеграла от 2sinx записывается как ∫2sinx dx = -2cosx + C, где символ ∫ обозначает интегрирование 2sinx, dx обозначает, что переменная — это x, а C — постоянная интегрирования. На изображении ниже показан интеграл формулы 2sinx:
Интеграл от 2sinx Доказательство
Теперь, когда мы знаем, что интеграл от 2sinx равен -2cosx + C, далее в этом разделе мы докажем этот результат, используя различные формулы интегрирования. Мы будем использовать следующие первообразные правила и формулы:
- ∫sinxdx = -cosx + C
- ∫kf(x) dx = k ∫f(x) dx
Используя приведенные выше формулы, мы имеем
∫2sinx dx = 2 ∫sinx dx
= 2[-cosx + K]
= -2cosx + 2K
= -2cosx + C, где C = 2K постоянная интегрирования.
Следовательно, мы доказали, что интеграл от 2sinx равен -2cosx + C.
Чтобы убедиться, что интегрирование от 2sinx равно -2cosx + C, мы можем взять производную от -2cosx + C. Мы знаем, что производная от cos x равна -sin x, то есть d(cos x)/dx = -sin x и производная постоянной функции равна нулю. Следовательно, имеем d(-2cosx + C)/dx = d(-2cosx)/dx + dC/dx = -2d(cosx)/dx + 0 = -2(-sinx) = 2sinx. Значит проверено. 9{\pi}\\&=(-2\cos\pi+C)-(-2\cos0 + C)\\&=-2\times (-1)+C+2\times1-C\\ &=2+2\\&=4 \end{align}\)
Следовательно, значение определенного интеграла от 2sinx с пределами от 0 до π равно 4.
Важные замечания по интегралу от 2sinx
- Интеграл от 2sinx математически записывается как ∫2sinx dx = -2cosx + C.
- Мы можем найти интегрирование 2sinx, используя интеграл от sinx.
☛ Статьи по теме:
- Интеграция sin4x
- Интеграция sec3x
- Интеграция коричневого квадрата x
Часто задаваемые вопросы по интегралу 2sinx
Что такое интеграл от 2sinx?
Интеграл от 2sinx равен -2cosx + C, где C — постоянная интегрирования.
Этот интеграл можно вычислить, используя формулу для интеграла от sin x.
Какова формула интеграции 2sinx?
Интеграл от 2sinx можно вычислить, используя формулу для интеграла от sinx, которая определяется как ∫2sin x dx = -2cos x + C, где C — постоянная интегрирования.
Как найти интеграл от 2sinx?
Мы можем найти интеграл от 2sinx, используя следующие правила и формулы первообразных:
- ∫sinx dx = -cosx + C
- ∫kf(x) dx = k ∫f(x) dx
Используя приведенные выше формулы, мы получаем, что интеграл от 2sinx равен -2cosx + C, где C является константой интегрирования.
Чему равен неопределенный интеграл от 2sinx по отношению к cosx?
Неопределенный интеграл от 2sinx по cosx определяется как ∫2sinx d(cosx) = ∫2sinx (-sinx) dx = ∫-2sin — sin2x/2) + C = -x + (1/2)sin2x + C. Следовательно, интеграл от 2sinx по cosx равен -x + (1/2)sin2x + C, где C — постоянная интеграции.
Каково значение интеграла от 2sinx от 0 до pi?
Значение определенного интеграла от 2sinx с пределами от 0 до π равно 4.