Статистика хи-квадрата с учетом выборки и дисперсии генеральной совокупности Калькулятор
✖Размер выборки — это общее количество лиц, присутствующих в данной выборке в исследуемой популяции.ⓘ Размер образца [N] | +10% -10% | ||
✖Выборочная дисперсия — это математическое ожидание квадрата отклонения случайной величины, связанной с данной выборкой, от генеральной совокупности.ⓘ Выборочная дисперсия [Vs] | +10% -10% | ||
✖Дисперсия населения — это математическое ожидание квадрата отклонения случайной величины, связанной с данным населением.ⓘ Дисперсия населения [Vσ] | +10% -10% |
|
✖Статистика хи-квадрат — это стандартный параметр, который характеризует выборку из совокупности с использованием стандартного отклонения выборки и стандартного отклонения совокупности. |
⎘ копия |
👎
Формула
сбросить
👍
Статистика хи-квадрата с учетом выборки и дисперсии генеральной совокупности Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Размер образца: 20 —> Конверсия не требуется
Выборочная дисперсия: 12 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
38 —> Конверсия не требуется
< 16 Основные формулы в статистике Калькуляторы
Значение P образца
Идти Значение P образца = (Образец пропорции-Предполагаемая доля населения)/sqrt((Предполагаемая доля населения*(1-Предполагаемая доля населения))/Размер образца)
Размер выборки с учетом значения P
Идти Размер образца = ((Значение P образца^2)*Предполагаемая доля населения*(1-Предполагаемая доля населения))/((Образец пропорции-Предполагаемая доля населения)^2)
т Статистика
Идти т Статистика = (Наблюдаемое среднее значение выборки-Теоретическое среднее значение выборки)/(Стандартное отклонение выборки/sqrt(Размер образца))
t Статистика нормального распределения
Идти t Статистика нормального распределения = (Выборочное среднее-Средняя численность населения)/(Стандартное отклонение выборки/sqrt(Размер образца))
Чи-квадрат Статистика
Идти Чи-квадрат Статистика = ((Размер образца-1)*Стандартное отклонение выборки^2)/(Стандартное отклонение населения^2)
Количество классов с учетом ширины класса
Идти Количество классов = (Самый большой элемент в данных-Наименьший элемент данных)/Ширина класса данных
Ширина класса данных
Идти Ширина класса данных = (Самый большой элемент в данных-Наименьший элемент данных)/Количество классов
Статистика хи-квадрата с учетом выборки и дисперсии генеральной совокупности
Идти Чи-квадрат Статистика = ((Размер образца-1)*Выборочная дисперсия)/Дисперсия населения
Количество отдельных значений с учетом остаточной стандартной ошибки
Идти Количество отдельных значений = (Остаточная сумма квадратов/(Остаточная стандартная ошибка данных^2))+1
Ожидание разности случайных величин
Идти Ожидание разности случайных величин = Ожидание случайной величины X-Ожидание случайной величины Y
F Значение двух образцов с заданными стандартными отклонениями выборки
Идти Значение F двух образцов = (Стандартное отклонение образца X/Стандартное отклонение образца Y)^2
Ожидание суммы случайных величин
Идти Ожидание суммы случайных величин = Ожидание случайной величины X+Ожидание случайной величины Y
Диапазон данных с учетом наибольшего и наименьшего элементов
Идти Диапазон данных = Самый большой элемент в данных-Наименьший элемент данных
Самый большой элемент в заданном диапазоне данных
Идти Самый большой элемент в данных = Диапазон данных+Наименьший элемент данных
Наименьший элемент в заданном диапазоне данных
Идти Наименьший элемент данных = Самый большой элемент в данных-Диапазон данных
Значение F двух образцов
Идти Значение F двух образцов = Дисперсия образца X/Дисперсия образца Y
Статистика хи-квадрата с учетом выборки и дисперсии генеральной совокупности формула
Чи-квадрат Статистика = ((Размер образца-1)*Выборочная дисперсия)/Дисперсия населения
χ2 = ((N-1)*Vs)/Vσ
Каково значение критерия хи-квадрат в статистике?
Тест хи-квадрат — это проверка статистической гипотезы, используемая при анализе таблиц непредвиденных обстоятельств при больших размерах выборки.
Проще говоря, этот тест в основном используется для проверки того, являются ли две категориальные переменные или два измерения таблицы непредвиденных обстоятельств независимыми в влиянии на статистику теста, то есть на значения в таблице. В стандартных приложениях этого теста наблюдения классифицируются во взаимоисключающие классы. Если нулевая гипотеза об отсутствии различий между классами в популяции верна, тестовая статистика, вычисленная на основе наблюдений, соответствует частотному распределению хи-квадрат. Цель теста — оценить, насколько вероятными будут наблюдаемые частоты, если предположить, что нулевая гипотеза верна.
Share
Copied!
Калькулятор CASIO FX-9750GII • Графические калькуляторы
Калькулятор CASIO FX-9750GII • Графические калькуляторыNavigation
by Fmeaddons
Современный графический калькулятор
с контрастным монохромным дисплеем,
основной памятью 61 Кбайт
и USB-разъемом
Серия: Графические
- Описание
- Технические характеристики
- Инструкция
Описание
- программная память 61 Кбайт
- большой контрастный монохромный дисплей
- 8 строк по 21 знаку
- символьное меню для выбора режима
- размер (В x Ш x Г): прим.
21,3 x 87,5 x 180,5 мм - масса: прим. 205 г с элементом питания
- элементы питания: 4 x AAA
- решение уравнений с интегральными, дифференциальными и вероятностными функциями
- Команда Ref и Rref для диагонализации матрицы или преобразования в уменьшенную ступенчатую матрицу
- случайные целые числа
- перевод единиц измерения
- функция НОД и НОК
- функция вычисления остатка (остаток)
- функция хи-квадрата согласия
- круговая и столбчатая диаграмма
- финансовая математика
– займы, списания - установленное приложение для регистрации результатов измерений ECON2
- дополнительный дисплей OH-9860 может использоваться со всеми FX-9750GII
- USB-разъем
21,3 x 87,5 x 180,5 ммТехнические характеристики
Экран
- Строки x позиции: 8 x 21
- Размер экрана (в пикселях): 64 x 128
Память / Memory
- Доступный объем памяти RAM/флэш-памяти: 61 kB
- Память значений/постоянная память: 28
- Вызов последнего введенного значения
Элементарная математика
- Нормализованный формат записи чисел: 10+2
- sin, cos, tan и arc
- Гиперболические и обратные гиперболические функции
- Пересчет единиц угловой меры (гоны, угловые градусы и радианы)
- Перевод из шестидесятеричной системы < > десятеричную
- Переключения между прямоугольной < > полярной системой координат
- Перевод единиц измерения
- Расчеты на основе n
- Экспоненциальные/логарифмические функции
- Таблицы значений
- Системы линейных уравнений: до 6
- Полиномиальные уравнения высшего порядка: до 6 градусов
- Логические операторы (AND/OR/…)
- Вычисления с комплексными числами
- Интерактивная программа решения уравнений
- Матрицы
- Функция REF/RREF
- Память повторений/ответов
- Рекурсивные последовательности
- Функция НОД и НОК
- Расчеты с остатком (Remainder)
Графическое изображение
- Количество прямоугольных функций: 20
- Количество параметрических функций: 20
- Количество полярных функций: 20
- X=f(Y) граф
- Неравенства
- Масштабирование, функция следа
- Режим кривых второго порядка (конические сечения)
Статистика
- Среднее значение, стандартное отклонение
- Линейная регрессия
- Медиана, квартиль
- Описательная статистика
- Комбинаторика и перестановки
- Модели регрессии: 12
- Гистограммы, дисперсия
- Диаграмма размаха
- Секторная/столбчатая диаграмма
- Количество списков: 26×6
- Макс. длина списков: 999
- Оценочная статистика
- Генератор случайных чисел
- Случайные целые числа
- Хи-квадрат, дисперсионный тест, F-тест
- Определение доверительных интервалов (Z и t)
- Распределение вероятностей
длина списков: 999Дифференцирование и интегрирование
- Интегрирование
- Дифференцирование
- Максимум, минимум
Программирование
- Память формул
- Программирование/пользовательское
- Строковая функция
Финансовая математика
- N, %, I, PMT, PV, FV
- Амортизация
- Преобразование процент. <> эффект. ставок
- Исчисление процентов и сложных процентов
- Сроки ежегодных платежей
- Расчет количества дней или даты
- Займы
- Амортизация
- Оценка капиталовложений
- Расчет точки безубыточности
Прочее
- Защитная жесткая крышка
- Кабель для соединения двух калькуляторов: необязательный
- Автоматическое отключение
- Возможно подключение к ПК
- Программа-эмулятор с идентичным управлением: необязательный
- Возможно соединение с EA-200/ECON2
- Главная батарея: 4 x AAA
- Размер (В x Ш x Г мм): 21,3 x 87,5 x 180,5
- Масса: 205 г
Инструкция
Спецификация может быть изменена без уведомления
© CASIO Europe Gmbh
Введите текст и нажмите “enter” для поиска
Информация об использовании файлов cookie на веб-сайте CASIO
Мы используем файлы cookie, чтобы максимально адаптировать наш веб-сайт к потребностям пользователей.
Нажмите «Подтвердить и продолжить», если вы хотите продолжить работу с нашим веб-сайтом.
Критерий хи-квадрат
| Холост: 47 Женат: 71 Разведен: 35 |
| Холост: 44 В браке: 85 Разведен: 40 |
Группы и числа
Вы исследуете две группы и распределяете их по категориям одинокие, женатые или разведенные:
Числа определенно разные, но…
- Это просто случайность?
- Или вы нашли что-то интересное?
Тест хи-квадрат дает значение «p», чтобы помочь вам принять решение!
Пример: «Какой праздник вы предпочитаете?»
| Пляж | Круиз | |
| Мужчины | 209 | 280 |
| Женщины | 225 | 248 |
Влияет ли пол на предпочтительный отпуск?
Если пол (мужской или женский) влияет ли на предпочтительный отпуск, мы говорим, что они зависимы .
Выполнив некоторые специальные вычисления (поясняемые позже), мы получаем значение «p»:
значение p равно 0,132
Теперь p < 0,05 является обычным тестом для зависимости .
В этом случае p больше, чем 0,05 , поэтому мы считаем, что переменные равны независимые (т.е. не связанные между собой).
Другими словами, мужчины и женщины, вероятно, , а не , по-разному предпочитают пляжный отдых или круизы.
Это были просто случайные различия, которые мы ожидаем при сборе данных.
Значение «p»
«p» — это вероятность того, что переменные независимы .
Представьте, что предыдущий пример на самом деле был двумя случайными выборками из мужчин каждый раз:
| Мужчины: Пляж 209, Круиз 280 | Мужчины: Пляж 225, Круиз 248 |
Неужели вероятно вы бы каждый раз получали такие разные результаты, опрашивая мужчин?
Что ж, значение «p» 0,132 говорит о том, что это действительно может происходить время от времени.
В конце концов, опросы случайны. Мы ожидаем немного разных результатов каждый раз, верно?
Таким образом, большинство людей хотят видеть значение p меньше, чем 0,05 , прежде чем они будут счастливы сказать, что результаты показывают, что группы имеют разные ответы.
Давайте посмотрим на другой пример:
Пример: «Какого питомца вы предпочитаете?»
| Кат | Собака | |
| Мужчины | 207 | 282 |
| Женщины | 231 | 242 |
Выполняя вычисления (показаны позже), мы получаем:
Значение P равно 0,043
являются независимыми от , а не от .
Другими словами, поскольку 0,043 < 0,05 , мы считаем, что пол связан с предпочтениями домашних животных (мужчины и женщины по-разному относятся к кошкам и собакам).
Просто из интереса заметьте, что числа в наших двух примерах похожи, но результирующие значения p очень разные: 0,132 и 0,043 .
Это показывает, насколько чувствителен тест!
Почему p
<0,05 ?Это просто выбор! Использование p<0,05 является обычным явлением , но мы могли бы выбрать p<0,01, чтобы быть еще более уверенными в том, что группы ведут себя по-разному, или любое значение на самом деле.
Расчет P-значения
Итак, как мы можем рассчитать это p-значение? Мы используем тест хи-квадрат!
Тест хи-квадрат
Примечание: Хи Звучит как «Привет», но с K , так что это звучит как « Ki квадрат»
И Chi это греческая буква Χ, так что мы можем также написать это Χ 2
Важные моменты, прежде чем мы начнем:
- Этот тест работает только для категориальных данных (данных в категориях), таких как пол {мужчины, женщины} или цвет {красный, желтый, зеленый, синий} и т. д., но не числовых данных, таких как рост или вес.
- Числа должны быть достаточно большими. Каждая запись должна быть 5 или больше. В нашем примере у нас есть такие значения, как 209, 282 и т. д., так что все готово.
В нашем примере у нас есть такие значения, как 209, 282 и т. д., так что все готово.Наш первый шаг — сформулировать наши
гипотезы :Гипотеза : Утверждение, которое может быть верным, которое затем можно проверить.
Две гипотезы есть.
- Пол и предпочтение кошек или собак не зависят друг от друга .
- Пол и предпочтение кошек или собак не являются независимыми .
Занесите данные в таблицу:
| Кот | Собака | |
| Мужчины | 207 | 282 |
| Женщины | 231 | 242 |
Сложить строки и столбцы:
| Кот | Собака | ||
| Мужчины | 207 | 282 | 489 |
| Женщины | 231 | 242 | 473 |
| 438 | 524 | 962 |
Рассчитайте «ожидаемое значение» для каждой записи:
Умножьте сумму каждой строки на сумму каждого столбца и разделите на общую сумму:
| Кот | Собака | ||
| Мужчины | 489×438 962 | 489×524 962 | 489 |
| Женщины | 473×438 962 | 473×524 962 | 473 |
| 438 | 524 | 962 |
Что дает нам:
| Кот | Собака | ||
| Мужчины | 222,64 | 266,36 | 489 |
| Женщины | 215,36 | 257,64 | 473 |
| 438 | 524 | 962 |
Вычесть ожидаемое из наблюдаемого, возвести его в квадрат, затем разделить на ожидаемое:
Другими словами, используйте формулу (O−E) 2 E где
- O = Наблюдаемое (фактическое) значение
- E = Ожидаемое значение
| Кот | Собака | ||
| Мужчины | (207−222,64) 2 222,64 | (282−266,36) 2 266,36 | 489 |
| Женщины | (231−215,36) 2 215,36 | (242−257,64) 2 257,64 | 473 |
| 438 | 524 | 962 |
Получается:
| Кот | Собака | ||
| Мужчины | 1,099 | 0,918 | 489 |
| Женщины | 1,136 | 0,949 | 473 |
| 438 | 524 | 962 |
Теперь сложите полученные значения:
1,099 + 0,918 + 1,136 + 0,949 = 4,102
Хи-квадрат равен 4,102
От хи-квадрата до p
Степени свободы
Сначала нам нужна «Степень свободы»
Степень свободы = (строки — 1) × (столбцы — 1 )
Для нашего примера у нас есть 2 строки и 2 столбца:
DF = (2 − 1)(2 − 1) = 1×1 = 1
p-значение
Остальная часть вычисления сложно, поэтому либо найдите его в таблице, либо воспользуйтесь калькулятором хи-квадрат.
Результат:
p = 0,04283
Готово!
Сигма-нотация)Итак, мы вычисляем (O−E) 2 E для каждой пары наблюдаемых и ожидаемых значений, затем суммируйте их все.
Значение P из калькулятора хи-квадрат
Онлайн-калькулятор значения хи-квадрат P предназначен для определения значения P с использованием стандартного метода хи-квадрат. Прежде чем мы продолжим обсуждение калькулятора, давайте сначала обратим внимание на концепцию значения P.
Что такое значение P?
В статистике значение P на самом деле представляет собой вероятность обнаружения наиболее экстремальных результатов, когда предполагаемая нулевая гипотеза верна. Мы не можем определить значение P с точки зрения прямой вероятности состояния.
Нулевая гипотеза (H0):
Состояние, при котором мы предполагаем, что нет разницы между наблюдаемым значением и ожидаемым значением данных.
Нам нужно определять нулевую гипотезу каждый раз, когда мы ищем решение проблемы.
Например:
Предположим, что Джек и Гарри — два друга. Оба они идут в больницу для вакцинации, но, к сожалению, Джек не получил вакцину. Теперь, после того, как Гарри введут дозу, мы скажем, что разницы в кровяном давлении у обоих друзей нет.
Альтернативная гипотеза (h2):
Если мы принимаем какие-либо значительные изменения в популяции после анализа, то мы должны принять альтернативную гипотезу, которая поддерживает любую дисперсию данных.
Например:
Вопрос:
Будет ли разница между кровяными давлениями двух сестер, если мы дадим одной сестре сахарную таблетку и панадол другой сестре?
Альтернативная гипотеза утверждает, что существуют существенные различия в физическом здоровье обеих сестер, потому что сахарная таблетка и панадол по-разному влияют на физическое и психическое здоровье тела.
92}{E} $$
Где;
O = наблюдаемое значение
E = ожидаемое значение
Чтобы рассчитать ожидаемое значение, мы должны следовать следующей формуле:
E = RT * CT / N
Где;
RT = сумма корней для строки, содержащей ячейки
CT = сумма столбца для столбца, содержащего ячейки
N = общее количество наблюдений
Калькулятор значения хи-квадрат P использует значение хи-квадрат для определения значения P.
Условия применения теста хи-квадрат:
Вам не разрешается каждый раз применять тест хи-квадрат для определения вероятности. Тест хи-квадрат применим только при следующих условиях:
- Каждая ячейка должна содержать 5 наблюдений, обычно предпочтительно 10 наблюдений. Если он <5, X2 завышен, что приводит к отклонению нулевой гипотезы.
- Все отдельные наблюдения должны быть случайными и полностью независимыми.
- Общий размер выборки (N) должен составлять не менее 50 наблюдений.
- Данные должны быть выражены в исходных единицах, что означает, что вы не можете выразить данные в процентах или отношениях.
Наш бесплатный онлайн-калькулятор значения хи-квадрат P работает для значения p, если выполняются вышеуказанные условия.
Значение P из хи-квадрата:
Тест хи-квадрат дает нам значение p. Чтобы определить значение p из теста хи-квадрат, вам необходимо понять несколько следующих терминов:
Степень свободы:
Максимальное количество значений в данных, которые могут свободно изменяться, называется степенью свободы. Вы можете оценить этот термин, используя следующее уравнение:
df = (r-1)(c-1)
где ;
r = количество строк
c = количество столбцов
Уровень значимости (α):
Когда нулевая гипотеза верна, то вероятность ее отклонения называется уровнем значимости.
Всякий раз, когда вы отвергаете нулевую гипотезу, выбор уровня значимости является произвольным. Обычно используются уровни 5%, 1% и 0,1%. Если вам не указан уровень значимости проблемы, то вы должны предположить, что это значение равно 5% (0,05)
Большинство авторов называют статистически значимое значение P < 0,05, а статистически высокозначимое значение P < 0,001 (менее один шанс из тысячи ошибиться).
Таблица хи-квадрат:
Вы можете легко определить значение p по диаграмме значения p хи-квадрат следующим образом:
Как рассчитать значение P из теста хи-квадрат?
Давайте обратим внимание на задачу по нахождению значения p с помощью метода хи-квадрат:
Задача:
Во время противомалярийной кампании в Америке хинин вводили людям из всего населения в 2000 человек.
число случаев лихорадки показано ниже:
| Лечение | Лихорадка | Без лихорадки | Всего |
| хинин | 20 | 480 | 500 |
| Без хинина | 100 | 1400 | 1500 |
| Всего | 120 | 1880 | 2000 |
92}{E} $$
Итак, для данных, приведенных в таблице, нам нужно определить ожидаемые значения для лиц, страдающих лихорадкой, и тех, кто не страдает лихорадкой.
E11 = E = RT * CT / N
= 500 * 120 / 2000
= 30
E12 = RT * CT / N
= 1500 * 120 / 2000
= 90
E21 = RT * CT / N
= 500 * 1880 / 2000
= 470
E22 = RT * CT / N
= 1500 * 1880 /2000
= 1410
Приведенные выше данные могут быть таблицы следующим образом:
| Лихорадка | Ожидаемое значение | Без лихорадки | Ожидаемое значение | Итого | |
| хинин | 20 | 30 | 480 | 470 | 500 |
| Без хинина | 100 | 90 | 1400 | 1410 | 1500 |
| Всего | 120 | – | 1880 | – | 2000 |
Для расчета хи-квадрата составим таблицу, содержащую наблюдаемые и ожидаемые значения:
| O наблюдаемое значение (O) | Ожидаемое значение (E) | (О – Э) | (О–Е)2 | (О – Е)2 / Е |
| 20 | 30 | -10 | 100 | 3,33 |
| 100 | 90 | +10 | 100 | 1. 11 |
| 480 | 470 | +10 | 100 | 0,21 |
| 1400 | 1410 | 92}{E} = 4,72 $$ Степень свободы вычисляется следующим образом: df = (r-1)(c-1) Поскольку у нас есть 2 строки и 2 столбца, мы имеем ; df = (2-1) * (2-1) Итак, для 1 степени свободы с уровнем значимости 5% (0,05) , значение хи-квадрат рассчитывается из диаграммы хи следующим образом: X20,05 = 3,84 (табличное значение хи-квадрат) Поскольку табличное значение хи-квадрат < расчетного значения хи-квадрат, мы отвергаем нулевую гипотезу. Следовательно, хинин эффективен при борьбе с малярией. Теперь мы должны вычислить значение chi -значения P, используя таблицу: Два хвостового значения P = 0,100087 левый хвост P Все значения значимы только при p < 0,05. Как работает калькулятор значения хи-квадрат?Вы можете легко найти двустороннее, левостороннее и правостороннее значение p с помощью калькулятора хи-квадрат значения p. Для получения результатов необходимо выполнить следующие шаги: Ввод:
Вывод: В зависимости от выбранных вами входных данных калькулятор вычисляет:
Часто задаваемые вопросы:Что нам говорит значение P? Значение p говорит нам, являются ли полученные нами результаты значимыми или нет. Что означает p-значение 0,05?Значение p меньше . 05 означает, что вероятность увидеть эти результаты составляет менее 5 процентов, когда нулевая гипотеза верна. Что подразумевается под низким значимым значением P?Низкое значимое значение p означает, что у нас есть достаточно доказательств, чтобы доказать, что наблюдаемое распределение не совпадает с ожидаемым распределением. Каково значимое значение P из хи-квадрат?На практике значение p 0,05 или выше считается значимым значением p для хи-квадрат. Заключение:Хи-квадрат позволяет нам сравнить наблюдаемые частоты и ожидаемые частоты. Статистики широко используют метод хи-квадрат для расчета хи-квадрат. Использование бесплатного онлайн-калькулятора значения хи-квадрат сводит к минимуму вероятность ошибки в вычислениях. Ссылки: Из источника википедии: критерий хи-квадрат Пирсона, поправка Йейтса на непрерывность. |
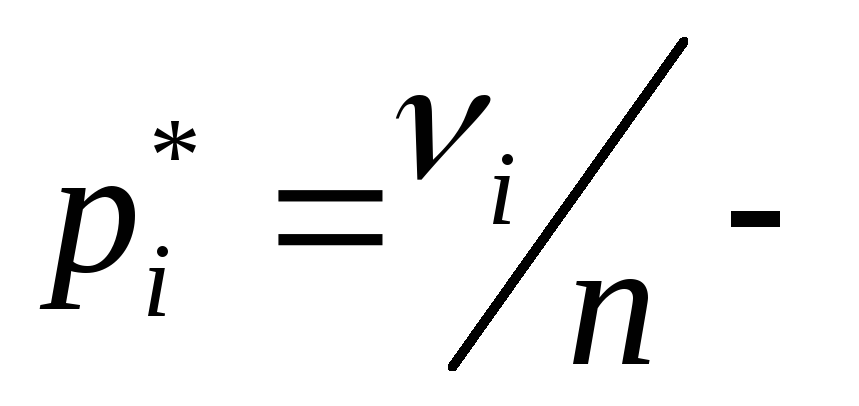
Калькулятор значения хи-квадрат p позволяет найти точное значение p.