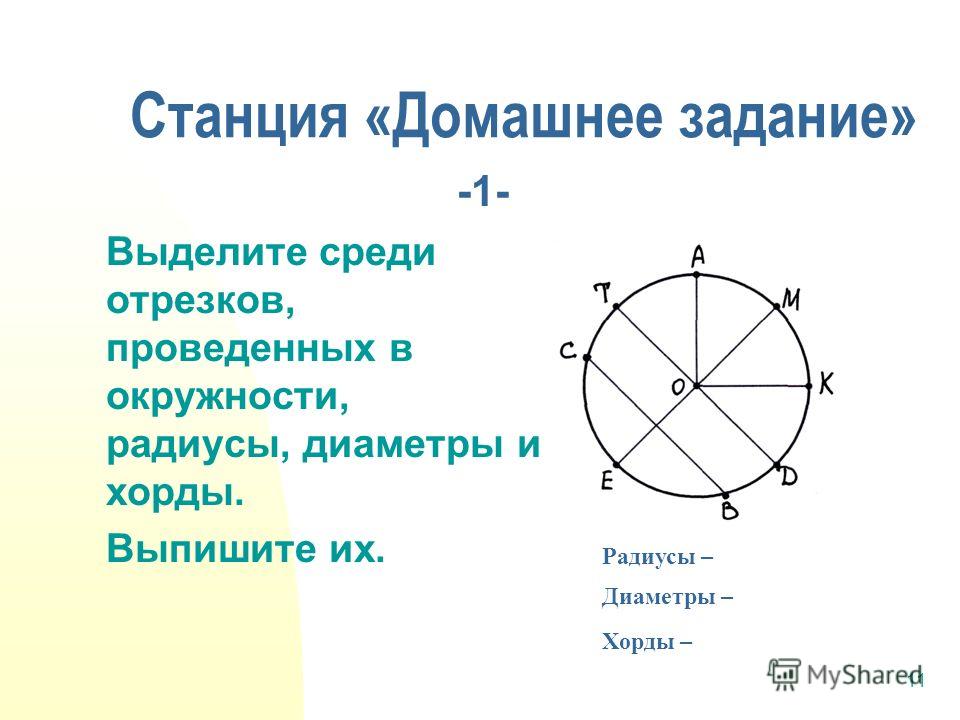
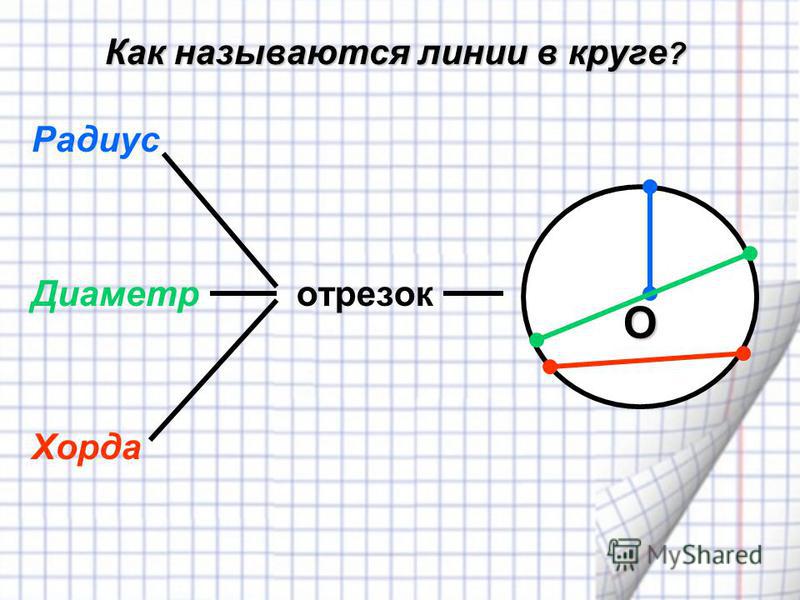
Что называется хордой окружности в математике и геометрии: определение, основные свойства
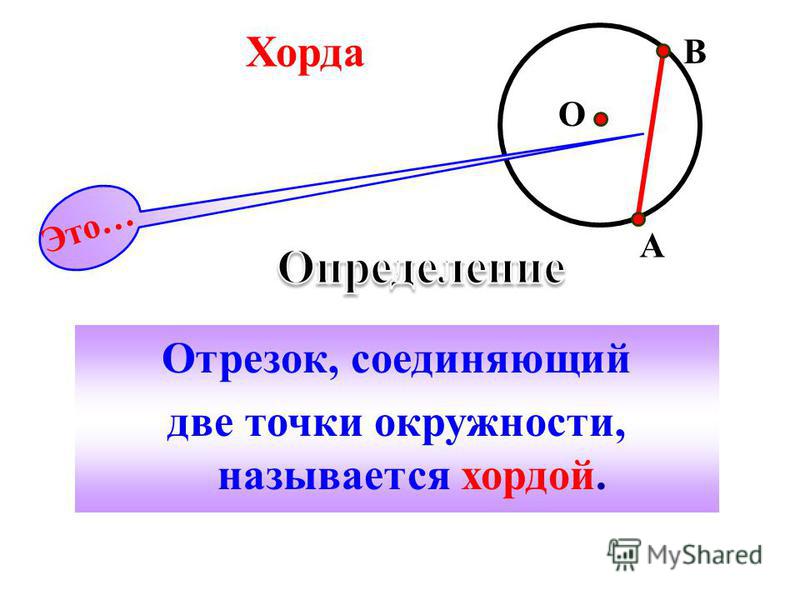
Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.
…
Оглавление:
- Как построить геометрическую хорду
- Свойства
- Взаимосвязь с радиусом и диаметром
- Хорда и радиус
- Отношения со вписанными углами
- Взаимодействия с дугой
Как построить геометрическую хорду
Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.
Это интересно: в геометрии луч — это что такое, основное понятие.
Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.
Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.
Свойства
Существует ряд закономерностей, связывающих между собой хорды и центр круга:
- Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
- Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
- Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности.
 И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше. - Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
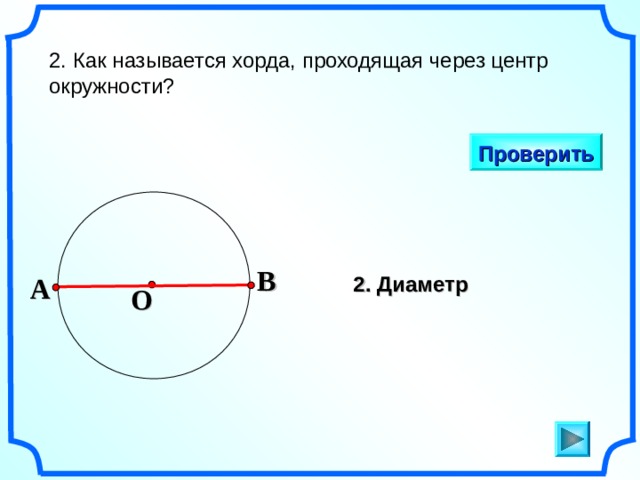
- Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
- Отрезок с наименьшей длиной представляет собой точку.
- Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.
Это интересно: разность векторов, определение разности.
Взаимосвязь с радиусом и диаметром
Вышеуказанные математические понятия связаны между собой следующими закономерностями:
- Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.

- С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
- Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
- Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
- Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
- Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.
Хорда и радиус
Между этими понятиями существуют следующие связи:
- Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
- Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.

- Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
- Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
- Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
- Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.
Отношения со вписанными углами
Углы, вписанные в окружность, подчиняются следующим правилам:
- Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
- Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
- Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.

- Вписанный угол, который опирается на диаметр круга, является прямым.
- Равные между собой по размеру отрезки стягивают равные центральные углы.
- Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
- Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.
Взаимодействия с дугой
Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:
- Две равные между собой хорды стягивают равные дуги.
- Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
- Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает.
 И чем больше дуга, тем меньше ограничивающая её хорда.
И чем больше дуга, тем меньше ограничивающая её хорда.
Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.
центр, хорда, диаметр и радиус. Вписанный угол. Центральный угол. Длина окружности, длина дуги – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Вопросы
Один из двух внутренних односторонних углов при параллельных прямых и секущей составляет 80% от другого.
 {\circ}\), AB = 15 см, BC = 22 см. Найдите расстояние между прямой \(AB\) и прямой проходящей через точку \(C \) параллельно \(AB.\)
{\circ}\), AB = 15 см, BC = 22 см. Найдите расстояние между прямой \(AB\) и прямой проходящей через точку \(C \) параллельно \(AB.\)К окружности с центром в точке О проведены касательная AB и секущая АО. Найдите радиус окружности, если AB = 15, АО = 17.
В окружности с центром O отрезки AC и BD — диаметры. Вписанный угол ACB равен 38°. Найдите центральный угол AOD.
Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности.
Найдите центральный угол AOB, если он на 15° больше вписанного угла ACB, опирающегося на ту же дугу.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12 см. Найдите радиус описанной окружности этой трапеции.
-
В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 и 12 см. Найдите катеты треугольника.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 5, считая от вершины, противолежащей основанию.
 Найдите периметр треугольника.
Найдите периметр треугольника.Найдите площадь круга, длина окружности которого равна \(50\sqrt{\pi}\).
Площадь круга, вписанного в правильный шестиугольник, равна 60,75π см2. Найдите периметр шестиугольника.
Найдите диаметр основания юрты, если ее радиус равен 4,5 м.
Расстояние от центра окружности до касательной равно 13 дм. Найдите радиус данной окружности.
Найдите величину дуги АВ, на которую опирается угол АВС, вписанный в окружность.

В окружности с центром в точке О проведена хорда АС. Найдите угол АОС, если известно, что хорда равна радиусу (АО = АС)
Восемь шариков для настольного тенниса нужно уложить в коробку плотно друг к другу. Какова длина коробки, если радиус одного шарика 2,5 см?
Центральный угол и вписанный угол опираются на одну дугу. Найдите эти углы, если центральный угол на 20° больше вписанного.
Прямая АВ касается окружности с центром в точке О и радиусом, равным 7 см, в точке А. Найдите ОВ, если АВ = 24 дм.
АВ и СD – хорды.
 АВ и СD пересекаются в точке Е. АЕ = 0,7 см, ВЕ = 0,5 см, СЕ = 0,4 см. Найдите DЕ и DС.
АВ и СD пересекаются в точке Е. АЕ = 0,7 см, ВЕ = 0,5 см, СЕ = 0,4 см. Найдите DЕ и DС.Вершины треугольника АВС делят описанную окружность в отношении 2: 3: 4. Найдите углы треугольника АВС.
Из точки А к окружности с центром в точке О проведена касательная АВ. Найдите радиус, если угол ОАВ равен 60°, АО =14\(\sqrt3\) см.
- К окружности с центром в точке О проведены две касательные, угол между которыми равен 120°. АО = 24 см. Найдите СА и DА, если С и D – точки касания.
Два угла треугольника равны 60° и 80°.
 Найдите градусную меру меньшей дуги, на которые вершины треугольника делят окружность.
Найдите градусную меру меньшей дуги, на которые вершины треугольника делят окружность.-
В треугольнике даны две стороны: a = 12, b = 8. Угол между ними равен 60°. Найдите третью сторону.
Основание равнобедренного треугольника – a, боковая сторона – b. Найдите биссектрису, проведенную из вершины, противолежащей основанию.
-
В треугольнике ABC угол A = 45°, угол C = 15°, сторона BC = 4\(\sqrt6\). Найдите длину стороны AC.
В треугольнике ABC угол A = 30°, угол B = 30°. Найдите соотношение сторон \(\frac{BC}{AB}\)
Какому неравенству удовлетворяет точка C, принадлежащая кругу с центром в точке O и радиусом R?
Вписанный угол ABC равен 30°.
 Найдите радиус окружности, если длина хорды AC, на которую он опирается, равна 17.
Найдите радиус окружности, если длина хорды AC, на которую он опирается, равна 17.
АВ – диаметр окружности. Точки С и D лежат на окружности по одну сторону от диаметра. Угол СВD равен 21°, угол DВА равен 49°. Найдите угол СDВ.
Вершины треугольника АВС делят окружность, описанную около этого треугольника в отношении 1: 3 : 5. Найдите углы треугольника.
Радиус окружности равен 10 см, расстояние от точки А, лежащей на окружности, до точки В – конца диаметра – равно 16 см. Найдите АС, если точка С – второй конец диаметра.
Из точки А к окружности с центром в точке О проведена касательная АВ.

АВ – диаметр окружности с центром в точке О. Точки С и К лежат на окружности по одну сторону от диаметра. Угол АВС равен 18°, угол СОК равен 46°. Найдите угол КАВ.
Точки А, В и С лежат на окружности с центром в точке О. Угол АОС равен 130°. Найдите угол АВС.
Прямая АВ касается в точке А окружности с центром в точке О. Найдите угол ОАВ.
- Вершины четырехугольника АВСD делят описанную окружность в отношении 1: 2 : 7 : 8. Найдите градусную меру большей дуги.

Расстояние от точки А, лежащей на окружности, до концов диаметра ВD равно 9 см, 12 см. Найдите радиус.
Хорды СК и АВ пересекаются в точке Е. АЕ = 4 см, ВЕ = 6 см, КЕ меньше СЕ на 5 см. Найдите СЕ.
Дана окружность с центром в точке О, АВ – диаметр. Точки С и К лежат на окружности по одну сторону от диаметра. Угол СКА равен 12°, угол СОК равен 64°. Найдите угол КАВ.
Хорды АВ и СН пересекаются в точке М. СМ = 4 см, НМ = 15 см, АМ:МВ = 3 : 5. Найдите АВ.
Диагонали ромба равны 6 и 8.
 \circ\), АВ = 3\(\sqrt2\), АС = 1. Найдите ВС.
\circ\), АВ = 3\(\sqrt2\), АС = 1. Найдите ВС.Сумма квадратов диагоналей прямоугольника равна 25. Найдите сумму квадратов его сторон.
Одна из сторон треугольника больше другой на 8 сантиметров, а угол между ними равен 120°. Найдите периметр треугольника, если длина третьей стороны равна 28 см.
Дан треугольник АВС. АВ = 15, ВС = 6, sin A = \(\frac15\). Найдите sin C.
В прямоугольной трапеции высота равна 12, большая боковая сторона равна 20, меньшее основание равно 5. Найдите большее основание.
Стороны треугольника равны 5\(\sqrt3\) см и 4 см, а угол между ними равен 30°.
 Найдите третью сторону треугольника.
Найдите третью сторону треугольника.Дан треугольник АВС. \(\angle\)B = 135°, AB = 2, BC = 2\(\sqrt2\). Найдите длину стороны АС.
Сообщить об ошибке
геометрия — Найдите длину хорды, зная диаметр окружности и стягиваемый угол
спросил
Изменено 5 лет, 3 месяца назад
Просмотрено 58 тысяч раз
$\begingroup$
Хорда окружности образует угол 89градусов в его центре. Найдите длину хорды, если диаметр окружности равен 11,4 см.
Проблема в том, что я не могу представить себе этот вопрос.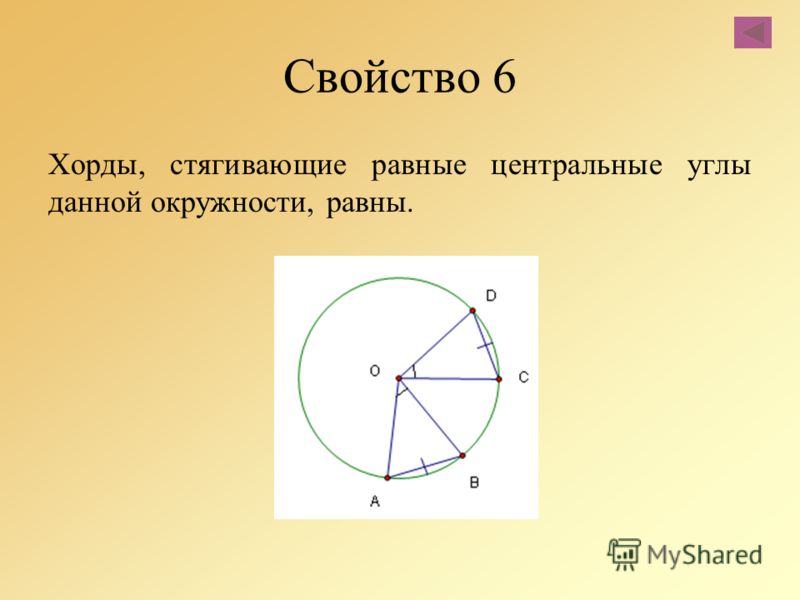 Я пытался нарисовать это, но все получалось беспорядочно, и я запутался, так что может ли кто-нибудь нарисовать диаграмму для меня? Это все, что мне нужно, потому что я могу работать с этого момента после.
Я пытался нарисовать это, но все получалось беспорядочно, и я запутался, так что может ли кто-нибудь нарисовать диаграмму для меня? Это все, что мне нужно, потому что я могу работать с этого момента после.
- геометрия
- тригонометрия
- круги
- треугольники
$\endgroup$
1
$\begingroup$
Вот как я интерпретирую задачу:
Задача состоит в том, чтобы найти длину красной линии.
$\endgroup$
$\begingroup$
Для этого есть формула:
$$ 2 \cdot 5.7 \cdot \sin \left(\frac{89 \pi }{360} \right) = 7,9903656130183 $$
Где A — угол в радианах, r — радиус.
$\endgroup$
4
$\begingroup$
Способ решения: Используйте формулу: 2r sin A/C
$OA = OB = 5,7$см, так как это радиус.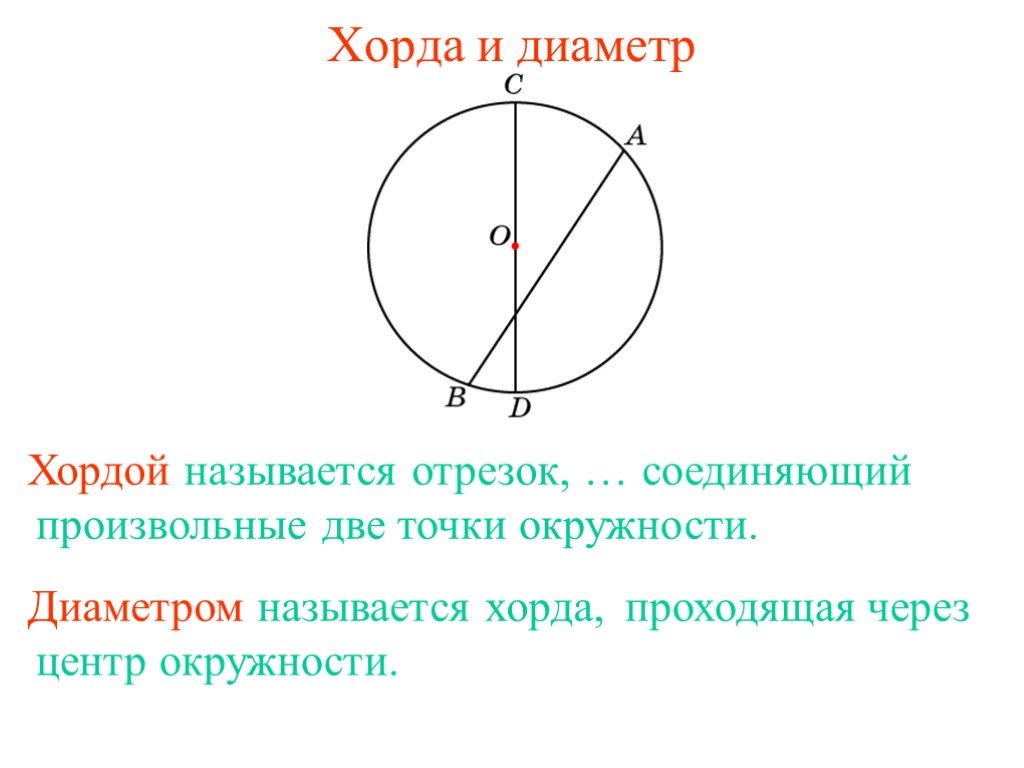 Таким образом, вы получите:
Таким образом, вы получите:
$2 \cdot 5.7 \cdot \sin \left(\frac{89 \pi }{360} \right) = 7,9903656130183$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Хорда окружности – определение, формулы, примеры
Что такое хорда окружности
Хорда окружности – это прямая линия, соединяющая две точки на окружности окружности. Диаметр, проходящий через центр окружности, является наибольшей хордой окружности.
Ниже показаны 3 аккорда AB, CD и EF. AB также является диаметром, поэтому это самая длинная хорда данного круга.
Хорда окружностиФормулы
Как найти хорду окружности
Существуют две основные формулы для определения длины хорды окружности. Обе формулы дают один и тот же результат, но используются на основе предоставленной информации. Рассмотрим каждую из них подробно с решаемыми примерами.
1) Когда известны радиус и перпендикулярное расстояние от центра
Если длина радиуса и расстояние между центром и хордой заданы, то формула для нахождения хорды приведена ниже.
Хорда окружности Формула Давайте решим пример, чтобы лучше понять концепцию.
Найдите длину хорды, если радиус окружности равен 16 см, а расстояние по перпендикуляру от хорды до центра равно 8 см.
Решение:
Как мы знаем,
Длина (L) хорды = 2√(r 2 – d 2 ), здесь r = 16 см, d = 8 см
= 2√(16 2 – 8 2 ) см
= 2√(256 – 64) см
= 2√ 192 см = 27,71 см
Расстояние по перпендикуляру от центра окружности до хорды составляет 12 дюймов. Вычислите длину хорды, если диаметр окружности равен 26 дюймам.
Решение:
Как мы знаем,
Длина (L) хорды = 2√(r 2 – d 2 ), здесь r = 26/2 = 13 дюймов, d = 12
= 2√(13 2 – 12 2 ) дюймов
= 2√(169 – 144) дюймов
= 2√25 дюймов = 10 дюймов
2) Известен
Если радиус и центральный угол хорды известны, то формула для нахождения хорды приведена ниже.
Вычислите длину хорды АВ на данной схеме.
Решение:
Как известно,
Длина (L) хорды = 2 × rsin (C/2), здесь r = 26 м, C = 75°
= 2 × 26 × sin (75°/2)
= 52 × sin 37,5°
= (52 × 0,60) м
= 31,2 м
Найдите длину шнура и центральный угол хорды на данном рисунке.
Решение:
Как мы знаем,
Длина (L) хорды = 2√(r 2 – d 2 ), здесь r = 50 м, d = 20 м
= 2√(50 2 – 20 2 ) м
= 2√(2500 – 400) м
= 2√2100 см = 91,65 м
Теперь для нахождения центрального угла
Длина (L) хорды = 2 × rsin (C/2), здесь r = 26 м, C = 75°
=> 91,65 = 2 × 50 × sin (C/2)
=> 91,65 = 100 sin (C/2)
=> 0,9165 = sin (C/2)
=> sin -1 0,9165 = C/2
=> 66,41 = C/2
=> C = 132,82°
Теоремы о хордах окружности
Связь между различными хордами и углом, образуемым ими с центром окружности можно установить с помощью приведенных ниже теорем.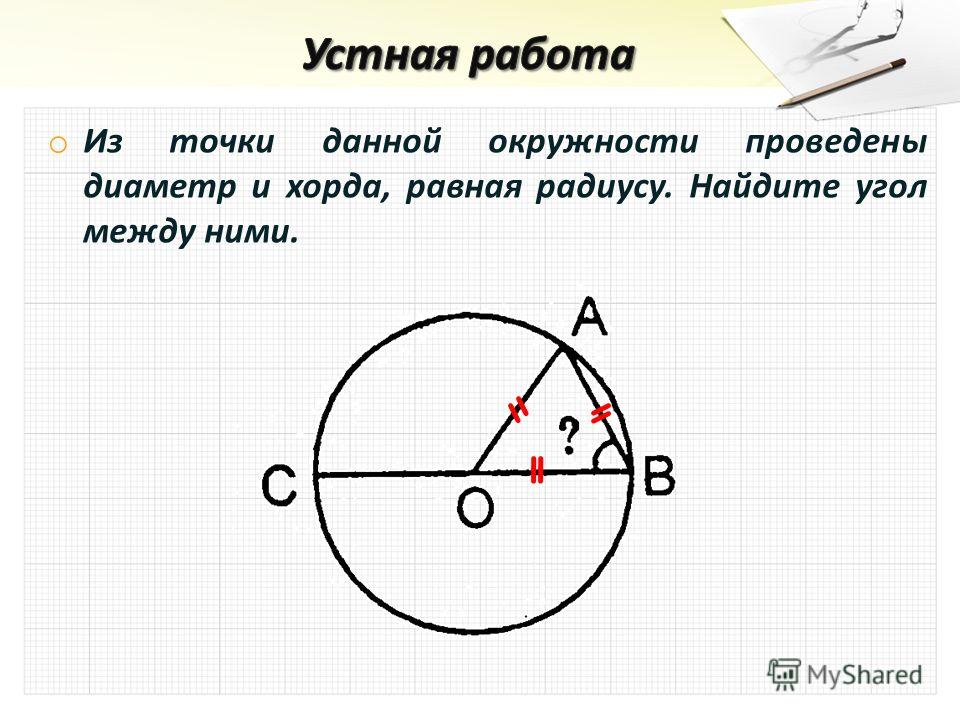

 И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.

 И чем больше дуга, тем меньше ограничивающая её хорда.
И чем больше дуга, тем меньше ограничивающая её хорда. {\circ}\), AB = 15 см, BC = 22 см. Найдите расстояние между прямой \(AB\) и прямой проходящей через точку \(C \) параллельно \(AB.\)
{\circ}\), AB = 15 см, BC = 22 см. Найдите расстояние между прямой \(AB\) и прямой проходящей через точку \(C \) параллельно \(AB.\)
 Найдите периметр треугольника.
Найдите периметр треугольника.
 АВ и СD пересекаются в точке Е. АЕ = 0,7 см, ВЕ = 0,5 см, СЕ = 0,4 см. Найдите DЕ и DС.
АВ и СD пересекаются в точке Е. АЕ = 0,7 см, ВЕ = 0,5 см, СЕ = 0,4 см. Найдите DЕ и DС. Найдите градусную меру меньшей дуги, на которые вершины треугольника делят окружность.
Найдите градусную меру меньшей дуги, на которые вершины треугольника делят окружность. Найдите радиус окружности, если длина хорды AC, на которую он опирается, равна 17.
Найдите радиус окружности, если длина хорды AC, на которую он опирается, равна 17.

 \circ\), АВ = 3\(\sqrt2\), АС = 1. Найдите ВС.
\circ\), АВ = 3\(\sqrt2\), АС = 1. Найдите ВС.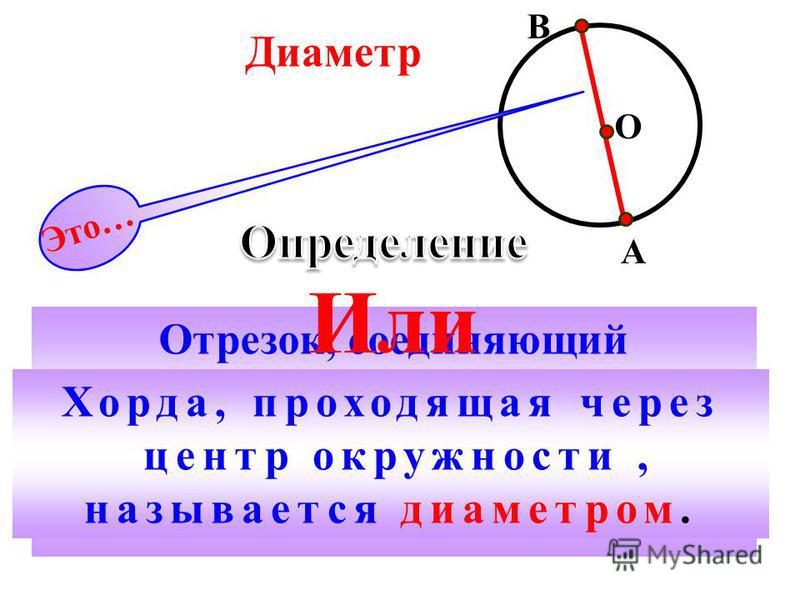 Найдите третью сторону треугольника.
Найдите третью сторону треугольника.