x в квадрате минус y в квадрате график
Вы искали x в квадрате минус y в квадрате график? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и x в квадрате функция, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «x в квадрате минус y в квадрате график».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как x в квадрате минус y в квадрате график,x в квадрате функция,y x в квадрате,y x квадрат,график икс в квадрате равен игрек в квадрате,график функции х в квадрате минус у в квадрате,график х у в квадрате,игрек в квадрате равен икс в квадрате,игрек равен,икс в квадрате плюс икс в квадрате график,икс квадрат равно игрек квадрат,икс равен игрек в квадрате,у х квадрат,функция x y в квадрате,функция x в квадрате,функция y x в квадрате,функция икс в квадрате,функция у в квадрате х в квадрате,функция х у в квадрате,х квадрат у квадрат график.
Где можно решить любую задачу по математике, а так же x в квадрате минус y в квадрате график Онлайн?
Решить задачу x в квадрате минус y в квадрате график вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Формулы сокращенного умножения
У нас есть сумма (разница) двух чисел и нам необходимо избавиться от скобок, используя формулы для сокращенного умножения: (x + y)2 = x2 + 2xy + y2
(x — y)2 = x2 — 2xy + y2
Пример: если x = 10, y = 5a
(10 + 5a)2 = 102 + 2.
(10 — 4)2 = 102 — 2.10.4 + 42 = 100 — 80 + 16 = 36
Конечно, если мы имеем следующую ситуацию:
25 + 20a + 4a2 = 52 + 2.2.5 + (2a)2 = (5 + 2a)2
(x + y)3 = x3 + 3x2y + 3xy2 + y3
(x — y)3 = x3 — 3x2y + 3xy2 — y3
Пример: (1 + a2)3 = 13 + 3.12.a2 + 3.1.(a2)2 + (a2)3 = 1 + 3a2 + 3a4 + a6
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2xz + 2yz
(x — y — z)2 = x2 + y2 + z2 — 2xy — 2xz + 2yz
x2 — y2 = (x — y)(x + y)
x2 + y 2 = (x + y)2 — 2xy
или
x2 + y2 = (x — y)2 + 2xy
Пример: 9a2 — 25b2 = (3a)2 — (5b)2 = (3a — 5b)(3a + 5b)
x3 — y3 = (x — y)(x2 + xy + y2)
x3 + y3 = (x + y)(x2 — xy + y2)
xn — yn = (x — y)(xn-1 + xn-2y +. {2}+2 a b+2 a c+2 b c$
{2}+2 a b+2 a c+2 b c$
Читать следующую тему: формула «квадрат разности».
Слишком сложно?
Квадрат суммы не по зубам? Тебе ответит эксперт через 10 минут!
Квадрат суммы и квадрат разности, разность квадратов
Квадрат суммы
Выражение (a + b)2 — это квадрат суммы чисел a и b. По определению степени выражение (a
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2.
Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Из правила следует, что общая формула квадрата суммы, без промежуточных преобразований, будет выглядеть так:
(a + b)2 = a2 + 2ab + b2.
Многочлен a2 + 2ab + b2 называется разложением квадрата суммы.
Так как a и b обозначают любые числа или выражения, то правило даёт нам возможность сокращённым путём возводить в квадрат любое выражение, которое может быть рассмотрено как сумма двух слагаемых.
Пример. Возвести в квадрат выражение 3x2 + 2xy.
Решение: Чтобы не производить дополнительных преобразований, воспользуемся формулой квадрата суммы. У нас должна получиться сумма квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(3x2 + 2xy)2 = (3x2)2 + 2(3x2 · 2xy) + (2xy)2.
Теперь, пользуясь правилами умножения и возведения в степень одночленов, упростим получившееся выражение:
Квадрат разности
Выражение (a — b)2 — это квадрат разности чисел a и b. Выражение (a — b)2 представляет собой произведение двух многочленов (a — b)(a — b). Следовательно, из квадрата разности мы можем сделать выводы, что
(a — b)2 = (a — b)(a — b) = a2 — ab — ab + b2 = a2 — 2ab + b2.
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Из правила следует, что общая формула квадрата разности, без промежуточных преобразований, будет выглядеть так:
(a — b)2 = a2 — 2ab + b2.
Многочлен a2 — 2ab + b2 называется разложением квадрата разности.
Это правило применяется к сокращённому возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.
Пример. Представьте квадрат разности в виде трёхчлена:
(2a2 — 5ab2)2.
Решение: Используя формулу квадрата разности, находим:
(2a2 — 5ab2)2 = (2a2)2 — 2(2a2 · 5ab2) + (5ab2)2.
Теперь преобразуем выражение в многочлен стандартного вида:
(2a2)2 — 2(2a2 · 5ab2) + (5ab2)2 = 4a4 — 20a3b2 + 25a2b4.
Разность квадратов
Выражение a2 — b2 — это разность квадратов чисел a и b. Выражение a2 — b2 представляет собой сокращённый способ умножения суммы двух чисел на их разность:
(a + b)(a — b) = a2 + ab — ab — b2 = a2 — b2.
Произведение суммы двух чисел на их разность равно разности квадратов этих чисел.
Из правила следует, что общая формула разности квадратов выглядит так:
a2 — b2 = (a + b)(a — b).
Это правило применяется к сокращённому умножению таких выражений, которые могут быть представлены: одно — как сумма двух чисел, а другое — как разность тех же чисел.
Пример. Преобразуйте произведение в двучлен:
Преобразуйте произведение в двучлен:
(5a2 + 3)(5a2 — 3).
Решение:
(5a2 + 3)(5a2 — 3) = (5a2)2 — 32 = 25a4 — 9.
В примере мы применили формулу разности квадратов справа налево, то есть, нам дана была правая часть формулы, а мы преобразовали её в левую:
(a + b)(a —
На практике все три рассмотренные формулы применяются и слева направо, и справа налево, в зависимости от ситуации.
Формулы сокращенного умножения
Продолжаем изучать многочлены. В данном уроке мы научимся перемножать многочлены с помощью формул сокращённого умножения.
Предварительные навыкиКвадрат суммы двух выражений
Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)2.
Таковым к примеру является случай (2x + 3y)2.
Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)
(2x + 3y)2 = (2x + 3y)(2x + 3y)
Получили умножение многочлена на многочлен. Выполним его:
(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4x2 + 6xy + 6xy + 9y2 = 4x2 + 12xy + 9y2
То есть выражение (2x + 3y)2 равно 4x2 + 12xy + 9y2
(2x + 3y)2 = 4x2 + 12xy + 9y2
Решим аналогичный пример, который попроще:
(a + b)2
Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (a + b)
(a + b)2 = (a + b)(a + b)
Выполним это умножение:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
То есть выражение (a + b)2 равно a2 + 2ab + b2
(a + b)2 = a2 + 2ab + b2
Оказывается, что случай (a + b)2 можно распространить для любых a и b. Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y
Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y
a = 2x
b = 3y
И далее можно воспользоваться тождеством (a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:
(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4x2 + 12xy + 9y2
Как и в прошлый раз получили многочлен 4x2 + 12xy + 9y2. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:
Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:
(2x + 3y)2 = 4x2 + 12xy + 9y2
Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.
Первый способ:
(2 + 3)2 = 52 = 25
Второй способ:
(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25
Пример 2.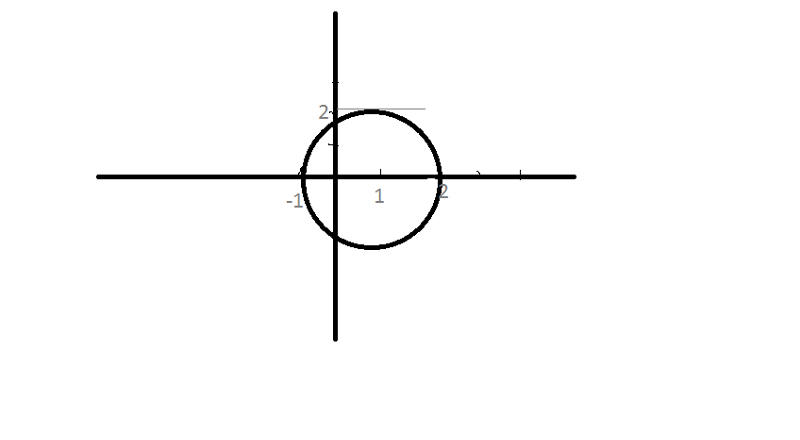 Преобразовать выражение (5a + 3)2 в многочлен.
Преобразовать выражение (5a + 3)2 в многочлен.
Воспользуемся формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9
Значит, (5a + 3)2 = 25a2 + 30a + 9.
Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:
(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9
Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.
Например, площадь квадрата со стороной a будет равна a2. Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2
Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2
Рассмотрим следующий рисунок:
Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.
Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b
В результате получается следующая сумма площадей:
a2 + ab + ab + b2
Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:
Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Квадрат разности двух выражений
Формула квадрата разности двух выражений выглядит следующим образом:
(a − b)2 = a2 − 2ab + b2
Эту формулу можно прочитать так:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)
(a − b)2 = (a − b)(a − b)
Если выполнить это умножение, то получится многочлен a2 − 2ab + b2
(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2
Пример 1.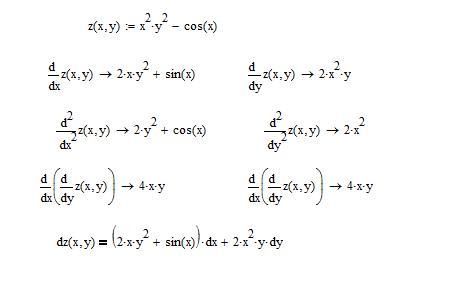 Преобразовать выражение (7x − 5)2 в многочлен.
Преобразовать выражение (7x − 5)2 в многочлен.
Воспользуемся формулой квадрата разности двух выражений:
(a − b)2 = a2 − 2ab + b2
(7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49x2 − 70x + 25
Значит, (7x − 5)2 = 49x2 − 70x + 25.
Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:
(7x − 5)2 = (7x − 5)(7x − 5) = 49x2 − 35x − 35x + 25 = 49x2 − 70x + 25.
Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a2, то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)2
Рассмотрим следующий рисунок:
Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b
У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b
Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:
Тогда можно написать следующее выражение: старая площадь a2 минус площадь ab минус площадь (a − b)b
a2 − ab − (a − b)b
Раскроем скобки в выражении (a − b)b
a2 − ab − ab + b2
Приведем подобные слагаемые:
a2 − 2ab + b2
В результате получается выражение a2 − 2ab + b2, которое является правой частью формулы квадрата разности двух выражений:
(a − b)2 = a2 − 2ab + b2
Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.
Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.
Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.
Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.
Например, если дано выражение (5x − 2y)2, и мы хотим воспользоваться формулой (a − b)2 = a2 − 2ab + b2, то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.
(5x − 2y)2
a = 5x
b = 2y
(5x − 2y)2 = (5x)2 − 2 × 5x × 2y + (2y)2 = 25x2 − 20xy + 4y2
Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:
(5x − 2y)2 = (5x + (−2y))2
и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:
(5x + (−2y)2
a = 5x
b = −2y
(5x + (−2y))2 = (5x)2 + 2 × 5x × (−2y) + (−2y)2 = 25x2 − 20xy + 4y2
Исключением могут быть выражения вида (x − (−y))2.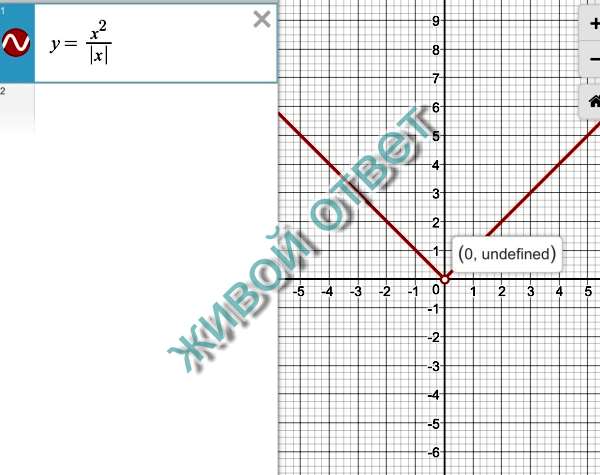 В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)
В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)
(x − (−y))2 = x2 − 2 × x × (−y) + (−y)2 = x2 + 2xy + y2
Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)2 и можно будет воспользоваться формулой квадрата суммы, а не разности:
(x + y)2 = x2 + 2xy + y2
Куб суммы и куб разности
Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Формулу куба суммы двух выражений можно прочитать так:
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
А формулу куба разности двух выражений можно прочитать так:
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.
Выведем формулу куба суммы самостоятельно:
(a + b)3
Выражение (a + b)3 представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)
(a + b)3 = (a + b)(a + b)(a + b)
Но выражение (a + b)3 также может быть записано как (a + b)(a + b)2
(a + b)3 = (a + b)(a + b)2
При этом сомножитель (a + b)2 является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a2 + 2ab + b2.
Этот квадрат суммы равен выражению a2 + 2ab + b2.
Тогда (a + b)3 можно записать как (a + b)(a2 + 2ab + b2).
(a + b)3 = (a + b)(a2 + 2ab + b2)
А это есть умножение многочлена на многочлен. Выполним его:
(a + b)3 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3
Аналогично можно вывести формулу куба разности двух выражений:
(a − b)3 = (a − b)(a2 − 2ab + b2) = a3 − 2a2b + ab2 − a2b + 2ab2 − b3 = a3 − 3a2b + 3ab2 − b3
Пример 1. Преобразуйте выражение (x + 1)3 в многочлен.
Преобразуйте выражение (x + 1)3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(x + 1)3 = x3 + 3 × x2 × 1 + 3 × x × 12 + 13 = x3 + 3x2 + 3x + 1
Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:
(x + 1)3 = (x + 1)(x + 1)(x + 1) = (x + 1)(x2 + 2x + 1) = x3 + 2x2 + x + x2 + 2x + 1 = x3 + 3x2 + 3x + 1
Пример 2. Преобразовать выражение (6a2 + 3b3)3 в многочлен.
Преобразовать выражение (6a2 + 3b3)3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(6a2 + 3b3)3= (6a2)3 + 3 × (6a2)2 × 3b3 + 3 × 6a2 × (3b3)2 + (3b3)3 = 216a6 + 3 × 36a4 × 3b3 + 3 × 6a2 × 9b6 + 27b9
Пример 3. Преобразовать выражение (n2 − 3)3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(a − b) = a3 − 3a2b + 3ab2 − b3
(n2 − 3)3 = (n2)3 − 3 × (n2)2 × 3 + 3 × n2 × 32 − 33 = n6 − 9n4 + 27n2 − 27
Пример 4. Преобразовать выражение (2x2 − x3)3 в многочлен.
Преобразовать выражение (2x2 − x3)3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(a − b) = a3 − 3a2b + 3ab2 − b3
(2x2 − x3)3 = (2x2)3 − 3 × (2x2)2 × x3 + 3 × 2x2 × (x3)2 − (x3)3 =
8x6 − 3 × 4x4 × x3 + 3 × 2x2 × x6 − x9 =
8x6 − 12x7 + 6x8 − x9
Умножение разности двух выражений на их сумму
Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:
Например:
(a − b)(a + b)
В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:
(a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2
То есть выражение (a − b)(a + b) равно a2 − b2
(a − b)(a + b) = a2 − b2
Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Случай (a − b)(a + b) можно распространить для любых a и b. Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.
Пример 1. Выполнить умножение (2x − 5)(2x + 5)
В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a2 − b2 имеем:
(2x − 5)(2x + 5) = (2x)2 − 52
Вычислим правую часть, получим 4x2 − 25
(2x − 5)(2x + 5) = (2x)2 − 52 = 4x2 − 25
Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a2 − b2. У нас получится тот же результат 4x2 − 25
(2x − 5)(2x + 5) = 4x2 − 10x + 10x − 25 = 4x2 − 25
Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(4x − 5y)(4x + 5y) = (4x)2 − (5y)2 = 16x2 − 25y2
Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)
Выполнить умножение (2a + 3b)(2a − 3b)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(2a + 3b)(2a − 3b) = (2a)2 − (3b)2 = 4a2 − 9b2
В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a2 − b2 разность располагается раньше.
Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a2 − b2, поскольку от перестановки сомножителей произведение не меняется.
Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b), так и (2a − 3b)(2a + 3b). Результат всё так же будет равен 4a2 − 9b2.
Пример 3. Выполнить умножение (7 + 3x)(3x − 7)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(7 + 3x)(3x − 7) = (3x)2 − 72 = 9x2 − 49
Пример 4. Выполнить умножение (x2 − y3)(x2 + y3)
(a − b)(a + b) = a2 − b2
(x2 − y3)(x2 + y3) = (x2)2 − (y3)2 = x4 − y6
Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)
Выполнить умножение (−5x − 3y)(5x − 3y)
В выражении (−5x − 3y) вынесем за скобки −1, тогда исходное выражение примет следующий вид:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)
Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2)
Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x)2. А это приведет к ошибке и изменению значения исходного выражения.
Далее вычисляем выражение в скобках:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25x2 − 9y2)
Теперь умножим −1 на выражение в скобках и получим окончательный результат:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) =
−1(25x2 − 9y2) = −25x2 + 9y2
Умножение разности двух выражений на неполный квадрат их суммы
Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:
Выглядит это произведение следующим образом:
(a − b)(a2 + ab + b2)
Первый многочлен (a − b) является разностью двух выражений, а второй многочлен (a2 + ab + b2) является неполным квадратом суммы этих двух выражений.
Неполный квадрат суммы это многочлен вида a2 + ab + b2. Он похож на обычный квадрат суммы a2 + 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Например, выражение 4x2 + 6xy + 9y2 является неполным квадратом суммы выражений 2x и 3y.
Действительно, первый член выражения 4x2 + 6xy + 9y2, а именно 4x2 является квадратом выражения 2x, поскольку (2x)2 = 4x2. Третий член выражения 4x2 + 6xy + 9y2, а именно 9y2 является квадратом выражения 3y, поскольку (3y)2 = 9y2. Член находящийся в середине 6xy, является произведением выражений 2x и 3y.
Третий член выражения 4x2 + 6xy + 9y2, а именно 9y2 является квадратом выражения 3y, поскольку (3y)2 = 9y2. Член находящийся в середине 6xy, является произведением выражений 2x и 3y.
Итак, умножим разность (a − b) на неполный квадрат суммы a2 + ab + b2
(a − b)(a2 + ab + b2) = a(a2 + ab + b2) − b(a2 + ab + b2) =
a3 + a2b + ab2 − a2b − ab2 − b3 = a3 − b3
То есть выражение (a − b)(a2 + ab + b2) равно a3 − b3
(a − b)(a2 + ab + b2) = a3 − b3
Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы. Эту формулу можно прочитать так:
Эту формулу можно прочитать так:
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.
Пример 1. Выполнить умножение (2x − 3y)(4x2 + 6xy + 9y2)
Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y. Второй многочлен 4x2 + 6xy + 9y2 это неполный квадрат суммы двух выражений 2x и 3y. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3. В нашем случае умножение (2x − 3y)(4x2 + 6xy + 9y2) можно заменить на разность кубов 2x и 3y
(2x − 3y)(4x2 + 6xy + 9y2) = (2x)3 − (3y)3 = 8x3 − 27y3
Попробуем решить этот же пример, не пользуясь формулой (a − b)(a2 + ab + b2) = a3 − b3. У нас получится тот же результат, но решение станет длиннее:
У нас получится тот же результат, но решение станет длиннее:
(2x − 3y)(4x2 + 6xy + 9y2) = 2x(4x2 + 6xy + 9y2) − 3y(4x2 + 6xy + 9y2) =
8x3 + 12x2y + 18xy2 − 12x2y − 18xy2 − 27y3 = 8x3 − 27y3
Пример 2. Выполнить умножение (3 − x)(9 + 3x + x2)
Первый многочлен (3 − x) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3
(3 − x)(9 + 3x + x2) = 33 − x3 = 27 − x3
Умножение суммы двух выражений на неполный квадрат их разности
Встречаются задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Выглядит это произведение следующим образом:
Выглядит это произведение следующим образом:
(a + b)(a2 − ab + b2)
Первый многочлен (a + b) является суммой двух выражений, а второй многочлен (a2 − ab + b2) является неполным квадратом разности этих двух выражений.
Неполный квадрат разности это многочлен вида a2 − ab + b2. Он похож на обычный квадрат разности a2 − 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Например, выражение 4x2 − 6xy + 9y2 является неполным квадратом разности выражений 2x и 3y.
(2x)2 − 2x × 3y + (3y)2 = 4x2 − 6xy + 9y2
Вернёмся к изначальному примеру. Умножим сумму a + b на неполный квадрат разности a2 − ab + b2
Умножим сумму a + b на неполный квадрат разности a2 − ab + b2
(a + b)(a2 − ab + b2) = a(a2 − ab + b2) + b(a2 − ab + b2) =
a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3
То есть выражение (a + b)(a2 − ab + b2) равно a3 + b3
(a + b)(a2 − ab + b2) = a3 + b3
Это тождество называют формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:
Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.
Пример 1. Выполнить умножение (2x + 3y)(4x2 − 6xy + 9y2)
Первый многочлен (2x + 3y) это сумма двух выражений 2x и 3y, а второй многочлен 4x2 − 6xy + 9y2 это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3. В нашем случае умножение (2x + 3y)(4x2 − 6xy + 9y2) можно заменить на сумму кубов 2x и 3y
(2x + 3y)(4x2 − 6xy + 9y2) = (2x)3 + (3y)3 = 8x3 + 27y3
Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:
У нас получится тот же результат, но решение станет длиннее:
(2x + 3y)(4x2 − 6xy + 9y2) = 2x(4x2 − 6xy + 9y2) + 3y(4x2 − 6xy + 9y2) =
8x3 − 12x2y + 18xy2 + 12x2y − 18xy2 + 27y3 = 8x3 + 27y3
Пример 2. Выполнить умножение (2x + y)(4x2 − 2xy + y2)
Первый многочлен (2x + y) является суммой двух выражений, а второй многочлен (4x2 − 2xy + y2) является неполным квадратом разности этих выражений. Это позволяет воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3
(2x + y)(4x2 − 2xy + y2) = (2x)3 + y3 = 8x3 + y3
Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:
У нас получится тот же результат, но решение станет длиннее:
(2x + y)(4x2 − 2xy + y2) = 2x(4x2 − 2xy + y2) + y(4x2 − 2xy + y2) =
8x3 − 4x2y + 2xy2 + 4x2y − 2xy2 + y3 = 8x3 + y3
Задания для самостоятельного решения
Задание 1. Преобразуйте выражение (m + n)2 в многочлен.
Решение:
(m + n)2 = m2 + 2mn + n2
Задание 2. Преобразуйте выражение (x + 8)2 в многочлен.
Решение:
(x + 8)2 = x2 + 2 × x × 8 + 82 = x2 + 16x + 64
Задание 3. Преобразуйте выражение (2x2 + 3x3)2 в многочлен.
Преобразуйте выражение (2x2 + 3x3)2 в многочлен.
Решение:
(2x2 + 3x3)2 = (2x2)2 + 2 × 2x2 × 3x3 + (3x3)2 = 4x4 + 12x5 + 9x6
Задание 4. Преобразуйте выражение (5a + 5)2 в многочлен.
Решение:
(5a + 5)2 = (5a)2 + 2 × 5a × 5 + 52 = 25a2 + 50a + 25
Задание 5. Преобразуйте выражение (9 − x)2 в многочлен.
Решение:
(9 − x)2 = 92 − 2 × 9 × x + x2 = 81 − 18x + x2
Задание 6. Преобразуйте выражение (x − 25)2 в многочлен.
Решение:
(x − 25)2 = x2 − 2 × x × 25 + 252 = x2 − 50x + 625
Задание 7. Преобразуйте выражение (3x2 − y3)2 в многочлен.
Преобразуйте выражение (3x2 − y3)2 в многочлен.
Решение:
(3x2 − y3)2 = (3x2)2 − 2 × 3x2 × y3 + ( y3)2 = 9x4 − 6x2y3 + y6
Задание 8. Выполните умножение (x − y)(x + y)
Решение:
(x − y)(x + y) = x2 − y2
Задание 9. Выполните умножение (2x − y)(2x + y)
Решение:
(2x − y)(2x + y) = (2x)2 − y2 = 4x2 − y2
Задание 10. Выполните умножение (7 + 3y)(3y − 7)
Решение:
(7 + 3y)(3y − 7) = (3y)2 − 72 = 9y2 − 49
Задание 11. Выполните умножение (x2 − 5)(x2 + 5)
Выполните умножение (x2 − 5)(x2 + 5)
Решение:
(x2 − 5)(x2 + 5) = (x2)2 − 52 = x4 − 25
Задание 12. Выполните умножение (a3 − b2)(a3 + b2)
Решение:
(a3 − b2)(a3 + b2) = (a3)2 − (b2)2 = a6 − b4
Задание 13. Выполните умножение (5a2 + 2b3)(5a2 − 2b3)
Решение:
(5a2 + 2b3)(5a2 − 2b3) = (5a2)2 − (2b3)2 = 25a4 − 4b6
Задание 14. Выполните умножение (9x − y2)(y2 + 9x)
Выполните умножение (9x − y2)(y2 + 9x)
Решение:
(9x − y2)(y2 + 9x) = (9x)2 − (y2)2 = 81x2 − y4
Задание 15. Выполните умножение (2 − x)(4 + 2x + x2)
Решение:
(2 − x)(4 + 2x + x2) = 23 − x3 = 8 − x3
Задание 16. Выполните умножение (3 − 2)(9 + 6 + 4)
Решение:
(3 − 2)(9 + 6 + 4) = 33 − 23 = 27 − 8 = 19
Задание 17. Выполните умножение (4x + 1)(16x2 − 4x + 1)
Решение:
(4x + 1)(16x2 − 4x + 1) = (4x)3 + 13 = 64x3 + 1
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Формулы сокращенного умножения / Блог / Справочник :: Бингоскул
Содержание:
- Таблица формул сокращенного умножения
- Примеры использования
- Формулы для квадратов
- Формулы для кубов
- Формулы для четвертой степени
Таблица формул сокращенного умножения
Примеры использования формул
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a+b)2 = a2+2ab+b2
Пример: (x + 3y)2 = x2 + 2 ·x·3y + (3y)2 = x2 + 6xy + 9y2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a-b)2 = a2-2ab+b2
Пример: (4x –y)2 = (4x)2-2·4x·y + y2 = 16x2 — 8xy + y2
Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.
a2–b2 = (a–b)(a+b)
Пример: 9x2 – 16y2 = (3x)2 – (4y)2 = (3x – 4y)(3x + 4y)
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a+b)3 = a3+3a2b+3ab2+b3
Пример: (x + 2y)3 = x3 + 3·x2·2y + 3·x·(2y)2 + (2n)3 = x3 + 6x2y + 12xy2 + 8y3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a-b)3 = a3— 3a2b+3ab2-b3
Пример: (2x – y)3 = (2x)3-3·(2x)2·y + 3·2x·y2 – y3 = 8x3 – 12x2y + 6xy2 – y3
Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.
a3+b3 = (a+b)(a2–ab+b2)
Пример: 125 + 8y3 = 53 + (2y)3 = (5 + 2y)(52 — 5·2y + (2y)2) = (5 + 2y)(25 – 10y + 4y2)
Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы. 2)
2)
В заданиях ЕГЭ по математике применяются формулы сокращенного умножения.
Решай с ответами задание 5 по математике база ЕГЭ
Смотри также: Основные формулы по математике
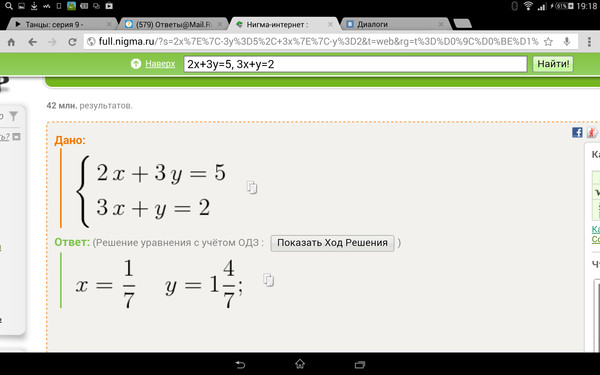
Система Икс плюс игрек равно 6 икс квадрат минус игрек квадрат равно 12
Ответ:
Объяснение:
Пусть Х — кол-во человек планировалось в 1 автобусе, тогда
150/х — автобусов заказали изначально;
Х-2 -чел разместились по факту
168/Х-2 — автобусов пришлось заказать (на 1 больше планируемого), значит:
168/х-2=150/х + 1
168х-150(х-2) /х(х-2) =1
18х+300=х²-2х
х²-20х-300=0
Д= 400+1200=1600
х1= (20-40)/2 = -10 не является решением
х2= (20+40)/2 = 30 чел. планировалось в 1 автобусе
планировалось в 1 автобусе
168÷(30-2) = 6 заказали в итоге.
Или 150:30=5 было заказано изначально
Пусть х — скорость первого
(х + 6) — скорость второго
2х — расстояние, пройденное первым за 2 часа после встречи
2 * (х +6) — расстояние, пройденное вторым за 2 часа после встречи
Уравнение находим с помощью теоремы Пифагора, т.к они двигались под прямым углом по отношению друг к другу.
(2х)² + (2х + 12)² = 60²
4х² + 4х² + 48 х + 144 = 3600
8х² + 48х — 3456 = 0
х² + 6х — 432 = 0
D = 6² — 4 * 1 * (- 432) = 36 + 1728 = 1764 = 42²
√D = 42
x₁ = (- 6 + 42)/2 = 36/2 = 18
x₂ = (- 6 — 42) /2 = — 24 отрицательное значение не уловлетворяет
18 км/ч — скорость первого
18 + 6 = 24 км/ч — скорость второго
Ответ: 18 км/ч; 24 км/ч
20ab-5(4+4b+b^2)
20ab-20-20ab-5b^2
-5b^2-20
-5b^2=20
b^2=4
b=2 или b= -2
Найдите вероятность того, что наугад выбранное двузначное число не будет кратно 25.
Решение:
Всего двузначных чисел — 90.
Кратны 25 три числа: 25,50,75.
Не кратны 25: 90-3=87 чисел.
Вероятностью называется отношение числа благоприятных исходов к общему числу равновозможных исходов.
Ответ:
12 квадратов: математические факты
Хотите увлекательный способ попрактиковаться в математических фактах для сложения, вычитания, умножения и / или деления? Попробуйте эту простую игру в кости под названием «12 квадратов». Он идеально подходит для быстрого просмотра в любое время, и в него можно играть несколькими способами! Я обнаружил, что это не только помогает с математическими фактами, но также требует некоторой логики!
В прошлом году я сделал несколько игр в кости на рождественскую тематику для нашей группы домашнего обучения, и это занятие произвело большой успех у наших младших школьников.Младшие дети (в основном детсадовцы и первоклассники) играли в нее со сложением и вычитанием, а старшие дети {со 2-го по 3-й классы} играли в нее со сложением, вычитанием, умножением и делением!
Для загрузки нажмите овальную кнопку в конце этого поста. Инструкции к каждой игре включены в загрузку.
Инструкции к каждой игре включены в загрузку.
* Этот пост содержит партнерские ссылки.
Веселая математическая игра
Мой сын {4-й класс} учится в замечательной частной школе для детей с трудностями в обучении в этом учебном году.Одно из его заданий каждую ночь — практиковать математические факты в течение 5 минут. Не знаю, как вы, но изучение математических фактов с помощью флеш-карт — это далеко не мое увлечение. Мы делали разные вещи, чтобы практиковать его факты, и эта игра — одна из таких.
Это может показаться простым, поскольку в нем используются только два кубика, но если вы добавите таймер или еще одного игрока, игра быстро станет сложной.
И мне нравится, что это требует от детей немного нестандартного мышления, расширяя свои представления о двух числах, которые они бросили на кости.В зависимости от того, что бросают дети, ответов может быть несколько. Задача ребенка — выяснить, какую операцию он хочет использовать, чтобы раскрыть (или скрыть) числа из своих 12 квадратов.
Например, если ребенок выбрасывает 6 и 3, он может сложить их, чтобы получить 9.
Или он мог бы вычесть 3 из 6, чтобы получить 3.
Или он мог бы даже разделить 3 на 6, чтобы получить 2.
В загрузке есть несколько версий.Я обнаружил, что при раскрытии лучше всего использовать прозрачные манипуляторы, чтобы дети могли легко видеть числа, например прозрачные счетчики.
В одной из версий игры детям предлагается накрыть доску. В этой игре вы можете использовать кубики привязки и складывать их, когда выпадает один и тот же ответ. Интересно посмотреть, какая «башня» вырастет выше всего.
Когда дети работают над чем-то самостоятельно, хорошо иметь часть подотчетности, чтобы вы могли «видеть», что сделал ребенок.Поскольку в этой игре нет встроенного элемента подотчетности, я его создал! Дети записывают составленные ими числовые предложения на листе для записи.
И если у вас есть два ученика, которые примерно равны в своих знаниях математических фактов, есть версия для двух игроков, которая делает игру немного более конкурентоспособной.
Другие задания по математике:
~ Бекки
квадратов сложения и умножения
Вы помните эту старую игру, в которую мы играли в детстве: нам требовались только квадратная бумага и ручки или карандаши разного цвета для каждого игрока.Затем каждый игрок в свой ход рисует одну сторону квадрата. Игрок, который рисует последнюю сторону квадрата, окрашивает этот квадрат в свой цвет и рисует еще одну линию. Когда все квадраты окрашены, игрок с наибольшим количеством цветных квадратов становится победителем. Используя ту же стратегию, добавляя некоторые числа, неопределенность и математику, игра в квадраты может стать более интересной, игровой и познавательной одновременно. Приблизительный уровень: Математика 1-го класса для сложения квадратов и Математика 3-го класса для квадратов умножения.Во-первых, я хотел бы поблагодарить Games 4 Gains за «математизацию» игры Squares. На своем сайте у них есть различные игры в квадраты для отработки математических навыков, такие как игры в квадраты для сложения, вычитания, умножения, деления, множителей, кратных, простых и составных чисел. Идея и основные правила игры те же, что и в старой игре Squares Game, а главное отличие заключается в способе получения чисел, который зависит от того, какой математический навык вы практикуете. Я выбрал для презентации два «математических» варианта игры — Квадраты сложения и умножения.Здесь вы можете найти игровые доски для этих игр, которые отличаются от игровых досок Games 4 Gains размером, частотой и распределением чисел, которые я объясню позже.
Приблизительный уровень: Математика 1-го класса для сложения квадратов и Математика 3-го класса для квадратов умножения.Во-первых, я хотел бы поблагодарить Games 4 Gains за «математизацию» игры Squares. На своем сайте у них есть различные игры в квадраты для отработки математических навыков, такие как игры в квадраты для сложения, вычитания, умножения, деления, множителей, кратных, простых и составных чисел. Идея и основные правила игры те же, что и в старой игре Squares Game, а главное отличие заключается в способе получения чисел, который зависит от того, какой математический навык вы практикуете. Я выбрал для презентации два «математических» варианта игры — Квадраты сложения и умножения.Здесь вы можете найти игровые доски для этих игр, которые отличаются от игровых досок Games 4 Gains размером, частотой и распределением чисел, которые я объясню позже.Дополнение Квадраты Игра
Позвольте мне объяснить правила игры в Addition Squares Game. Игра рассчитана на 2 и более игроков в возрасте от 7 лет и старше.
 Вам понадобится игровая доска (квадраты с числами, которые вы можете скачать по ссылкам ниже), 2 кубика и карандаш разного цвета для каждого игрока. Вот правила игры:
Вам понадобится игровая доска (квадраты с числами, которые вы можете скачать по ссылкам ниже), 2 кубика и карандаш разного цвета для каждого игрока. Вот правила игры: - Сначала, бросив кости, решите, кто начнет игру.Игрок с наибольшим номером начинает первым.
- На каждом ходу игрок бросает оба кубика и складывает числа.
- Затем игрок ищет на доске квадрат, содержащий сумму чисел, и рисует одну сторону этого квадрата.
- Если игрок вытащил последнюю сторону квадрата, он окрашивает этот квадрат в свой цвет и снова бросает оба кубика, в противном случае очередь игрока бросает кубики.
- Если на доске нет доступного квадрата, содержащего сумму чисел, ход игрока заканчивается, и следующий игрок бросает оба кубика.
- Игра окончена, когда все квадраты на доске окрашены, и игрок с наибольшим количеством цветных квадратов становится победителем.
Чем привлекательна эта игра для детей и их учителей? Это игра, и в ней можно выиграть.
 Итак, стратегия нужна каждый раз, когда принимается решение о раскраске стороны квадрата. И самое главное — даже дети с низкими математическими навыками могут выиграть игру! Бросок кубиков неуверен, и, несмотря на математические навыки, могут быть выброшены благоприятные числа.Эта функция делает игру более увлекательной для этих детей. Они отрабатывают математические навыки, не сосредотачиваясь на практике, что дает учителям еще один эффективный образовательный инструмент для их класса математики.
Итак, стратегия нужна каждый раз, когда принимается решение о раскраске стороны квадрата. И самое главное — даже дети с низкими математическими навыками могут выиграть игру! Бросок кубиков неуверен, и, несмотря на математические навыки, могут быть выброшены благоприятные числа.Эта функция делает игру более увлекательной для этих детей. Они отрабатывают математические навыки, не сосредотачиваясь на практике, что дает учителям еще один эффективный образовательный инструмент для их класса математики. Хочу отметить, что игра с добавлением квадратов может занять много времени, если используется большое игровое поле 10 × 10. Итак, я сделал две меньшие игровые доски, среднюю игровую доску 7 × 7 и маленькую игровую доску 5 × 5. Рекомендую начинать играть на досках меньшего размера. Вы можете загрузить игровые доски и инструкции к игре, щелкнув ссылку для загрузки рядом с каждой игрой Addition Squares:
Игра в квадраты умножения
Как вы полагаете, с помощью квадратов умножения вместо того, чтобы складывать числа, выпавшие на обоих кубиках, мы их умножаем. Опять же, игра рассчитана на 2 или более игроков, но теперь от 8 лет и старше. Вам понадобится игровая доска для квадратов умножения (вы можете скачать по ссылкам ниже), 2 кубика и карандаш разного цвета для каждого игрока. Вот правила этой игры:
Опять же, игра рассчитана на 2 или более игроков, но теперь от 8 лет и старше. Вам понадобится игровая доска для квадратов умножения (вы можете скачать по ссылкам ниже), 2 кубика и карандаш разного цвета для каждого игрока. Вот правила этой игры: - Сначала, бросив кости, решите, кто начнет игру. Игрок с наибольшим номером начинает первым.
- На каждом ходу игрок бросает оба кубика и умножает числа.
- Затем игрок ищет на доске квадрат, который содержит произведение чисел, и рисует одну сторону этого квадрата.
- Если игрок вытащил последнюю сторону квадрата, он окрашивает этот квадрат в свой цвет и снова бросает оба кубика, в противном случае очередь игрока бросает кубики.
- Если на доске нет доступных квадратов, содержащих произведение чисел, ход игрока заканчивается, и следующий игрок бросает оба кубика.
- Игра окончена, когда все квадраты на доске окрашены, и игрок с наибольшим количеством цветных квадратов становится победителем.

Опять же, рекомендуется начать с меньших игровых досок.Вы можете загрузить игровые доски и инструкции к игре, щелкнув ссылку для загрузки рядом с каждой игрой в квадраты умножения:
Как я делал игровые доски?
Я объясню здесь конструкцию игрового поля для Addition Squares. Поскольку мы играем двумя кубиками, это означает, что сумма чисел на кубиках — это число от 2 до 12 включительно. Но не все суммы выпадут с одинаковой вероятностью. Например, сумма, равная 2, может появиться только в том случае, если на обоих кубиках будет 1, а сумма, равная 4, может появиться, если у нас есть 1 и 3, 2 и 2 или 3 и 1.И поскольку каждое число от 1 до 6 с одинаковой вероятностью выпадет на кубике, это означает, что вероятность выпадения суммы, равной 4, в три раза выше, чем суммы, равной 1. Следовательно, если мы хотим получить более реалистичную сумму игровое поле, мы должны поставить на него в три раза больше четверок, чем двоек.
В следующей таблице показано количество различных способов получить каждую из сумм от 2 до 12 путем броска двух кубиков и вероятность (в процентах) выпадения соответствующей суммы.
Теперь на доске 10 × 10 100 квадратов и 2.78% из них должны быть 2s, 5,56% из них должны быть 3s, 8,33% из них должны быть 4s и так далее, или 2,78 квадрата должны быть 2s, 5,56 квадрата должны быть 3s, 8,33 квадрата должны быть 4s и т. Д. на. Но количество квадратов также должно быть целым числом, поэтому я округлил их до ближайшего целого числа, а затем внес некоторые поправки, чтобы сохранить их сумму равной 100. Таким образом я получил следующее приближение количества квадратов. за каждую сумму, которую нужно положить на доску 10 × 10:
Пока я распределял числа на доске, я помещал числа с меньшей вероятностью появления внутри доски.По краям и углам доски я помещаю числа, у которых больше шансов появиться, так как эти квадраты имеют менее общие стороны с другими квадратами на доске. Таким образом я получил следующую большую доску для сложения квадратов:
Я проделал то же самое для досок 7 × 7 и 5 × 5, которые имеют 49 и 25 квадратов соответственно. Вы можете найти эти доски по указанным выше ссылкам для скачивания.
Вы можете найти эти доски по указанным выше ссылкам для скачивания.
Определив вероятность появления всех возможных продуктов, я сделал те же поправки в количестве квадратов с тем же продуктом, что и с дополнительными квадратами, и для доски 10 × 10 я получил следующее приближение количества квадратов для каждый возможный товар, который следует поставить на доску:
И снова я распределил более вероятные продукты по краям и углам доски, а менее вероятные продукты — внутри доски.Таким образом я получил следующую большую доску для квадратов умножения:
Вы можете найти две другие доски меньшего размера, 7 × 7 и 5 × 5, по указанным выше ссылкам для скачивания.
 Вы также можете создавать свои собственные квадраты сложения и умножения, даже с разными размерами досок.
Вы также можете создавать свои собственные квадраты сложения и умножения, даже с разными размерами досок.Надеюсь, вам и вашим детям понравятся эти математические игры.
квадратов Суперкубка | Блог Serendipit Consulting
Как играть на квадратах Суперкубкаквадратов Суперкубка — один из старейших способов повеселиться во время большой игры.Вы можете создать свою собственную сетку или загрузить нашу бесплатную распечатанную сетку квадратов Суперкубка здесь. Сэкономьте время на создание сетки и поиск линейки — просто распечатайте нашу сетку!
Серые прямоугольники представляют возможные комбинации очков в игре, левые серые прямоугольники представляют чемпиона команды NFC (Каролина Пантерс), а верхние серые прямоугольники представляют командного чемпиона AFC (Денвер Бронкос).
Правила игры Есть 100 игровых полей (белые квадраты).Серые прямоугольники, идущие слева и вверху игры, предназначены для случайного присвоения чисел от 0 до 9 ПОСЛЕ того, как все белые квадраты будут заполнены.
Чтобы заполнить сетку из белых квадратов, участники пишут свои имена, на каких квадратах они хотят. «Комиссар» игры (ВЫ!) Определяет цену за квадрат. 1, 2, 5 или 10 долларов — все, что вы считаете, будет работать для вашей группы друзей, семьи или коллег. Собирайте деньги по мере того, как люди заполняют свои квадраты, чтобы вы могли отслеживать и не гоняться за игроками за деньги.
Будьте готовы заполнить серые квадраты слева и над белыми квадратами. Напишите числа от 0 до 9 на отдельных листах бумаги, сложите их и положите в миску или шляпу. Вы будете случайным образом рисовать числа, чтобы заполнить левое и верхнее серые поля, чтобы игра в квадраты была честной и не давала преимущества никому, включая вас. После того, как вы нарисуете все числа и заполните левые серые поля (двигайтесь сверху вниз), сложите числа обратно, поместите их обратно в шляпу и затем повторите процесс для верхних серых прямоугольников, начиная с слева направо.
Убедитесь, что ваша сетка квадратов Суперкубка заполнена до начала большой игры! Соберите все деньги и определите, как вы хотите наградить победителя (ов). Обычно в конце каждого квартала определяется один победитель. Победитель определяется текущим счетом игры. Например: если в конце игры счет Денвер 10, Каролина 21, вы найдете число 0 в верхнем ряду и число 1 в левом ряду и найдете белое поле, где эти два числа пересекаются.Человек, имя которого указано в поле, в победителе данной четверти.
Обычно в конце каждого квартала определяется один победитель. Победитель определяется текущим счетом игры. Например: если в конце игры счет Денвер 10, Каролина 21, вы найдете число 0 в верхнем ряду и число 1 в левом ряду и найдете белое поле, где эти два числа пересекаются.Человек, имя которого указано в поле, в победителе данной четверти.
«Комиссар» игры в квадраты должен решить, будет ли определен победитель 4-й четверти по счету в 4-й четверти или по общему счету игры в случае овертайма. В большинстве случаев окончательный счет игры определяет победителя 4-й четверти.
Пример структуры выплат Super Bowl SquaresНаиболее распространенный способ структурирования выплаты — один победитель в каждой четверти (1-й, 2-й и 3-й), а затем 4-й победитель в финальном квадрате.Выплаты могут быть равными или увеличиваться с каждым кварталом, при этом наибольший выигрыш в игре достигается за счет окончательного результата игры.
Допустим, вы получаете скидку 10 долларов за квадрат.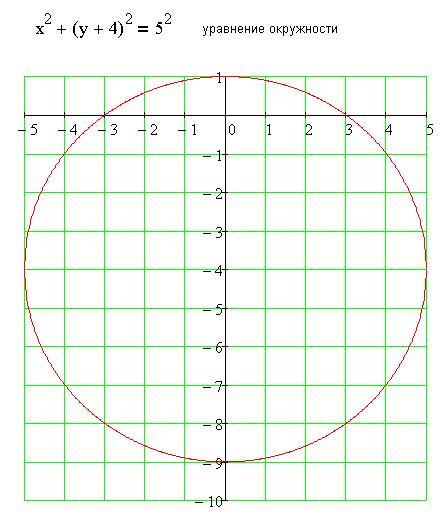 Это дает вам банк в размере 1000 долларов, который можно разделить между 4 четвертями игры. Вы можете разделить его поровну, с 250 долларами каждому победителю в конце каждого квартала, или вы можете чередовать выигрыши, чтобы увеличиваться с каждым кварталом. Пример может выглядеть так: 1-й квартал: 150 долларов — 2-й квартал: 200 долларов — 3-й квартал: 300 долларов — 4-й квартал: 350 долларов.Вы можете разделить выигрыш, как хотите, но просто убедитесь, что он четко обозначен для каждого игрока, прежде чем продавать квадраты.
Это дает вам банк в размере 1000 долларов, который можно разделить между 4 четвертями игры. Вы можете разделить его поровну, с 250 долларами каждому победителю в конце каждого квартала, или вы можете чередовать выигрыши, чтобы увеличиваться с каждым кварталом. Пример может выглядеть так: 1-й квартал: 150 долларов — 2-й квартал: 200 долларов — 3-й квартал: 300 долларов — 4-й квартал: 350 долларов.Вы можете разделить выигрыш, как хотите, но просто убедитесь, что он четко обозначен для каждого игрока, прежде чем продавать квадраты.
Имейте в виду — один человек может выиграть более одного раза… все зависит от того, где находятся их квадраты, поскольку игроки могут покупать столько квадратов, сколько захотят. Если у вас большая группа или офис, возможно, вам сначала придется ограничить количество квадратов для каждого игрока, чтобы у всех была возможность играть.
Пусть начинается самое интересное!
Гольф — Правила карточной игры
Спасибо многим людям, которые предоставили информацию о различных версиях этой игры.
Введение
Гольф — карточная игра для двух или более игроков, цель которой — набрать как можно меньше очков, как в игре в гольф. Перед каждым игроком выложены карты, расположенные в квадрате или прямоугольнике, и игроки улучшают свои очки, вытягивая новые карты взамен ненужных карт, которые они сбрасывают. Каждая сделка рассматривается как эквивалент лунки в гольф, и во многих версиях полная игра состоит из 9 или 18 раздач, соответствующих длине поля для гольфа.
Хотя карточная игра Гольф довольно широко распространена в Северной Америке, Великобритании и, возможно, других англоязычных странах, ее редко можно найти в книгах по карточным играм. Гольф также иногда называют Polish Polka или Polish Poker ; 4-карточная игра известна некоторыми игроками как Turtle , 6-карточная игра как Hara Kiri , а 9-карточная игра как Crazy Nines . Игра в гольф, описанная на этой странице, не имеет никакого отношения к одноименной игре «Пасьянс» («Терпение»).
У каждого игрока есть раскладка карт, изначально лицом вниз, которые могут быть последовательно заменены новыми картами, взятыми из колоды или стопки сброса. Цель состоит в том, чтобы макет как можно меньше набирал очки. Счет в конце игры иногда считается количеством ударов, сделанных для игры в лунку. Обычно разыгрывается серия из девяти раздач или «лунок», в конце которой побеждает игрок с наименьшим общим счетом.
Есть две основные формы игры, которые я назову 4-карточным гольфом и 6-карточным гольфом, в зависимости от количества карт в раскладке каждого игрока.В 4-карточный гольф иногда играют с картами силы, которые позволяют игроку выполнить действие, например, взглянуть на карту, поменять местами карту с другим игроком и так далее. Есть также 8-карточные, 9-карточные и 10-карточные формы гольфа, но они, кажется, менее распространены.
Основное различие между версиями Golf заключается в способе завершения игры.
- Первый метод, наиболее часто используемый в 4-карточном гольфе, заключается в том, что если вы думаете, что у вас наименьшее количество очков, вы можете использовать свой ход, чтобы сбить ногу, вместо того, чтобы вытягивать одну из своих карт.
 Это приводит к тому, что игра заканчивается после того, как каждый из других игроков сделает еще один ход.
Это приводит к тому, что игра заканчивается после того, как каждый из других игроков сделает еще один ход. - Второй метод, который чаще всего используется с макетами с 6 и более крупными картами, заключается в том, что всякий раз, когда карта макета заменяется, новая карта кладется лицевой стороной вверх. Игра заканчивается, как только любой игрок оказывается лицом вверх.
Гольф с четырьмя картами
Игроки, карты и сделки
Используется стандартный набор из 52 карт, и теоретически количество игроков может составлять от двух до восьми и более, хотя считается, что в игре лучше всего четыре.При большом количестве игроков, скажем, восьми или более, две колоды могут быть перемешаны вместе. Раздача и игра идут по часовой стрелке.
Дилер раздает по четыре карты каждому игроку. Карты каждого игрока должны быть выложены лицевой стороной вниз в виде квадрата. Оставшиеся невыносимые карты кладутся лицевой стороной вниз в центр стола, чтобы сформировать колоду для вытягивания. Верхняя карта колоды переворачивается лицевой стороной вверх и кладется рядом с колпаком, чтобы начать колоду сброса. Перед началом игры каждый игрок может один раз взглянуть на две ближайшие карты своей квадратной раскладки, не показывая их никому.После этого карты раскладки нельзя просматривать снова, пока они не будут сброшены во время игры или не будут подсчитаны в конце игры.
Верхняя карта колоды переворачивается лицевой стороной вверх и кладется рядом с колпаком, чтобы начать колоду сброса. Перед началом игры каждый игрок может один раз взглянуть на две ближайшие карты своей квадратной раскладки, не показывая их никому.После этого карты раскладки нельзя просматривать снова, пока они не будут сброшены во время игры или не будут подсчитаны в конце игры.
Игра
Начинает игрок слева от дилера, и ход игры проходит по часовой стрелке. В свой ход вы должны либо вытянуть верхнюю карту из лежащей лицом вниз, либо взять верхний сброс, либо стукнуть, чтобы игра закончилась.
- Если вы вытягиваете карту, вы можете использовать ее для замены одной из четырех карт вашего макета, но вам не разрешено просматривать любую из ваших карт макета, прежде чем решить, какую из них заменить.Вы кладете вытянутую карту лицевой стороной вниз в свою раскладку, стараясь запомнить, что это такое, и сбрасываете карту, которая ранее занимала эту позицию, кладя ее лицевой стороной вверх поверх стопки сброса.
 Затем наступает очередь следующего игрока.
Затем наступает очередь следующего игрока. - Если вы берете карту из колоды и решаете, что не хотите использовать ее в своей раскладке, вы можете просто сбросить вытянутую карту лицевой стороной вверх в стопку сброса, и тогда наступает очередь следующего игрока. Однако, если вы решите взять сброс, вы должны использовать его, чтобы заменить одну из ваших карт раскладки — вы не можете просто положить его обратно в стопку сброса, оставив ситуацию в прежнем виде.
- Если вы стучите, вы больше ничего не делаете в свой ход. У каждого из остальных игроков в очереди есть еще один обычный ход (в котором они берут карту из колоды или стопки сброса, но не могут сбить с ног), и затем игра заканчивается.
Обратите внимание, что если вы посмотрите на любую карту, лежащую лицом вниз, в своем раскладе вы увидите, что карта должна быть сброшена и заменена на карту, которую вы вытащили. Невозможно проверить значение закрытой карты и оставить ее на месте.
Подсчет очков
В конце игры квадрат из четырех карт каждого игрока переворачивается лицом вверх и оценивается следующим образом.
- Каждая цифровая карта имеет номинальную стоимость (Туз = 1, Двойка = 2 и т. Д.)
- Каждый валет или дама получает 10 очков.
- Каждый Король получает ноль очков.
Побеждает игрок, набравший наименьшее совокупное количество очков после девяти раздач.
Варианты четырехкарточного гольфа
Глядя в карты
Некоторые игры, в которых вы можете выбрать любые две карты для просмотра перед началом игры — не обязательно две ближайшие к вам карты. Некоторые считают, что вначале вы можете смотреть только одну из своих четырех карт.
Некоторая игра, в которой вы можете смотреть любую из своих четырех карт во время игры, по цене 1 очко за каждый раз, когда вы смотрите на карту, добавляемую к вашему счету в конце руки.
В некоторых играх вы можете смотреть на две карты, которые вы видели в начале, или на их замену в вашем раскладе так часто, как вам нравится во время игры. Некоторые играют так, что вы держите эти две карты в руке, чтобы вы (но не другие игроки) могли видеть их в любое время. Некоторые даже играют так, что вы держите в руке все четыре карты, что устраняет необходимость запоминать какие-либо карты и устраняет неуверенность в отношении ваших двух невидимых карт.
Некоторые даже играют так, что вы держите в руке все четыре карты, что устраняет необходимость запоминать какие-либо карты и устраняет неуверенность в отношении ваших двух невидимых карт.
Замена карт
Некоторые считают, что две карты, которые вы не смотрели вначале, можно заменить только один раз. Две карты, которые вы видите в начале, можно менять так часто, как вы хотите.
Переворачивание карт лицом вверх; окончание пьесы
Этот вариант характерен для гольфа с шестью или более картами, но иногда в него играют и в гольф с четырьмя картами. Каждый раз, когда карта заменяется, новая карта кладется в раскладку лицевой стороной вверх. Когда все карты, принадлежащие одному игроку, открыты, игра заканчивается после того, как у каждого из других игроков будет еще один ход.
Некоторые играют так, что все четыре карты начинаются рубашкой вверх, а карта, лежащая лицом вверх, не может быть заменена. Если вы заменяете карту лицевой стороной вниз, новая карта кладется лицевой стороной вверх. Если вы берете карту из колоды и сбрасываете ее, вы должны перевернуть одну из карт вашего расклада лицевой стороной вверх, и эта карта не может быть впоследствии заменена. В результате на каждом ходу открывается еще одна карта вашего макета. Игра заканчивается, когда все игроки открывают все свои карты.
Если вы берете карту из колоды и сбрасываете ее, вы должны перевернуть одну из карт вашего расклада лицевой стороной вверх, и эта карта не может быть впоследствии заменена. В результате на каждом ходу открывается еще одна карта вашего макета. Игра заканчивается, когда все игроки открывают все свои карты.
Альтернативные методы подсчета очков
Некоторые играют так, что если ваш расклад содержит пару равных карт (например, две девятки), счет для этой пары карт равен нулю.Если есть три одинаковые карты, таким образом аннулируются только две из них; если все четыре карты равны, весь макет получает ноль. Некоторые играют, что пары получают ноль, только если карты вместе в ряд или столбец; одинаковые карты, находящиеся в противоположных по диагонали углах, не отменяются.
В некоторых вариантах ферзям дается более высокий балл — 12, 13 или даже 20 очков вместо 10; в одном варианте дама пик получает 40 очков, а в других — 10; в этом же варианте восьмерки получают ноль.
Некоторые играют, что одноглазые валеты являются дикими — их можно объединить в пару с любой картой, в результате чего пара получит ноль.
В некоторых играх валеты получают ноль, например короли. Другие играют, что валеты получают ноль, дамы 12 и короли 13.
В некоторых играх валеты получают 20 очков, и когда валет сбрасывается, следующий игрок пропускает ход — ход игры переходит к следующему игроку.
Некоторые добавляют в колоду два джокера; оценка за джокер минус 5, поэтому общая оценка за раскладку может быть отрицательной.
Оценка для молотка
Некоторые играют, что игрок, который ударил, но не набрал наименьшее количество очков, наказывается. Есть несколько альтернативных версий этого, в которых играют разные группы:
- Молоток добавляет штраф в размере 10 очков.
- Оценка ударника за руку удваивается и добавляется 5 очков.
- Молоток набирает очки, равные игроку, набравшему наибольшее количество очков в этой руке.

Если количество очков у молотка меньше всего, некоторые игроки дают ему преимущество в виде уменьшенного количества очков.
- Некоторые играют, что молоток получает ноль, если самый низкий.
- Согласно другим данным, оценка метателя уменьшается на количество игроков, если оно наименьшее, и удваивается в противном случае — например, в игре с четырьмя игроками игрок выбивает с 3 очками и получает -1 очко (3-4), если это наименьшее количество. , но 6 баллов (2 x 3) в противном случае.
Некоторые играют с банком, в который в начале все вносят одинаковый вклад. Игрок забирает этот банк, если у него наименьшее количество очков, и удваивает его в противном случае.Чтобы такие выплаты не становились слишком большими, может быть разумным согласовать максимальную сумму, которую можно выиграть из банка или выплатить в банк.
Конец игры
Если вы хотите более длительную игру, вы можете сыграть 18 лунок (раздач) вместо 9.
Вместо того, чтобы играть фиксированное количество лунок, вы можете согласиться играть до тех пор, пока счет одного игрока не достигнет или не превысит 100 (или другую заранее оговоренную цель). Затем побеждает игрок с наименьшим количеством очков.
Затем побеждает игрок с наименьшим количеством очков.
Гольф с картами питания
В этой группе вариантов четырехкарточного гольфа несколько карт обозначены как карты силы, которые могут иметь особые эффекты при вытягивании из колоды.Они носят разные названия, такие как Cambio или Pablo или Cabo или Cactus . Были опубликованы как минимум две проприетарные версии с использованием специально разработанных карт: Cabo появился в 2010 году, а Kombio — в 2019 году.
Основные правила такие же, как и в четырехкарточном гольфе. Каждый игрок начинает с четырьмя закрытыми картами — в ряд или в квадрат — и лично смотрит на две из них. Ход начинается вытягиванием верхней карты из колоды или стопки сброса и заканчивается сбросом карты лицом вверх поверх стопки сброса.Вытянутую карту можно использовать для замены карты в раскладке игрока, не глядя предварительно на заменяемую карту. Как обычно, цель состоит в том, чтобы получить макет с низким рейтингом.
Некоторые карты обозначены как карты силы. Если одна из них вытаскивает из закрытой карты , ее можно использовать как обычную карту или использовать ее особую силу, после чего ее нужно сбросить. Сброшенная карта силы не может быть снова использована в качестве карты силы — если она вытаскивается из стопки сброса следующим игроком, она может использоваться только как обычная карта.Некоторые способности могут приводить к тому, что игрок получает или теряет карты в раскладке, поэтому в некоторых версиях игроки могут закончить игру с более или менее четырьмя закрытыми картами.
Я получил описания нескольких версий этого варианта карты силы, и из источников этих отчетов кажется вероятным, что он возник в Испании или Латинской Америке. Испанское слово cambio означает обмен, который является одной из возможных способностей, так что это могло быть первоначальное название этого варианта. Основные различия между версиями заключаются в свойствах специальных карт, количестве очков карт и способе окончания игры.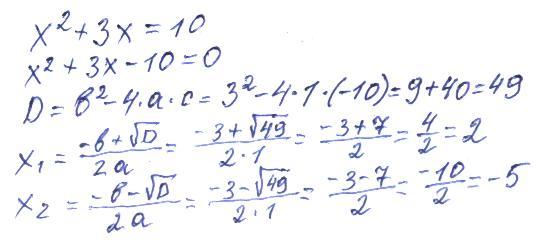
Ашбир Диллон описывает простую форму этой игры, в которую играют в Малайзии с использованием стандартной колоды из 52 карт и двух джокеров.
- Значения карт: от туза до 10 номиналом, все графические карты и джокеры являются картами силы и считаются по 10 каждая.
- Джек: посмотрите на одну из своих карт наедине
- Королева: внимательно посмотрите на карту, принадлежащую оппоненту
- Король: поменяйте местами одну из своих карт на карту, принадлежащую оппоненту, не глядя ни на одну из карт
- Джокер: требуется, чтобы один противник перетасовал свои карты, чтобы они больше не знали, какая из них какая
- Стука нет.Игра продолжается до тех пор, пока стопка запасов не иссякнет. Побеждает игрок с наименьшим количеством очков.
Джон Робертс описывает версию под названием «Пабло», в которой также используется колода из 52 карт плюс два джокера. Семерки и восьмерки — карты силы.
- Значения карт: номинал от туза до 10, карточки с картинками (JQK) 10, джокеры -5.

- Игрок может использовать вытянутую карту для замены двух или более карт с одинаковым рангом в своем раскладе. Если это удается, все равные карты сбрасываются, и в раскладе игрока меньше карт, чем раньше.Если карты, которые игрок пытается заменить, оказываются не равными, они остаются в раскладе вместе с картой, которая должна была их заменить. В этом ходу игрок не сбрасывает карты, и теперь в раскладке игрока на одну карту больше, чем раньше.
- Игрок, который вытягивает из запаса семь , может выполнить обмен . Игрок обменивает одну карту у соперника на одну карту в собственном раскладе. Игрок выбирает карту оппонента, затем смотрит на нее наедине, затем выполняет обмен, не глядя на карту, переданную противнику взамен.Затем семерка сбрасывается.
- Игрок, который вытягивает восемь , может в частном порядке посмотреть любую карту — либо в собственном раскладе игрока, либо в раскладе оппонента. Затем восьмерка сбрасывается.

- В конце игры игрок произносит «Пабло» в конце своего хода. У каждого из других игроков есть еще один ход, после чего подсчитываются расстановки. Игрок, сказавший «Пабло», получает -10 очков, если у него самый низкий результат. В противном случае игрок Пабло оценивает стоимость своей раскладки плюс ценность раскладки оппонента, набравшего наибольшее количество очков.В любом случае все остальные игроки оценивают свои раскладки. Если Пабло сравнивает с другим игроком наименьшее количество очков, каждый получает значение своей раскладки.
- Дальнейшие раздачи разыгрываются до тех пор, пока счет игрока не достигнет 100 или более очков, и в это время побеждает игрок с наименьшим количеством очков.
Эндрю Соул описывает версию под названием « Cumbia », в которой используется колода из 52 карт без джокеров.
- Значения карт: 2 бубны -10, красные короли -5, черные короли 0, дамы 12, валеты 11, остальные карты номиналом.
- Карты силы: 4, 5, 6, 7, 10, J.
 Эти не могут быть размещены в раскладке игрока: игрок должен либо выполнить действие, либо просто сбросить карту.
Эти не могут быть размещены в раскладке игрока: игрок должен либо выполнить действие, либо просто сбросить карту. - 4 или 5: игрок смотрит на одну из своих карт в частном порядке.
- 6 или 7: игрок смотрит на карту оппонента конфиденциально
- 10: Игрок переключает любые две карты, принадлежащие любым игрокам, не глядя на них.
- Валет: игрок смотрит на одну из своих карт и одну карту, принадлежащую оппоненту, и может поменять их местами, если пожелает.
- Каждый раз, когда сбрасывается карта, любой игрок может взять одну совпадающую карту из любой раскладки и сбросить ее поверх сброса. Игрок не может смотреть карту первым. Если она совпадает и была взята из раскладки оппонента, игрок, который ее сбросил, перемещает одну карту, не глядя на нее, из своей раскладки на раскладку оппонента. Таким образом, расклад успешного игрока всегда уменьшается на одну карту. Если вторая сброшенная карта не совпадает, игрок, который ее переместил, заменяет карту в раскладе, из которого она была взята, и, если она была взята из раскладки оппонента, получает 10-балльный штраф.
 Примечание: допинг красного короля не соответствует черному королю, а 2 не соответствует другому 2: значения карты должны быть равны. Примечание: только , одна дополнительная карта может быть сброшена как матч поверх обычного сброса.
Примечание: допинг красного короля не соответствует черному королю, а 2 не соответствует другому 2: значения карты должны быть равны. Примечание: только , одна дополнительная карта может быть сброшена как матч поверх обычного сброса. - Чтобы закончить игру, игрок называет «Камбию» в любой момент своего хода. Каждый игрок получает еще один ход, а затем каждый оценивает свою раскладку. Специального бонуса за наименьшее количество очков в сделке нет. После согласованного количества сделок — например, 7 — побеждает игрок с наименьшим общим счетом.
Крис Смит описывает версию под названием « Cabo », в которой используется колода из 52 карт без джокеров.
- Значения карт: бубновый король 0, другие короли 13, дамы 12, валеты 11, 10 до номинала туза. 7, 8, 9, 10, J и Q — это карты силы, чьи способности запоминаются с помощью следующих рифм:
- Семь или восемь, знайте свою судьбу : посмотрите на одну из своих карт, а затем положите ее обратно (только вы можете ее увидеть)
- Девять или десять, узнайте друга : посмотрите одну карточку от кого-то другого, а затем положите ее обратно (только вы можете ее увидеть)
- Валет или Дама, переключитесь между : поменяйте местами любые две карты на столе (за исключением колоды)
- В любой ход вместо добавления вытянутой карты в раскладку или использования ее силы, если таковая имеется, вы можете сопоставить ее с такой же картой или картами из любого расклада (ов).
 Все короли подходят друг другу, включая бриллианты. Все совпавшие карты сбрасываются, за ними следует карта, инициировавшая сопоставление. Любые совпавшие карты из раскладок оппонентов заменяются картами из вашего собственного расклада, не глядя на заменяющие карты. Если вы пытаетесь сопоставить карту, которая оказывается не равна соответствующей карте, карта остается на месте и в качестве штрафа за каждую такую неудачу вы берете дополнительную карту из запаса и добавляете ее в свой макет, не глядя на Это.
Все короли подходят друг другу, включая бриллианты. Все совпавшие карты сбрасываются, за ними следует карта, инициировавшая сопоставление. Любые совпавшие карты из раскладок оппонентов заменяются картами из вашего собственного расклада, не глядя на заменяющие карты. Если вы пытаетесь сопоставить карту, которая оказывается не равна соответствующей карте, карта остается на месте и в качестве штрафа за каждую такую неудачу вы берете дополнительную карту из запаса и добавляете ее в свой макет, не глядя на Это. - Чтобы закончить игру, игрок называет «Кабо» в любой момент своего хода. Каждый игрок получает еще один ход, а затем каждый оценивает свою раскладку. Игра также заканчивается, если игрок выбрасывает все карты из своей раскладки или если стопка карт заканчивается.
Коннор Чу описывает версию из Ванкувера, Канада, известную как « Cactus ». В нее играют колодой из 52 карт без джокеров, и считается, что она лучше всего подходит для двух игроков, хотя могут играть трое и более.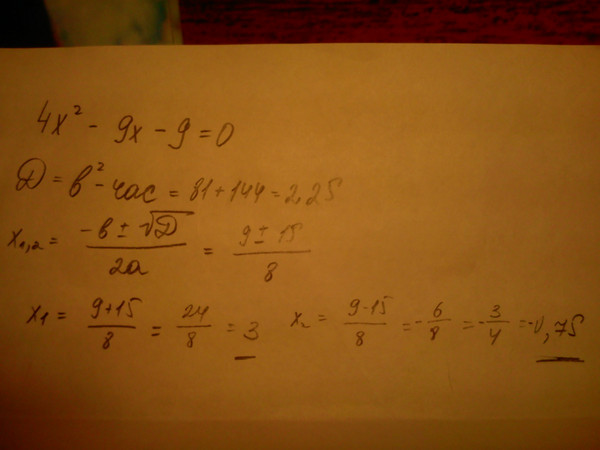
- Ни одна карта не переворачивается лицом вверх в конце раздачи: первый игрок должен взять из колоды, и его сброс начинает стопку сброса.
- Значения карт: Туз: 1 Король: 0 Дама: 10 Валет: 10, номинал остальных карт.
- Карты силы: 6, 7, 8, 9, 10, валет, дама.
- 6, 7 или 8: игрок смотрит на одну из своих карт в частном порядке.
- 9, 10 или валет: игрок смотрит на карту противника конфиденциально.
- Королева: игрок обменивает любую из своих карт с одной из карт оппонента, не глядя ни на одну из них.
- Туз, Король, 2, 3, 4 и 5 не имеют силы, и никакие уникальные способности не предоставляются, когда они сбрасываются.
- Игрок может использовать свой ход, чтобы использовать силу карты, лежащей лицом вверх в стопке сброса, если предыдущий игрок еще не использовал ее силу. Фактически их ход состоит из взятия карты, используя ее силу, и повторного сброса той же карты. Например, если игрок A вытягивает 2 из колоды и обменивает ее на валета в своей раскладке, то игрок B может использовать свой ход, чтобы применить силу сброшенного валета, чтобы посмотреть на одну из карт игрока A.

- В любой момент игры, независимо от того, чей это ход, игрок может сбросить карту, которая соответствует верхней карте в стопке сброса. Игрок, который быстрее всего сбросил свою карту, может сделать это, не считая хода. Если игрок ошибается и пытается сбросить карту, которая не соответствует стопке сброса, он забирает свою карту и берет еще две карты.
- Раунд завершается, когда один игрок называет «Кактус» в конце своего хода. Затем у их оппонентов есть еще один ход.
- Если вы называете «Кактус» и после того, как все сделали свой последний ход, ваша раскладка имеет наименьшее значение в очках, вы ничего не получаете. Если какой-либо противник имеет значение очков, равное или меньшее, чем у вас, вы добавляете ценность вашего макета плюс дополнительные 10 штрафных очков к вашему счету.
- Если ваш оппонент называет «Кактус» и после вашего последнего хода ваша раскладка имеет более высокое значение, чем у вызывающей стороны, вы добавляете ценность вашей раскладки к вашему счету.
 Если ваш балл равен или ниже, чем у вызывающего абонента, вы ничего не набираете.
Если ваш балл равен или ниже, чем у вызывающего абонента, вы ничего не набираете. - «Победитель» каждого раунда играет первым в следующем раунде. Победителем становится игрок с наименьшим значением расклада. Звонящий теряет связь. В случае ничьей между двумя противниками вызывающего абонента, они берут карты, чтобы решить, кто начнет следующий раунд.
- Играется несколько раундов, пока игрок не наберет 100 очков. В этот момент игрок с наименьшим количеством очков выигрывает игру. В игре с более чем двумя игроками может быть ничья для самого низкого: в этом случае могут быть сыграны дальнейшие раунды до тех пор, пока не будет найден единственный победитель.
Шестикарточный гольф
В этой версии пара одинаковых карт в столбце получает нулевой балл. Поэтому основная цель игры — составлять пары, сохраняя при этом как можно меньше непарных карт.
Игроки, карты и сделки
Два, три или четыре игрока используют стандартную колоду из 52 карт. Если игроков больше четырех, добавляется второй пакет и третий пакет, если их больше восьми. Раздача и игра идут по часовой стрелке.
Если игроков больше четырех, добавляется второй пакет и третий пакет, если их больше восьми. Раздача и игра идут по часовой стрелке.
Дилер раздает по шесть карт каждому игроку по одной, раскладывая их лицом вниз в прямоугольнике перед каждым игроком следующим образом:
Оставшиеся невыносимые карты кладутся лицевой стороной вниз в центр стола, чтобы сформировать колоду для вытягивания.Верхняя карта колоды переворачивается лицевой стороной вверх и кладется рядом с колпаком, чтобы начать колоду сброса. Перед началом игры каждый игрок переворачивает любые две карты в своей раскладке лицевой стороной вверх. Карты других раскладок нельзя смотреть, пока они не будут сброшены или открыты в ходе игры, или пока они не будут подсчитаны в конце игры.
Игра
Начинает игрок слева от дилера, и ход игры проходит по часовой стрелке. В свой ход вы должны либо взять верхнюю карту из закрытой колоды, либо взять верхний сброс.Вы можете использовать вытянутую карту для замены любой из шести карт в вашем раскладе, но если вы решите заменить карту лицом вниз, вам не разрешается смотреть на нее, прежде чем принять решение о замене.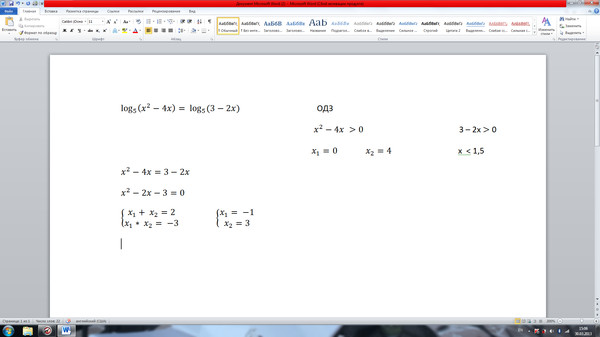 Вы кладете новую карту в раскладку лицевой стороной вверх, а карта, которая ранее занимала эту позицию, кладется лицевой стороной вверх наверх стопки сброса. Затем наступает очередь следующего игрока.
Вы кладете новую карту в раскладку лицевой стороной вверх, а карта, которая ранее занимала эту позицию, кладется лицевой стороной вверх наверх стопки сброса. Затем наступает очередь следующего игрока.
Если вы вытащите карту из колоды, лежащую рубашкой вверх, вы можете решить, что она вам больше не нужна.В этом случае вы просто сбрасываете вытянутую карту лицом вверх в стопку сброса, и наступает очередь следующего игрока. Однако запрещено брать верхнюю карту из стопки сброса и снова сбрасывать ту же карту, оставляя ситуацию без изменений: если вы решите взять сброс, вы должны использовать его для замены одной из ваших карт раскладки.
Игра заканчивается, как только последняя из шести карт игрока оказывается открытой. Затем рука оценивается.
Подсчет очков
В конце игры каждый игрок из шести карт переворачивается лицом вверх и оценивается следующим образом.
- Каждый туз приносит 1 очко.
- Каждые два отсчета минус два очка.

- Каждая цифровая карта от 3 до 10 очков номинала.
- Каждый валет или дама получает 10 очков.
- Каждый Король получает ноль очков.
- Пара равных карт в одном столбце приносит ноль очков в столбце (даже если одинаковые карты — двое).
Побеждает игрок, набравший наименьшее совокупное количество очков после девяти раздач.
Гэри Гловер предоставил пустые листы с результатами до 8 игроков, до 11 игроков и до 12 игроков в виде файлов MS Word.Дэн Вагнер предоставил таблицу результатов в формате PDF для 8 игроков.
Варианты шестикарточного гольфа
Карты
Некоторые игроки используют две колоды с четырьмя, тремя или даже только двумя игроками. Это мало влияет на игру и снижает вероятность того, что карты закончатся.
У некоторых игроков есть джокеры — по два на колоду. В этом случае двойки приносят 2 очка, а джокеры — -2.
Открытие карт в начале
Некоторые считают, что две открытые карты должны находиться в одном столбце расклада; другие играют наоборот, согласно правилу, согласно которому две открытые карты должны быть , а не в одном столбце. Некоторые требуют, чтобы одна карта была перевернута из центрального столбца и одна — из одного из внешних столбцов.
Некоторые требуют, чтобы одна карта была перевернута из центрального столбца и одна — из одного из внешних столбцов.
Некоторые играют так, что после открытия двух карт вы можете переставить карты в своей раскладке (не глядя ни на одну из закрытых карт) так, чтобы расположить ваши открытые карты в любых желаемых положениях.
Некоторые играют, что в начале не открываются карты; вместо этого каждый из игроков может один раз взглянуть на ближайший к нему ряд из трех карт, положив их рубашкой вверх.
Открытие карт во время игры
Некоторые игры, в которые вы можете использовать свой ход, просто чтобы перевернуть одну из ваших закрытых карт лицом вверх.
Некоторые играют так, что если вы берете карту из колоды и решаете сбросить ее, а не кладете в свою раскладку, вы должны также перевернуть одну из своих закрытых карт лицом вверх, если только у вас нет только одной закрытой карты. оставшиеся, в этом случае вы можете оставить его рубашкой вверх.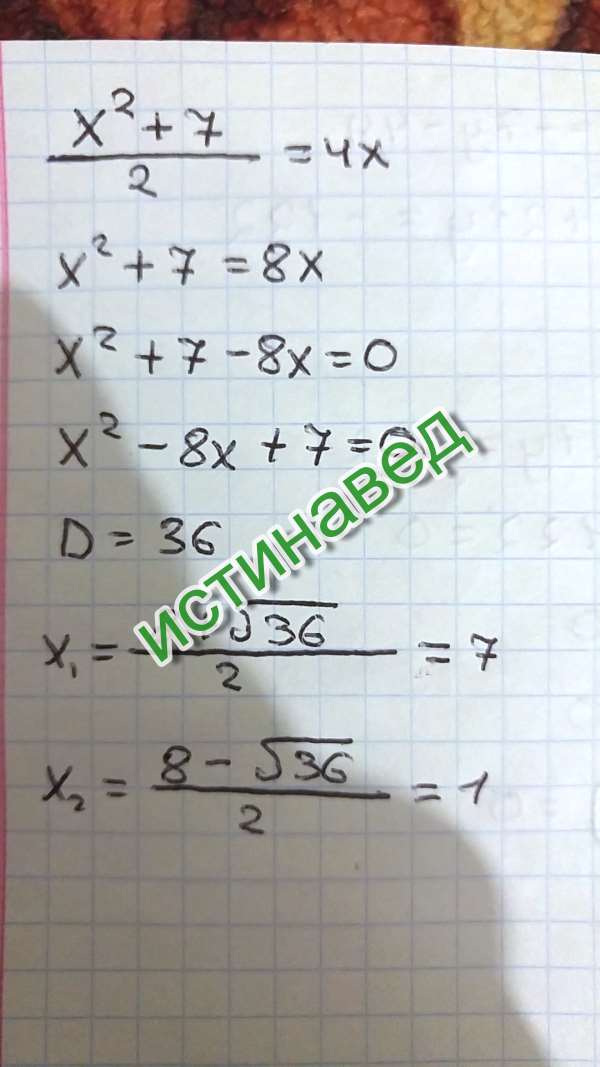
Окончание спектакля
Некоторые розыгрыши, которые вы можете использовать в свой ход, чтобы завершить игру, перевернув все ваши оставшиеся закрытые карты лицом вверх.
Многие играют так, что после того, как открыта последняя карта игрока, каждый из других игроков играет еще один ход до того, как рука будет подсчитана.
Подсчет очков
Некоторые игроки присуждают отрицательную оценку, например -10 очков, за четыре равные карты, расположенные в два столбца (например, два столбца по две семерки). Когда используются две или более колод, некоторые дают более высокий отрицательный результат, например -20 очков, за раскладку из шести одинаковых карт.
Некоторые награды минус 20 очков за четыре равные карты вместе в квадратном блоке. В этом варианте при игре двойной колодой блок из 6 одинаковых карт должен набрать минус 40 очков, так как он содержит два (перекрывающихся) квадрата.
Некоторые играют так, что пара одинаковых карт в любом месте расклада получает нулевой результат — они не обязательно должны быть в одном столбце.
Некоторые игроки включают в колоду двух джокеров, которые, по мнению разных игроков, могут приносить -5, -3, -2 или ноль очков. В этом случае двойки приносят +2 балла, а не -2. Некоторые также считают, что одноглазые валеты не стоят ноль.
Когда две двойки (или джокеры, если они используются) появляются вместе в столбце, некоторые игроки позволяют им сохранить свое отрицательное значение (-4 для столбца, если каждая карта равна -2).Некоторые присуждают более высокое отрицательное значение, когда четыре такие карты расположены в два столбца — например, при игре двумя колодами четыре джокера в двух столбцах имеют значение -20.
Конец игры
Как и в четырехкарточном гольфе, игра может продолжаться на 18 лунках вместо девяти
Восьмикарточный гольф
Эта игра очень похожа на шестикарточный гольф, но в раскладке каждого игрока четыре столбца по две карты, а не три.
На бывшем веб-сайте Билла Уитнака «Карточные игры» описывалась версия, в которой использовалась двойная колода из 52 карт с четырьмя джокерами (108 карт).Можно добавить больше колод и джокеров, если игроков больше четырех. Дилер сдает каждому игроку восемь карт рубашкой вверх, размещенных в сетке, четыре карты в ширину и две в высоту, и кладет следующую карту лицевой стороной вверх на стол, чтобы начать сброс колоды, а оставшуюся часть колоды кладут рубашкой вверх рядом с ней. сформировать чертежный запас. Игрок слева от дилера начинает игру, и ход игры переходит по часовой стрелке.
Каждый игрок начинает свой первый ход , переворачивая одну колонку из двух карт лицом вверх, как показано на следующей диаграмме.
Игрок продолжает вытягивать либо неизвестную верхнюю карту колоды, либо открытую верхнюю карту стопки сброса. Затем у игрока есть три варианта:
- Используйте вытянутую карту, чтобы заменить одну из открытых карт в раскладке игрока, и сбросьте замененную карту лицевой стороной вверх в стопку сброса.
- Используйте вытянутую карту, чтобы заменить одну из закрытых карт в раскладе игрока. Заменяемую карту следует выбирать без предварительного просмотра и сбрасывать лицевой стороной вверх в стопку сброса, даже если это карта, которую игрок хотел бы оставить.
- Если карта была взята из колоды лицевой стороной вниз, сбросьте ее лицевой стороной вверх поверх стопки сброса и переверните одну из закрытых карт в раскладке игрока лицевой стороной вверх.
После того, как у каждого игрока будет один ход, у всех будут две или три карты лицом вверх. Игра продолжается по часовой стрелке. Теперь каждый ход состоит из вытягивания верхней карты из стопки запаса или из стопки сброса и использования ее в соответствии с любым из трех вариантов, описанных выше.
Игрок, в раскладе которого осталась только одна закрытая карта, имеет дополнительную возможность: взять карту из колоды и сбросить ее , не переворачивая последнюю карту расклада.
Когда игрок переворачивает последнюю карту своего расклада лицом вверх, у каждого из остальных игроков есть еще один ход. Затем все оставшиеся закрытые карты в раскладках всех игроков переворачиваются лицом вверх, и раскладки оцениваются следующим образом:
| Джокеры | Минус 5 баллов за каждые |
| Короли | 0 баллов |
| Дамы, валеты | по 10 очков |
| Тузы | 1 балл за каждое |
| Карточки с цифрами 2-10 | Номинал |
| Пара в столбик | 0 баллов |
| Две равные пары в любых двух столбцах | Минус 10 баллов |
Возможен отрицательный общий балл.Разыгрывается девять раздач (что соответствует девяти лункам поля для гольфа), и игрок с наименьшим общим счетом становится победителем.
Примеры выставления баллов:
Первый столбец 8 (6 + 2), второй столбец 0 (пара), третий столбец 1 (0 + 1), четвертый столбец 0 (пара), всего 9.
Первый столбец 1 (1 + 0), второй столбец 0 (пара), третий столбец 10 (6 + 4), четвертый столбец -10 (пара, равная паре в столбце 2), всего 1.
Вариант
Некоторые из них позволяют игроку перевернуть любые две карты лицом вверх в первый ход и разыграть так, что после того, как обе карты столбца перевернуты, эти карты больше нельзя будет обменивать.
Девятикарточный гольф
В эту игру, также известную как Crazy Nines или просто Nines , играют с двумя или более колодами карт. Каждому игроку раздаются девять карт в квадрате три на три, и он переворачивает три карты лицом вверх, чтобы начать игру. Механизм игры и подсчет очков по сути такие же, как и в шестикарточном гольфе, за исключением того, что пара равных карт не дает нулевых очков. Вместо этого столбец из трех одинаковых карт дает ноль.
Как и в других версиях, существует множество вариаций.
- Некоторые играют так, что в начале перевернуты только две карты.
- Некоторые играют, что двойки набирают +2, а не -2, и включают джокеров, которые набирают -2.
- Некоторые играют, что ферзи забивают 12, а не 10.
- Некоторые играют так, что не только вертикальный ряд из трех равных карт дает ноль, но также горизонтальный ряд или диагональная линия из трех равных карт.
- Некоторые также считают, что блок из четырех одинаковых карт вместе в квадрате дает отрицательный результат, например -25.
- Некоторые играют так, что игрок с наименьшим счетом для лунки получает ноль, и что если игрок, который первым открыл все свои карты (известный как , вызывающий ), не имеет наименьшего количества очков, этот игрок добавляет счет игрок с наименьшим количеством очков к своему собственному. Я не знаю, как разрешаются связи в этом методе.
Игроки должны согласовать, что произойдет, если у вас есть две пересекающиеся строки равных карт или строка, пересекающая квадратный блок, если вы получите бонус за блок.Некоторые решают эту проблему, немедленно удаляя из разметки любую строку или блок одинаковых карт. Игра продолжается, используя только оставшуюся часть расклада, оставляя позиции, из которых были удалены карты, пустыми.
Если вы предпочитаете оставить все девять карточек на месте, вам нужно договориться о том, как оценивать такие раскладки, как эти:
пример (а): пересекающиеся линии
пример (б): блокировать перекрывающуюся строку
Стивен Морако описал версию 9-карточного гольфа, в которой каждая пара одинаковых карт, расположенных рядом по горизонтали или вертикали, приносит ноль.Одна и та же карта может использоваться как часть более чем одной пары, поэтому одинаковые строки и столбцы также будут иметь нулевой балл, поскольку они состоят из двух пар.
На своей странице «Девятки» (архивная копия) Джесси Фукс описал версию, в которой в начале не было карт. Дамы считают ноль, короли — десять, джокеры — -2. Строки и столбцы из трех одинаковых карт удаляются при формировании.
Десятькарточный гольф
Для этой игры необходимо как минимум две колоды. Каждому игроку раздается десять карт, разбитых на пять столбцов по две, и он переворачивает любые две карты лицом вверх.Игра такая же, как и в шестикарточном гольфе.
Другие веб-страницы, посвященные гольфу
Страница изобретенных вариаций гольфа, представленных читателями этого сайта.
Краткое описание четырехкарточного гольфа появилось на сайте Real Beer (архивная копия).
Архивная копия страницы Билла Уитнака о восьмикарточном гольфе.
Версии девятикарточного гольфа Стивена Морако и Джесси Фукса (архивная копия).
Программное обеспечение для гольфа и онлайн-игры
Компания Стивена Морако Iron Sheep Productions выпустила 9-карточную игру в гольф для iPhone / iPad.
Джозеф МакМюррей выпустил приложение для игры в гольф с 6 картами для Android.
КомпанияGlowing Eye выпустила приложение для игры в гольф для iOS, которое позволяет играть в гольф с 4 и 6 картами.
Gaming Safari предлагает бесплатную онлайн-игру в гольф с 6 картами для Windows.
ВGolf можно играть онлайн в TrapApps.
Эта страница частично основана на информации, предоставленной: Ванда Бартолмай, Даниэль Карлсон, Майкл Дэвис, Джери Дэй, Стив Доусон, Ашбир Диллон, Билл Гарднер, Джерри Грей, Бет Гроув, Винсент Герин, Ким Хэтч, Боб Хирдинк, Эрни Хойер, Джим Кеннеди, Ли Мурра, Джейн Маскато, Николас Пфайффенбергер, Марк Рио, Джон Робертс, Крис Смит, Эндрю Соул, Марк Спинелли, Яш Шривастава, Шерман Стаффер, Гэри Салливан, Джеймс Томас, Стэн Томпсон, Билл Уитнак, Дейтон Уильямс, Тони Янг , Вирджиния Зиглер.
квадратов и квадратных корней
Сначала узнайте о квадратах, затем квадратные корни — это просто.
Как возвести число в квадрат
Чтобы возвести число в квадрат: , умножьте его на само себя .
Пример: Что такое 3 в квадрате?
| 3 Квадрат | = | = 3 × 3 = 9 |
«В квадрате» часто записывают как две маленькие цифры:
Это говорит о том, что «4 в квадрате равно 16»
(маленькая 2 говорит
число появляется дважды при умножении)
Квадраты от 0
2 до 6 2| 0 Квадрат | = | 0 2 | = | 0 × 0 | = | 0 |
| 1 Квадрат | = | 1 2 | = | 1 × 1 | = | 1 |
| 2 Квадрат | = | 2 2 | = | 2 × 2 | = | 4 |
| 3 Квадрат | = | 3 2 | = | 3 × 3 | = | 9 |
| 4 квадрат | = | 4 2 | = | 4 × 4 | = | 16 |
| 5 Квадрат | = | 5 2 | = | 5 × 5 | = | 25 |
| 6 Квадрат | = | 6 2 | = | 6 × 6 | = | 36 |
Отрицательные числа
Мы также можем возвести в квадрат отрицательных чисел .
Это было интересно!
Когда мы возводим в квадрат отрицательное число , мы получаем положительный результат .
То же, что и возведение положительного числа в квадрат:
(Подробнее см. Квадраты и квадратные корни в алгебре)
Квадратные корни
Квадратный корень из идет в обратном направлении:
3 в квадрате равно 9, поэтому квадратный корень из 9 это 3
Квадратный корень числа равен…
… значение, которое можно умножить на само на себя , чтобы получить исходное число.
Квадратный корень из 9 равен …
… 3 , потому что , когда 3 умножается на само , мы получаем 9 .
Это как спросить:
Что можно умножить само на себя, чтобы получить это?
Чтобы помочь вам вспомнить , подумайте о корне дерева: «Я знаю дерево , но какой корень его сделал? » В данном случае дерево — «9», а корень — «3». |
Вот еще несколько квадратов и квадратных корней:
| 4 | 16 | |
| 5 | 25 | |
6 | 36 | |
7 | 49 | |
Десятичные числа
Также работает с десятичными числами.
Попробуйте использовать ползунки ниже (примечание: «…» означает, что десятичные дроби остаются неизменными):
Использование ползунков:
- Что такое квадратный корень из 8 ?
- Что такое квадратный корень из 9 ?
- Что такое квадратный корень из 10 ?
- Что такое 1 в квадрате?
- Что такое 1,1 в квадрате?
- Что такое 2,6 в квадрате?
Негативы
Ранее мы обнаружили, что можем возводить в квадрат отрицательные числа:
Пример: (−3) в квадрате
(−3) × (−3) = 9
И, конечно же, 3 × 3 = 9 тоже.
Таким образом, квадратный корень из 9 может быть −3 или +3
Пример. Каковы квадратные корни из 25?
(−5) × (−5) = 25
5 × 5 = 25
Таким образом, квадратные корни из 25 равны −5 и +5
Символ квадратного корня
| Это специальный символ, означающий «квадратный корень», это что-то вроде галочки, и фактически началось сотни лет назад в виде точки с движением вверх. Он называется радикалом и всегда делает математику важной! |
Мы используем это так:
, и мы говорим, что «квадратный корень из 9 равен 3»
Пример: Что такое √25?
25 = 5 × 5, другими словами, когда мы умножаем 5 сам по себе (5 × 5) получаем 25
Итак, ответ:
√25 = 5
Но подождите минутку! Разве квадратный корень не может быть −5 ? Потому что (−5) × (−5) = 25 тоже.
- Итак, квадратный корень из 25 может быть -5 или +5.
- Но когда мы используем радикальный символ √ , мы даем только положительный (или нулевой) результат .
Пример: Что такое √36?
Ответ: 6 × 6 = 36, поэтому √36 = 6
Идеальные квадраты
Совершенные квадраты (также называемые «квадратными числами») — это квадраты целых чисел:
| Perfect Квадраты | |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
| и др… |
Попытайтесь запомнить их до 12.
Вычисление квадратного корня
Легко вычислить квадратный корень из полного квадрата, но он действительно сложно найти , чтобы вычислить другие квадратные корни.
Пример: что такое √10?
Итак, 3 × 3 = 9 и 4 × 4 = 16, поэтому мы можем угадать ответ от 3 до 4.
- Давайте попробуем 3,5: 3,5 × 3,5 = 12,25
- Попробуем 3.2: 3,2 × 3,2 = 10,24
- Давайте попробуем 3,1: 3,1 × 3,1 = 9,61
- …
Приближаемся к 10, но чтобы получить хороший ответ, потребуется много времени!
В этот момент я достаю свой калькулятор, и он говорит: 3,1622776601683793319988935444327 Но цифры могут продолжаться и продолжаться без всякого рисунка. Так даже ответ калькулятора — только приближение ! |
Примечание: подобные числа называются иррациональными числами, если вы хотите узнать больше.
Самый простой способ вычислить квадратный корень
| Используйте кнопку квадратного корня вашего калькулятора! |
А также руководствуйтесь здравым смыслом, чтобы убедиться, что у вас есть правильный ответ.
Интересный способ вычислить квадратный корень
Существует забавный метод вычисления квадратного корня, который с каждым разом становится все точнее:
| a) начните с предположения (предположим, что 4 — это квадратный корень из 10) | |
| б) разделить на предположение (10/4 = 2.5) c) добавьте это к предположению (4 + 2,5 = 6,5) d) затем разделите , полученный результат на 2, другими словами, уменьшите его вдвое. (6,5 / 2 = 3,25) e) теперь установите это как новое предположение и начните с b) снова |
- Наша первая попытка позволила нам подняться с 4 до 3,25
- Возвращаясь снова ( b к e ), мы получаем: 3,163
- Возвращаясь снова ( b к e ), мы получаем: 3,1623
Итак, через 3 раза ответ будет 3.1623, что неплохо, потому что:
3,1623 x 3,1623 = 10,00014
А теперь … почему бы вам, , не попытаться вычислить квадратный корень из 2 таким способом?
Как угадать
Что, если нам нужно угадать квадратный корень для такого сложного числа, как «82 163» …?
В этом случае мы могли бы подумать, что «82 163» состоит из 5 цифр, поэтому квадратный корень может состоять из 3 цифр (100 x 100 = 10 000), а квадратный корень из 8 (первая цифра) примерно равен 3 (3×3 = 9), поэтому 300 хорошее начало.
День квадратного корня
4 апреля 2016 г. — День квадратного корня, потому что дата выглядит как 4/4/16
Следующее за этим 5 мая 2025 г. (05.05.25)
309 310 315, 1082, 1083, 2040, 3156, 2041, 2042, 3154
Кадриль
Научите своих игроков избегать контакта с этой простой игрой, которая работает на постепенном преодолении «пробок», стараясь не натолкнуться на других бегунов, которые также хотят набрать очки.
Установка
Круг длиной 20 м с конусами разного цвета и игроком на каждом конусе. Иметь одинаковое количество цветных конусов: например, 3 красных, 3 зеленых, 3 синих.
Квадрат 2 м внутри круга содержит по одному мячу на каждого игрока (рисунок 1).
Правила
По вашему призыву «Вперед!» Игроки выбегают на квадрат, хватают мяч, затем касаются им другого конуса того же цвета, с которого они начали. Итак, игрок, который начинает с синего, пробегает, берет мяч и бежит к другому синему конусу (рисунок 2).
После того, как каждый игрок коснулся конуса, он бежит обратно в квадрат, кладет мяч и берет другой. Затем они бегут к последнему конусу своего цвета (рисунок 3).
Играть одну минуту. Сделайте столько кругов, сколько позволят игроки.
Подсчет очков
- Игроки считают, сколько конусов они коснулись, не задев другого игрока — с мячом или без него — или не уронив мяч.
- Сложите баллы, чтобы найти победный цвет на каждом круге.Сложите все очки вместе, чтобы найти общий выигрышный цвет.
Скажите им
«Мяч всегда в две руки»
«Постоянно смотрите налево и направо, когда владеете»
«Посмотри на пространство, беги в него».
Советы тренера
Часто вам приходится преодолевать «пробки», чтобы добраться до пункта назначения. Эта игра позволяет игрокам практиковать навыки бега, защищая мяч и выполняя другую задачу.
Информация об Имонне Хогане
Имонн был тренером с 1991 года и провел годы в RAF, оттачивая свои навыки, работая в Англии, Шотландии и Германии.Покинув армию, Имонн посвятил свое время Лестерской академии тигров, тренируя на клубном, конституционном и региональном уровнях в Мидлендсе, а также получил много опыта во многих государственных и независимых школах. Здесь он работал преподавателем по спорту и физкультуре и в отделе специальных образовательных потребностей, что еще больше расширило его навыки современного тренера. С 2005 года он много раз ездил в США и близко наблюдал за их ростом как нации регби, и ему посчастливилось встретиться и поработать вместе со многими их тренерами более высокого уровня и некоторыми из их зарубежных гостей из Южного полушария.В 2016 году Имонн был единственным иностранным тренером, которого пригласили поработать на первых профессиональных соревнованиях по регби в США, где он работал с Ohio Aviators. Обладая профессиональным подходом и находясь под сильным влиянием его многочисленных добровольных действий, Имонн испытывает сильное сочувствие к современным тренерам и требованиям, которые могут быть предъявлены к их времени, поскольку он сам пережил многие из этих опытов. Имонн пишет для Rugby Coach Weekly с 2012 года и является автором двух наших книг, специально разработанных для тренеров, работающих с молодыми игроками.Связанные
Побег из тюрьмы
в Работа ногами и уклонение, Маленькие игры, Разминка
Веселая игра, которая поможет отработать защитную работу ног, а также навыки уклонения от атакующих.Развивает навыки уклонения, а также защитную работу ног и общение. БОЛЬШЕ
Управление возвратом в отбор при заземлении …
в Упражнениях по регби, Малые игры, Отбор мяча
Тренируя в моем местном клубе по возвращении в регби, проблемы помогали игрокам вспомнить, как нужно бороться. Это особенно когда они не хотели приземляться на твердую землю. БОЛЬШЕ
Игра стандартов
в играх с малой стороной
Мне повезло, что Эдди Джонс провел несколько сессий.Это игра, с которой он начал, и она отлично подходит для закрепления ключевых идей, касающихся основных навыков или принципов игры. БОЛЬШЕ
Повышение уверенности в контакте: Touch-Tackle-Ruck
в игре Rucking & Mauling, Упражнения по регби, Игры с малыми сторонами
Познакомьте игроков со смешанными способностями с контактом, развивая навыки в играх и задавая вопросы. Я обнаружил, что, используя эту последовательность действий, игроки вместе развивают навыки контакта.Вы можете настроить размеры поля и тайминги в соответствии с вашими игроками. БОЛЬШЕ
Круг как ограничение игры на …
в играх с малой стороной
Используйте это необычное поле, чтобы ставить перед игроками задачи. По мере того, как они отрабатывают способы набрать очки, они начнут использовать управляемость и поддержку, чтобы увеличить ширину своей игры. БОЛЬШЕ
Атакуйте пространство, атакуйте края, атакуйте в темпе
в Работа ногами и уклонение, Маленькие игры
Поощряйте своих носителей мяча бегать в темпе, стараясь избегать контакта, предугадывая, где находятся места.Это упражнение на сканирование только для игрока с мячом. Они будут делать ошибки, но начнут настраиваться на поиск пробелов. БОЛЬШЕ
Математические пазлы
Большое удовлетворение вызывает то, что можно получить, решив математическую головоломку. Здесь очень много головоломки на этой странице, все с математической связью, которые просто ждет своего решения. Вы можете заработать Transum Trophies, решая головоломки. решать.
Номера самолетов
Расположите числа на плоской сетке, чтобы получить заданные суммы
Криптографические
Заполните квадраты в соответствии с подсказками, указанными в цепочке чисел для каждой строки и столбца.
Без ведома
Некоторые головоломки с сеткой изображений, которые можно решить, используя одновременные уравнения.
Группы по четыре человека
Упрощенная математическая версия задачи, показанной в британской телепрограмме Only Connect. Найдите связи между терминами.
Частичные пирамиды
Подсчитайте недостающие числа в этих частично завершенных головоломках-пирамидах.
Пазл-пирамида
Числа в кубиках можно найти, сложив два кубика сразу под ними вместе.Сможете ли вы достичь поставленной цели?
Пазл с разбитой шахматной доской
Шахматная доска разбита на 13 частей. Вы можете собрать его обратно?
Рассечение пончиков
Головоломка, в которой нужно найти четыре разных способа получить 900 путем умножения трех разных чисел.
Power Shift
Расположите указанные числа как основания и индексы в трехчленной сумме, чтобы получить целевую сумму.
Удовлетворение
Это довольно сложная головоломка с группировкой чисел, требующая знания простых, квадратных и треугольных чисел.
Squorder
Версия Transum традиционной головоломки с раздвижной плиткой.
Найти шахту
Найдите, где спрятаны мины, не наступая на них.
Пентамино
Расположите двенадцать пентамино по контуру прямоугольника.
Лобзик номер
Онлайн, интерактивные пазлы из сеток чисел.
Головоломка с римскими цифрами
Интерактивная онлайн-головоломка из сетки римских цифр.
Лобзик Magic Square
Интерактивные головоломки из четырех магических квадратов.
плюс
Пазл с семью уровнями сложности.
Площадь лабиринта
Используйте свои знания о прямоугольных областях, чтобы вычислить недостающие размеры этих составных диаграмм.
Пазл о парковке
Можете ли вы вывести свою машину из переполненной стоянки, переместив другие машины вперед или назад?
Только одна цифра
Найдите выражения с использованием только одной цифры, которые соответствуют заданным целям.
Центровыражение
Расположите числа от 1 до 9, чтобы получить выражение со значением 100.
Идеальный магический квадрат
Расположите шестнадцать чисел в сетке четыре на четыре так, чтобы группы из четырех чисел в образце составляли одну и ту же сумму.
Octagram Star
Расположите шестнадцать чисел на октаграмме так, чтобы сумма чисел в каждой строке равнялась одинаковой сумме.
Гексаграмма Звезда
Расположите двенадцать чисел на гексаграмме так, чтобы сумма чисел в каждой строке равнялась одинаковой сумме.
Треугольная гексаграмма
Расположите двенадцать чисел в треугольниках гексаграммы так, чтобы сумма чисел в каждой строке из пяти треугольников равнялась одинаковой сумме.
Awe-Sum
Расположите указанные цифры так, чтобы получилось шесть 3-значных чисел, которые прекрасно сочетаются друг с другом.
Целевые продукты
Расположите пронумерованные футбольные мячи на стойках ворот, чтобы получилось три одинаковых продукта с 3 номерами.
Обхват
Довольно сложная головоломка с числами, состоящими из дробей.
Магический квадрат
Каждая строка, столбец и диагональ должны давать одинаковую сумму.
Unmagic Square
Как магический квадрат, но все суммы должны быть разными.
Тоннель с одним факелом
Решите задачу прохождения четырех человек через туннель с одним фонариком за минимальное время.
Разлученные близнецы
Сможете ли вы найти 6-значное число, содержащее по две цифры каждая из цифр от 1 до 3, которое подчиняется данным правилам?
Не отрывая карандаш
Можете ли вы нарисовать эти схемы, не отрывая карандаш от бумаги? Это интерактивная версия традиционной головоломки.
Переход через реки
Традиционное испытание на переходе через реки.Сможете ли вы сделать это за наименьшее количество ходов?
Digivide
Расставьте числа от 1 до 6 в полях, чтобы расчет деления был правильным.
Разведчики в лодке
Организуйте расписание для скаутов, чтобы они путешествовали на лодках, чтобы они были с разными людьми каждый день.
Quad Area
Вычислите площади всех возможных четырехугольников, которые можно построить, соединив точки на этой сетке.
Четыре суммы
Расположите плитки с заданными числами так, чтобы получилось два двузначных числа, которые в сумме дают заданное общее количество.
Путь Головоломка
Отличная головоломка, требующая от вас использовать все карты, чтобы создать непрерывную красную линию от начала до конца.
Лимонный закон
Измените числа на яблоках так, чтобы число на лимоне равнялось заданной сумме.
Головоломка с расписанием
Составьте расписание 24-часового дартс-марафона, которое учтет все запросы и сделает всех счастливыми.
Интернет-экстрасенс
Позвольте экстрасенсу прочитать карты и волшебным образом открыть число, которое вы тайно выбрали. Какая математика заставляет этот трюк работать?
Numskull
Интерактивная логическая головоломка на основе чисел, генерируемая случайным образом, для развития навыков счета.
Addle
Расставьте числа от 1 до 14 в полях, чтобы суммы были правильными. Как быстро ты сможешь это сделать?
Суко Судзико
Интерактивные логические головоломки на основе чисел, похожие на те, что публикуются в ежедневных газетах.
Пазлы с латинскими квадратами
Расположите указанные цифры так, чтобы получился латинский квадрат с заданными результатами вычисления строки и столбца.
Многоугольник
Расставьте девять частей головоломки на сетке, чтобы образовать разные многоугольники.
Пу Вианг
Задача с минимальным количеством ходов и встречным обменом, изобретенная в северном Таиланде.
Разочарование
Логическая задача, требующая стратегии для обновления каждого из чисел в сетке.
Prime Square
Перетащите числа в красные ячейки так, чтобы сумма трех чисел в каждой строке и каждом столбце была простым числом.
Смеси
Разложите карточки, чтобы составить верное математическое утверждение.
Масленица
Перемешивайте блины, пока они не будут аккуратно сложены по размеру.Найдите, как это сделать, используя наименьшее количество ходов.
Поиск слова
Найдите математические слова в сетке букв.
Вектор Менты
Помогите полицейским поймать грабителей, найдя векторы, которые положат конец погоне.
Трафальгарская площадь
Решите числовые головоломки, нарисованные на тротуаре Трафальгарской площади в Лондоне.
Triside Totals
Расположите цифры от 1 до 9 в треугольнике так, чтобы сумма чисел на каждой стороне была равна заданной сумме.
Множество
Расположите указанные цифры так, чтобы получилось три числа так, чтобы третье было произведением первого и второго.
Двойной тройной
Расположите цифры так, чтобы получилось три трехзначных числа так, чтобы второе было в два раза больше первого, а третье было в три раза больше первого.
Не слишком близко
Учащиеся с номерами от 1 до 8 должны сесть на стулья, чтобы никакие два последовательно пронумерованных ученика не сидели рядом друг с другом.
Инструменты
Сколько разных способов можно расположить числа, чтобы получить одинаковые итоги?
Вид из окна
Перетащите 20 цветов в сад, чтобы из каждого окна дома было видно по 9 цветов.
Фигуры в звездах
Соединяйте звезды, чтобы найти скрытые правильные многоугольники.
Удовлетворение
Поместите девять чисел в таблицу так, чтобы они соответствовали заголовкам строк и столбцов о свойствах чисел.
T Пазл
Используйте части головоломки T, чтобы вписаться в предоставленные контуры.Интерактивная задача перетаскивания, поворота и падения.
Маневровые пазлы
Как можно быстрее переместите трамваи на указанные стоянки на маневровой дворе.
Пазл Magic Square
Найдите все возможные способы получения магической суммы из чисел в этом магическом квадрате четыре на четыре.
Cubical Net Challenge
Найдите все способы раскрашивания граней кубиков, используя только два цвета.
Девять цифр
Расположите указанные цифры так, чтобы получилось три числа так, чтобы два из них в сумме давали третье.
Стол Tangram
Используйте части пазла танграм, чтобы сделать основные формы, затем заполните таблицу, показывающую, какие формы возможны.
слов в калькуляторе
Переверните калькулятор, чтобы составить слова из ответов на эти вопросы.
Гласный
Из математических слов было удаленогласных. Вы их узнаете?
Палочки для захвата
Если бы вы брали палки из этой кучи и всегда снимали верхнюю палку, какой расчет вы бы создали?
Разделительный
Расположите цифры с первого по девять в отведенных местах, чтобы произвести два вычисления деления, кратные трем.
Go Рисунок
Расположите цифры от одного до девяти, чтобы четыре вычисления были правильными.
Олимпийские кольца
Разместите цифры от одной до девяти в каждой из областей, созданных олимпийскими кольцами, так, чтобы сумма чисел в каждом кольце была одинаковой.
Арифмагоны
Найдите недостающие числа в этих треугольных головоломках с функцией самопроверки и откройте для себя чудеса этих увлекательных построек.
Пазлы для стен
Разделите сетку на прямоугольные части так, чтобы площадь каждой части была такой же, как и число, которое она содержит.
Рождественские украшения
Практическое задание, требующее от студентов сложить рождественские украшения в квадратную коробку.
Pentadd Quiz
Найдите пять чисел, которые при попарном сложении или умножении дают заданные суммы или произведения.
Прайм Лабиринт
Найдите путь к центру лабиринта, двигаясь по простым числам.
Жестокий
Сможете ли вы расположить семь жетонов на сетке, несмотря на их агрессивное поведение?
Математический кроссворд
Интерактивный математический кроссворд для вас онлайн.Найдите недостающие слова из заданных подсказок.
Истерика
Игра, головоломка и задача, в которой фишки размещаются по углам квадрата на сетке.
Подлецы и негодяи
Расставьте негодяев и негодяев на стульях так, чтобы числа любых двух сидящих рядом друг с другом составляли простое число.
Нет партнера
Найдите, какие числа в данном списке не сочетаются с другими числами в списке, чтобы получить заданную сумму.
трижды
Можете ли вы расположить все фишки на сетке в 10 линий по три фишки?
Домино Пазл
Разложите домино на семи квадратах. Количество точек на каждой стороне квадрата должно быть равно числу в середине
.Флер-де-Лис
Нажмите на шесть геральдических лилий, чтобы оставить четное число в каждой строке и столбце.
Головоломка Миллера
Это интерактивная версия головоломки, описанной Генри Эрнестом Дудени в The Canterbury Puzzles
.Восхитительно делимый
Расположите цифры от одного до девяти, чтобы получилось число, которое делится описанным способом.
Девять Девять Девять
Используйте цифры от 1 до 9, чтобы составить три трехзначных числа, которые в сумме дают 999.
Спинсум
Расположите числа на квадратах так, чтобы суммы по каждой линии из трех квадратов были равны.
Ключи к шаблонам
Интерактивное задание, в котором вам предстоит воспроизвести узор из цветных квадратов в соответствии с заданными подсказками.
Brainbox
Головоломка, требующая расположения чисел на функциональных машинах, чтобы связать заданные входные числа с правильными выходными.
Zygo
Интерактивная логическая головоломка на основе чисел, генерируемая случайным образом, для развития навыков счета.
Судоку онлайн
Интерактивная онлайн-версия популярной головоломки с числами.
Пазл Cube Net
Куб-головоломка с беспорядочными движущимися блоками показан как сеть.Вы можете это решить?
Где Валлаби?
Найдите спрятанного валлаби, используя подсказки в выбранных координатах.
Кувшины
Можно ли приготовить 4 литра, если у вас есть только кувшины на 7 и 5 литров?
Взломщик кода
Взломайте код, заменив зашифрованные буквы в данном тексте.Есть много подсказок о методах взлома кода.
Сколько квадратов? 2
Сколько разных наборов из четырех точек можно соединить в квадрат?
Ханойская башня
Перемещайте части башни с места на место за минимальное количество ходов.
Людикросс
Расположите указанные числа на кресте так, чтобы сумма чисел на обеих диагоналях была одинаковой.
Самый крупный продукт
Операция перетаскивания, в которой вам нужно расположить цифры для получения максимально возможного продукта.
Подсказка Судоку
Другой способ решить головоломку Судоку с подсказками, доступными на каждом этапе.
Пазлы для начинающих
На сайте Transum есть еще много головоломок.
Следующие головоломки взяты из ежемесячных информационных бюллетеней и подкастов Transum.
Половина среднего угла
Найдите размер угла в точке A, если он составляет половину среднего значения углов в точках B и C.
Newsletter Podcast
Продовольственная инфляция
Стоимость еды увеличивается на 4% до целого числа фунтов.
Подкаст информационного бюллетеня
Крис и его непредсказуемые дети
Подумайте о головоломке с числами с непредсказуемым элементом.
Подкаст информационного бюллетеня
Кейт и Кэт
Найдите возраст Кейта и Кэт по предоставленным подсказкам.
Подкаст информационного бюллетеня
Two-Faced and Blue
Сколько маленьких кубиков, составляющих куб 3×3, имеют две грани, окрашенные в синий цвет?
Подкаст информационного бюллетеня
Санта крутой
Какая температура указывается с использованием одного и того же числа в градусах Цельсия и Фаренгейта?
Подкаст информационного бюллетеня
Три тройки троек, трижды
Простой вопрос, на который ошиблись семьдесят два процента группы людей.
Подкаст информационного бюллетеня
Поезда вместе
Как далеко друг от друга будут находиться поезда за полчаса до встречи?
Подкаст информационного бюллетеня
Six Ropes
Могут ли пираты завоевать свободу, связав шесть кусков веревки в одну большую петлю?
Подкаст информационного бюллетеня
Богдан и Уолли
В каком порядке вы должны играть в Ultimate Noughts and Crosses против Уолли и Богдана?
Подкаст информационного бюллетеня
математических дней
Какая дата следующего дня теоремы Пифагора?
Подкаст информационного бюллетеня
Eva’s Eggs and Fickle Fractions
Сколько яиц Ева вывела на рынок, чтобы сделать эти странные половинки продаж?
Подкаст информационного бюллетеня
Кормление дураков и лошадей
Как долго лошадь будет кормить лошадей после того, как некоторые из них покинули конюшню?
Подкаст информационного бюллетеня
Балансировка воздушных шаров
Сколько воздушных шаров Джейми должен дать Бену, чтобы сбалансировать уравнение воздушного шара?
Подкаст информационного бюллетеня
Головоломка от Карла
Головоломка Карла представляет собой результат деления произведения возраста его родителей на его возраст вдвое.
Подкаст информационного бюллетеня
Коэффициенты от событий до 2020 года
Вычтите сумму нечетных чисел меньше 2020 из суммы четных чисел меньше 2020 года.
Подкаст информационного бюллетеня
Ноэль в Лапландии
Определите продолжительность поездки Ноэля в Лапландию, учитывая подробности погодных условий.
Подкаст информационного бюллетеня
Несколько остатков
Какое второе наименьшее число такое, что при делении на 5 остаток равен 4, а при делении на 7 остаток равен 6?
Подкаст информационного бюллетеня
Автобусы до Кембриджа
Можете ли вы выяснить, на каком автобусе я ехал, когда ехал в Кембридж?
Подкаст информационного бюллетеня
Дети Перси Кода
Перси Код говорил о своих детях.Можете ли вы определить их возраст с учетом соотношений?
Подкаст информационного бюллетеня
Морковноеды
Определите, сколько животных каждого вида находится в поле, по их морковные привычки.
Новостная рассылка Подкаст
Площадь Красной Стрелки
Какую часть квадрата закрывает красная стрелка?
Новостная рассылка Подкаст
Пэтси любит Перси
Странный случай с Перси, который, кажется, очень быстро стареет
Новостная рассылка Подкаст
Обезьяны, котята и собаки
Кто, скорее всего, сможет вычислить квадратный корень из 121?
Новостная рассылка Подкаст
Покормить лошадей
Как Долго ли хватит оставшегося корма для не проданных лошадей?
Новостная рассылка Подкаст
Странное дополнение
Если Я начинаю с пяти и добавляю шесть, я получаю одиннадцать, но если я начинаю с шести и добавляю семь Я получаю.
Новостная рассылка Подкаст
Простые перестановки
Из всех перестановок от 1 до 9, используемых для получения девятизначных чисел, сколько главные?
Новостная рассылка Подкаст
4-значный код сейфа в гостиничном номере
Можете ли вы определить, какой номер я использовал, чтобы запирать и отпирать сейф в номере отеля?
Новостная рассылка Подкаст
Цвет глаз хора
Выясните процент участников хора, у которых нет голубых глаз данные подсказки.
Новостная рассылка Подкаст
Клавиши калькулятора в углах Прямоугольник
Вопрос про четыре клавиши по углам прямоугольника на калькуляторе.
Новостная рассылка Подкаст
Среднее количество домов
Определите номера домов по подсказкам о среднем, медиане и моде.
Новостная рассылка Подкаст
Часы в зеркале
Какое время на самом деле показывали часы в зеркале?
Новостная рассылка Подкаст
Восхитительно делимый
Найдите панцифровое число, которое восхитительно делится.
Новостная рассылка Подкаст
Пять целых чисел с произведением 12
Сможете ли вы найти пять целых чисел, которые при умножении дают двенадцать?
Новостная рассылка Подкаст
Квадрат в прямоугольнике
Какой самый большой квадрат можно нарисовать в углу 10 см на 15 см? прямоугольник?
Новостная рассылка Подкаст
Лондонский марафон
A вопрос о средней скорости, необходимой для второй половины марафон.
Новостная рассылка Подкаст
Стрижка газона
Айнюк и Айли вырезали половину газона. Какова длина каждой стороны квадратный газон?
Новостная рассылка Подкаст
Найден недостающий фунт
Действительно замечательный ответ на загадку о пропавшем фунте.
Новостная рассылка Подкаст
Сорок пять в четырех частях
Разделите число 45 на четыре части в соответствии с предоставленной информацией.
Новостная рассылка Подкаст
Сморщенные палочки
Определите вес картофеля, оставленного на солнце. сушить.
Новостная рассылка Подкаст
Ошибка транспозиции
Получив информацию об ошибке транспонирования, рассчитайте банковский баланс.
Новостная рассылка Подкаст
Подсчет овец
Работа из числа имеющихся у Перси и Пэтси овец.
Новостная рассылка Подкаст
Жонглирование таймерами для яиц
Можете ли вы рассчитать ровно девять минут, используя четырех- и семиминутное яйцо? таймеры?
Новостная рассылка Подкаст
Сумма перестановок
Какова сумма всех четырехзначных чисел, содержащих все цифры: единица до четырех?
Новостная рассылка Подкаст
Нечетная вероятность
Какова вероятность того, что два случайных числа будут одинаковыми, даже если они не оба ли странные?
Новостная рассылка Подкаст
Области в кругах
Подсчитайте количество областей в круге, образованном пересекающимися хордами.
Новостная рассылка Подкаст
Братья и сестры
Можете ли вы определить количество детей в семье Нумлов, учитывая подсказки о братьях и сестрах?
Новостная рассылка Подкаст
Среднее значение за экзамен
Что оценка требуется на последнем экзамене для достижения 80% общего среднего?
Новостная рассылка Подкаст
Торт нарезанный
Где следует ли разрезать последний кусок торта, чтобы получить два равных куска?
Новостная рассылка Подкаст
Holy Sphere
Вычислите оставшийся объем сферы после того, как цилиндрическое отверстие пробурено через центр
Новостная рассылка Подкаст
Блоха в прыжках
Как много разных мест могла найти блоха после 8-футовых прыжков на север, юг, восток или запад?
Новостная рассылка Подкаст
Последняя цифра
Сколько положительные двузначные числа, квадрат и куб которых оканчиваются на такая же цифра?
Новостная рассылка Подкаст
Центральный вокзал
вероятность того, что следующий поезд отправится на север, составляет пять раз вероятность того, что следующий поезд отправится на юг.
Новостная рассылка Подкаст
Очередь в столовую
Это Можно ли ответить на вопрос, если возраст Бетси неизвестен?
Новостная рассылка Подкаст
Разлученные близнецы
Разработайте комбинацию сейфа по подсказкам о парах чисел.
Новостная рассылка Подкаст
делится на три
Головоломка о двухзначных числах, которые можно составить из десяти разных цифр.
Новостная рассылка Подкаст
Буквы в цифрах
Совершенно новая головоломка, в которой буквы в числах записываются как слова.
Новостная рассылка Подкаст
Квадратный треугольник
Углы треугольника — это квадратные числа. Кто они такие?
Новостная рассылка Подкаст
Головоломка с тремя перекрестками
Какова вероятность того, что три машины не дойдут до развязки? попасть в аварию?
Новостная рассылка Подкаст
Два основных квадрата
Какое наименьшее квадратное число (больше единицы) не может быть выражается как сумма двух простых чисел?
Новостная рассылка Подкаст
Недостающий фунт
Куда делся недостающий фунт в этой истории о трех людях, посетивших ресторан?
Новостная рассылка Подкаст
Клещи, тактики, галстуки и вытачки
Найдите, как клещи соотносятся с тактиками, закрепками и защипами, исходя из предоставленной информации.
Новостная рассылка Подкаст
Сила Рождества
Вопрос об индексах, который заставит вас задуматься математически на этом праздничном время года.
Новостная рассылка Подкаст
Муравей и Дек
Что Единственный вопрос, который Дек мог бы задать Ant, чтобы узнать, о чем он думает?
Новостная рассылка Подкаст
Книжный червь
Как далеко путешествует ли книжный червь во время еды?
Новостная рассылка Подкаст
Три математика
Как может третий математик быть настолько уверенным, что все хотят выпить?
Новостная рассылка Подкаст
Незаконченная игра
Если игра с подбрасыванием монет была прервана, как бы вы поделились выигрышем?
Новостная рассылка Подкаст
Буквенно-цифровой
Вопросы о буквах, используемых в натуральных числах.
Новостная рассылка Подкаст
Лучшие кости
Какие из необычные кости, которые вы выбрали бы, чтобы дать вам больше шансов выиграть приз?
Новостная рассылка Подкаст
Проблема дня рождения
Какова вероятность того, что два или более ученика в классе будут иметь одинаковые день рождения?
Новостная рассылка Подкаст
Гласные буквы Enigma
A Вопрос по кодированию навеян фильмом «Игра в имитацию».
Новостная рассылка Подкаст
Смещенная монета
A математический вопрос, который задают интервьюеры Microsoft и Google.
Новостная рассылка Подкаст
Двенадцать дней Рождества
Сможете ли вы точно подсчитать, сколько подарков посылает настоящая любовь во время двенадцать дней рождественских праздников?
Новостная рассылка Подкаст
За медведем
A головоломка о исследователе, преследуемом медведем, а также вопрос о Британские и метрические меры с помощью Measurement Man
Новостная рассылка Подкаст
Подставки для Хэллоуина
A головоломка о том, почему Хэллоуин похож на Рождество вместе с новостями о новом Опись умений и навыков
Новостная рассылка Подкаст
Torch Tunnel
A загадка про четырех человек, пробирающихся через туннель с одним факел вместе с новостями новой нумерологии страница
Новостная рассылка Подкаст
Кубик в молоке
A головоломка о кубике, который опускают в ведро с молоком, а также новости о новые маневровые пазлы
Новостная рассылка Подкаст
Следующие головоломки относятся к Transum Advanced Starters.
Алгебраическое произведение
Найти значение выражения проще, чем вы думаете!
Продвинутый стартер
Угловое мышление
Найдите диапазон возможных углов x, для которых tan x> cos x> sin x
Продвинутый стартер
Средняя скорость езды на велосипеде
Определите среднюю скорость двух поездок. Очевидный ответ не является правильным.
Продвинутый стартер
Вернуться на завод
Найдите все числа ниже 1000, которые имеют ровно 20 множителей
Продвинутый стартер
Barmy BIDMAS
Вводящий в заблуждение способ сформулировать ответ на простой расчет.
Продвинутый стартер
Парадокс коробки Бертрана
Парадокс коробки Бертрана — парадокс элементарной теории вероятностей, впервые сформулированный Джозефом Бертраном в 1889 году
Продвинутый стартер
Best Dice
Какие из необычных игральных костей вы бы выбрали, чтобы дать вам больше шансов выиграть приз?
Продвинутый стартер
Неравенства автомобилей
Решите три одновременных неравенства, чтобы узнать, сколько автомобилей у меня есть.
Продвинутый стартер
Charging Rhinos
Найдите простой способ решить эту кинематическую задачу с участием мухи и двух носорогов.
Продвинутый стартер
День рождения Шерил
Используйте процесс исключения, чтобы определить правильную дату из данных подсказок.
Продвинутый стартер
Координатное расстояние
Найдите k, учитывая, что (-2, k) находится на расстоянии 13 единиц от (10,9)
Продвинутый стартер
Кубоид
Найдите размеры кубоида, соответствующие приведенному описанию
Продвинутый стартер
Делится на 11
Можете ли вы доказать, что трехзначное число, первая и третья цифры которого в сумме дают значение второй цифры, должно делиться на одиннадцать?
Продвинутый стартер
Двойная или половина?
При изменении десяти процентов в день удвоение достигается быстрее, чем уменьшение вдвое?
Продвинутый стартер
Превышает на 99
Найдите число, удвоение которого превышает половину ровно на 99.
Продвинутый стартер
Оптимизация забора
Найдите длину прямоугольника, охватывающего максимально возможную площадь.
Продвинутый стартер
Задача Ферми
Классическая задача Ферми с использованием стандартных методов оценки
Продвинутый стартер
Найдите радиус
Найдите радиус круга из небольшого количества предоставленной информации.
Продвинутый стартер
Деление на четыре дроби
Объясните, почему ответом на серию дробных делений является целое число.
Продвинутый стартер
GDC Challenge
Построить данный график на графическом калькуляторе
Продвинутый стартер
Geometry Snack
Найдите значение отмеченного угла на этой диаграмме из книги Geometry Snacks
Продвинутый стартер
Бабушка
Как далеко ушла бы бабушка после достаточно большого количества дней, учитывая ее режим ходьбы?
Продвинутый стартер
Руки вместе
Стрелки часов вместе в полночь.В какое время они будут вместе?
Продвинутый стартер
HCF и LCM даны
Если даны HCF, LCM и меньшее из двух чисел, можете ли вы найти другое?
Продвинутый стартер
Сколько левшей?
Определите количество членов, если дана вероятность случайного выбора левых элементов.
Продвинутый стартер
Сто пятьдесят процентов
Разделите 110 на две части так, чтобы большая часть составляла 150% меньшей части.
Продвинутый стартер
Key Eleven
Докажите, что построенное определенным образом четырехзначное число будет кратно одиннадцати.
Продвинутый стартер
Log Perfection
Определите, верны ли данные утверждения, содержащие логарифмы
Продвинутый стартер
Логарифмическое уравнение
Решите уравнение, содержащее логарифмы с разными основаниями
Продвинутый стартер
Максимум продукта
В сумме два числа дают 10.Какой самый крупный продукт, который они могли бы иметь?
Продвинутый стартер
Кратное сумме цифр
Какое число в шесть раз больше суммы его цифр?
Продвинутый стартер
Девятизначные числа
Сколько у них различных девятизначных чисел, которые содержат каждую из цифр от одного до девяти?
Продвинутый стартер
Пол другого ребенка
Какова вероятность того, что второй ребенок тоже мальчик?
Продвинутый стартер
Пропорции бумаги
Рассчитайте соотношение сторон листа бумаги формата A4 без каких-либо измерений.
Продвинутый стартер
Paper Surprising Perimeter
Найдите периметр сложенного листа бумаги формата A4, как описано в этом коротком видео.
Продвинутый стартер
Параллельные графики
Определите по их уравнениям, какие из прямых графиков параллельны и перпендикулярны.
Продвинутый стартер
Пенни-мешки
Можете ли вы поместить 63 пенни в мешки таким образом, чтобы вы могли раздать любую сумму денег (от 1 пенни до 63 пенни), отдав выбор из этих расфасованных пакетов?
Продвинутый стартер
Perennial Rivals
Какая футбольная команда первой выиграет четыре матча?
Продвинутый стартер
Перестановочные функции
Найдите пары функций, коммутативные относительно композиции.
Продвинутый стартер
Часть веревки
Найдите место, где нужно разрезать веревку так, чтобы получился круг и квадрат одинаковой площади.
Продвинутый стартер
Pizza Slice
Задача, которую можно решить, рассматривая площади треугольника и сектора круга.
Продвинутый стартер
Произведение индексов
Найдите произведение неизвестных индексов, входящих в два уравнения
Продвинутый стартер
Середины четырехугольника
Какая форма создается, когда середины сторон четырехугольника соединяются вместе?
Продвинутый стартер
Сдержанная блоха
Сколько разных мест может найти блоха после 8-футовых прыжков на север, юг, восток или запад?
Продвинутый стартер
Обратное соединение
Найдите общее правило для разницы между двузначным числом и тем же числом с перевернутыми цифрами.
Продвинутый стартер
Рис на шахматной доске
Сколько зерен риса находится на шахматной доске, если в каждом квадрате содержится вдвое больше зерен, чем в предыдущем квадрате.
Продвинутый стартер
Богатые или бедные?
Интересный результат процентного увеличения и уменьшения
Продвинутый стартер
Дорожные соединения
Спроектируйте дороги, чтобы соединить четыре дома, которые находятся на углах квадрата со стороной длиной в одну милю, чтобы минимизировать общую длину дорог.
Продвинутый стартер
Сумма одного ряда
Найдите арифметический ряд и геометрический ряд, в которых сумма первых пяти членов одинакова.
Продвинутый стартер
Одинаковые три цифры
Найдите выражения, содержащие индексы, и оцените числа, содержащие одинаковые цифры.
Продвинутый стартер
Семнадцать верблюдов
Объясните математику классической истории разделения дробей девятнадцатого века.
Продвинутый стартер
Single Fraction
Упростите выражение, включающее дроби, показатели степени и квадратный корень.
Продвинутый стартер
Круги скорости
Найдите диаметры окружностей в углах квадрата.
Продвинутый стартер
Отверстие в сфере
Найдите объем оставшейся части сферы после того, как в ней было просверлено 10-сантиметровое цилиндрическое отверстие.
Продвинутый стартер
Квадрат в прямоугольнике
Найдите площадь квадрата, нарисованного под диагональю прямоугольника
Продвинутый стартер
Tan 22,5
Найдите точное значение tan 22,50 без использования калькулятора.
Продвинутый стартер
Результаты тестов
Изучите заблуждение о том, что при сложении дробей вы складываете и числители, и знаменатели
Продвинутый стартер
Три прямоугольных треугольника
Вычислите длины сторон без меток этих прямоугольных треугольников.
Продвинутый стартер
Transum Tonic
Какое наибольшее количество флаконов невозможно купить, если они поставляются в упаковках по 6, 9 и 20?
Продвинутый стартер
Tri-Junction
Реальная жизненная ситуация, которую можно проанализировать с помощью древовидной диаграммы.
Продвинутый стартер
Треугольник или четырехугольник
Может ли четырехугольник иметь прямой угол?
Продвинутый стартер
Два равно одному
Что не так с алгебраическими рассуждениями, которые показывают, что 2 = 1?
Продвинутый стартер
Два действительных числа
Сумма обратных двух действительных чисел равна -1, а сумма их кубиков равна 4.Кто они такие?
Продвинутый стартер
Незаконченная игра
Разделите приз в справедливом соотношении, в зависимости от вероятности желания каждого игрока.
Продвинутый стартер
Unlucky Seven Eleven
Следуйте инструкциям, чтобы умножить выбранное число, а затем объясните полученный результат.
Продвинутый стартер
Код гласного
Сколько способов вы можете создать код для гласных, назначив каждой гласной разные гласные?
Продвинутый стартер
Сводки погоды
Какие пять различных целых чисел умножаются и дают 12?
Продвинутый стартер
Какой вопрос?
Запишите все возможные вопросы, которые можно было бы задать, если бы это была диаграмма из учебника математики.
Продвинутый стартер
X Разделено на 2 года
Почему разные калькуляторы не согласовывают порядок операций?
Продвинутый стартер
.

 Это приводит к тому, что игра заканчивается после того, как каждый из других игроков сделает еще один ход.
Это приводит к тому, что игра заканчивается после того, как каждый из других игроков сделает еще один ход. Затем наступает очередь следующего игрока.
Затем наступает очередь следующего игрока.


 Эти не могут быть размещены в раскладке игрока: игрок должен либо выполнить действие, либо просто сбросить карту.
Эти не могут быть размещены в раскладке игрока: игрок должен либо выполнить действие, либо просто сбросить карту. Примечание: допинг красного короля не соответствует черному королю, а 2 не соответствует другому 2: значения карты должны быть равны. Примечание: только , одна дополнительная карта может быть сброшена как матч поверх обычного сброса.
Примечание: допинг красного короля не соответствует черному королю, а 2 не соответствует другому 2: значения карты должны быть равны. Примечание: только , одна дополнительная карта может быть сброшена как матч поверх обычного сброса. Все короли подходят друг другу, включая бриллианты. Все совпавшие карты сбрасываются, за ними следует карта, инициировавшая сопоставление. Любые совпавшие карты из раскладок оппонентов заменяются картами из вашего собственного расклада, не глядя на заменяющие карты. Если вы пытаетесь сопоставить карту, которая оказывается не равна соответствующей карте, карта остается на месте и в качестве штрафа за каждую такую неудачу вы берете дополнительную карту из запаса и добавляете ее в свой макет, не глядя на Это.
Все короли подходят друг другу, включая бриллианты. Все совпавшие карты сбрасываются, за ними следует карта, инициировавшая сопоставление. Любые совпавшие карты из раскладок оппонентов заменяются картами из вашего собственного расклада, не глядя на заменяющие карты. Если вы пытаетесь сопоставить карту, которая оказывается не равна соответствующей карте, карта остается на месте и в качестве штрафа за каждую такую неудачу вы берете дополнительную карту из запаса и добавляете ее в свой макет, не глядя на Это.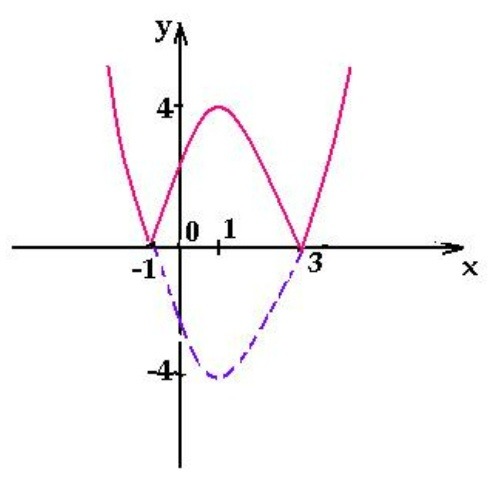
 Если ваш балл равен или ниже, чем у вызывающего абонента, вы ничего не набираете.
Если ваш балл равен или ниже, чем у вызывающего абонента, вы ничего не набираете.