Игры с природой теория игр: Игры с природой / Хабр

alexxlab / / Разное

Содержание

Игры с природой / Хабр

Затянувшееся продолжение цикла статей о теории игр.

Ближе к практике

В прошлой статье о теории игр были рассмотрены ситуации, в которых предполагалась логичность дествий двух игроков, каждый из которых хочет получить для себя максимум выгоды. Следующим этапом являются так называемые игры с природой. Формально изучение игр с природой, так же, как и стратегических, должно начинаться с построения платежной матрицы, что является, по существу, наиболее трудоемким этапом подготовки принятия решения. Ошибки в платежной матрице не могут быть компенсированы никакими вычислительными методами и приведут к неверному итоговому результату.

Отличительная особенность игры с природой состоит в том, что в ней сознательно действует только один из участников, в большинстве случаев называемый игроком один. Игроку два (природа) не важен результат, либо он не способен к осмысленным решениям. Или, возможно, условия не зависят от действий игрока, а определяются внешними факторами: реакция рынка, который не будет вредить одному конкретному игроку, государственная политика, реальная природа.

Виды задач и критерии выбора

Различают два вида задач в играх с природой:

  • Задача о принятии решений в условиях риска, когда известны вероятности, с которыми природа принимает каждое из возможных состояний;
  • Задачи о принятии решений в условиях неопределенности, когда нет возможности получить информацию о вероятностях появления состояний природы;

Чтобы быть ближе к реальным ситуациям, для примера возьмем относительно реальную ситуацию. Первого игрока, за которого мы будем принимать решения, будет представлять Samsung со своим Galaxy S5. Вторым игроком, играющим «природу», будет компания Apple, и его iPhone 6.

Подходит время выпуска нового смартфона, прошла презентация, эксперты высказали свое мнение, и игрок один должен принять важное решение, когда выпустить продукт? Упростив ситуацию, у нас останется три варианта: до конкурента (А

1), вместе с ним (А2) или после (А3). Естественно, пока не выйдет новый iPhone мы не узнаем, будет он намного лучше нашего (В1), таким же (В3) или сильно уступающим в качестве (В3). Посчитав прибыль во всех случаях, в итоге получим матрицу:

В1 В2 В3
А1 5 5 7
А2 3 4 6
А3 2 4 8

Теперь же, для принятия решения, у нас есть несколько критериев.

1. Критерий Вальда (максиминный). Игрок рассчитывает, что природа пойдет по наихудшему для него пути, и следует выбрать вариант с максимальной прибылью при самом плохом исходе, поэтому данный критерий считается пессимистическим. Представить его можно в виде max (min i)

При данном критерии:

для А1 минимальной прибылью (5) выльются действия природы В1 и В2
для А2 минимальная прибыль 3 после действия В1
для А3 минимальная прибыль 2 после действия В1

Таким образом из 5, 3 и 2 максимум прибыли (5) нам даст вариант А1

2. Критерий максимума (максимаксный) является оптимистическим, т.е. мы надеемся на самый благоприятный для нас исход.представляется как max (max i).

для А1 максимальная прибыль 7
для А2 максимальная прибыль 6
для А3 максимальная прибыль 8

Из 7, 6 и 8 максимальную прибыль принесет вариант А3

3. Критерий Гурвица рекомендует стратегию, определяемую по формуле max (A*max i + (1-A)*min i), где А — степень оптимизма и изменяется в пределах от 0 до 1. Критерий выдает результат, учитывающий возможность как наихудшего, так и наилучшего поведения природы. При А=1 данный критерий можно заменить критерием максимума, а при А=0 — критерием Вальда. Величина А зависит от степени ответственности игрока один: чем она выше, тем ближе А к единице. Для данного примера примем А=0,4.

для А1 прибыль равна 0,4*7 + 0,6*5 = 5,8
для А2 прибыль равна 0,4*6 + 0,6*3 = 4,2
для А3 прибыль равна 0,4*8 + 0,6*2 = 4,4

Из полученных ответов максимыльную прибль приносит действие А1

4. Критерий Сэвиджа (минимаксный). Суть его заключается в выборе стратегии, не допускающей слишком высоких потерь. Для этого используется матрица рисков, в которой вычисляется максимальная прибыль при каждом варианте действия игрока, и среди результатов выбирается наименьший. Его формула выглядит как min (max i)

При данном критерии:

для А1 максимальной прибылью (7) выльется действие природы В3
для А2 максимальная прибыль 6 после действия В3
для А3 максимальная прибыль 8 после действия В3

Таким образом из 7, 6 и 8 минимум прибыли (6) нам даст вариант А2

5. По критерию Байеса предлагается придать равные вероятности всем рассматриваемым стратегиям, после чего принять ту из них, при которой ожидаемый выигрыш окажется наибольшим. Критерий имеет один недостаток: не всегда можно точно определить вероятность того или иного события со стороны природы. Формулой для него является max (Σ q*i).

Сначала мы положили вероятность наступления каждого из собитий природы равной 0,33, и получили

для А1 5*0,33 + 5*0,33 + 7*0,33 = 5,61
для А2 3*0,33 + 4*0,33 + 6*0,33 = 4,29
для А3 2*0,33 + 4*0,33 + 8*0,33 = 7,63

Очевидно что максимальную прибыль мы получим от варианта А3. Однако, обратившись к экспертам, мы получили вероятности событий для природы 0,5; 0,4; 0,1; соответственно. Таким образом

для А1 5*0,5 + 5*0,4 + 7*0,1 = 5,2
для А2 3*0,5 + 4*0,4 + 6*0,1 = 3,7
для А3 2*0,5 + 4*0,4 + 8*0,1 = 3,4

Думаю результат комментировать бессмысленно.

Основная задача состоит в том, чтобы найти оптимальные (или хотя бы рациональные) стратегии, наилучшим образом приводящие систему к цели при заданных внешних условиях. Для выбора стратегий в условиях неопределенности можно применять любые критерии, в условиях риска действеннее критерий Байеса. Однако выбор между самими критериями основывается обычно на интуиции, зависит от характера принимающего решение (в частности, его склонности к риску).

Если решение принимается в условиях неопределенности, то лучше использовать несколько критериев. В том случае, если рекомендации совпадают, можно с уверенностью выбирать наилучшее решение. Если рекомендации противоречивы, решение надо принимать более взвешенно, с учетом сильных и слабых сторон.

Игры с природой онлайн

Назначение сервиса. Данный тип задач относится к задачам принятия решений в условиях неопределенности. С помощью сервиса можно выбрать оптимальную стратегию, используя:
  • критерий минимакса, критерий максимакса, критерий Байеса, критерий Вальда, критерий Сэвиджа, критерий Лапласа, критерий Ходжа-Лемана;
  • критерий Гурвица, обобщенный критерий Гурвица с расчетом эффективности;
  • множество Паретто.
Также проводится планирование идеального эксперимента. Результаты онлайн вычислений оформляются в отчете формата Word.
  • Шаг №1
  • Шаг №2
  • Видеоинструкция

Инструкция. Для выбора оптимальной стратегии в онлайн режиме необходимо задать размерность матрицы. Затем в новом диалоговом окне выбрать необходимые критерии и коэффициенты. Также можно вставить данные из Excel. Размерность платежной матрицы (целевая функция ЗПР в условиях неопределенности)
2345678910 x 2345678910
Примечание: Сначала, если возможно, упрощают матрицу, вычеркивая невыгодные стратегии A. Стратегии природы вычеркивать нельзя, т. к. каждое из состояний природы может наступить случайным образом, независимо от действий A.

Любую хозяйственную деятельность человека можно рассматривать как игру с природой. В широком смысле под «природой» понимается совокупность неопределенных факторов; влияющих на эффективность принимаемых решений. Безразличие природы к игре (выигрышу) к возможность получения экономистом (статистиком) дополнительной информации о ее состоянии отличают игру экономиста с природой от обычной матричной игры, в которой принимают участие два сознательных игрока.

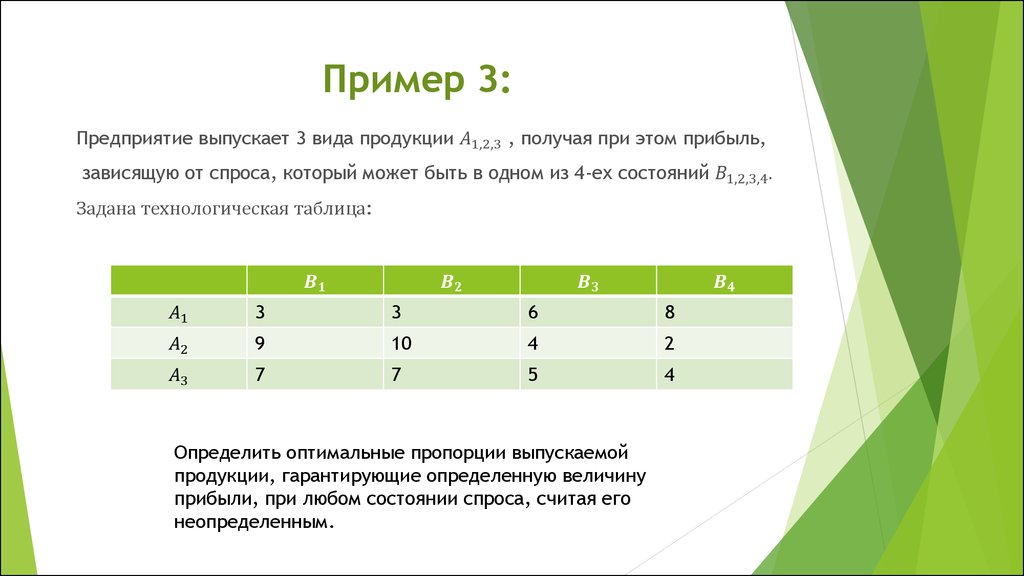
Пример. Предприятие может выпускать 3 вида продукции А1, А2 и А3, получая при этом прибыль, зависящую от спроса, который может быть в одном из 4-х состояний (В1, В2, В3, В4). Элементы платежной матрицы характеризуют прибыль, которую получат при выпуске i-й продукции при j-м состоянии спроса. Игра предприятия А против спроса В задана платежной матрицей:

В1В2В3В4
А12786
А22873
А34342
Определить оптимальные пропорции в выпускаемой продукции, гарантирующие максимизацию средней величины прибыли при любом состоянии спроса, считая его определенным. Задача сводится к игровой модели, в которой.

Решение.
Критерий максимакса.

AiП1П2П3П4max(aij)
A127868
A228738
A343424
Выбираем из (8; 8; 4) максимальный элемент max=8
Вывод: выбираем стратегию N=1.

Критерий Лапласа.

AiП1П2П3П4∑(aij)
A10.51.7521.55.75
A20.521.750.755
A310. 7510.53.25
pj0.250.250.250.25
Выбираем из (5.75; 5; 3.25) максимальный элемент max=5.75
Вывод: выбираем стратегию N=1.

Критерий Вальда.

AiП1П2П3П4min(aij)
A127862
A228732
A343422
Выбираем из (2; 2; 2) максимальный элемент max=2
Вывод: выбираем стратегию N=1.

Критерий Севиджа.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r11 = 4 — 2 = 2; r21 = 4 — 2 = 2; r31 = 4 — 4 = 0;
2. Рассчитываем 2-й столбец матрицы рисков.
r12 = 8 — 7 = 1; r22 = 8 — 8 = 0; r32 = 8 — 3 = 5;
3. Рассчитываем 3-й столбец матрицы рисков.
r13 = 8 — 8 = 0; r23 = 8 — 7 = 1; r33 = 8 — 4 = 4;
4. Рассчитываем 4-й столбец матрицы рисков.
r14 = 6 — 6 = 0; r24 = 6 — 3 = 3; r34 = 6 — 2 = 4;

AiП1П2П3П4
A12100
A22013
A30544
Результаты вычислений оформим в виде таблицы.
AiП1П2П3П4max(aij)
A121002
A220133
A305445
Выбираем из (2; 3; 5) минимальный элемент min=2
Вывод: выбираем стратегию N=1.

Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A1.

Пример. Предлагается три проекта инвестиций и прогноз получения доходов за год (дивиденды и повышение стоимости капитала) при различных возможных исходах.

Проект инвестиций 1
возможные исходы:		Проект инвестиций 2
возможные исходы:		Проект инвестиций 3
возможные исходы:
123123123
404020302030203020

Теория игр

Что такое теория игр?

Теория игр — это теоретическая основа для понимания социальных ситуаций между конкурирующими игроками. В некотором смысле теория игр — это наука о стратегии или, по крайней мере, об оптимальном принятии решений независимыми и конкурирующими субъектами в стратегической обстановке.

Ключевые выводы

  • Теория игр — это теоретическая основа для понимания социальных ситуаций между конкурирующими игроками.
  • Теория игр предназначена для обеспечения оптимального принятия решений независимыми и конкурирующими субъектами в стратегической обстановке.
  • Используя теорию игр, можно разработать реальные сценарии для таких ситуаций, как ценовая конкуренция и выпуск продуктов (и многие другие), и предсказать их результаты.
  • Сценарии включают дилемму заключенного и игру в диктатора среди многих других.
  • Различные типы теории игр включают кооперативную/некооперативную, с нулевой суммой/ненулевой суммой и одновременную/последовательную.
Теория игр

Как работает теория игр

Ключевыми пионерами теории игр были математик Джон фон Нейман и экономист Оскар Моргенштерн в XIX веке. 40с. Многие считают математика Джона Нэша первым значительным продолжением работы фон Неймана и Моргенштерна.

В центре внимания теории игр находится игра, которая служит моделью интерактивной ситуации между рациональными игроками. Ключ к теории игр состоит в том, что выигрыш одного игрока зависит от стратегии, реализуемой другим игроком.

Игра определяет личность, предпочтения и доступные стратегии игроков, а также то, как эти стратегии влияют на результат. В зависимости от модели могут потребоваться различные другие требования или допущения.

Теория игр имеет широкий спектр приложений, включая психологию, эволюционную биологию, войну, политику, экономику и бизнес. Несмотря на многочисленные достижения, теория игр все еще остается молодой и развивающейся наукой.

Согласно теории игр действия и выбор всех участников влияют на результат каждого из них. Предполагается, что игроки в игре рациональны и будут стремиться максимизировать свои выигрыши в игре.

Полезные термины теории игр

Каждый раз, когда у нас возникает ситуация с двумя или более игроками, которая включает известные выплаты или поддающиеся количественной оценке последствия, мы можем использовать теорию игр, чтобы определить наиболее вероятные исходы. Начнем с определения нескольких терминов, обычно используемых при изучении теории игр:

  • Игра : Любой набор обстоятельств, результат которого зависит от действий двух или более лиц, принимающих решения (игроков)
  • Игроки : Принятие стратегических решений в контексте игры
  • Стратегия : Полный план действий, которые игрок предпримет с учетом набора обстоятельств, которые могут возникнуть в игре
  • Выплата :   Выплата, которую игрок получает за достижение определенного результата (Выплата может быть в любой измеримой форме, от долларов до полезности.)
  • Информационный набор : Информация, доступная в данный момент в игре (Термин информационный набор чаще всего применяется, когда в игре есть последовательный компонент. )
  • Равновесие : Момент в игре, когда оба игрока приняли решение и достигнут результат

Равновесие Нэша

Равновесие Нэша — это достигнутый результат, который означает, что ни один игрок не может увеличить выигрыш, изменив решения в одностороннем порядке. Это также можно рассматривать как «без сожалений» в том смысле, что после принятия решения игрок не будет сожалеть о решениях с учетом последствий.

В большинстве случаев равновесие Нэша достигается со временем. Однако, как только равновесие Нэша будет достигнуто, оно не будет отклоняться от него. После того, как мы научимся находить равновесие Нэша, посмотрим, как одностороннее движение повлияет на ситуацию. Есть ли в этом смысл? Так не должно быть, и поэтому равновесие Нэша описывается как «без сожалений». Как правило, в игре может быть более одного равновесия.

Однако это обычно происходит в играх с более сложными элементами, чем два выбора двумя игроками. В одновременных играх, которые повторяются с течением времени, одно из этих множественных равновесий достигается после некоторых проб и ошибок. Этот сценарий различных вариантов выбора в течение долгого времени до достижения равновесия чаще всего разыгрывается в деловом мире, когда две фирмы определяют цены на продукты с высокой степенью взаимозаменяемости, такие как авиабилеты или безалкогольные напитки.

Вы когда-нибудь видели, чтобы тренер соперника брал тайм-аут прямо перед тем, как кикер другой команды должен попытаться забить победный бросок с игры? Th

Влияние теории игр

Теория игр присутствует почти в каждой отрасли или области исследований. Его обширная теория может относиться ко многим ситуациям, что делает ее универсальной и важной теорией для понимания. Вот несколько областей исследований, на которые непосредственно повлияла теория игр.

Экономика

Теория игр произвела революцию в экономике, решив важнейшие проблемы предшествующих математических экономических моделей. Например, неоклассическая экономическая теория изо всех сил пыталась понять предпринимательское ожидание и не могла справиться с несовершенной конкуренцией. Теория игр переключила внимание с установившегося равновесия на рыночный процесс.

Экономисты часто используют теорию игр для понимания поведения олигополистических фирм. Это помогает предсказать вероятные результаты, когда фирмы участвуют в определенных действиях, таких как установление цен и сговор.

Бизнес

В бизнесе теория игр полезна для моделирования конкурирующего поведения между экономическими агентами. У предприятий часто есть несколько стратегических вариантов, которые влияют на их способность получать экономическую выгоду. Например, предприятия могут столкнуться с такими дилеммами, как отказаться от существующих продуктов, разработать новые или использовать новые маркетинговые стратегии.

Компании также часто могут выбирать своего противника. Некоторые сосредотачиваются на внешних силах и конкурируют с другими участниками рынка. Другие ставят внутренние цели и стремятся быть лучше предыдущих версий себя. Будь то внешние или внутренние компании, они всегда конкурируют за ресурсы, пытаясь нанять лучших кандидатов у своих конкурентов и отвлечь внимание клиентов от конкурирующих товаров.

Теория игр в бизнесе может больше всего напоминать игровое дерево, как показано ниже. Компания может начать с первой позиции и должна выбрать два исхода. Однако постоянно приходится принимать другие решения; окончательная сумма выплаты не известна до тех пор, пока не будет принято окончательное решение.

Пример дерева игры.

Интернет-энциклопедия философии

Управление проектами

Управление проектами включает социальные аспекты теории игр, поскольку разные участники могут иметь разное влияние. Например, руководитель проекта может быть поощрен за успешное завершение проекта по развитию здания. Между тем, строитель может быть заинтересован в том, чтобы работать медленнее из соображений безопасности или отложить проект, чтобы потратить больше оплачиваемых часов.

При работе с внутренней командой теория игр может быть менее распространенной, поскольку все участники, работающие на одного и того же работодателя, часто имеют более общий интерес к успеху. Однако сторонние консультанты или внешние стороны, помогающие проекту, могут быть поощрены другими способами, не связанными с успехом проекта.

Цены на потребительские товары

Стратегия покупок в Черную пятницу лежит в основе теории игр. Концепция гласит, что если компании снизят цены, больше потребителей купят больше товаров. Отношения между потребителем, товаром и финансовым обменом для передачи права собственности играют важную роль в теории игр, поскольку у каждого потребителя свой набор ожиданий.

Помимо масштабных распродаж в преддверии праздников, компании должны использовать теорию игр при установлении цен на продукты для запуска или в ожидании конкуренции со стороны конкурирующих товаров. Компания должна сбалансировать слишком низкую цену на товар и не получать прибыль, но слишком высокая цена на товар может отпугнуть покупателей от товара-заменителя.

Типы теорий игр

Кооперативные и некооперативные игры

Хотя существует множество типов теорий игр (например, симметричные/асимметричные, одновременные/последовательные и т. д.), наиболее распространенными являются кооперативные и некооперативные теории игр. Кооперативная теория игр имеет дело с тем, как взаимодействуют коалиции или кооперативные группы, когда известны только выигрыши. Это игра между коалициями игроков, а не между отдельными людьми, и в ней ставится вопрос о том, как формируются группы и как они распределяют выигрыш между игроками.

Некооперативная теория игр имеет дело с тем, как рациональные экономические агенты взаимодействуют друг с другом для достижения своих целей. Наиболее распространенной некооперативной игрой является стратегическая игра, в которой перечислены только доступные стратегии и результаты, являющиеся результатом комбинации выборов. Упрощенный пример реальной некооперативной игры — камень-ножницы-бумага.

Игры с нулевой суммой и игры с ненулевой суммой

Когда существует прямой конфликт между несколькими сторонами, стремящимися к одному и тому же результату, этот тип игры часто представляет собой игру с нулевой суммой. Это означает, что на каждого победителя приходится проигравший. В качестве альтернативы это означает, что полученная коллективная чистая выгода равна потерянной коллективной чистой выгоде. Почти каждое спортивное событие представляет собой игру с нулевой суммой, в которой одна команда побеждает, а другая проигрывает.

Игра с ненулевой суммой — это игра, в которой все участники могут выиграть или проиграть одновременно. Рассмотрите деловые партнерства, которые являются взаимовыгодными и способствуют повышению ценности для обеих сторон. Вместо того, чтобы конкурировать и пытаться «выиграть», выигрывают обе стороны.

Инвестирование и торговля акциями иногда считается игрой с нулевой суммой. Ведь один участник рынка купит акцию, а другой участник продаст ту же акцию по той же цене. Однако, поскольку разные инвесторы имеют разные аппетиты к риску и цели инвестирования, сделка может быть взаимовыгодной для обеих сторон.

Игры с одновременным ходом или с последовательным ходом

Много раз в жизни теория игр представляла собой ситуации с одновременными ходами. Это означает, что каждый участник должен постоянно принимать решения, в то время как их противник принимает решения. По мере того, как компании разрабатывают свои планы маркетинга, разработки продуктов и операционных планов, конкурирующие компании одновременно делают то же самое.

В некоторых случаях имеет место преднамеренное чередование этапов принятия решений, когда одна сторона может видеть действия другой стороны, прежде чем делать свои собственные. Это обычно всегда присутствует на переговорах; одна сторона перечисляет свои требования, затем у другой стороны есть определенное количество времени, чтобы ответить и перечислить свои собственные.

Один выстрел против повторных игр

Наконец, теория игр может начинаться и заканчиваться в одном экземпляре. Как и многое в жизни, лежащее в основе соревнование начинается, развивается, заканчивается и не может быть переделано. Это часто имеет место в случае с фондовыми трейдерами, которые должны мудро выбирать свою точку входа и точку выхода, поскольку их решение не может быть легко отменено или повторено.

С другой стороны, некоторые повторяющиеся игры продолжаются и никогда не заканчиваются. В играх такого типа часто каждый раз участвуют одни и те же участники, и каждая сторона знает, что произошло в прошлый раз. Например, рассмотрим конкурирующие компании, пытающиеся установить цену на свои товары. Всякий раз, когда один из них корректирует цену, это может сделать и другой. Эта круговая конкуренция повторяется в течение цикла продукта или сезонности продаж.

В приведенном ниже примере показано изображение дилеммы заключенного (обсуждается в следующем разделе). В этом изображении после первой итерации выигрыша нет. Вместо этого происходит вторая итерация игры, приносящая с собой новый набор результатов, невозможных в играх с одним выстрелом.

Пример повторяющейся игры.

Интернет-энциклопедия философии

Примеры теории игр

Теория игр анализирует несколько «игр». Ниже мы лишь кратко опишем некоторые из них.

Дилемма заключенного

Дилемма заключенного — самый известный пример теории игр. Рассмотрим пример двух преступников, арестованных за преступление. У прокуратуры нет веских доказательств, чтобы осудить их. Однако для получения признания чиновники выводят заключенных из одиночных камер и допрашивают каждого в отдельных камерах. Ни один из заключенных не имеет возможности общаться друг с другом. Официальные лица представляют четыре сделки, часто отображаемые в виде поля 2 x 2.

  1. Если оба признаются, каждый из них получит по пять лет тюремного заключения.
  2. Если Заключенный 1 признается, а Заключенный 2 нет, Заключенный 1 получит три года, а Заключенный 2 — девять лет.
  3. Если Заключенный 2 признается, а Заключенный 1 нет, Заключенный 1 получит 10 лет, а Заключенный 2 — два года.
  4. Если ни один из них не признается, каждый будет отбывать по два года тюрьмы.

Самая благоприятная стратегия — не признаваться. Однако ни один из них не знает о стратегии другого, и без уверенности в том, что один из них не признается, оба, вероятно, признаются и получат пятилетний тюремный срок. Равновесие Нэша предполагает, что в дилемме заключенного оба игрока сделают ход, который лучше для них по отдельности, но хуже для них в совокупности.

Выражение «око за око» было определено как оптимальная стратегия для оптимизации дилеммы заключенного. Око за око было введено Анатолием Рапопортом, который разработал стратегию, в которой каждый участник повторяющейся дилеммы заключенного следует курсу действий, согласующемуся с предыдущим ходом их противника. Например, если его спровоцировать, игрок впоследствии ответит возмездием; если это неспровоцировано, игрок сотрудничает.

На изображении ниже показана дилемма, когда выбор участника в столбце и выбор участника в строке могут конфликтовать. Например, обе стороны могут получить наиболее благоприятный исход, если обе выберут строку/столбец 1. Однако каждая из сторон сталкивается с риском сильных неблагоприятных исходов, если другая сторона не выберет такой же исход.

Пример статической игры для двух человек.

Интернет-энциклопедия философии

Игра «Диктатор»

Это простая игра, в которой игрок А должен решить, как разделить денежный приз с игроком Б, который не имеет никакого отношения к решению игрока А. Хотя это не стратегия теории игр как таковая , она дает некоторые интересные сведения о поведении людей. Эксперименты показывают, что около 50 % оставляют все деньги себе, 5 % делят их поровну, а остальные 45 % отдают другому участнику меньшую долю.

Игра «диктатор» тесно связана с ультиматумной игрой, в которой игроку А дается определенная сумма денег, часть которой должна быть отдана игроку Б, который может принять или отклонить данную сумму. Суть в том, что если второй игрок отклоняет предложенную сумму, то и A, и B ничего не получают. Игры с диктатором и ультиматумом содержат важные уроки по таким вопросам, как благотворительность и филантропия.

Дилемма волонтера

В дилемме волонтера кто-то должен взять на себя работу по дому или работу для общего блага. Наихудший возможный результат реализуется, если никто не добровольно. Например, рассмотрим компанию, в которой процветает бухгалтерское мошенничество, хотя высшее руководство не знает об этом. Некоторые младшие сотрудники бухгалтерского отдела знают о мошенничестве, но не решаются сообщить об этом высшему руководству, потому что это приведет к увольнению сотрудников, причастных к мошенничеству, и, скорее всего, к судебному преследованию.

Если вас заклеймят как разоблачителя, это также может иметь некоторые последствия в будущем. Но если никто не согласится, крупномасштабное мошенничество может привести к банкротству компании и потере работы всеми.

Игра «Сороконожка»

Игра «Сороконожка» — это игра в расширенной форме в теории игр, в которой два игрока поочередно получают шанс получить большую долю медленно растущего денежного запаса. Это устроено так, что если игрок передает тайник своему противнику, который затем забирает тайник, игрок получает меньшую сумму, чем если бы он взял банк.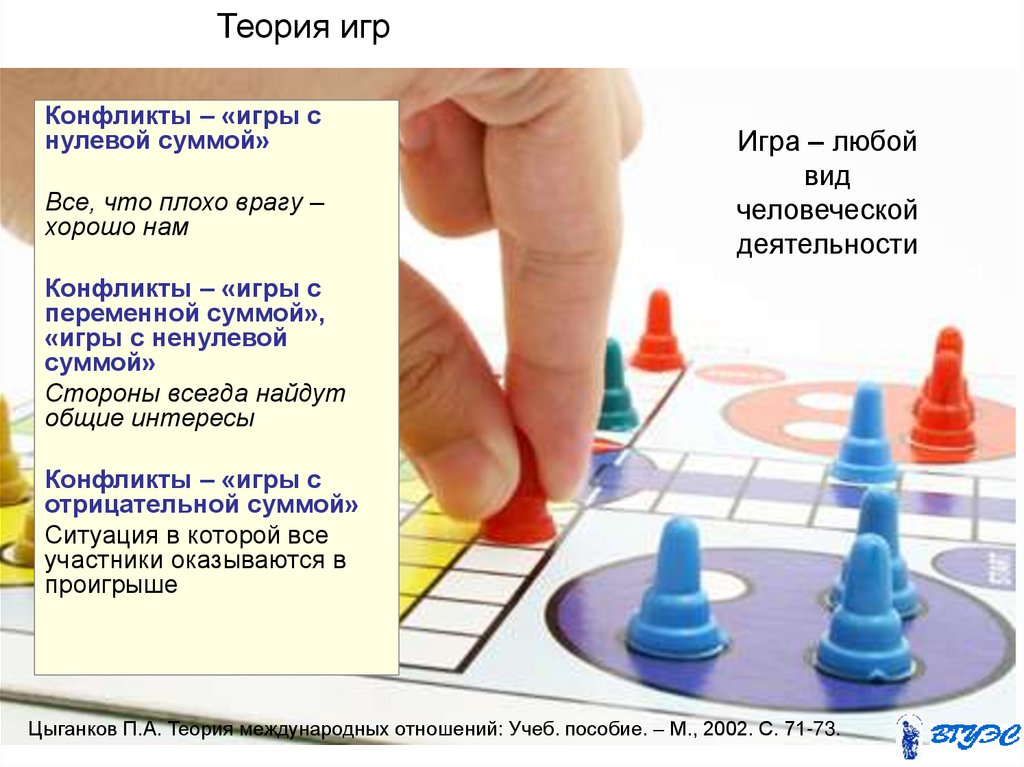

Игра с многоножкой завершается, как только игрок забирает тайник, при этом этот игрок получает большую часть, а другой игрок получает меньшую часть. В игре есть предопределенное общее количество раундов, которое заранее известно каждому игроку.

Теория игр существует почти во всех сферах жизни. Поскольку решения других людей вокруг вас влияют на ваш день, теория игр относится к личным отношениям, покупательским привычкам, просмотру СМИ и хобби.

Типы стратегий теории игр

Участники теории игр могут выбирать между несколькими основными способами игры. В общем, каждый участник должен решить, на какой уровень риска он готов пойти и как далеко он готов зайти, чтобы добиться наилучшего возможного результата.

Максимакс Стратегия

Максимаксная стратегия не предполагает хеджирования. Участник либо ва-банк, либо весь в ауте; они либо выиграют по-крупному, либо столкнутся с худшими последствиями. Рассмотрим новые начинающие компании, выводящие на рынок новые продукты. Их новый продукт может привести к увеличению рыночной капитализации компании в пятьдесят раз. С другой стороны, неудачный запуск продукта сделает компанию банкротом. В любой ситуации участник готов рискнуть для достижения наилучшего результата, даже если возможен худший результат.

Максимин Стратегия

Максиминная стратегия в теории игр приводит к тому, что участник выбирает лучший выигрыш из худшего. Участник решил хеджировать риск и пожертвовать полной выгодой в обмен на избежание худшего исхода. Часто компании сталкиваются с этой стратегией и принимают ее при рассмотрении судебных исков. Договариваясь во внесудебном порядке и избегая публичного судебного разбирательства, компании соглашаются на неблагоприятный исход. Однако этот исход мог быть и хуже из-за подвигов суда или еще худшего судебного решения.

Доминирующая стратегия

В доминирующей стратегии участник выполняет действия, которые являются лучшим результатом для игры, независимо от того, что решили сделать другие участники. В бизнесе это может быть ситуация, когда компания решает масштабироваться и выйти на новый рынок, независимо от того, решила ли конкурирующая компания также выйти на рынок. В «Дилемме заключенного» доминирующей стратегией будет признание.

Чистая стратегия

Чистая стратегия влечет за собой наименьшее количество стратегических решений, поскольку чистая стратегия — это просто определенный выбор, который делается независимо от внешних сил или действий других. Рассмотрим игру «камень-ножницы-бумага», в которой один участник решает бросать одну и ту же фигуру в каждом испытании. Поскольку исход для этого участника заранее определен (исходы либо определенной формы, либо не такой конкретной формы), стратегия определяется как чистая.

Смешанная стратегия

Смешанная стратегия может показаться случайной, но для разработки плана смешивания элементов или действий требуется много размышлений. Рассмотрим отношения между бейсбольным питчером и отбивающим. Питчер не может каждый раз бросать одну и ту же подачу; в противном случае отбивающий мог бы предсказать, что будет дальше. Вместо этого питчер должен смешивать свою стратегию от подачи к подаче, чтобы создать ощущение непредсказуемости, от которого он надеется извлечь выгоду.

Ограничения теории игр

Самая большая проблема с теорией игр заключается в том, что, как и большинство других экономических моделей, она основана на предположении, что люди — это рациональные действующие лица, преследующие собственные интересы и стремящиеся к максимизации полезности. Конечно, мы социальные существа, которые часто сотрудничают за свой счет. Теория игр не может объяснить тот факт, что в одних ситуациях мы можем попасть в равновесие по Нэшу, а в других — нет, в зависимости от социального контекста и игроков.

Кроме того, теория игр часто с трудом учитывает такие человеческие элементы, как лояльность, честность или сочувствие. Хотя статистические и математические расчеты могут диктовать, каким должен быть наилучший курс действий, люди могут не пойти по этому пути из-за непредсказуемых и сложных сценариев самопожертвования или манипуляции. Теория игр может анализировать набор моделей поведения, но не может точно предсказать человеческий фактор.

В какие игры играют в теории игр?

Это называется теорией игр, поскольку теория пытается понять стратегические действия двух или более «игроков» в данной ситуации, содержащей установленные правила и исходы. Хотя теория игр используется в нескольких дисциплинах, она в первую очередь используется в качестве инструмента при изучении бизнеса и экономики.

«Игры» могут заключаться в том, как две конкурирующие фирмы будут реагировать на снижение цен другой, должна ли одна фирма приобретать другую или как трейдеры на фондовом рынке могут реагировать на изменения цен. Теоретически эти игры можно разделить на дилеммы заключенного, игру в диктатора, ястреб-и-голубь, Баха или Стравинского.

Какие предположения об этих играх?

Как и многие экономические модели, теория игр также содержит ряд строгих допущений, которые должны выполняться, чтобы теория могла делать хорошие прогнозы на практике. Во-первых, все игроки являются рациональными акторами, стремящимися к максимизации полезности и обладающими полной информацией об игре, правилах и последствиях. Игрокам не разрешается общаться или взаимодействовать друг с другом. Возможные исходы не только известны заранее, но и не могут быть изменены. Теоретически количество игроков в игре может быть бесконечным, но в большинстве игр будет только два игрока.

Что такое равновесие Нэша?

 Равновесие Нэша – важная концепция, относящаяся к стабильному состоянию в игре, когда ни один игрок не может получить преимущество, в одностороннем порядке изменив стратегию, при условии, что другие участники также не меняют свои стратегии. Равновесие Нэша обеспечивает концепцию решения в некооперативной (состязательной) игре. Он назван в честь Джона Нэша, получившего Нобелевскую премию в 1994 году за свою работу.

Кто придумал теорию игр?

Теория игр в значительной степени связана с работами математика Джона фон Неймана и экономиста Оскара Моргенштерна в 1940-х годах и широко развивалась многими другими исследователями и учеными в 1950-х годах. Это остается областью активных исследований и прикладной науки по сей день.

Итог

Теория игр — это исследование того, как конкурентные стратегии и действия участников могут влиять на исход ситуации. Имея отношение к войне, биологии и многим аспектам жизни, теория игр используется в бизнесе для представления стратегических взаимодействий, в которых результат одной компании или продукта зависит от действий, предпринимаемых другими компаниями или продуктами.

Теория игр в биологии: 50 лет и позже

1. Maynard Smith J, Price GR. 1973. Логика конфликта животных. Природа 246 , 15-18. ( 10.1038/246015a0) [CrossRef][Google Scholar]

2. Чарнов Е.Л. 1982. Теория распределения полов. Принстон, Нью-Джерси: Издательство Принстонского университета. [Google Scholar]

3. Дарвин К. 1871. Происхождение человека и отбор в отношении пола. Лондон, Великобритания: Джон Мюррей. [Google Scholar]

4. Дюзинг К. 1884. Die Regulierung des Geschlechtsverhältnisses bei der Vermehrung der Menschen, Tiere und Pflanzen [ Регуляция соотношения полов в репродукции человека, животных и растений ]. Йена, Германия: Густав Фишер. [На немецком языке.] [Google Scholar]

5. Эдвардс AWF. 2000. Карл Дюзинг (1884 г.) о регулировании соотношения полов. Теор. Народ. биол. 58 , 255-257. (10.1006/tpbi.2000.1482) [PubMed] [CrossRef] [Google Scholar]

6. Фишер Р.А. 1930. Генетическая теория естественного отбора. Оксфорд, Великобритания: Clarendon Press. [Google Scholar]

7. Shaw RF, Mohler JD. 1953. Селективное значение соотношения полов. Являюсь. Нац. 87 , 337-342. ( 10.1086/281794) [CrossRef] [Google Scholar]

8. Hamilton WD. 1967. Необычное соотношение полов. Наука 156 , 477-488. ( 10.1126/science.156.3774.477) [PubMed] [CrossRef] [Google Scholar]

9. Hamilton WD, May RM. 1977. Расселение в стабильных местообитаниях. Природа 269 , 578-581. ( 10.1038/269578a0) [CrossRef] [Google Scholar]

10. Общий MR. 1996. Альтернативные репродуктивные стратегии и тактики: разнообразие полов. Тенденции Экол. Эвол. 11 , 92-98. ( 10.1016/0169-5347(96)81050-0) [PubMed] [CrossRef] [Google Scholar]

11. Trivers RL. 1971. Эволюция взаимного альтруизма. Q. Преподобный Биол. 46 , 35-57. ( 10.1086/406755) [CrossRef] [Google Scholar]

12. Axelrod R, Hamilton WD. 1981. Эволюция сотрудничества. Наука 211 , 1390-1396. ( 10.1126/science.7466396) [PubMed] [CrossRef] [Google Scholar]

13. Фишер Р.А. 1958 год. Полиморфизм и естественный отбор. Дж. Экол. 46 , 289-293. ( 10.2307/2257396) [CrossRef] [Google Scholar]

14. Фишер Р.А. 1934. Рандомизация и старая загадка карточной игры. Мат. Газ. 18 , 294-297. ( 10.2307/3605473) [CrossRef] [Google Scholar]

15. Райт С. 1977. Эволюция и генетика популяций, т. 1, с. 3. Чикаго, Иллинойс: Издательство Чикагского университета. [Google Scholar]

16. Маллет Дж. 2015. Новые геномы проясняют эволюцию мимикрии. Нац. Жене. 47 , 306-307. ( 10.1038/ng.3260) [PubMed] [CrossRef] [Google Scholar]

17. Левонтин Р.С. 1961. Эволюция и теория игр. Дж. Теор. биол. 1 , 382-403. ( 10.1016/0022-5193(61)

-8) [PubMed] [CrossRef] [Google Scholar]

18. Maynard Smith J. 1972. Об эволюции. Эдинбург, Великобритания: Издательство Эдинбургского университета. [Google Scholar]

19. Мейнард Смит Дж. 1974. Теория игр и эволюция конфликтов животных. Дж. Теор. биол. 47 , 209-221. ( 10.1016/0022-5193(74)

-6) [PubMed] [CrossRef] [Google Scholar]

20. Мейнард Смит Дж. 1976. Эволюция и теория игр. Являюсь. науч. 64 , 41-45. [PubMed] [Google Scholar]

21. Эшель И. 1983. Эволюционная и непрерывная стабильность. Дж. Теор. биол. 103 , 99-111. ( 10.1016/0022-5193(83)

-1) [CrossRef] [Google Scholar]

22. Taylor PD. 1989. Эволюционная устойчивость однопараметрических моделей при слабом отборе. Теор. Народ. биол. 36 , 125-143. ( 10.1016/0040-5809(89)

-7) [CrossRef] [Google Scholar]

23. Винн-Эдвардс В.К. 1962 год. Расселение животных по отношению к социальному поведению. Нью-Йорк, штат Нью-Йорк: издательство Hafner Publishing Company. [Google Scholar]

24. Лоренц К. 1963. Das sogenannte Böse. Вена, Австрия: доктор Г. Борота-Шолер Верлаг. [На немецком; перевод МК Уилсон. 1966 Об агрессии . Лондон, Великобритания: Routledge.] [Google Scholar]

25. Maynard Smith J, Parker GA. 1976 год. Логика асимметричных состязаний животных. Аним. Поведение 24 , 159-175. ( 10.1016/S0003-3472(76)80110-8) [CrossRef] [Google Scholar]

26. Шеллинг ТС. 1960. Стратегия конфликта. Кембридж, Массачусетс: Издательство Гарвардского университета. [Google Scholar]

27. Харман О. 2010. Цена альтруизма. Нью-Йорк, штат Нью-Йорк: WW Norton. [Google Scholar]

28. Харман О. 2011. Рождение первой ESS: Джордж Прайс, Джон Мейнард Смит и открытие утерянной бумаги «Оленьи рога». Дж. Эксп. Зоол. Б 316 , 1-9. ( 10.1002/jez.b.21377) [PubMed] [CrossRef] [Google Scholar]

29. Gale JS, Eaves LJ. 1975. Логика конфликта животных. Природа 254 , 463. (10.1038/254463b0) [CrossRef] [Google Scholar]

30. Huxley J. 1966. Дискуссия о ритуализации поведения у животных и человека. Фил. Транс. R Соц. Лонд. Б 251 , 249-271. ( 10.1098/rstb.1966.0010) [CrossRef] [Google Scholar]

31. Паркер Г.А. 1974. Стратегия оценки и эволюция боевого поведения. Дж. Теор. биол. 47 , 223-243. ( 10.1016/0022-5193(74)

-8) [PubMed] [CrossRef] [Google Scholar]

32. Дэвис Н.Б., Холлидей Т.Р. 1978 год. Глубокое кваканье и боевая оценка у жаб Bufo bufo . Природа 274 , 683-685. ( 10.1038/274683a0) [CrossRef] [Google Scholar]

33. Clutton-Brock TH, Albon SD. 1979. Рев благородного оленя и эволюция честной рекламы. Поведение 69 , 145-170. ( 10. 1163/156853979X00449) [CrossRef] [Google Scholar]

34. Clutton-Brock TH, Albon SD, Gibson RM, Guinness FE. 1979. Логический олень: адаптивные аспекты борьбы благородного оленя ( Cervus elaphus L.). Аним. Поведение 27 , 211-225. ( 10.1016/0003-3472(79)
-6) [CrossRef] [Google Scholar]

35. Geist V. 1966. Эволюция рогообразных органов. Поведение 27 , 175-214. ( 10.1163/156853966X00155) [CrossRef] [Google Scholar]

36. Эмлен Д.Дж. 2008. Эволюция оружия животных. Анну. Преподобный Экол. Эвол. Сист. 39 , 387-413. ( 10.1146/annurev.ecolsys.39.110707.173502) [CrossRef] [Google Scholar]

37. Enquist M, Leimar O. 1983. Эволюция боевого поведения: правила принятия решений и оценка относительной силы. Дж. Теор. биол. 102 , 387-410. ( 10.1016/0022-5193(83)

-4) [CrossRef] [Google Scholar]

38. Leimar O, Enquist M. 1984. Эффекты асимметрии в конфликтах между собственником и злоумышленником. Дж. Теор. биол. 111 , 475-491. ( 10.1016/S0022-5193(84)80235-0) [CrossRef] [Google Scholar]

39. Enquist M, Leimar O. 1987. Эволюция боевого поведения: влияние изменения стоимости ресурсов. Дж. Теор. биол. 127 , 187-205. ( 10.1016/S0022-5193(87)80130-3) [CrossRef] [Google Scholar]

40. Enquist M, Leimar O. 1990. Эволюция смертельных боев. Аним. Поведение 39 , 1-9. ( 10.1016/S0003-3472(05)80721-3) [CrossRef] [Google Scholar]

41. Leimar O, Austad S, Equist M. 1991. Тест последовательной оценочной игры: борьба в тарелке и салфетке с пауком Frontinella pyramitela . Эволюция 45 , 862-874. ( 10.2307/2409694) [PubMed] [CrossRef] [Google Scholar]

42. Энквист М., Леймар О., Юнгберг Т., Мальнер Ю., Сегердал Н. 1990. Тест последовательной оценочной игры: борьба с цихлидами Nannacara anomala . Аним. Поведение 40 , 1-14. ( 10.1016/S0003-3472(05)80660-8) [CrossRef] [Google Scholar]

43. Хантингфорд Ф.А., Тейлор А.С., Смит И.П., Торп К.Е. 1995. Поведенческие и физиологические исследования агрессии крабов-плавунцов. Дж. Эксп. Мар биол. Экол. 193 , 21-39. ( 10.1016/0022-0981(95)00108-5) [CrossRef] [Google Scholar]

44. Хантингфорд Ф.А., Тейлор А.С., Снеддон Л.У., Нит Ф.К. 2000. Доблесть и разрешение звериных боев. В Animal signal (под редакцией Y Espmark, T Amundsen, G Rosenqvist), стр. 259–276. Тронхейм, Норвегия: Tapir Academic Press.

45. Тейлор П.В., Элвуд Р.В. 2003. Неправильная оценка состязаний животных. Аним. Поведение 65 , 1-8. ( 10.1006/anbe.2003.2169) [CrossRef] [Google Scholar]

46. Arnott G, Elwood RW. 2009. Оценка бойцовских способностей в соревнованиях животных. Аним. Поведение 77 , 991-1004. ( 10.1016/j.anbehav.2009.02.010) [CrossRef] [Google Scholar]

47. Dawkins R, Krebs JR. 1978 год. Сигналы животных: информация или манипуляция? В Behavioral ecology (ред. Дж. Р. Кребс, Н. Б. Дэвис), стр. 282–309. Оксфорд, Великобритания: Научные публикации Блэквелла.

48. Мейнард Смит Дж. 1979. Теория игр и эволюция поведения. проц. Р. Соц. Лонд. Б 205 , 475-488. ( 10.1098/rspb.1979.0080) [PubMed] [CrossRef] [Google Scholar]

49. Мейнард Смит Дж. 1982. Эволюция и теория игр. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar]

50. Спенс М. 1973. Сигнализация рынка труда. QJ Econ. 87 , 355-374. ( 10.2307/1882010) [CrossRef] [Google Scholar]

51. Захави А. 1975. Выбор мата — выбор на гандикап. Дж. Теор. биол. 53 , 205-214. ( 10.1016/0022-5193(75)

-3) [PubMed] [CrossRef] [Google Scholar]

52. Захави А. 1977. Цена честности (дальнейшие замечания о принципе гандикапа). Дж. Теор. биол. 67 , 603-605. ( 10.1016/0022-5193(77)-3) [PubMed] [CrossRef] [Google Scholar]

53. Графен А. 1990. Биологические сигналы как помехи. Дж. Теор. биол. 144 , 517-546. ( 10.1016/S0022-5193(05)80088-8) [PubMed] [CrossRef] [Google Scholar]

54. Enquist M. 1985. Общение во время агрессивных взаимодействий с особым упором на изменение выбора поведения. Аним. Поведение 33 , 1152-1161. ( 10.1016/S0003-3472(85)80175-5) [CrossRef] [Google Scholar]

55. Hurd PL, Enquist M. 2001. Отображение угрозы у птиц. Может. Дж. Зул. 79 , 931-942. ( 10.1139/z01-062) [CrossRef] [Google Scholar]

56. Lange H, Leimar O. 2003. Функция отображения угрозы у зимующих больших синиц. Аним. Поведение 65 , 573-584. ( 10.1006/anbe.2003.2088) [CrossRef] [Google Scholar]

57. Андерссон М. 1980. Почему так много показов угроз? Дж. Теор. биол. 86 , 773-781. ( 10.1016/0022-5193(80)

-0) [PubMed] [CrossRef] [Google Scholar]

58. Hammerstein P, Riechert SE. 1988 год. Выигрыши и стратегии в территориальных спорах: анализ ESS двух экотипов паука Agelenopsis aperta . Эвол. Экол. 2 , 115-138. ( 10.1007/BF02067272) [CrossRef] [Google Scholar]

59. Хьюстон А.И., Макнамара Дж.М. 1991. Эволюционно устойчивые стратегии в повторяющейся игре ястреб-голубь. Поведение Экол. 2 , 219-227. ( 10.1093/beheco/2.3.219) [CrossRef] [Google Scholar]

60. Gilley DC. 2001. Поведение медоносных пчел ( Apis mellifera ligustica ) во время поединков королев. этология 107 , 601-622. ( 10.1046/j.1439-0310.2001.00692.x) [CrossRef] [Google Scholar]

61. Hamilton WD. 1979. Бескрылые и боевые самцы у фиговых ос и других насекомых. В Репродуктивная конкуренция, выбор партнера и половой отбор у насекомых (ред. М.С. Блюм, Н.А. Блюм), стр. 167–220. Нью-Йорк, штат Нью-Йорк: Academic Press.

62. Гамильтон WD. 1996. Узкие дороги в землю генов, том. 1. Нью-Йорк, штат Нью-Йорк: WH Freeman and Company. [Академия Google]

63. Вест С.А., Мюррей М.Г., Мачадо К.А., Гриффин А. С., Эрре Э.А. 2001. Проверка правила Гамильтона на соревновании между родственниками. Природа 409 , 510-513. ( 10.1038/35054057) [PubMed] [CrossRef] [Google Scholar]

64. Hammerstein P. 1981. Роль асимметрии в состязаниях животных. Аним. Поведение 29 , 193-205. ( 10.1016/S0003-3472(81)80166-2) [CrossRef] [Google Scholar]

65. Hammerstein P, Parker GA. 1982. Асимметричная война на истощение. Дж. Теор. биол. 96 , 647-682. ( 10.1016/0022-5193(82)

-1) [CrossRef] [Google Scholar]

66. Davies NB. 1978 год. Территориальная защита в крапчатой ​​древесной бабочке ( Pararge aegeria ): резидент всегда побеждает. Аним. Поведение 26 , 138-147. ( 10.1016/0003-3472(78)-1) [CrossRef] [Google Scholar]

67. Wickman P-O, Wiklund C. 1983. Территориальная защита и ее сезонный спад у крапчатой ​​древесной бабочки ( Pararge aegeria ). Аним. Поведение 31 , 1206-1216. ( 10.1016/S0003-3472(83)80027-X) [CrossRef] [Google Scholar]

68. Бергман М., Олофссон М., Виклунд К. 2010. Исход конкурса в территориальной бабочке: роль мотивации. проц. Р. Соц. Б 277 , 3027-3033. ( 10.1098/rspb.2010.0646) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

69. Bishop DT, Cannings C, Maynard Smith J. 1978. Война на истощение со случайными наградами. Дж. Теор. биол. 74 , 377-388. ( 10.1016/0022-5193(78)-5) [PubMed] [CrossRef] [Google Scholar]

70. Mesterton-Gibbons M, Dai Y, Goubault M. 2016. Моделирование эволюции эффектов победителя и проигравшего: обзор и проспект. Мат. Бионауч. 274 , 33-44. ( 10.1016/j.mbs.2016.02.002) [PubMed] [CrossRef] [Google Scholar]

71. Mesterton-Gibbons M. 1994. Новый взгляд на игру «Ястреб-Голубь»: влияние постоянного изменения потенциала удержания ресурсов на частоту эскалации. Эвол. Экол. 8 , 230-247. ( 10.1007/BF01238275) [CrossRef] [Google Scholar]

72. Местертон-Гиббонс М., Алан Дугаткин Л. 1995. К теории иерархий доминирования: эффекты оценки, размер группы и различия в боевых способностях. Поведение Экол. 6 , 416-423. ( 10.1093/beheco/6.4.416) [CrossRef][Google Scholar]

73. Дугаткин Л.А. 1997. Эффекты победителя и проигравшего и структура иерархии доминирования. Поведение Экол. 8 , 583-587. ( 10.1093/beheco/8.6.583) [CrossRef] [Google Scholar]

74. van Doorn GS, Hengeveld GH, Weissing FJ. 2003. Эволюция социального доминирования I: модели двух игроков. Поведение 140 , 1305-1332. ( 10.1163/156853

1980611) [CrossRef] [Google Scholar]

75. van Doorn GS, Weissing FJ, Hengeveld GM. 2003. Эволюция социального доминирования II: многопользовательские модели. Поведение 140 , 1333-1358. ( 10.1163/156853

1980611) [CrossRef] [Google Scholar]

76. Хсу Ю., Эрли Р.Л., Вольф Л.Л. 2006. Модуляция агрессивного поведения боевым опытом: механизмы и исходы соревнований. биол. Преподобный Кэмб. Фил. соц. 81 , 33-74. ( 10.1017/S146479310500686X) [PubMed] [CrossRef] [Google Scholar]

77. Rutte C, Taborsky M, Brinkhof MWG. 2006. Что определяет шансы на победу и поражение? Тенденции Экол. Эвол. 21 , 16-21. ( 10.1016/j.tree.2005.10.014) [PubMed] [CrossRef] [Google Scholar]

78. Дугаткин Л.А. 2001. Эффекты свидетеля и структура иерархии доминирования. Поведение Экол. 12 , 348-352. ( 10.1093/beheco/12.3.348) [CrossRef] [Google Scholar]

79. McNamara JM, Leimar O. 2020. Теория игр в биологии: концепции и границы. Оксфорд, Великобритания: Издательство Оксфордского университета. [Академия Google]

80. Леймар О. 2021. Эволюция социального доминирования через обучение с подкреплением. Являюсь. Нац. 197 , 560-575. ( 10.1086/713758) [PubMed] [CrossRef] [Google Scholar]

81. Леймар О., Бшари Р. 2022. Влияние репродуктивного перекоса на затраты на борьбу и эффекты победителя-проигравшего в эволюции социального доминирования.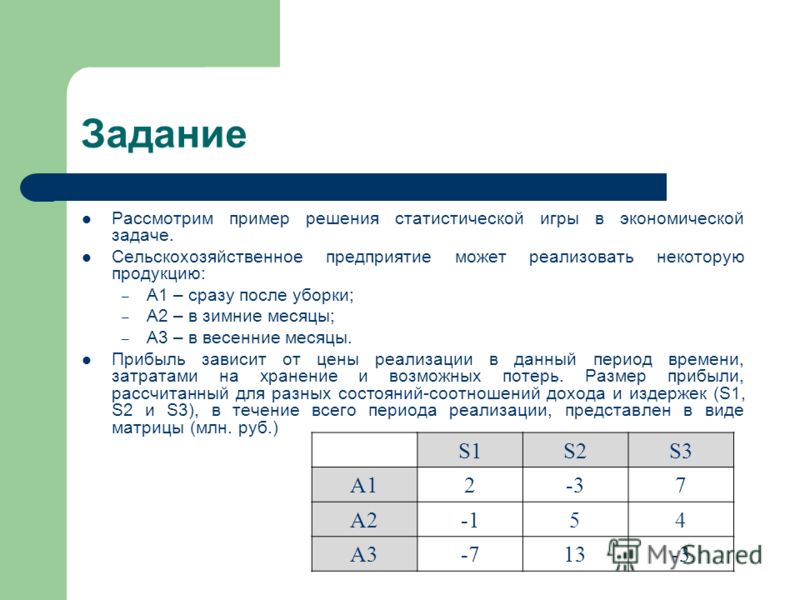 Дж. Аним. Экол. 91 , 1036-1046. ( 10.1111/1365-2656.13691) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

82. Rapoport A, Chammah AM. 1965. Дилемма заключенного. Исследование конфликта и сотрудничества. Анн-Арбор, Мичиган: University of Michigan Press. [Google Scholar]

83. Бшари Р., Ноэ Р. 2003. Биологические рынки. В Генетическая и культурная эволюция сотрудничества (изд. П. Хаммерштейн), стр. 167–184. Кембридж, Массачусетс: MIT Press.

84. Зубербюлер К., Дженни Д., Бшари Р. 1999. Функция отпугивания хищников сигналами тревоги приматов. этология 105 , 477-490. ( 10.1046/j.1439-0310.1999.00396.x) [CrossRef] [Google Scholar]

85. Бергстрем К.Т., Лахманн М. 2001. Звонки тревоги как дорогостоящие сигналы бдительности против хищников: бдительная игра болтунов. Аним. Поведение 61 , 535-543. ( 10.1006/anbe.2000.1636) [CrossRef] [Google Scholar]

86. Rothstein SI, Pierotti R. 1988. Различия между взаимным альтруизмом, родственным отбором и сотрудничеством и модель начальной эволюции благотворного поведения. этанол Социобиол. 9 , 189-209. ( 10.1016/0162-3095(88)

-0) [CrossRef] [Google Scholar]

87. Аксельрод Р. 1984. Эволюция сотрудничества. Нью-Йорк, штат Нью-Йорк: Основные книги. [Google Scholar]

88. Петерсон М. (ред.). 2015. Дилемма заключенного. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar]

89. Hammerstein P, Hoekstra RF. 1995. Мутуализм в движении. Природа 376 , 121-122. ( 10.1038/376121a0) [PubMed] [CrossRef] [Google Scholar]

90. Hammerstein P. 2003. Почему взаимность так редка у социальных животных? Протестантский призыв. В Генетическая и культурная эволюция сотрудничества (изд. П. Хаммерштейн), стр. 83–93. Кембридж, Массачусетс: MIT Press.

91. Selten R, Hammerstein P. 1984. Пробелы в аргументации Харли об эволюционно стабильных правилах обучения и в логике «око за око». Поведение наук о мозге. 7 , 115-116. ( 10.1017/S0140525X00026479) [CrossRef] [Google Scholar]

92. Рапопорт А., Сил Д.А., Колман А.М. 2015. Око за око ответ? О выводах турниров Аксельрода. ПЛОС ОДИН 10 , e0134128. ( 10.1371/journal.pone.0134128) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

93. Boyd R. 1989. Ошибки обеспечивают эволюционную стабильность в повторяющейся игре с дилеммой заключенного. Дж. Теор. биол. 136 , 47-56. ( 10.1016/S0022-5193(89)80188-2) [PubMed] [CrossRef] [Google Scholar]

94. Новак М., Зигмунд К. 1993. Стратегия «выиграл-остался, проиграл», которая превосходит «око за око» в игре «Дилемма заключенного». Природа 364 , 56-58. ( 10.1038/364056a0) [PubMed] [CrossRef] [Google Scholar]

95. Зельтен Р. 1983. Эволюционная стабильность в обширных играх на двоих. Мат. Социальные науки. 5 , 269-363. ( 10.1016/0165-4896(83)

  • -4) [CrossRef] [Google Scholar]

    96. Леймар О. 1997. Повторяющиеся игры: подход в пространстве состояний. Дж. Теор. биол. 184 , 471-498. ( 10.1006/jtbi.1996.0286) [CrossRef] [Google Scholar]

    97. McNamara JM, Leimar O. 2010. Вариация и реакция на вариацию как основа успешного сотрудничества. Фил. Транс. Р. Соц. Б 365 , 2627-2633. ( 10.1098/rstb.2010.0159) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

    98. McNamara JM, Barta Z, Houston AI. 2004. Различия в поведении способствуют сотрудничеству в игре «Дилемма заключенного». Природа 428 , 745-748. ( 10.1038/nature02432) [PubMed] [CrossRef] [Google Scholar]

    99. Daniel WJ. 1942 г. Совместное решение проблем у крыс. Дж. Комп. Психол. 34 , 361-368. ( 10.1037/h0062264) [CrossRef] [Google Scholar]

    100. Флад М., Ленденманн К., Рапопорт А. 1983. Игры 2 × 2, в которые играют крысы: различные задержки подкрепления в качестве выплат. Поведение науч. 28 , 65-78. ( 10.1002/bs.3830280108) [CrossRef] [Google Scholar]

    101. Гарднер Р.М., Корбин Т.Л., Белтрамо Дж.С., Никелл Г.С. 1984. Игра «Дилемма заключенного» и сотрудничество в крысе. Психол. Респ. 55 , 687-696. ( 10.2466/pr0.1984.55.3.687) [CrossRef] [Google Scholar]

    102. Wood RI, Kim JY, Li GR. 2016. Кооперация крыс, играющих в итерированную игру «Дилемма заключенного». Аним. Поведение 114 , 27-35. ( 10.1016/j.anbehav.2016.01.010) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

    103. Rutte C, Taborsky M. 2007. Генерализованная реципрокность у крыс. PLoS биол. 5 , 1421-1425. ( 10.1371/journal.pbio.0050196) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

    104. Schweinfurth MK, Aeschbacher J, Santi M, Taborsky M. 2019. Самцы норвежских крыс сотрудничают в соответствии с прямыми, но не обобщенными правилами взаимности. Аним. Поведение 152 , 93-101. ( 10.1016/j.anbehav. 2019.03.015) [CrossRef] [Google Scholar]

    105. Швайнфурт М.К., Таборский М. 2020. Крысы играют «око за око» вместо того, чтобы интегрировать социальный опыт в несколько взаимодействий. проц. Р. Соц. Б 287 , 20192423. ( 10.1098/rspb.2019.2423) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

    106. Clements KC, Stephens DW. 1995. Апробация моделей неродственного сотрудничества: мутуализм и дилемма заключенного. Аним. Поведение 50 , 527-535. ( 10.1006/anbe.1995.0267) [CrossRef] [Google Scholar]

    107. Eberhard MJW. 1975 год. Эволюция социального поведения путем родственного отбора. Q. Преподобный Биол. 50 , 1-33. ( 10.1086/408298) [CrossRef] [Google Scholar]

    108. Браун Дж.Л. 1983. Кооперация — дилемма биолога. Доп. Изучение поведения. 13 , 1-37. ( 10.1016/S0065-3454(08)60284-3) [CrossRef] [Google Scholar]

    109. Connor RC. 1986 год. Псевдо-взаимность: инвестирование в мутуализм. Аним. Поведение 34 , 1562-1566. ( 10.1016/S0003-3472(86)80225-1) [CrossRef] [Google Scholar]

    110. Connor RC. 1995. Преимущества мутуализма: концептуальная основа. биол. преп. 70 , 427-457. ( 10.1111/j.1469-185X.1995.tb01196.x) [CrossRef] [Google Scholar]

    111. Leimar O, Connor RC. 2003. Побочные выгоды, взаимность и псевдо-взаимность в мутуализме. В Генетическая и культурная эволюция сотрудничества (изд. П. Хаммерштейн), стр. 203–222. Кембридж, Массачусетс: MIT Press.

    112. Сакс Дж.Л., Мюллер У.Г., Уилкокс Т.П., Булл Дж.Дж. 2004. Эволюция сотрудничества. Q. Преподобный Биол. 79 , 135-160. ( 10.1086/383541) [PubMed] [CrossRef] [Google Scholar]

    113. Leimar O, Hammerstein P. 2010. Сотрудничество для прямой выгоды фитнеса. Фил. Транс. Р. Соц. Б 365 , 2619-2626. ( 10.1098/rstb.2010.0116) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

    114. McNamara JM, Gasson CE, Houston AI. 1999. Включение правил реагирования в эволюционные игры. Природа 401 , 368-371. ( 10.1038/43872) [PubMed] [CrossRef] [Google Scholar]

    115. Kokko H, Johnstone RA, Clutton-Brock TH. 2001. Эволюция кооперативного разведения через групповое увеличение. проц. Р. Соц. Лонд. Б 268 , 187-196. ( 10.1098/rspb.2000.1349) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

    116. Friedman JW, Hammerstein P. 1991. Торговать или не торговать; вот в чем вопрос. В Модели игрового равновесия I: эволюция и игровая динамика (изд. R Selten), стр. 257–275. Берлин, Германия: Springer.

    117. Энквист М., Леймар О. 1993. Эволюция сотрудничества в мобильных организмах. Аним. Поведение 45 , 747-757. ( 10.1006/anbe.1993.1089) [CrossRef] [Google Scholar]

    118. Noë R, Hammerstein P. 1994. Биологические рынки: спрос и предложение определяют эффект выбора партнера в сотрудничестве, мутуализме и спаривании. Поведение Экол. Социобиол. 35 , 1-11. ( 10.1007/BF00167053) [CrossRef] [Google Scholar]

    119. Ноэ Р., Хаммерштейн П. 1995. Биологические рынки. Тенденции Экол. Эвол. 10 , 336-339. (10.1016/S0169-5347(00)89123-5) [PubMed] [CrossRef] [Google Scholar]

    120. Kiers ET, et al. 2011. Взаимное вознаграждение стабилизирует сотрудничество в микоризном симбиозе. Наука 333 , 880-882. ( 10.1126/science.1208473) [PubMed] [CrossRef] [Google Scholar]

    121. Wyatt GAK, Kiers ET, Gardner A, West SA. 2014. Биологический анализ рынка растительно-микоризного симбиоза. Эволюция 68 , 2603-2618. ( 10.1111/evo.12466) [PubMed] [CrossRef] [Google Scholar]

    122. Бронштейн Дж.Л. 2001. Эксплуатация мутуализмов. Экол. лат. 4 , 277-287. ( 10.1046/j.1461-0248.2001.00218.x) [CrossRef] [Google Scholar]

    123. Бшари Р., Груттер А.С. 2002. Возможности асимметричного мошенничества и контроль партнера в мутуализме чистой рыбы. Аним. Поведение 63 , 547-555. ( 10.1006/anbe.2001.1937) [CrossRef] [Google Scholar]

    124. Бшары Р., Груттер А.С. 2005. Наказание и смена партнера вызывают кооперативное поведение в чистящем мутуализме. биол. лат. 1 , 396-399. ( 10.1098/rsbl.2005.0344) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

    125. Johnstone RA, Bshary R. 2008. Мутуализм, рыночные эффекты и партнерский контроль. Дж. Эвол. биол. 21 , 879-888. ( 10.1111/j.1420-9101.2008.01505.x) [PubMed] [CrossRef] [Google Scholar]

    126. Hammerstein P, Noë R. 2016. Биологическая торговля и рынки. Фил. Транс. Р. Соц. Б 371 , 20150101. ( 10.1098/rstb.2015.0101) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

    127. Triki Z, Li Richter X-Y, Demairé C, Kurokawa S, Bshary R. 2022. Взаимность морской очистки бросает вызов стандартной логике спроса и предложения. Являюсь. Нац. 199 , 455-467. ( 10.1086/718315) [PubMed] [CrossRef] [Google Scholar]

    128. Clutton-Brock T. 2009. Сотрудничество между неродственными в животных обществах. Природа 462 , 51-57. ( 10.1038/nature08366) [PubMed] [CrossRef] [Google Scholar]

    129. Curio E. 1978. Адаптивное значение птичьего моббинга. З. Тирпсихол. 48 , 175-183. ( 10.1111/j.1439-0310.1978.tb00254.x) [CrossRef] [Google Scholar]

    130. Krams I, Krama T, Igaune K, Mänd R. 2008. Экспериментальное свидетельство взаимного альтруизма у мухоловки-пеструшки. Поведение Экол. Социобиол. 62 , 599-605. ( 10.1007/s00265-007-0484-1) [CrossRef] [Google Scholar]

    131. Wheatcroft D, Price TD. 2018. Коллективные действия, продвигаемые ключевыми лицами. Являюсь. Нац. 192 , 401-414. ( 10.1086/698874) [PubMed] [CrossRef] [Google Scholar]

    132. Уиткрофт DJ, Price TD. 2008. Взаимное сотрудничество в птичьем моббинге: хорошая игра. Тенденции Экол. Эвол. 23 , 416-419. ( 10.1016/j.tree.2008.04.011) [PubMed] [CrossRef] [Google Scholar]

    133. Милинский М. 1987. ТО ЗА ТО у колюшек и эволюция кооперации. Природа 325 , 433-435. ( 10.1038/325433a0) [PubMed] [CrossRef] [Google Scholar]

    134. Noë R. 2006. Эксперименты по сотрудничеству: координация через общение или совместное действие порознь. Аним. Поведение 71 , 1-18. ( 10.1016/j.anbehav.2005.03.037) [CrossRef] [Google Scholar]

    135. Raihani NJ, Bshary R. 2011. Решение повторяющейся дилеммы заключенного: теория и реальность. Дж. Эвол. биол. 24 , 1628-1639. ( 10.1111/j.1420-9101.2011.02307.x) [PubMed] [CrossRef] [Google Scholar]

    136. Wilkinson GS. 1984. Взаимный обмен едой у летучей мыши-вампира. Природа 308 , 181-184. ( 10.1038/308181a0) [CrossRef] [Google Scholar]

    137. Картер Г.Г., Уилкинсон Г.С. 2013. Разделение еды в летучих мышах-вампирах: взаимная помощь предсказывает пожертвования больше, чем родство или домогательства. проц. Р. Соц. Б 280 , 20122573. ( 10.1098/rspb.2012.2573) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

    138. Carter GG. 2021. Кооперация и эволюция разделения пищи у летучих мышей-вампиров. этология 127 , 837-849. ( 10.1111/eth.13146) [CrossRef] [Google Scholar]

    139. McNamara JM. 2022. Теория игр в биологии: выход за рамки функциональных счетов. Являюсь. Нац. 199 , 179-193. ( 10.1086/717429) [PubMed] [CrossRef] [Google Scholar]

    140. McNamara JM, Houston AI. 2009 г.. Интеграция функции и механизма. Тенденции Экол. Эвол. 24 , 670-675. ( 10.1016/j.tree.2009.05.011) [PubMed] [CrossRef] [Google Scholar]

    141. Savage LJ. 1972. Основа статистики. Нью-Йорк, штат Нью-Йорк: Dover Publications. [Google Scholar]

    142. Бинмор К. 2009. Рациональные решения. Принстон, Нью-Джерси: Издательство Принстонского университета. [Google Scholar]

    143. Тверски А., Канеман Д.

    No related posts.

    • Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *