Уравнения и неравенства, содержащие переменную под знаком модуля
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
• СОДЕРЖАНИЕ
Понятие
модуля
Уравнения,
содержащие
переменную
под знаком модуля
Неравенства,
содержащие
переменную
под знаком модуля
3. Понятие модуля
Модулем числа а называется расстояние от началаотсчета до точки с координатой а
а|
|
Например:
|-7|=7
-7
Таким образом:
х
а
0
|
7 | =7
0
а, если а 0,
а
а, если а 0
х
7
оглавление
4.
 Уравнения.содержащие переменную под знаком модуля
Уравнения.содержащие переменную под знаком модуля| f(x) | = a
| f(x) | = |g(x) |
| f(x) | = g(x)
| f(x) | + | g(x) | = h(x)
5. Уравнение вида | f(x) | = a
Если а < 0, то уравнение решений не имеет
Если а = 0, то f(x) = 0
Если а > 0, то f(x) = а или f(x) = — а
Пример:
Решить уравнение: | 2х – 5 | = 13
Решение: 2х – 5 = 13 или 2х – 5 = — 13
2х = 13 + 5
2х = — 13 + 5
2х = 18
х =9
2х = — 8
х = -4
Ответ: х = 9 , х = — 4
Задачи для самостоятельного решения
оглавление
другой вид
6. Уравнение вида | f(x) | = a
Решите уравнение• 1) | 2х — 3| = 7
Ответ
• 2) .|х2 – х — 5| = 1 Ответ
• 3) | |х| — 2 |= 2
Ответ
оглавление
другой вид
• Ответ: х = 5, х = — 2
• Показать решение
назад
• Ответ: x = — 2, x = 3
• Показать решение
х
1
назад
17
2
• Ответ: x= 4, x= — 4 , x = 0
• Показать решение
назад
РЕШЕНИЕ:
| 2х – 3 | = 7
2х – 3 = 7 или
2х = 7 + 3 или
2х = 10 или
х = 5 или
2х – 3 = — 7
2х = — 7 + 3
2х = — 4
х =- 2
назад
РЕШЕНИЕ:
| х2 – х — 5 | = 1
х2 – х — 5 = 1 или
х2 – х — 6 = 0
D = 25
x1 = — 2, x2 = 3
х2 – х — 5 = -1
х2 – х — 4 = 0
D = 17
1 17
х1, 2
2
назад
РЕШЕНИЕ:
| |x| -2 | = 2
|x| -2 = 2
или |x| -2 = — 2
|x| = 2+ 2
|x| = — 2 +2
|x| = 4
|x| = 0
x = 4 или х = — 4
x = 0
назад
13.
 Уравнение вида | f(x) | = g(x)• 1) определить условие, при котором уравнение имеет решение:
Уравнение вида | f(x) | = g(x)• 1) определить условие, при котором уравнение имеет решение:g(x) ≥ 0
• 2) f(x) = g(x) или f(x) = — g(x)
• 3) Решить уравнения и выбрать корни, удовлетворяющие
условиюg(x) ≥ 0
• Пример: Решить уравнение:| х + 2| = 2( 3 – х)
• Определим при каких значениях х уравнение имеет решение
2( 3 – х) ≥ 0 => х ≤ 3
• Распишем данное уравнение на два:
х + 2 = 2( 3 – х) или х + 2 = — 2( 3 – х)
х = 4/3
х = 8 не удовлетворяет условию х ≤ 3
• Ответ: х = 4/3
Задачи для самостоятельного
решения
другой вид
Уравнение вида | f(x) | = g(x)
Решите уравнения
1) |5х + 2| = 3 – 3х
2) |х2 — 2х| = 3 — 2х
Ответ:
Ответ
другой вид
• Ответ: х = 1/8, х = — 2,5
• Показать решение
назад
• Ответ: х = 3 , х = 1
• Показать решение
назад
РЕШЕНИЕ:
• |5х + 2| = 3 – 3х
• Определим при каких значениях х уравнение
имеет решение: 3 – 3х ≥ 0 => х ≤ 1
• Распишем данное уравнение на два:
• 5х + 2 = 3 – 3х или 5х + 2 = — (3 – 3х)
• 5х + 3х = 3 – 2
5х — 3х = — 3 – 2
• 8х = 1
2х = — 5
• х = 1/8
х = — 2,5
• Оба корня удовлетворяют условию х ≤ 1
назад
РЕШЕНИЕ:
• |х2 -2 х| = 3 — 2х
• Определим при каких значениях х уравнение имеет
решение: 3 — 2х ≥ 0 => х ≤ 1,5
• Распишем данное уравнение на два:
• х2 –2 х =3 — 2х
или
х2 – 2х = — (3 — 2х )
• х2 = 3
х2 – 4х +3 = 0
• х= 3
х1 = 1 х2 = 3
Корни 3 и 3 не удовлетворяют условию х ≤ 1,5
Ответ: х = 3 х = 1
назад
19.
 Уравнение вида | f(x) | = | g(x)|
Уравнение вида | f(x) | = | g(x)|1способ: f(x) = g(x) или f(x) = — g(x)
2способ: возвести обе части уравнения в квадрат
Пример Решить уравнение: |х + 2| = |2х — 6|
1 способ: х + 2 = 2х – 6 или х + 2 = — (2х – 6)
х = 8
3х = 4
х = 4/3
2 способ: (|х + 2|)2 = (|2х — 6|)2 Воспользуемся свойством |а|2=а2
(х + 2)2 = (2х — 6)2
3х2 – 28х + 32 = 0 => х = 8, х = 4/3
Задачи для самостоятельного
решения
другой вид
Уравнение вида | f(x) | = |g(x)|
Решите уравнения
1) |х2 + х — 2| = |х +2|
2) |3 + х |= |х|
Ответ:
Ответ
другой вид
• Ответ: х = -2, х = 0, х = 2
• Показать решение
назад
• Ответ: х = -1,5
• Показать решение
назад
• РЕШЕНИЕ
|х2 + х — 2| = |х +2|
х2 + х — 2 = х +2 или х2 + х — 2 = — (х +2)
х2 = 4
х2 + 2х = 0
х = 2, х = — 2
х(х + 2) = 0
х = 0 х = -2
Ответ: х = -2, х = 0, х = 2
назад
• РЕШЕНИЕ
|3 + х| = |х|
3+х =х
или
3= 0
решений нет
Ответ: х = -1,5
назад
3+х =-х
2х = -3
х = -1,5
25.
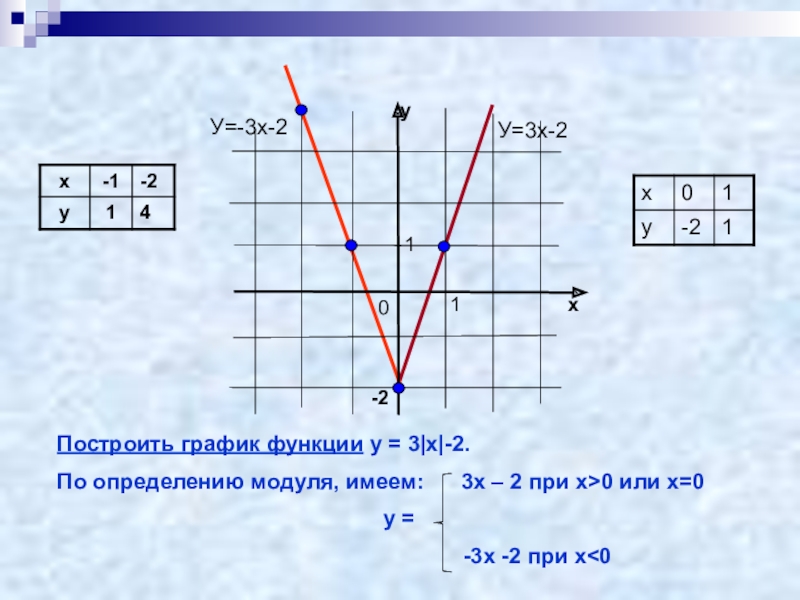 Уравнение вида | f(x) | + | g(x)| = h(x)• При решении уравнений данного вида используется
Уравнение вида | f(x) | + | g(x)| = h(x)• При решении уравнений данного вида используетсяправило раскрытия модуля.
• Пример: Решить уравнение:|х-3| + |2х-1| =8
1
• Найдем нули функций, стоящих под знаком модуля: х= 3, х= 2
• Отметим эти точки на числовой прямой и определим знаки функций на
получившихся промежутках
1
2
х 3
2х 1
3
Рассмотрим решение уравнения на каждом промежутке
1
х
2
1
х 3
2
Задачи для самостоятельного
решения
х 3
Ответ:
оглавление
26. Уравнение вида | f(x) | + | g(x)| = h(x)
• Пример: Решить уравнение: |х-3| + |2х-1| =8х
1
1 2
3
х 3
2х 1
2
Раскроем модули с учетом знака функций на этом промежутке
— ( х-3 ) – ( 2х-1 ) = 8
— 3х +4 = 8
4
удовлетворяет условию
х
3
х
1
2
назад
27. Уравнение вида | f(x) | + | g(x)| = h(x)
Пример: Решить уравнение:|х-3| + |2х-1| =81
2
3
х 3
2х 1
1
х 3
2
Раскроим модули с учетом знака функций на этом промежутке
— ( х-3 ) + ( 2х-1 ) = 8
х+2=8
х=6 не удовлетворяет условию 1 х 3
2
назад
28.
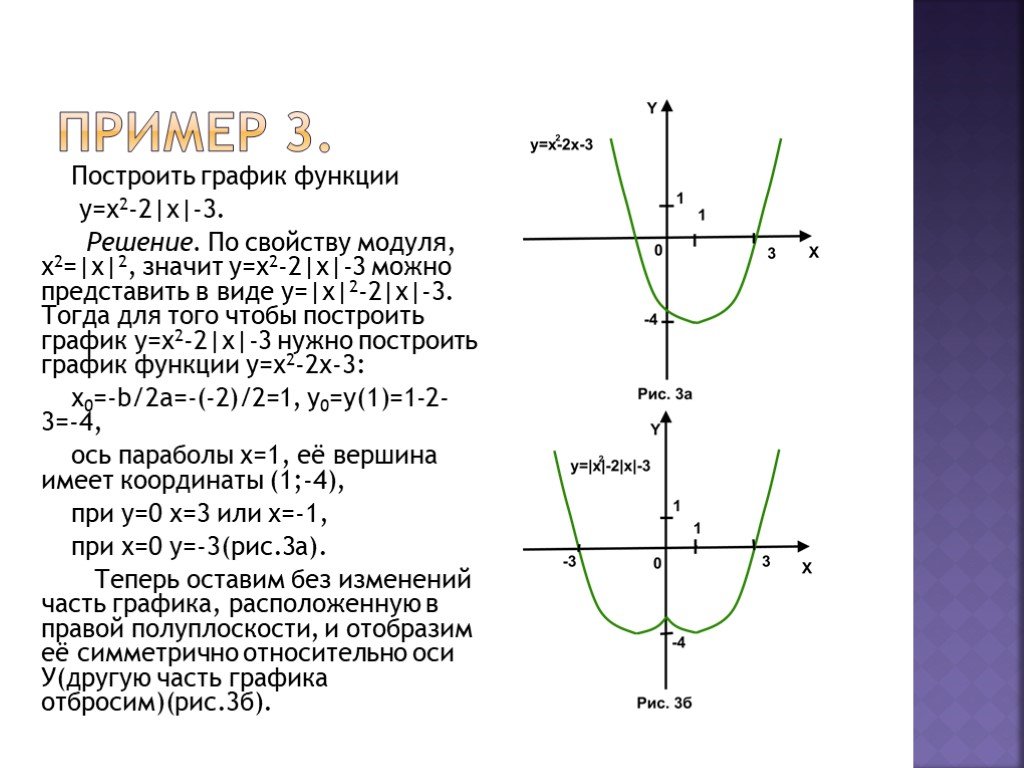 Уравнение вида | f(x) | + | g(x)| = h(x)Пример: Решить уравнение:|х-3| + |2х-1| =8
Уравнение вида | f(x) | + | g(x)| = h(x)Пример: Решить уравнение:|х-3| + |2х-1| =81
2
3
х 3
х 3
2х 1
• Раскроем модули с учетом знака функций на этом
промежутке
( х-3 ) + ( 2х-1 ) = 8
3х — 4 = 8
х=4 удовлетворяет условию х 3
назад
29. Уравнение вида | f(x) | + | g(x)| = h(x)
Объединим все ответы1
2
1
х
2
х
4
3
3
1
х 3
2
решений нет
Ответ: х
4
3
Задачи для самостоятельного
решения
х 3
2х 1
х 3
х 4
х 4
назад
30. Раскрытие модуля
а, если а 0,а
а, если а 0
• Решить уравнение: | 2х — 4| = х +6
Раскроем модуль.
Если 2х – 4 ≥ 0 , т. е. х ≥ 2,
то 2х – 4 = х +6
х = 10 – удовлетворяет условию х ≥ 2
Если 2х – 4 < 0, т. е. х < 2,
то -(2х – 4) = х +6
х = — 2/3 – удовлетворяет условию х < 2
Ответ: х = -2/3, х = 10
Второй способ
оформления
31. Раскрытие модуля
а, если а 0,а
а, если а 0
• Решить уравнение: | 2х — 4| = х +6
Раскроем модуль.

Найдем нули функции, стоящей внутри знака модуля
2х – 4 = 0 => х = 2
Отметим точку с координатой 2 на прямой.
—
2
+
Определим знаки функции на получившихся промежутках
Рассмотрим неравенство отдельно на каждом промежутке:
Если х < 2, то 2х – 4 < 0 => -(2х – 4) = х +6
х = — 2/3 – удовлетворяет условию х < 2
Если х ≥ 2, то 2х – 4 ≥ 0 => 2х – 4 = х +6
х = 10 – удовлетворяет условию х ≥ 2
Ответ: х = -2/3, х = 10
назад
32. Уравнение вида | f(x) | + | g(x)| = h(x)
Решите уравнения2 х 3 х 1 2х 1
3 х 3 х 5 2х
х 2 х 2 2х
Ответ:
Ответ:
Ответ:
оглавление
• Ответ:
x 2
2
3
х 4
• Показать решение
назад
• Ответ:
x 2
• Показать решение
назад
• Ответ:
x ;0
• Показать решение
назад
36. Уравнение вида | f(x) | + | g(x) | = h(x)
• Задача 1. Решить уравнение 2 х 3 х 1 2х 1Найдем нули функций (х-3) и (х+1) , отметим эти точки на числовой
прямой и определим знаки этих функций на получившихся
промежутках
+
х-3
х+1
+
3 +
-1
х 1
2 х 3 ( х 1) 2х 1
2 х 6 х 1 2 х 1
5х 6
6
х
5
не
удовлетворяет условию
х 1
1 х 3
2 х 3 ( х 1) 2х 1
2 x 6 х 1 2 х 1
3x 8
2
x 2
3
удовлетворяет условию
х 3
2 х 3 ( х 1) 2х 1
2 x 6 х 1 2 х 1
х 4
удовлетворяет условию
х 3
1 х 3
Ответ:
x 2
2
х 4
3
назад
37.
 Уравнение вида | f(x) | + | g(x) | = h(x)• Задача 1. Решить уравнение 3 х 3 х 5 2 х
Уравнение вида | f(x) | + | g(x) | = h(x)• Задача 1. Решить уравнение 3 х 3 х 5 2 хНайдем нули функций (3-х) и (х+5) , отметим эти точки на числовой
прямой и определим знаки этих функций на получившихся
промежутках
+
+
3-х
х+5
+
3 +
-5
х 5
5 х 3
3 х 3( х 5) 2х
3 х 3х 15 2х
18 0
3 х 3( х 5) 2х
3 x 3х 11 2х
6x 12
решений нет
x 2
удовлетворяет условию
х 3
3 х 3( х 5) 2х
3 x 3х 15 2х
х 9,5
не удовлетворяет условию
х 3
5 х 3
Ответ:
x 2
назад
38. Уравнение вида | f(x) | + | g(x) | = h(x)
• Задача 1. Решить уравнение х 2 х 2 2хНайдем нули функций (х-3) и (х+1) , отметим эти точки на числовой
прямой и определим знаки этих функций на получившихся
промежутках
+
х-2
х
+
2 +
0
х 0
х 2 х 2 2х
х 2 х 2 2х
2 2
верно при всех х
0 х 2
х 2 х 2 2х
x 2 х 2 2х
2x 0
с учетом условия
х 0
х ;0
x 0
удовлетворяет условию
0 х 2
Ответ:
х 2
х 2 х 2 2х
x 2 х 2 2х
х ;0
x 1
не удовлетворяет условию
х 2
назад
40.
 Неравенствасодержащие переменную под знаком модуля
Неравенствасодержащие переменную под знаком модуля|x| <a
| f(x) | < a
| f(x) | < |g(x) |
| f(x) | > |g(x) |
|x| >a
| f(x) | > a
| f(x) | + | g(x) | < h(x)
| f(x) | + | g(x) | > h(x)
41. Неравенства вида |x| < a
Неравенства вида |x| < a• Опираясь на понятие модуля:
|x| < a — это значит: расстояние от начала координат до точек,
удовлетворяющих данному условию должно быть меньше а.
На координатной прямой эти точки будут находиться правее нуля
до точки с координатой (а) и левее нуля до точки с координатой (а)
-а
х а; а
х
а
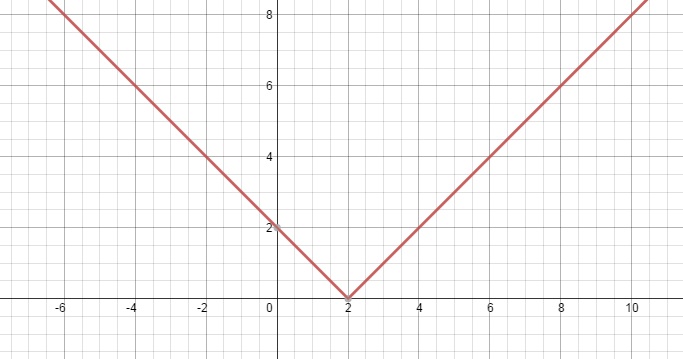
Пример: Решите неравенство |х| ≤ 6
Решение: Отметим на координатной прямой точки с координатами 6 и 6.
Решением будет множество точек, находящихся на отрезке 6;6
Ответ:
-6
6;6
6
Другой вид
х
42. Неравенства вида |x| > a
Неравенства вида |x| > aОпираясь на понятие модуля:
|x| > a — это значит: расстояние от начала координат до точек,
удовлетворяющих данному условию должно быть больше а.
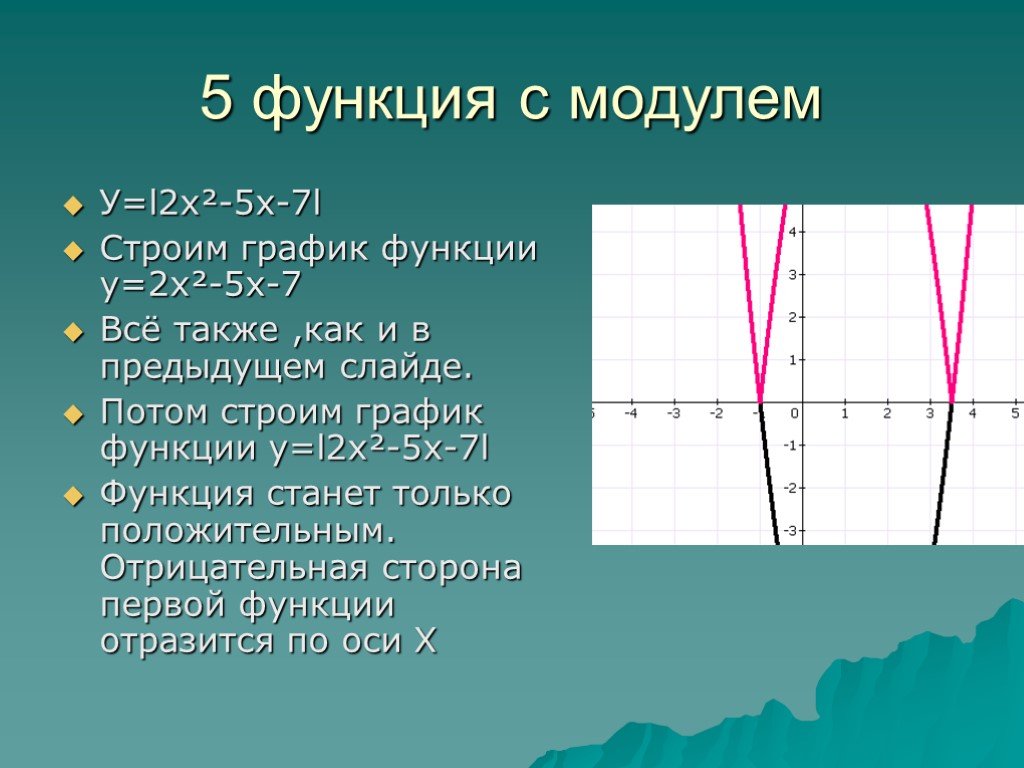
На координатной прямой эти точки будут находиться правее с
координатой (а) и левее точки с координатой (-а)
-а
х
а
х ; а а;
Пример: Решите неравенство: | х| > 9
Решение: Отметим на координатной прямой точки с координатами
-9 и 9. Решением неравенства будет являться множество точек,
координаты которых меньше – 9 или больше 9
-9
Ответ : х ; 9 9;
9
х
Задачи для самостоятельного
решения
43. Решите неравенства
х 8Ответ : 8 х 8
х 3 8
Ответ : 11 х 11
х 2 16 Ответ : х 14 или х 14
13 2 х 5 Ответ : х 4 или х 4
x 2 16 0
Ответ : 4 х 4
Показать решение
75 3 x 2 0 Ответ : х 5 или х 5 Показать решение
ДРУГОЙ ВИД
44. Решение неравенства
x 2 16 0x 2 16
Извлекаем корень из обеих частей уравнения,
2
не забывая свойства : х х
х 4
-4
4
х
Ответ : 4 х 4
НАЗАД
45. Решение неравенства
75 3 x 2 03 x 2 75
x 2 25
Извлекаем корень из обеих частей уравнения,
не забывая свойства : х х
2
х 5
-5
5
х
Ответ : х 5 или х 5
Другой вид
46.
 Неравенства вида |f(x)| < aНеравенства вида |f(x)| < a
Неравенства вида |f(x)| < aНеравенства вида |f(x)| < a• Аналогично неравенству вида |x| < a , решением данного
неравенства будет являться множество точек, удовлетворяющих
условию — a < f(x) < a
Пример 1: Решите неравенство: | 2х — 3| ≤ 11
Решение: Это неравенство равносильно двойному неравенству
— 11 ≤ 2х — 3 ≤ 11
— 11 + 3 ≤ 2х ≤ 11 + 3
-8 ≤ 2х ≤14
-4 ≤ х ≤7
Ответ : х 4; 7
Другой вид
47. Неравенства вида |f(x)| > a
Неравенства вида |f(x)| > a• Аналогично неравенству вида |x| > a , решением данного
неравенства будет являться множество точек, удовлетворяющих
условиям f(x) < — a или f(x) > a
Пример 1: Решите неравенство: | х + 6| ≥ 4
Решение: Это неравенство равносильно неравенствам:
х + 6 ≤ — 4 или х + 6 ≥ 4
х ≤-4-6
х≥ 4-6
х≥ -2
х ≤ — 10
Ответ : х ; 10 2;
Задачи для
самостоятельного решения
48. Решите неравенства
2 х 3Ответ:
х 3 1 5
Ответ:
2 х 4 2 12
Ответ:
13 2 4 3х 5
Ответ:
ДРУГОЙ ВИД
2 х 3
Ответ : 1 х 5
Показать решение
назад
х 3 1 5
Ответ : 9 х 3
Показать решение
назад
2 х 4 2 12
Ответ : х 3 или х 7
Показать решение
назад
13 2 4 3х 5
8
Ответ : х 0 или х
3
Показать решение
назад
53.
 Решение неравенства2 х 3
Решение неравенства2 х 33 2 х 3
3 2 х 3 2
5 х 1
5 х 1
1 х 5
-1
5
Ответ : 1 х 5
х
НАЗАД
54. Решение неравенства
х 3 1 5х 3 6
6 х 3 6
6 3 х 6 3
9 х 3
-9
3
Ответ : 9 х 3
х
НАЗАД
55. Решение неравенства
2 х 4 2 122 х 4 10
2 х 4 10 или 2 х 4 10
2 х 6 или 2 х 14
х 3 или х 7
-3
7
Ответ : х 3 или х 7
х
НАЗАД
56. Решение неравенства
13 2 4 3х 52 4 3х 5 13
2 4 3х 8
4 3х 4
4 3 х 4 или 4 3 х 4
3 х 8 или 3 х 0
8
х
или х 0
3
0
8
3
8
Ответ : х 0 или х
3
х
НАЗАД
57. Неравенства вида
f ( x) g ( x)Неравенства вида f ( x) g ( x) или f ( x) g ( x)
можно решать двумя способами:
1. возведением обеих частей в квадрат
2. раскрывая модули по определению
Пример: Решить неравенство: 3х 2 х 1
1 способ: Т. к. обе части неравенства неотрицательны, то их можно
2
2
3
х
2
х
1
возвести в квадрат
Используя известное свойство, получим: (3х 2) 2 ( х 1) 2
Перенесем все слагаемы в левую часть и разложим на множители
по формуле разность квадратов:
(3х 2) ( х 1) (3х 2) ( х 1) 0
2 х 3 4 х 1 0
Решая методом интервалов, получим:
1 3
х
;
4 2
Второй
способ
58.
 Неравенства видаf ( x) g ( x)
Неравенства видаf ( x) g ( x)Пример: Решить неравенство: 3х 2 х 1
2 способ: Найдем нули функции, стоящей внутри знака модуля, отметим эти
числа на числовой прямой и определим знаки этих функций на
получившихся промежутках:
—
—
+
-1
Решим неравенство на каждом промежутке:
х 1
3х-2
+
1 х
2
3
2
3
х+1
+
х
2
3
(3x 2) ( x 1)
(3 x 2) ( x 1)
(3x 2) ( x 1)
2x 3
4x 1
1
x
4
2x 3
x 1,5
x 1,5
с учетом данного условия:
-1
1
1,5
Решений нет
1
4
2
3
1 2
х
;
4 3
2
3
3
2
2 3
х
;
3 2
Объединяем второе и третье решение
1 3
х
;
4
2
59. Решите неравенство
2 х 2x 1Ответ:
ДРУГОЙ ВИД
2 х 2x 1
1
Ответ : x ; 3 ;
3
Показать решение
другой вид
61. Решение неравенства
2 х 2x 12 x
2
Возведем обе части в квадрат
2 x 1
2
Перенесем все в левую часть
и разложим по формуле разность квадратов
( 2 x 2 x 1)( 2 x 2 x 1) 0
( 3 x 1)( x 3) 0
—
+
Решаем неравенство методом интервалов
—
1
31
Ответ : x ; 3 ;
3
-3
х
НАЗАД
Неравенства вида
f ( x) g ( x) h( x)
• Неравенства данного вида решаются
методом раскрытия модулей, как и
уравнения такого типа .

• Рассмотрим решение данного вида
неравенств на примере:
63. Неравенства вида
f ( x) g ( x) h( x)3х 2 х 1 2 x
Пример: Решить неравенство:
2 способ: Найдем нули функции, стоящей внутри знака модуля, отметим эти
получившихся промежутках:
—
—
+
-1
Решим неравенство на каждом промежутке:
х 1
1 х
2
3
2
3
(3x 2) ( x 1) 2 x (3x 2) ( x 1) 2 x
4x 3
3
x
4
с учетом данного условия:
1
3
4
Решений нет
6x 1
1
x
6
-1
3х-2
+
1
6
х+1
+
х
2
3
(3 x 2) ( x 1) 2 x
0x 3
Неравенство верно при всех х
2
3
1 2
х
;
6 3
2
3
2
х
;
3
Объединяем второе и третье решение
1
х
;
4
English Русский Правила
2-x-1=0$ по модулю $11$. Я уже знаю, что решения $x=4$ по модулю $11$ и $x=8$ по модулю $11$, но я получил этот результат, попробовав. Я также знаю, что могу получить эти решения, используя обычную квадратичную формулу и выполняя некоторые сравнения следующим образом:
$$x=\frac{1\pm \sqrt{5}}{2}\equiv_{11}\frac{1\pm \sqrt{16}}{2}\equiv_{11}\frac{1\pm 4}{2}$$
$$x_+\equiv_{11}\frac{1+ 4}{2}\equiv_{11}\frac{5}{2}\equiv_{11}\frac{16}{2}=8$$
$$x_-\equiv_{11}\frac{1- 4}{2}\equiv_{11}\frac{-3}{2}\equiv_{11}\frac{8}{2}=4$$
Однако в этом методе я должен суммировать $11$ с некоторыми числами, пока не получу число, которое находится в $\mathbb{F}_{11}$. Что, если я продолжаю суммировать и суммировать, а в $\mathbb{F}_{11}$ ничего не получится? Когда можно сделать вывод, что уравнение не имеет решения? Есть ли лучший способ сделать это? 92$, поэтому мы могли бы продолжать вычитать 11$ из $x$ (или прибавлять 11$) до тех пор, пока $x$ не окажется в нужном диапазоне.
Я также знаю, что могу получить эти решения, используя обычную квадратичную формулу и выполняя некоторые сравнения следующим образом:
$$x=\frac{1\pm \sqrt{5}}{2}\equiv_{11}\frac{1\pm \sqrt{16}}{2}\equiv_{11}\frac{1\pm 4}{2}$$
$$x_+\equiv_{11}\frac{1+ 4}{2}\equiv_{11}\frac{5}{2}\equiv_{11}\frac{16}{2}=8$$
$$x_-\equiv_{11}\frac{1- 4}{2}\equiv_{11}\frac{-3}{2}\equiv_{11}\frac{8}{2}=4$$
Однако в этом методе я должен суммировать $11$ с некоторыми числами, пока не получу число, которое находится в $\mathbb{F}_{11}$. Что, если я продолжаю суммировать и суммировать, а в $\mathbb{F}_{11}$ ничего не получится? Когда можно сделать вывод, что уравнение не имеет решения? Есть ли лучший способ сделать это? 92$, поэтому мы могли бы продолжать вычитать 11$ из $x$ (или прибавлять 11$) до тех пор, пока $x$ не окажется в нужном диапазоне. Таким образом, вы должны попробовать каждую возможность между $0$ и $10$: или, используя переформулирование этого вычисления «прибавьте $11$ к $5$, пока не получите квадратное число», вы должны повторить процесс $10$ раз (пока достигнув $5+11\times 10=115$), чтобы установить, что решения не существует.
, так что
$$2x\equiv \begin{случаи} +4+1=5\эквив16\\ -4+1=-3\экв8 \end{случаи} $$
, следовательно, $x\equiv8$ и $4$.
Суть здесь в том, что $5$ является квадратичным вычетом по модулю $11$. Можно узнать, какие числа являются квадратичными остатками (а какие нет), не обязательно зная их «квадратный корень», но для небольших простых чисел, таких как $11$, пробежаться по возможностям так же быстро, как и применить любую причудливую теорию.
$\endgroup$ 92-x-12=(x-4)(x+3).$$ Решения равны $4$ и $-3,$ по модулю $11$ они равны $$4 \quad \text{и} \quad 8.$$ $\endgroup$ $\begingroup$Если проблема заключается в нахождении квадратного корня из $5\bmod 11$, это можно сделать с помощью того, что я называю «методом возведения в степень».
Поскольку $11-1$ делится на $2$, но не на $4$, любой квадратичный вычет $r$ будет иметь квадратный корень, являющийся также степенью $r\bmod 11$. Затем квадратный корень можно вычислить как степень, что требует $O(\log n)$ умножения, где $n$ — показатель степени. 92\экв5$. (Если бы это не удалось, квадратный корень и, следовательно, квадратное уравнение не имели бы решения.) Таким образом, мы можем с уверенностью ввести эти значения для квадратных корней из $5$ с ограниченным методом проб и ошибок и исходить из этого.
Затем квадратный корень можно вычислить как степень, что требует $O(\log n)$ умножения, где $n$ — показатель степени. 92\экв5$. (Если бы это не удалось, квадратный корень и, следовательно, квадратное уравнение не имели бы решения.) Таким образом, мы можем с уверенностью ввести эти значения для квадратных корней из $5$ с ограниченным методом проб и ошибок и исходить из этого.
абстрактная алгебра — $\Bbb F_2[X]$ модули с 8 элементами
Пусть $L$ полный список неизоморфных $\Bbb{F}_2[X]$-модулей порядка $8$. Тогда по аргументу подсчета, который вы привели выше, $L$ должен содержаться в следующем списке: 93+X+1$ неприводимы в $\Bbb{F}_2[X]$, так как не имеют корней в $\Bbb{F}_2$.
Снова применяя структурную теорему к окончательным формам каждого из этих (классов изоморфизма) модулей, мы можем заключить, что $L$ — это в точности указанный список.
Также обратите внимание, что 1-8 в $L$ — это полный список неизоморфных циклических $\Bbb{F}_2[X]$-модулей порядка $8$.
