Выпуклость и вогнутость графика функции. Точки перегиба (Лекция №10)
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Примеры.
- Полуокружность выпукла на [–1; 1].
- Парабола y = x2 вогнута на интервале (-∞; +∞).
- График функции в одних интервалах может быть выпуклым, а в других вогнутым. Так график функции y = sin x на [0,2; π], выпуклый в интервале (0; π) и вогнутый в (π; 2π).
Рассмотрим достаточный признак, позволяющий установить,
будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f »(x) < 0, то график функции на этом интервале выпуклый, если же f»(x) > 0 – вогнутый.
Доказательство. Предположим для определенности, что f»(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
Итак, уравнение кривой имеет вид y
= f(x). Обозначим ординату касательной,
соответствующую абсциссе x.
Тогда . Следовательно, разность ординат кривой и касательной при
одном и том же значении x будет .
Разность f(x) – f(x0) преобразуем по теореме Лагранжа , где c между x и x0.
Таким образом,
.
К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: , где c1 между c0 и x0. По условию теоремы f »(x) < 0. Определим знак произведения второго и третьего сомножителей.
- Предположим, что x>x0. Тогда x0<c1<c<x,
следовательно, (
- Пусть x<x0, следовательно, x < c
< c1 < x0 и (x – x0)
< 0, (c – x0) < 0.
Поэтому вновь .
Поэтому вновь .
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 Î (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
Примеры.
- Установить интервалы
выпуклости и вогнутости кривой y = 2 – x2.
Найдем y » и определим, где вторая производная положительна и где отрицательна. y‘ = –2x, y» = –2 < 0 на (–∞; +∞), следовательно, функция всюду выпукла.
- y = ex. Так как y» = ex
> 0 при любых x, то кривая всюду вогнута.
- y = x3. Так как y» = 6x, то y» < 0 при x
< 0 и y» > 0 при x
> 0. Следовательно, при x < 0 кривая выпукла, а
при x > 0 вогнута.
Следовательно, при x < 0 кривая выпукла, а
при x > 0 вогнута.
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
Определим достаточные условия того, что данная точка кривой является точкой перегиба.
Теорема. Пусть кривая определяется уравнением y = f(x). Если f »(x0) = 0 или f »(x0) не существует и при переходе через значение x = x0 производная f »(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть
f »(x) < 0 при x
< x0 и f
»(x) > 0 при x
> x0.
Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с
абсциссой x0
Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Примеры. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривых.
Найдем производные заданной функции до второго порядка.
.
. Вторая производная не существует при x = 1. Исследуем эту точку на возможный перегиб.
Итак, точка перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞; 1).
Возможные точки перегиба найдем, решив уравнение 2x2 – 1 = 0. Отсюда .
Точки перегиба . Функция выпукла на и вогнута на .
- y = ln (1 – x2). Область определения функции D(y) = (-1; 1).
.
при всех x из (–1; 1).
Следовательно, f(x) выпуклая на (–1; 1).
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.
Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
Прямая называется асимптотой графика функции y = f(x), если расстояние от
переменной точки M графика до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.
е. точка графика функции при своем стремлении
в бесконечность должна неограниченно приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.
Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
Пусть при x→ x0 с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной величине, т.е. или или . Тогда из определения асимптоты следует, что прямая
Таким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x0 – 0 или x → x0 + 0, x = x0
Следовательно,
для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный
разрыв).
Тогда вертикальная асимптота имеет уравнение x = x0.
Примеры.
- Найти вертикальные асимптоты графика функции . Так как , то прямая x = 2 является вертикальной асимптотой.
- .
Прямая x = 0 – вертикальная асимптота.
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.
Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда . Аналогичное утверждение верно и при x → –∞.
Доказательство. Пусть MP –
длина отрезка, равного расстоянию от точки M до асимптоты. По условию . Обозначим через φ угол наклона асимптоты к
оси Ox.
Тогда из ΔMNP
следует, что . Так как φ постоянный угол (φ ≠ π/2), то , но
MN = MK – NK = y — yас= f(x) — (kx+b).
Следовательно, мы можем записать следующее равенство .
Так как x → +∞, то должно выполняться равенство . Но при постоянных k и b и . Следовательно, , т.е. .
Если число k уже известно, то , поэтому .
Для доказательства в случае x → –∞ все рассуждения аналогичны.
Докажем обратное утверждение. Предположим, что существуют пределы, определяющие числа k и b. Тогда несложно заметить, что выполняется равенство . Действительно
Следовательно, прямая y = kx + b есть асимптота. Теорема полностью доказана.
Сделаем несколько замечаний.
Замечание 1. Теорема
показывает, что для нахождения асимптот достаточно найти два указанных предела.
Причем, если хотя бы один из пределов не существует или обращается в бесконечность,
то кривая асимптот не имеет.
Замечание 2. В случае, когда k = 0 асимптота y = b называется горизонтальной асимптотой. Наличие горизонтальной асимптоты означает, что существуют пределы
.
Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞ и, следовательно, график функции может иметь две различные асимптоты при x → +∞ и x → –∞.
Примеры. Найти асимптоты кривых.
- .
- Вертикальные:
x = 0 – вертикальная асимптота.
- Наклонные:
.
При x → — ∞ получим те же значения k и b. Следовательно, прямая y = x + 2 является наклонной асимптотой.
- Вертикальные:
- y = e–x sin x + x.
- Функция определена и непрерывна на всей числовой прямой, следовательно,
вертикальных асимптот нет.
-
а) .
Итак, при x → +∞ наклонная асимптота у= х.
б) , т. к.
, поэтому при x → — ∞ наклонных асимптот нет.
- Функция определена и непрерывна на всей числовой прямой, следовательно,
вертикальных асимптот нет.
- y = x – 2arctg x.
- Вертикальных асимптот нет.
-
а) .
. Наклонная асимптота y = x – π при .
б) при .
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Как построить график функций точек перегиба
Все ресурсы по исчислению 1
10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Исчисление 1 Помощь » Функции » Графические функции » Точки » Точки перегиба » Как построить график функций точек перегиба
Найдите точки перегиба .
Возможные ответы:
Правильный ответ:
Объяснение:
Точки перегиба могут возникать только тогда, когда вторая производная равна нулю или не определена. Здесь у нас есть
.
Следовательно, возможные точки перегиба возникают в и . Однако, чтобы получить точку перегиба, мы должны убедиться, что знак второй производной отличается по обе стороны от точки. Здесь у нас есть
.
Следовательно, обе точки перегиба
Сообщить об ошибке
Ниже приведен график . Сколько у него точек перегиба?
Возможные ответы:
Недостаточно информации
Правильный ответ:
Объяснение: Возможные точки перегиба возникают, когда .
Это происходит при трех значениях . Однако, чтобы быть точкой перегиба, знак должен быть разным по обе стороны от критического значения. Следовательно, только являются критическими точками.
Сообщить об ошибке
Найдите точки перегиба для функции .
Возможные ответы:
Точек перегиба нет.
и
и
Правильный ответ:
Объяснение:
Точка перегиба находится там, где график (или изображение) функции изменяет вогнутость. Чтобы найти это алгебраически, мы хотим найти, где вторая производная функции меняет знак с отрицательного на положительный или наоборот. Итак, находим вторую производную заданной функции
Первая производная с использованием правила степени
равна
и вторая производная
Затем мы находим, где эта вторая производная равна .
когда .
Затем мы смотрим, меняет ли знак вторая производная в этой точке. Как графически, так и алгебраически мы можем видеть, что функция действительно меняет знак в точке и только в точке , так что это наша точка перегиба.
Сообщить об ошибке
Найти все точки перегиба
.
Возможные ответы:
Точки перегиба отсутствуют.
Правильный ответ:
Объяснение:
Чтобы найти точки перегиба, нам нужно найти используя степенное правило, .
Теперь устанавливаем и находим.
Чтобы убедиться, что это истинная точка перегиба, нам нужно подставить значение, которое меньше ее, и значение, которое больше ее, во вторую производную. Если вокруг точки происходит смена знака, то это истинная точка перегиба.
Пусть
Теперь пусть
Поскольку знак меняется с положительного на отрицательный вокруг точки, мы можем заключить, что это точка перегиба.
Сообщить об ошибке
Найти все точки перегиба
Возможные ответы:
Нет точек перегиба.
Правильный ответ:
Объяснение:
Чтобы найти точки перегиба, нам нужно найти с помощью степенного правила.
Теперь, чтобы найти точки перегиба, нам нужно установить .
.
Теперь мы можем использовать квадратное уравнение.
Напомним, что квадратное уравнение имеет вид
,
, где a,b,c относятся к коэффициентам уравнения .
В этом случае a=12, b=0, c=-4.
Таким образом возможные точки заражения
.
Теперь, чтобы проверить, являются ли и какие точки перегиба, нам нужно подставить значение выше и ниже каждой точки. Если есть смена знака, то точка является точкой перегиба.
Для проверки подключим.
Следовательно, это точка перегиба.
Теперь давайте проверим с .
Следовательно, это также точка перегиба.
Сообщить об ошибке
Найти все точки заражения
.
Возможные ответы:
Точек перегиба нет.
Правильный ответ:
Объяснение:
Чтобы найти точки перегиба, нам нужно найти с помощью степенного правила.
Теперь давайте помножим.
Теперь, чтобы найти точки перегиба, нам нужно установить .
.
Из этого уравнения мы уже знаем одну из точек перегиба, .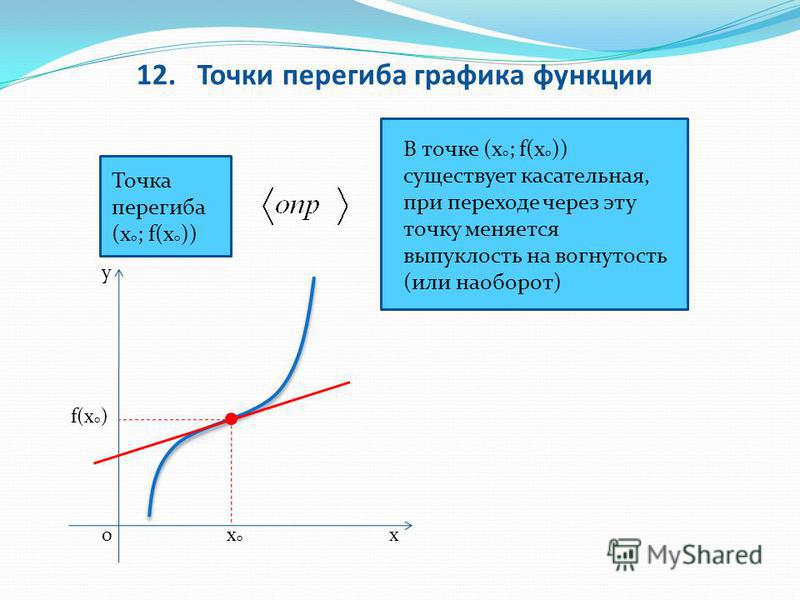
Чтобы вычислить остальные точки перегиба, мы можем использовать квадратное уравнение.
Напомним, что квадратное уравнение имеет вид
, где a,b,c относятся к коэффициентам уравнения
.
В этом случае a=20, b=0, c=-18.
Таким образом, другие 2 точки заражения — это
Чтобы убедиться, что все они являются точками перегиба, нам нужно подставить значения выше и ниже каждого значения и посмотреть, изменится ли знак.
Давайте подключим
Поскольку в каждой точке происходит смена знака, все они являются точками перегиба.
Сообщить об ошибке
Найти точки перегиба
.
Возможные ответы:
Точек перегиба нет.
Правильный ответ:
Точек перегиба нет.
Пояснение:
Чтобы найти точки перегиба, нам нужно найти
Теперь устанавливаем.
.
Это последнее утверждение говорит, что никогда не будет. Таким образом, точек перегиба нет. 9
Возможные ответы:
Правильный ответ: 909 909 9 9 Пояснение: Точками перегиба данной функции являются значения, при которых вторая производная функции равна нулю. Первая производная функции равна , а производная этой функции (вторая производная исходной функции) равна . Обе производные были найдены с помощью степенного правила . Решение , . Чтобы убедиться, что эта точка является истинной точкой перегиба, нам нужно подставить значение, которое меньше точки, и значение, которое больше точки, во вторую производную. Подключаем, . Теперь подключите . Следовательно, это единственная точка перегиба функции. Сообщить об ошибке Найти все точки перегиба . Возможные ответы: Правильный ответ: Объяснение: Чтобы найти все точки перегиба, мы сначала находим, используя правило степени дважды, . Теперь устанавливаем. . Теперь факторизуем левую часть. Из этого мы видим, что есть одна точка перегиба в . Для точки перегиба давайте найдем x для уравнения в скобках. Отчет о ошибке Найдите все точки перегиба: .
Если между двумя числами есть смена знака, то рассматриваемая точка является точкой перегиба.