Математика: Справ. материалы
Математика: Справ. материалы
ОглавлениеГЛАВА I. ЧИСЛА3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре.  Переменные.11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа § 4. Комплексные числа ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ § 6. Целые рациональные выражения 52. Многочлены. Приведение многочленов к стандартному виду. § 7. Дробные рациональные выражения Глава III. ФУНКЦИИ И ГРАФИКИ § 9. Свойства функций § 10. Виды функций 95. Обратная функция. График обратной функции. 96. Логарифмическая функция. 96. Определение тригонометрических функций. § 11. Преобразования графиков ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. 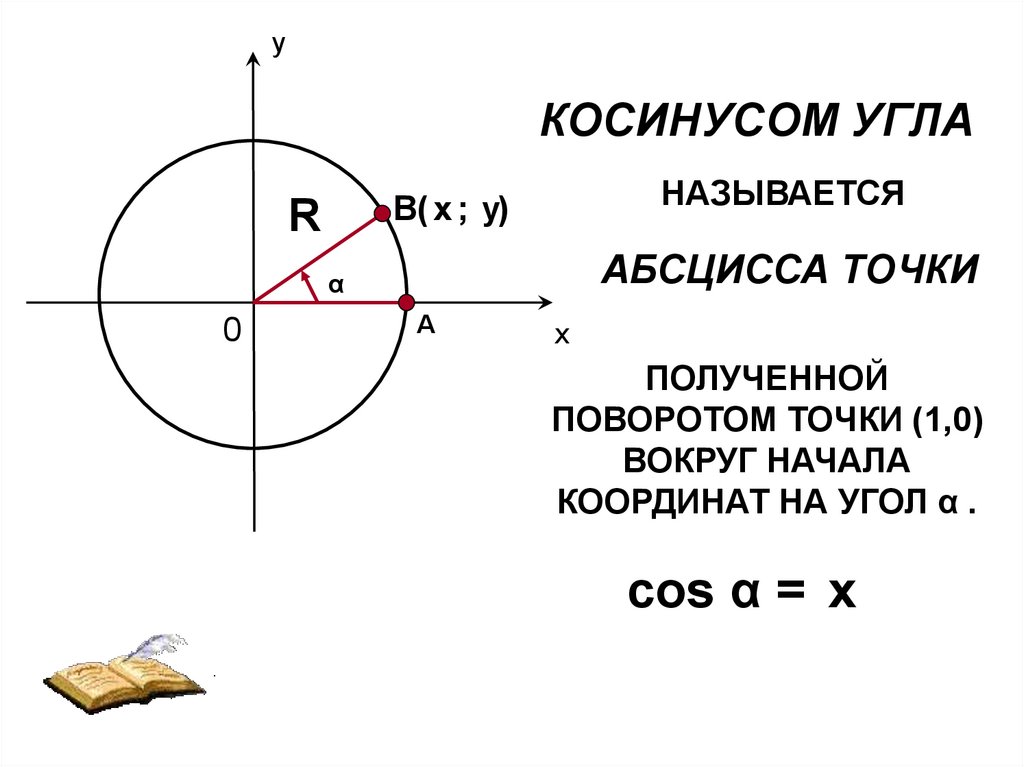 Преобразование выражений, содержащих переменную под знаком логарифма§ 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной § 15. Уравнения с двумя переменными § 16. Системы уравнений Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной § 18. Доказательство неравенств ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности § 20. Предел функции § 21. Производная и ее применения § 22. Первообразная и интеграл ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ § 1. О строении курса геометрии § 2. Основные свойства простейших геометрических фигур § 3. Геометрические построения на плоскости § 4. Четырехугольники § 5. Многоугольники § 6. Решение треугольников § 7. Площади плоских фигур 38. Площади подобных фигур. ГЛАВА II. Прямые и плоскости в пространстве § 8. 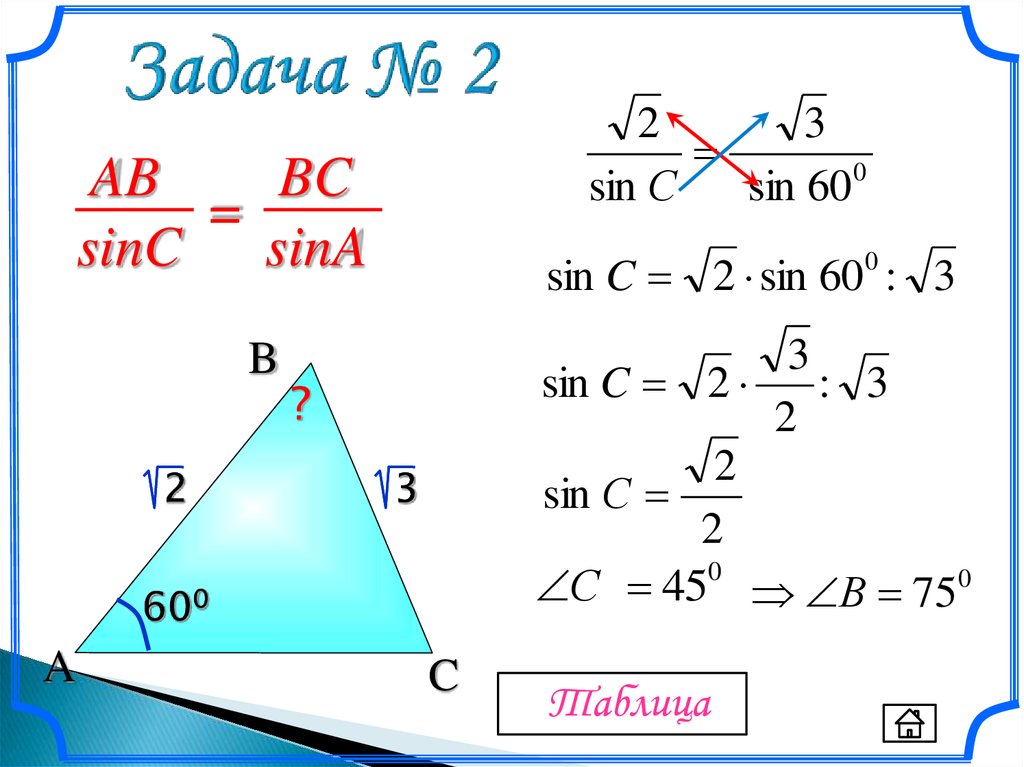 Аксиомы стереометрии и некоторые следствия из них§ 9. Параллельность прямых и плоскостей § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники § 12. Тела вращения § 13. Изображение пространственных фигур на плоскости § 14. Объемы тел § 15. Площади поверхностей тел ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве § 17. Уравнения фигур на плоскости § 18. Уравнения фигур в пространстве ГЛАВА V. ПРЕОБРАЗОВАНИЯ ФИГУР § 19. Движение § 20. Подобие фигур ГЛАВА VI. ВЕКТОРЫ § 21. Введение понятия вектора § 22. Операции над векторами ОСНОВНЫЕ ФОРМУЛЫ И СООТНОШЕНИЯ I. Основные законы алгебры ГЕОМЕТРИЯ |
Урок геометрии в 8 классе «Соотношения между сторонами и углами в прямоугольном треугольнике. Синус, косинус и тангенс острого угла в прямоугольном треугольнике» | План-конспект урока по геометрии (8 класс) на тему:
Урок геометрии в 8 классе
«Соотношения между сторонами и углами в прямоугольном треугольнике.
Синус, косинус и тангенс острого угла в прямоугольном треугольнике»
Цель урока: ввести понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника и ознакомить с правилом нахождения катета и гипотенузы, закрепить полученные сведения.
Образовательные задачи урока:
- научить восьмиклассников находить неизвестные элементы, синус, косинус и тангенс острого угла прямоугольного треугольника;
- сформировать познавательный интерес у школьников через исследовательскую деятельность;
Развивающие задачи урока:
- развивать творческие способности, дифференцируя учебный материал на несколько уровней, прививать навык самообразовательной деятельности;
- развивать умение осуществлять культурную коммуникацию с учителем и со сверстниками;
Воспитательные задачи урока:
- развивать навыки контроля и самоконтроля, способность преодолевать трудности при решении учебной задачи
Тип урока: урок объяснения нового материала
Формы работы учащихся: фронтальная, индивидуальная
Оборудование: презентация Power Point,мультимедиа проектор, опорные листы.
Ход урока
1.Организационный момент:
По мнению Галилео Галилея: «Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать» (Слайд 1)
2.Актуализация знаний
Один мудрец сказал: «Клетка геометрии – это треугольник, он так же неисчерпаем, как и Вселенная»
Сегодня мы продолжим с вами беседу о прямоугольном треугольнике. Вспомним, что мы о нём уже знаем. Открываем тетради, записываем число, «Классная работа».
(Слайд 2)- (Слайд 7)
1.«Треугольник, у которого один угол прямой называется…»
А) остроугольный Б) равнобедренный
В) равносторонний Г) прямоугольный
2. «Прямоугольный треугольник изображен на рисунке … »
А) Б) В)
3.Как называются стороны в прямоугольном треугольнике?
А) боковые Б) основания
В) катеты и гипотенуза Г) параллельные стороны
4.
Один из острых углов прямоугольного треугольника равен 30°, чему равен другой острый угол?
А) 90° Б) 60° В) 30° С) 180°
5. Катет прямоугольного треугольника, лежащий напротив угла в 30°, равен
А) гипотенузе Б) другому катету В) половине гипотенузы Г) острому углу
6. В данном прямоугольном треугольнике по теореме Пифагора
выполняется следующее равенство:
b c А) a2 = b2 + c2 Б) b2 = a2 + c2 В) c2 = a2 + b2 Г) c2 = a2 – b2
a
Выполним проверку.
(Слайд 8)
(Слайд 9)
Перед вами три треугольника:
1) 2) 3)
3 10 4 5
3 3
5
Ответьте на вопросы:
1.
Что их объединяет? (Они прямоугольные)
2. Чем отличаются? (Длинами сторон и величиной острых углов)
3. Что мы знаем об этих треугольниках? (Знаем длины некоторых сторон)
4. Можем найти длины неизвестных сторон? Каким образом?
5. Можем найти градусные меры углов в этих треугольниках? Какие правила надо использовать? Как связаны длины сторон с величинами углов в этих треугольниках?
В третьем треугольнике не можем найти градусные меры углов. Нам не хватает знаний. Какова сегодняшняя задача? (Найти зависимость между длинами сторон прямоугольного треугольника и его острыми углами)
Правильно, надо найти каково соотношение между сторонами и углами прямоугольного треугольника. (Слайд 10)
В тетради запишите тему урока.
Задача каждого провести небольшие исследования, выполнять определенные задания. Давайте делиться своими идеями, которые придут вам в голову, и не бойтесь ошибиться, ведь недаром народная мудрость гласит «не ошибается тот, кто ничего не делает».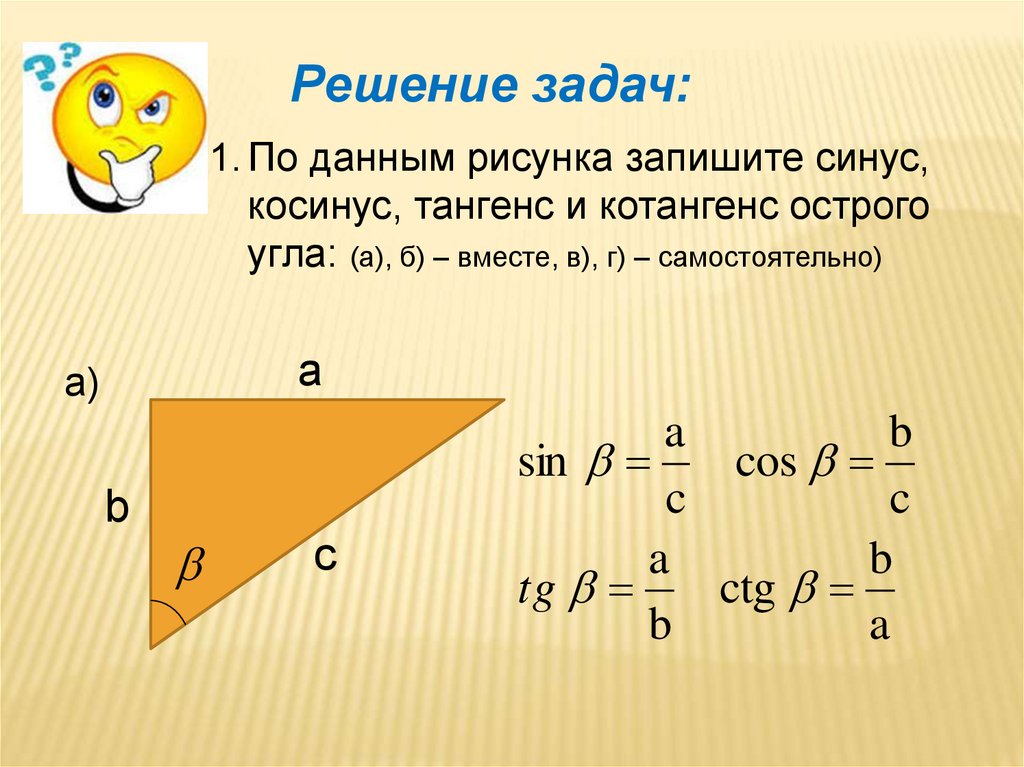
3. Изучение нового материла:
Итак, ребята, давайте еще раз озвучим, какой треугольник называется прямоугольным? … ….
Совершенно верно, это треугольник у которого один угол прямой.
А может ли быть у прямоугольного треугольника еще один прямой или тупой угол?
А почему? Конечно, т. к. сумма углов треугольника =180, значит сколько градусов приходится на оставшиеся два угла? Действительно, оба они острые.
Начертите прямоугольный треугольник ABC с прямым углом С. (Слайд 11)
Назовите катеты и гипотенузу этого треугольника.
То есть гипотенуза АВ лежит напротив прямого угла С. Обозначим ее маленькой буквой с.
Назовите катет лежащий против острого угла В, его мы обозначим b, катет лежащий против острого угла А, его мы обозначим а.
Какой катет прилежит углу В? Да, катет а .
Какой катет прилежит углу А? Да, катет b.
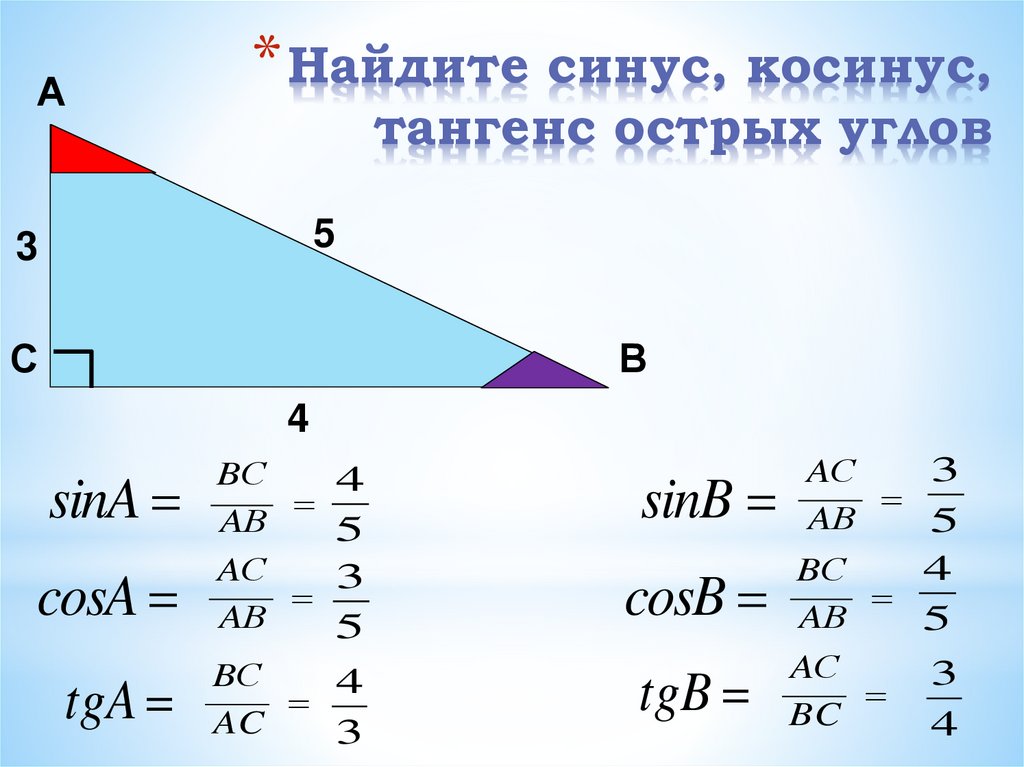
Треугольник и треугольник, подумаешь! Что с ним делать? А вот древние люди знали, что делать! Повторим их действия. Измерим сторону в. Сторона в равна четырём клеточкам. Ладно. Измерим сторону а. Три клеточки.
А теперь поделим длину стороны а на длину стороны в. Или, как ещё говорят, возьмём отношение а к в. а/в = 3/4.
Можно наоборот, поделить в на а. Получим 4/3. Можно в поделить на с. Гипотенузу с по клеточкам не посчитать, но она равна 5. Получим в/с = 4/5. Итак, можно делить длины сторон друг на друга и получать какие-то числа.
Ну и что? Какой смысл в этом интересном занятии? Пока никакого. Бестолковое занятие, прямо скажем.
А теперь сделаем вот что. Увеличим треугольник. Продлим стороны в и с, но так, чтобы треугольник остался прямоугольным. Угол α, естественно, не меняется. Стороны а, в и с превратятся в m, n, k, и, понятное дело, длины сторон изменятся.
А вот их отношения – нет!
Отношение а/в было: а/в = 3/4, стало m/n = 6/8 = 3/4. Отношения других соответствующих сторон также не изменятся.
Можно как угодно менять длины сторон в прямоугольном треугольнике, увеличивать, уменьшать, не меняя угла α – отношения соответствующих сторон не изменятся. Можно проверить, а можно поверить древним людям на слово.
А вот это уже очень важно! Отношения сторон в прямоугольном треугольнике никак не зависят от длин сторон (при одном и том же угле). Это настолько важно, что отношения сторон заслужили свои специальные названия. Свои имена, так сказать. (Слайд 12)
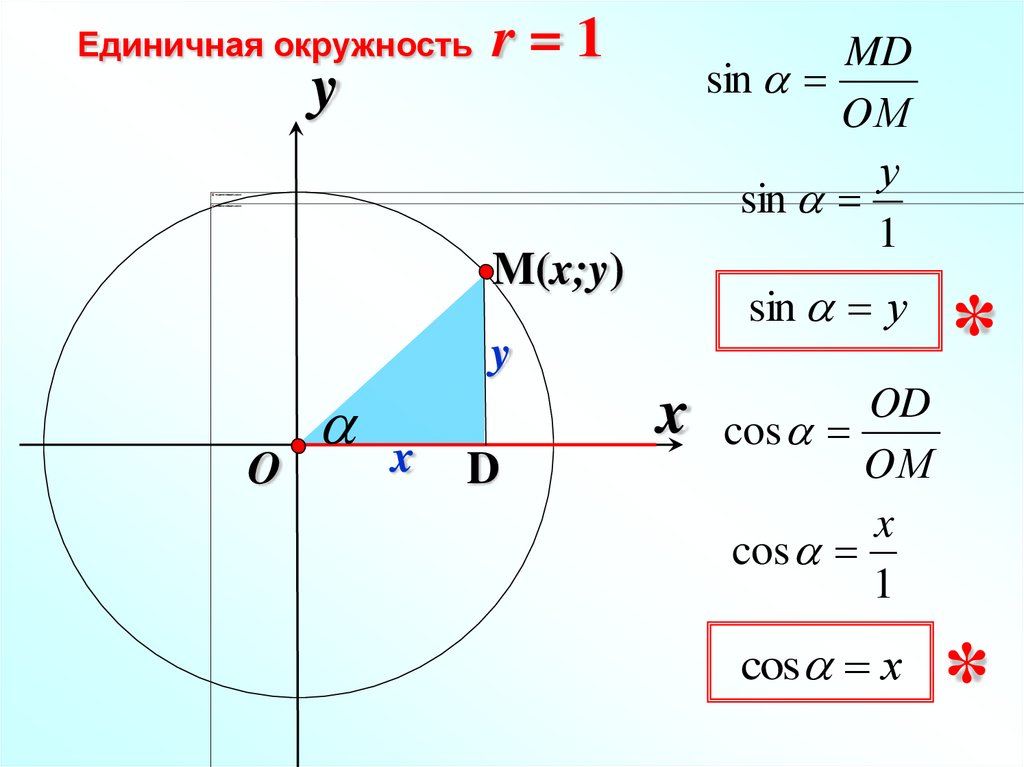
Что такое синус угла α? (Слайд 13)
Это отношение противолежащего катета к гипотенузе:
Что такое косинус угла α?
Это отношение прилежащего катета к гипотенузе:
Что такое тангенс угла α?
Это отношение противолежащего катета к прилежащему:
Что такое котангенс угла α?
Это отношение прилежащего катета к противолежащему:
сtg α = в/а
Всё очень просто. Синус, косинус, тангенс и котангенс – это некоторые числа.
Безразмерные. Просто числа. Для каждого угла – свои.
Это надо запомнить.
Запоминание можно облегчить. Фраза «Начнём издалека…» знакома? Вот и начинайте издалека.
Синус угла – это отношение дальнего от угла катета к гипотенузе.
Косинус – отношение ближнего к гипотенузе.
Тангенс угла – это отношение дальнего от угла катета к ближнему. Котангенс – наоборот.
Или (Слайд 14): косинус-коснуться-близкий-прилежащий;
тангенс-там- далёкий- противолежащий
Уже проще, правда?
Ну а если запомнить, что в тангенсе и котангенсе сидят только катеты, а в синусе и косинусе гипотенуза появляется, то всё станет совсем просто.
У каждого угла есть свой синус и косинус. И почти у каждого — свой тангенс и котангенс. Это важно. Считается, что если нам дан угол, то его синус, косинус, тангенс и котангенс нам известны! И наоборот. Дан синус, или любая другая тригонометрическая функция – значит, мы знаем угол.
Всю эту славную семейку – синус, косинус, тангенс и котангенс называют ещё тригонометрическими функциями.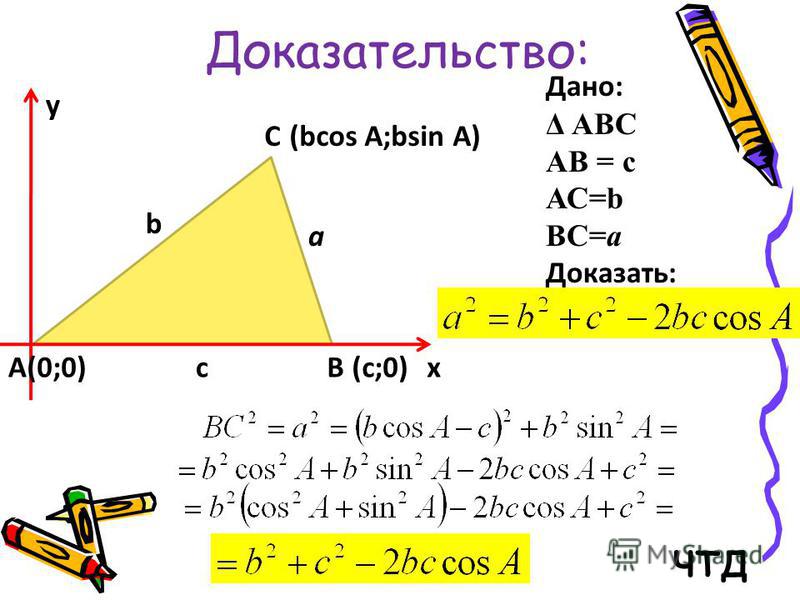
Таким образом мы с вами сегодня немного приоткрыли дверь нового для вас раздела математики — тригонометрии — науки, изучающей связи между сторонами и углами в треугольнике. Истоки тригонометрии уходят в далекую древность, когда у людей возникла потребность следить за небесными светилами и по этим наблюдениям вести календарь, рассчитывали сроки сева, время разлива рек; ориентировались в пути по звездам.
Повторим ещё раз: (Слайд 15)
Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
если нам нужно выразить из этих формул катет или гипотенузу мы воспользуемся свойством пропорции
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
отсюда,
Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
отсюда,
Ребята, как вы видите, мы получили очень много формул, но этого не нужно страшиться, ведь зная определение синуса, косинуса и тангенса острого угла прямоугольного треугольника, вы всегда сможете вывести все остальные формулы.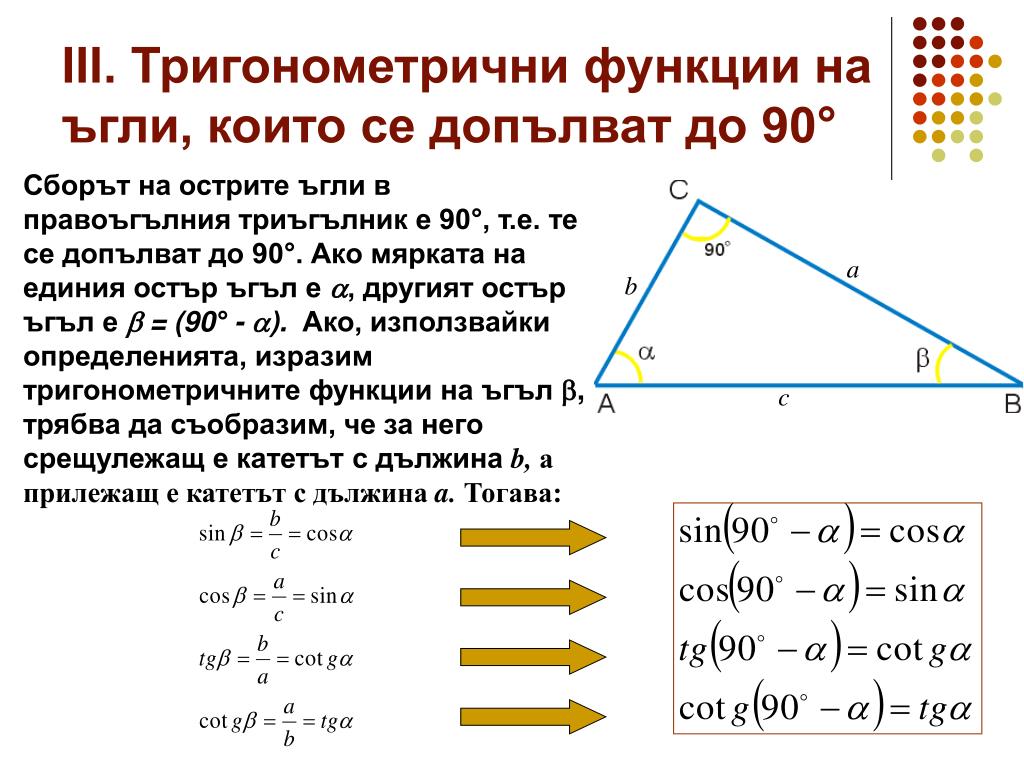
4.Закрепление изученного материала: (Слайд 16)
Перед вами прямоугольный треугольник, запишите верные соотношения для синусов, косинусов и тангенсов острого угла. Найдите синус, косинус и тангенс угла М.
Все ли данные у нас есть для решения задачи?
Неизвестна гипотенуза, как нам ее найти?
Верно, по теореме Пифагора, ну а потом, зная все необходимые элементы треугольника, найдем синус, косинус и тангенс острого угла М.
(с последующей проверкой)
(Слайд 17) (Кто-то из учащихся делает на доске)
Дан треугольник PQR.
А) Используя определения, запишите чему равны
sin∟R, cos∟R и tg∟R.
Б) Найдите отношение синуса угла R к косинусу угла R.
Что можно сказать об этом отношении? (Оно равно тангенсу этого же угла)
Какое правило можем добавить? (Тангенс острого угла прямоугольного треугольника равен отношению синуса к косинусу этого угла).
5.
Рефлексия. (Слайд 18)
Перед вами опять прямоугольный треугольник. Что можно найти в этом треугольнике, зная длины его катетов? (Гипотенузу, площадь, периметр, синусы, косинусы, тангенсы острых углов, среднюю линию…).
6.Домашнее задание №591 (а, в), повторить записи в тетради, для тех, кто увлекается геометрией составить ребусы, кроссворды.
7. (Слайд 19) Подведение итогов:
Какие определения вы сегодня узнали?
Что показалось самым трудным?
Какой этап урока был самым интересным для вас?
Ребята, я благодарю вас за урок, вы сегодня очень хорошо поработали особенно я хотела бы отметить…….
С каким настроением вы уйдете с урока, нарисуйте соответствующий смайлик на полях своей тетради.
Как вы можете отличить, когда использовать SohCahToa и когда использовать правила синуса/косинуса?
Как отличить, когда использовать SohCahToa, а когда использовать правила синуса/косинуса? | MyTutorAnswers>Maths>GCSE>Article
SohCahToa
Мы используем SohCahToa, чтобы вычислить неизвестный угол или сторону в прямоугольном треугольнике.
В вопросах вы увидите прямоугольный треугольник с двумя заданными сторонами (чтобы вы могли вычислить угол) или с углом и стороной (чтобы вы могли вычислить другую сторону).
Например:
Чтобы найти угол x , мы будем использовать SohCahToa, а именно «Toa». Это происходит потому, что: Это прямоугольный треугольник Даны две стороны: противолежащая и прилежащая
. Мы знаем противолежащую и прилежащую стороны этого угла, поэтому тангенс x = противолежащий / прилежащий = 5/7. Чтобы найти x само по себе, мы затем используем функцию обратного тангенса (tan-1) в нашем ответе, чтобы получить 35,5
Правило синусов
Правило синусов может быть организовано для вычисления углов или длин и выглядит следующим образом:
Где a, b и c — стороны, а A, B и C — противоположные им углы. Это может быть использовано для любого типа треугольника. Мы можем использовать это правило, когда нам даны две стороны и угол, противолежащий одной из сторон (для вычисления угла), или когда у нас есть одна сторона и любые два угла (для вычисления стороны).
Поэтому в вопросе ищите любой тип треугольника и эту информацию.
Например:
Чтобы найти угол x , нам нужно использовать правило синусов. Это потому, что:
Это треугольник (в данном случае не прямоугольный). Нам даны две стороны и угол, противоположный одной из этих сторон.
Следовательно, используя SinA/a = SinB/b , мы можем подставить данные значения, чтобы получить sinx/4 = sin74/9.
Затем мы можем изменить это, чтобы сделать sin x подлежащим: sinx = 4 x sin75 / 9. Если мы введем это в калькулятор, он даст 0,4293. Затем мы можем применить обратную функцию sin (sin-1), чтобы выделить x , что даст значение 25,4°.
Правило косинуса
Правило косинуса может использоваться для вычисления углов или длин и выглядит следующим образом:
Где a, b и c — стороны, а A, B и C — соответствующие им противоположные углы. Правило косинуса также может быть использовано в любом типе треугольника.
Мы можем использовать это правило, когда известны три стороны (для вычисления угла), или когда известны две стороны и угол между ними (для вычисления стороны. Поэтому в вопросе ищите любой тип треугольника и эту информацию.
Например:
Чтобы найти сторону x , нам нужно использовать правило косинуса. Это потому, что:
Это треугольник (в данном случае не прямоугольный треугольник). Нам даны две стороны и угол между этими сторонами.
Обратите внимание: если бы мы попытались использовать здесь правило синусов, это бы не сработало! У нас нет противоположных углов ни для одной из сторон, которые нам даны.
Используя правило косинуса, мы можем подставить данные значения, чтобы получить ответ. Следовательно, x2 = 32 + 72 — 2 x 3 x 7cos35. Затем мы должны извлечь из ответа квадратный корень, чтобы получить x, потому что прямо сейчас у нас есть значение x2. Это дает нам ответ 4,86 см.
Ответ Mansi C. • Maths Tutor
6989 Просмотров
См.
Аналогичные математические репетиторыСвязанные Maths GCSE. любого нечетного числа всегда также является нечетным числом.
Решите одновременное уравнение: 6x+3y=13, 14x-9y=9?
Нарисуйте график y = x2 + 3x + 2
Правила синусов и косинусов
Правила синусов и косинусов | Информационные бюллетениКрасивые и простые в использовании информационные бюллетени.
Авторизоваться
Зарегистрируйтесь сейчас (это бесплатно)
В этой главе вы узнаете:
- Тригонометрия прямоугольного треугольника
- Подшипники
- Тригонометрия с тупыми углами
- Правило синусов
- Использование правила синусов для нахождения неизвестного
- Правило косинуса
- Использование правила косинуса для нахождения неизвестного
- Площади треугольников и синусов
- 0 9 правило косинуса
- Смещение и радиальные съемки
С программой можно ознакомиться здесь (стр.
90)
Терминология
1. Прямоугольная тринометрия
- рисовать диаграммы для представления информации о прямоугольном треугольнике
- решать задачи с использованием тригонометрических соотношений в одном или нескольких прямоугольных треугольниках
- решать задачи, связанные с углами возвышения и депрессии, учитывая соответствующую диаграмму
Некоторые студенты:
- Запомните инициалы SOH CAH TOA, или
- Используйте пневмонику
❤² Тригонометрия: Прямоугольные треугольники… Как? (математика)
2.
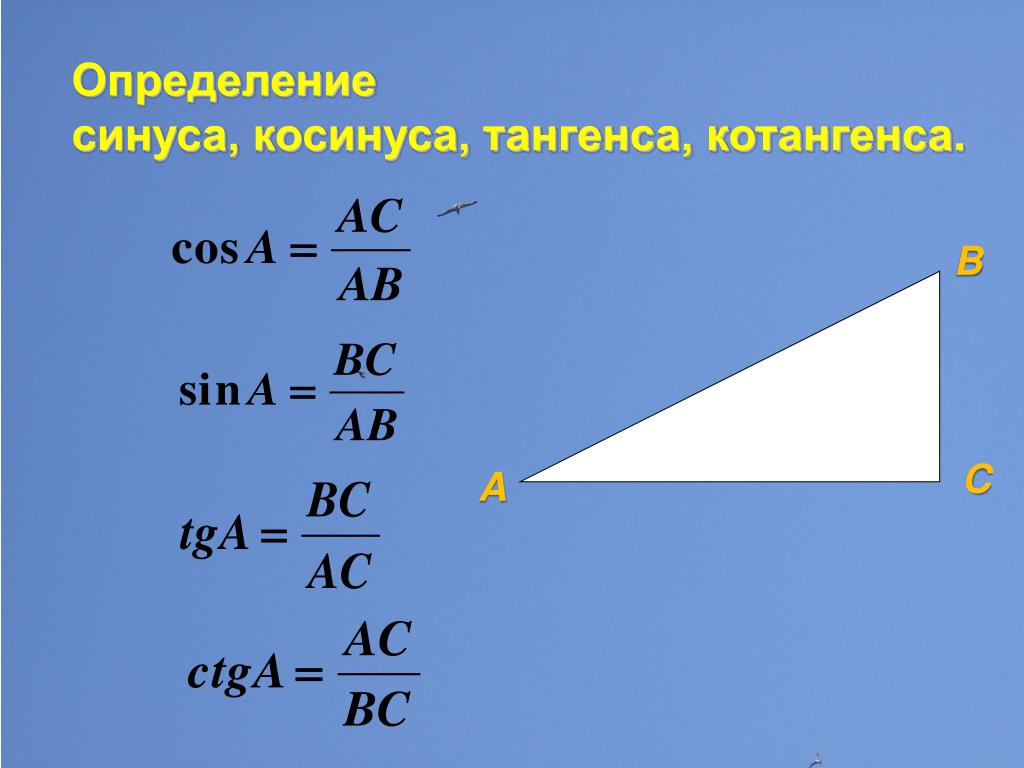Подшипники- используют азимуты по компасу (только восемь точек) и истинные азимуты (трехзначные азимуты) при решении задач, связанных с картами и схемами от заданной точки
Истинные азимуты или трехзначные азимуты измеряются по часовой стрелке от истинного севера 000 до 360
Компасные азимуты относятся к восьми точкам компаса: N, NE, E, SE, S, ЮЗ, З, СЗ.
3. Тригонометрия с тупыми углами
- установить соотношения синуса, косинуса и тангенса для тупых углов с помощью калькулятора
- определить знак вышеприведенных соотношений для тупых углов
Необходимо уметь устанавливать синус , коэффициенты косинуса и тангенса для тупых углов с помощью калькулятора
5.04 Правилом синусов
- определяют знак приведенных выше соотношений для тупых углов
- используйте правило синусов для нахождения длин сторон и углов треугольников
правило синусов представляет собой соотношение между двумя сторонами треугольников и двумя углами.
Учебник по математике: Тригонометрия Закон синусов / Правило синусов
6. Правило косинуса
- Используйте правило косинуса для нахождения длин сторон и углов треугольников
Правило равно 90 стороны треугольника и один из его углов
Закон косинусов | Триггерные тождества и примеры | Тригонометрия | Khan Academy
7.
- использование правила косинуса для нахождения длин сторон и углов треугольников
правило косинуса — нахождение неизвестного угла
8. Площадь треугольника треугольник
- вычислить площадь треугольника по формуле A = 1/2 absinC
Площадь треугольника можно рассчитать в тригонометрии по следующей формуле:
9. Применение правила синусов и косинусов прямоугольные и дана диаграмма
- выбрать и использовать соответствующие тригонометрические соотношения и формулы для решения задач на прямоугольные и непрямоугольные треугольники
10.
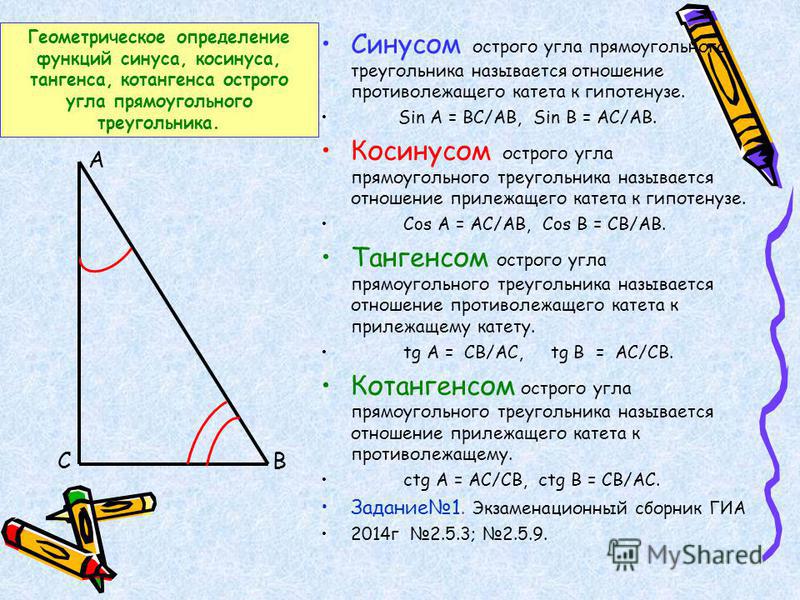Выносная и радиальная съемки- проведение радиальной (планшета и компаса) съемки
- решение задач, связанных с тригонометрией непрямоугольного треугольника, теоремой Пифагора и площадями при выносной и радиальной съемке
Геодезия включает в себя определение позиций предполагаемых строительных или инженерных работ. Он включает в себя измерение границ поля и расчет периметра площадей. Существует ряд методов съемки, в том числе:
- Основной обзор (предварительный курс)
- Правило Симпсона (глава третья)
- ТАБЛИЦА ТАБЛИЦА
- Радиальные обследования Compass Radial
- ТРИУНГОЛЯЦИЯ
Планета Radial Radial Surve поле и расстояния до каждого угла измеряются и отмечаются на большом листе бумаги, приколотом к столу. Слово «радиальный» означает исходящий из центральной точки, такой как радиус или луч.
Радиальная съемка с компасом
Аналогичен съемке на планшете, за исключением того, что каждый угол измеряется компасом, расположенным в центре поля
Полное имя:
Электронная почта:
На ваш почтовый ящик будет отправлено письмо с подтверждением.