Свойства определённого интеграла.
1. .
Это свойство часто бывает нужно при заменах переменной в определённом интеграле. Так, например, если замена , то большему будет соответствовать меньшее и наоборот. То есть, интеграл получится от большего числа до меньшего, и надо будет поменять пределы интегрирования обратно, и при этом сменится знак.
2. .
Кстати, свойство верно даже в том случае, если , тогда просто получится, что интегралы по и взаимоуничтожатся.
Следующие два свойства относятся к уже знакомому понятию «линейность»: можно вынести константу и интеграл от суммы функций разбить на сумму двух интегралов.
3. и 4. .
5. Если то .
Действительно, если в интегральной сумме все числа положительны (отрицательны) то и сумма положительна (отрицательна).
6. если то .
Свойство 6 следует из 5, ведь можно рассмотреть .
Свойство 7.
(Модуль интеграла меньше или равен, чем интеграл модуля).
Действительно, если сначала вычислить интеграл, то площади, расположенные выше и ниже оси, частично вычитаются, и число получается меньше. А если заранее взять модуль функции, то эти площади не вычитаются, а складываются:
Равенство здесь возможно лишь в том случае, когда в области интегрирования функция нигде не меняет знак.
Свойство 8. Если то .
Площадь прямоугольника, соответствующего минимальной высоте графика функции, это и есть , что меньше, чем площадь криволинейной трапеции, а наоборот, больше, ведь это площадь прямоугольника, соответствущего максимальной высоте графика.
А теперь представьте себе, что высота прямоугольника плавно растёт от до . Площадь при этом растёт от до значения . Но ведь значение интеграла между этими числами, следовательно, при какой-то высоте , площадь растущего прямоугольника сравняется со значением интеграла.
Свойство 9. Существует такое , где , что .
Свойство 10. Если f непрерывна, то существует точка , такая, что: .
Отличие от прошлого свойства в том, что это среднее значение не просто существует, а ещё достигается в какой-то точке, то есть обязательно найдётся точка графика на этой высоте. Для разрывной могло быть и не так: например, если ступенчатая функция на одной половине отрезка навна 1, а на второй половине 2, то средняя высота графика 1,5 но ведь график нигде не проходит через эту высоту.
Основной формулой в теме «определённый интеграл» является формула Ньютона-Лейбница . Она позволяет сразу же вычислить определённый интеграл, если известен неопределённый.
Но на самом деле, связь между этими двумя видами интегралов двусторонняя, т.е. и неопределённый интеграл может быть вычислен с помощью определённого. А именно, если рассматривать функцию то есть определённый интеграл с переменным верхним пределом.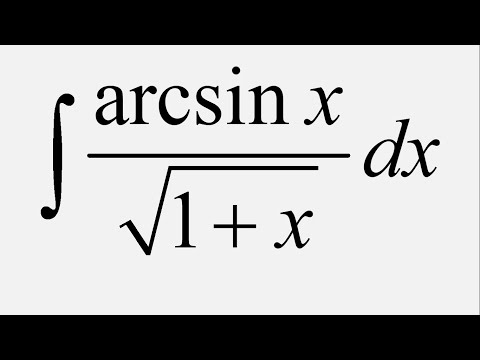
Теорема 1. Функция является первообразной от функции .
Доказательство. Нужно доказать, что .
Рассмотрим подробнее производную функции . По определению,
.
В данном случае, это , по свойству 2, интеграл по отрезку можно представить в виде суммы двух интегралов, а именно, по и . Чертёж:
При этом интеграл по там в разности есть ещё и со знаком «минус», то есть он в итоге сокращается.
= .
По свойству 10, интеграл по отрезку можно представить как некоторое среднее значение, т.е. в какой-то точке , умноженное на длину отрезка.
В общем случае длина была равна , а для данного отрезка это просто . Тогда: = = .
Однако точка , поэтому при , точка , которая находится где-то между и , стремится к левой границе отрезка: . Поэтому в итоге = .
Теорема 2.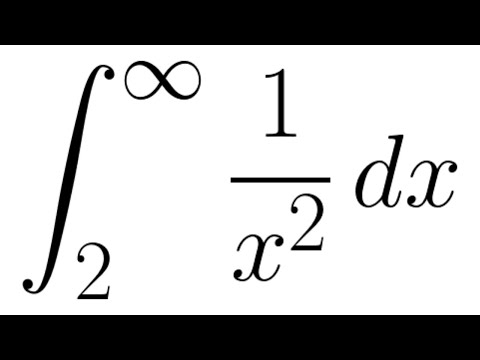
(Ньютона-Лейбница). Если — какая-либо первообразная от , то верна формула: .
Доказательство. Если есть произвольная первообразная, то она отличается на какую-то константу от той первообразной, которую мы рассматривали в теореме 1. То есть , что означает
. Запишем это равенство в точке , получится но ведь интеграл по одной точке это 0, там нулевая длина основания, а значит и нулевая площадь. Тогда . вот, кстати, мы заодно и установили, как связана константа с выбором начальной точки .
, а на сколько по высоте отличается от любая другая первообразная — это и есть значение .
Итак, теперь ясно, что .
А теперь рассмотрим это выражение в точке .
, то есть . Но ведь переменная вводилась исключительно для того, чтобы отличать внутри функции и на верхнем пределе интеграла. Теперь, когда перешли к фиксированным границам в интеграле, можно сделать тривиальную замену и запись примет вид , что и требовалось доказать.
Примеры вычисления по формуле Ньютона-Лейбница.
Пример. Найти интеграл .
Решение. = .
Пример. Найти интеграл .
Решение. = .
Пример. Найти интегралы и .
Решение. = .
= .
Пример. Найти интеграл .
Решение. = = = .
Пример. Найти интеграл .Решение. = = .
Вид формулы интегрирования по частям для определённого интеграла: .
Особенности замены переменной в определённом интеграле (пересчёт пределов интегрирования, и можно не возвращаться к старой переменной, то есть не делать обратную замену).
Пример. Вычислить интеграл
Решение. При замене мы адаптируем границы к новой переменной, то есть, если , то = .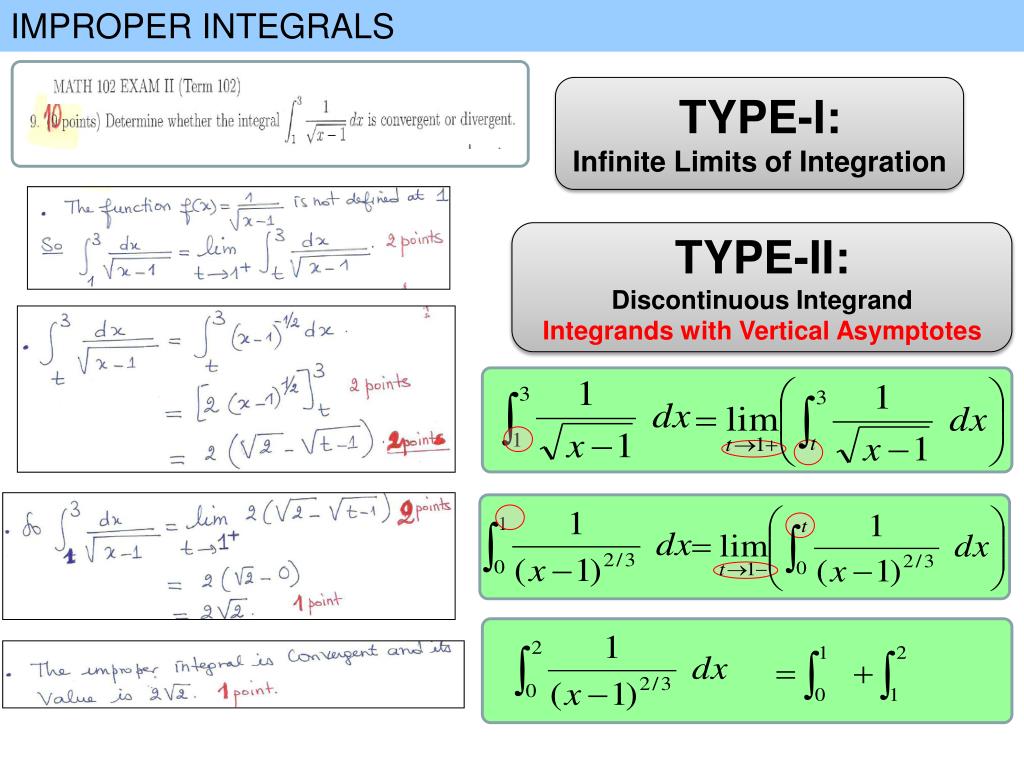
Тогда = = = 8.
Конечно, старые границы могут остаться прежними, например, при такой замене отобразится в . Но, как правило, при замене верхний и нижний предел интегрирования тоже изменяются.
Замена в определённом интеграле должна задаваться взаимно-однозначной функцией , то есть монотонной функцией. Иначе можно столкнуться с такими парадоксами: например, , интеграл от 0 до . Тогда по переменной получаем интеграл по промежутку , и он был бы в любом случае равен 0. Чтобы избежать такого противоречия, надо было бы разбить исходный интеграл по переменной на 2 части, по и .
Дата добавления: 2017-04-05; просмотров: 3156; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
линейность, монотонность, аддитивность, оценка модуля интеграла, формула среднего значения
Утверждения
3. Свойства криволинейного интеграла 1 рода
. Линейность. Если , а для функции существует криволинейный
интеграл по кривой
,
то для функции также существует криволинейный интеграл
по кривой
,
причем .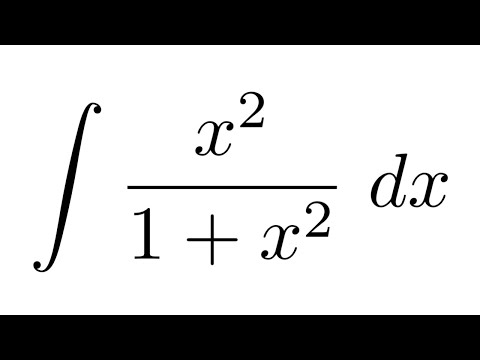
. Линейность. Если для функций и существуют криволинейные интегралы по кривой и если и — любые постоянные, то для функции также существует криволинейный интеграл по кривой , причем .
. Аддитивность. Если дуга составлена из двух дуг и , не имеющих общих внутренних точек, и если для функции существует криволинейный интеграл по кривой , то для этой функции существует криволинейный интеграл по каждой из дуг и , причем .
. Монотонность. Если функция — неотрицательная интегрируемая функция, то всегда .
. Оценка модуля интеграла. Если существует криволинейный интеграл по кривой от функции , то существует и криволинейный интеграл по кривой АB от функции , причем .
. Теорема о среднем. Если функция непрерывна вдоль кривой , то на этой кривой найдется точка , такая что .
. Независимость криволинейного интеграла
1-го рода от направления кривой. Выбор
направления на дуге
не влияет на величину интеграла от
скалярной функции
по этой дуге, то есть
.
11. Интегральная сумма по координатам, определение криволинейного интеграла второго рода
2. Рассмотрим на плоскости хОу некоторую спрямляемую кривую L, не имеющую точек самопересечения и участков самоналегания.
Предположим, что эта кривая определяется параметрическими уравнениями
И сначала будем считать ее незамкнутой и ограниченной точками и .
Пусть на L =AB определена f (x,y), являющаяся непрерывной. Разобьем сегмент при помощи точек на частичных сегментов . При этом кривая L распадется на частичных дуг , где точки имеют координаты . Выберем на каждой частичной дуге произвольную точку , координаты которой отвечают некоторому принадлежащему сегменту значению параметра , так что . Обозначим символом длину -ой частичной дуги .
Составим интегральную
сумму , которую назовем интегральной суммой
по координатам.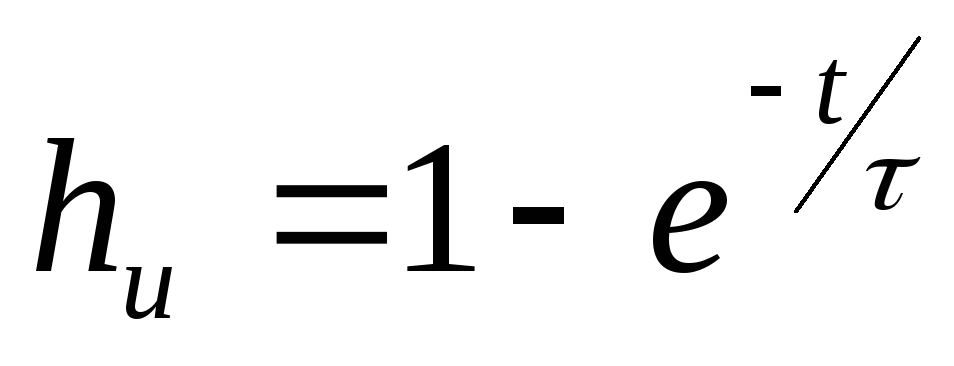
4. Если существует предел интегральной суммы (соответственно ) при , то этот предел называется криволинейным интегралом второго рода от функции ( ) по кривой и обозначается символом: ( ).
5. Сумму принято называть общим криволинейным интегралом второго рода и обозначать символом: .
Утверждения
2. Условия существования криволинейного интеграла 2 рода
Пусть — гладкая кривая, заданная уравнениями , и пусть — вектор-функция, заданная на этой кривой. Тогда
и интеграл слева существует, если существует определенный интеграл, стоящий справа; при этом — значение параметра , отвечающее точке , а — значение, отвечающее точке .
12. Свойства криволинейного интеграла второго рода
Утверждения
5. Свойства криволинейного интеграла 2 рода
. Линейность. Если
— постоянный множитель, то
можно выносить за знак интеграла, причем .
. Аддитивность. Если дуга составлена из двух дуг и , не имеющих общих внутренних точек, и если для функций и существуют криволинейные интегралы по кривой , то для этих функций существуют криволинейные интегралы по каждой из дуг и , причем .
. Зависимость криволинейного интеграла 2-го рода от направления кривой . Криволинейный интеграл 2-го рода зависит от ориентации кривой , по которой этот интеграл берется, а именно, при изменении ориентации этой кривой интеграл меняет знак:
Новости Modulus Data
НОВОСТИ
Данные Modulus представлены в серии PBS In Depth, организованной Лоуренсом Фишбёрном
В этом видео о тенденциях в области технологий Modulus Data назвал «идейным лидером, влияющим на бизнес».
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Отдел кадров Fedcap Group экономит 30 минут на каждом новом приеме на работу с помощью Oracle HCM и ADP Workforce Now Integration
Глобальная социальная компания автоматизирует свой основной рабочий процесс HR для расчета заработной платы с помощью автоматической интеграции данных.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Команда по подбору персонала M3 экономит драгоценное время с теплицей и интеграцией прогнозных индексов
Одна из самых популярных компаний-разработчиков программного обеспечения для бухгалтерского учета в индустрии гостеприимства в США освобождает свою команду по подбору персонала от задач двойного ввода данных.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Решения B-Stock экономят время и деньги за счет интеграции парниковых и ADP-систем
Быстрорастущая торговая площадка для продажи товаров B2B освобождает отдел кадров от необходимости двойного ввода данных вручную.
НОВОСТИ
Workstream объединяется с Modulus Data для предоставления клиентам коннекторов для интеграции данных
Клиенты Workstream теперь могут подключать Workstream к любому приложению HR для оптимизации рабочих процессов HR.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Отдел кадров компании National Automotive Parts автоматизирует оценку кандидатов с помощью UKG для интеграции прогнозных индексов
Успешный дистрибьютор автозапчастей с сотнями офисов по всей Америке и более чем 3000 сотрудников оптимизирует рабочий процесс управления персоналом за счет интеграции данных.
INSIDE MODULUS DATA
Интервью со Шри Сешей Бхаргави Сетталури, старшим специалистом по технической интеграции, профессиональные услуги
Узнайте об опыте старшего специалиста по технической интеграции в Modulus Data.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Ресторанная группа Wen JAI кардинально меняет эффективность рабочего процесса с помощью интеграции ADP в Aloha POS
Успешный франчайзи ресторана Wendy’s с более чем 200 заведениями автоматизирует свой HRIS в систему точек продаж с помощью автоматической интеграции данных.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Команда отдела кадров One Concern экономит 20 часов в месяц благодаря интеграции BambooHR и Paylocity
Передовая компания, занимающаяся технологиями стихийных бедствий и климатических технологий, освобождает свои отделы кадров и расчетов заработной платы от двойного ввода данных.
INSIDE MODULUS DATA
Интервью с Салливаном Идролле, разработчиком программного обеспечения для исследований и разработок
Узнайте об опыте разработчика программного обеспечения для исследований и разработок в Modulus Data.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
HR-команда Logicalis оптимизирует рабочий процесс с помощью интеграции Workday с ADP
Workday с интеграцией ADP Пример из практики: глобальная компания, занимающаяся ИТ-решениями, автоматизирует свой основной рабочий процесс HR для расчета заработной платы с помощью автоматической интеграции данных.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Финансовая группа Roostify экономит 32 часа в месяц благодаря интеграции ADP в NetSuite
Пример интеграции ADP в Oracle NetSuite. Ведущий поставщик ипотечных технологий освобождает свои финансовые и кадровые отделы от двойного ввода данных.
NEWS
Modulus Data побеждает в номинации «Лучший сервис и поддержка» на саммите партнеров ADP Marketplace 2022 года
Специалисты по интеграции данных HR Modulus Data побеждает за ориентированный на клиента подход к интеграции данных.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Standard Bank успешно передает все интеграции HR-приложений в Modulus Data
Standard Bank модернизирует предоставление данных и освобождает своих специалистов по персоналу от двойного ввода данных.
НОВОСТИ
Modulus Data названа лучшим сотрудником UKG в 2021 году
UKG (Ultimate Kronos Group), ведущий мировой поставщик решений для HCM, расчета заработной платы, предоставления услуг в области управления персоналом и управления персоналом, назвал Modulus Data сотрудником года UKG 2021 года среди технологических партнеров по управлению персоналом.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Global Manufacturing Company оптимизирует процессы управления персоналом с помощью интеграции Workday в ADP
Пример интеграции Workday в ADP: глобальный производитель с более чем 55 000 сотрудников освобождает своих специалистов по персоналу от двойного ввода данных.
NEWS
Modulus Data назван победителем в категории iPaaS для G2!
На основании отзывов клиентов компания Modulus Data была выбрана G2 как обладающая «Лучшей поддержкой клиентов» летом 2021 года.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Пример использования Flexspring iPaaS: Быстрорастущая компания-разработчик программного обеспечения осуществляет внутреннюю интеграцию данных, используя Flexspring
ClearCompany выбирает Flexspring iPaaS как более быстрый способ экономически эффективной интеграции данных.
НОВОСТИ
Обзор лучших поставщиков решений NetSuite на 2021 год по версии CIO Review: главная история Modulus Data
CIO Review составляет ежегодный список 10 лучших поставщиков решений NetSuite на 2021 год. в качестве прикрытия.
NEWS
Интеграция Quinyx с ADP теперь доступна
Интеграция Quinyx с ADP теперь доступна с использованием коннекторов данных от Modulus Data. Делитесь данными о сотрудниках, табелями учета рабочего времени и данными об отпусках практически в режиме реального времени.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Расчет заработной платы ADP в журнальные записи NetSuite по модулю Данные для быстрорастущей компании среднего размера
Хотите интегрировать записи журнала заработной платы ADP в NetSuite General Ledger без использования рук? Наслаждайтесь этим примером интеграции данных для быстрорастущей компании.
ПРИМЕР ИНТЕГРАЦИИ ДАННЫХ
Интеграция Greenhouse в UKG с помощью Modulus Data для крупной облачной коммуникационной компании
Рассматриваете возможность интеграции данных Greenhouse в UKG? Наслаждайтесь этим примером интеграции данных для компании масштаба предприятия, включающим новых сотрудников и базовые данные.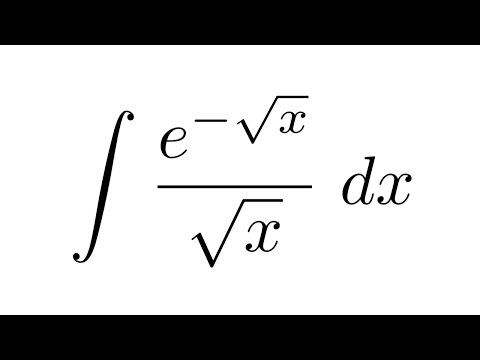
NEWS
Modulus Data названа платиновым партнером ADP Marketplace
Modulus Data с гордостью сообщает, что мы стали партнером ADP Marketplace Platinum в 2020 году.
СОБЫТИЯ
Как Modulus Data помогает HR-консультантам увеличить прибыль
Modulus Data делает все возможное, чтобы помочь сообществу HR-консультантов адаптироваться к быстро меняющейся среде HR.
СОБЫТИЯ
Посещение Modulus Data на конференции ADP Meeting of the Minds: 7 октября 2020 г.
Партнер по интеграции данных HR Modulus Data продемонстрирует разъемы ADP на виртуальной конференции ADP Meeting of the Minds.
НОВОСТИ
Новые готовые соединители Беспрепятственный обмен данными между Workday или Oracle HCM и ServiceNow
Интеграция ServiceNow стала быстрой и простой благодаря готовым соединителям от Modulus Data.
НОВОСТИ
Интеграция HR-данных: сейчас больше, чем когда-либо
Поскольку HR-специалисты преодолевают эти трудные времена, последнее, на что у вас есть время, — это двойной ввод данных вручную между приложениями HR.