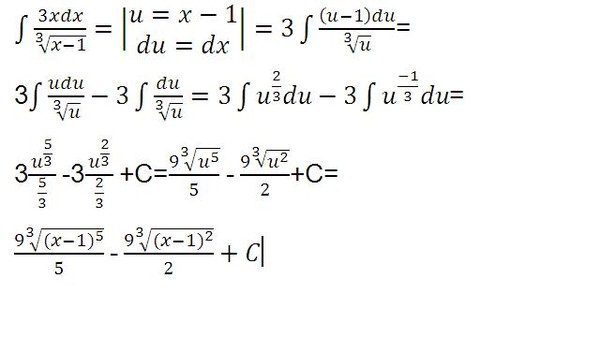Интеграл от x в степени x: Интеграл от (x в степени x)

Алгебра Неопределённый интеграл

Материалы к уроку

Конспект урока

Неопределённый интеграл

Вспомним правила вычисления первообразной функции. ПРАВИЛО 1: Первообразная суммы равна сумме первообразных. ПРАВИЛО 2: Постоянный множитель выносится за знак первообразной. ПРАВИЛО 3: Если игрек, равное эф большое от икс, — первообразная для функции эф малое от икс, то первообразной для функции игрек равно эф малое от ка икс плюс эм является функция игрек, равная один, делённое на ка, умноженное на эф большое от ка икс плюс эм.
Докажем теорему. Если y=F(x) (игрек равно эф большое от икс) — первообразная для функции y=F(x) (игрек равно эф малое от икс) на промежутке Х (икс большое), то у функции y=F(x)игрек равно эф малое от икс) бесконечно много первообразных и все они имеют вид y=F(x)+C (игрек равен эф большое от икс плюс це).	Теорема: Если y=F(x) – первообразная для функции y=f(x) на промежутке Х, то у функции  бесконечно много первообразных и все они имеют вид y=F(x)+C
1.Пусть y=F(x) (игрек равен эф от икс большое) — первообразная для функции y=f(x) (игрек равен эф малое от икс) на промежутке Х (икс большое). Значит, для всех х принадлежащих Х (икс большое) выполнено равенство: F(x)=f(x)(производная от эф большое равна эф малая). Найдём производную любой функции вида y=F(x) +C (игрек равен эф большое от икс плюс це): (F(x)+C)=F(x)+C=f(x)+0=f(x)   Известно, что производная суммы равна сумме производных, поэтому мы можем отдельно найти производную от эф большое и це. Производная от первообразной эф большое – есть сама функция эф малое, производная от постоянной це равна нулю, тогда мы получим, что производная любой функции вида y=F(x)+C есть сама функция эф малая. Значит, функция игрек равен эф большое от икс плюс це является первообразной для функции игрек равен эф малое от икс. Таким образом, мы доказали, что если у функции игрек равен эф малое от икс существует первообразная игрек равен эф от икс большое, то у функции игрек равен эф малое от икс бесконечное множество первообразных вида игрек равен эф большое от икс плюс це.   2.Теперь докажем, что таким видом функции исчерпывается всё множество первообразных. Пусть игрек равен эф один от икс и игрек равен эф два от икс — две первообразные для функции игрек равен эф малое от икс на промежутке Х (икс большое). Значит, для всех икс малое из промежутка икс большое выполнены соотношения: производные функций эф большое от икс и эф большое один от икс равны самой функции эф малое. Рассмотрим функцию игрек равен эф большое один от икс минус эф большое от икс и найдём её производную: (F1(x)-F(x))=F1(x)-F(x)=f(x)-f(x)=0   Применяя правило нахождения суммы производных, разбиваем функцию на два слагаемых и находим производную от эф один большое от икс и от эф большое от икс. Так как производные функций эф большое от икс и эф большое один от икс равны самой функции эф малое, то разность этих производных равна нулю. Известно, что если производная функции на промежутке Х (икс большое) тождественно равна нулю, то функция постоянна на данном промежутке Х (икс большое). Мы получили, что разность функций эф большое один от икс и эф большое от икс постоянна, то есть эф большое один от икс равно эф большое от икс плюс це. Теорема доказана.	1. Пусть -первообразная для функции y=f(x) на промежутке Х. Значит, для всех х принадлежащих Х выполнено равенство: f(x)+F(x). Найдём производную любой функции вида y=F(x)+C: (F(x)+C)=F(x)+C=f(x)+0=f(x)                 Итак, (F(x)+C)=f(x)⇒ y=F(x)+C -первообразная для y=f(x).   Доказали, что если у функции y=f(x).  есть первообразная y=F(x). , то у функции y=f(x). бесконечно много первообразных вида y=F(x)+C                 2. Пусть y=F1(x) и y=F2(x) y=F1(x) и y=F2(x) -две первообразные для функции y=f(x) на  промежутке Х.         Тогда для любого X верно: F(x)=f(x), F1(x)=f(x)           Рассмотрим y=F1(x)-F(x) и найдём производную: (F1(x)-F(x))=F1(x)-F(x)=f(x)-f(x)=0                                       Если производная функции на промежутке Х тождественно равна нулю, то функция постоянна на данном промежутке Х—F1(x)-F(x)=C—F1(x)=F(x)+C

 

Составим таблицу неопределённых интегралов, для этого воспользуемся табличными значениями первообразной. С(це) — константа, т.е. постоянная. 1.Неопределённый интеграл от дэ икс равен икс плюс це. 2. Неопределённый интеграл от икс в степени эн дэ икс равен икс в степени эн плюс один, делённое на эн плюс один, и плюс це, где эн принадлежит множеству натуральных чисел. 3. Неопределённый интеграл от дэ икс, делённое на икс в квадрате, равен минус один, делённое на икс плюс це. 4. Неопределённый интеграл от дэ икс, делённое на корень квадратный из икс, равен два корень из икс плюс це. 5. Неопределённый интеграл от синус икс дэ икс равен минус косинус икс плюс це. 6. Неопределённый интеграл от косинус икс дэ икс равен синус икс плюс це. 7. Неопределённый интеграл от  дэ икс, делённое на синус в квадрате икс, равен минус котангенс  икс плюс це. 8. Неопределённый интеграл от  дэ икс, делённое на косинус в квадрате икс, равен тангенс  икс плюс це.

Вычислим неопределённый интеграл функции, применяя полученные знания. ЗАДАНИЕ 1: Найти неопределённый интеграл от три, делённое на корень квадратный из икс, минус пять, делённое на икс в квадрате, дэ икс. Решение: Разобьем интеграл разности на разность двух интегралов, затем вынесем постоянные множители три и пять за знак интеграла. Мы получили табличные интегралы: Неопределённый интеграл от дэ икс делённое на корень квадратный из икс равен два корень из икс плюс це. Неопределённый интеграл от дэ икс делённое на икс в квадрате равен минус один делённое на икс плюс це. Перемножая три и два корня из икс, минус пять и минус один делённое на икс, в результате получим: шесть корней из икс плюс пять делённое на икс плюс це.

Задание 2: Найти неопределённый интеграл от дэ икс, деленное на косинус в квадрате три икс минус пи на три.   Решение: Воспользуемся третьим правилом интегрирования Правило 3:   Неопределённый интеграл от сложной функции равен первообразной этой функции, делённой на постоянный множитель при икс и плюс це., а так же табличным интегралом: неопределённый интеграл от  дэ икс, делённое на косинус в квадрате икс, равен тангенс икс плюс це. Получим: Одна третья тангенс три икс минус пи на три плюс цэ.

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

3.

1.7. Возведение в степень

При возведении в целую положительную степень комплексного числа в показательной или тригонометрической форме его модуль возводится в эту степень, а аргумент умножается на данную степень.

Пусть тогда

или

Запишем результат возведения в целую степень в тригонометрической форме

Эту формулу называют формулой Муавра.

Пример 5. Вычислить

Решение. Перейдем к показательной форме. Найдем модуль и аргумент комплексного числа .

3.1.8. Извлечение корня

Извлечение корня n-ой степени из комплексного числа можно рассматривать как операцию возведения комплексного числа в дробную степень т.е. .

Если комплексное число в показательной форме, то

.

Придавая k – значения от 0 до n – 1 получим n – различных комплексных чисел, у которых модули одинаковые, а аргументы разные:

При k = 0

При k = 1

При k = 2

…………..

При k = n – 1

При k = n

Последнее значение аргумента числа совпадает с первым при k = 0.

Итак, корень n-ой степени из комплексного числа имеем n – различных значений.

Пример 6. Найти все значения корня .

Действительное число –1 можно рассматривать как комплексное, у которого действительная часть: α = –1, а мнимая β = 0, т.е.:

Запишем это число в тригонометрической форме. Для этого найдем его модуль и аргумент.

Т ак как tgφ = 0 при φ = 0 и φ = π, построим число «–1» на комплексной плоскости (Рис.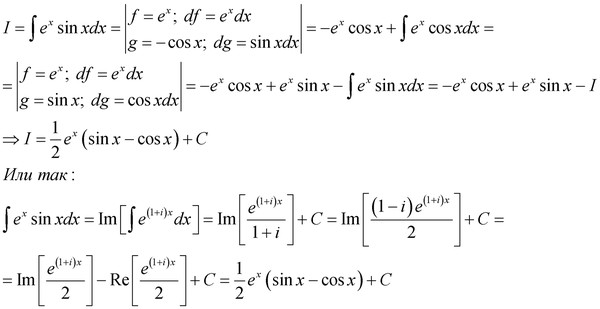 3.1.4), его аргумент равен

arg(–1) = φ = π

следовательно, тригонометрическая форма числа «–1» следующая:

.

Согласно формуле вычисления корня имеем:

.

К орень четвертой степени имеет четыре значения, которые можно найти, если положить к равным 0, 1, 2, 3.

При k = 0

При k = 1

При k = 2

При k = 3

Все четыре значения корня имеют одинаковы модули и отличаются друг от друга только значением аргумента (Рис.3.1.5).

Лекция 3.2. Первобразная и неопределенный интеграл. Геометрический смысл, свойства. Таблица простейших интегралов. Интегрирование подведением под знак дифференциала

3.2.1.Определение, геометрическая иллюстрация

Основной задачей дифференциального исчисления является задача нахождения дифференциала или производной данной функции, т. е. задача нахождения скорости изменения значений какой-нибудь функции, при изменении аргумента. На практике часто бывает важно решить обратную задачу: зная скорость изменения значений функции (по отношению к аргументу), найти эту функцию.

Так в механике по заданной скорости определяют закон движения материальной точки, а также закон изменения скорости (со временем) по заданному ее ускорению. Эти задачи приводят к проблеме отыскания функции по ее производной f(x). Неизвестная функция, обозначим ее F(x), получила название первообразной по отношению к своей производной.

Определение. Функцию F(x) называют первообразной для функции f(x) на числовом промежутке Х, если в любой его точке х она дифференцируема и имеет производную F‘(x), равную f(x), т.е.

F‘(x) = f(x).

Числовым промежутком мы будем называть множество точек числовой оси заключенных между двумя точками, и определяемых неравенствами:

α < x < b, α ≤ x ≤ b, α ≤ x < b, α < x ≤ b, – ∞ < x < ∞.

Пример 1. Функция является первообразной для функции на интервале (–1;1), так как в любой его точке х выполняется равенство:

Пример 2. Функция – есть первообразная для функции f(x)= cosx на интервале (–∞; ∞), ибо в каждой его точке х справедливо равенство:

(sinx)’ = cosx.

Если F(x) является первообразной для функции f(x) на числовом промежутке Х, то и функция F(x) + С, где С – любая постоянная, также является первообразной для f(x) на Х.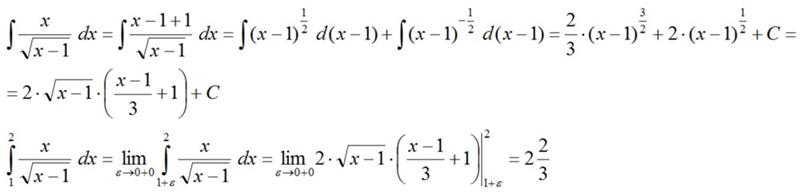 Действительно:

(F(x) + C)’ = F‘(x) + (C)’ = F‘(x) = f(x).

Следовательно, данная функция имеет бесконечное множество первообразных. Связь между различными первообразными для одной и той же функции f(x) выражена следующей основной теоремой.

Теорема 1. Две различные первообразные одной и той же функции, определенной в некотором промежутке Х, отличаются друг от друга в этом промежутке на постоянное слагаемое.

Пример 3. Функция f(x) = sinx · cosx имеет первообразные:

(проверьте).

Покажем, что разность между ними равна числу. Преобразуем функцию F₃(x):

т.е. или

Аналогично:

Таким образом, если F(x) – есть одна из первообразных для функции f(x) на числовом промежутке Х, то выражение F(x) + C, где С – произвольная постоянная, исчерпывает множество всех первообразных для f(x). (Предполагается, что рассматриваемые функции непрерывны на числовом промежутке Х).

Определение. Отыскание первообразных называют неопределенным интегрированием, а выражение, охватывающее множество всех первообразных от данной функции f(x) – неопределенным интегралом от f(x) и обозначают:

где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, х – переменная интегрирования.

Согласно данного определения, неопределенный интеграл записывают так:

, (3.2.1)

где F(x) – одна из первообразных (F‘(x) = f(x)),

(F(x) + C) – множество всех первообразных.

График каждой из первообразных для функции y=f(x), называют интегральной кривой.

Если Y=F₁(x) и Y=F₂(x) – первообразные одной и той же функции f(x), то касательные к их графикам в точках с общей абсциссой х параллельны между собой:

(рисунок 3.2.1).

Р асстояние между этими кривыми, считая вдоль оси Oу, остается постоянным:

т.е. кривые в некотором смысле «параллельны» друг другу. Поэтому, неопределенный интеграл геометрически представляется множеством всех интегральных кривых, полученных при параллельном движении одной из них по направлению оси Oу.

(9𝑥) д𝑥.

Стенограмма видео

Определить неопределенный интеграл двойки в степени девятки 𝑥 относительно 𝑥.

В этом вопросе нас просят вычислить интеграл экспоненциальной функции. И мы можем отметить, что это выглядит очень аналогично одному из наших интегральных результатов. Для любой положительной константы 𝑎 не равен единице, интеграл от 𝑎 в степени 𝑥 по 𝑥 равен 𝑎 в степени 𝑥 разделить на натуральный логарифм 𝑎 плюс константа интеграция 𝐶. Однако в этом случае наш показатель не просто равно 𝑥; у нас девять 𝑥. Таким образом, мы не можем просто напрямую применить этот интегральный результат. И есть два способа, которыми мы можем попробовать и исправить это. Мы могли бы попробовать использовать 𝑢-замена. 𝑢 девять 𝑥. Это позволило бы нам переписать наш интеграл в этой форме. Однако на самом деле есть более простой метод.

Мы можем просто применить наши законы экспоненты. Два в девятой степени все подняты в степени 𝑥 будет равно двум в степени девяти, умноженной на 𝑥. Итак, мы можем переписать наш интеграл в виде интеграл от двух в девятой степени, возведенный в степень 𝑥 по отношению к 𝑥. Тогда наше значение 𝑎 равно двум девятая власть. Теперь мы можем оценить два в девятой степени как 512. Однако мы просто собираемся подставить 𝑎 равно двум в степени девять в наш интегральный результат. Это дает нам от двух до девятого все степени возводятся в степень 𝑥 все делятся на натуральный логарифм от двух до девятая степень плюс постоянная интегрирования 𝐶. И это может помочь нам понять, почему полезно оставить это как два в девятой степени, а не оценивать.

Мы можем упростить числитель на используя наши законы показателей, и мы можем упростить наш знаменатель, используя степень правило для логарифмов. Во-первых, в числителе двойка поставлена в степени девять все возведенное в степень 𝑥 будет два в степени девять раз 𝑥.