Вычисление поверхностных интегралов: теория и примеры
Поверхностный интеграл — обобщение понятия криволинейного интеграла на случаи, когда интегрирование происходит не по отрезку кривой, а по ограниченной поверхности. Как и криволинейные интегралы, поверхностные интегралы бывают первого рода и второго рода.
Поверхностный интеграл первого рода записывается в виде
,
где f(M) = f(x,y,z) – функция трёх переменных, а поверхность σ — область интегрирования этой функции. Если f(x,y,z) равна единице, то поверхностный интеграл равен площади поверхности.
Представьте себе довольно большой подсолнух с очень-очень маленькими семечками. Тогда по сумме поверхностей очень-очень маленьких семечек, расположенных на поверхности подсолнуха, можно вычислить поверхность подсолнуха — таким может быть упрощённое толкование поверхностного интеграла. Почему так?
Давайте перейдём к более формальному определению поверхностного интеграла. Поверхность σ разбита на n частей с площадями Δσ1, Δσ2, …, Δσn. Если выбрать на каждой частичной поверхности (семечке) произвольную точку Mi с координатами (ζi, ηi, ςi,), то можно составить сумму
.
Эта сумма называется интегральной суммой для функции f(M) по поверхности σ. Теперь будем максимально увеличивать число таких маленьких частей, а наибольший диаметр Δσi — наоборот, уменьшать. Если интегральная сумма при стремлении наибольшего из диаметров частей к нулю (то есть, как мы уже отмечали, все части очень маленькие) имеет предел, то этот предел и называется поверхностным интегралом первого рода от функции f(M) по поверхности σ.
Вычисление поверхностного интеграла первого рода производится сводением к двойному интегралу.
Пусть поверхность σ задана уравнением z = z(x, y), её проекцией на плоскость xOy является область Dxy, при этом функция z = z(x, y) и её частные производные и непрерывны в области Dxy.
Тогда
Это и есть формула, выражающая поверхностный интеграл первого рода через двойной интеграл по проекции поверхности σ на плоскость xOy.
Пример 1. Вычислить поверхностный интеграл первого рода
Решение. Чертёж:
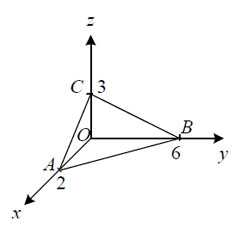
Из уравнения плоскости получаем выражение «зет»: .
Тогда частные производные: , и
.
Поверхность σ является изображённым на чертеже треугольником ABC, а его проекцией на плоскость xOy — треугольником AOB, который ограничен прямыми x = 0, y = 0 и 3x + y = 6. От поверхностного интеграла перейдём к двойному интегралу и решим его:
 .
.
Прежде чем перейти к определению поверхностного интеграла второго рода, требуется познакомиться с понятиями стороны поверхностей и ориентированных поверхностей.
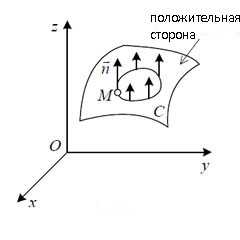
Пусть в пространстве дана гладкая поверхность σ. На этой поверхности выберем произвольную точку M и проведём через неё вектор нормали к поверхности. Через точку M проведём также на поверхности σ произвольный контур, не имеющий общих точек с границей поверхности σ. Точку M вместе с вектором нормали будем перемещать по контуру так, чтобы вектор нормали постоянно был перпендикулярен поверхности σ. По возвращении точки M в начальное положение возможны два случая: направление вектора нормали сохранится или же поменяется на противоположное.
Если направление вектора нормали не поменяется, то поверхность σ называется двусторонней. Если же при обходе контура направление вектора нормали поменяется на противоположное, то поверхность называется односторонней. Двусторонние поверхности называются ориентированными поверхностями, односторонние — неориентированными поверхностями.
Пример односторонней поверхности — лист Мёбиуса (на рисунке выше), который можно сделать из полоски бумаги, одна сторона которой повёрнута на 180 градусов, и затем концы склеены. И вот что здесь важно: для односторонней поверхности понятие поверхностного интеграла второго рода не вводится.
Так что будем рассматривать только двусторонние поверхности. Примеры двусторонних поверхностей — плоскости, сфера, эллипсоил, параболоид.
Положительную сторону двустороней поверхности определяет направление вектора нормали. Противоположная сторона поверхности называется отрицательной. Положительной стороной поверхности называется её верхняя сторона. Если единичные векторы нормали составляют острые углы с осью Oz, то выбрана верхняя сторона поверхности z
= z(x, y), если углы тупые, то нижняя сторона поверхности.Как и в случае поверхностного интеграла первого рода, поверхность можно разбить на n частей. При формулировке понятия поверхностного интеграла первого рода в интегральной сумме присутствовали площади каждой из частей, на которые умножаются значения функции f(Mi). В случае поверхностного интеграла второго рода берутся площади не самих частей, а площади их проекций на координатные плоскости. А функцию трёх переменных для отличия от интеграла первого рода обозначим R(x,y,z). Тогда интегральная сумма запишется так:
,
где Δsi — площади упомянутых проекций частей стороны поверхности на координатную ось (пока будем считать, что на ось xOy).
При таких соглашениях и обозначениях определение поверхностного интеграла второго рода аналогично определению интеграла первого рода. А именно: поверхностным интегралом второго рода называется предел данной интегральной суммы при стремлении к нулю наибольшего из диаметров частей рассматриваемой поверхности.
Записывается он так:
.
В данном случае функция R(x,y,z) интегрируема по переменным x и y, так как части поверхности проецировались на плоскость xOy.
Аналогично можно записать и два других поверхностных интеграла второго рода:
(функция P(x,y,z) интегрируема по переменным y и z, так как части поверхности проецируются на плоскость yOz),
(функция Q( x,y,z) интегрируема по переменным z и x, так как части поверхности проецируются на плоскость zOx).
Сумма этих интегралов
называется общим поверхностным интегралом второго рода и обозначается
Поверхностный интеграл второго рода вычисляется путём разложения общего поверхностного интеграла второго рода на сумму поверхностных интегралов (см. окончание предыдущего параграфа) и сведением каждого из них к двойному интегралу.
Рассмотрим подробно вычисление интеграла
.
Пусть поверхность σ задана уравнением z = z(x, y). Положительную сторону поверхности обозначим , отрицателную , а проекцию на плоскость xOy — Dxy.
.
Если выбрана отрицательная сторона поверхности, то знак интеграла меняется:
.
Аналогично вычисляются два других отдельных интеграла — слагаемых общего:
,
.
Пример 2. Вычислить поверхностный интеграл второго рода
,
где σ — верхняя сторона части плоскости , отсечённая плоскостями y = 0 и y = 4 и находящаяся в первом октанте.
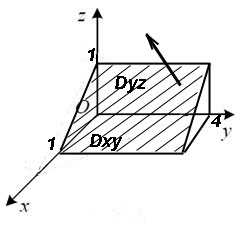
Решение. Чертёж — на рисунке сверху. По определению получаем сумму трёх двойных интегралов:
Второй интеграл равен нулю, так как плоскость σ параллельна оси Oy. Поэтому найдём первый и третий интегралы:
Остаётся лишь сложить все отдельные интегралы и получить общий поверхностный интеграл второго рода:
.
Если требуется вычислить поверхностный интеграл второго рода по замкнутой поверхности, можно перейти к тройному интегралу, используя формулу Остроградского. Тогда, если функции P(x,y,z), Q(x,y,z) и R(x,y,z) и их частные производные , , — непрерывные функции в области W, которую ограничивает замкнутая поверхность σ, то при интегрировании по внешней стороне поверхности в силе равенство
Пример 4. Вычислить поверхностный интеграл первого рода
,
где σ — боковая поверхность конуса при .
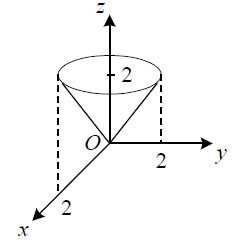
Решение. Так как частные производные , , то
Сводим данный поверхностный интеграл к двойному:
.
Проекцией поверхности на плоскость xOy является круг с центром в начале координат и радиусом R = 2, поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:
Получаем следующий интеграл, который окончательно и решаем:

Пример 5. Вычислить поверхностный интеграл второго рода
,
где σ — верхняя часть треугольника, образованного пересечением плоскости с координатными плоскостями.
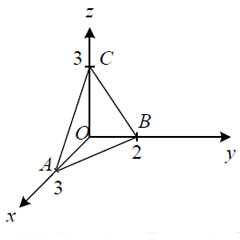
Решение. Данный поверхностный интеграл разделим на сумму двух интегралов
, где
,
.
Чтобы вычислить интеграл I1, построим проекцию поверхности σ на плоскость yOz. Проекцией является треугольник OCB, который на плоскости yOz ограничивают прямые или , y = 0 и z = 0. Из уравнения плоскости выводится . Поэтому можем вычислить интеграл I1:

Чтобы вычислить интеграл I2, построим проекцию поверхности σ на плоскость zOx. Проекцией является треугольник AOC, который ограничивают прямые или , x = 0 и z = 0. Вычисляем:

Складываем два полученных интеграла и окончательно получаем данный поверхностный интеграл:
.
Пример 6. Вычислить поверхностный интеграл второго рода
,
где σ — внешняя поверхность пирамиды, образованной плоскостью и координатными плоскостями.
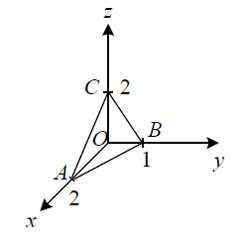
Решение. Данный поверхностный интеграл вычислим двумя способами
1) интегрируя по каждой грани пирамиды;
2) используя формулу Остроградского.
1) Вычисление интегрированием по каждой грани пирамиды.
а) Вычислим интеграл по треугольнику ABC. Для этого разделим интеграл на сумму трёх интегралов, которые отдельно решим:

;
Складываем и получаем:
.
б) Вычислим поверхностный интеграл по треугольнику AOB, который находится в плоскости z = 0. Тогда dz = 0 и, учитывая, что нормальный вектор плоскости образует с осью Oz тупой угол, получаем
в) Треугольник AOC находится в плоскости y = 0, таким образом, dy = 0 и (нормальный вектор плоскости образует с осью Oy тупой угол) получаем
г) Осталось вычислить поверхностный интеграл по треугольнику CBO находится в плоскости x = 0, таким образом, dx = 0 и получаем
.
В результате получаем данный поверхностный интеграл второго рода:
.
2) Используя формулу Остроградского, от поверхностного интеграла по замкнутой поверхности перейдём к тройному интегралу, где W — область, ограниченная поверхностью σ. Так как P = xz, Q = 1, R = 2y, то частные производные , , .
Получаем следующее решение данного поверхностного интеграла:

В последнем примере вернёмся к вычислению поверхностного интеграла первого рода.
Пример 7. Вычислить площадь поверхности параболоида во внутренней части сферы .
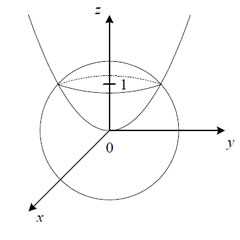
Решение. Определим, при каком значении z данные поверхности пересекаются:
Значение −3 не подходит, поэтому остаётся только z = 1.
Обозначим через C часть поверхности данного параболоида во внутреней стороне сферы. Проекция поверхности C (обозначим её D) на плоскость xOy является кругом с центром в начале координат и радиусом √2, так как при z = 1 получаем уравнение окружности . Решаем поверхностный интеграл первого рода:
.
Так как
то
.
Проекцией поверхности на плоскость xOy является круг, поэтому при вычислении двойного интеграла перейдём к полярной системе координат. Для этого сделаем замену переменных:
Получаем окончательное решение данного поверхностного интеграла:

Кратные и криволинейные интегралы
Поделиться с друзьями
function-x.ru
Вычисление площади поверхности / Двойной интеграл / 3dstroyproekt.ru
Пример 1
Пусть в пространстве задана кусочно-гладкая поверхность $\sigma $, однозначно проектирующаяся в область $\mathbf { \textit { D } } $ на плоскости $\mathbf { \textit { Оху } } $. Пусть эта поверхность задаётся уравнением $\sigma :\;z=f(x,y),\;(x,y)\in D$. Тогда площадь этой поверхности выражается формулой
$ s(\sigma )=\iint\limits_D { \sqrt { 1+\left( { \frac { \partial f } { \partial x } }\right)^2+\left( { \frac { \partial f } { \partial y } }\right)^2 } dxdy } . $
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } $ = 2$\mathbf { \textit { ax } } $ из сферы $\mathbf { \textit { x } } ^ { 2 } +\mathbf { \textit { y } } ^ { 2 } +\mathbf { \textit { z } } ^ { 2 } $ = 4$\mathbf { \textit { a } } ^ { 2 } $ .
Решение:
На рисунке изображён верхний из этих лепестков. Уравнение поверхности $z=\sqrt { 4a^2-x^2-y^2 } ,$ вычисляем производные $\frac { \partial z } { \partial x } =-\frac { x } { \sqrt { 4a^2-x^2-y^2 } } , \quad \frac { \partial z } { \partial y } =-\frac { y } { \sqrt { 4a^2-x^2-y^2 } } ,$ и $s(\sigma )=\iint\limits_D { \sqrt { 1+\frac { x^2+y^2 } { 4a^2-x^2-y^2 } dxdy } } =2a\iint\limits_D { \frac { dxdy } { \sqrt { 4a^2-x^2-y^2 } } } $.
Область $\mathbf { \textit { D } } $ — сдвинутый на $\mathbf { \textit { а } } $ единиц по оси $\mathbf { \textit { Ох } } $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $\mathbf { \textit { Оху } } $ и $\mathbf { \textit { Охz } } $:
$s(\sigma )=4\cdot 2a\iint\limits_ { D_ { r,\varphi } } { \frac { rdrd\varphi } { \sqrt { 4a^2-r^2 } } } =8a\int\limits_0^ { \pi /2 } { d\varphi \int\limits_0^ { 2a\cos \varphi } { \left( { 4a^2-r^2 }\right)^ { -1/2 } rdr } } =-8a\int\limits_0^ { \pi /2 } { d\varphi \left. { \left( { 4a^2-r^2 }\right)^ { 1/2 } }\right|_0^ { 2a\cos \varphi } } = \\ =8a\int\limits_0^ { \pi /2 } { \left[ { 2a-2a\sqrt { 1-\cos ^2\varphi } }\right]d\varphi } =16a^2\left. { \left( { \varphi +\cos \varphi }\right) }\right|_0^ { \pi /2 } =16a^2\left( { \pi /2-1 }\right)$.
Пример 2
Вычислить площадь cферы радиуса (a.)
Решение:
Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ { { x^2 } + { y^2 } + { z^2 } = { a^2 } } \;\; { \text { или } \;\;z = \sqrt { { a^2 } — { x^2 } — { y^2 } } . } $
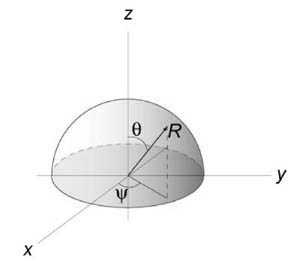
Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ { S_ { \large\frac { 1 } { 2 } \normalsize } } = \iint\limits_R { \sqrt { 1 + { { \left( { \frac { { \partial z } } { { \partial x } } }\right) } ^2 } + { { \left( { \frac { { \partial z } } { { \partial y } } }\right) } ^2 } } dxdy } .$
Найдем частные производные. $ { \frac { { \partial z } } { { \partial x } } } = { \frac { \partial } { { \partial x } } \sqrt { { a^2 } — { x^2 } — { y^2 } } } = { \frac { { — { 2 } x } } { { { 2 } \sqrt { { a^2 } — { x^2 } — { y^2 } } } } } = { — \frac { x } { z } , } $ $ { \frac { { \partial z } } { { \partial y } } } = { \frac { \partial } { { \partial y } } \sqrt { { a^2 } — { x^2 } — { y^2 } } } = { \frac { { — { 2 } y } } { { { 2 } \sqrt { { a^2 } — { x^2 } — { y^2 } } } } } = { — \frac { y } { z } . } $
Подставляя найденные производные, получаем $ { { S_ { \large\frac { 1 } { 2 } \normalsize } } = \iint\limits_R { \sqrt { 1 + { { \left( { \frac { { \partial z } } { { \partial x } } }\right) } ^2 } + { { \left( { \frac { { \partial z } } { { \partial y } } }\right) } ^2 } } dxdy } } = { \iint\limits_R { \sqrt { 1 + \frac { { { x^2 } } } { { { z^2 } } } + \frac { { { y^2 } } } { { { z^2 } } } } dxdy } } = { \iint\limits_R { \sqrt { \frac { { { z^2 } + { x^2 } + { y^2 } } } { { { z^2 } } } } dxdy } } = { \iint\limits_R { \frac { a } { z } dxdy } . } $
Преобразуем двойной интеграл в полярные координаты. $ { { S_ { \large\frac { 1 } { 2 } \normalsize } } = \iint\limits_R { \frac { a } { z } dxdy } } = { \int\limits_0^ { 2\pi } { \int\limits_0^a { \frac { a } { { \sqrt { { a^2 } — { r^2 } } } } rdrd\theta } } } = { a\int\limits_0^ { 2\pi } { d\theta } \int\limits_0^a { \frac { { rdr } } { { \sqrt { { a^2 } — { r^2 } } } } } } = { — 2\pi a\int\limits_0^a { \frac { { d\left( { { a^2 } — { r^2 } }\right) } } { { 2\sqrt { { a^2 } — { r^2 } } } } } } = { — 2\pi a\left. { \left( { \sqrt { { a^2 } — { r^2 } } }\right) }\right|_ { r = 0 } ^a } = { — 2\pi a\left( { 0 — a }\right) = 2\pi { a^2 } . } $
Площадь поверхности полной сферы, соответственно, равна $S = 2 { S_ { \large\frac { 1 } { 2 } \normalsize } } = 4\pi { a^2 } .$
3dstroyproekt.ru
16.4.3. Поверхностный интеграл первого рода (по площади поверхности).
16.4.3.1. Определение
поверхностного интеграла первого рода. Пусть в
пространстве переменных x,y,z задана
кусочно-гладкая поверхность  ,
на которой определена функция f(x,y,z). Разобьём
поверхность на
,
на которой определена функция f(x,y,z). Разобьём
поверхность на  частей ,
на каждой из частей
частей ,
на каждой из частей  выберем произвольную точку ,
найдём
и площадь части
выберем произвольную точку ,
найдём
и площадь части  (которую будем обозначать тем же символом
(которую будем обозначать тем же символом  ),
и составим интегральную сумму
),
и составим интегральную сумму 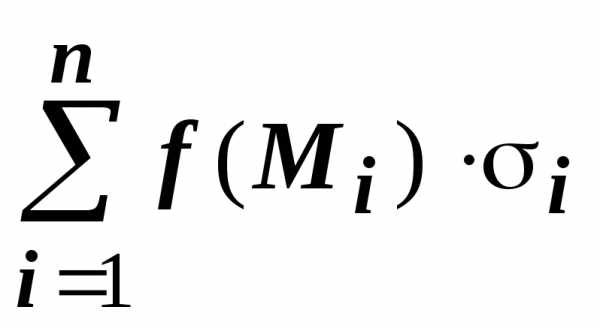 .
Если существует предел последовательности
интегральных сумм при ,
не зависящий ни от способа разбиения
поверхности
.
Если существует предел последовательности
интегральных сумм при ,
не зависящий ни от способа разбиения
поверхности  на части ,
ни от выбора точек
на части ,
ни от выбора точек 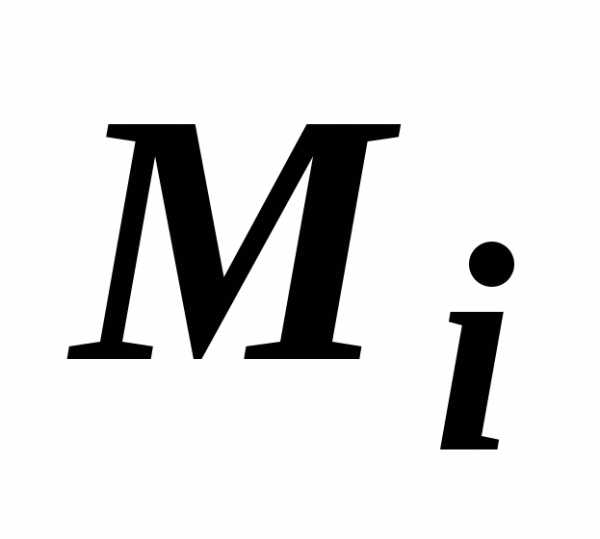 ,
то функция f(x,y,z)
называется интегрируемой по поверхности
,
то функция f(x,y,z)
называется интегрируемой по поверхности  ,
а значение этого предела называется
поверхностным интегралом первого рода,
или поверхностным интегралом по площади
поверхности, и обозначается
,
а значение этого предела называется
поверхностным интегралом первого рода,
или поверхностным интегралом по площади
поверхности, и обозначается 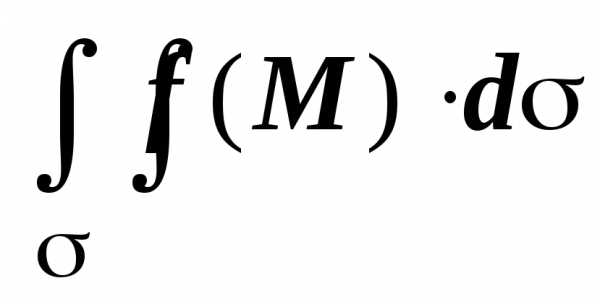 .
.
Теорема
существования. Если функция f(x,y,z)
непрерывна на поверхности  ,
то она интегрируема по этой поверхности.
,
то она интегрируема по этой поверхности.
16.4.3.2. Свойства поверхностного интеграла первого рода. Для этого интеграла имеют место основные шесть свойств, справедливых для определённого, двойного, тройного интеграла, от линейности до теоремы о среднем. Сформулировать и доказать их самостоятельно. Седьмое, персональное, свойство — независимость поверхностного интеграла первого рода от выбора стороны поверхности.
16.4.3.3. Вычисление поверхностного интеграла первого рода.
16.4.3.3.1. Определение
единичного вектора нормали к поверхности.
Выражения для элемента площади
поверхности. Предположим,
что поверхность  задаётся неявным уравнением
(
— непрерывно дифференцируемая функция)
и взаимно однозначно проецируется в
область
задаётся неявным уравнением
(
— непрерывно дифференцируемая функция)
и взаимно однозначно проецируется в
область 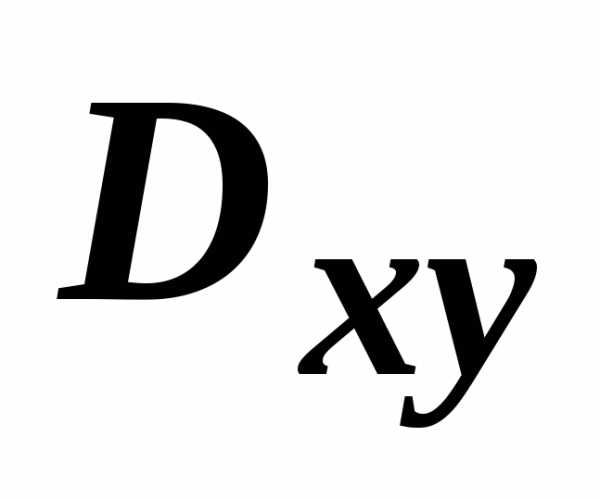 на плоскости Оху. Из
теории функций нескольких переменных
известно, что градиент функции ортогонален
поверхности уровня этой функции,
проходящей через точку, в которой найден
градиент. Рассматривая уравнение
как уравнение поверхности уровня функции
трёх переменных ,
получаем, что в каждой точке поверхности
на плоскости Оху. Из
теории функций нескольких переменных
известно, что градиент функции ортогонален
поверхности уровня этой функции,
проходящей через точку, в которой найден
градиент. Рассматривая уравнение
как уравнение поверхности уровня функции
трёх переменных ,
получаем, что в каждой точке поверхности  ортогонален
ортогонален  ,
т.е. является нормальным к
,
т.е. является нормальным к  вектором. Чтобы получить единичный
нормальный вектор, достаточно просто
пронормировать :
,
где знак перед дробью соответствует
возможности выбора двух возможных
взаимно противоположных направлений
нормали. В координатной форме
вектором. Чтобы получить единичный
нормальный вектор, достаточно просто
пронормировать :
,
где знак перед дробью соответствует
возможности выбора двух возможных
взаимно противоположных направлений
нормали. В координатной форме 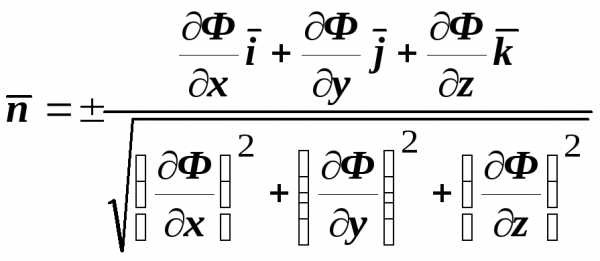 ,
где
,
где  — базисные орты. Если сравнить это
выражение с представлением градиента
через направляющие косинусы: ,
то
— базисные орты. Если сравнить это
выражение с представлением градиента
через направляющие косинусы: ,
то 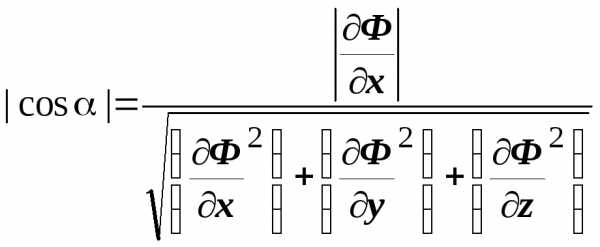 ,
, 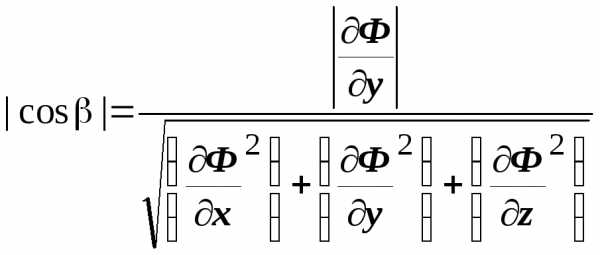 ,
, 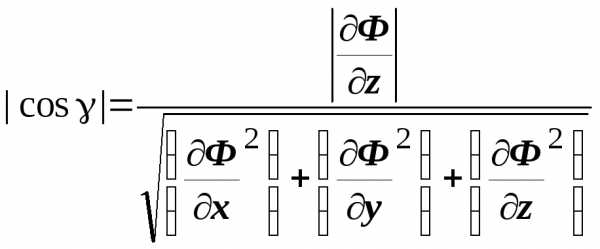 .
Теперь мы можем выразить элемент площади
поверхности через элемент площади в
каждой координатной плоскости: ,
,
.
В частном случае задания уравнения
поверхности в явном виде
получим ,
т.е. ,
.
Теперь мы можем выразить элемент площади
поверхности через элемент площади в
каждой координатной плоскости: ,
,
.
В частном случае задания уравнения
поверхности в явном виде
получим ,
т.е. , 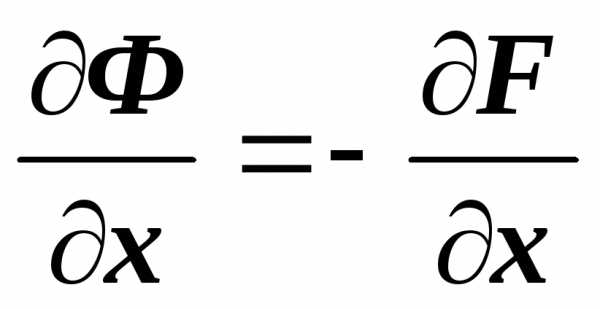 ,
, 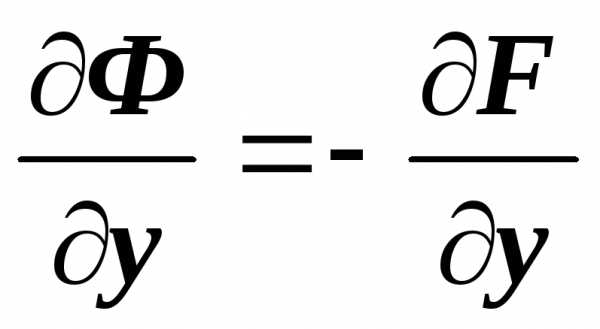 ,
, 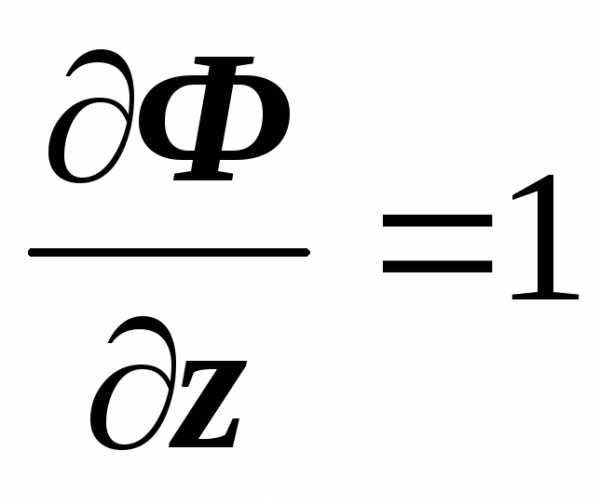 ,
поэтому ,
,
,
поэтому ,
, 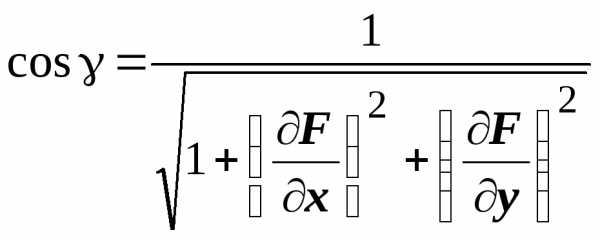 ,
и .
Мы уже пользовались этой формулой при
вычислении площади поверхности с помощью
двойного интеграла.
,
и .
Мы уже пользовались этой формулой при
вычислении площади поверхности с помощью
двойного интеграла.
16.4.3.3.2.
Выражение поверхностного интеграла
через двойной интеграл по проекции
поверхности на координатную плоскость.Пусть поверхность  взаимно однозначно проецируется в
область
взаимно однозначно проецируется в
область 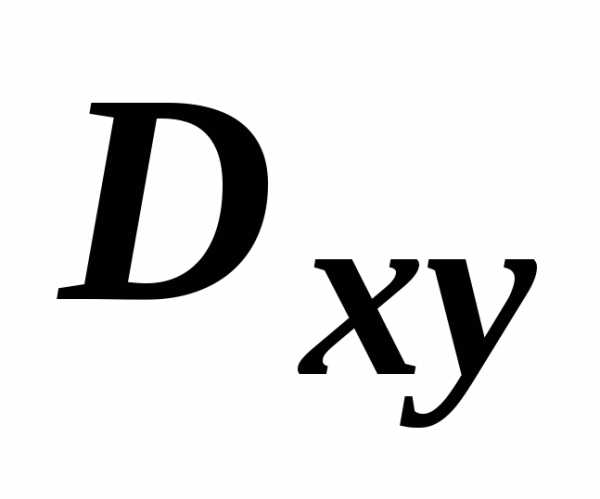 на плоскости Оху. Будем
считать, что поверхность задана уравнением
,
.
В интегральной сумме
на плоскости Оху. Будем
считать, что поверхность задана уравнением
,
.
В интегральной сумме 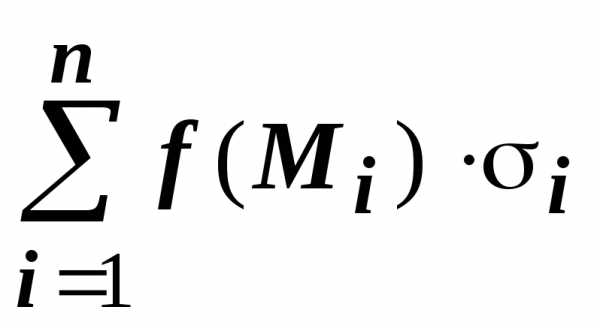 выразим площадь
выразим площадь  через двойной интеграл по её проекции
через двойной интеграл по её проекции 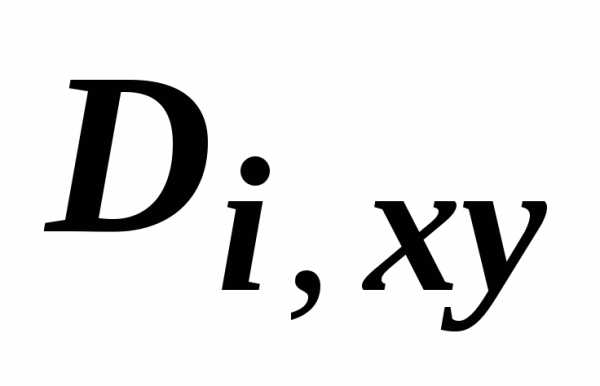 на плоскость Оху:
.
Применим к этому интегралу теорему о
среднем: существует точка
такая, что .
Значение подынтегральной функции
будем вычислять в точке ,
такой, что .
Тогда .
на плоскость Оху:
.
Применим к этому интегралу теорему о
среднем: существует точка
такая, что .
Значение подынтегральной функции
будем вычислять в точке ,
такой, что .
Тогда .
Слева стоит интегральная сумма для поверхностного интеграла, справа — для двойного; переход к пределу при (при этом и ) даёт
.
Эта формула и применяется для вычисления поверхностных интегралов. Естественно, в каждой задаче надо выбирать, на какую из координатных плоскостей предпочтительней проецировать поверхность; если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
Примеры. 1. Найти 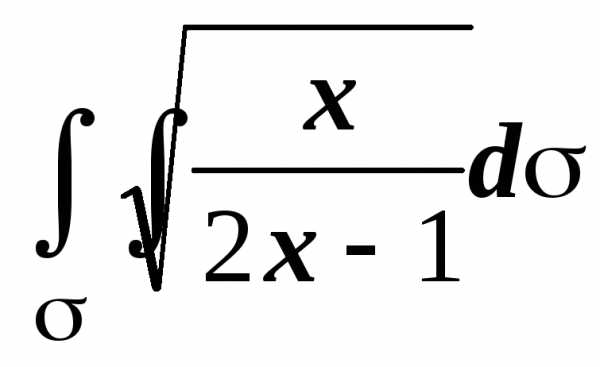 ,
где
— часть цилиндра x2 + z2 = 2x,
вырезаемая гиперболоидом x2 — y2 + z2 = 1 и
плоскостью z = 0 (z > 0).
,
где
— часть цилиндра x2 + z2 = 2x,
вырезаемая гиперболоидом x2 — y2 + z2 = 1 и
плоскостью z = 0 (z > 0).
Решение: Найдем проекцию поверхности на плоскость OXY. Исключим из уравнений цилиндра и гиперболоида переменную z:
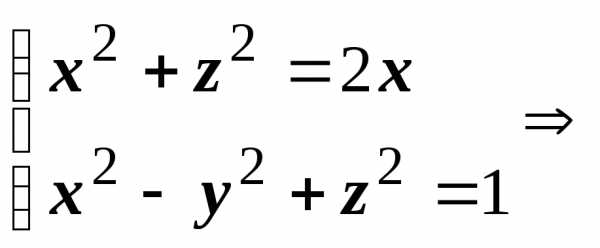 2x = y2+1
— уравнение проекции линии пересечения
двух поверхностей на OXY.
П
2x = y2+1
— уравнение проекции линии пересечения
двух поверхностей на OXY.
П олагая
в уравнении цилиндраz = 0, получим уравнение линии пересечения
цилиндра и плоскости OXY.
Таким образом, поверхность
проецируется в область D,
ограниченную параболой x =
олагая
в уравнении цилиндраz = 0, получим уравнение линии пересечения
цилиндра и плоскости OXY.
Таким образом, поверхность
проецируется в область D,
ограниченную параболой x =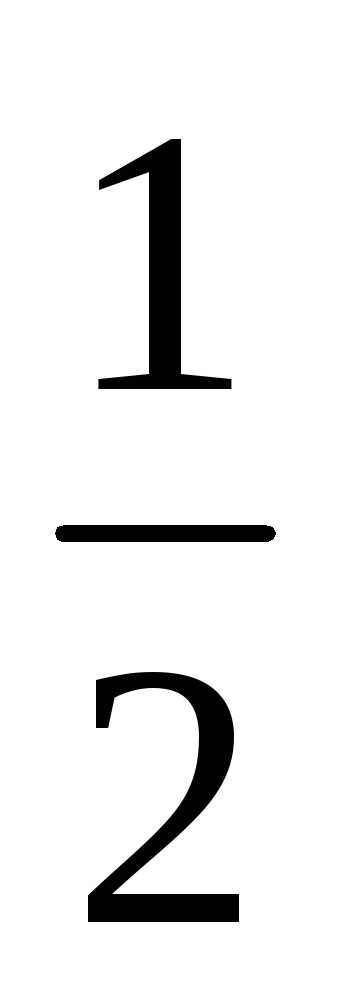 (y2+1)
и прямой x=2.
Часть цилиндра, удовлетворяющая условию z>0,
задается уравнением z =
(y2+1)
и прямой x=2.
Часть цилиндра, удовлетворяющая условию z>0,
задается уравнением z = 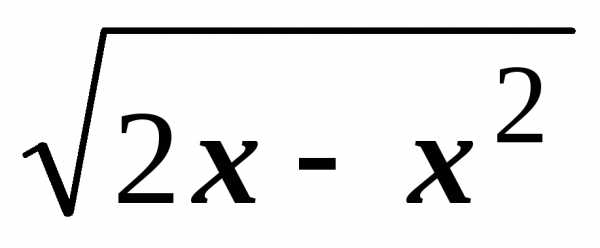 .
Тогда
.
Тогда 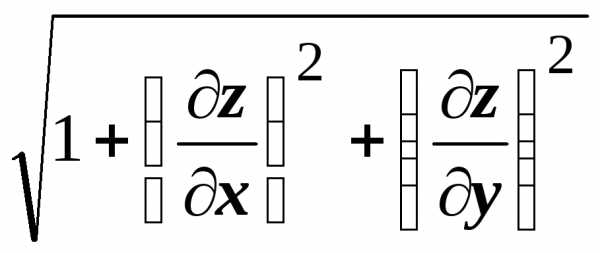 =
= 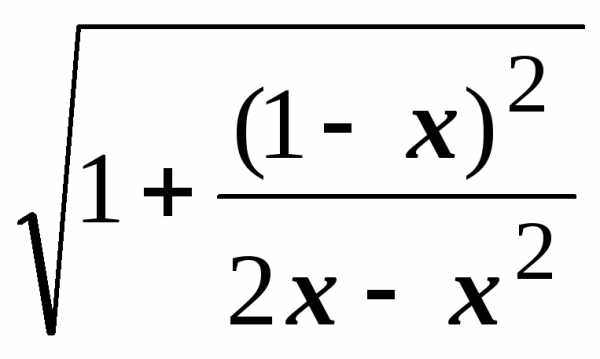 =
=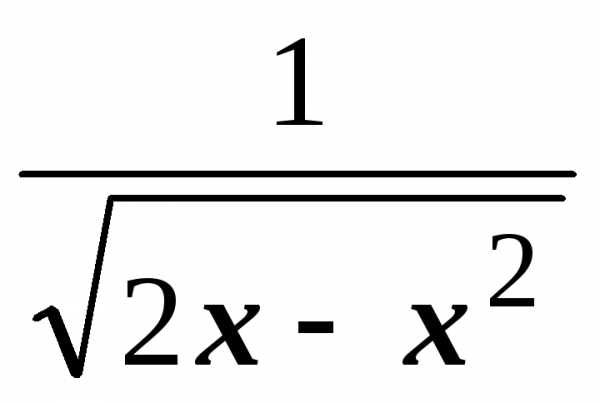 .
Таким образом, .
.
Таким образом, .
2.
Найти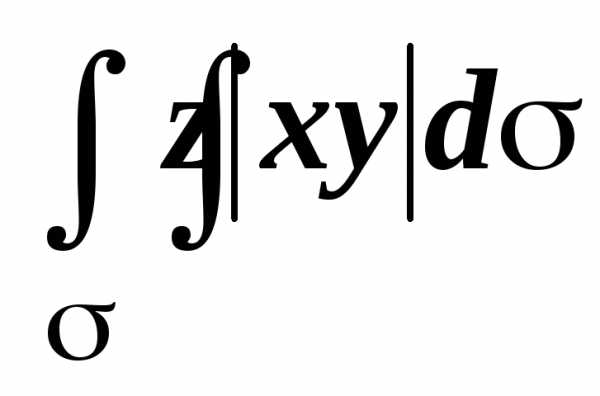 ,
где
— полная поверхность цилиндра x2+y2 = 1, 0 ≤ z ≤
1.
,
где
— полная поверхность цилиндра x2+y2 = 1, 0 ≤ z ≤
1.
Решение:
Искомый интеграл равен сумме трех
интегралов: по нижнему и верхнему
основаниям 1 и 2 и боковой поверхности (рис.18). Так как
на нижнем основании z=0, то  =0.
Для верхнего основания2 имеем z(x,y)=1,
=0.
Для верхнего основания2 имеем z(x,y)=1, 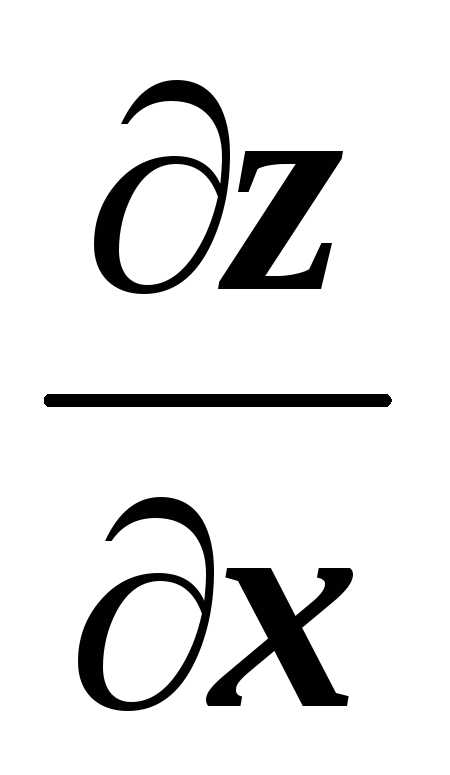 =
=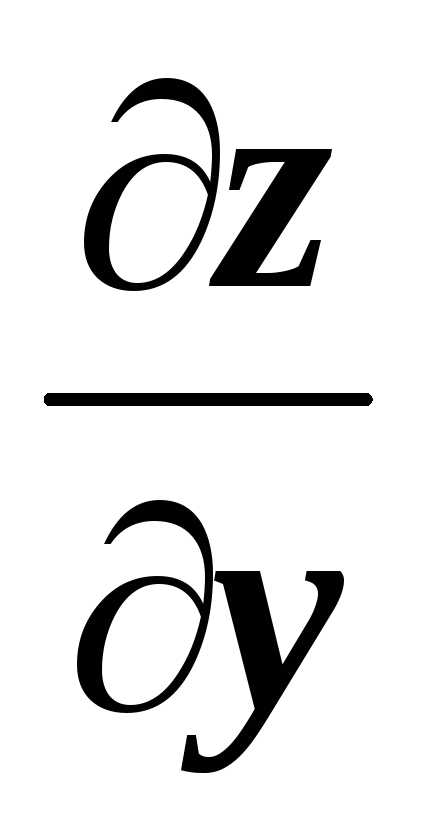 =0,
поэтому поверхностный интеграл по2 совпадает с двойным интегралом от
функции z(x,y)|xy|
= |xy|,
взятым по кругу D ={x2+ y2<1}:
=0,
поэтому поверхностный интеграл по2 совпадает с двойным интегралом от
функции z(x,y)|xy|
= |xy|,
взятым по кругу D ={x2+ y2<1}:
Найдем интеграл по боковой поверхности. Она состоит из двух частей: 3 и 4 , симметричных относительно плоскости OYZ. Так как функция z|xy| — четная по x, то интегралы по 3 и 4 равны.
Проекция 3 на плоскость OYZ — прямоугольник D:{-1
≤ у ≤
1, 0 ≤ z ≤1}.
Уравнение 3 : х=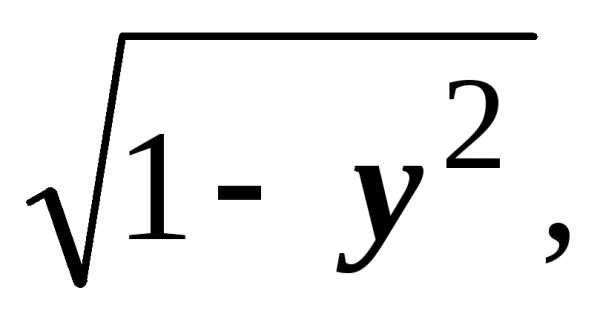 Отсюда:
Отсюда:
Окончательно получаем:
3. Найти 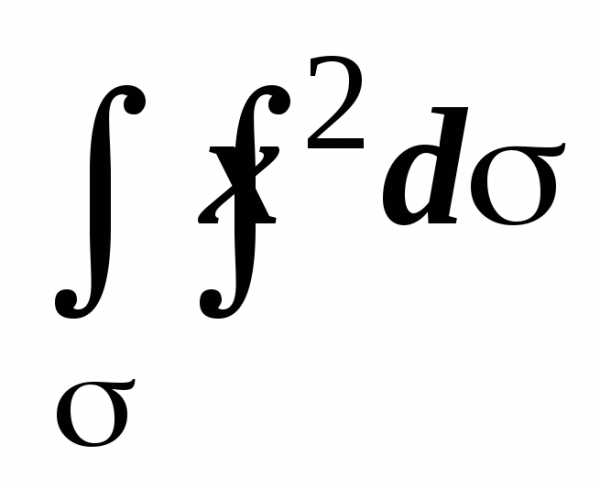 ,
где
— сфера x2 + y2 + z2 = R2.
,
где
— сфера x2 + y2 + z2 = R2.
Решение: Использование соображений симметрии позволяет иногда существенно упростить вычисление интегралов. Очевидно, что для сферы . Тогда
studfiles.net
Поверхностный интеграл первого рода и его свойства / Поверхностный интеграл / 3dstroyproekt.ru
Определение поверхностного интеграла первого рода
Пусть в пространстве переменных $\mathbf { \textit { x,y,z } } \mathbf { } $ задана кусочно-гладкая поверхность $\sigma $, на которой определена функция $\mathbf { \textit { f } } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } $,$\mathbf { \textit { z } } )$.$\mathbf { } $
Разобьём поверхность на $n$ частей $\sigma _1 ,\sigma _2 ,\ldots \sigma _i ,\ldots \sigma _n $, на каждой из частей $\sigma _i $ выберем произвольную точку $M_i (x_i ,y_i ,z_i )$, найдём $f(M_i )=f(x_i ,y_i ,z_i )$ и площадь части $\sigma _i $ { которую будем обозначать тем же символом $\sigma _i )$ и составим интегральную сумму $\sum\limits_ { i=1 } ^n { f(M_i )\cdot \sigma _i } $.
Если существует предел последовательности интегральных сумм при $\mathop { \max } \limits_ { i=1,2,\ldots n } diam\sigma _i \to 0$, не зависящий ни от способа разбиения поверхности $\sigma $ на части $\sigma _i (i=1,2,\ldots ,n)$, ни от выбора точек $M_i $, то функция $\mathbf { \textit { f } } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } $,$\mathbf { \textit { z } } )$ называется интегрируемой по поверхности $\sigma $, а значение этого предела называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности и обозначается $\iint\limits_\sigma { f(M)\cdot d\sigma } $.
Теорема существования Если функция $\mathbf { \textit { f } } (\mathbf { \textit { x } } $,$\mathbf { \textit { y } } $,$\mathbf { \textit { z } } )$ непрерывна на поверхности $\sigma $, то она интегрируема по этой поверхности.
Свойства поверхностного интеграла первого рода
Аналогичны по формулировке и доказательству свойствам рассмотренных ранее интегралов первого рода.
- Линейность. $\iint\limits_\sigma { (\lambda \,f+ } \mu \,g)d\sigma =\lambda \iint\limits_\sigma { fd\sigma } +\mu \iint\limits_\sigma { gd\sigma } $
- Аддитивность $\iint\limits_ { \sigma _1 \cup \sigma _2 } { fd\sigma } =\iint\limits_ { \sigma _1 } { fd\sigma } \iint\limits_ { \sigma _2 } { fd\sigma } $
- $\iint\limits_\sigma { d\sigma } =S_\sigma -$ площадь поверхности.
- Если $f(x,\,y,\,z)\geqslant g(x,\,y,\,z)$, то $\iint\limits_\sigma { fd\sigma \geqslant \iint\limits_\sigma { gd\sigma } } $ { если $f\geqslant 0$, то $\iint\limits_\sigma { fd\sigma } \geqslant 0)$,
- Теорема об оценке Если $m\leqslant f\left( { x,\,y,\,z }\right)\leqslant M$, то $mS_\sigma \leqslant \iint\limits_\sigma { fd\sigma } \leqslant MS_\sigma $,
- Теорема о среднем Пусть функция $f(M)=f(x,\,y,\,z)$ непрерывна на кусочно-гладкой ограниченной поверхности $\sigma $. Тогда на поверхности найдется точка С, такая что $f(C)=\frac { 1 } { S_\sigma } \iint\limits_\sigma { f\left( { x,\,y,\,z }\right)d\sigma } $
Доказательство
Первые четыре свойства доказываются аналогично подобным свойствам в двойном, тройном интегралах, криволинейном интеграле первого рода { записью соотношений в интегральных суммах и предельным переходом } . Во втором свойстве используется возможность такого разбиения поверхности на две части, чтобы ни один элемент разбиения не содержал граничные точки этих частей в качестве своих внутренних точек.
Теорема об оценке следует из свойств 3, 4.
Теорема о среднем, как и ранее, использует теоремы Вейерштрасса и Больцано-Коши для функций, непрерывных на замкнутых ограниченных множествах.
Седьмое, персональное, свойство — независимость поверхностного интеграла первого рода от выбора стороны поверхности
3dstroyproekt.ru
16.4.3. Поверхностный интеграл первого рода (по площади поверхности).
16.4.3.1. Определение
поверхностного интеграла первого рода. Пусть в
пространстве переменных x,y,z задана
кусочно-гладкая поверхность  ,
на которой определена функция f(x,y,z). Разобьём
поверхность на
,
на которой определена функция f(x,y,z). Разобьём
поверхность на  частей ,
на каждой из частей
частей ,
на каждой из частей  выберем произвольную точку ,
найдём
и площадь части
выберем произвольную точку ,
найдём
и площадь части  (которую будем обозначать тем же символом
(которую будем обозначать тем же символом  ),
и составим интегральную сумму
),
и составим интегральную сумму 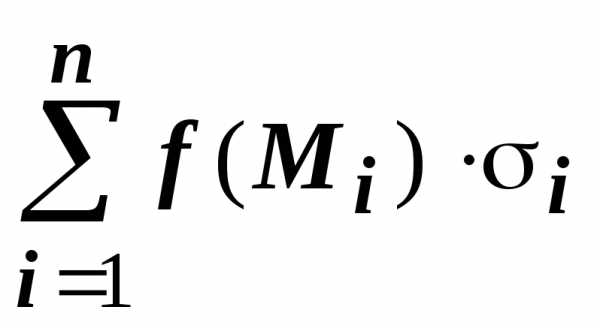 .
Если существует предел последовательности
интегральных сумм при ,
не зависящий ни от способа разбиения
поверхности
.
Если существует предел последовательности
интегральных сумм при ,
не зависящий ни от способа разбиения
поверхности  на части ,
ни от выбора точек
на части ,
ни от выбора точек 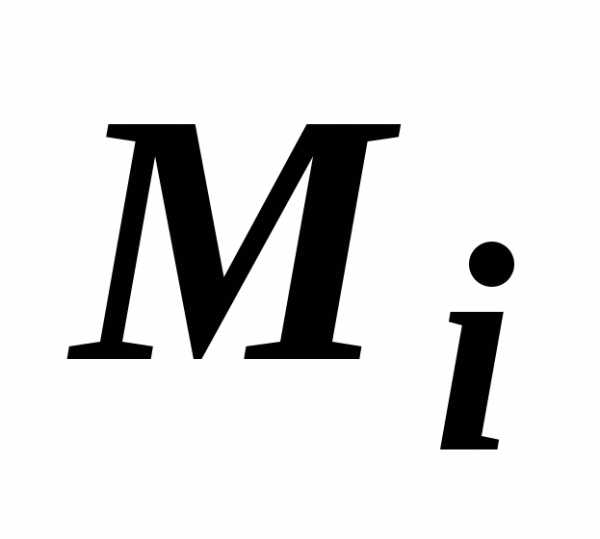 ,
то функция f(x,y,z)
называется интегрируемой по поверхности
,
то функция f(x,y,z)
называется интегрируемой по поверхности  ,
а значение этого предела называется
поверхностным интегралом первого рода,
или поверхностным интегралом по площади
поверхности, и обозначается
,
а значение этого предела называется
поверхностным интегралом первого рода,
или поверхностным интегралом по площади
поверхности, и обозначается 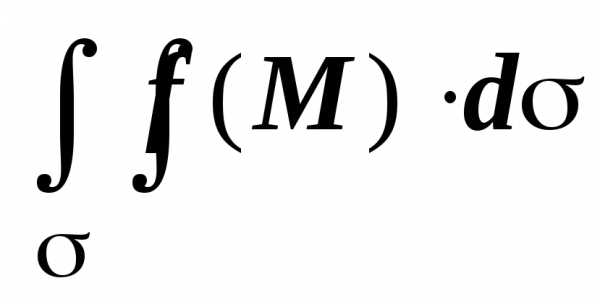 .
.
Теорема
существования. Если функция f(x,y,z)
непрерывна на поверхности  ,
то она интегрируема по этой поверхности.
,
то она интегрируема по этой поверхности.
16.4.3.2. Свойства поверхностного интеграла первого рода. Для этого интеграла имеют место основные шесть свойств, справедливых для определённого, двойного, тройного интеграла, от линейности до теоремы о среднем. Сформулировать и доказать их самостоятельно. Седьмое, персональное, свойство — независимость поверхностного интеграла первого рода от выбора стороны поверхности.
16.4.3.3. Вычисление поверхностного интеграла первого рода.
16.4.3.3.1. Определение
единичного вектора нормали к поверхности.
Выражения для элемента площади
поверхности. Предположим,
что поверхность  задаётся неявным уравнением
(
— непрерывно дифференцируемая функция)
и взаимно однозначно проецируется в
область
задаётся неявным уравнением
(
— непрерывно дифференцируемая функция)
и взаимно однозначно проецируется в
область 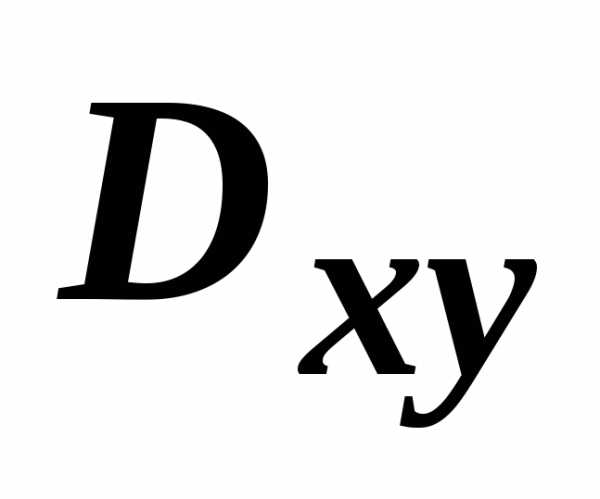 на плоскости Оху. Из
теории функций нескольких переменных
известно, что градиент функции ортогонален
поверхности уровня этой функции,
проходящей через точку, в которой найден
градиент. Рассматривая уравнение
как уравнение поверхности уровня функции
трёх переменных ,
получаем, что в каждой точке поверхности
на плоскости Оху. Из
теории функций нескольких переменных
известно, что градиент функции ортогонален
поверхности уровня этой функции,
проходящей через точку, в которой найден
градиент. Рассматривая уравнение
как уравнение поверхности уровня функции
трёх переменных ,
получаем, что в каждой точке поверхности  ортогонален
ортогонален  ,
т.е. является нормальным к
,
т.е. является нормальным к  вектором. Чтобы получить единичный
нормальный вектор, достаточно просто
пронормировать :
,
где знак перед дробью соответствует
возможности выбора двух возможных
взаимно противоположных направлений
нормали. В координатной форме
вектором. Чтобы получить единичный
нормальный вектор, достаточно просто
пронормировать :
,
где знак перед дробью соответствует
возможности выбора двух возможных
взаимно противоположных направлений
нормали. В координатной форме 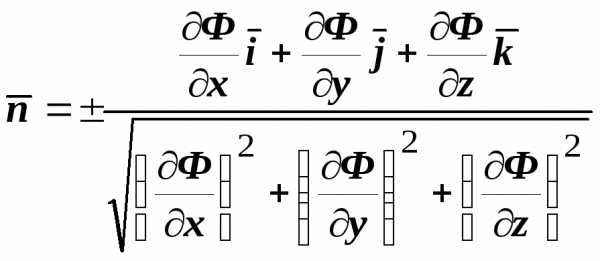 ,
где
,
где  — базисные орты. Если сравнить это
выражение с представлением градиента
через направляющие косинусы: ,
то
— базисные орты. Если сравнить это
выражение с представлением градиента
через направляющие косинусы: ,
то 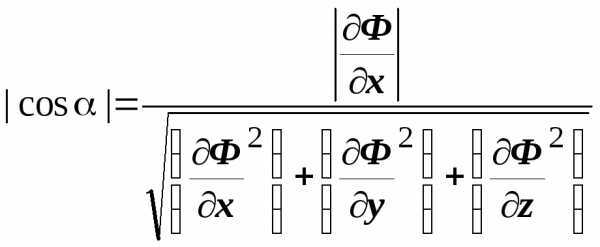 ,
, 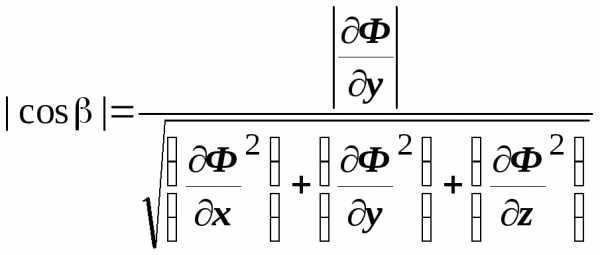 ,
, 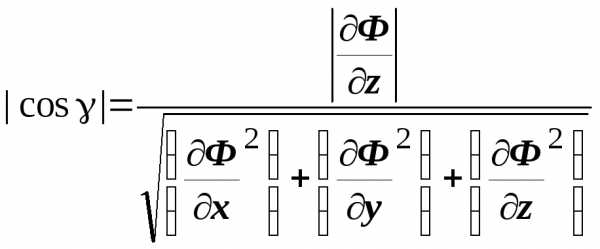 .
Теперь мы можем выразить элемент площади
поверхности через элемент площади в
каждой координатной плоскости: ,
,
.
В частном случае задания уравнения
поверхности в явном виде
получим ,
т.е. ,
.
Теперь мы можем выразить элемент площади
поверхности через элемент площади в
каждой координатной плоскости: ,
,
.
В частном случае задания уравнения
поверхности в явном виде
получим ,
т.е. , 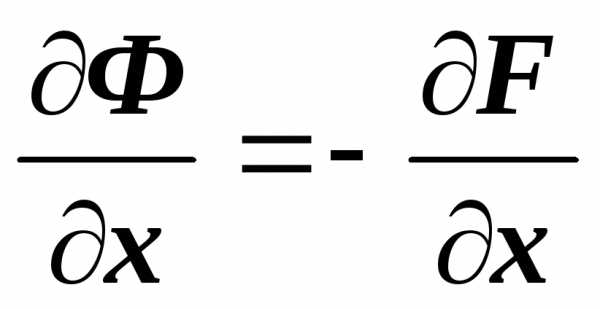 ,
, 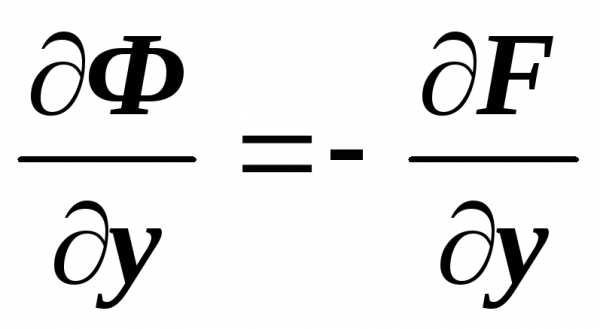 ,
, 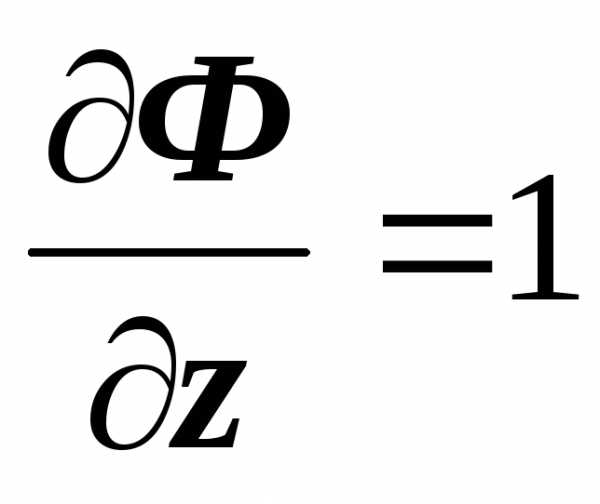 ,
поэтому ,
,
,
поэтому ,
, 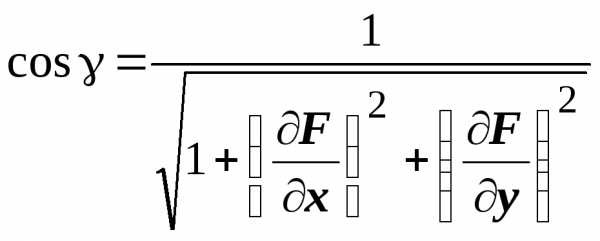 ,
и .
Мы уже пользовались этой формулой при
вычислении площади поверхности с помощью
двойного интеграла.
,
и .
Мы уже пользовались этой формулой при
вычислении площади поверхности с помощью
двойного интеграла.
16.4.3.3.2.
Выражение поверхностного интеграла
через двойной интеграл по проекции
поверхности на координатную плоскость.Пусть поверхность  взаимно однозначно проецируется в
область
взаимно однозначно проецируется в
область 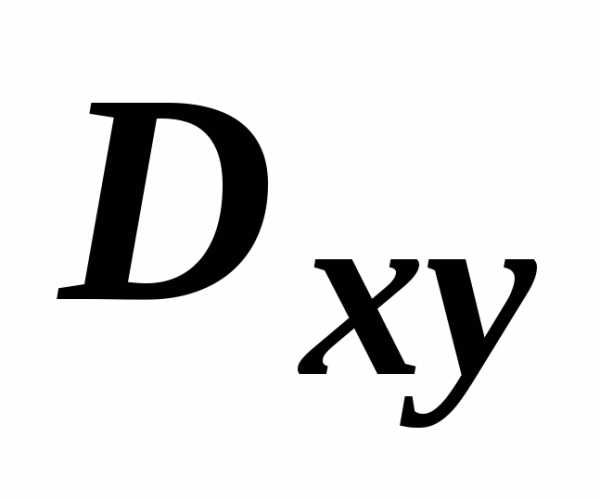 на плоскости Оху. Будем
считать, что поверхность задана уравнением
,
.
В интегральной сумме
на плоскости Оху. Будем
считать, что поверхность задана уравнением
,
.
В интегральной сумме 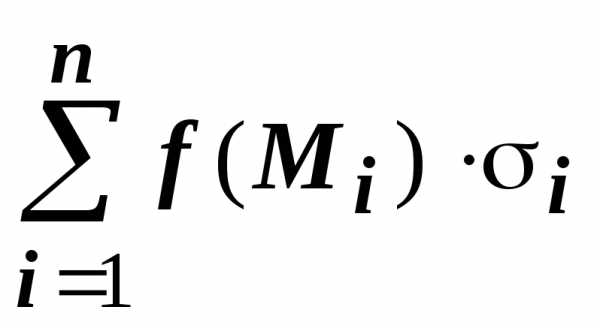 выразим площадь
выразим площадь  через двойной интеграл по её проекции
через двойной интеграл по её проекции 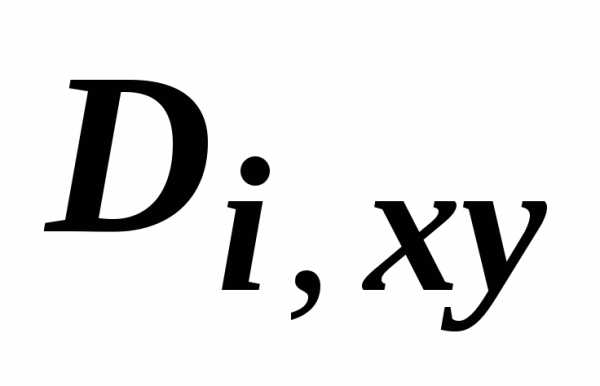 на плоскость Оху:
.
Применим к этому интегралу теорему о
среднем: существует точка
такая, что .
Значение подынтегральной функции
будем вычислять в точке ,
такой, что .
Тогда .
на плоскость Оху:
.
Применим к этому интегралу теорему о
среднем: существует точка
такая, что .
Значение подынтегральной функции
будем вычислять в точке ,
такой, что .
Тогда .
Слева стоит интегральная сумма для поверхностного интеграла, справа — для двойного; переход к пределу при (при этом и ) даёт
.
Эта формула и применяется для вычисления поверхностных интегралов. Естественно, в каждой задаче надо выбирать, на какую из координатных плоскостей предпочтительней проецировать поверхность; если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
Примеры. 1. Найти 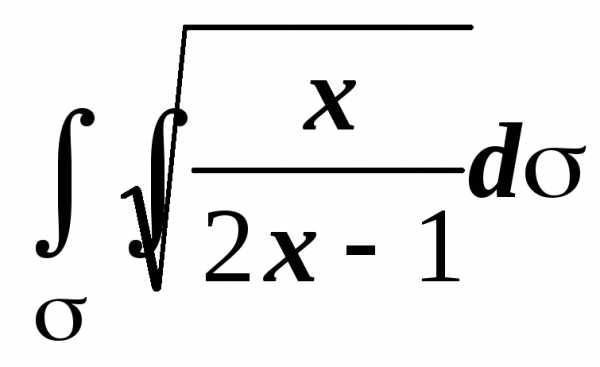 ,
где
— часть цилиндра x2 + z2 = 2x,
вырезаемая гиперболоидом x2 — y2 + z2 = 1 и
плоскостью z = 0 (z > 0).
,
где
— часть цилиндра x2 + z2 = 2x,
вырезаемая гиперболоидом x2 — y2 + z2 = 1 и
плоскостью z = 0 (z > 0).
Решение: Найдем проекцию поверхности на плоскость OXY. Исключим из уравнений цилиндра и гиперболоида переменную z:
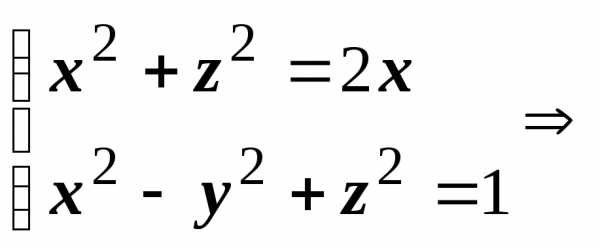 2x = y2+1
— уравнение проекции линии пересечения
двух поверхностей на OXY.
П
2x = y2+1
— уравнение проекции линии пересечения
двух поверхностей на OXY.
П олагая
в уравнении цилиндраz = 0, получим уравнение линии пересечения
цилиндра и плоскости OXY.
Таким образом, поверхность
проецируется в область D,
ограниченную параболой x =
олагая
в уравнении цилиндраz = 0, получим уравнение линии пересечения
цилиндра и плоскости OXY.
Таким образом, поверхность
проецируется в область D,
ограниченную параболой x = (y2+1)
и прямой x=2.
Часть цилиндра, удовлетворяющая условию z>0,
задается уравнением z =
(y2+1)
и прямой x=2.
Часть цилиндра, удовлетворяющая условию z>0,
задается уравнением z = 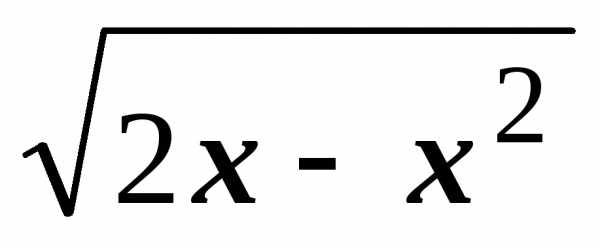 .
Тогда
.
Тогда 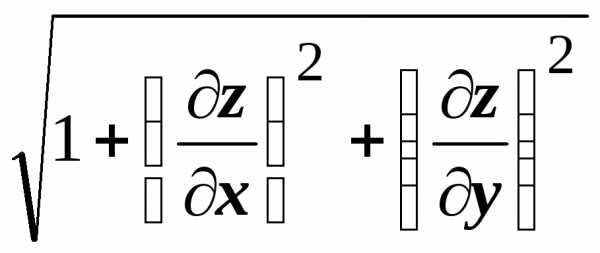 =
= 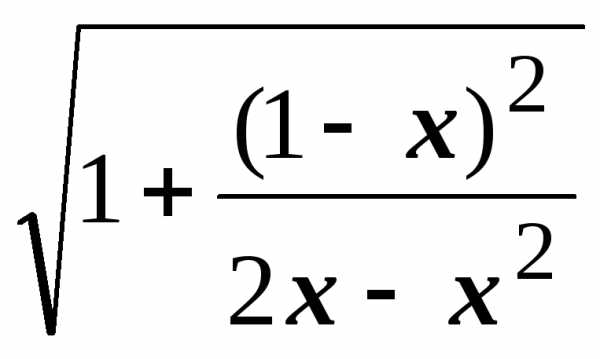 =
=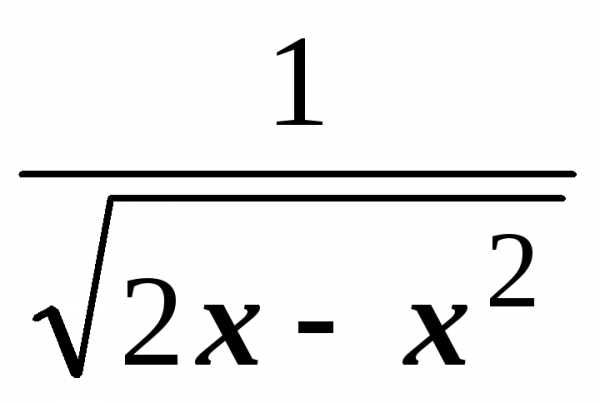 .
Таким образом, .
.
Таким образом, .
2.
Найти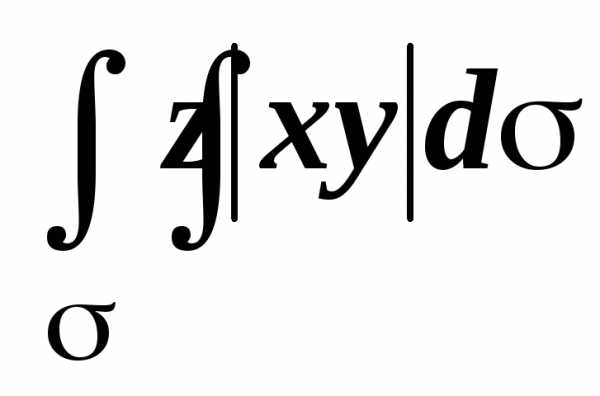 ,
где
— полная поверхность цилиндра x2+y2 = 1, 0 ≤ z ≤
1.
,
где
— полная поверхность цилиндра x2+y2 = 1, 0 ≤ z ≤
1.
Решение:
Искомый интеграл равен сумме трех
интегралов: по нижнему и верхнему
основаниям 1 и 2 и боковой поверхности (рис.18). Так как
на нижнем основании z=0, то 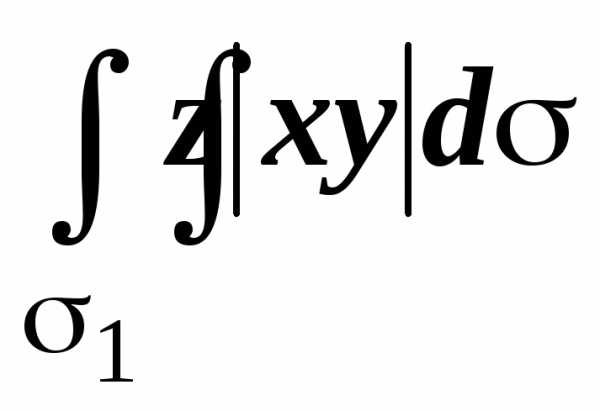 =0.
Для верхнего основания2 имеем z(x,y)=1,
=0.
Для верхнего основания2 имеем z(x,y)=1, 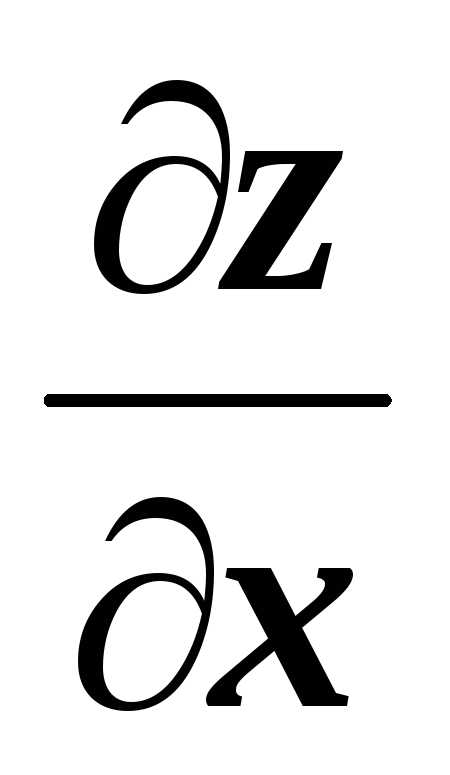 =
=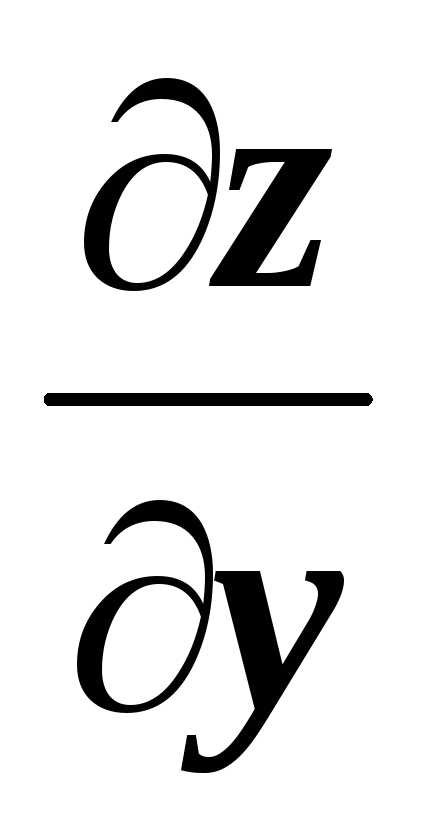 =0,
поэтому поверхностный интеграл по2 совпадает с двойным интегралом от
функции z(x,y)|xy|
= |xy|,
взятым по кругу D ={x2+ y2<1}:
=0,
поэтому поверхностный интеграл по2 совпадает с двойным интегралом от
функции z(x,y)|xy|
= |xy|,
взятым по кругу D ={x2+ y2<1}:
Найдем интеграл по боковой поверхности. Она состоит из двух частей: 3 и 4 , симметричных относительно плоскости OYZ. Так как функция z|xy| — четная по x, то интегралы по 3 и 4 равны.
Проекция 3 на плоскость OYZ — прямоугольник D:{-1
≤ у ≤
1, 0 ≤ z ≤1}.
Уравнение 3 : х=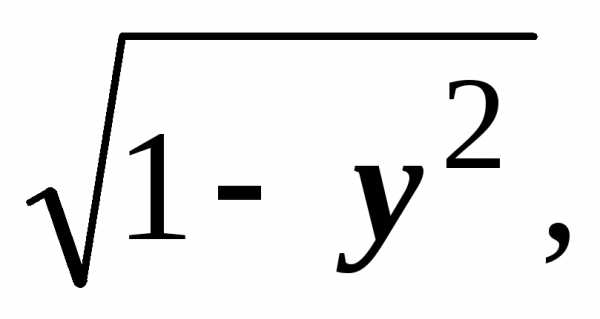 Отсюда:
Отсюда:
Окончательно получаем:
3. Найти 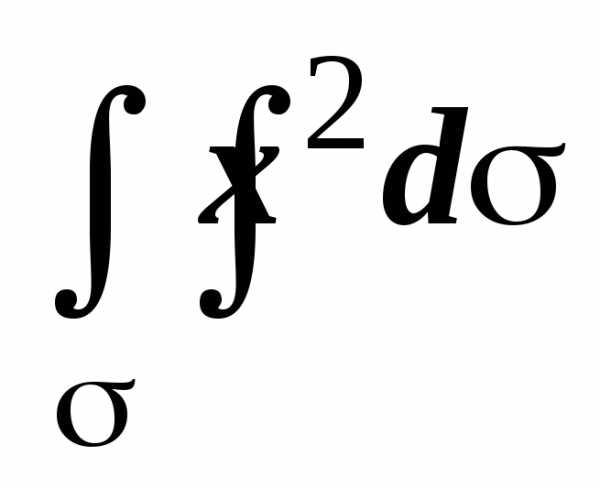 ,
где
— сфера x2 + y2 + z2 = R2.
,
где
— сфера x2 + y2 + z2 = R2.
Решение: Использование соображений симметрии позволяет иногда существенно упростить вычисление интегралов. Очевидно, что для сферы . Тогда
studfiles.net
3.3. Интеграл и задача об определении площади
Заканчивая главу о первообразной, покажем, как понятие первообразной (неопределенного интеграла) теснейшим образом связано с определением площади плоской фигуры. Причем воспользуемся здесь интуитивным представлением о площади плоской фигуры, отложив точную постановку этого вопроса.
Пусть имеем непрерывную на отрезке [a,b] функциюf(x), принимающую лишь положительные (неотрицательные) значения.
Рассмотрим фигуру ABCD(рис. 24), ограниченную кривойy =f(x), прямымиx = a,x =bи отрезком оси0X; такую фигуру
называют криволинейной трапецией.
Изучим вопрос о площади криволинейной
трапеции. Для этого возьмем некоторую
переменную точкуx, лежащую на
интервале [a,b], и рассмотрим
площадь фигурыABLK. При измененииxэта последняя площадь будет, очевидно,
соответственно изменяться, причем
каждому значению переменнойxотвечает вполне определенное значение
площади криволинейной трапеции. Поэтому
площадь криволинейной трапецииABLKявляется некоторой функцией отx;
обозначим эту функциюS(x). Найдем
(если это возможно) производную функцииS(x) при измененииx. Для этого
дадимxприращение (например,
положительное)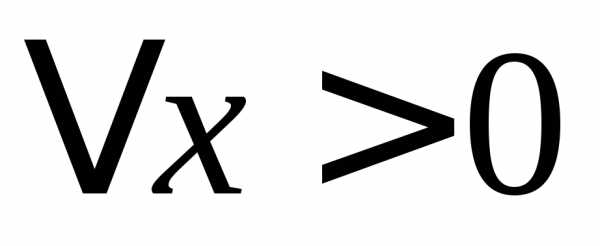 ;
тогда площадьS(x) получит
приращение
;
тогда площадьS(x) получит
приращение .
ОбозначимmиMсоответственно
наименьшее и наибольшее значенияf(x)
на промежуткеи сравним площадь
.
ОбозначимmиMсоответственно
наименьшее и наибольшее значенияf(x)
на промежуткеи сравним площадь с площадями прямоугольников
с площадями прямоугольников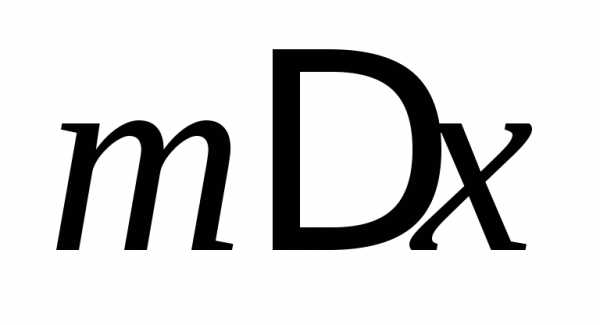 и
и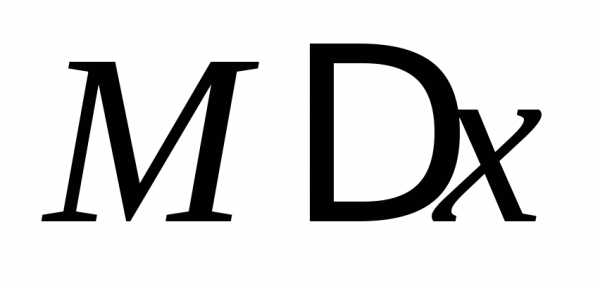 .
Очевидно,или.
.
Очевидно,или.
Рис. 24
Если теперь  ,
то,
вследствие непрерывностиf(x)
значения,;
существует предел.
Таким образом, мы получили замечательный
результат.
,
то,
вследствие непрерывностиf(x)
значения,;
существует предел.
Таким образом, мы получили замечательный
результат.
Теорема.Производная от переменной площади по переменной абсциссеxравна значению функции в этой переменной точкеf(x).
Иными словами, переменная площадь S(x) представляет собой одну из первообразных – для данной функцииy =f(x):.
Так как все первообразные отличаются друг от друга на постоянную величину c, то еслиF(x) какая-либо первообразная дляf(x), тогдаS(x) =F(x) +c.
Положив здесь x=aи считая (очевидно)S(a)=0, получим 0 =F(a) +c,c= –F(a).
Окончательно, S(x)=F(x)–F(a), гдеx– любая точка из интервала [a,b]. В частности, для получения площади всей криволинейной трапецииABCDследует взятьx=b:
.
Этот важный результат называют теоремой Ньютона-Лейбница. Мы еще встретимся с этой теоремой в дальнейшем: площадь криволинейной трапеции Sравна разности значений (произвольной) первообразнойF(x) в концах интервала [a,b].
3.4. Определенный интеграл
Вернемся вновь к задаче определения площади криволинейной трапеции, ограниченной непрерывной кривой y=f(x),, прямымиx=a,x=bи отрезком осиOX.
Разобьем отрезок [a,b] точкаминаnравных частей (рис. 25). Получимn“малых” отрезков; длина каждого отрезкаобозначается, k=1, 2, …,n; в нашем случае длины всех отрезков одинаковы:.
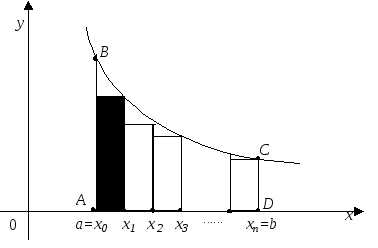
Рис. 25
Проведя через точки деления прямые, параллельные оси 0Y, мы разобьем криволинейную трапециюABCDнаnмалых криволинейных трапеций – полосок с площадью(k=1, 2,…,n). Очевидно, площадь всей криволинейной трапецииABCD
.
Эту последнюю сумму записывают так: , где греческая буква ∑ – это знак суммы, а символозначает, что суммируютсяnслагаемых при изменении индексаkот 1 доn.
Заменим теперь площадь малой криволинейной фигурыMLPQ(рис. 26) площадью прямоугольникаMLPQ, равной. Искомая площадьSкриволинейной трапеции приближенно равна площади ступенчатой фигуры:
.
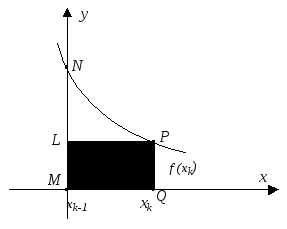
Рис. 26
Очевидно, чем меньше длина промежутков ,тем точнее ступенчатая фигура приближает нашу криволинейную трапецию.
Будем теперь увеличивать вдвое число n точек деления, уменьшая вдвое длину интервалов разбиения.
Получим последовательность сумм
, (*)
где 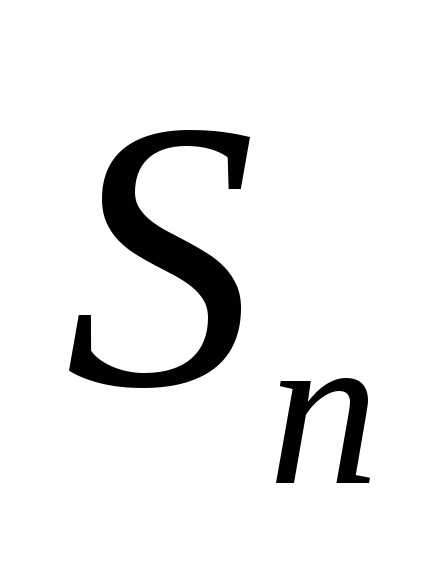 – площадь ступенчатой фигуры изnпрямоугольников. Естественно за точное
значение площадиSкриволинейной
трапеции принять предел последовательности
– площадь ступенчатой фигуры изnпрямоугольников. Естественно за точное
значение площадиSкриволинейной
трапеции принять предел последовательности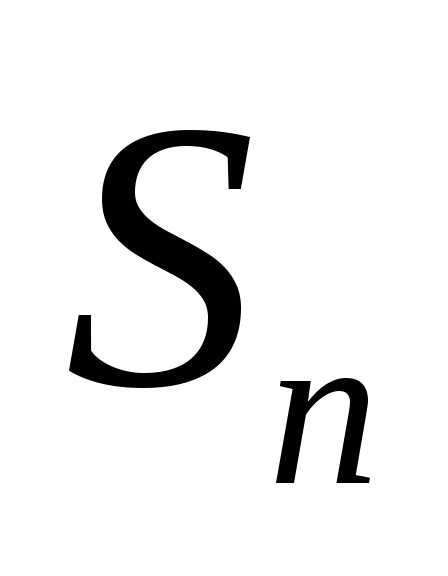 площадей ступенчатых фигур, когда(при этом все длины
площадей ступенчатых фигур, когда(при этом все длины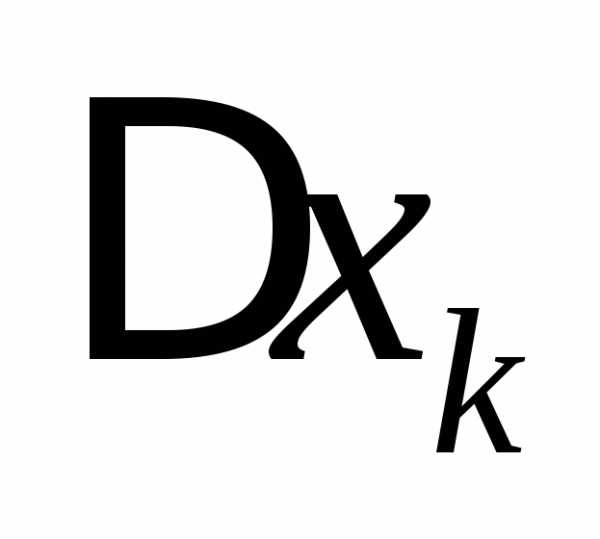 стремятся к нулю,).
стремятся к нулю,).
Сумма вида (*)называется интегральной суммой, а
предел, к которому стремится
последовательность интегральных сумм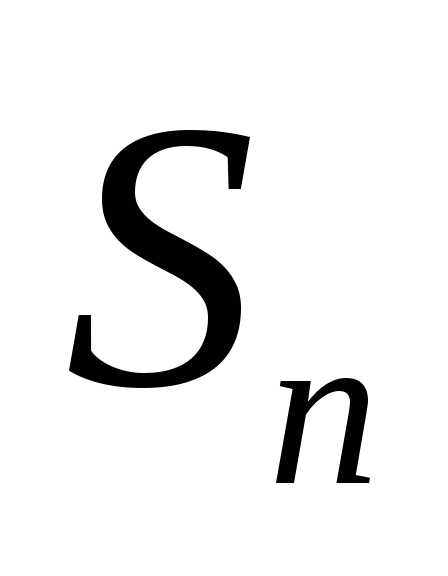 при,
если такой предел существует, называется
определенным интегралом функцииf(x)
на отрезке [a,b] и обозначается
символом(читается – интеграл отaдоbфункцииf(x)).
при,
если такой предел существует, называется
определенным интегралом функцииf(x)
на отрезке [a,b] и обозначается
символом(читается – интеграл отaдоbфункцииf(x)).
Итак,
.
Замечание.Мы
рассмотрели здесь только частный случай
последовательности интегральных сумм:
разбиение отрезка [a,b] сделано
так, что все(k=1, 2,…,n) равны между собой,, точки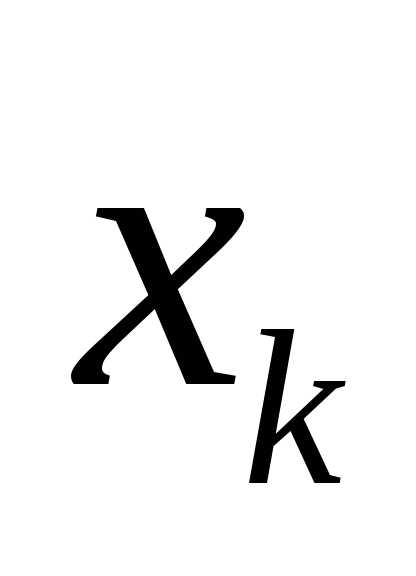 являются правыми концами промежутка,
а функцияf(x) – непрерывна и
неотрицательна. Вообще говоря,
рассматриваются интегральные суммы
более общего вида, а именно:
являются правыми концами промежутка,
а функцияf(x) – непрерывна и
неотрицательна. Вообще говоря,
рассматриваются интегральные суммы
более общего вида, а именно:
1) точки деления выбираются произвольно, не обязательно на равном расстоянии друг от друга;
2) на каждом отрезке
длинывыбирается произвольная точка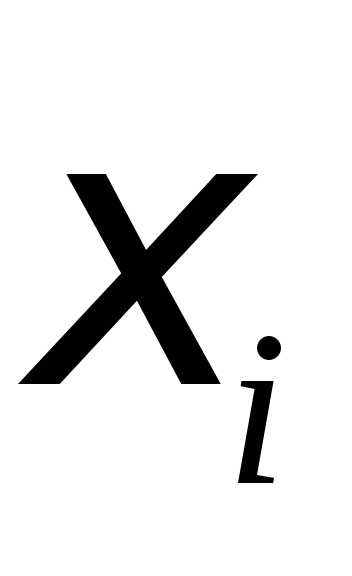 ;
;
3) сумму называют интегральной суммой (Римана) для функцииf(x) на отрезке [a, b];
4) определенным интеграломназывается такое числоI, которое удовлетворяет условию: для любого (сколь угодно малого) положительного числанайдется такое положительное числоδ, что прии любом выборе точеквыполняется неравенство
.
Фактически определенный интеграл Iявляется пределом интегральных сумм при стремлении к нулю всех отрезков разбиения, если этот предел существует и не зависит от выбора точек деленияи выбора точек.
Функции f(x), для которых определенный интегралсуществует, называются интегрируемыми (по Риману) на отрезке [a,b]. К таким функциям относятся любые непрерывные на [a,b] функции, а также кусочно-непрерывные, т.е. имеющие на отрезке интегрирования лишь конечное число точек разрыва первого рода. Очевидно, что интегрируемые на отрезке функции ограничены на этом отрезке.
Возвращаясь к задаче о площади, с которой мы начали, видим, что площадь криволинейной трапеции, ограниченной непрерывной кривой y=f(x), гдена [a,b], численно равна определенному интегралу.
Этот факт выражает геометрический смысл определенного интеграла.
studfiles.net
16.4.3. Поверхностный интеграл первого рода (по площади поверхности).
16.4.3.1. Определение
поверхностного интеграла первого рода. Пусть в
пространстве переменных x,y,z задана
кусочно-гладкая поверхность  ,
на которой определена функция f(x,y,z). Разобьём
поверхность на
,
на которой определена функция f(x,y,z). Разобьём
поверхность на  частей ,
на каждой из частей
частей ,
на каждой из частей  выберем произвольную точку ,
найдём
и площадь части
выберем произвольную точку ,
найдём
и площадь части  (которую будем обозначать тем же символом
(которую будем обозначать тем же символом  ),
и составим интегральную сумму
),
и составим интегральную сумму 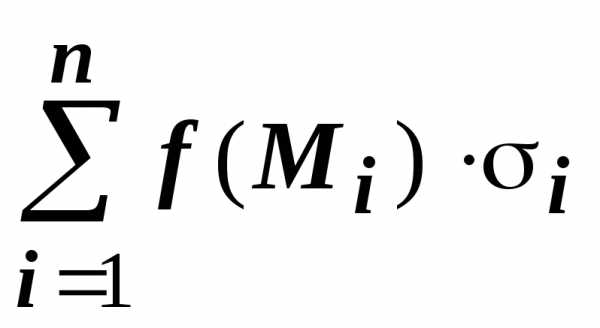 .
Если существует предел последовательности
интегральных сумм при ,
не зависящий ни от способа разбиения
поверхности
.
Если существует предел последовательности
интегральных сумм при ,
не зависящий ни от способа разбиения
поверхности  на части ,
ни от выбора точек
на части ,
ни от выбора точек 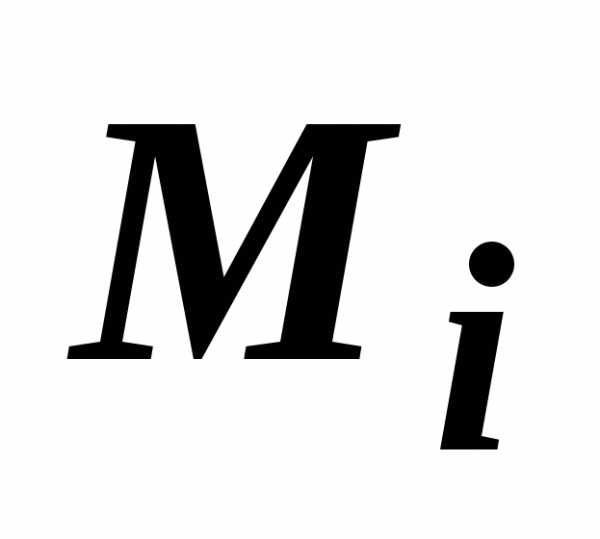 ,
то функция f(x,y,z)
называется интегрируемой по поверхности
,
то функция f(x,y,z)
называется интегрируемой по поверхности  ,
а значение этого предела называется
поверхностным интегралом первого рода,
или поверхностным интегралом по площади
поверхности, и обозначается
,
а значение этого предела называется
поверхностным интегралом первого рода,
или поверхностным интегралом по площади
поверхности, и обозначается 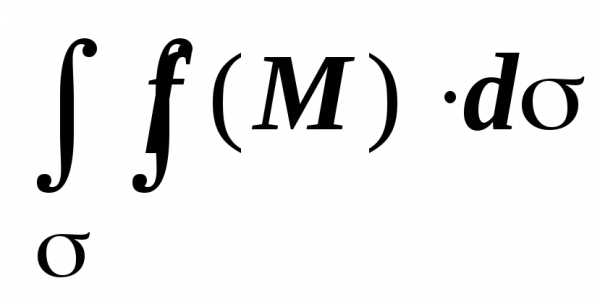 .
.
Теорема
существования. Если функция f(x,y,z)
непрерывна на поверхности  ,
то она интегрируема по этой поверхности.
,
то она интегрируема по этой поверхности.
16.4.3.2. Свойства поверхностного интеграла первого рода. Для этого интеграла имеют место основные шесть свойств, справедливых для определённого, двойного, тройного интеграла, от линейности до теоремы о среднем. Сформулировать и доказать их самостоятельно. Седьмое, персональное, свойство — независимость поверхностного интеграла первого рода от выбора стороны поверхности.
16.4.3.3. Вычисление поверхностного интеграла первого рода.
16.4.3.3.1. Определение
единичного вектора нормали к поверхности.
Выражения для элемента площади
поверхности. Предположим,
что поверхность  задаётся неявным уравнением
(
— непрерывно дифференцируемая функция)
и взаимно однозначно проецируется в
область
задаётся неявным уравнением
(
— непрерывно дифференцируемая функция)
и взаимно однозначно проецируется в
область 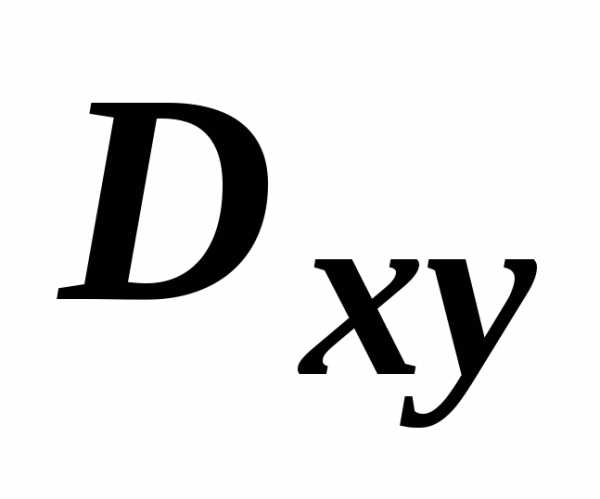 на плоскости Оху. Из
теории функций нескольких переменных
известно, что градиент функции ортогонален
поверхности уровня этой функции,
проходящей через точку, в которой найден
градиент. Рассматривая уравнение
как уравнение поверхности уровня функции
трёх переменных ,
получаем, что в каждой точке поверхности
на плоскости Оху. Из
теории функций нескольких переменных
известно, что градиент функции ортогонален
поверхности уровня этой функции,
проходящей через точку, в которой найден
градиент. Рассматривая уравнение
как уравнение поверхности уровня функции
трёх переменных ,
получаем, что в каждой точке поверхности  ортогонален
ортогонален  ,
т.е. является нормальным к
,
т.е. является нормальным к  вектором. Чтобы получить единичный
нормальный вектор, достаточно просто
пронормировать :
,
где знак перед дробью соответствует
возможности выбора двух возможных
взаимно противоположных направлений
нормали. В координатной форме
вектором. Чтобы получить единичный
нормальный вектор, достаточно просто
пронормировать :
,
где знак перед дробью соответствует
возможности выбора двух возможных
взаимно противоположных направлений
нормали. В координатной форме 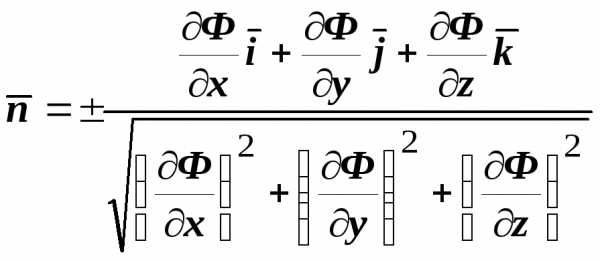 ,
где
,
где 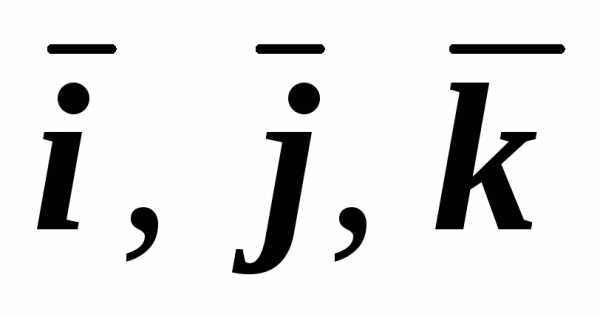 — базисные орты. Если сравнить это
выражение с представлением градиента
через направляющие косинусы: ,
то
— базисные орты. Если сравнить это
выражение с представлением градиента
через направляющие косинусы: ,
то 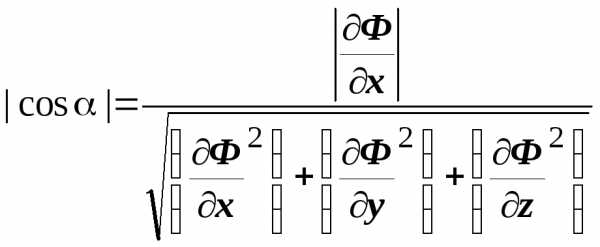 ,
, 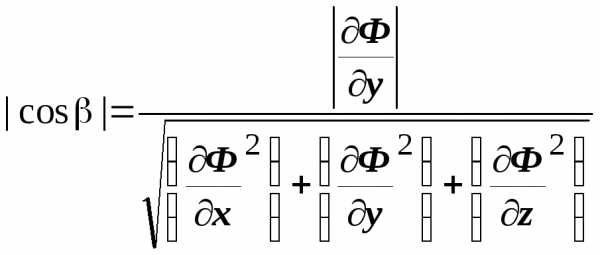 ,
, 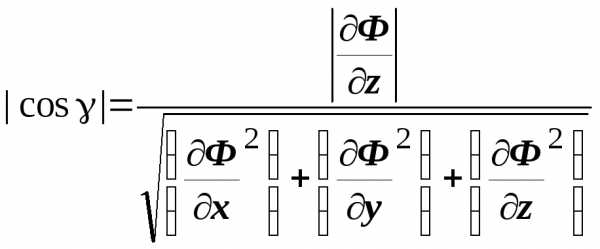 .
Теперь мы можем выразить элемент площади
поверхности через элемент площади в
каждой координатной плоскости: ,
,
.
В частном случае задания уравнения
поверхности в явном виде
получим ,
т.е. ,
.
Теперь мы можем выразить элемент площади
поверхности через элемент площади в
каждой координатной плоскости: ,
,
.
В частном случае задания уравнения
поверхности в явном виде
получим ,
т.е. , 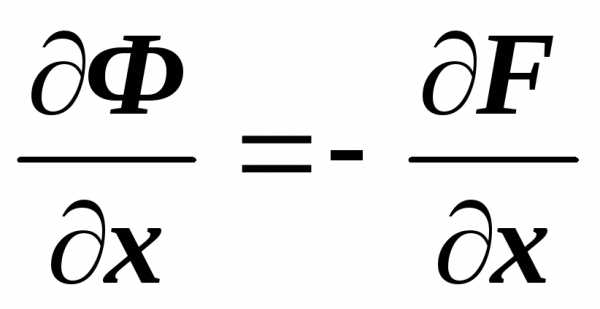 ,
, 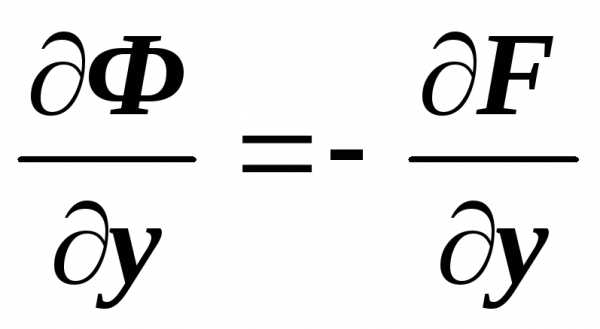 ,
, 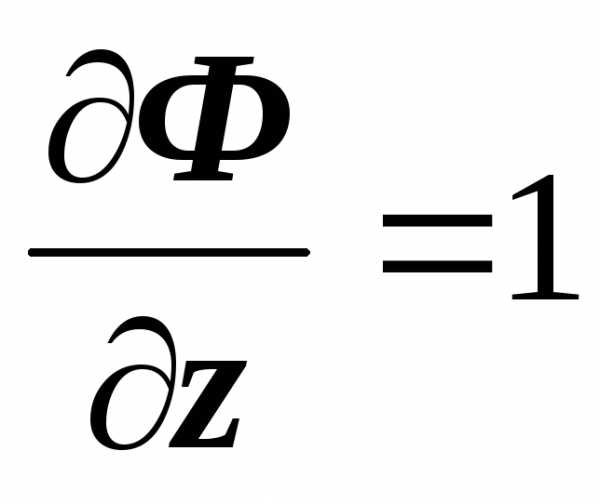 ,
поэтому ,
,
,
поэтому ,
, 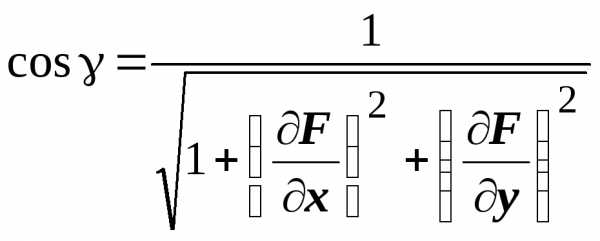 ,
и .
Мы уже пользовались этой формулой при
вычислении площади поверхности с помощью
двойного интеграла.
,
и .
Мы уже пользовались этой формулой при
вычислении площади поверхности с помощью
двойного интеграла.
16.4.3.3.2.
Выражение поверхностного интеграла
через двойной интеграл по проекции
поверхности на координатную плоскость.Пусть поверхность  взаимно однозначно проецируется в
область
взаимно однозначно проецируется в
область 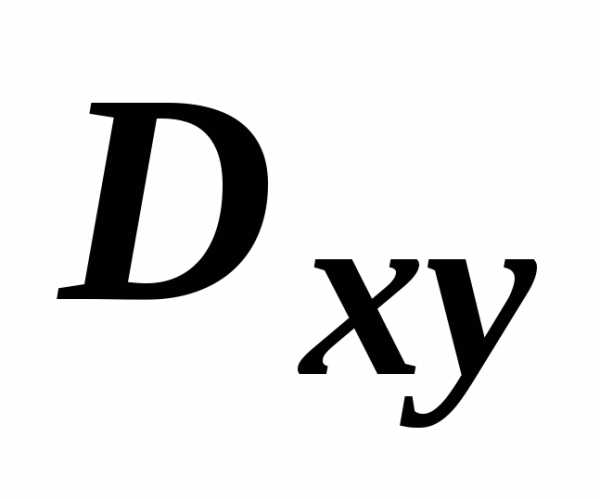 на плоскости Оху. Будем
считать, что поверхность задана уравнением
,
.
В интегральной сумме
на плоскости Оху. Будем
считать, что поверхность задана уравнением
,
.
В интегральной сумме 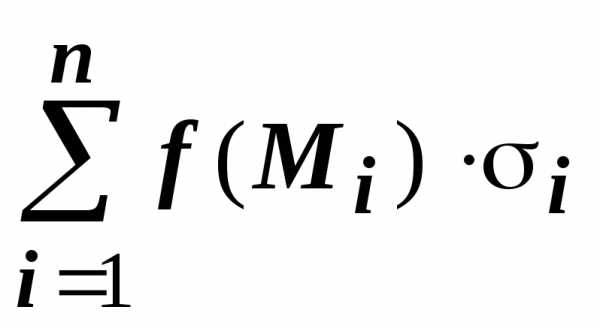 выразим площадь
выразим площадь  через двойной интеграл по её проекции
через двойной интеграл по её проекции 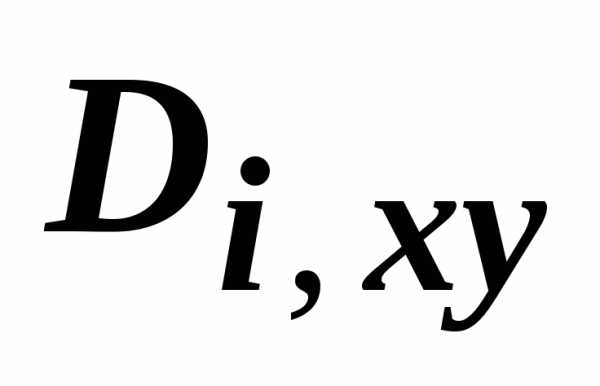 на плоскость Оху:
.
Применим к этому интегралу теорему о
среднем: существует точка
такая, что .
Значение подынтегральной функции
будем вычислять в точке ,
такой, что .
Тогда .
на плоскость Оху:
.
Применим к этому интегралу теорему о
среднем: существует точка
такая, что .
Значение подынтегральной функции
будем вычислять в точке ,
такой, что .
Тогда .
Слева стоит интегральная сумма для поверхностного интеграла, справа — для двойного; переход к пределу при (при этом и ) даёт
.
Эта формула и применяется для вычисления поверхностных интегралов. Естественно, в каждой задаче надо выбирать, на какую из координатных плоскостей предпочтительней проецировать поверхность; если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.
Примеры. 1. Найти 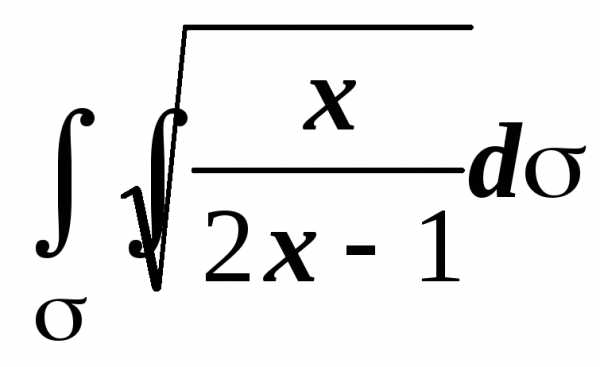 ,
где
— часть цилиндра x2 + z2 = 2x,
вырезаемая гиперболоидом x2 — y2 + z2 = 1 и
плоскостью z = 0 (z > 0).
,
где
— часть цилиндра x2 + z2 = 2x,
вырезаемая гиперболоидом x2 — y2 + z2 = 1 и
плоскостью z = 0 (z > 0).
Решение: Найдем проекцию поверхности на плоскость OXY. Исключим из уравнений цилиндра и гиперболоида переменную z:
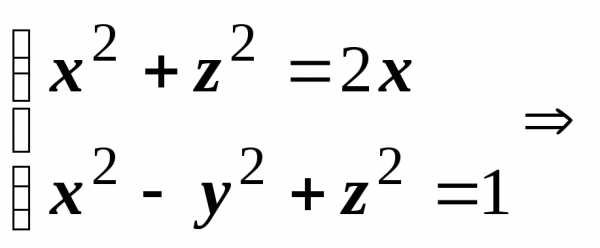 2x = y2+1
— уравнение проекции линии пересечения
двух поверхностей на OXY.
П
2x = y2+1
— уравнение проекции линии пересечения
двух поверхностей на OXY.
П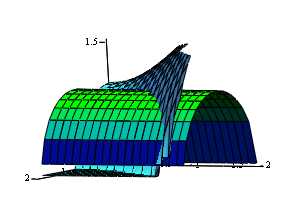 олагая
в уравнении цилиндраz = 0, получим уравнение линии пересечения
цилиндра и плоскости OXY.
Таким образом, поверхность
проецируется в область D,
ограниченную параболой x =
олагая
в уравнении цилиндраz = 0, получим уравнение линии пересечения
цилиндра и плоскости OXY.
Таким образом, поверхность
проецируется в область D,
ограниченную параболой x =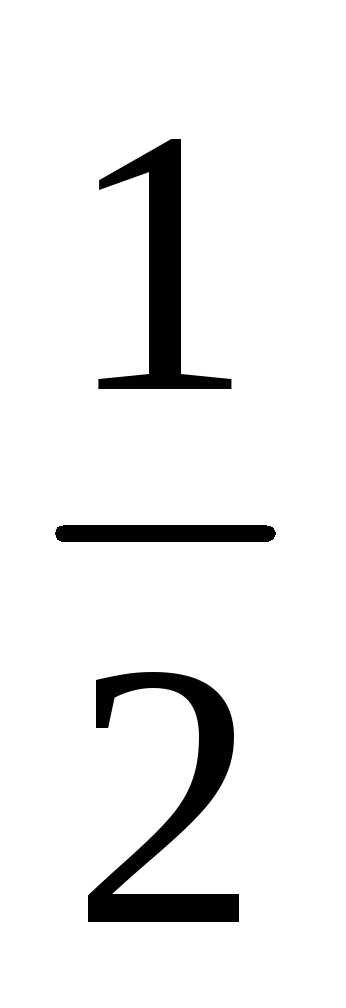 (y2+1)
и прямой x=2.
Часть цилиндра, удовлетворяющая условию z>0,
задается уравнением z =
(y2+1)
и прямой x=2.
Часть цилиндра, удовлетворяющая условию z>0,
задается уравнением z = 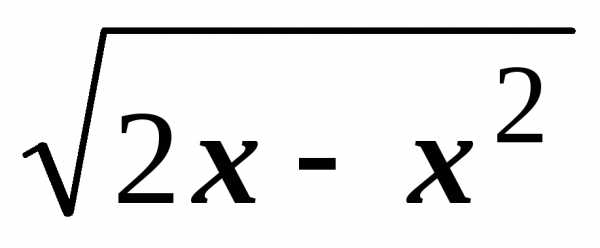 .
Тогда
.
Тогда 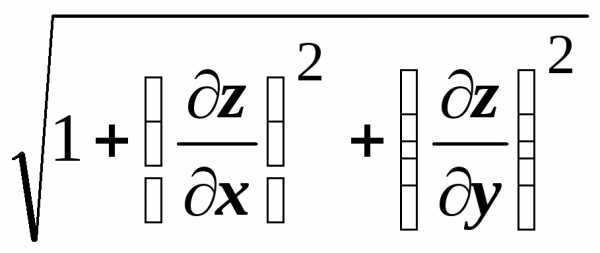 =
=  =
=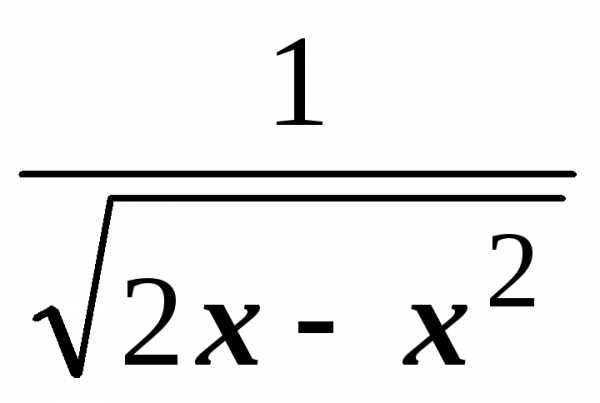 .
Таким образом, .
.
Таким образом, .
2.
Найти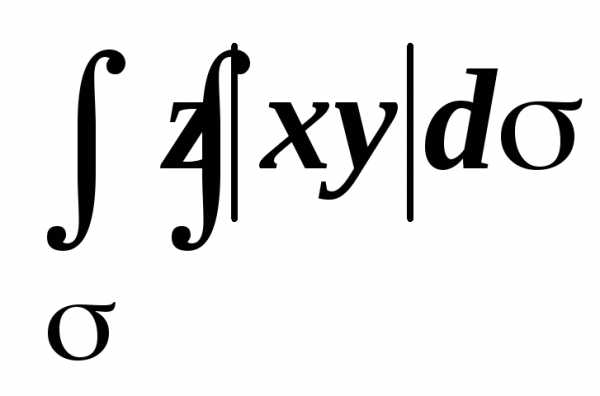 ,
где
— полная поверхность цилиндра x2+y2 = 1, 0 ≤ z ≤
1.
,
где
— полная поверхность цилиндра x2+y2 = 1, 0 ≤ z ≤
1.
Решение:
Искомый интеграл равен сумме трех
интегралов: по нижнему и верхнему
основаниям 1 и 2 и боковой поверхности (рис.18). Так как
на нижнем основании z=0, то 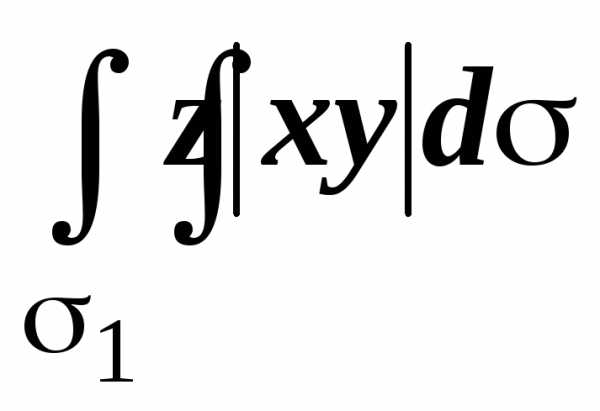 =0.
Для верхнего основания2 имеем z(x,y)=1,
=0.
Для верхнего основания2 имеем z(x,y)=1, 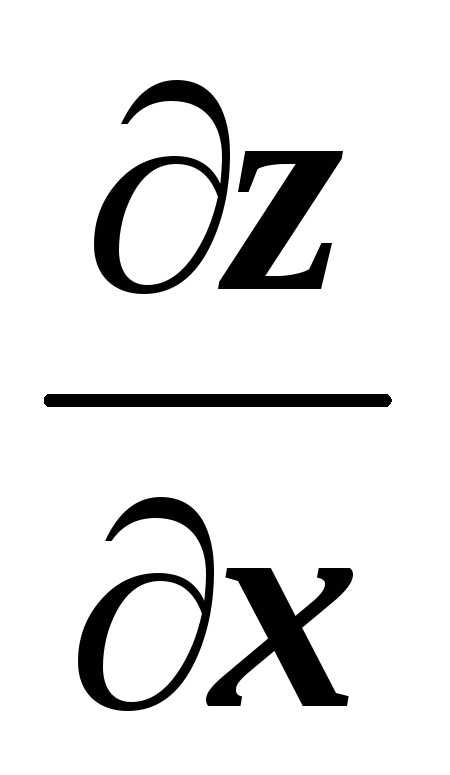 =
=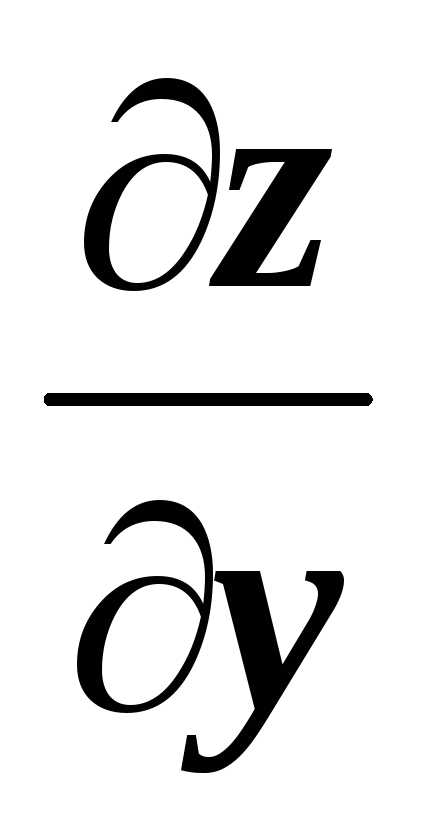 =0,
поэтому поверхностный интеграл по2 совпадает с двойным интегралом от
функции z(x,y)|xy|
= |xy|,
взятым по кругу D ={x2+ y2<1}:
=0,
поэтому поверхностный интеграл по2 совпадает с двойным интегралом от
функции z(x,y)|xy|
= |xy|,
взятым по кругу D ={x2+ y2<1}:
Найдем интеграл по боковой поверхности. Она состоит из двух частей: 3 и 4 , симметричных относительно плоскости OYZ. Так как функция z|xy| — четная по x, то интегралы по 3 и 4 равны.
Проекция 3 на плоскость OYZ — прямоугольник D:{-1
≤ у ≤
1, 0 ≤ z ≤1}.
Уравнение 3 : х=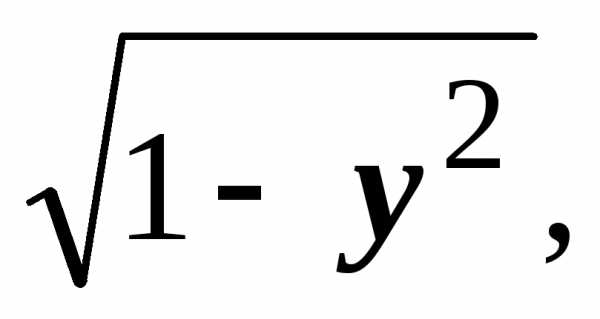 Отсюда:
Отсюда:
Окончательно получаем:
3. Найти 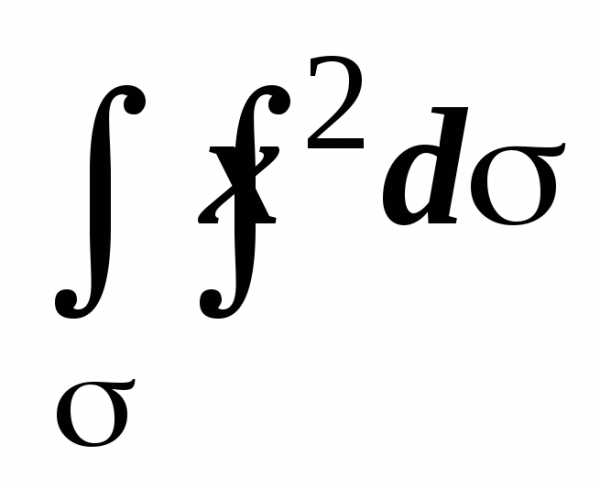 ,
где
— сфера x2 + y2 + z2 = R2.
,
где
— сфера x2 + y2 + z2 = R2.
Решение: Использование соображений симметрии позволяет иногда существенно упростить вычисление интегралов. Очевидно, что для сферы . Тогда
studfiles.net
