Интегрирование по частям, формулы и примеры решений
Содержание:
- Объяснение
- Примеры решения интегралов данным методом
Рассмотрим функции $u=u(x)$ и $v=v(x)$, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
$d(u v)=u d v+v d u$
Проинтегрировав левую и правую части последнего равенства, получим:
$\int d(u v)=\int(u d v+v d u) \Rightarrow u v=\int u d v+\int v d u$
Полученное равенство перепишем в виде:
$\int u d v=u v-\int v d u$
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл $\int u d v$ можно свести к нахождению интеграла $\int v d u$, который может быть более простым.
Замечание
В некоторых случаях формулу интегрирования частями нужно применять неоднократно.
Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:
1) $\int P_{n}(x) e^{k x} d x$ ; $\int P_{n}(x) \sin (k x) d x$ ; $\int P_{n}(x) \cos (k x) d x$
Здесь $P_{n}(x)$ — многочлен степени
$n$,
$k$ — некоторая константа.
{2}-1\right) \sin x+2 x \cos x+C$
2)$\int P_{n}(x) \arcsin x d x$ ; $\int P_{n}(x) \arccos x d x$ ; $\int P_{n}(x) \ln x d x$
Здесь принимают, что $d v=P_{n}(x) d x$, а в качестве $u$ оставшиеся сомножители.
Пример
Задание. Найти интеграл $\int \ln x d x$
Решение. В исходном интеграле выделим функции $u$ и $v$, затем выполним интегрирование по частям.
$$\int \ln x d x\left\|\begin{array}{l} u=\ln x \quad d v=d x \\ d u=\frac{d x}{x} \quad v=x \end{array} \quad\right\|=x \ln x-\int x \cdot \frac{d x}{x}=$$
$=x \ln x-\int d x=x \ln x-x+C=x(\ln x-1)+C$
Ответ. $\int \ln x d x=x(\ln x-1)+C$
Больше примеров решений Решение интегралов онлайн
Пример
Задание. Найти интеграл $\int \arcsin x d x$
Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям.
{2 x+1} \sin x}{5}+C$
Больше примеров решений Решение интегралов онлайн
Читать дальше: простейшие дроби.
Интегрирование по частям: объяснение, решение примеров
- Суть метода интегрирования по частям
- Применяем интегрирование по частям вместе
- Применить интегрирование по частям самостоятельно, а затем посмотреть решение
- Снова применяем интегрирование по частям вместе
- Интегрирование по частям для вывода рекуррентных формул
Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:
Для
применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя.
Один из них обозначается через u, а остальная часть относится ко второму множителю и
обозначается через dv. Затем дифференцированием находится du и интегрированием —
функция v.
При этом за u следует брать такую часть подынтегральной функции,
которая при дифференцировании сильно не усложняется, а за dv — такую часть подынтегрального
выражения, которая легко интегрируется.
Когда выгодно применять метод интегрирования по частям? Тогда, когда подынтегральная функция содержит:
1) — логарифмические
функции, а также обратные тригонометрические функции (с приставкой «arc»), тогда на основании продолжительного опыта
интегрирования по частям эти функции обозначаются через
2) , , — синус, косинус и экспоненту, умноженные на P(x) — произвольный многочлен от икса, тогда эти функции обозначают через dv, а многочлен — через u;
3) , , , , в этом случае интегрирование по частям применяется дважды.
Поясним ценность метода интегрирования по частям на примере первого случая.
Пусть выражение
под знаком интеграла содержит логарифмическую функцию (таким будет пример 1). Применением интегрирования по частям
такой интеграл сводится вычислению интеграла только алгебраических функций (чаще всего многочлена), то есть
не содержащих логарифмическую или обратную тригонометрическую функцию. Применяя данную
в самом начале урока формулу интегрирования по частям
,
получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) — функцию, не содержащую логарифма. Интеграл алгебраической функции намного проще интеграла, под знаком которого находятся отдельно или вместе с алгебраическим множителем логарифмическая или обратная тригонометрическая функция.
Таким образом, с помощью формулы интегрирования по частям интегрирование не выполняется сразу:
нахождение данного интеграла сводится к нахождению другого. Смысл формулы интегрирования по частям
состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал
проще первоначального.
Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций:
то её можно записать в виде
,
который и был приведён в самом начале урока.
При нахождении интегрированием функции v для неё получается бесконечное множество первообразных функций. Чтобы применить формулу интегрирования по частям, можно взять любую из них, а значит, и ту, которая соответствует произвольной постоянной С, равной нулю. Поэтому при нахождении функции v произвольную постоянную С вводить не следует.
Есть у метода интегрирования по частям совершенно особенное применение: с его помощью
можно выводить рекуррентные формулы для нахождения первообразных функций, когда требуется понизить степень функций
под знаком интеграла. Понижение степени необходимо, когда не существует табличных интегралов для таких, например,
функций, как синусы и косинусы в степени более второй и их произведения.
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 1. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. В подынтегральном выражении — логарифм, который, как мы уже знаем, разумно обозначить через u. Полагаем, что , .
Тогда , .
Находим (как уже говорилось в пояснении к теоретической справке, сразу же получаем в первом слагаемом
(без интеграла) логарифмическую функцию, а во втором слагаемом
(под знаком интеграла) — функцию, не содержащую логарифма, сводящуюся к
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
И снова логарифм…
Пример 2. Найти неопределённый интеграл:
.
Решение. Пусть , .
Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как
сложную функцию. Находим, пользуясь производной 6 в таблице производных сложных функций:
,
.
Применяя формулу интегрирования по частям, получаем:
Второй интеграл вновь находим по частям и получаем уже упомянутое преимущество (в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) — функцию, не содержащую логарифма, сводящуюся к табличному интегралу 9).
Находим изначальный интеграл:
Пример 3. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Арктангенс, как и логарифм, лучше обозначить через u. Итак, пусть , .
Тогда, пользуясь табличной производной 12, получаем
,
.
Применяя формулу интегрирования по частям, получаем:
Второй интеграл находим методом замены переменной
Возвращаясь к переменной x, получаем
.
Находим изначальный интеграл:
.
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
Пример 4. Найти неопределённый интеграл методом интегрирования по частям:
Решение. Экспоненту лучше обозначить через dv. Разбиваем подынтегральное выражение на два множителя. Полагая, что
находим
(воспользовались табличной производной 16).
- Пригодится: тригонометрические тождества для преобразования выражений
Нет времени вникать в решение? Можно заказать работу!
Пример 5. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Пусть , . Тогда , (воспользовались табличной производной 4 в таблице производных сложной функции).
Используя формулу интегрирования по частям (1), находим:
Пример 6. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Синус, как и экспоненту, удобно обозначить через dv. Пусть , .
Тогда , .
По формуле интегрирования по частям находим:
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 7.
Найти неопределённый интеграл методом интегрирования по частям:
.
Посмотреть правильное решение и ответ.
Пример 8. Найти неопределённый интеграл методом интегрирования по частям:
.
Посмотреть правильное решение и ответ.
Пример 9. Найти неопределённый интеграл методом интегрирования по частям:
.
Посмотреть правильное решение и ответ.
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
Пример 10. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Как и во всех подобных случаях, косинус удобно обозначить через dv. Обозначаем
,
(производная 7 в
таблице производных сложной функции).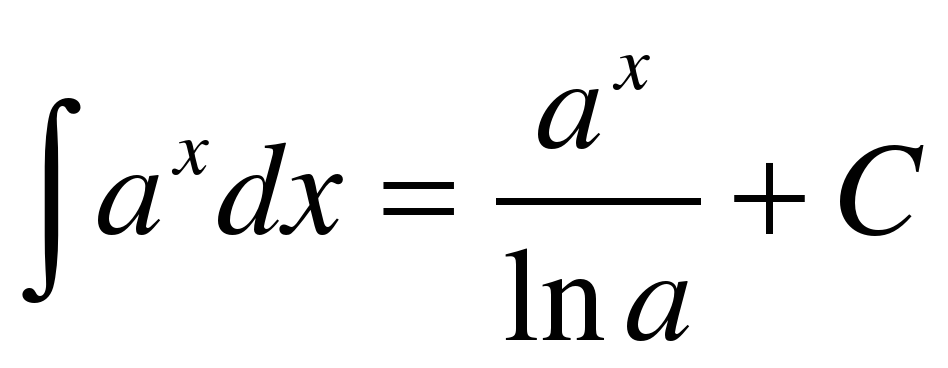
Тогда (табличные производные 3 и 2), ().
По формуле интегрирования по частям получаем:
Ко второму слагаемому также применяем интегрирование по частям. Обозначаем , .
Тогда , .
Применив эти обозначения, интегрируем упомянутое слагаемое:
Теперь находим требуемый интеграл:
Среди интегралов, которые можно решить методом интегрирования по частям, есть и такие,
которые не входят ни в одну из трёх упомянутых в теоретической части групп, относительно которых из
практики известно, что лучше обозначать через u, а что через dv. Поэтому в этих случаях
нужно пользоваться соображением удобства, также приведённым в параграфе «Суть метода интегрирования по частям»:
за u следует брать такую часть подынтегральной функции,
которая при дифференцировании сильно не усложняется, а за dv — такую часть подынтегрального
выражения, которая легко интегрируется.
Последний пример этого урока — решение именно такого интеграла.
Пример 11. Найти неопределённый интеграл методом интегрирования по частям:
.
Решение. Примем как руководство к действию общее соображение относительно обозначений. Обозначаем , (табличная производная 8).
Тогда , .
По формуле интегрирования по частям получаем:
- Пригодится: тригонометрические тождества для преобразования выражений
Случаев, когда требуется понижения степени подынтегральной функции, мы уже коснулись во вводной части урока. Теперь — практика использования для этой цели метода интегрирования по частям.
Пример 12. Используя интегрирование по частям, вывести рекуррентную формулу для
,
найти I4.
Решение.
Для удобства приведём исходный интеграл к такому выражению, в котором присутствовали
бы и синус, и косинус. Используя тригонометрические тождества, получаем
Ко второму слагаемому — интегралу — применяем метод интегрирования по частям. Для этого обозначим
Тогда
Находим это второе слагаемое — интеграл:
Теперь находим рекуррентную формулу для исходного интеграла:
С помощью полученной формулы найдём I4:
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Интеграл
Начало темы «Интеграл»
Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов
Найти неопределённый интеграл: начала начал, примеры решений
Метод замены переменной в неопределённом интеграле
Интегрирование подведением под знак дифференциала
Продолжение темы «Интеграл»
Интегрирование дробей
Интегрирование рациональных функций и метод неопределённых коэффициентов
Интегрирование некоторых иррациональных функций
Интегрирование тригонометрических функций
Определённый интеграл
Несобственные интегралы
Площадь плоской фигуры с помощью интеграла
Объём тела вращения с помощью интеграла
Вычисление двойных интегралов
Длина дуги кривой с помощью интеграла
Площадь поверхности вращения с помощью интеграла
Определение работы силы с помощью интеграла
Поделиться с друзьями
Правила интеграции
Интеграция
Интеграцию можно использовать для поиска площадей, объемов, центральных точек и многих других полезных вещей.
Он часто используется для нахождения области под графиком функции и оси x .
Первое правило, которое нужно знать, это то, что интегралы и производные противоположны!
Иногда мы можем вычислить интеграл,
потому что мы знаем соответствующую производную.
Правила интеграции
Вот наиболее полезные правила с примерами ниже:
| Общие функции | Функция | Интеграл |
|---|---|---|
| Константа | ∫а дх | топор + С |
| Переменная | ∫x дх | x 2 /2 + С |
| Квадрат | ∫x 2 дх | x 3 /3 + С |
| Взаимное | ∫(1/х) дх | лн|х| + С |
| Экспоненциальный | ∫е х дх | е х + С |
| ∫а х дх | а х /ln(а) + С | |
| ∫ln(x)dx | х пер(х) — х + С | |
| Тригонометрия (x в радианах) | ∫cos(x) дх | грех(х) + С |
| ∫sin(x)dx | -cos(x) + С | |
| ∫сек 2 (х) дх | загар(х) + С | |
| Правила | Функция | Интеграл |
| Умножение на константу | ∫cf(x)dx | c∫f(x)dx |
| Степенное правило (n≠−1) | ∫x п дх | x n+1 n+1 + C |
| Правило суммы | ∫(f + g) дх | ∫f дх + ∫g дх |
| Правило различия | ∫(е — г) дх | ∫f дх — ∫g дх |
| Интеграция по частям | См. Интеграция по частям | |
| Правило замены | См. Интеграция путем замены | |
Примеры
Пример: чему равен интеграл sin(x) ?
Из приведенной выше таблицы это указано как −cos(x) + C
Записано как:
∫sin(x) dx = −cos(x) + C
Пример: чему равен интеграл от 1/x ?
В приведенной выше таблице указан номер 9.0007 лн|х| + C
Записывается как:
∫(1/x) dx = ln|x| + C
Вертикальные стойки || по обе стороны от x означают абсолютное значение, потому что мы не хотим придавать отрицательные значения функции натурального логарифма ln .
Силовое правило
Пример: Что такое ∫x
3 dx ?Вопрос: «Какой интеграл от x 3 ?»
Мы можем использовать правило мощности, где n=3:
∫x N DX = x N + 1 N + 1 + C
∫x 3 DX = x 4 4 166161666.
X 4 4 4 6666661666.
Пример: Что такое ∫√x dx ?
√x также x 0,5
Мы можем использовать правило мощности, где n = 0,5:
∫x N DX = x N+1 n+1 +C+C+1 N+1 +1 +1 +1 +1
∫x 0,5 dx = x 1,5 1,5 + C
Умножение на константу
Пример: Что такое ∫6x
2 dx ?Мы можем переместить 6 за пределами интеграла:
∫6x 2 DX = 6∫x 2 DX
и теперь используйте правило мощности на X 2 :
= 6 x 3 . 3 + C
Упрощение:
= 2x 3 + C
Правило суммы
Пример: Что такое ∫(cos x + x) dx ?
Используйте правило суммы:
∫(cos x + x) dx = ∫cos x dx + ∫x dx
Вычислите интеграл каждого из них (используя таблицу выше):
= sin x + x 2 /2 + C
Правило различия
Пример: Что такое ∫(e
w − 3) dw ?Используйте правило разности:
∫(e w − 3) dw =∫e w dw − ∫3 dw
Затем вычислите интеграл каждого (используя таблицу выше):
= e ш
— 3ш + ССумма, разность, постоянное умножение и правила степени
Пример: Что такое ∫(8z + 4z
3 − 6z 2 ) dz ?Используйте правило суммы и разности:
∫ (8Z + 4Z 3 — 6Z 2 ) DZ = ∫8Z DZ + ∫4Z 3 DZ — 2 DZ
9004= 8∫Z DZ + 4∫Z 3 DZ — 6∫Z 2 DZ
Правило мощности:
= 8Z 2 /2 + 4Z 4 /4 — 6Z 3 /3Z 4 /4 — 6Z 3 /3 + C
Упрощение:
= 4z 2 + з 4 − 2з 3 + С
Интеграция по частям
См.
Интеграция по частям
Правило замены
См. Интеграция путем замены
Заключительный совет
- Много практики
- Не забудьте dx (или dz и т. д.)
- Не забудьте + C
6834, 6835, 6836, 6837, 6838, 6839, 6840, 6841, 6842, 6843
Интегралы как умножение – BetterExplained
Интегралы часто описываются как нахождение площади под кривой. Это описание слишком узкое: это все равно, что сказать, что умножение существует для нахождения площади прямоугольников. Поиск площади является полезным приложением , но не целью умножения.
Основная идея: интегралы помогают нам комбинировать числа, когда умножение не может.
Хотел бы я побыть наедине с собой в школьном исчислении:
«Псс! Интегралы позволяют «перемножать» изменяющиеся числа. Мы привыкли к «3 x 4 = 12», но что, если одна величина меняется? Мы не можем умножать изменяющиеся числа, поэтому интегрируем.
Вы я буду слышать много разговоров о площади — площадь — это просто один из способов визуализировать умножение. Ключ не в площади, а в идее объединения величин в новый результат. Мы можем интегрировать («умножить») длину и ширину, чтобы получить простую старую площадь, конечно. Но мы можем интегрировать скорость и время, чтобы получить расстояние, или длину, ширину и высоту, чтобы получить объем.0005
Когда мы хотим использовать обычное умножение, но не можем, мы достаем большую пушку и интегрируем. Площадь — это просто техника визуализации , не слишком зацикливайтесь на ней. А теперь иди, изучай исчисление!»
Это мой ага-момент: интегрирование — это «лучшее умножение», которое работает с вещами, которые изменяются. Давайте научимся видеть интегралы в этом свете. время:
- Для целых чисел (3 x 4) умножение равно повторному сложению
- С действительными числами (3,12 x $\sqrt{2}$) умножение равно в масштабе
- С отрицательными числами (-2,3 * 4,3) умножение равно с переворотом и масштабированием
- С комплексными числами (3 * 3i) умножение равно вращению и масштабированию
Мы движемся к общему понятию «применения» одного числа к другому, и свойства, которые мы применяем (повторяющийся счет, масштабирование, переворачивание или вращение), могут различаться.
Интеграция — еще один шаг на этом пути.
Понимание области
Область — это детальная тема. На сегодня давайте посмотрим на площадь как визуальное представление умножения :
С каждым счетом на другой оси мы можем «применить их» (3 применительно к 4) и получить результат (12 квадратных единиц). Свойства каждого входа (длина и длина) переносились в результат (квадратные единицы).
Просто, правда? Ну, становится сложно. Умножение может привести к «отрицательной области» (3 x (-4) = -12), которой не существует.
Мы понимаем, что граф представляет собой представление умножения, и используем аналогию так, как она нам служит. Если бы все были слепы и у нас не было диаграмм, мы все равно могли бы прекрасно умножать. Площадь — это просто интерпретация.
Умножение по частям
Теперь давайте умножим 3 x 4,5:
Что происходит? Ну, 4,5 не считается, но мы можем использовать операцию «по частям». Если 3×4 = 3 + 3 + 3 + 3, то
3 x 4,5 = 3 + 3 + 3 + 3 + 3×0,5 = 3 + 3 + 3 + 3 + 1,5 = 13,5
Берем 3 (значение) 4,5 раза.
То есть мы объединили 3 с 4 целыми отрезками (3 х 4 = 12) и одним неполным отрезком (3 х 0,5 = 1,5).
Мы так привыкли к умножению, что забыли, насколько хорошо оно работает. Мы можем разбить число на части (целые и частичные), умножить каждую часть и сложить результаты. Заметили, как мы поступили с дробной частью? Это начало интеграции.
Проблема с числами
Числа не всегда остаются на месте, чтобы мы могли их подсчитать. Сценарии типа «Вы едете со скоростью 30 миль в час в течение 3 часов» предназначены для удобства, а не для реализма.
Формулы типа «расстояние = скорость * время» только маскируют проблему; нам все еще нужно подключить статические числа и умножить. Так как же нам найти пройденное расстояние, если наша скорость меняется со временем?
Описание изменения
Наша первая задача — описать изменяющееся число. Мы не можем просто сказать: «Моя скорость изменилась с 0 до 30 миль в час». Это недостаточно конкретно: как быстро это меняется? Это гладко?
Теперь давайте конкретнее: каждую секунду я еду в два раза быстрее, чем в милях в час.
В 1 секунду я еду 2 мили в час. 2 секунды, 4 мили в час. 3 секунды это 6 миль в час, и так далее:
Это хорошее описание, достаточно подробное, чтобы в любой момент узнать мою скорость. Формальное описание: «скорость есть функция времени», что означает, что мы можем подключить любое время (t) и найти нашу скорость в этот момент («2t» миль в час).
(Это не говорит , почему скорость и время связаны. Возможно, я ускоряюсь из-за гравитации или из-за того, что меня тянет лама. Мы просто говорим, что с изменением времени меняется и наша скорость.)
Итак, наше умножение «расстояние = скорость * время», пожалуй, лучше записать:
где скорость(t) это скорость в любой момент. В нашем случае скорость(t) = 2t, поэтому мы пишем:
Но это уравнение все равно выглядит странно! «t» по-прежнему выглядит как одно мгновение, которое нам нужно выбрать (например, t = 3 секунды), что означает, что скорость (t) примет одно значение (6 миль в час).
Это не хорошо.
При обычном умножении мы можем взять одну скорость и предположить, что она справедлива для всего прямоугольника. Но изменяющаяся скорость требует от нас объединения скорости и времени по частям (посекундно). Ведь каждое мгновение могло быть разным.
Это большой сдвиг перспективы:
- Обычное умножение (прямоугольное): возьмите расстояние, пройденное за одну секунду, предположим, что оно одинаково для всех секунд, и «увеличьте его».
- Интеграция (по частям): смотрите на время как на серию мгновений, каждое из которых имеет свою собственную скорость. Сложите расстояние, пройденное за секунду за секундой.
Мы видим, что регулярное умножение является частным случаем интегрирования, когда величины не меняются.
Насколько велик «кусок»?
Насколько велик «кусок» при сборке по частям? Второй? Миллисекунда? Наносекунда?
Быстрый ответ: достаточно мало, чтобы значение выглядело одинаково на протяжении всего времени.
Нам не нужна идеальная точность.
Более длинный ответ: такие понятия, как пределы, были изобретены, чтобы помочь нам выполнять кусочное умножение. Хотя они и полезны, они являются решением проблемы и могут отвлекать от понимания «комбинирования вещей». Меня беспокоит, что ограничения вводятся в самом начале исчисления, до того, как мы понимаем проблему, для решения которой они были созданы (например, показать кому-то ремень безопасности еще до того, как он увидит машину). Конечно, это полезная идея, но Ньютон, похоже, довольно хорошо разбирался в исчислении и без них.
Что насчет начала и конца?
Допустим, мы рассматриваем интервал от 3 до 4 секунд.
Скорость в начале (3×2 = 6 миль в час) отличается от скорости в конце (4×2 = 8 миль в час). Итак, какое значение мы используем, когда делаем «скорость * время»?
Ответ заключается в том, что мы разбиваем наши фрагменты на достаточно маленькие куски (от 3,00000 до 3,00001 секунды) до тех пор, пока разница в скорости в начале и в конце интервала не будет иметь для нас значения.
Опять же, это более длинная дискуссия, но «поверьте мне», что есть период времени, который делает разницу бессмысленной.
На графике представьте каждый интервал как одну точку на линии. Вы можете нарисовать прямую линию для каждой скорости, и ваша «площадь» будет набором линий, которые измеряют умножение.
Где находится «кусок» и какова его стоимость?
Отделение части от ее значения было для меня проблемой.
«Кусок» — это рассматриваемый нами интервал (1 секунда, 1 миллисекунда, 1 наносекунда). «Позиция» — это место, где начинается этот секундный, миллисекундный или наносекундный интервал. Значение — это наша скорость в этой позиции.
Например, рассмотрим интервал от 3,0 до 4,0 секунд:
- «Ширина» отрезка времени составляет 1,0 секунды
- Позиция (начальное время) 3.0
- Значение (скорость(t)) равно скорости(3,0) = 6,0 миль в час
Опять же, исчисление позволяет нам сжимать интервал до тех пор, пока мы не сможем определить разницу в скорости в начале и в конце интервала.
Следите за более широкой картиной: мы умножаем коллекцию кусочков.
Понимание интегральной записи
У нас есть неплохое представление о «кусочном умножении», но мы не можем его выразить. «Расстояние = скорость (t) * t» по-прежнему выглядит как обычное уравнение, где t и скорость (t) принимают одно значение.
В исчислении мы записываем соотношение следующим образом:
Знак интеграла (кривая в форме буквы S) означает, что мы умножаем вещи по частям и складываем их вместе.
dt представляет конкретный «кусок» времени, который мы рассматриваем. Это называется «дельта t», а не «d умножить на t».
t представляет положение dt (если dt — это диапазон от 3,0 до 4,0, t равно 3,0).
скорость(t) представляет значение, на которое мы умножаем (скорость(3.0) = 6.0))
У меня есть несколько претензий к этому обозначению:
- То, как используются буквы, сбивает с толку.
«dt» выглядит как «d, умноженное на t», в отличие от всех уравнений, которые вы видели ранее. - Пишем скорость(t) * dt вместо скорости(t_dt) * dt. Последнее дает понять, что мы рассматриваем «t» в нашем конкретном фрагменте «dt», а не в какой-то глобальной «t» 9.0420
- Вы часто будете видеть $\int speed(t)$ с неявным dt. Это позволяет легко забыть, что мы выполняем пошаговое умножение на два элемента .
«dt» выглядит как «d, умноженное на t», в отличие от всех уравнений, которые вы видели ранее.Слишком поздно менять способ записи интегралов. Просто помните концепцию более высокого уровня «умножения» того, что изменяется.
Чтение в голове
Когда я вижу
, я думаю: «Расстояние равно скорости, умноженной на время» (читая сначала левую часть) или «объединить скорость и время, чтобы получить расстояние» (читая правую часть). первый).
Я мысленно перевожу «скорость(t)» в скорость и «dt» во время, и получается умножение, помня, что скорость может изменяться. Такое абстрагирование интеграции помогает мне сосредоточиться на том, что происходит («Мы комбинируем скорость и время, чтобы увеличить расстояние!»), а не на деталях операции.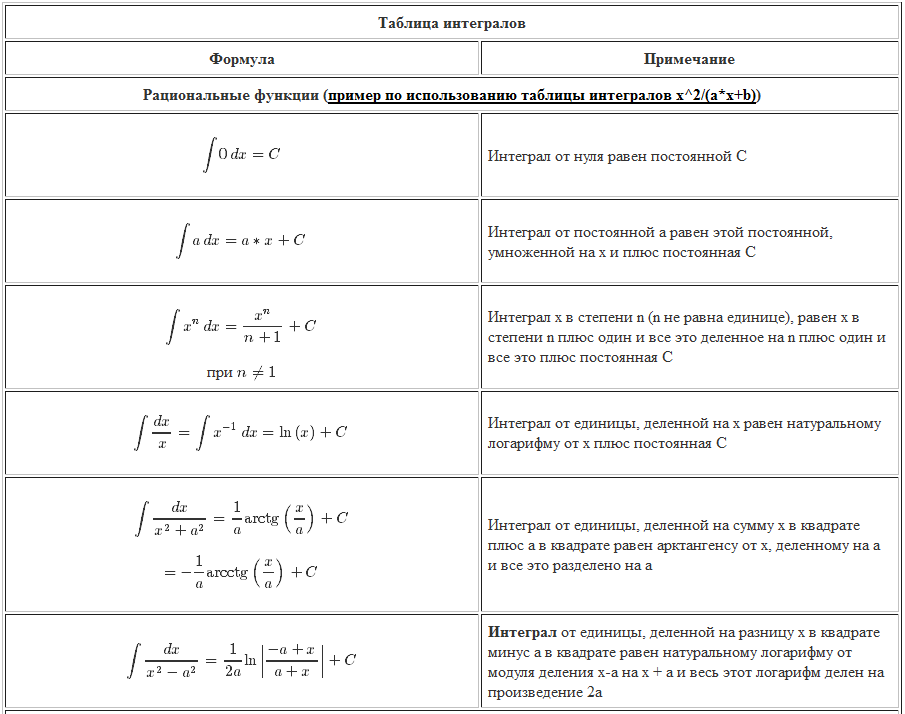
Бонус: последующие идеи
Интегралы — это глубокая идея, как и умножение. У вас могут возникнуть дополнительные вопросы, основанные на этой аналогии:
- Если интегралы умножают изменяющиеся величины, есть ли что-то, что их делит? (Да — производные)
- А интегралы (умножение) и производные (деление) сокращаются? (Да, с некоторыми оговорками).
- Можем ли мы изменить уравнения с «расстояние = скорость * время» на «скорость = расстояние/время»? (Да.)
- Можем ли мы объединить несколько изменяющихся вещей? (Да — это называется множественной интеграцией)
- Имеет ли значение порядок, в котором мы объединяем несколько вещей? (обычно нет)
Когда вы начинаете рассматривать интегралы как «лучшее умножение», вы начинаете искать такие понятия, как «лучшее деление», «повторное интегрирование» и так далее. Придерживаясь «области под кривой», эти темы кажутся несвязанными. (Для ботаников-математиков, рассматривающих «площадь под кривой» и «наклон» как обратные величины, это многого требует от студента).
Чтение интегралов
Интегралы имеют множество применений. Один из них — объяснить, что две вещи «умножаются» вместе, чтобы получить результат.
Вот как можно выразить площадь круга:
Мы хотели бы получить площадь круга с помощью умножения. Но мы не можем — высота меняется по ходу движения. Если мы «развернём» круг, мы увидим, что площадь, вносимая каждой частью радиуса, равна «радиус * длина окружности». Мы можем записать это соотношение, используя приведенный выше интеграл. (Подробнее см. Введение в исчисление).
А вот и интеграл, выражающий идею «масса = плотность * объем»:
О чем это говорит? Rho: $\rho$ — это функция плотности, говорящая нам, насколько плотен материал в определенном положении, r. dv — это бит объема, на который мы смотрим. Итак, мы умножаем небольшую часть объема (dv) на плотность в этой позиции $\rho(r)$ и складываем их все, чтобы получить массу.
Мы хотели бы умножить плотность и объем, но если плотность меняется, нам нужно интегрировать.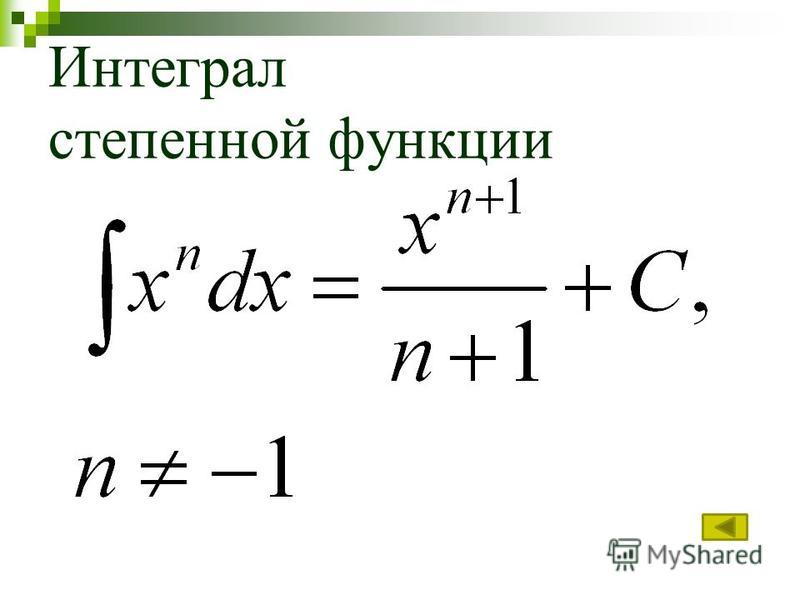
Нижний индекс V означает сокращение от «интеграла объема», который на самом деле представляет собой тройной интеграл длины, ширины и высоты! Интеграл включает четыре «умножения»: 3 для нахождения объема и еще одно для умножения на плотность.
Возможно, мы не решим эти уравнения, но сможем понять, что они выражают.
Вперед вверх
Сегодняшняя цель не в том, чтобы строго понять исчисление. Это чтобы расширить нашу ментальную модель и понять, что есть другой способ комбинировать вещи: мы можем складывать, вычитать, умножать, делить… и объединять.
Воспринимайте интегралы как лучший способ умножения: вычисления станут проще, и вы будете знать такие понятия, как множественные интегралы и производная. Счастливая математика.
(PS. Зак из SMBC изобразил себя в… ммм… комиксе об этой интуиции).
