Как решать интегралы для чайников, примеры решений
Как решать?
Процесс решения интегралов в науке под названием «математика» называется интегрированием. С помощью интегрирования можно находить некоторые физические величины: площадь, объем, массу тел и многое другое.
Интегралы бывают неопределенными и определенными. Рассмотрим вид определенного интеграла и попытаемся понять его физический смысл. Представляется он в таком виде: $$ \int ^a _b f(x) dx $$. Отличительная черта написание определенного интеграла от неопределенного в том, что есть пределы интегрирования a и b. Сейчас узнаем для чего они нужны, и что всё-таки значит определенный интеграл. В геометрическом смысле такой интеграл равен площади фигуры, ограниченной кривой f(x), линиями a и b, и осью Ох.
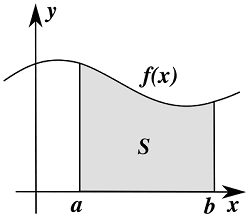
Из рис.1 видно, что определенный интеграл — это и есть та самая площадь, что закрашена серым цветом. Давайте, проверим это на простейшем примере. Найдем площадь фигуры на изображении представленном ниже с помощью интегрирования, а затем вычислим её обычным способом умножения длины на ширину.
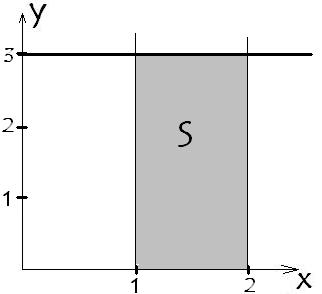
Из рис.2 видно, что $ y=f(x)=3 $, $ a=1, b=2 $. Теперь подставим их в определение интеграла, получаем, что $$ S=\int _a ^b f(x) dx = \int _1 ^2 3 dx = $$ $$ =(3x) \Big|_1 ^2=(3 \cdot 2)-(3 \cdot 1)=$$ $$=6-3=3 \text{ед}^2 $$ Сделаем проверку обычным способом. В нашем случае длина = 3, ширина фигуры = 1. $$ S = \text{длина} \cdot \text{ширина} = 3 \cdot 1 = 3 \text{ед}^2 $$ Как видим, всё отлично совпало.
Появляется вопрос: как решать интегралы неопределенные и какой у них смысл? Решение таких интегралов — это нахождение первообразных функций. Этот процесс противоположный нахождению производной. Для того, чтобы найти первообразную можно использовать нашу помощь в решении задач по математике или же необходимо самостоятельно безошибочно вызубрить свойства интегралов и таблицу интегрирования простейших элементарных функций. Нахождение выглядит так $$ \int f(x) dx = F(x) + C \text{где} F(x) $ — первообразная $ f(x), C = const $.
Для решения интеграла нужно интегрировать функцию $ f(x) $ по переменной. Если функция табличная, то записывается ответ в подходящем виде. Если же нет, то процесс сводится к получению табличной функции из функции $ f(x) $ путем хитрых математических преобразований. Для этого есть различные методы и свойства, которые рассмотрим далее.
Свойства интегралов
- Вынос константы из под знака интеграла: $$ $$ $$ \int Cg(x) dx = C\int g(x) dx $$
- Интеграл суммы/разности двух функций равен сумме/разности интегралов этих функций: $$ \int ( f(x) \pm g(x)) dx = \int f(x) dx \pm \int g(x) dx $$
- Изменение направления интегрирования: $$ \int _a ^b f(x) = -\int _b ^a f(x) dx $$
- Разбиение отрезка интегрирования: $$ \int_a^b f(x) dx = \int_a^c f(x) dx + \int_c^b f(x) dx $$ $$ c \in (a,b) $$
Итак, теперь составим алгоритм как решать интегралы для чайников?
Алгоритм вычисления интегралов
- Узнаем определенный интеграл или нет.
- Если неопределенный, то нужно найти первообразную функцию $ F(x) $ от подынтегральной $ f(x) $ с помощью математических преобразований приводящих к табличному виду функцию $ f(x) $.
- Если определенный, то нужно выполнить шаг 2, а затем подставить пределы $ а $ и $ b $ в первообразную функцию $ F(x) $. По какой формуле это сделать узнаете в статье «Формула Ньютона Лейбница».
Примеры решений
| Пример 1 |
| $$ \int x dx $$ |
| Решение |
$$ \int x dx = \frac{x^2}{2} + C, C=const $$ Данный интеграл содержит под своим знаком табличную функцию, а это значит, что можно сразу записать ответ взятый из таблицы. |
| Ответ |
| $$ \int x dx = \frac{x^2}{2} + C $$ |
| Пример 2 |
| $$ \int 3xdx $$ |
| Решение |
$$ \int 3xdx = 3\int xdx = \frac{3x^2}{2}+C $$ Замечаем, что под знаком интеграла есть постоянная 3. По первому свойству можно ее вынести за значок интеграла. Далее, видим, что подынтегральная функция является табличной и получаем из нее первообразную для f(x)=x. |
| Ответ |
| $$ \int 3xdx = \frac{3x^2}{2}+C $$ |
| Пример 3 |
| $$ \int (x^3+\frac{1}{2\sqrt{x}}) dx $$ |
| Решение |
$$ \int (x^3+\frac{1}{2\sqrt{x}}) dx =$$ $$ = \int x^3 dx + \int \frac{1}{2\sqrt{x}}dx =$$ $$ = \frac{x^4}{4}+\sqrt{x} + C, C=const $$ Проанализировав неопределенный интеграл заметили, что подынтегральные функции являются табличными. И дана их сумма. Можно воспользоваться свойством номер 2. Значит, производим операции над функцией $ f(x) $ и $ g(x) $ согласно указанным в табличке преобразованиям. Так как интеграл неопределенный, то получаем в ответе первообразную. |
| Ответ |
| $$ \int (x^3+\frac{1}{2\sqrt{x}}) dx = \frac{x^4}{4}+\sqrt{x} + C $$ |
Итак, вы узнали как решать интегралы для чайников, примеры решения интегралов разобрали по полочкам. Узнали физический и геометрический их смысл. О методах решения будет изложено в других статьях.
Решение интегралов. Рассказываем, как решать интегралы.
Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы!
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.
Решение интегралов (интегрирование) есть операция обратная диференциированию.
Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.
В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .
Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.
Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим:
Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.
Попробуем решить тоже самое не прибегая к построению, используя интегрирование:
Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной.
F(x) – первообразная. Дифференцируя первообразую, мы получим исходное подинтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференциируем полученный ответ и сравниваем с исходным выражением.
Основные функции и первообразные для них приведены в таблице:
Таблица первообразных для решения интегралов
Основные приемы решения интегралов:
Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду.
Сначала следует запомнить основные свойства интегралов:
Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим
Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.
Основные приемы решения интегралов
1. Замена переменной.
Для выполнения данного приема потребуется хороший навык нахождения производных.
2. Интегрирование по частям. Пользуются следующей формулой.
Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.
3. Интегрирование дробно-рациональных функций.
— разложить дробь на простейшие
— выделить полный квадрат.
— создать в числителе дифференциал знаменателя.
4. Интегрирование дробно-иррациональных функций.
— выделить под корнем полный квадрат
— создать в числителе дифференциал подкоренного выважения.
5. Интегрирование тригонометрических функций.
При интегрировании выражений вида
применяет формулы разложения для произведения.
Для выражений
m-нечетное, n –любое, создаем d(cosx). Используем тождество sin2+cos2=1
m,n – четные, sin2x=(1-cos2x)/2 и cos2x=(1+cos2x)/2
Для выражений вида:
— Применяем свойство tg2x=1/cos2x — 1
С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм:
Алгоритм обучения решению интегралов:
1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первобразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференциируем полученное выражение и сравниваем с исходным интегралом.
Отработаем основные моменты на нескольких примерах:
Примеры решения интегралов
Пример 1:
Решить интеграл: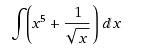
Интеграл неопределенный. Находим первообразную.
Для этого интеграл суммы разложим на сумму интегралов.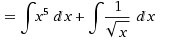
Каждый из интегралов табличного вида. Смотрим первообразные по таблице.
Решение интеграла: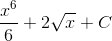
Проверим решение(найдем производную):
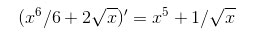
Пример 2. Решаем интеграл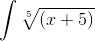
Интеграл неопределенный. Находим первообразную.
Сравниваем с таблицей. В таблице нет.
Разложить, пользуясь свойствами, нельзя.
Смотрим приемы. Наиболее подходит замена переменной.
Заменяем х+5 на t5. t5 = x+5 . Получаем.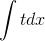
Но dx нужно тоже заменить на t. x= t5 — 5, dx = (t5 — 5)’ = 5t4. Подставляем: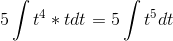
Интеграл из таблицы. Считаем:
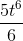
Подставляем в ответ вместо t ,
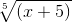
Решение интеграла:
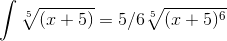
Пример 3. Решение интеграла: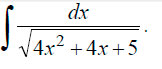
Для решения в этом случае необходимо выделить полный квадрат. Выделяем: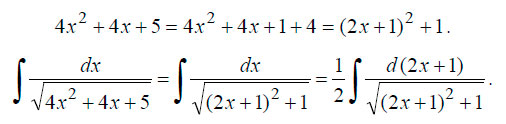
В данном случае коэфециент ? перед интегралом получился в результате замены dx на ?*d(2x+1). Если вы найдете производные x’ = 1 и ?*(2x+1)’= 1, то поймете почему так.
Находим первообразную.
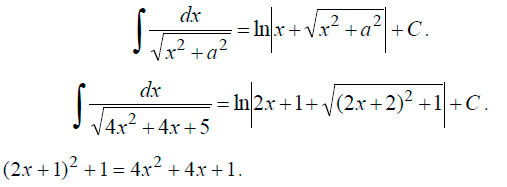
В итоге получаем:
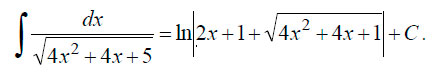
Для закрепления темы интегралов рекомендуем также посмотреть видео.
В нем мы на примере физики показываем практическое применение интегрирования, а также решаем еще несколько задач.
Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.
Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию. Программирование одна из дочек математики!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Первообразная
Определение 1. Функцию F (x) , определенную на интервале (a, b), называют первообразной функции f (x) , определенной на интервале (a, b), если для каждого  выполнено равенство
выполнено равенство
F’ (x) = f (x) .
Например, из справедливости равенства
(sin 2x)’ = 2 cos 2x
вытекает, что функция F (x) = sin 2x является первообразной функции f (x) = 2 cos 2x .
Замечание. Функция F (x) = sin 2x не является единственной первообразной функции f (x) = 2 cos 2x , поскольку функция F (x) = sin 2x + 10 , или функция F (x) = sin 2x – 3 , или функции вида F (x) = sin 2x + c , где c – любое число, также являются первообразными функции f (x) = 2 cos 2x .
Справедлива следующая теорема, доказательство которой выходит за рамки школьного курса математики.
Теорема 1. Если функция F (x) является первообразной функции f (x) на интервале (a, b) , то любая другая первообразная функции f (x) на интервале (a, b) имеет вид
F (x) + с ,
где c – некоторое число.
Неопределенный интеграл
Определение 2. Множество всех первообразных функции f (x) называют неопределенным интегралом от функции f (x) и обозначают
 | (1) |
Обозначение (1) читается так: «Неопределенный интеграл от функции f (x) по dx» .
Если F (x) является первообразной f (x) , то в силу теоремы 1 смысл формулы (1) заключается в следующем:
  | (2) |
Однако для упрощения формулу (2) принято записывать в виде
 | (3) |
подразумевая, но не указывая специально, что c – любое число.
В формуле (3) функцию f (x) называют подынтегральной функцией, выражение f (x) dx нызывают подынтегральным выражением, а число c называют постоянной интегрирования.
Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.
Правила интегрирования. Замена переменной в неопределенном интеграле
Вычисление интегралов (интегрирование) основано на применении следующих правил, которые непосредственно вытекают из правил вычисления производных.
Правило 1 (интеграл от произведения числа на функцию). Справедливо равенство

где k – любое число.
Другими словами, интеграл от произведения числа на функцию равен произведению этого числа на интеграл от функции.
Правило 2 (интеграл от суммы функций). Интеграл от суммы функций вычисляется по формуле

то есть интеграл от суммы функций равен сумме интегралов от этих функций.
Правило 3 (интеграл от разности функций). Интеграл от разности функций вычисляется по формуле

то есть интеграл от разности функций равен разности интегралов от этих функций.
Правило 4 (интегрирование при помощи замены переменной). Из справедливости формулы

вытекает, что
 | (4) |
если все входящие в формулу (4) функции f (φ (x)), φ’ (x), F (φ (x)) определены.
Доказательство правила 4. Воспользовавшись формулой для производной сложной функции, вычислим производную от правой части формулы (4):


Мы получили подынтегральную функцию из левой части формулы (4), что и требовалось.
Замечание. Рассмотрим частный случай формулы (4), когда функция φ (x) является линейной функцией, то есть
φ (x) = kx + b ,
что k и b – произвольные числа,  .
.
В этом случае
φ’ (x) = k ,
и формула (4) принимает вид
 | (5) |
Формула (5) часто используется при решении задач.
Таблица интегралов
Следующая таблица неопределенных интегралов составлена на основе таблицы производных часто встречающихся функций, а также на основе таблицы производных сложных функций
| Основная формула | Обобщения |
 |
|
где n – любое число, не равное – 1 |
где n, k, b – любые числа, |
где n – любое число, | |
|
где k, b – любые числа, |
где φ (x) > 0 | |
 |
где k, b – любые числа, |
 | |
где a – любое положительное число, не равное 1 |
где a – любое положительное число, не равное 1, k, b – любые числа, |
где a – любое положительное число, не равное 1 | |
 |
где k, b – любые числа, |
 | |
 |
где k, b – любые числа, |
 | |
|
где k, b – любые числа, |
| |
|
где k, b – любые числа, |
| |
|
где k, b – любые числа, |
| φ (x) | < 1 | |
где a, b – любые числа, | |
 |
где k, b – любые числа, |
 | |
где a, b – любые числа, |
Основная формула:
Обобщения:
|
Основная формула:
где n – любое число, не равное – 1 . Обобщения:
где n, k, b – любые числа, _____
где n – любое число, |
Основная формула:
Обобщения:
где k, b – любые числа, _____
где φ (x) > 0 |
Основная формула:
Обобщения:
где k, b – любые числа, _____
|
Основная формула:
где a – любое положительное число, не равное 1 . Обобщения:
где a – любое положительное число, не равное 1, k, b – любые числа, _____
где a – любое положительное число, не равное 1 |
Основная формула:
Обобщения:
где k, b – любые числа, _____
|
Основная формула:
Обобщения:
где k, b – любые числа, _____
|
Основная формула:
где Обобщения:
где k, b – любые числа, _____
где |
Основная формула:
где Обобщения:
где k, b – любые числа, _____
|
Основная формула:
Обобщения:
где k, b – любые числа, _____
где | φ (x) | < 1 _____
где a, b – любые числа, |
Основная формула:
Обобщения:
где k, b – любые числа, _____
_____
где a, b – любые числа, |
Примеры решения задач
Пример 1. Вычислить интеграл

Решение. Воспользовавшись свойствами степеней, а затем правилами интегрирования и формулами из таблицы неопределенных интегралов формулами из таблицы неопределенных интегралов, получаем


Ответ.
Пример 2. Значение первообразной F (x) функции f (x) = – 4 sin x в точке x = 0 равно 9. Найти  .
.
Решение. Поскольку Поскольку

то
Подставляя в формулу (6) значение x = 0 , находим значение постоянной интегрирования c:
F (0) = 4 cos 0 + c = 9,
4 + c = 9, c = 5.
Следовательно,
F (x) = 4 cos x + 5
Поэтому

Ответ. 7
Пример 3. Найти первообразную F (x) функции

если F (2π) = 2e + 3.
Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов

для функции φ (x) = cos x , получаем

Следовательно,
 | (7) |
Подставляя в формулу (7) значение x = 2π, находим значение постоянной интегрирования c:

Итак,
c = 3e +3 .
Ответ. 
Пример 4. Вычислить интеграл

Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов

для функции φ (x) = ex, получаем

Ответ. 

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
как вычислить интеграл с заменой переменной, его свойства и методы вычисления с подробным решением
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Интегралы для чайников: как решать, правила вычисления, объяснение

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие «интеграл»
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x). Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов

Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции.
Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры.
Это и есть определенный интеграл, который записывается так:

Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
Производная от интеграла равна подынтегральной функции:

Константу можно выносить из-под знака интеграла:

Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла
Знак интеграла изменяется, если поменять местами пределы интегрирования:
- При любых точках a, b и с:
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в х.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Источник: https://Zaochnik-com.ru/blog/integraly-dlya-chajnikov-kak-reshat-pravila-vychisleniya-obyasnenie/
Первообразная и неопределенный интеграл, их свойства
Для начала, дадим определение понятиям, которые будут использоваться в данном разделе. В первую очередь это первообразная функции. Для этого введем константу C.
Первообразная функции f(x) на промежутке (a; b) это такая функция F(x), при которое формула F'(x)=f(x) превращается в равенство для любого x из заданного промежутка.
Следует учитывать тот факт, что производная от константы C будет равна нулю, что позволяет нам считать верным следующее равенство F(x)+C’=f(x).
Получается, что функция f(x) имеет множество первообразных F(x)+C, для произвольной константы C. Эти первообразные отличаются друг от друга на произвольную постоянную величину.
Определение неопределенного интеграла
Все множество первообразных функции f(x) можно назвать неопределенным интегралом этой функции. С учетом этого формула будет иметь вид ∫f(x)dx=F(x)+C. При этом, выражение f(x)dx является подынтегральным выражением, а f(x) – это подынтегральная функция. Подынтегральное выражение представляет собой дифференциал функции f(x).
Имея заданный дифференциал функции, мы можем найти неизвестную функцию.
Результатом неопределенного интегрирования будет не одна функция F(x), а множество ее первообразных F(x)+C.
Зная свойства производной, мы можем сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
∫f(x)dx’=F(x)+C’=f(x)
Производная результата интегрирования равна подынтегральной функции.
∫d(F(x))=∫F'(x)dx=∫f(x)dx=F(x)+C
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
∫k·f(x)dx=k·∫f(x)dx, где k – произвольная константа. Коэффициент можно выносить за знак неопределенного интеграла.
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
∫f(x)±g(x))dx=∫f(x)dx±∫g(x)dx
Промежуточные равенства первого и второго свойств неопределенного интеграла мы привели в качестве пояснения.
Для того, чтобы доказать третье и четвертое свойства, необходимо найти производные от правых частей равенств:
k·∫f(x)dx’=k·∫d(x)dx’=k·f(x)∫f(x)dx±∫g(x)dx’=∫f(x)dx’±∫g(x)dx’=f(x)±g(x)
Производные правых частей равенств равны подынтегральным функциям, что является доказательством первого свойства. Его же мы используем в последних переходах.
Как видите, задача интегрирования представляет собой обратный процесс по отношению к задаче дифференцирования. Обе эти задачи тесно связаны между собой.
Первое свойство может быть использовано для проведения проверки интегрирования. Для проверки нам достаточно вычислить производную полученного результата. Если полученная функция будет равна подынтегральной функции, то интегрирование проведено верно.
Благодаря второму свойству по известному дифференциалу функции мы можем найти ее первообразную и использовать ее для вычисления неопределенного интеграла.
Рассмотрим пример.
Пример 1
Найдем первообразную функции f(x)=1x, значение которой равно единице при х=1.
Решение
Используя таблицу производных основных элементарных функций получаем:
- d(ln x)=(ln x)’dx=dxx=f(x)dx∫f(x)dx=∫dxx=∫d(ln(x))
Используя второе свойство ∫d(ln(x))=ln(x)+C, мы получаем множество первообразных ln(x)+C. При х=1 получим значение ln(1)+C=0+C=C. Согласно условию задачи, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид ln(x)+1.
Ответ: f(x)=1x=ln(x)+1
Пример 2
Необходимо найти неопределенный интеграл ∫2sinx2cosx2dx и проверить результат вычисления дифференцированием.
Решение
Используем для проведения вычислений формулу синуса двойного угла из курса тригонометрии 2sinx2cosx2=sin x, получим ∫2sinx2cosx2dx=∫sin xdx.
Используем таблицу производных для тригонометрических функций, получим:
- d(cos x)=cos x’dx=-sin xdx⇒sin xdx=-d(cos x)
- То есть, ∫sin xdx=∫(-d(cos x))
- Используя третье свойство неопределенного интеграла, мы можем записать ∫-d(cos x)=-∫d(cos x).
- По второму свойству получаем -∫d(cos x)=-(cos x+C)
- Следовательно, ∫2sin x2cosx2dx=-cos x-C.
- Проверим полученный результат дифференцированием.
- Продифференцируем полученное выражение:
-cos x-C’=-(cos x)’-(C)’=-(-sin x)=sin x=2sinx2cosx2
В результате проверки мы получили подынтегральную функцию. Это значит, что интегрирование было проведено нами верно. Для осуществления последнего перехода мы использовали формулу синуса двойного угла.
Ответ: ∫2sin x2cosx2dx=-cos x-C
Если таблицу производных основных элементарных функций переписать в виде дифференциалов, то из нее по второму свойству неопределенного интеграла можно составить таблицу первообразных.
Источник: https://Zaochnik.com/spravochnik/matematika/integraly-integrirovanie/pervoobraznaja-i-neopredelennyj-integral-ih-svojst/
Примеры решений неопределенных интегралов
- Попробуйте решить приведенные ниже неопределенные интегралы.
- Нажмите на изображение интеграла, и вы попадете на страницу с подробным решением.
Примеры на основные формулы и методы интегрирования
См раздел
Основные формулы и методы интегрирования > > >
Решение > > >
Решение > > >
Решение > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования рациональных функций (дробей)
См раздел
Интегрирование рациональных функций (дробей) > > >
> > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования иррациональных функций (корней)
См раздел
Методы интегрирования иррациональных функций (корней) > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования тригонометрических функций
См раздел
Методы интегрирования тригонометрических функций > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Автор: Олег Одинцов. Опубликовано:
Для чего был изобретен интеграл и дифференциал, какое математическое действие лежит в их основе и их значение для естественных и технических наук?
В отличие от других ответчиков я начну с интеграла, а не с производной. Интеграл в жизни имеет конкретный физический смысл. Это площадь фигуры ограниченной осью абцисс Х и графиком функции. Далеко от жизни? Сейчас приблизим. Представим себе машину, которая едет. Отложим по оси Х время в пути, а по Y — скорость в каждый, конкретный момент времени, и начертим график скорости от времени. Если скорость постоянная — это будет горизонтальная прямая. Фигура ограниченная этой прямой и осью Х — будет прямоугольником. Ширина прямоугольника — время в пути, а высота — скорость машины. Ширина*высота=площадь. Но при этом время*скорость=расстояние. Т.е. расстояние равно площади! И пройденное расстояние — это интеграл скорости.
А теперь начинается магия математики. Как посчитать путь, который пройдет машина, если у неё непрерывно меняется скорость, и её график извилистая кривая? А очень просто. Ведь ничего не изменилось — надо только найти площадь фигуры на графике! Как мы будем искать эту площадь — не важно. Можно просто посчитать клеточки на бумаге (это будет численным интегрированием, которое всегда приблизительное). А если скорость описана функцией от времени — можно найти её интеграл и сразу получить точный ответ.
А диференцирование — это это действие обратное интегрированию. Если продиференцировать функцию расстояния от времени, которую получили интегрированием скорости — мы обратно получим скорость. Ту самую скорость, с которой меняется пройденный путь машины. Сейчас скорость большая, километровые столбы мелькают, и пройденный путь быстро растет, а когда скорость падает и пройденные километры набираются медленно. На графике пути от времени, скорость это наклон самого графика. Грфик идет вверх — скорость положительная, мы едем вперед и расстояние растет. График пошел вниз — скорость отрицательная, мы едем обратно, а расстояние до точки старта уменьшается. График горизонтальная линия (наклона нет) -скорость равна нулю, мы стоим и расстояние неизменно.
Немного решил дописать.
Вообще интеграл в изменяющихся физических процессах очень востребован. А любой процесс описывает какую-то жизненную ситуацию.
Это сколько воды натекло через трубу в пресловутый бассейн при переменном напоре. Сколько киловатт накрутил электросчетчик при переменной нагрузке на сеть. До какой температуры нагрелась вода в кастрюле, если в процессе нагрева мы регулировали мощность плиты.
Любой процесс изменяемый во времени можно интегрировать и получить полезный результат. То же касается и дифенциала, который показывает скорость изменения общего результата.
Быстрое вычисление определенных интегралов с использованием основной теоремы
- Образование
- Математика
- Исчисление
- Быстрое вычисление определенных интегралов с использованием основной теоремы
Марк Райан
Вот супер-пупер-сокращенная теорема интеграции, которую вы будете использовать до конца своих естественных дней рождения — или, по крайней мере, до конца вашего срока с расчетами. Этот сокращенный метод — все, что вам нужно для большинства задач интеграции со словами.
Основная теорема исчисления (вторая версия или сокращенная версия): Пусть F будет любой первообразной функции f; , затем
Эта теорема дает вам супер-ярлык для вычисления определенного интеграла, такого как
площадь под параболой y = x 2 + 1 между 2 и 3. Вы можете получить эту площадь, вычтя площадь между 0 и 2 из области между 0 и 3, но для этого вам необходимо чтобы знать, что конкретная функция площади выметает область, начинающуюся с нуля,
(с нулевым значением C ).
Прелесть теоремы быстрого доступа в том, что вам даже не нужно использовать функцию площади, например
Вы просто находите любую первообразную F ( x ) вашей функции и выполняете вычитание F ( b ) — F ( a ). Самая простая первообразная в использовании — та, где C = 0. Итак, вот как вы используете теорему, чтобы найти площадь под вашей параболой от 2 до 3.
является первообразной x 2 + 1.Тогда теорема дает вам:
Этот ярлык работает независимо от функции, и вам не нужно беспокоиться о функциях области. Все, что вам нужно сделать, это F ( b ) — F ( a ).
Вот еще один пример: какова площадь под f ( x ) = e x , между x = 3 и x = 5? Производная e x равна e x , поэтому e x является первообразной e x , и, следовательно,
Что может быть попроще?
Области выше кривой и ниже x — ось считается как отрицательная областей. Прежде чем продолжить, важно коснуться отрицательных сторон. Обратите внимание, что в двух показанных здесь примерах, параболе y = x 2 + 1 и экспоненциальной функции y = e x , вычисляемые области под кривыми и над по оси x . Эти области считаются обычными, положительная области. Но если функция идет ниже оси x , области выше кривой и ниже оси x считаются как отрицательные области .
Хорошо, теперь у вас есть супер-ярлык для вычисления площади под кривой. И если одного большого ярлыка было недостаточно, чтобы сделать ваш день, в этой таблице перечислены некоторые правила относительно определенных интегралов, которые могут значительно облегчить вашу жизнь.
Об авторе книги
Марк Райан — основатель и владелец The Math Center, учебного центра по математике и подготовке к тестам в Виннетке, штат Иллинойс.Он является автором «Учебного пособия по исчислению для чайников », «Основы исчисления для чайников » и трех книг по геометрии из серии «Для чайников» серии . Райан преподает математику в средней и средней школе с 1989 года. Он живет в Эванстоне, штат Иллинойс.
,Интегралы, связь между интеграцией и дифференциацией
Интересная статья: Исчисление для чайников Джона Габриэля
Производная неопределенного интеграла. Первая фундаментальная теорема исчисления
Теперь мы подошли к замечательной связи, существующей между интегрированием и дифференцированием. Отношения между этими двумя процессами в некоторой степени аналогичны отношениям между «возведением в квадрат» и «извлечением квадратного корня».x f (t) \ dt = A (x + h) — A (x) $
Показанный пример является непрерывным на протяжении всего интервала [x, x + h]. Следовательно, по теореме о среднем значении для интегралов имеем
A (x + h) — A (x) = hf (Z), где x ≤ z ≤ x + h.
Следовательно, мы имеем
(5.2) [A (x + h) — A (x)] / h = f (z),
и, поскольку x ≤ z ≤ x + h, находим, что f (z) → f (x) при h → 0 через положительные значения. Аналогичный аргумент действителен, если h → 0 через отрицательные значения. Следовательно, A ‘(x) существует и равно f (x).
Этот аргумент предполагает, что функция f непрерывна в некоторой окрестности точки x.{x + h} [f (t) — f (x)] \ dt = 0 $
Именно в этой части доказательства используется непрерывность в точке x.
Обозначим второй член справа в (5.3) через G (h). Нам нужно доказать, что G (h) -f 0 при h —f 0. Используя определение предела, мы должны показать, что для любого ε> 0 существует такое δ> 0, что
(5.4) | G (h ) | Непрерывность f в точке x говорит нам, что, если задано ε, существует такое положительное δ, что
(5.5) | f (t) -f (x) | всякий раз, когда (5.6) x — δ Если мы выберем h так, чтобы 0 $ | \ int _x ^ {x + h} [f (t) — f (x)] \ dt | \ leq \ int _x ^ {x + h} | f (t) — f (x) | \ dt \ leq \ int _x ^ {x + h} \ frac {1} {2} \ epsilon \ dt = \ frac {1} {2} h \ epsilon Если мы разделим на h, мы увидим, что (5.4) выполняется при 0
Теорема о нулевой производной
Если функция f постоянна на открытом интервале (a, b), ее производная равна нулю всюду на (a, b). Мы доказали этот факт ранее как непосредственное следствие определения производной. Мы также доказали, как часть (c) теоремы 4.7, обратное этому утверждению, которое мы переформулируем здесь как отдельную теорему.
ТЕОРЕМА 5.2. ТЕОРЕМА НУЛЕВОЙ ПРОИЗВОДНОЙ. Если f ‘(x) = 0 для каждого x в открытом интервале I, то f постоянна на I.
Эта теорема, когда используется в сочетании с первой фундаментальной теоремой исчисления, приводит ко второй фундаментальной теореме, которая описана в следующем разделе.
5.3 Примитивные функции и вторая основная теорема исчисления
Определение примитивной функции
Функция P называется примитивной (или первообразной) функции f на открытом интервале I, если производная P равна f, то есть если P ‘(x) = f (x) для всех x в I.
Например, функция синуса является примитивом косинуса на каждом интервале, потому что производная синуса является косинусом. Мы говорим о примитиве, а не о примитиве, потому что если P является примитивом off, то P + k будет таким же для любой константы k. И наоборот, любые две примитивы P и Q одной и той же функции f cari отличаются только константой, потому что их разность P — Q имеет производную
P ‘(x) — Q’ (x) = f (x) — f (x) = 0
для любого x из I и, следовательно, по теореме 5.2, P — Q постоянно на Z.
Первая фундаментальная теорема исчисления говорит нам, что мы всегда можем построить примитив непрерывной функции интегрированием. Когда мы объединяем это с тем фактом, что два примитива одной и той же функции могут отличаться только константой, мы получаем вторую фундаментальную теорему исчисления.
Вторая основная теорема исчисления
Предположим, что f непрерывна на открытом интервале I, и пусть P — любой примитив вне I. Тогда для каждого c и каждого x в I мы имеем
(5.7) & nbs
Введение в интеграцию
Интеграция — это способ добавления фрагментов для поиска целого.
Integration можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей. Но проще всего начать с поиска области под кривой функции следующим образом:
Какова площадь под y = f (x) ?
Ломтики
Мы можем вычислить функцию в нескольких точках, и сложить срезы шириной Δx вот так (но ответ будет не очень точным): | ||
Мы можем сделать Δx намного меньше, а сложить много маленьких кусочков (ответ становится все лучше): | ||
И когда срезы приближаются к нулю по ширине , ответ приближается к истинному ответу . Теперь мы запишем dx , чтобы обозначить, что ширина срезов Δx приближается к нулю. |
Это очень много!
Но складывать их не нужно, есть «ярлык». Потому что …
… нахождение интеграла — это , обратный нахождения производной.
(Так что вам действительно следует знать о производных финансовых инструментах, прежде чем читать больше!)
Как здесь:
Пример: Что такое интеграл от 2x?
Мы знаем, что производная x 2 равна 2x…
… так что интеграл от 2x равен x 2
Вы увидите другие примеры позже.
Обозначение
Символ «Интеграл» — стильная буква «S» |
После символа интеграла мы помещаем функцию, интеграл от которой мы хотим найти (называемую интегралом),
, а затем закончите с dx , чтобы обозначить, что срезы идут в направлении x (и приближаются к нулю по ширине).
А вот как пишем ответ:
плюс C
Мы написали ответ как x 2 , но почему + C?
Это «Константа интеграции». Это из-за всех функций, производная которых равна 2x :
Производная x 2 +4 равна 2x , а производная x 2 +99 также равна 2x и так далее! Потому что производная константы равна нулю.
Итак, когда мы меняем операцию (чтобы найти интеграл), мы знаем только 2x , но там могла быть константа любого значения.
Итак, мы завершаем идею, просто написав + C в конце.
Кран и резервуар
Интеграция похожа на наполнение бака из-под крана.
Вход (до интегрирования) — расход от крана.
Объединение потока (складывание всех маленьких кусочков воды) дает нам объема воды в резервуаре.
Простой пример: постоянный расход
Интеграция: при расходе 1 объем резервуара увеличивается на x
Производная: если объем резервуара увеличивается на x , то расход равен 1
Это показывает, что интегралы и производные противоположны!
Теперь для увеличения расхода
Представьте, что поток начинается с 0 и постепенно увеличивается (возможно, двигатель медленно открывает кран).
По мере увеличения расхода бак наполняется все быстрее и быстрее.
Интеграция: при расходе 2x объем резервуара увеличивается на x 2
Производная: если объем резервуара увеличивается на x 2 , то расход должен быть 2x
Пример: с расходом в литрах в минуту и баком, начинающимся с 0
Через 3 минуты ( x = 3 ):
- расход достиг 2x = 2 × 3 = 6 л / мин,
- и объем достиг x 2 = 3 2 = 9 литров
И через 4 минуты ( x = 4 ):
- расход достиг 2x = 2 × 4 = 8 л / мин,
- и объем достиг x 2 = 4 2 = 16 литров
Мы можем сделать и обратное:
Представьте, что вы не знаете скорость потока.
Вы знаете только, что объем увеличивается на x 2 .
Мы можем пойти в обратном направлении (используя производную, которая дает нам наклон) и найти, что скорость потока равна 2x .
Пример:
- Через 1 минуту объем увеличивается на 2 литра / минуту (наклон объема равен 2)
- Через 2 минуты объем увеличивается со скоростью 4 литра / минуту (наклон объема равен 4)
- Через 3 минуты объем увеличивается со скоростью 6 л / мин (наклон 6)
- и т. Д.
Итак, интеграл и производная — это противоположности. |
Мы можем записать это так:
Интеграл от расхода 2x сообщает нам объем воды: | ∫2x dx = x 2 + C | |
И наклон увеличения объема x 2 + C возвращает нам скорость потока: | (x 2 + C) = 2x |
И, эй, мы даже получили хорошее объяснение этого значения «C»… может быть, в баке уже есть вода!
- Поток по-прежнему увеличивает объем на ту же величину
- И увеличение объема может вернуть нам скорость потока.
Которая учит нас всегда добавлять «+ C».
Прочие функции
Итак, мы уже поиграли с y = 2x , так как же нам интегрировать другие функции?
Если нам посчастливится найти функцию на стороне производной result , тогда (зная, что производные и интегралы противоположны), мы получим ответ.Но не забудьте добавить C.
Пример: что такое ∫cos (x) dx?
Из таблицы Rules of Derivatives мы видим, что производная sin (x) равна cos (x), поэтому:
∫cos (x) dx = sin (x) + C
Но многое из этого «обращения» уже сделано (см. Правила интеграции).
Пример: Что такое ∫x 3 dx?
В правилах интеграции есть «Правило власти», которое гласит:
∫x n dx = x n + 1 n + 1 + C
Мы можем использовать это правило с n = 3:
∫x 3 dx = x 4 4 + C
Знание того, как использовать эти правила, является ключом к успешной интеграции.
Итак, познакомьтесь с этими правилами и получите много практики .
Изучите правила интеграции и практикуйтесь! Практика! Практика!
(для начала вам нужно задать несколько вопросов)
Определенные и неопределенные интегралы
До сих пор мы выполняли неопределенных интегралов .
Определенный интеграл имеет фактические значения для вычисления между ними (они помещаются внизу и вверху буквы «S»):
| Неопределенный Интегральный | Определено Интегральное |
Прочтите Определенные интегралы, чтобы узнать больше.
,Основные рабочие инструменты в исчислении, производные и интегральные пронизывают все аспекты моделирования природы в физических науках. Производная функции может быть геометрически интерпретирована как наклон кривой математической функции f (x), построенной как функция от x. Но его значение для моделирования природы гораздо глубже, чем может предполагать это простое геометрическое приложение. В конце концов, вы можете увидеть, как вы рисуете конечные треугольники, чтобы определить наклон, так почему же производная так важна? Его важность заключается в том, что многие физические объекты, такие как скорость, ускорение, сила и т. Д., Определяются как мгновенные скорости изменения некоторой другой величины.Производная может дать вам точное внутреннее значение для этой скорости изменения и привести к точному моделированию желаемой величины. Интеграл функции можно геометрически интерпретировать как площадь под кривой математической функции f (x), построенной как функция от x. Вы можете увидеть, как вы рисуете большое количество блоков, чтобы аппроксимировать область под сложной кривой, и получите лучший ответ, если вы используете больше блоков. Интеграл дает вам математический способ нарисовать бесконечное количество блоков и получить точное аналитическое выражение для площади.Это очень важно для геометрии — и чрезвычайно важно для физических наук, где определения многих физических объектов могут быть представлены в математической форме, такой как площадь под кривой. Площадь небольшого блока под кривой можно представить как ширину полосы, взвешенную на высоту полосы (то есть умноженную на нее). Многие свойства непрерывных тел зависят от взвешенных сумм, которые, чтобы быть точными, должны быть бесконечными взвешенными суммами — задача, специально созданная для интеграла.Например, определение центра масс непрерывного тела включает взвешивание каждого элемента массы по его расстоянию от оси вращения, процесс, для которого необходим интеграл, если вы собираетесь получить точное значение. Огромное количество физических проблем включает в себя такие бесконечные суммы в своих решениях, что делает интеграл важным инструментом для физика. | Указатель Производные концепции Интегральные концепции |

 , где k – любое число
, где k – любое число
 ,
,

 , x > 0
, x > 0 ,
,
 ,
,
 ,
, ,
, ,
, ,
,
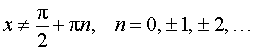
 ,
,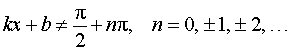
 ,
,

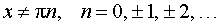
 ,
,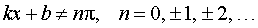
 ,
,
 | x | < 1
| x | < 1



 ,
,
