Интегралы определенные онлайн с подробным решением: Интегралы. Пошаговый калькулятор

вычисление интегралов определенных онлайн

Вы искали вычисление интегралов определенных онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление определенного интеграла, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление интегралов определенных онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вычисление интегралов определенных онлайн,вычисление определенного интеграла,вычисление определенного интеграла онлайн,вычисление определенного интеграла онлайн с подробным решением,вычисление определенных интегралов,вычисление определенных интегралов онлайн,вычисление определенных интегралов онлайн с подробным решением,вычислите определенный интеграл,вычислить значение определенного интеграла,вычислить интеграл онлайн с подробным решением определенный,вычислить несобственный интеграл онлайн,вычислить определенные интегралы,вычислить определенные интегралы онлайн с решением,вычислить определенный интеграл,вычислить определенный интеграл онлайн,вычислить определенный интеграл онлайн калькулятор,вычислить определенный интеграл онлайн с подробным решением,вычислить определенный интеграл онлайн с решением,интеграл онлайн определенный,интеграл определенный онлайн,интеграл решение определенный,интегралы онлайн несобственные,интегралы онлайн определенные,интегралы определенные онлайн,интегралы определенные онлайн с подробным решением,как вычислить определенный интеграл,калькулятор интегралов онлайн определенных,калькулятор интегралов онлайн определенных интегралов,калькулятор интегралов определенных,калькулятор онлайн вычислить определенный интеграл,калькулятор онлайн определенные интегралы,калькулятор онлайн определенный интеграл,калькулятор онлайн определенный интеграл с подробным решением,калькулятор онлайн определенных интегралов,калькулятор определенного интеграла,калькулятор определенного интеграла онлайн,калькулятор определенный интеграл,калькулятор определенных интегралов,калькулятор определенных интегралов онлайн,калькулятор определенных интегралов онлайн с решением,калькулятор определенных интегралов онлайн с решением подробным,калькулятор определенных интегралов с подробным решением онлайн,калькулятор определенных интегралов с решением онлайн,найти определенный интеграл,найти определенный интеграл онлайн,найти определенный интеграл онлайн с подробным решением,нахождение определенного интеграла,нахождение определенного интеграла онлайн,несобственные интегралы онлайн,несобственный интеграл онлайн,онлайн вычисление определенных интегралов,онлайн калькулятор вычислить определенные интегралы,онлайн калькулятор интегралов определенных,онлайн калькулятор интегралов с подробным решением определенных,онлайн калькулятор интегралы определенные,онлайн калькулятор определенного интеграла,онлайн калькулятор определенные интегралы,онлайн калькулятор определенный интеграл,онлайн калькулятор определенных интегралов,онлайн калькулятор определенных интегралов с подробным решением,онлайн нахождение определенного интеграла,онлайн решение определенного интеграла,онлайн решение определенного интеграла с подробным решением,онлайн решение определенных интегралов,онлайн решение определенных интегралов с подробным решением,определенные интегралы калькулятор онлайн,определенные интегралы онлайн,определенные интегралы онлайн калькулятор,определенные интегралы онлайн с подробным решением,определенный интеграл калькулятор,определенный интеграл калькулятор онлайн,определенный интеграл калькулятор онлайн с подробным решением,определенный интеграл онлайн,определенный интеграл онлайн калькулятор,определенный интеграл онлайн калькулятор с подробным решением,определенный интеграл онлайн с подробным решением,определенный интеграл онлайн тройной,определенный интеграл решение,определенный интеграл решить,определенный интеграл решить онлайн,определенный интеграл решить онлайн с подробным решением,посчитать интеграл онлайн определенный,посчитать онлайн определенный интеграл,посчитать определенный интеграл онлайн,решение интегралов онлайн определенных,решение несобственных интегралов онлайн,решение определенного интеграла,решение определенного интеграла онлайн,решение определенного интеграла онлайн с подробным решением,решение определенный интеграл,решение определенных интегралов,решение определенных интегралов онлайн,решение определенных интегралов онлайн с подробным решением,решение определенных интегралов онлайн с подробным решением бесплатно,решить интеграл определенный,решить онлайн определенный интеграл,решить определенный интеграл,решить определенный интеграл онлайн,решить определенный интеграл онлайн с подробным решением,сходимость интеграла онлайн.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вычисление интегралов определенных онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычисление определенного интеграла онлайн).

Где можно решить любую задачу по математике, а так же вычисление интегралов определенных онлайн Онлайн?

Решить задачу вычисление интегралов определенных онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Калькулятор Интегралов — определенный & неопределенный

Онлайн-калькулятор интегралов поможет вам вычислить интегралы функций по отношению к задействованной переменной и покажет вам полные пошаговые вычисления. Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-интеграл калькулятор:

• Определенные интегралы
• Неопределенные интегралы (первообразная)

Интегральный расчет довольно сложно решить вручную, так как он включает в себя различные сложные формулы интегрирования. Итак, рассмотрим интерактивный интегральный решатель, который решает простые и сложные функции решение интегралов онлайн и показывает вам пошаговые вычисления.

Итак, сейчас самое время понять формулы интегрирования, как интегрировать функцию шаг за шагом, с помощью калькулятора интегрирования и многое другое. Во-первых, давайте начнем с основ:

Читать дальше!

Что такое интеграл?

В математике интеграл функций описывает площадь, смещение, объем и другие понятия, которые возникают, когда мы объединяем бесконечные данные. В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.

Вы также можете использовать бесплатную версию онлайн-калькулятора факторов, чтобы найти факторы, а также пары факторов для положительных или отрицательных целых чисел.

• Процесс нахождения интегралов, называемый интегрированием
• Интегрируемая функция называется подынтегральной функцией.
• В интегральных обозначениях ∫3xdx, ∫ – символ интеграла, 3x – интегрируемая функция, а dx – дифференциал переменной x.

Где f (x) – функция, а A – площадь под кривой. Наш бесплатный калькулятор интегралов легко вычисляет интегралы и определяет площадь под заданной функцией. Что ж, теперь поговорим о типах интегралов:

Типы интегралов:

По сути, есть два типа интегралов:

• Неопределенные интегралы
• Определенные интегралы

Неопределенные интегралы:

определенный интеграл онлайн функции принимает первообразную другой функции. Взять первообразную функции – это самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.

Определенные интегралы:

Определенный интеграл функции имеет начальное и конечное значения. Просто существует интервал [a, b], который называется пределами, границами или границами. Этот тип можно определить как предел интегральных сумм, когда диаметр разбиения стремится к нулю. Наш интеграл онлайн калькулятор определенных интегралов с оценками вычисляет интегралы, учитывая верхний и нижний предел функции. Разницу между определенным и неопределенным интегралами можно понять по следующей диаграмме:

Основные формулы для интеграции:

Существуют разные формулы для интеграции, но здесь мы перечислили некоторые общие:

• ∫1 dx = x + c
• ∫xn dx = xn + 1 / n + 1 + c
• ∫a dx = ax + c
• ∫ (1 / х) dx = lnx + c
• ∫ ax dx = ax / lna + c
• ∫ ex dx = ex + c
• ∫ sinx dx = -cosx + c
• ∫ cosx dx = sinx + c
• ∫ tanx dx = – ln | cos x | + c
• ∫ cosec2x dx = – детская кроватка x + c
• ∫ sec2x dx = tan x + c
• ∫ cotx dx = ln | sinx | + c
• ∫ (secx) (tanx) dx = secx + c
• ∫ (cosecx) (cotx) dx = -cosecx + c

Помимо этих уравнений интегрирования, есть еще несколько важных формул интегрирования, которые упомянуты ниже:

• ∫ 1 / (1-x2) 1/2 dx = sin-1x + c
• ∫ 1 / (1 + x2) 1/2 dx = cos-1x + c
• ∫ 1 / (1 + x2) dx = tan-1x + c
• ∫ 1 / | x | (x2 – 1) 1/2 dx = cos-1x + c

Запоминание всех этих формул интегрирования и выполнение вычислений вручную – очень сложная задача. Просто введите функцию в предназначенное для этого поле онлайн-калькулятор интегралов, который использует эти стандартизированные формулы для точных вычислений.

Как решать интегралы вручную (шаг за шагом):

Большинство людей раздражается начинать с вычислений интегральной функции. Но здесь мы собираемся решать интегральные примеры шаг за шагом, что поможет вам разобраться, как легко интегрировать функции! Итак, это точки, которым нужно следовать для вычисления решение интегралов онлайн:

• Определить функцию f (x)
• Возьмите первообразную функции
• Вычислить верхний и нижний предел функции
• Определите разницу между обоими пределами

Если вас интересует вычисление первообразной (неопределенного интеграла), тогда возьмите онлайн-калькулятор первообразной, который быстро решит первообразную данной функции.

Смотрит на примеры:

Пример 1:

Решить интегралы от ∫ x3 + 5x + 6 dx?

Решение:

Шаг 1:

Применяя правило функциональной мощности для интегрирования:

∫xn dx = xn + 1 / n + 1 + c

∫ x3 + 5x + 6 dx = x3 + 1/3 + 1 + 5 x1 + 1/1 + 1 + 6x + c

Шаг 2:

∫ x3 + 5x + 6 dx = x4 / 4 + 5 x2 / 2 + 6x + c

Шаг 3:

∫ x3 + 5x + 6 dx = x4 + 10×2 + 24x / 4 + c

Этот калькулятор неопределенного интеграла помогает интегрировать интеграл калькулятор функции шаг за шагом, используя формулу интегрирования. 1_5 x * lnx dx = –14

Поскольку это очень сложно для решения интегралов, когда две функции умножаются друг на друга. Для удобства просто введите функции в онлайн-калькулятор интегралов по частям, который помогает выполнять вычисления двух функций (по частям), которые точно умножаются друг на друга.

Пример 3 (Интеграл от тригонометрической функции):

Вычислить определенный интеграл для ∫sinx dx с интервалом [0, π / 2]?

Решение:

Шаг 1:

Используйте формулу для тригонометрической функции:

∫ sinx dx = -cosx + c

Шаг 2:

Вычислите верхний и нижний предел для функций f (a) и f (b) соответственно:

Поскольку a = 0 и b = π / 2

Итак, f (a) = f (0) = cos (0) = 1

f (b) = f (π / 2) = cos (π / 2) = 0

Шаг 3:

Рассчитайте разницу между верхним и нижним пределами:

f (а) – f (b) = 1 – 0

f (а) – f (b) = 1

Теперь вы можете использовать бесплатный калькулятор частичных интегралов для проверки всех этих примеров и просто добавлять значения в поля назначения для мгновенного вычисления интегралов.

Как найти первообразную и вычислить интегралы с помощью калькулятора интегралов:

Вы можете легко вычислить интеграл от определенных и неопределенных функций с помощью лучшего интегратора. Вам просто нужно следовать указанным пунктам, чтобы получить точные результаты:

Проведите по!

Входы:

• Во-первых, введите уравнение, которое вы хотите интегрировать.
• Затем выберите зависимую переменную, входящую в уравнение
• Выберите на вкладке определенный или определенный интеграл онлайн
• Если вы выбрали конкретный вариант, то вам следует ввести нижнюю и верхнюю границу или предел в предназначенное для этого поле.
• После этого пора нажать на кнопку расчета.

Выходы:

Интегральный оценщик показывает:

• Определенный интеграл
• неопределенный интеграл онлайн
• Выполните пошаговые расчеты

Часто задаваемые вопросы (FAQ):

Какое целое значение?

В математике интеграл – это числовое значение, равное площади под графиком некоторой функции на некотором интервале. Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.

Как вы оцениваете интеграл, используя основную теорему исчисления?

Прежде всего, мы должны найти первообразную функции, чтобы решить интеграл, используя фундаментальную теорему. Затем используйте основную теорему исчисления для вычисления решение интегралов онлайн. Или просто введите значения в предназначенное для этого поле этого калькулятора интеграции и мгновенно получите результаты.

Что такое двойной интеграл?

Двойные интегралы – это способ интегрирования по двумерной области. Двойные интегралы позволяют вычислить объем поверхности под кривой. Они имеют две переменные и рассматривают функцию f (x, y) в трехмерном пространстве.

Заключительные слова:

Интегралы широко используются для улучшения архитектуры зданий, а также для мостов. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом.

Other Languages: Integral Calculator, Integral Hesaplama, Kalkulator Integral, Kalkulator Integralny, Integralrechner, 積分計算, 적분계산기, Integrály Kalkulačka, Calculadora De Integral, Calcul Intégrale En Ligne, Calculadora De Integrales, Calcolatore Integrali, حساب متكامل, Integraatio Laskin, Integreret Lommeregner, Integral Kalkulator, Integralni Kalkulator, เครื่องคำนวณอินทิกรัล, Integrale Rekenmachine.

Исчисление I. Определение определенного интеграла

Онлайн-заметки Пола
Главная / Исчисление I / Интегралы / Определение определенного интеграла

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 5.6: Определение определенного интеграла 9*} \справа)\Дельта х} \]

Определенный интеграл определяется как предел и сумма, которые мы рассмотрели в предыдущем разделе, чтобы найти чистую площадь между функцией и осью \(x\). Также обратите внимание, что обозначение определенного интеграла очень похоже на обозначение неопределенного интеграла. Причина этого со временем станет очевидной.

Есть также немного терминологии, которую мы должны здесь убрать. Число «\(a\)», стоящее под знаком интеграла, называется 9.0020 нижний предел интеграла и число «\(b\)» над знаком интеграла называется верхним пределом интеграла. Кроме того, несмотря на то, что \(a\) и \(b\) были заданы как интервал, нижний предел не обязательно должен быть меньше верхнего предела. В совокупности мы часто будем называть \(a\) и \(b\) интервалом интегрирования .

Давайте рассмотрим быстрый пример. В этом примере будут использоваться многие свойства и факты из краткого обзора нотации суммирования в главе «Дополнительно». 9*\). Чтобы упростить нашу жизнь, мы будем использовать правильные конечные точки каждого интервала.

Из предыдущего раздела мы знаем, что для общего \(n\) ширина каждого подынтервала равна

\[\Delta x = \frac{{2 — 0}}{n} = \frac{2}{n}\]

Тогда подынтервалы равны

\[\left[ {0,\frac{2}{n}} \right]\,\,\,\,\left[ {\frac{2}{n},\frac{4}{n} } \right],\,\,\,\left[ {\frac{4}{n},\frac{6}{n}} \right],\,\,\ldots\,\,\, \,\left[ {\frac{{2\left({i — 1} \right)}}{n},\frac{{2i}}{n}} \right],\,\, \ldots\ , \, \, \, \ влево [ {\ гидроразрыва {{2 \ влево ( {n — 1} \ вправо)}} {п}, 2} \ вправо] \] 93}}} + \frac{2}{n}} \right)} \end{align*}\]

Теперь нам нужно ограничить это. Это означает, что нам нужно будет «оценить» это суммирование. Другими словами, нам придется использовать формулы, приведенные в обзоре обозначений суммирования, чтобы исключить фактическое суммирование и получить формулу для этого для общего \(n\).

Чтобы сделать это, нам нужно будет признать, что \(n\) является константой, насколько это касается обозначения суммирования. Когда мы циклически перебираем целые числа от 1 до \(n\), при суммировании изменяется только \(i\), поэтому все, что не является \(i\), будет константой и может быть исключено из суммирования. В частности, любой \(n\), который находится в суммировании, может быть вынесен за скобки, если нам нужно. 92}}}\\ & = \frac{{14}}{3}\end{align*}\]

Мы рассмотрели несколько способов работы с ограничением в этой задаче, поэтому мы оставляем вам возможность проверить результаты.

Вау, это было много работы для довольно простой функции. Есть гораздо более простой способ их оценки, и в конце концов мы до него доберемся. Основная цель этого раздела — изложить основные свойства и факты об определенном интеграле. Мы обсудим, как мы вычисляем их на практике, начиная со следующего раздела. 9{{\,b}}{{f\left( t \right)\,dt}}\). Смысл этого свойства в том, чтобы заметить, что пока функция и пределы одинаковы, переменная интегрирования, которую мы используем в определенном интеграле, не повлияет на ответ.

Доказательство свойств 1–4 см. в разделе «Доказательство различных интегральных свойств» главы «Дополнительно». Свойство 5 доказать непросто, поэтому оно здесь не показано. Свойство 6 на самом деле не является свойством в полном смысле этого слова. Здесь нужно только признать, что пока функция и ограничения одинаковы, не имеет значения, какую букву мы используем для переменной. Ответ будет таким же. 9{{\,12}}{{f\left( x \right)\,dx}}\).

Показать решение

Этот пример в основном является примером свойства 5, хотя в решении также есть пара применений свойства 1.

Нам нужно выяснить, как правильно разбить интеграл, используя свойство 5, чтобы мы могли использовать данные фрагменты информации. Во-первых, отметим, что существует интеграл, который имеет «-5» в одном из пределов. Это не нижний предел, но мы можем использовать свойство 1, чтобы исправить это в конечном итоге. Другой предел равен 100, так что это число \(c\), которое мы будем использовать в свойстве 5. 9{{\, б}} {{\ влево | {е\влево( х \вправо)\,} \вправо|dx}}\)

Доказательство этих свойств см. в разделе «Доказательство различных интегральных свойств» главы «Дополнительно».

Интерпретации определенного интеграла

Здесь мы можем дать несколько быстрых интерпретаций определенного интеграла.

Во-первых, как мы упоминали в предыдущем разделе, одна из возможных интерпретаций определенного интеграла состоит в том, чтобы дать чистую площадь между графиком \(f\left( x \right)\) и осью \(x\) на интервале \(\left[ {a,b} \right]\). Итак, чистая площадь между графиком \(f\left( x \right) = {x^2} + 1\) и осью \(x\) на \(\left[ {0,2} \ справа]\) есть, 9{{\,b}}{{f’\left( x \right)\,dx}} = f\left( b \right) — f\left( a \right)\]

— чистое изменение \(f\left( x \right)\) на интервале \(\left[ {a,b} \right]\).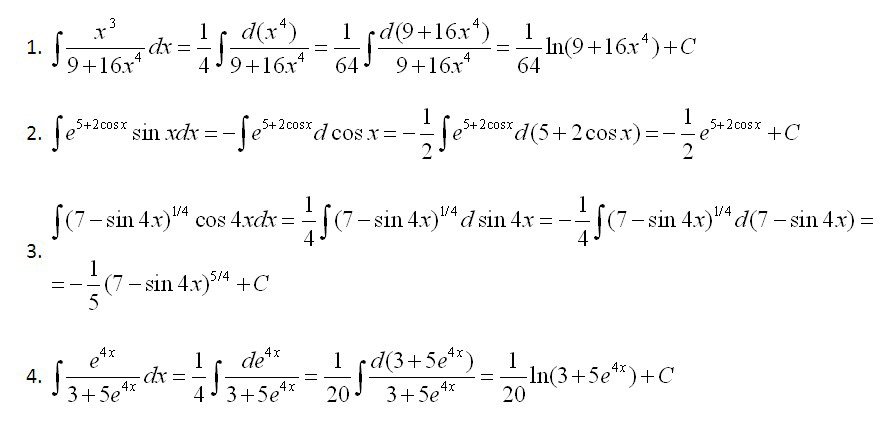 Другими словами, вычислите определенный интеграл скорости изменения, и вы получите чистое изменение количества. Мы можем видеть, что значение определенного интеграла \(f\left( b \right) — f\left( a \right)\) на самом деле дает нам чистое изменение \(f\left( x \ правильно)\) и, таким образом, этим утверждением действительно нечего доказывать. На самом деле это просто подтверждение того, что говорит нам определенный интеграл скорости изменения. 9{{\,{t_2}}}{{V’\left( t \right)\,dt}} = V\left( {{t_2}} \right) — V\left( {{t_1}} \right )\]

— чистое изменение объема по мере перехода от времени \({t_1}\) к времени \({t_2}\).

Аналогично, если \(s\left( t \right)\) является функцией, задающей положение некоторого объекта в момент времени \(t\), мы знаем, что скорость объекта в любой момент времени \(t\) равна : \(v\влево(t\вправо) = s’\влево(t\вправо)\). Следовательно, смещение объекта от времени \({t_1}\) до времени \({t_2}\) равно 9{{\,{t_2}}}{{v\left( t \right)\,dt}} = s\left( {{t_2}} \right) — s\left( {{t_1}} \right) \]

Обратите внимание, что в этом случае, если \(v\left( t \right)\) является как положительным, так и отрицательным ( т. е. объект перемещается как вправо, так и влево) во временном интервале, это НЕ даст общее расстояние путешествовал. Это даст только смещение, , т.е. , разницу между тем, где объект начал и где он закончился. Чтобы получить общее расстояние, пройденное объектом, нам нужно вычислить 9{{\,{t_2}}}{{\left| {v\left( t \right)} \right|\,dt}}\]

Здесь важно отметить, что теорема о чистом изменении действительно имеет смысл только в том случае, если мы интегрируем производную функции.

Фундаментальная теорема исчисления, часть I

Как указано в заголовке выше, это только первая часть Фундаментальной теоремы исчисления. Мы дадим вторую часть в следующем разделе, так как это ключ к простому вычислению определенных интегралов, и это предмет следующего раздела. 92} + 1}}\,dt}}\) Показать решение

Над этим нужно немного поработать, прежде чем мы сможем использовать основную теорему исчисления. Первое, на что следует обратить внимание, это то, что Основная теорема исчисления требует, чтобы нижний предел был константой, а верхний предел был переменной. 2} + 1}}\,dt}} \]

Следующее, на что следует обратить внимание, это то, что Фундаментальная теорема исчисления также требует \(x\) в верхнем пределе интегрирования, и мы получили x ² . Чтобы сделать эту производную, нам понадобится следующая версия цепного правила.

\[\frac{d}{{dx}}\left( {g\left( u \right)} \right) = \frac{d}{{du}}\left( {g\left( u \right )} \right)\,\,\frac{{du}}{{dx}}\hspace{0.5in}{\mbox{где }}u = f\left( x \right)\] 9{{\,u\left( x \right)}}{{f\left( t \right)\,dt}} = u’\left( x \right)f\left( {u\left( x \ верно-верно)\]

Это просто цепное правило для подобных проблем.

Далее мы можем получить формулу для интегралов, в которой верхний предел есть константа, а нижний предел есть функция \(x\). Все, что нам нужно сделать, это поменять местами пределы интеграла (конечно, добавив знак минус), а затем использовать приведенную выше формулу, чтобы получить

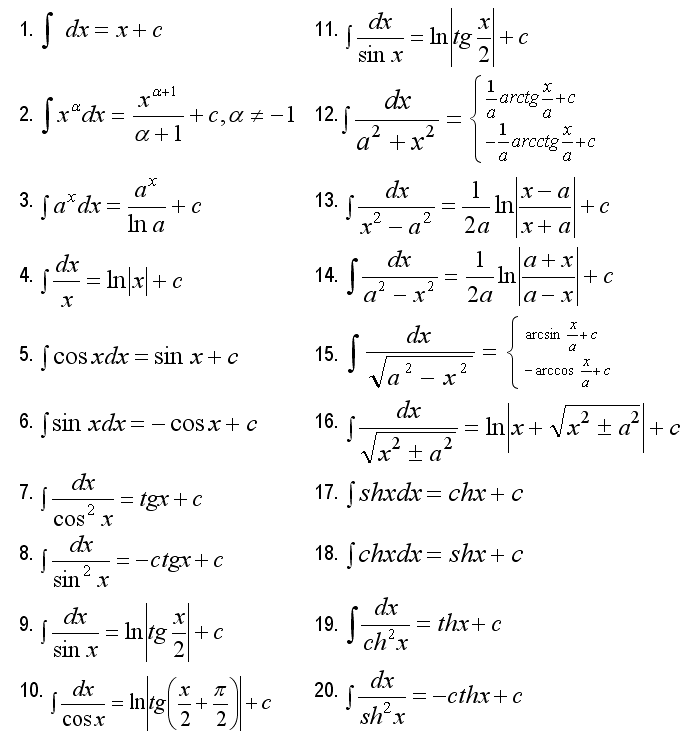. {{\,v\left( x \right)}}{{f\left( t \right)\,dt }} = — v’\left( x \right)f\left( {v\left( x \right)} \right)\] 92}} \right)\end{align*}\]

Интегральное исчисление — формулы, методы, примеры

Интегральное исчисление помогает найти первообразные функции. Эти первообразные также называются интегралами функции. Процесс нахождения первообразной функции называется интегрированием. Обратным процессом нахождения производных является нахождение интегралов. Интеграл функции представляет собой семейство кривых. Нахождение как производных, так и интегралов составляет фундаментальное исчисление. В этом разделе мы рассмотрим основы интегралов и вычисления интегралов.

1.	Что такое интегральное исчисление?
2.	Основные теоремы интегралов
3.	Типы интегралов
4.	Свойства интегралов
5.	Интегральные формулы
6.	Методы интегралов
7.	Применение интегралов
8.	Часто задаваемые вопросы по интегралам

Что такое интегральное исчисление?

Интегралы — это значения функции, найденные в процессе интегрирования. Процесс получения f(x) из f'(x) называется интегрированием. Интегралы присваивают номера функциям таким образом, что описывают задачи перемещения и движения, проблемы площади и объема и т. д., возникающие при объединении всех небольших данных. Зная производную f’ функции f, мы можем определить функцию f. Здесь функция f называется первообразной или интегралом от f’.

Пример: Дано: f(x) = x ² .

Производная f(x) = f'(x) = 2x = g(x)

если g(x) = 2x, то антипроизводная g(x) = ∫ g(x) = x ²

Определение интеграла

F(x) называется первообразной или интегралом Ньютона-Лейбница или примитивной функции f(x) на интервале I. F'(x) = f(x) для каждого значения x в I.

Интеграл представляет площадь области под кривой. Мы аппроксимируем фактическое значение интеграла, рисуя прямоугольники. Определенный интеграл функции можно представить как площадь области, ограниченной ее графиком данной функции между двумя точками прямой. Площадь области находят, разбивая ее на тонкие вертикальные прямоугольники и применяя нижний и верхний пределы, площадь области суммируют. Зададим интеграл функции по интервалу, на котором этот интеграл определен. 9b f(x) dx\) = f(b) — f(a). Это известно как определенный интеграл от f в диапазоне [a,b], где a — нижний предел, а b — верхний предел.

Типы интегралов

Интегральное исчисление используется для решения задач следующих типов.

а) задача о нахождении функции, если задана ее производная.

б) задача нахождения площади, ограниченной графиком функции при заданных условиях. Таким образом, интегральное исчисление делится на два типа.

• Определенные интегралы (значения интегралов определенные)
• Indefinite Integrals (значение интеграла неопределенно с произвольной константой, C)

Неопределенные интегралы

Это интегралы, которые не имеют ранее существовавшего значения пределов; тем самым делая окончательное значение интеграла неопределенным. ∫g'(x)dx = g(x) + c. Неопределенные интегралы относятся к семейству параллельных кривых.

Определенные интегралы

9b f(x) dx = f(b) — f(a)\)

Свойства интегрального исчисления

Изучим свойства неопределенных интегралов, чтобы работать над ними.

• Производная интеграла — это сама подынтегральная функция. ∫ f(x) dx = f(x) +C
• Два неопределенных интеграла с одной и той же производной приводят к одному и тому же семейству кривых, поэтому они эквивалентны. ∫ [ f(x) dx -g(x) dx] =0
• Интеграл суммы или разности конечного числа функций равен сумме или разности интегралов отдельных функций. ∫ [ f(x) dx+g(x) dx] = ∫ f(x) dx + ∫ g(x) dx
• Константа вынесена за знак интеграла. ∫ k f(x) dx = k ∫ f(x) dx, где k ∈ R.
• Два предыдущих свойства объединяются, чтобы получить форму: ∫ [k\(_1\)f\(_1\)(x) + k\(_2\)f\(_2\)(x) +… k \(_n\)f\(_n\)(x)] dx = k\(_1\)∫ f\(_1\)(x)dx + k\(_2\)∫ f\(_2\)(x )dx+ … k\(_n\) ∫ f\(_n\)(x)dx

Интегральные формулы

Мы можем запомнить формулы производных некоторых важных функций. Вот соответствующие интегралы этих функций, которые запоминаются как стандартные формулы интегралов.

• ∫ x ⁿ dx=x ⁿ⁺¹ /n+1+C, где n ≠ -1
• ∫ дх =х+С
• ∫ cosxdx = sinx+C
• ∫ sinxdx = -cosx+C
• ∫ сек ² x dx = tanx+C
• ∫ cosec ² x dx = -cotx+C
• ∫ сек ² x dx = tanx+C
• ∫ secx tanxdx = secx+C
• ∫ cscx cotx dx = -cscx+C
• ∫1/(√(1-x ² ))= sin ^-1 х + С
• ∫-1/(√(1-x ² ))= cos ^-1 x + C
• ∫1/(1+x ² )= тангенс ^-1 x + C
• ∫-1/(1+x ² )= детская кроватка ^-1 x + C
• ∫1/(x√(x ² -1))= сек ^-1 x + C
• ∫-1/(x√(x ² -1))= cosec ^-1 x + C
• ∫ e ^x dx=e ^x + C
• ∫dx/x=ln|x| + С
• ∫ ^x dx=a ^x /ln a + C

Методы нахождения интегралов

Существует несколько методов нахождения неопределенных интегралов. Известные методы:

• Нахождение интегралов путем интегрирования методом подстановки
• Нахождение интегралов интегрированием по частям
• Нахождение интегралов интегрированием по неполным дробям.

Нахождение интегралов методом подстановки

Несколько интегралов находятся методом подстановки. Если u является функцией x, то u’ = du/dx.

∫ f(u)u’ dx = ∫ f(u)du, где u = g(x).

Нахождение интегралов интегрированием по частям

Если две функции имеют вид произведения, интегралы находятся методом интегрирования по частям.

∫f(x)g(x) dx = f(x)∫ g(x) dx — ∫ (f'(x) ∫g(x) dx) dx.

Нахождение интегралов интегрированием дробей

Интегрирование рациональных алгебраических функций, числитель и знаменатель которых содержат положительные целые степени x с постоянными коэффициентами, производится путем их разложения на частные дроби.

Чтобы найти ∫ f(x)/g(x) dx, разложите эту неправильную рациональную функцию на правильную рациональную функцию и затем проинтегрируйте.

∫f(x)/g(x) dx = ∫ p(x)/q(x) + ∫ r(x)/s(x), где g(x) = a(x) . с(х)

Применение интегрального исчисления

Используя интегрирование, мы можем найти расстояние, зная скорость. Определенные интегралы представляют собой мощный инструмент для нахождения площади под простыми кривыми, площади, ограниченной кривой и линией, площади между двумя кривыми, объема твердых тел. Задачи о перемещении и движении также находят свое применение интегралов. Площадь области, заключенной между двумя кривыми y = f(x) и y = g(x) и линиями x =a, x =b, равна 92)dx\)

= x ² /2- x ³ /3

= 1/2-1/3

= 1/6 кв.

Важные примечания

• Примитивное значение функции, найденное в процессе интегрирования, называется интегралом.
• Интеграл — это математический объект, который можно интерпретировать как площадь или обобщение площади.
• При интегрировании полиномиальной функции степень интеграла увеличивается на 1.

☛ Также проверьте:

• Интеграция формулы УФ
• Формула определенного интеграла

Часто задаваемые вопросы по интегральному исчислению

Что такое интегралы?

Интегралы – это значения функции, найденные в процессе интегрирования. Интеграл определяется как площадь области под кривой, представленной в виде функции y = f(x).

Как называется символ интеграла?

Целочисленный символ ∫. Это означает, что она привязана к пределу от низшего к высшему и что интегралы представляют собой площадь кривой под графиком функции.

Какие существуют типы интегралов?

Два типа интегралов: определенный интеграл и неопределенный интеграл. Определенные интегралы ограничены пределами. Неопределенные интегралы не привязаны к ранее существовавшим значениям.

Может ли интеграл иметь два ответа?

Да, неопределенный интеграл может иметь бесконечные ответы в зависимости от значения постоянного члена; а определенный интеграл будет постоянной величиной.

Для чего используется двойной интеграл?

Двойной интеграл используется для вычисления площадей областей, нахождения объемов данной поверхности, а также среднего значения любой заданной функции в плоской области.

Как найти интегралы?

Нахождение интегралов — это операция, обратная нахождению производных. Некоторые интегралы запоминаются как формулы. Например, ∫ x ⁿ = x ⁿ⁺¹ / (n+1) + C. Таким образом, x ⁶ = x ⁶⁺¹ / 6+1 = x ⁷ / 7 + C. В некоторых интегралах используются методы интегрирования по частям, интегрирования по неполным дробям, метода подстановки и т. д.

Как использовать интегралы в тригонометрии?

Используйте тригонометрические тождества и упростите функцию до интегрируемой функции, а затем примените формулы и примените процедуры интегрирования, чтобы найти интегралы с помощью тригонометрии.

Что такое интеграл от sin x?

Интеграл от синуса x равен -cos x + C.