Интегралы сложные: Нескучные интегралы / Хабр

Нескучные интегралы / Хабр

Некоторые из вас, вероятно, видали на просторах сети эту задачку: какое число продолжает следующий ряд?

Предлагался такой очевидный правильный ответ:

Для тех, кому неочевидно, как он получен, предлагалось объяснение. Пусть (ну и 1 при x = 0, хотя неважно). Тогда каждый член ряда — это значение следующего интеграла в цепочке:

Пока всё идёт хорошо, но тут внезапно:

В принципе, этого достаточно, чтобы повеселить друзей-математиков, но мне захотелось узнать, как вообще считаются такие интегралы и почему получается такой смешной результат. Если кому-то ещё охота тряхнуть стариной и вспомнить матан с функаном, прошу читать дальше.

Начинает сказка сказываться

Для начала отдельно посмотрим на первый интеграл:

Некоторое время назад я подумал: «Эй, я ещё не совсем забыл матан! Дайте-ка я возьму этот интеграл как неопределённый, а потом подставлю пределы.

Наверняка пару раз по частям, и дело в шляпе. Вот сейчас на бумажке всё решу без посторонней помощи». Хочу предостеречь вас: не повторяйте моей ошибки. Вас ждёт бессонная ночь, а потом вы заглянете в справочник и узнаете, что неопределённый интеграл не берётся в элементарных функциях. Для него даже специальную функцию ввели.

Однако с данными конкретными пределами взять интеграл можно разными способами. Мы пойдём путём, который требует минимум базовых знаний (самое суровое — то же интегрирование по частям). Для начала сделаем внезапную замену:

Вы спросите: откуда вообще это взялось и зачем нам ещё один интеграл, мало что ли? Спокойно, так надо (знакомые со свойствами преобразования Лапласа весело ухмыляются). Подставим замену в исходную формулу и поменяем порядок интегрирования:

Внутри получился почти классический интеграл по dx, которым всех пугали у нас в физматшколе. Его можно взять и как неопределённый, дважды использовав формулу интегрирования по частям.

Тогда справа получится какая-то муть и ещё раз тот же самый интеграл, домноженный на что-то, и в результате можно будет решить уравнение относительно этого интеграла и получить ответ, а потом подставить пределы. Кому интересно, проделайте это сами, а я лениво запишу готовый результат:

Ну а теперь совсем всё просто: это табличный интеграл из средней школы, который равен арктангенсу. В бесконечности пи-пополам, в нуле — ноль, вот мы и получили ответ.
Интеграл, кстати, настолько хорош, что у него есть своё имя — интеграл Дирихле. По ссылке вы можете найти другие способы взять его.

Скоро сказка сказывается, а не скоро дело делается

Для следующего путешествия нам понадобятся четыре вещи: прямоугольная функция, косинусное преобразование Фурье, свёртка и теорема Парсеваля. Сперва скажу пару слов об этих замечательных штуках.

Прямоугольная функция — это у нас будет такая ступенька вокруг нуля:

Значение 1/2 в точках разрыва нужно в основном для соблюдения свойств преобразования Фурье, в целом для нашей задачи оно непринципиально.

Косинусное преобразование Фурье. Для простоты мы немного отступим от математической точности и сформулируем грубовато. Для достаточно хорошей чётной функции f(x) выполняются такие соотношения:

Функция и называется косинусным преобразованием Фурье (FCT) от f(x) (её ещё называют образом f). То есть, косинусное преобразование от косинусного преобразования даёт снова исходную функцию f(x)!

Людям, знакомым с обработкой сигналов, хорошо известно, что FCT от прямоугольной функции — это . Это легко доказать, пользуясь вышеприведёнными формулами и школьными знаниями. Так как прямоугольная функция за пределами промежутка [-a, a] равна нулю, то можно просто интегрировать cos(xt) dt по этому промежутку, тут простая замена переменной и табличный интеграл. Приведённое выше свойство говорит, что FCT от — это прямоугольная функция.

Свёртка — это ещё одна прекрасная штука, без которой не обходится обработка сигналов. Для двух функций f₁(x) и f₂(x) можно определить функцию-свёртку (обозначается звёздочкой) вот так:

У свёртки есть прекрасное свойство, за которое её любят: преобразование Фурье превращает её в умножение, а умножение — в свёртку. Если точнее, косинусное преобразование произведения двух хороших чётных функций есть свёртка их образов, делённая на корень из двух пи: .

Теорема Парсеваля — это очень крутое утверждение о равенстве энергии сигнала и его спектра, которое записывают по-разному в разных целях. Нам потребуется такая версия: для чётных и достаточно хороших функций .

Доселева Макар огороды копал, а нынече Макар в воеводы попал

Возьмём второй интеграл из нашей чудесной последовательности. Как многие уже догадались, мы воспользуемся теоремой Парсеваля и заменим множители на их FCT-образы:

Первая прямоугольная функция под интегралом равна единице для аргументов меньше единицы и нулю для аргументов больше единицы. Поэтому ничто нам не мешает убрать её из интеграла, откорректировав пределы интегрирования:

Под интегралом осталась ступенька высотой 3 и шириной 1/3. Такой интеграл возьмёт даже третьеклассник: надо всего лишь умножить 3 и 1/3.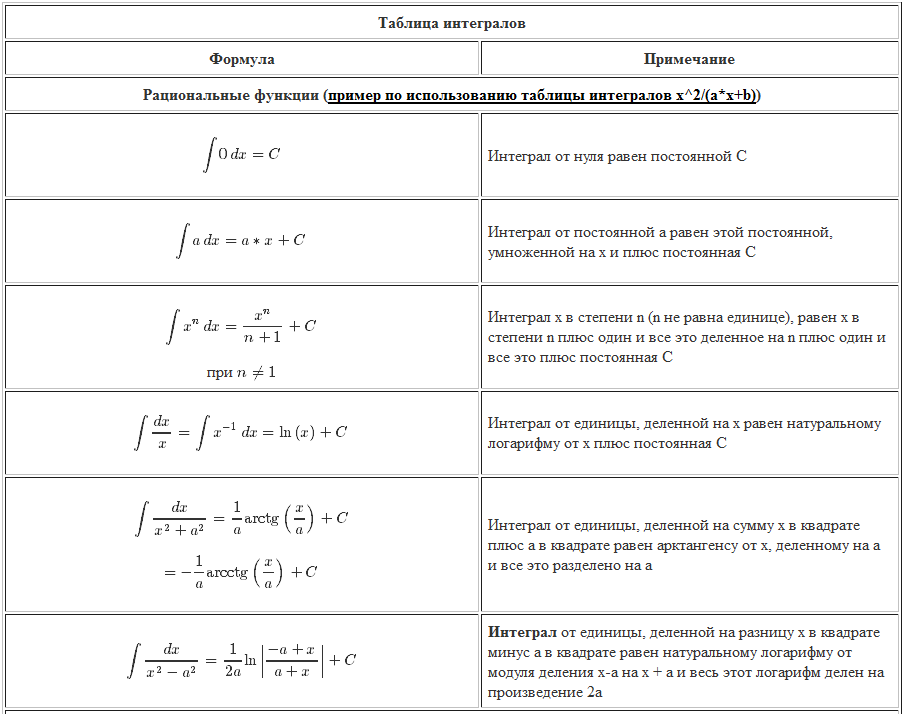 От интеграла остаётся единица, и мы имеем искомое пи-пополам! Таким образом мы почти честно взяли второй интеграл из ряда. Кто желает сделать это совсем честно, тому придётся разобраться, что же такое хорошесть функции, и доказать, что наши функции хорошие.

Чтобы дальше было проще, обозначим эту ступеньку под интегралом как F₁(x) и нарисуем её график:

Пойдём веселиться дальше и посмотрим на интеграл с тремя множителями. Чтобы применить теорему Парсеваля, мы теперь все множители со второго будем считать одним множителем: . С образом первого множителя всё уже понятно, а образ второго множителя, выражается через свёртку:

На первый взгляд жутковато. Но можно кое-чего повыносить, кое-чего посокращать и подставить нашу F₁(x). Тогда получим:

Внутренний интеграл — это просто прямоугольный фильтр, эдакий «блюр» для функции F₁(x): мы просто для каждой точки усредняем все значения в окрестности плюс-минус одна пятая. Можно опять же избавиться от прямоугольной функции, подшаманив пределы интегрирования. И со внешним интегралом сделаем такую же процедуру. Вот что получится в итоге:

Слева график функции F₂(x), которая на самом деле — сглаженная F₁(x). Нетрудно доказать, что после сглаживания функции по нормированному ядру её интеграл не меняется. Ну, вообще-то речь об интеграле от -∞ до +∞, но для чётной функции это верно и для интеграла от нуля. В данном случае ядром была ступенька от -1/5 до +1/5, умноженная на 5/2. Площадь под ступенькой единица, значит, ядро нормировано. Тут тоже можно сравнить с блюром в фотошопе: после применения блюра картинка в целом не становится светлее или темнее. А раз так, то интеграл F₂(x) в точности равен интегралу F₁(x), то есть единице, поэтому и третий интеграл равен пи-пополам!

Дальше процедура во многом похожая. Четвёртый интеграл сгруппируем так: . Сначала теорему Парсеваля, для скобок свёртку, причём мы уже умеем выразить образ внутренней скобки через

F₂(x). Дальше всё то же самое, что в прошлый раз, и в результате получим:

Теперь мы уже имеем F₃(x), которая на самом деле — сглаженная F₂(x) с ядром шириной 2/7. Ядро нормировано, значит, интеграл F₃(x) равен интегралу F₂(x), то есть единице, и мы снова имеем пи-пополам!

Отлично, мы теперь щёлкаем эти интегралы как орехи. Но по идее, если так и дальше пойдёт, они все до бесконечности будут равны пи-пополам? Давайте смотреть дальше. Пятый интеграл:

Вроде всё то же самое. Ладно, шестой интеграл:

И здесь никаких проблем. Хорошо, берём седьмой:

Ничего нового! Ладно, а восьмой?

Стоп-стоп-стоп! Здесь нам не обойтись без команды CSI!

Функция протекла через единицу! Интеграл F₇(x)

всё ещё равен единице, но это если интегрировать от 0 до ∞. А мы-то интегрируем до единицы! До сих пор все функции были нулевыми при x больше единицы, но рано или поздно это должно было кончиться.

А как понять, когда наступает конец? Это очень просто. F₁(x) была ненулевой при x<1/3. F₂(x) сглаживала её по ±1/5, значит, была ненулевой при x<1/3+1/5. Аналогичным образом можно найти границу ненулевых значений для всех этих функций, и для F₇(x) эта граница впервые превышает единицу:

Несложно даже посчитать, сколько конкретно утекло, и тем самым вычислить точное значение восьмого интеграла. Заметим, что слева от границы F₁(x) — это константа 3. F₂(x)

— минус интеграл этой константы с коэффициентом 5/2, то есть прямая с коэффициентом 3×5/2. F₃(x) в достаточной близости к границе 1/3+1/5+1/7 — это интеграл той прямой с коэффициентом 7/2, то есть что-то вроде . Продолжая аналогичные рассуждения, получим формулу для F₇(x) в окрестности границы:

Собственно, обычная парабола шестой степени, сдвинутая и домноженная. Если проинтегрировать её от единицы и до границы 1/3+1/5+1/7+1/9+1/11+1/13+1/15, то мы узнаем, сколько функции утекло за пределы единицы. Можно решить эту задачу целиком в обыкновенных дробях. Получится вот сколько:

Если эту цифру вычесть из единицы и домножить на пи-пополам, мы получим окончательное значение восьмого интеграла:

Такие интегралы называются борвейновскими интегралами в честь Давида и Джонатана Борвейнов, которые их описали. Если вы хотите строгие математические доказательства (без всяких «хороших функций») и другие свойства этих замечательных интегралов, почитайте статью авторов.

Заключение: троллинг восьмидесятого уровня

Открыв эти интегралы, Джонатан Борвейн ввёл их в программный пакет Maple и, убедившись, что Maple корректно берёт все восемь интегралов, сообщил разработчикам о «баге»: мол, восьмой интеграл тоже должен быть пи-пополам, а у вас получается чёрт-те-что. Три дня и три ночи убил Жак Каретт, один из разработчиков Maple, в поисках ошибки, пока не понял, что над ним жестоко пошутили. А ещё говорят, что математики — скучные люди!

Примеры решения интегралов иррациональных функций.

Сложные интегралы

Универсального способа решения иррациональных уравнений нет, так как их класс отличается количеством. В статье будут выделены характерные виды уравнений с подстановкой при помощи метода интегрирования.

Для использования метода непосредственного интегрирования необходимо вычислять неопределенные интегралы типа ∫ k x + b p d x , где p является рациональной дробью, k и b являются действительными коэффициентами.

Пример 1

Найти и вычислить первообразные функции y = 1 3 x — 1 3 .

Решение

По правилу интегрирования необходимо применить формулу ∫ f (k · x + b) d x = 1 k · F (k · x + b) + C , а таблица первообразных говорит о том, что имеется готовое решение данной функции. Получаем, что

∫ d x 3 x — 1 3 = ∫ (3 x — 1) — 1 3 d x = 1 3 · 1 — 1 3 + 1 · (3 x — 1) — 1 3 + 1 + C = = 1 2 (3 x — 1) 2 3 + C

Ответ: ∫ d x 3 x — 1 3 = 1 2 (3 x — 1) 2 3 + C .

Имеют место быть случаи, когда можно использовать метод подведения под знак дифференциала. Это решается по принципу нахождения неопределенных интегралов вида ∫ f » (x) · (f (x)) p d x , когда значение p считается рациональной дробью.

Пример 2

Найти неопределенный интеграл ∫ 3 x 2 + 5 x 3 + 5 x — 7 7 6 d x .

Решение

Отметим, что d x 3 + 5 x — 7 = x 3 + 5 x — 7 » d x = (3 x 2 + 5) d x . Тогда необходимо произвести подведение под знак дифференциала с использованием таблиц первообразных. Получаем, что

∫ 3 x 2 + 5 x 3 + 5 x — 7 7 6 d x = ∫ (x 3 + 5 x — 7) — 7 6 · (3 x 2 + 5) d x = = ∫ (x 3 + 5 x — 7) — 7 6 d (x 3 + 5 x — 7) = x 3 + 5 x — 7 = z = = ∫ z — 7 6 d z = 1 — 7 6 + 1 z — 7 6 + 1 + C = — 6 z — 1 6 + C = z = x 3 + 5 x — 7 = — 6 (x 3 + 5 x — 7) 6 + C

Ответ: ∫ 3 x 2 + 5 x 3 + 5 x — 7 7 6 d x = — 6 (x 3 + 5 x — 7) 6 + C .

Решение неопределенных интегралов предусматривает формулу вида ∫ d x x 2 + p x + q , где p и q являются действительными коэффициентами. Тогда необходимо выделить полный квадрат из-под корня. Получаем, что

x 2 + p x + q = x 2 + p x + p 2 2 — p 2 2 + q = x + p 2 2 + 4 q — p 2 4

Применив формулу, расположенную в таблице неопределенных интегралов, получаем:

∫ d x x 2 ± α = ln x + x 2 ± α + C

Тогда вычисление интеграла производится:

∫ d x x 2 + p x + q = ∫ d x x + p 2 2 + 4 q — p 2 4 = = ln x + p 2 + x + p 2 2 + 4 q — p 2 4 + C = = ln x + p 2 + x 2 + p x + q + C

Пример 3

Найти неопределенный интеграл вида ∫ d x 2 x 2 + 3 x — 1 .

Решение

Для вычисления необходимо вынести число 2 и расположить его перед радикалом:

∫ d x 2 x 2 + 3 x — 1 = ∫ d x 2 x 2 + 3 2 x — 1 2 = 1 2 ∫ d x x 2 + 3 2 x — 1 2

Произвести выделение полного квадрата в подкоренном выражении. Получим, что

x 2 + 3 2 x — 1 2 = x 2 + 3 2 x + 3 4 2 — 3 4 2 — 1 2 = x + 3 4 2 — 17 16

Тогда получаем неопределенный интеграл вида 1 2 ∫ d x x 2 + 3 2 x — 1 2 = 1 2 ∫ d x x + 3 4 2 — 17 16 = = 1 2 ln x + 3 4 + x 2 + 3 2 x — 1 2 + C

Ответ: d x x 2 + 3 x — 1 = 1 2 ln x + 3 4 + x 2 + 3 2 x — 1 2 + C

Интегрирование иррациональных функций производится аналогичным способом. Применимо для функций вида y = 1 — x 2 + p x + q .

Пример 4

Найти неопределенный интеграл ∫ d x — x 2 + 4 x + 5 .

Решение

Для начала необходимо вывести квадрат знаменателя выражения из-под корня.

∫ d x — x 2 + 4 x + 5 = ∫ d x — x 2 — 4 x — 5 = = ∫ d x — x 2 — 4 x + 4 — 4 — 5 = ∫ d x — x — 2 2 — 9 = ∫ d x — (x — 2) 2 + 9

Табличный интеграл имеет вид ∫ d x a 2 — x 2 = a r c sin x a + C , тогда получаем, что ∫ d x — x 2 + 4 x + 5 = ∫ d x — (x — 2) 2 + 9 = a r c sin x — 2 3 + C

Ответ: ∫ d x — x 2 + 4 x + 5 = a r c sin x — 2 3 + C .

Процесс нахождения первообразных иррациональных функций вида y = M x + N x 2 + p x + q , где имеющиеся M , N , p , q являются действительными коэффициентами, причем имеют схожесть с интегрированием простейших дробей третьего типа. Это преобразование имеет несколько этапов:

подведение дифференциала под корень, выделение полного квадрата выражения под корнем, применение табличных формул.

Пример 5

Найти первообразные функции y = x + 2 x 2 — 3 x + 1 .

Решение

Из условия имеем, что d (x 2 — 3 x + 1) = (2 x — 3) d x и x + 2 = 1 2 (2 x — 3) + 7 2 , тогда (x + 2) d x = 1 2 (2 x — 3) + 7 2 d x = 1 2 d (x 2 — 3 x + 1) + 7 2 d x .

Рассчитаем интеграл: ∫ x + 2 x 2 — 3 x + 1 d x = 1 2 ∫ d (x 2 — 3 x + 1) x 2 — 3 x + 1 + 7 2 ∫ d x x 2 — 3 x + 1 = = 1 2 ∫ (x 2 — 3 x + 1) — 1 2 d (x 2 — 3 x + 1) + 7 2 ∫ d x x — 3 2 2 — 5 4 = = 1 2 · 1 — 1 2 + 1 · x 2 — 3 x + 1 — 1 2 + 1 + 7 2 ln x — 3 2 + x — 3 2 — 5 4 + C = = x 2 — 3 x + 1 + 7 2 ln x — 3 2 + x 2 — 3 x + 1 + C

Ответ: ∫ x + 2 x 2 — 3 x + 1 d x = x 2 — 3 x + 1 + 7 2 ln x — 3 2 + x 2 — 3 x + 1 + C .

Поиск неопределенных интегралов функции ∫ x m (a + b x n) p d x осуществляется при помощи метода подстановки.

Для решения необходимо ввести новые переменные:

1. Когда число p является целым, тогда считают, что x = z N , а N является общим знаменателем для m , n .
2. Когда m + 1 n является целым числом, тогда a + b x n = z N , а N является знаменателем числа p .
3. Когда m + 1 n + p является целым числом, то необходим ввод переменной a x — n + b = z N , а N является знаменателем числа p .

Пример 6

Найти определенный интеграл ∫ 1 x 2 x — 9 d x .

Решение

Получаем, что ∫ 1 x 2 x — 9 d x = ∫ x — 1 · (- 9 + 2 x 1) — 1 2 d x . Отсюда следует, что m = — 1 , n = 1 , p = — 1 2 , тогда m + 1 n = — 1 + 1 1 = 0 является целым числом. Можно ввести новую переменную вида — 9 + 2 x = z 2 . Необходимо выразить x через z . На выходы получим, что

9 + 2 x = z 2 ⇒ x = z 2 + 9 2 ⇒ d x = z 2 + 9 2 » d z = z d z — 9 + 2 x = z

Необходимо произвести подстановку в заданный интеграл.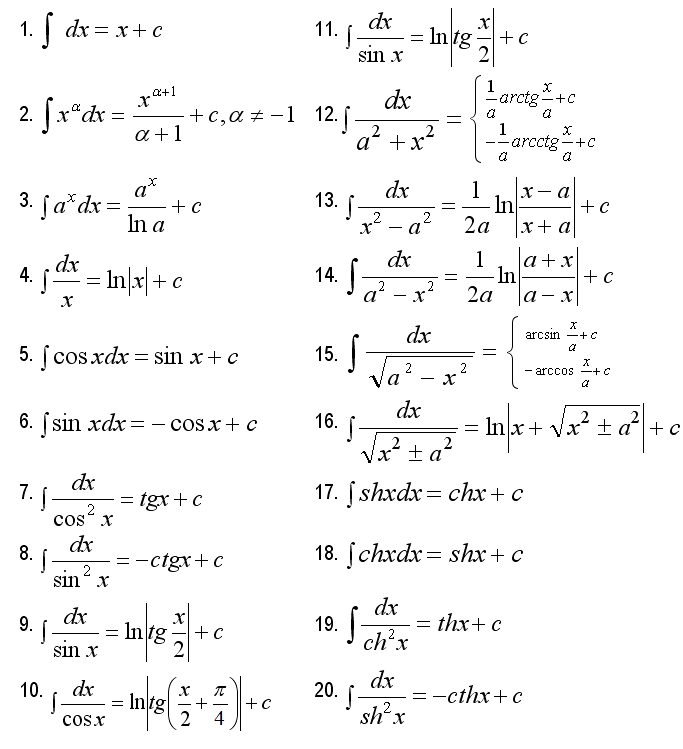 Имеем, что

∫ d x x 2 x — 9 = ∫ z d z z 2 + 9 2 · z = 2 ∫ d z z 2 + 9 = = 2 3 a r c t g z 3 + C = 2 3 a r c c t g 2 x — 9 3 + C

Ответ: ∫ d x x 2 x — 9 = 2 3 a r c c t g 2 x — 9 3 + C .

Для упрощения решения иррациональных уравнений применяются основные методы интегрирования.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Под иррациональным понимают выражение, в котором независимая переменная %%x%% или многочлен %%P_n(x)%% степени %%n \in \mathbb{N}%% входят под знак радикала (от латинского radix — корень), т.е. возводятся в дробную степень. Некоторые классы иррациональных относительно %%x%% подынтегральных выражений заменой переменной удается свести к рациональным выражениям относительно новой переменной.

Понятие рациональной функции одной переменной можно распространить на несколько аргументов. Если над каждым аргументом %%u, v, \dotsc, w%% при вычислении значения функции предусмотрены лишь арифметические действия и возведение в целую степень, то говорят о рациональной функции этих аргументов, которую обычно обозначают %%R(u, v, \dotsc, w)%%. 2 + bx + c}\right) \mathrm{d}x%% используются

Вспоминаем счастливые школьные годы. Пионеры на уроках математики, приступая к изучению корней, в первую очередь знакомились с квадратным корнем. Мы пойдем тем же путем.

Пример 1

Найти неопределенный интеграл

Анализируя подынтегральную функцию, приходишь к печальному выводу, что она совсем не напоминает табличные интегралы. Вот если бы всё это добро находилось в числителе – было бы просто. Или бы корня внизу не было. Или многочлена. Никакие методы интегрирования дробей тоже не помогают. Что делать?

Основной приём решения иррациональных интегралов – это замена переменной, которая избавит нас от ВСЕХ корней в подынтегральной функции.

Отметим, что эта замена немного своеобразная, ее техническая реализация отличается от «классического» способа замены, который рассмотрен на уроке Метод замены в неопределенном интеграле .

В данном примере нужно провести замену x = t 2 , то есть, вместо «икса» под корнем у нас окажется t 2 . Почему замена именно такая? Потому что , и в результате замены корень пропадёт.

Если бы в подынтегральной функции вместо квадратного корня у нас находился , то мы бы провели замену . Если бы там был , то провели бы и так далее.

Хорошо, у нас превратится в . Что произойдет с многочленом ? Сложностей нет: если , то .

Осталось выяснить, во что превратится дифференциал . Делается это так:

Берем нашу замену и навешиваем дифференциалы на обе части :

(распишем максимально подробно).

Оформление решения должно выглядеть примерно так:

.

Проведем замену: .

.

(1) Проводим подстановку после замены (как, что и куда, уже рассмотрено).

(2) Выносим константу за пределы интеграла. Числитель и знаменатель сокращаем на t .

(3) Получившийся интеграл является табличным, готовим его для интегрирования, выделяя квадрат.

(4) Интегрируем по таблице, используя формулу

.

(5) Проводим обратную замену. Как это делается? Вспоминаем, от чего плясали: если , то .

Пример 2

Найти неопределенный интеграл

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Как-то так получилось, что в Примерах 1, 2 «голый» числитель с одиноким дифференциалом . Исправим ситуацию.

Пример 3

Найти неопределенный интеграл

Предварительный анализ подынтегральной функции опять показывает, что лёгкого пути нет. А поэтому нужно избавляться от корня.

Проведем замену: .

Заобозначаем ВСЁ выражение под корнем . Замена из предыдущих примеров здесь не годится (точнее, сделать-то её можно, но это не избавит нас от корня).

Навешиваем дифференциалы на обе части:

С числителем разобрались. Что делать с в знаменателе?

Берем нашу замену и выражаем из неё: .

Если , то .

(1) Проводим подстановку в соответствии с выполненной заменой.

(2) Причесываем числитель. Константу здесь я предпочел не выносить за знак интеграла (можно делать и так, ошибкой не будет)

(3) Раскладываем числитель в сумму. Еще раз настоятельно рекомендуем ознакомиться с первым параграфом урока Интегрирование некоторых дробей . Канители с разложением числителя в сумму в иррациональных интегралах будет предостаточно, очень важно отработать это прием.

(4) Почленно делим числитель на знаменатель.

(5) Используем свойства линейности неопределенного интеграла. Во втором интеграле выделяем квадрат для последующего интегрирования по таблице.

(6) Интегрируем по таблице. Первый интеграл совсем простой, во втором используем табличную формулу высокого логарифма .

(7) Проводим обратную замену. Если мы проводили замену , то, обратно: .

Пример 4

Найти неопределенный интеграл

Это пример для самостоятельного решения, если вы невнимательно проработали предыдущие примеры, то допустите ошибку! Полное решение и ответ в конце урока.

Принципиально так же решаются интегралы с несколькими одинаковыми корнями, например

И т.д. А что делать, если в подынтегральной функции корни разные ?

Пример 5

Найти неопределенный интеграл

Вот и пришла расплата за голые числители. Когда встречается такой интеграл, обычно становится страшно. Но страхи напрасны, после проведения подходящей замены подынтегральная функция упрощается. Задача состоит в следующем: провести удачную замену, чтобы сразу избавиться от ВСЕХ корней.

Когда даны разные корни, удобно придерживаться определённой схемы решения.

Сначала выписываем на черновике подынтегральную функцию, при этом все корни представляем в виде :

Нас будут интересовать знаменатели степеней:

Комплексный анализ

←Комплексный анализ→

---

Магия и сила исчисления в конечном итоге основываются на том удивительном факте, что дифференцирование и интеграция являются взаимно обратными операциями. И так же, как сложные функции обладают замечательной дифференцируемостью свойства, которых нет у их реальных аналогов, поэтому возвышенная красота сложной интеграции далеко выше своего реального прародителя.

Питер Дж. Оливер bf\left(z(t)\right)z'(t)\,dt. b v(t)\,dt \end{эквнаррай}

Теперь запишем подынтегральную функцию $$f(z)= u(x,y)+ iv(x,y)$$ через его действительную и мнимую части, а также дифференциал $$dz=\frac{dz}{dt}dt = \left(\frac{dx}{dt}+ i \frac{dy}{dt}\right)dt = dx+ i dy$$ Тогда комплексный интеграл (\ref{contour-integral}) распадается на пару вещественных линейных интегралов: \begin{eqnarray}\label{действительные интегралы} \int_C f(z)\,dz = \int_C\left(u+iv\right)\left(dx+idy\right) = \int_C\left(u\,dx-v\,dy\right) + i \int_C\влево(v\,dx+u\,dy\вправо). \end{эквнаррай} 9{2\пи} dt= 2\пи \,я. \end{выравнивание*}

---

Численная оценка комплексных интегралов

Разведка 1

Используйте следующий апплет для численного исследования интеграла $$\int_C \overline{z}\, dz$$ с разными контурами $C$:

• Сегменты линий.
• Полукруги.
• Круги, позитивно и негативно ориентированные.

Вы также можете изменить параметр отображения цвета домена. Перетаскивайте точки и внимательно наблюдайте, что происходит. Затем решить упражнение 1 ниже. 92 . Затем проанализируйте значения $I_2$ в следующих случаях:

1. $C$ — любой контур от $z_0=-i$ до $z_1 = i$. Что происходит, когда вы выбираете Line Segment в апплете? Что случается когда вы выбираете Полукруги ?
2. $C$ — окружность с центром $z_0$ и радиусом $r\gt 0$, $|z-z_0|= г$; позитивно или негативно ориентированы. В этом случае выберите Circle ↺ или Circle ↻ . Что произойдет, если $z = 0$ окажется внутри или вне круга? Что произойдет, если $z=0$ лежит на контуре, например когда $z_0=1$ и $r=1$? 92}$ от это?

   ---

   Антидеривативы

   Хотя значение контурного интеграла функции $f (z)$ от фиксированной точки $z_0$ до фиксированная точка $z_1$ зависит, вообще говоря, от выбранного пути, существуют определенные функции, интегралы которых от $z_0$ до $z_1$ имеют значения, не зависящие от пути, как вы видели в упражнениях 2 и 3. Эти примеры также иллюстрируют тот факт, что значения интегралов вокруг замкнутых путей иногда, но не всегда, нуль. Следующая теорема полезна для определения того, когда интегрирование является независимым. пути и, тем более, когда интеграл по замкнутому пути имеет нулевое значение. Это известно как сложная версия 9{b} \frac{d}{dt} F \left(z(t)\right) dt \\ &=& F\влево(z(b)\вправо) — F\влево(z(a)\вправо) \\ &=& F\влево(z_1\вправо) — F\влево(z_0\вправо) \end{выравнивание*} где $z_0= z(a)$ и $z_1= z(b)$ — концы контура $C$. $\черный квадрат$

   СЛЕДУЮЩАЯ: Интегралы функций с ветвями

   4.2: Сложные линейные интегралы — Математика LibreTexts

   1. Последнее обновление

   2. Сохранить как PDF

3. Идентификатор страницы

   6481

• Джереми Орлофф
• Массачусетский технологический институт через MIT OpenCourseWare

  ---

  6

  Линейные интегралы также называются интегралами по траекториям или контурам. Учитывая ингредиенты, мы определяем комплексный линейный интеграл \ (\ int _ {\ gamma} f (z) \ dz \) как 92\). Кроме того, убедитесь, что вы понимаете, что произведение \(f(\gamma (t)) \gamma ‘(t)\) — это просто произведение комплексных чисел.

  Альтернативная запись использует \(dz = dx + idy\) для записи

  \[\int_{\gamma} f(z)\dz = \int_{\gamma} (u + iv) (dx + idy) \label{4.2.2}\]

  Давайте проверим, что уравнения \ref{4.2.1} и \ref{4.2.2} совпадают. Уравнение \ref{4.2.2} на самом деле представляет собой исчисление с несколькими переменными, поэтому, представляя \(\gamma (t)\) как \((x(t), y(t))\), оно становится

  9{2\pi} i \ dt = 2\pi i.\nonumber\]

  ---

  Эта страница под названием 4.2: Комплексные линейные интегралы распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джереми Орлоффом (MIT OpenCourseWare) посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами.

  No related posts.