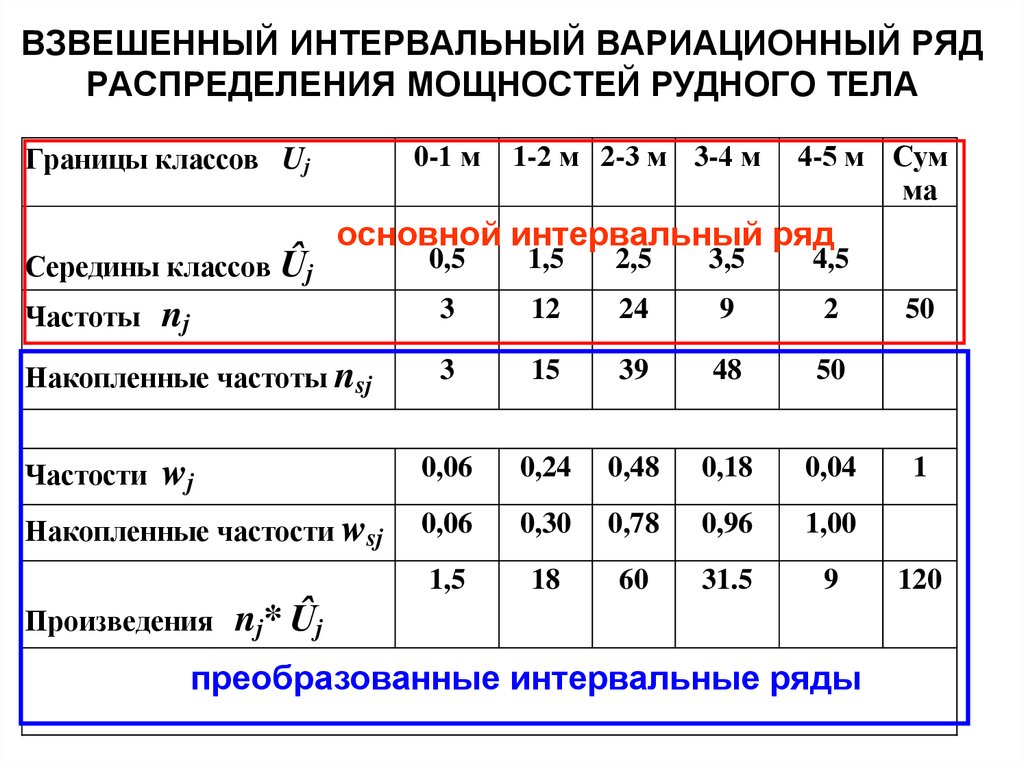
Определение числа групп при построении гистограммы
Сегодня, говоря о статистике, я буду обсуждать гистограммы. Вообще говоря, гистограмма является наглядным отображением метода группировки, то есть распределения множества результатов измерений какой-либо величины по группам, в соответствии с существенным для данной группы признаком. Методы группировки широко применяются для обработки первичных данных.
Под первичными данными в статистике мы понимаем статистические ряды, которые называют рядами динамики, если речь идет об изменении явления во времени, либо рядами распределения, если речь идет о составе или структуре исследуемого явления.
Если речь идет о рядах, построенных на основе качественных признаков (например, предприятия по формам собственности), то такие ряды называются атрибутивными, если ряды построены по количественным признакам (например, предприятия по объему товарооборота), то они называются вариационными.
В зависимости от прерывности вариации признака различают дискретные и интервальные вариационные ряды.
Гистограмма представляет собой столбчатый график, построенный по полученным данным, которые разбиваются на несколько групп. Число данных, попавших в каждую группу (частота), выражается высотой столбика, соответствующего данной группе.
Гистограмму можно строить для любых рядов, при этом, если это атрибутивный либо дискретный вариационный ряд (например, число рабочих в каждом тарифном разряде), то число выделяемых групп равно числу вариантов значений признака. В случае же интервального вариационного ряда число групп будет зависеть от величины интервала, используемого для группировки данных.
Интервал — разница между максимальным и минимальным значениями признака в каждой группе. Понятно, что чем больше групп, тем меньше интервал и наоборот. Группы в таком случае иногда называют также классами интервалов.
Например, можно разбить полученные данные о численности рабочих на предприятиях на следующие группы:
до 25 человек,
25–50 человек,
50–100 человек,
свыше 100 человек.
Тогда гистограмма будет содержать 4 столбика, высота которых будет соответствовать числу предприятий попавших в данную группу.
Заметим, кстати, что вышеприведенное распределение является примером использования неравных интервалов, выделенных, что называется, программой исследования, т. е. нами самими.
Вопрос выбора величины интервала (числа групп), используемого для группировки элементов интервального вариационного ряда, далеко не праздный. Помимо того, что гистограмма является отличным средством визуализации данных, она также является ни чем иным, как приближением функции распределения вероятности (см. картинку). Т. е. величина столбика каждой группы показывает вероятность того, что следующее значение измеряемой величины попадет в данную группу.
Слишком большое число групп может дать слишком «скачущий» график, слишком малое – слишком «сглаженный». В идеале, очевидно, хотелось бы иметь число групп, дающее наименьшее отклонение от функции распределения вероятности, т.
е. позволяющее дать наиболее точную оценку настоящей функции распределения вероятности изучаемого явления.
В общем, математики этим занялись.
Первым, по всей видимости, был Стерджесc (Sturges, 1926). Он рассмотрел идеализированную частотную гистограмму из k классов, где i-ое значение было равно биномиальному коэффициенту . При достаточно больших k форма гистограммы приближалась к форме нормального распределения. Сумма всех значений была равна
.
Таким образом, для n результатов измерений величины, подчиняющейся нормальному распределению, число классов, используемых при построении гистограммы следует брать как и форма полученной гистограммы будет приближаться к форме нормального распределения для достаточно большого k. Это и есть формула Стерджесса. В этом виде она попала практически во все учебники по статистике.
Формула эта в настоящее время подвергается критике как раз за то, что она явным образом использует биномиальное распределение для аппроксимации нормального распределения, что не всегда применимо.
Считается, что эта формула позволяет строить удовлетворительные гистограммы при числе измерений менее 200.
Существует целый ряд альтернативных формул, некоторые из которых вычисляют длину интервала, после чего определяется число требуемых классов (см. здесь).
Рассмотрим пару таких формул:
Формула Скотта (Scott, 1979)
, где h — длина интервала, s — стандартное отклонение значений ряда измерений
Формула Фридмана Диакониса (Freedman and Diaconis, 1981)
, где h — длина интервала, (IQ) — разница между верхним и нижним квартилем.
Эти формулы довольно просты и обоснованы статистической теорией, и считаются предпочтительнее формулы Стерджесса.
Калькулятор ниже использует в качестве результатов измерений результаты генератора случайных чисел, встроенного в Javascript.
Поскольку функция распределения генератора практически постоянная, случайное число, полученное от генератора, можно дополнительно модифицировать, выбрав в поле «Функция .
..» что-нибудь интересное. Собственно, это позволит наблюдать более веселые графики, вместо практически прямой линии.
Помимо построения гистограммы с использованием числа классов, полученных по формуле Стерджесса, строятся гистограммы с числом классов по Скотту и Фридману/Диаконису, а также с числом классов, произвольно заданных пользователем.
Конечно, практического применения в этом калькуляторе никакого, но зато можно посмотреть на разницу в числе классов и внешний вид гистограммы.
Формула Стерджесса и другие способы определения числа групп при построении гистограммы
Число наблюдений
Число случайно генерируемых результатов наблюдений
Масштаб
Модифицирующая функцияНетЛогарифмКвадратКубКвадратный корень
Функция, модифицирующая результаты генератора случайных чисел
Задать свое число классов
Точность вычисления
Знаков после запятой: 2
Число классов по Стерджессу
Группировка с использованием формулы Стерджесса
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Среднее
Стандартное отклонение
Число классов по Скотту
Скотт
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Первая квартиль
Третья квартиль
Число классов по Фридману/Диаконису
Фридман/Диаконис
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Свое число классов
Группировка с использованием своего числа классов
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
группировка интервалы Статистика теория вероятности формула Скотта формула Стерджесса формула Фридмана Диакониса
НОУ ИНТУИТ | Лекция | Сводка и группировка статистических данных
< Лекция 12 || Лекция 3: 123
Аннотация: После того как статистическая информация получена в виде данных статистических анкет, отчетности и других документов, возникает задача ее систематизации и упорядочивания, поскольку из разрозненных сведений первичных документов, содержащих информацию только по одной единице наблюдения, нельзя сделать правильного вывода обо всей совокупности в целом.
Для этого полученную информацию сводят воедино, группируют, подводят итоги по группам и совокупности в целом. Таким образом, наступает следующий этап статистического исследования — сводка и группировка статистических материалов.
Ключевые слова: массив, ПО, идентификация, значение, связь, прямой, разбиение, объединение, интервал, длина, отрезок
3.1. Задачи и виды статистической сводки
Статистическая сводка — это первичная обработка данных статистического наблюдения с целью их систематизации. Она предполагает сведение полученной статистической информации о единицах наблюдения в массив данных, упорядоченных по значению какого-либо признака.
По глубине обработки материала различают простую и сложную сводку.
Простая сводка предполагает сведение полученных данных в статистические таблицы, подведение общих итогов по совокупности в целом.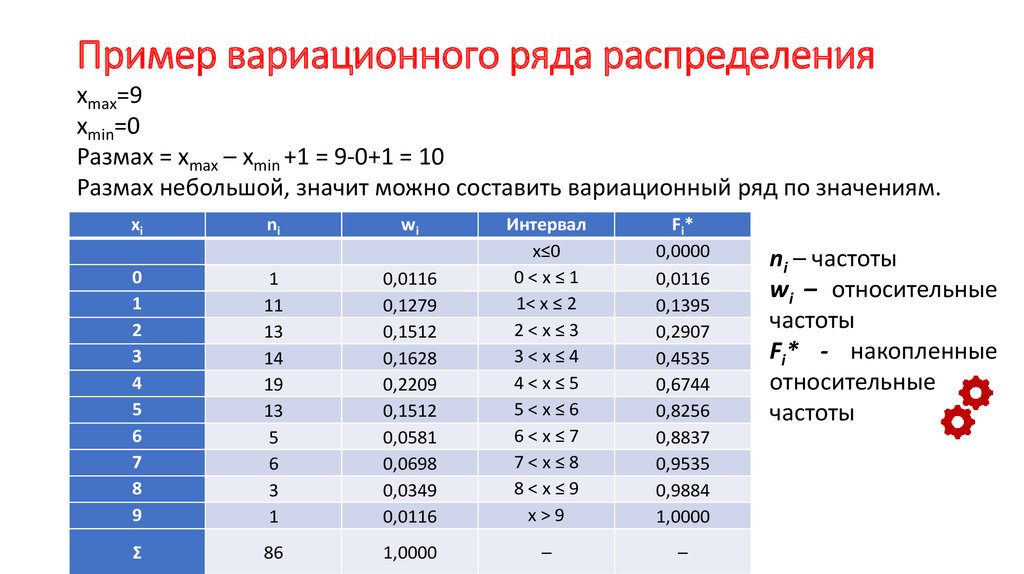
Сложная сводка осуществляется с применением метода группировок по определенной программе, предусматривающей следующие этапы:
- выбор группировочных признаков;
- определение порядка формирования групп;
- разработка системы показателей для характеристики групп и статистической совокупности в целом;
- разработка макетов статистических таблиц для представления результатов сводки;
- распределение единиц наблюдения на группы по изучаемым признакам;
- подведение групповых и общих итогов;
- оформление результатов сводки в виде статистических таблиц.
По технике выполнения различают ручную сводку и сводку с использованием компьютерных технологий.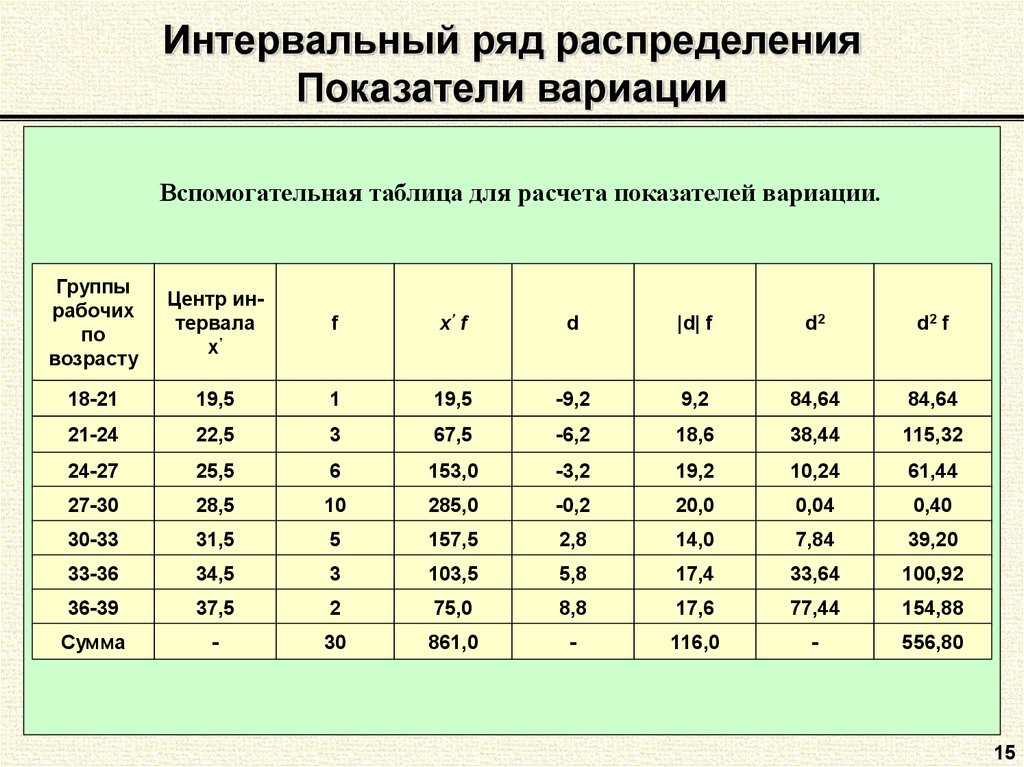
Результатом проведения статистической сводки является получение обобщающих статистических таблиц, которые содержат итоговые данные по показателям, характеризующим единицы наблюдения. Этими итоговыми данными могут быть суммарные значения показателей, рассчитанные как для всей совокупности в целом, так и для отдельных групп единиц, если проводилась разбивка на группы; средние значения, относительные показатели.
Дальше >>
< Лекция 12 || Лекция 3: 123
Настройте тренировки на Apple Watch
Вы можете настроить тренировки на Apple Watch в соответствии со своими целями в фитнесе.
Изменить цели времени, калорий и расстояния; добавить время разогрева и восстановления; и добавить интервалы работы и восстановления.
Изменение целей тренировки на Apple Watch
В watchOS 9 вы можете изменять существующие тренировки и создавать только те, которые вам нужны.
Откройте приложение «Тренировка» на Apple Watch.
Поверните колесико Digital Crown на желаемую тренировку.
Коснитесь , затем коснитесь «Создать тренировку».
Коснитесь цели, такой как Калории, Расстояние или Время; выбрать значение; затем нажмите «Готово».
Коснитесь отредактированной цели, чтобы начать тренировку.
Вы также можете нажать <, чтобы сохранить отредактированную тренировку, а затем коснуться ее, когда будете готовы начать.
Чтобы удалить отредактированные цели из тренировки, выделите тренировку, коснитесь , коснитесь рядом с измененной целью, прокрутите вниз, коснитесь «Удалить тренировку», затем коснитесь «Удалить».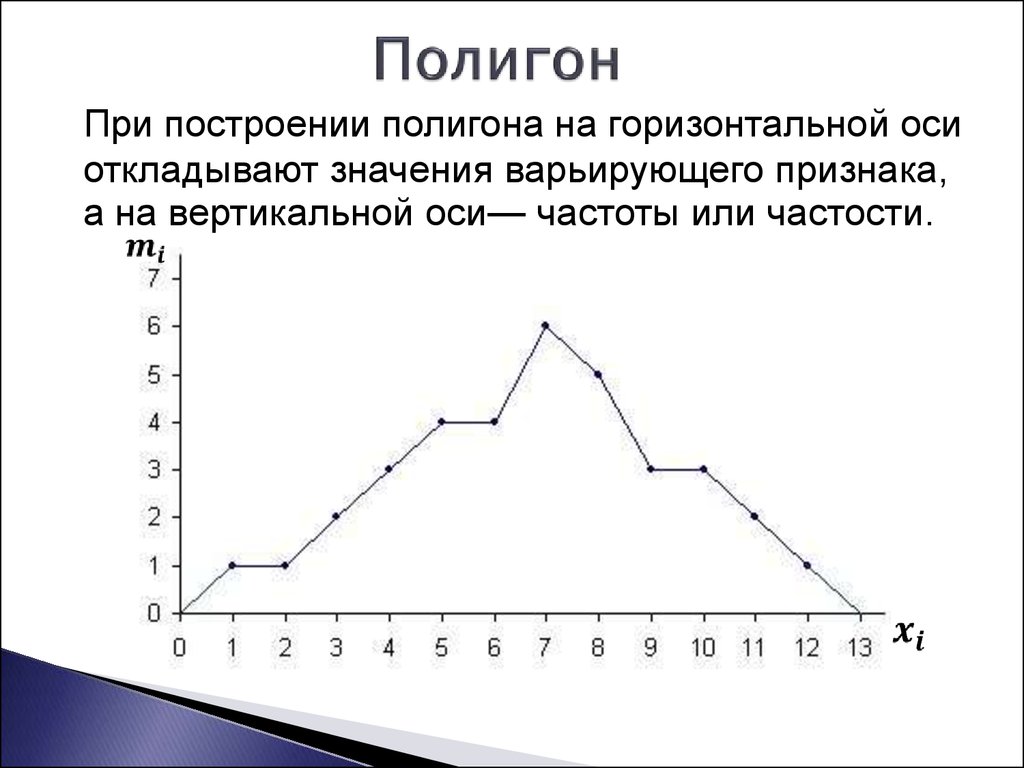
Добавьте интервалы разминки, работы, восстановления и заминки
Вы можете настроить свои тренировки, включив в них период разминки, повторяющиеся интервалы работы и восстановления, а также время для заминки.
Откройте приложение «Тренировка» на Apple Watch.
Поверните колесико Digital Crown на желаемую тренировку.
Коснитесь , прокрутите вниз, затем коснитесь «Создать тренировку».
Нажмите «Пользовательский», где вы можете сделать следующее:
Добавьте период прогрева: Нажмите «Прогрев», затем нажмите «Время», «Расстояние» или «Открытие». Вы также можете добавить оповещение о частоте сердечных сокращений в период разминки.
Добавление интервалов работы и восстановления: Нажмите «Добавить», нажмите «Работа» или «Восстановление», затем выберите «Время», «Расстояние» или «Открыть».
Вы можете добавить несколько интервалов работы и восстановления.
Добавить период восстановления: Нажмите «Время восстановления», затем нажмите «Время», «Расстояние» или «Открытие». Когда вы выбираете «Открыть», вы также можете добавить оповещение о частоте сердечных сокращений.
Назовите тренировку: Нажмите «Без названия» под «Пользовательским названием», затем введите имя.
Примечание: Если вы выполняете стационарную тренировку — например, на эллиптическом тренажере или пилатесе — дистанция не подходит.
Нажмите «Создать тренировку».
Кнопка «Создать тренировку» активна, только если вы добавили интервал работы или восстановления.
Чтобы удалить периоды разминки или восстановления, коснитесь рядом с тренировкой, коснитесь на плитке «Пользовательские», коснитесь «Разминка» или «Заминка», затем коснитесь «Пропустить». Чтобы удалить интервал работы или восстановления, коснитесь его, затем коснитесь «Удалить интервал».
Пользовательские тренировки доступны для всех типов тренировок, кроме мультиспорта, плавания в бассейне и плавания в открытой воде.
Добавление оповещений к тренировке
Вы можете получать различные оповещения во время тренировки. Например, во время тренировки на свежем воздухе вы можете получить предупреждение, когда частота сердечных сокращений упадет в пределах 133–141 удара в минуту.
Чтобы настроить оповещения, выполните следующие действия.
Откройте приложение «Тренировка» на Apple Watch.
Поверните колесико Digital Crown на желаемую тренировку.
Коснитесь , коснитесь кнопки редактирования плитки, затем коснитесь «Оповещения».
Коснитесь оповещения, которое вы хотите получать, затем настройте оповещение.
Оповещения, которые вы добавляете, используются каждый раз, когда вы выполняете эту тренировку.
Методы классификации данных—ArcGIS Pro | Documentation
Когда вы классифицируете свои данные, вы можете использовать один из многих стандартных методов классификации, предоставляемых в ArcGIS Pro, или вы можете вручную определить свои собственные пользовательские диапазоны классов.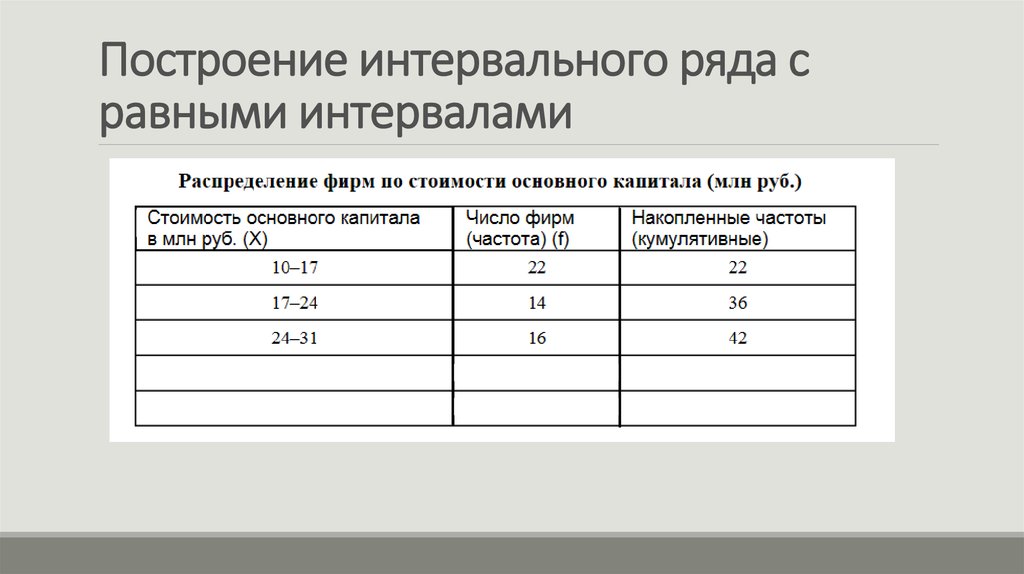
Интервал вручную
Используйте интервал вручную, чтобы определить собственные классы, вручную добавить разрывы классов и задать диапазоны классов, соответствующие данным. Кроме того, вы можете начать с одной из стандартных классификаций и вносить коррективы по мере необходимости.
Заданный интервал
Используйте заданный интервал, чтобы указать размер интервала для определения серии классов с одинаковым диапазоном значений. Например, если размер интервала равен 75, каждый класс будет охватывать 75 единиц. Количество классов, исходя из размера интервала и максимального размера выборки, определяется автоматически. Размер интервала должен быть достаточно мал, чтобы соответствовать минимально допустимому количеству классов, равному трем.
Равный интервал
Используйте равный интервал, чтобы разделить диапазон значений атрибута на поддиапазоны одинакового размера.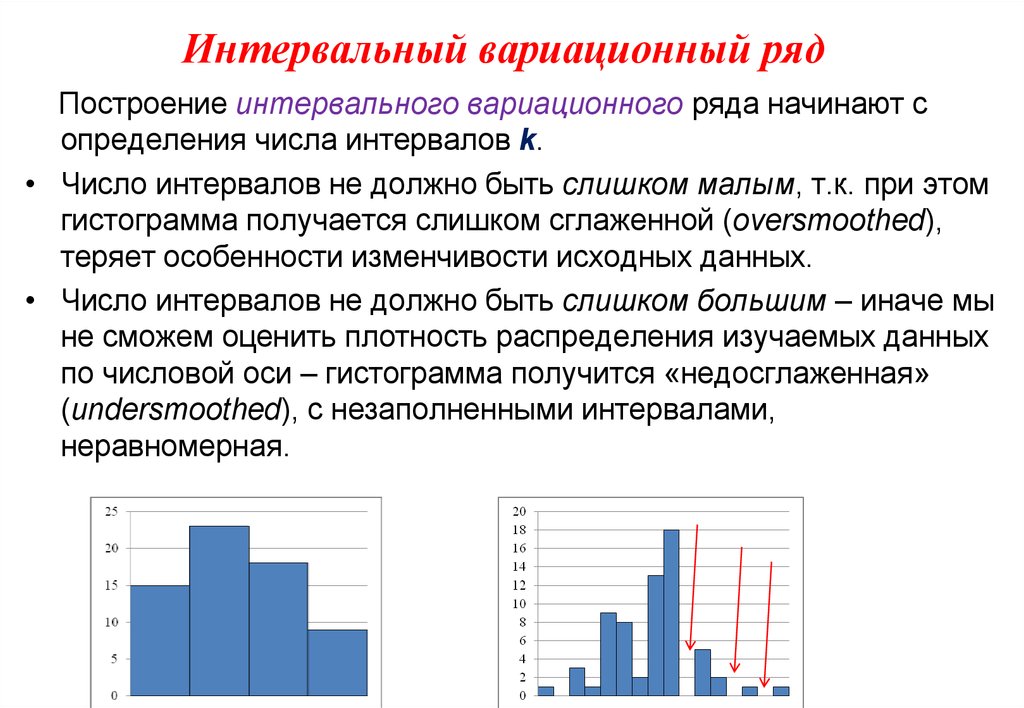
Это позволяет указать количество интервалов, а разрывы классов на основе диапазона значений определяются автоматически. Например, если вы укажете три класса для поля, значения которого находятся в диапазоне от 0 до 300, будут созданы три класса с диапазонами от 0 до 100, 101–200 и 201–300.
Равный интервал лучше всего применять к знакомым диапазонам данных, таким как проценты и температура. Этот метод подчеркивает количество значения атрибута по отношению к другим значениям. Например, он показывает, что магазин входит в группу магазинов, на долю которых приходится треть всех продаж.
Квантиль
В квантильной классификации каждый класс содержит равное количество признаков. Квантильная классификация хорошо подходит для линейно распределенных данных. Квантиль присваивает одинаковое количество значений данных каждому классу. Нет пустых классов или классов со слишком малым или слишком большим количеством значения.
Поскольку объекты группируются в равных количествах в каждом классе с использованием квантильной классификации, результирующая карта часто может вводить в заблуждение.
Подобные функции могут быть помещены в соседние классы, или функции с сильно различающимися значениями могут быть помещены в один и тот же класс. Вы можете свести к минимуму это искажение, увеличив количество классов.
Естественные разломы (Дженкс)
При классификации естественных разломов (Дженкс) классы основаны на естественных группировках, присущих данным. Разрывы классов создаются таким образом, чтобы наилучшим образом сгруппировать схожие значения и максимизировать различия между классами. Признаки разделены на классы, границы которых устанавливаются там, где имеются относительно большие различия в значениях данных.
Естественные разломы — это классификации, зависящие от данных, и они бесполезны для сравнения нескольких карт, построенных на основе различной исходной информации.
Эта классификация основана на алгоритме естественных перерывов Дженкса. Для получения дополнительной информации см. Схемы одномерной классификации в Geospatial Analysis—A Comprehensive Guide, 6th edition; 2007–2018 годы; де Смит, Гудчайлд, Лонгли.
Геометрический интервал
Геометрический интервал Схема классификации создает разрывы классов на основе интервалов классов, которые имеют геометрический ряд. Геометрический коэффициент в этом классификаторе может измениться один раз (на обратный) для оптимизации диапазонов классов. Алгоритм создает геометрические интервалы путем минимизации суммы квадратов количества элементов в каждом классе. Это гарантирует, что каждый диапазон классов будет иметь примерно одинаковое количество значений в каждом классе и что изменение между интервалами будет достаточно согласованным.
Этот алгоритм был специально разработан для работы с непрерывными данными. Это компромисс между равноинтервальными, естественными интервалами (Дженкса) и квантильными методами. Он создает баланс между выделением изменений в средних и крайних значениях, тем самым создавая визуально привлекательный и картографически полный результат.
Одним из примеров использования геометрической интервальной классификации является набор данных об осадках, в котором только 15 из 100 метеостанций (менее 50 процентов) зарегистрировали осадки, а остальные не зарегистрировали осадки, поэтому значения их атрибутов равны нулю.