Читать дальше: понятие экстремума функции.
Страница не найдена – ФГОС online
Извините, страница не найдена. Она была удалена или переименована. Но вы можете перейти на главную страницу либо на страницу любой олимпиады.
Олимпиады для работников ДОУ
Олимпиады для учителей и
педагогов
Олимпиады для студентов
Олимпиады для дошкольников
Олимпиады по предметам
Олимпиады 1 класс
Олимпиады 2 класс
Олимпиады 3 класс
Олимпиады 4 класс
Олимпиады 5 класс
Олимпиады 6 класс
Олимпиады 7 класс
Олимпиады 8 класс
Олимпиады 9 класс
Олимпиады 10 класс
Олимпиады 11 класс
ТОП курсов повышения квалификации
ТОП курсов профессиональной переподготовки
| Функциональная грамотность школьников | Организация деятельности педагогических работников по классному руководству |
| Система сопровождения ребенка с ОВЗ в общеразвивающем детском саду | Основы религиозных культур и светской этики (ОРКСЭ): теория и методика преподавания в образовательной организации |
| Патриотическое воспитание в системе работы воспитателя общеобразовательной организации | Организация деятельности педагога-воспитателя группы продленного дня |
| Активизация познавательной деятельности младших школьников с ограниченными возможностями здоровья (ОВЗ) как стратегия повышения успешной учебной деятельности | Профилактика коронавируса, гриппа и других острых респираторных вирусных инфекций в образовательных организациях |
| Здоровьесберегающие технологии в физическом развитии дошкольников и их применение в условиях ФГОС ДО | Применение современных педагогических технологий в образовательном процессе в условиях реализации ФГОС |
| Дистанционное обучение как современный формат преподавания | Гражданская оборона и защита от чрезвычайных ситуаций природного и техногенного характера |
| Организация образовательной деятельности в соответствии с требованиями ФГОС НОО (федерального государственного образовательного стандарта начального общего образования), утвержденного приказом Министерства просвещения РФ № 286 от 31 мая 2021 года | Охрана труда |
| Организация образовательной деятельности в соответствии с требованиями ФГОС ООО (федерального государственного образовательного стандарта основного общего образования), утвержденного приказом Министерства просвещения РФ № 287 от 31 мая 2021 года | Оказание первой помощи детям и взрослым |
| Пожарно-технический минимум (ПТМ) | Пожарная безопасность |
Калькулятор монотонных функций — Онлайн-тестер возрастания/убывания
Поиск инструмента
Поиск инструмента в dCode по ключевым словам:Просмотр полного списка инструментов dCode
Монотонная функция
Инструмент для вычисления монотонности (или нет) функции, т.
е. проверки направления ее изменения, если функция (строго? ) монотонный (возрастающий или убывающий)
Результаты
Монотонная функция — dCode
Тег(и) : Функции
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Тестер монотонной функции
Функция f=Переменная
| Изучение | всей области определения следующего интервала |
Нижняя граница
Верхняя граница
См. также: Функция возрастания — Функция убывания
Ответы на вопросы (FAQ)
Что такое монотонная функция? (Определение)
монотонная функция — это функция $ f $ такая, что для любых $ x_1, x_2 $ if $ x_1 возрастающая функция) или $ f(x_1) > f(x_2) $ (убывающая функция), но не обе .
Другими словами, монотонная функция — это функция, сохраняющая или изменяющая порядок. 92 $, вычисление $ f'(x) >= 0 $ всегда проверяется, каким бы ни было значение $ x $, поэтому функция $ f $ является монотонной (и возрастающей) на $ \mathbb{R} $
— Вычисление по уравнению: известно, что некоторые функции являются монотонными (либо возрастающими, либо убывающими): экспоненциальная функция и т. д. — Расчет с кривой функции: монотонная 9Функция 0056 имеет свою кривую, которая идет либо всегда вниз, либо всегда вверх
Что такое монотонная последовательность?
Монотонная последовательность представляет собой ряд чисел, либо всегда возрастающих, либо всегда убывающих.
Исходный код
dCode сохраняет за собой право собственности на исходный код «Монотонной функции». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Монотонная функция», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Монотонной функции».
функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или доступ к API для «Монотонной функции» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Cite dCode
Копирование и вставка страницы «Монотонная функция» или любых ее результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Monotonic Function на dCode.fr [онлайн-сайт], получено 20 февраля 2023 г., https://www.dcode.fr/monotonic-function
Сводка
- Тестер монотонной функции
- Что такое монотонная функция? (Определение)
- Как определить, является ли функция монотонной?
- Что такое монотонная последовательность?
Similar pages
- Decreasing Function
- Increasing Function
- Differential Equation Solver
- Intersection Point
- Linear Equation
- Square Root
- Lagrange Interpolating Polynomial
- DCODE’S TOOLS LIST
Support
- Paypal
- Патреон
- Еще
Форум/Помощь
Ключевые слова
монотонный, возрастающий, убывающий, функция, направление, вариация
Ссылки
▲
исчисление — Разница между возрастающей и монотонно возрастающей функцией
спросил
Изменено 8 месяцев назад
Просмотрено
36 тысяч раз
93$$ монотонно возрастает, т.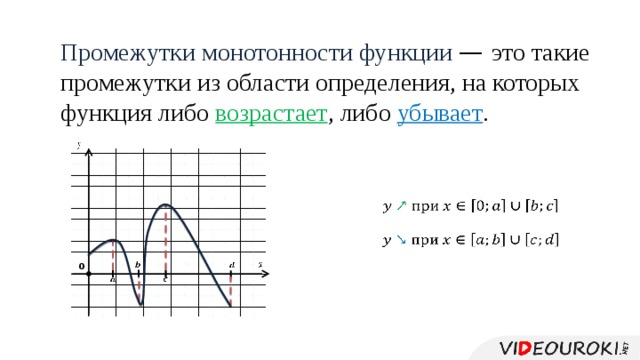
е. если $$x_2 \gt x_1$$, то $$f(x_2) \gt f(x_1)$$, и в некоторых книгах такие функции приводятся как строго возрастающие функции.
Но если
$$f(x)= \begin{case} х & х\leq 1 \\ 1 & 1\leq х\leq 2\\ х-1 и 2\leq х \end{случаи} $$
Является ли эта функция монотонно возрастающей?
- исчисление
- производные
$\endgroup$
1
$\begingroup$
Я привык к следующему: $f$
возрастает, если $x< y \Rightarrow f(x)\le f(y)$
строго возрастает, если $x< y \Rightarrow f(x) < f(y)$
убывающие и строго убывающие: аналогично, но неравенства для $f$ меняются местами.
Монотонный: либо возрастающий, либо убывающий
строго монотонный: либо строго возрастающий, либо строго убывающий.
В частности, монотонно возрастать то же, что возрастать, строго монотонно возрастать то же, что строго возрастать.
(Вообще всегда есть некоторая свобода в определениях, поэтому я и написал «привык». Если вы читаете учебник по анализу, то автор должен определить эти термины, а затем придерживаться их) .
$\endgroup$
9
$\begingroup$
Как я всегда это понимал (и различные ссылки в Интернете, кажется, следуют этой традиции), так это то, что когда кто-то говорит, что функция возрастает или строго возрастает, они имеют в виду, что это происходит в некотором подмножестве области определения функции. Сказать, что функция монотонна, означает, что она демонстрирует одно и то же поведение во всей области. То есть монотонно возрастающая функция не убывает в своей области определения, а также является возрастающей функцией, поскольку она не убывает в любом подмножестве области определения. Точно так же строго монотонно возрастающая функция — это функция, которая строго возрастает по всей своей области определения, а не просто возрастает по подмножеству области (как определено из теста возрастания/убывания в исчислении).