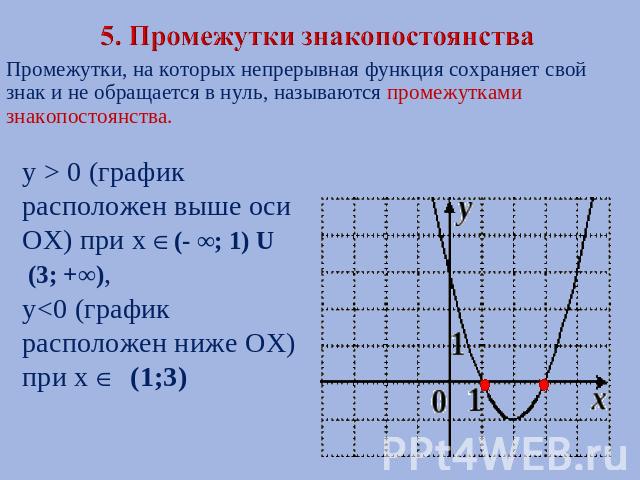
Что исследует?
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции:
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
- Минимум и максимум функции: Да
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- DiracDelta(x)
- Дельта-функция Дирака
- Heaviside(x)
- Функция Хевисайда
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
×
Где учитесь?
Для правильного составления решения, укажите:
(не выбрано)9 класс10 класс11 класс1-й курс2-й курс3-й курс4-й курсдругое
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Шар радиусом 5 см пересекли плоскостью на расстоянии 3 см от центра кули.Знайдить площадь сечения
Решено
Помогите решить: 1)Sin (2x П/2)=0…
Решено
Решите уравнение: а)sinxsin5x=1 б) sinxcos4x=-1.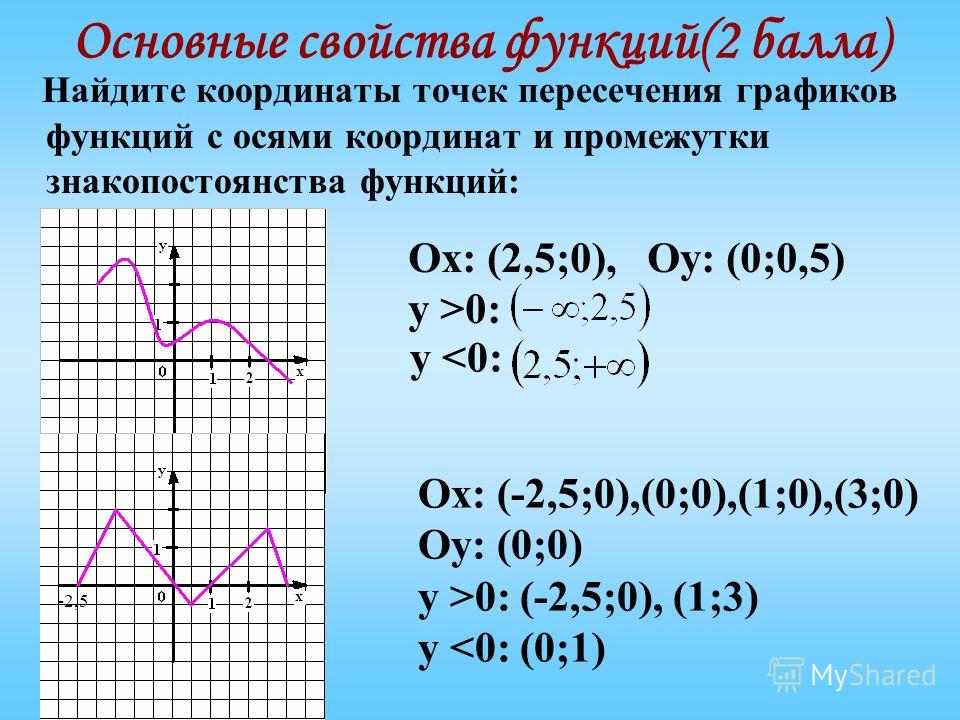 ..
..
Формулы приведения
Пользуйтесь нашим приложением
Постоянство интервала между выбросом лютеинизирующего гормона и овуляцией у овец | Биология репродукции
Фильтр поиска панели навигации Биология размноженияЭтот выпускБиология развитияРазмножение, рост и развитиеКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Биология размноженияЭтот выпускБиология развитияРазмножение, рост и развитиеКнигиЖурналыOxford Academic Термин поиска на микросайте
Расширенный поиск
Статья журнала
И. А. Камминг,
И. А. Камминг
А. Камминг
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Дж. М. Бакмастер,
Дж. М. Бакмастер
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
М. А. деБ. Блоки,
М. А. деБ. Блоки
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Дж. Р. Годинг,
Дж. Р. Годинг
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
К. Г. Уинфилд,
CG Winfield
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Р. В. Бакстер
В. Бакстер
Р. В. Бакстер
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Биология размножения , том 9, выпуск 1, 1 августа 1973 г., страницы 24–29, https://doi.org/10.1093/biolreprod/9.1.24
Опубликовано:
01 августа 1973 г.
3 История статьи
Получено:
06 июля 1972 г.
Принято:
08 января 1973 г.
Опубликовано:
01 августа 1973 г.
Фильтр поиска панели навигации Биология размноженияЭтот выпускБиология развитияРазмножение, рост и развитиеКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Биология размноженияЭтот выпускБиология развитияРазмножение, рост и развитиеКнигиЖурналыOxford Academic Термин поиска на микросайте
Расширенный поиск
Для изучения временных соотношений между предовуляторным пиком ЛГ и овуляцией у овец был разработан «короткий» радиоиммуноанализ для измерения концентрации ЛГ в плазме. Этот короткий анализ позволил определить концентрацию ЛГ в течение 6 часов после отбора проб. Затем интервал от пика ЛГ до овуляции определяли путем однократной лапаротомии у каждой овцы через известный интервал после начала выброса ЛГ, чтобы определить для каждого интервала долю овец, у которых произошла овуляция.
Этот короткий анализ позволил определить концентрацию ЛГ в течение 6 часов после отбора проб. Затем интервал от пика ЛГ до овуляции определяли путем однократной лапаротомии у каждой овцы через известный интервал после начала выброса ЛГ, чтобы определить для каждого интервала долю овец, у которых произошла овуляция.
С помощью этого метода было исследовано время между пиком ЛГ и овуляцией у 47 овец с нормальным эстральным циклом, у 11 молодых и 16 старых овец, переживших вторую течку после изъятия пропитанных кронолоном губок, и у 19 овец, переживших первую течку. после изъятия таких губок.
Результаты показали, что у овец с нормальным циклом овуляция происходит через 21–26 часов после пика LII, в то время как у молодых и старых овец и овец, получавших кронолон, овуляция происходит через 22–26 часов после выброса ЛГ. Через 23 часа овулировали 16,6% овец из всех четырех групп, тогда как через 24 часа овулировали 66,6% овец, что указывает на то, что большая часть овец овулировала между 23-24 часами после начала пика ЛГ.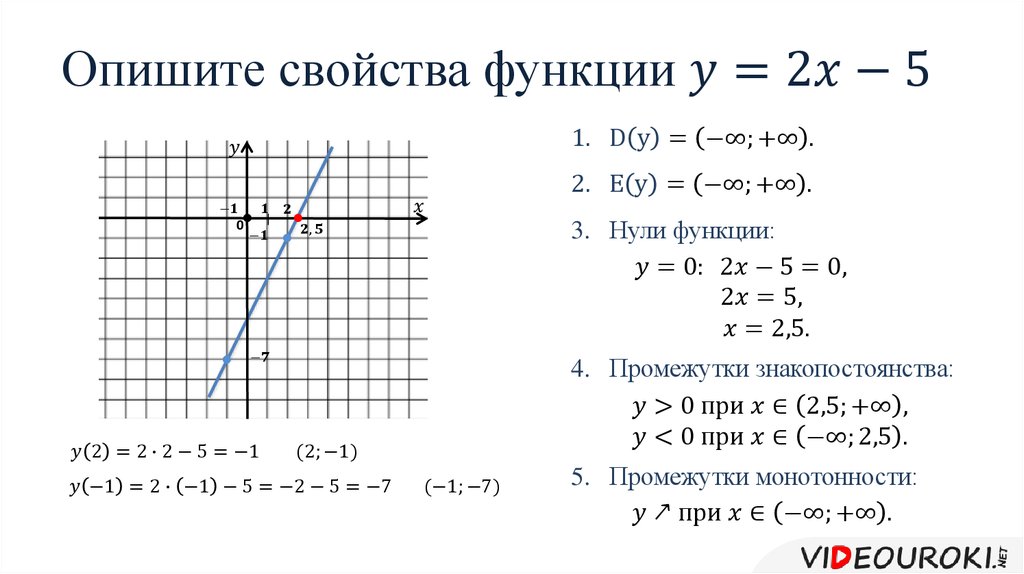
Сделан вывод, что постоянство интервала между высвобождением ЛГ и овуляцией в этих экспериментальных ситуациях подтверждает важность роли ЛГ в овуляторном механизме.
Этот контент доступен только в формате PDF.
авторское право © 1973 Общества изучения репродукции
авторское право © 1973 Общество изучения репродукции
Выпуск Раздел:
Статья
Скачать все слайды
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Оповещение о теме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Ссылки на статьи по телефону
Последний
Самые читаемые
Самые цитируемые
Передача сигналов Hedgehog регулирует развитие вольфовых протоков через первичную ресничку
MDSCs при беременности и осложнениях, связанных с беременностью: обновление
Снижение уровня B7-h4 способствует необъяснимому привычному невынашиванию беременности через сигнальный путь RhoA/ROCK2 и регулирует секрецию децидуальных NK-клеток
Митохондриальная убиквитинлигаза E3 MARCH5 необходима для мейотического созревания ооцитов мыши
Оценка качества ооцитов: обзор инженерных подходов к решению клинических задач
Реклама
pr.
 probability — предсказуемая квадратичная вариация имеет те же интервалы постоянства, что и процесс
probability — предсказуемая квадратичная вариация имеет те же интервалы постоянства, что и процессспросил
Изменено 6 лет, 7 месяцев назад
Просмотрено 981 раз
$\begingroup$
Из
Ревуз и Йор — Непрерывные мартингалы и броуновское движение 1999
Глава IV Предложение 1.13
доказано, что для непрерывного локального мартингала $M_t$ интервалы постоянства равны интервалам постоянства предсказуемой квадратичной вариации $
Интересно, останется ли это верным, если $M_{t}$ будет просто càdlàg. Думаю, нет.
Думаю, нет.
Итак, давайте рассмотрим эту настройку: Дан интегрируемый с квадратом мартингал $X_t=F_t-a\cdot K_{t}$ с предсказуемой квадратичной вариацией $b\cdot K_{t}$, где $a,b$ — константы, а $K_{t}$ непрерывна, но $ F_{t}$ только càdlàg. Чтобы заключить, что $K_{t}$ постоянна на каком-то интервале (предсказуемая квадратичная вариация — это непрерывный процесс постоянной $K_{t}$), следует, что $X_{t}$ постоянна на этом интервале и, следовательно, $ F_{t}$ на интервале. Где $K_{0}=0$, $K_{t}\rightarrow \infty$ п.н. и неубывающий процесс.
- пр.вероятность
- случайные процессы
- мартингалы
$\endgroup$
3
$\begingroup$
Не работает для càdlàg мартингалов.
Пусть $N_t$ — пуассоновский процесс интенсивности $\lambda$,
положим $M_t=N_t-\lambda t$. Это càdlàg мартингал,
$

 3
3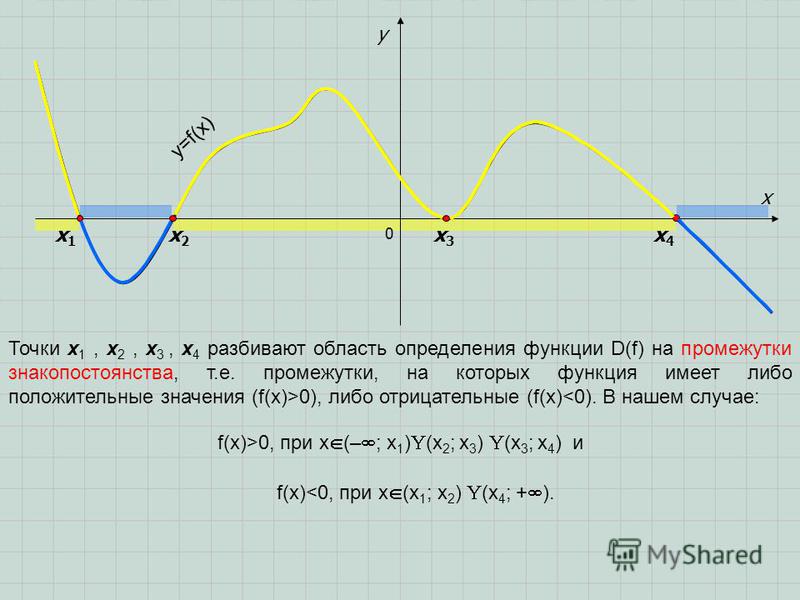 14159..
14159..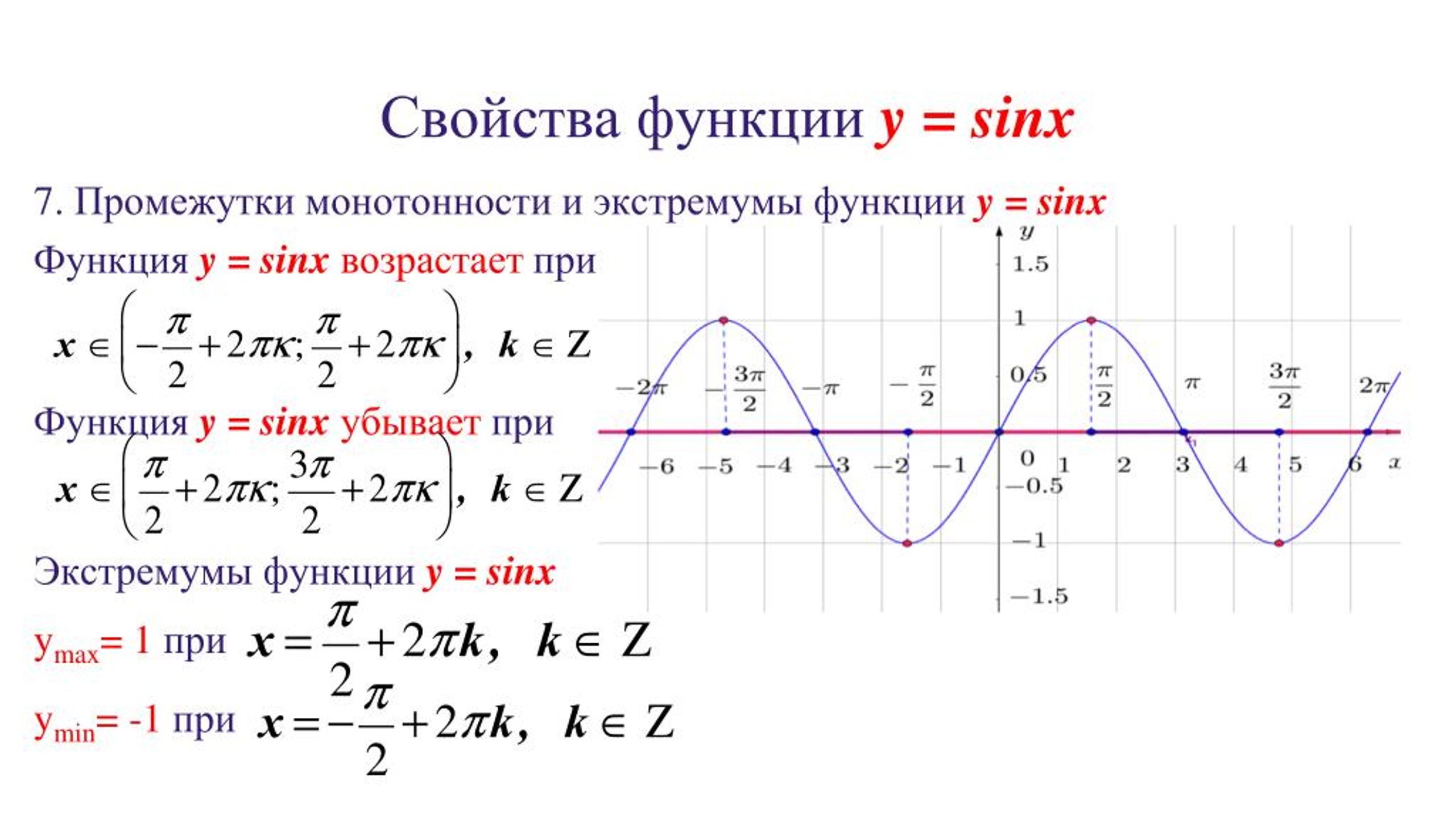 02.14
02.14
 A. Cumming, J. M. Buckmaster, M. A. deB. Блоки, Дж. Р. Годинг, К. Г. Уинфилд, Р. В. Бакстер, Постоянство интервала между высвобождением лютеинизирующего гормона и овуляцией у овец, Биология репродукции , том 9, выпуск 1, 1 августа 1973 г., страницы 24–29, https://doi .org/10.1093/biolreprod/9.1.24
A. Cumming, J. M. Buckmaster, M. A. deB. Блоки, Дж. Р. Годинг, К. Г. Уинфилд, Р. В. Бакстер, Постоянство интервала между высвобождением лютеинизирующего гормона и овуляцией у овец, Биология репродукции , том 9, выпуск 1, 1 августа 1973 г., страницы 24–29, https://doi .org/10.1093/biolreprod/9.1.24