Иррациональные числа действительные числа: Какие числа называются действительными?

4. Действительные числа. Пропорция. Проценты

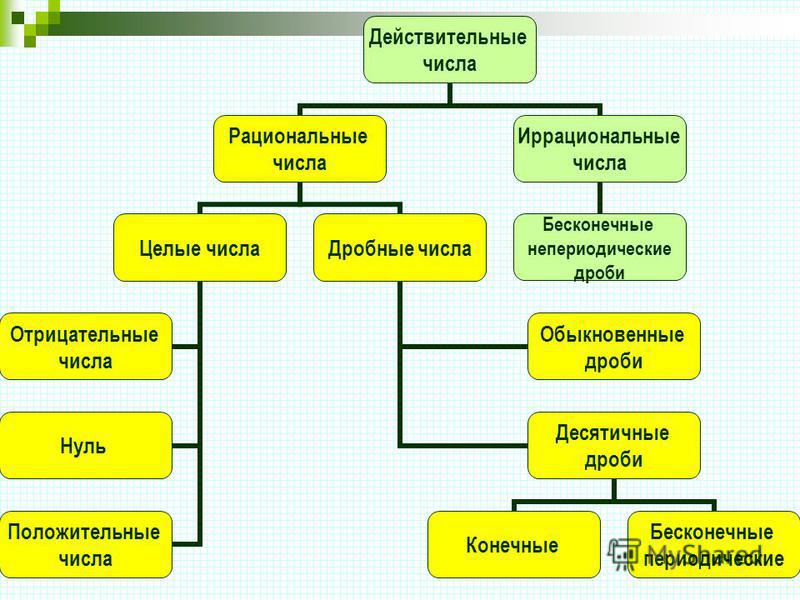
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Действительные числа

Рациональное число – число, представляемое обыкновенной дробью m/n, где числитель m – целое число, а знаменатель n – натуральное число. Любое рациональное число представимо в виде периодической бесконечной десятичной дроби. Множество рациональных чисел обозначается Q.
Примеры: 

Если действительное число не является рациональным, то оно иррациональное число. Десятичные дроби, выражающие иррациональные числа бесконечны и не периодичны. Множество иррациональных чисел обычно обозначается заглавной латинской буквой I.

Примеры иррациональных чисел:

1. Бесконечная непериодическая десятичная дробь 4,10110011100011110000… (количество единиц и нулей каждый раз увеличивается на одну) является иррациональным числом. 

2.

 −22,353335333335… (число троек, разделяющих восьмерки, каждый раз увеличивается на две).
3. Арифметический квадратный корень из двух,  равный 1,414213… .

4.  Число «пи»,  равное 3,141592….

---

Действительные числа – это рациональные и иррациональные числа. Множество действительных  чисел обозначается R.

---

Стандартный вид числа N — это запись его в виде а·10^k, где 1≤a≤9 и k – целое число. Число k называется порядком числа N.
Например, 125,5687=1,255687·10^2;     0,0036987=3,6987·10^-3

---

Пропорция

Отношением числа х к числу у называется частное чисел х и у, т.е. х : у.
Отношение х/у  показывает, во сколько раз х больше у или какую часть числа у составляет число х.

Пропорцией называется равенство двух отношений, т.е.

; а и у называются крайними членами, х и b — средними членами пропорции.

Свойства пропорции

1. Произведение крайних членов пропорции равно произведению средних членов пропорции:

2. В пропорции можно менять местами крайние и средние члены или те и другие одновременно:

3. Чтобы найти неизвестный крайний член пропорции, надо произведение средних членов разделить на известный крайний член пропорции.

 Чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.

---

Процент

Процентом называется сотая часть какого-либо числа. Процент обозначается знаком %.

Если данное число принять за 1, то 1% составляет 0,01 этого числа. Например, 50% составляют 0,5 числа.

Основные задачи на проценты

1. Нахождение процентов данного числа.

Чтобы найти а% от числа b, надо b умножить на а и разделить на 100..

Например, 25% от 80 составляют 25*80:100=20.

2. Нахождение числа по его процентам.
Если известно, что а% числа х равно b, то число х можно найти разделив b на а и умножив на 100.
Например, если 3% числа составляют 150, то все число равно 150:3*100=5000.

3. Нахождение процентного отношения чисел.
Чтобы найти процентное отношение двух чисел a и b, надо отношение этих чисел умножить на 100%, т.е. a : b*100%.
Например, ученик должен был решить 10 задач, но решил 8, тогда он выполнил задание на 8 : 10 *100%=80%.

---

УПРАЖНЕНИЯ

1. Выпишите числа, которые являются иррациональными:

Решение:

а) иррациональными являются числа:

---

2. Округлите числа до тысячных:

а)  0,2451872;  2547,2354;  12,2567;      б)  10,019812;  1235,123458; 0,001999.

Решение:

а)  0,245;  2547,235;  12,257. 

---

3. Выпишите верные равенства:

Решение:

а) верные равенства: 

---

4. Запишите в стандартном виде числа:

а) 54800; 0,025;  102,256;   б) 0,02394;  12501; 569,4501.

Решение:

а) 54800= 5,48·10⁴;   0,025=2,5·10^-2;  102,256=1,02256·10²

---

5. Найдите число, если:

а) 39 % от него равны 1,3;    б) 64% от него равны 1,6.

Решение:

а) 1,3 : 39% * 100% = 10/3

Ответ: 

---

6. Найдите, какой процент число 25 составляет:

а) от числа 750;    б) от числа 125.

Решение:

а) 25 : 750 *100% = 10/3%

Ответ: %

---

7. Найдите:

Решение:

а) найдем само число: 

вычислим 80% от числа 4:     4 : 100% * 80% = 3,2.

Ответ: 3,2.

---

8. а) Какое число увеличили на 15% и получили в результате 69.

    б) Какое число увеличили на 45% и получили в результате 290.

Решение:

а) Пусть х — исходное число, оно равно 100%, после увеличения на 15% число стало (100%+15%) =115%.

х   — 100%

69 — 115%

х= 69 * 100% : 115% = 60.

Ответ: 60.

---

9. а) Какой процент разность чисел 3,5 и 2,5 составляет от их суммы?

    б) Какой процент разность чисел 8,5 и 6 составляет от их суммы?

Решение:
а) Сумма чисел : 3,5+2,5=6, разность чисел: 3,5-2,5=1.
Процентное отношение разности чисел к их сумме: 1 : 6 * 100% = 100/6%.
Ответ:

---

10. а)  Представьте число 36 в виде суммы двух слагаемых, пропорциональных числам  4 и  5.
      б) Представьте число 51 в виде суммы двух слагаемых, пропорциональных числам  3 и  5.
Решение:
а) Т.к. слагаемые пропорциональны числам 4 и 5, то всего частей 4+5=9. 
36 : 9 = 4 — на одну часть.
4 * 4 = 16 — первое слагаемое.
4 * 5 = 20 — второе слагаемое.
Ответ:  16; 20.

---

11. Найдите х из пропорции:

Решение:
а) Упростим выражение: 
Воспользуемся свойством пропорции:

---

12. а) Число 48 увеличили на 12%, а затем полученное число увеличили на 10%. Найдите число, которое получилось в результате.
      б) Число 80 увеличили на 40%, а затем полученное число уменьшили на 25%, Найдите число, которое получилось в результате.

Решение:
а) увеличим число 48 на 12%: 48 + 48 : 100 *12% = 48 + 5,76 = 53,76.
Увеличим полученное число 53,76 на 10%: 53,76 + 53,76 : 100 * 10% = 53,76 + 5,376 = 59,136.
Ответ: 59,136.

---

13. а) На сколько процентов изменилось число, если его увеличили на 6/25?
      б) На сколько процентов изменилось число, если его уменьшили на 3/10?
Решение:
а) Пусть 1 — исходное число, оно составляет 100%.

    1 — 100%
6/25 — х%
Составим пропорцию и найдем х: 
1 : 6/25 = 100 * х;
х =  100 * 6/25;
х = 24.
Ответ: увеличилось на 24%.

---

14. Избавьтесь от иррациональности в знаменателе:

Решение:
а) К числителю прибавим корень из двух и разделим выражение почленно. При решении пользуемся домножением на сопряженное выражение.

---

15. Найдите значение выражения (№ 1.5.42 [7]):

Решение:
а) Выделим в выражении  полный квадрат:

Аналогично, 

Получим:

Ответ: 2/3.

---

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Выпишите числа, являющиеся рациональными:

2. Выпишите числа, представленные в стандартном виде:

3,9·10⁹;   0,1·10^-5;    18·10⁵;   5·10³;    10^-2

^3.  Найдите число, если:

а) 15 % от него равны 19;    б) 42% от него равны 50.

4. а) Найдите 16% от числа 3,7;   б) найдите 58% от числа 1,9.

5. Найдите число, если 30% от него равны

6. Из 42 поездов, приходящих на станцию, отношение пассажирских к скорым составляет 4:3. Сколько скорых поездов приходит на станцию?

7. Во сколько раз 2% от 4 больше, чем 0,4% от 1?

8. Найдите положительное число, если 45% от него равны 20% от числа, ему обратного.

9. Что больше: 20% от 25% торта или 15% от 30% торта?

10. Докажите, что значение выражения является рациональным числом

---

ПРОВЕРЬТЕ СЕБЯ

Действительные числа (вещественные числа) — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Действительные числа (вещественные числа).

МОУ СОШ №63 с УИП
Сарыгин Никита.

2. Оглавление: указание страниц.

3. Ввеедение
4. Определение
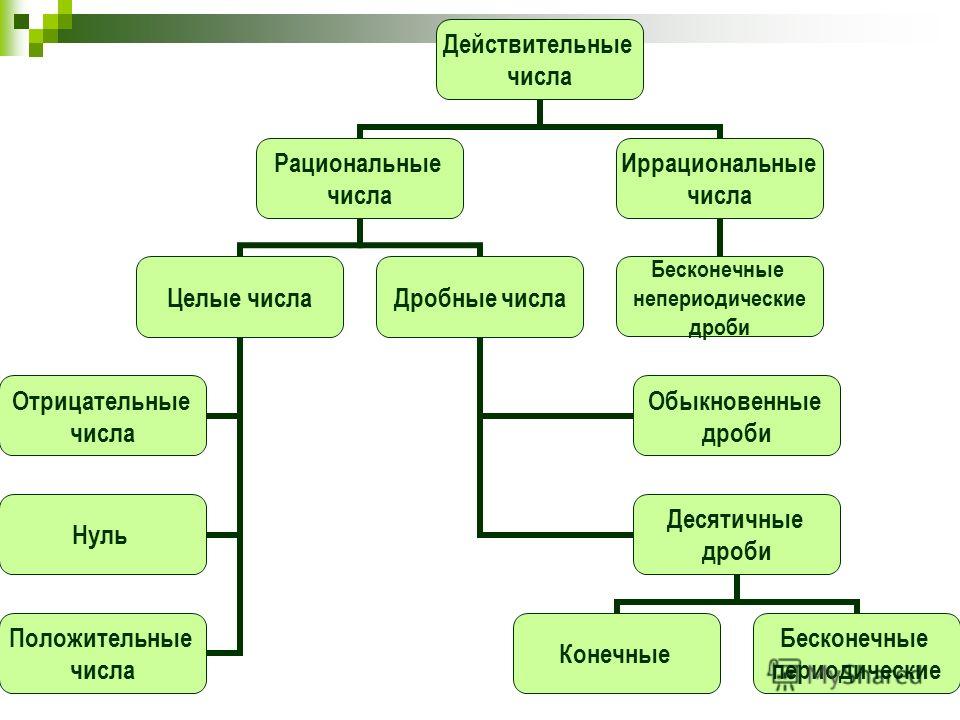
5. Действительные числа разделяются на рациональные и иррациональные
6. Правила
7.Период дроби
8. Иррациональное число
9.Осноаные числовые множества
10.Множество. Элемент множества
11.Подмножество
12.Пересечение и объединение множеств
13.Модуль действительного числа
14.Заключение
15.Список используемых источников.

3. Введение:

Что это такое? Действительное число (вещественное число) – это любое положительное число, отрицательное число или ноль.
Математический объект, возникший из потребности измерения геометрических и физических величин окружающего мира, а
также проведения таких вычислительных операций, как извлечение корня, вычисление логарифмов, решение алгебраических
уравнений, исследование поведения функций.

4. Определение

В период зарождения современной математики в 17 веке при разработке методов изучения непрерывных процессов и методов
приближённых вычислений. И. Ньютон во «Всеобщей арифметике» даёт определение понятия действительного числа: «Под
числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой-нибудь величины к другой величине
того же рода, принятой нами за единицу». Позже, в 70 годах 19 века, понятие действительного числа было уточнено на основе
анализа понятия непрерывности Р. Дедекиндом, Г. Кантором и К. Вейерштрассом. Введение понятия

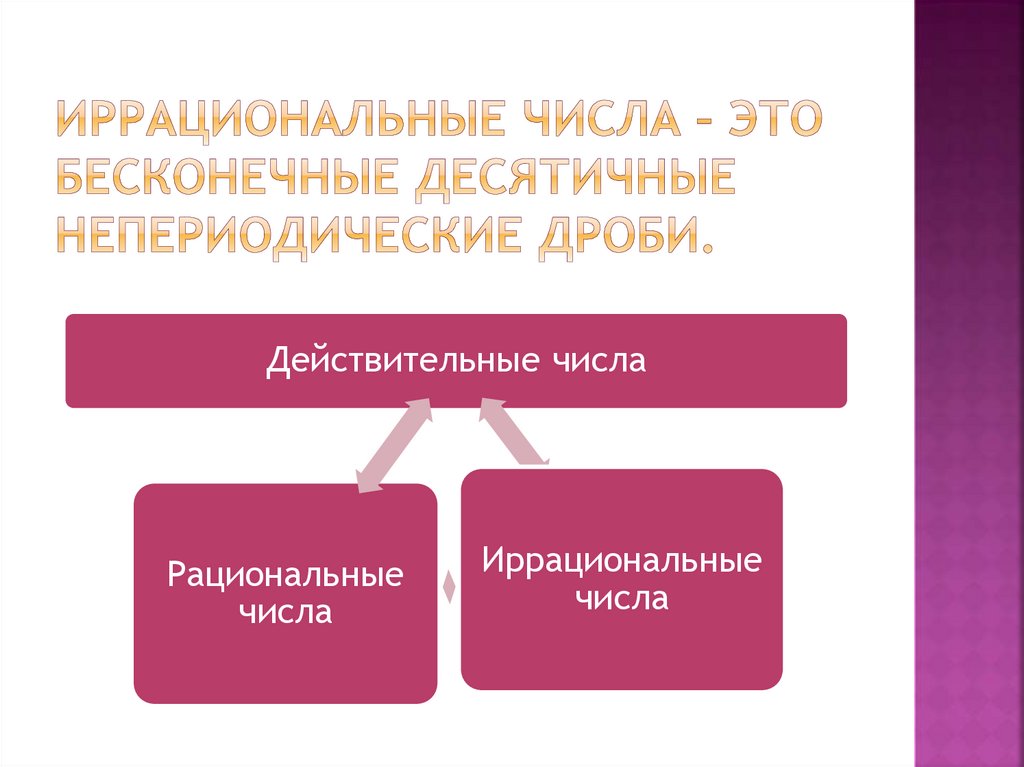
5. Действительные числа разделяются на рациональные и иррациональные

Существуют рациональные (Q) и иррациональные числа. Рациональные разделяются на целые (Z) и дробные. Целые
разделяются на натуральные (N), 0 и противоположные натуральным. Дробные разделяются на обыкновенные дроби,
смешанные числа и десятичные дроби.

6. Правила

При сложении и умножении натуральных чисел всегда получаются натуральные числа. Разность и частное натуральных чисел
могут не быть натуральными числами. При сложении, умножении, вычитании целых чисел всегда получаются целые числа.
Каждое рациональное число можно представить в бесконечной периодической десятичной дроби.

7. Период дроби

Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется
одна и та же цифра или группа цифр – период дроби.

8. Иррациональное число

Иррациональным числом называется бесконечная десятичная непериодическая дробь.

9. Основные числовые множества

.
Основные числовые множества
Натуральные числа — числа 1, 2, 3 и т.д. то те числа, которые мы используем для счёта объектов. Множество натуральных чисел
обозначается N.
Простые числа (P) — натуральные числа, имеющие ровно два различных натуральных делителя: 1 и самого себя. Все остальные
натуральные числа, кроме 1, называются составными. Все составные числа могут быть представлены как произведение простых чисел.
Целые числа (Z) — это числа …, -3, -2, -1, 0, 1, 2, 3, … То есть множество целых чисел есть ноль и «плюс-минус натуральные».
Рациональные числа (Q) — числа, которые можно представить дробью m/n, где m – целое число, а n – натуральное.
Действительные (вещественные) числа (R) — расширение множества рациональных чисел. Множество вещественных чисел
можно представить в виде числовой прямой: на прямой отметим нулевую точку, выберем направление и единицу длины для
измерения отрезков. Тогда каждая точка этой прямой будет соответствовать единственному вещественному числу и каждому
вещественному числу на числовой прямой будет соответствовать единственная точка.
Иррациональные числа — это все вещественные числа, которые не являются рациональными.

10. Множество. Элемент множества

Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита —
от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми
же буквами: N — множество натуральных чисел, Z — множество целых чисел.
Элемент множества — это любой объект, входящий в состав множества.
Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество —
множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и
целых чисел. Множества не содержащие ни одного элемента называются пустыми.

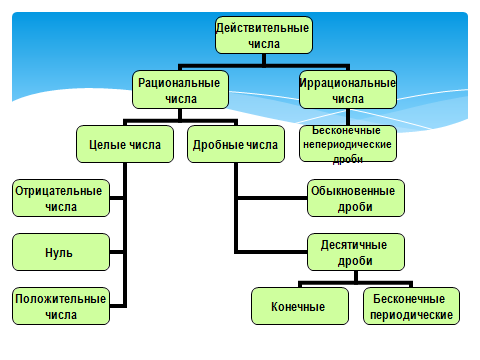
11. Подмножество

Подмножество — это множество, все элементы которого, являются частью другого множества. Визуально продемонстрировать
отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические
схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.

12. Пересечение и объединение множеств

Пересечение двух множеств — это совокупность элементов, принадлежащих каждому из этих множеств, то есть их общая
часть.
Объединением двух множеств называется множество, содержащее все элементы исходных множеств в единственном
экземпляре, то есть если один и тот же элемент встречается в обоих множествах, то в новое множество этот элемент будет
включён только один раз.

13. Модуль действительного числа

Модулем (или абсолютной величиной) числа называется величина, равная ему, если оно неотрицательное, и равная
противоположному к нему, если число отрицательное.
Примеры:
|5| = 5;
|-3.5| = 3.5;
|0| = 0.

14. Заключение

Таким образом, мы выяснили, что действительные числа (вещественные числа)
бывают разными (Натуральные числа, целые числа, рациональные числа и
иррациональные числа). Действительные числа помогают измерить геометрические и
физические величины окружающего мира, извлекать корни, вычислять логарифмы,
решать алгебраические уравнения и исследовать поведение функций.

15. Список используемых источников.

1. https://ru.wikipedia.org/wiki/
2. https://izamorfix.ru/matematika/algebra/mnojestva.html
3. https://umath.ru/theory/osnovnye-chislovye-mnozhestva/

English     Русский Правила

Разница между иррациональными и действительными числами

Ключевая разница: Иррациональное число не может быть представлено в виде дроби с ненулевым знаменателем. Это прямо противоположно рациональному числу. Вещественное число — это число, которое может принимать любое значение на числовой прямой. Это могут быть любые рациональные и иррациональные числа.

Проще говоря, иррациональные числа — это те действительные числа, которые не могут быть представлены в виде дроби. Иррациональные числа — это просто противоположности рациональных чисел. Другими словами, иррациональные числа можно представить как частное двух целых чисел. Важно отметить, что многие квадратные корни, кубические корни и т. д. попадают в категорию иррациональных чисел. Однако не все корни являются иррациональными числами. Иррациональные числа могут быть представлены как непрерывающиеся, неповторяющиеся десятичные дроби. Следует отметить один важный момент: десятичное расширение иррационального числа не заканчивается и не повторяется (блоками одинаковой длины). Однако он может иметь вид 0,101001000100… 

Действительные числа определяют набор значений, лежащих между положительной и отрицательной бесконечностью. Они используются для представления различных типов непрерывных физических величин, таких как расстояние, время и температура. Действительные числа состоят из всех рациональных и иррациональных чисел. Систему действительных чисел можно далее разделить на множество подмножеств:

Натуральные числа (1, 2, 3,….)

Целые числа (0, 1, 2, 3, 4, 5,…)

Целые числа ( ….., -3, -2, -1, 0, 1, 2, 3,…..)

Действительные числа представляют количество вдоль непрерывной линии, известной как числовая линия. Числа стоят во взаимно однозначном соответствии с непрерывными точками на числовой прямой. Они состоят из целых (0, 1, 3, 9, 26), рациональных (6/9, 78,98) и иррациональных чисел (квадратный корень из 3, пи). Бесконечность не попадает в категорию действительных чисел. Квадратный корень из -1 также не является действительным числом, поэтому его называют мнимым числом. Действительное число может быть представлено как возможно бесконечно длинное и неповторяющееся десятичное число.

Сравнение иррационального и действительного числа:

	Реальный номер	Иррациональное число
Определение	Вещественное число — это число, которое может принимать любое значение на числовой прямой. Это могут быть любые рациональные и иррациональные числа.	Иррациональное число не может быть представлено в виде дроби с ненулевым знаменателем.
Номер строки	Можно нанести на числовую прямую.	Может быть нанесен на числовую прямую на основе близости.
Включает	Сюда входят (но не ограничиваются) положительные и отрицательные числа, целые и рациональные числа, квадратные корни, кубические корни, π (пи) и т. д.	Квадратный корень из пяти, так как его нельзя упростить дальше. 4/0, так как знаменатель отличен от нуля Пи (3,14159265358….) — самое известное иррациональное число. Однако в некоторых расчетах приблизительным значением числа Пи считается . Число Эйлера (2,7182818284……) Золотое сечение (1.6180339887………)
Важные моменты, которые следует помнить	Объединение множеств рациональных и иррациональных чисел. Действительные числа включают ноль.	Десятичные числа никогда не повторяются. Десятичные числа никогда не заканчиваются.

Иррациональные числа

Эта запись была опубликована 15 октября 2022 г. автором Anne Helmenstine (обновлено 19 октября 2022 г. )

---

Любые рациональные числа p/q можно записать в виде дроби целых чисел. Вы не можете записать иррациональное число в виде целой дроби.

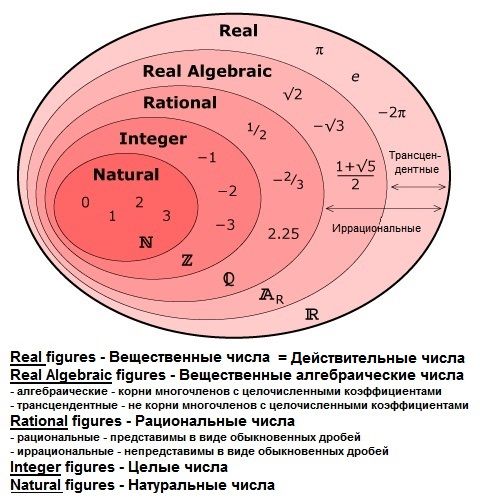
В математике иррациональное число — это число, которое нельзя представить в виде дроби или отношения двух целых чисел. Например, не существует дроби, равной √ 2. Десятичное значение иррационального числа не повторяется регулярно и не заканчивается. Напротив, рациональное число может быть выражено как дробь двух целых чисел p/q. Вместе набор рациональных и иррациональных чисел образует действительных числа . Множество иррациональных чисел является несчетно бесконечным множеством.

Символ иррациональных чисел

Наиболее распространенным символом иррационального числа является заглавная буква «P». Между тем, «R» представляет собой действительное число, а «Q» представляет собой рациональное число. Иногда набор иррациональных чисел равен R-Q или R|Q.

Примеры иррациональных чисел

Иррациональные числа могут быть положительными или отрицательными. Есть много примеров иррациональных чисел:

• √ 2 (постоянная Пифагора)
• Другим способом выражения √ 2 является гипотенуза треугольника, две стороны которого равны 1, или диагональ квадрата с стороны, имеющие длину 1.
• Многие другие квадратные и кубические корни, такие как √3 и √99. Обратите внимание, что некоторые квадратные и кубические корни рациональны (√4 = 2, √9= 3).
• π или PI , или о окружности круга до его радиуса
• — π
• -√ 2
80
• -√ 2
• 80
• -ждать 2
80
• . 8. 9008 9008 6-3
• . 9008. 9008.
79
• . 9073
70
• . 9073
70
• . 9073
70
• . или Номер Эйлера
• φ или Золотое соотношение
• E ^π
• π
• π
  9
• π
  9. π
  9,
• 119, 1999,

, 199,

. 0080

i ⁱ , где i — мнимое число, √-1

трансцендентных действительных чисел , где трансцендентные числа не являются алгебраическими (не являются корнем ненулевого многочлена). Примеры: π и e . Обратите внимание, что все трансцендентные числа иррациональны, но не все иррациональные числа трансцендентны.

Примеры неиррациональных чисел

Неиррациональные числа включают рациональные числа и мнимые числа. Вы можете записать рациональное число в виде дроби. Как десятичное число оно либо заканчивается, либо повторяется. Мнимое число — это действительное число, умноженное на i , где i — это квадратный корень из -1.

Examples of numbers that are not irrational include:

• 1/3, 2/3, and their decimal equivalents, which repeat
• i
• 0
• -42
• 13.2
• 7
• ⁵ / ₄
• -12

Свойства иррациональных чисел

Иррациональные числа являются подмножеством действительных чисел, поэтому они обладают всеми свойствами действительных чисел. У них также есть свойства, которые отличают их от рациональных чисел.

• Сложение рационального и иррационального числа дает иррациональное число.
• Сложение или умножение двух иррациональных чисел может дать или не дать рациональное число. Например, умножение √ 2x√ 2= 2. Но π x π = π ² , что иррационально.
• Множество иррациональных чисел не замыкается при умножении. Множество действительных чисел закрыто при умножении, то есть умножение любых двух рациональных чисел дает другое рациональное число.
• Умножение иррационального числа на любое ненулевое рациональное число дает иррациональное число.
• Любые два иррациональных числа могут иметь или не иметь общее наименьшее кратное.

Ссылки

• Бриджер, Марк (2007). Реальный анализ: конструктивный подход с помощью интервальной арифметики . Джон Уайли и сыновья. ISBN 978-1-470-45144-8.
• Чойке, Джеймс Р. (1980) «Пентаграмма и открытие иррационального числа».

  No related posts.