Действительные числа
Вы уже знакомы с конечными, бесконечными периодическими десятичными дробями, которые являются рациональными числами.
Но в математике существуют и непериодические бесконечные десятичные дроби, которые не являются рациональными числами.
Например, вот такое число: … . Это число является иррациональным.
Итак, иррациональным числом называется бесконечная десятичная непериодическая дробь.
Кстати, иррациональные числа, как и рациональные, могут быть как положительными, так и отрицательными. К примеру, следующие числа:
Первое число положительное иррациональное число, второе – отрицательное иррациональное число.
Числа
, , , ,, являются иррациональными
числами, так как эти числа можно представить в виде 
С понятием иррациональных чисел мы с вами разобрались. Теперь давайте перейдём к действиям с ними. И ответим на такой вопрос: какие же числа получают в результате выполнения арифметических действий с иррациональными числами?
При сложении, вычитании, умножении и делении иррациональных чисел результат может оказаться как рациональным, так и иррациональным числом.
Множество иррациональных чисел принято обозначать заглавной латинской буквой .
Рациональные и иррациональные числа вместе образуют множество действительных чисел.
Множество действительных чисел принято обозначать заглавной латинской буквой . Запись означает, что является действительным числом.
Действительным
числом называется бесконечная десятичная дробь, то есть … или …, где – целое
неотрицательное число, а каждая из букв , , и так далее – это
одна из десяти цифр: , , , , , , , , , .
Например, в записи числа …
, , , , , …
В записи действительного числа …
, , , ,, …
В записи действительного числа …
, , , ,…
В записи действительного числа …
, , , , при .
Действительные числа могут быть как положительными, так и отрицательными, а могут и равняться нулю.
Если все цифры записи бесконечной десятичной дроби равны нулю, то и дробь равна нулю. А если бесконечная десятичная дробь не равна нулю и перед ней стоит знак «+» либо вообще не стоит знака, то это положительное действительное число. А если стоит знак «–», то это отрицательное действительное число.
Все
основные действия и правила над рациональными числами, которые вы
знаете, сохраняются и для действительных чисел. Например,
переместительный, сочетательный и распределительный законы, правила сравнения,
правила раскрытия скобок и так далее.
Только арифметические операции над действительными числами, как правило, заменяют операциями над их приближениями.
Например, давайте вычислим
…
…
Если вычислять сумму этих корней с точностью до единицы, то
.
Если вычислять эту же сумму, но с точностью до одной десятой, то
.
А вот если вычислять сумму наших корней с точностью до одной сотой, то
.
Обратите внимание:; ; и так далее являются последовательными десятичными приближениями значения . Причём первые два числа с избытком, последнее с недостатком. Заметим, что при вычислении и корня из сами числа и корень мы заменяли на их приближения, то есть рациональными числами, а затем выполняли сложение чисел по известным правилам.
Так же, как и для рациональных чисел, модуль действительного числа обозначается и определяется так:
Например,
…
…
И
ещё нам с вами осталось дать геометрическое истолкование действительных чисел.
Итак, геометрически действительные числа изображаются точками числовой прямой. Множество действительных чисел «заполняет» всю числовую прямую. Причём каждому действительному числу соответствует единственная точка на числовой прямой
Точку, изображающую действительное число , также обозначают буквой .
Отметим, что если действительное число меньше действительного числа , то на числовой прямой точка будет лежать левее точки .
А теперь давайте приступим к практической части нашего урока.
Задание 1. Сравните числа , и .
Решение.
…
…
…
Видим: у данных чисел совпадают целые части и цифры десятых.
Значит ,.
Теперь сравним и .
Видим:
у этих чисел совпадают первые четыре цифры после запятой, а вот пятая цифра
после запятой у значения.
Следовательно
Отсюда получаем,
Задание 2. Выясните, каким числом (рациональным или иррациональным) является числовое значение выражения .
Решение. Раскроем скобки в нашем выражении, применяя формулу квадрата суммы. Воспользуемся следствием из определения квадратного корня.
.
Затем применим свойство корня из произведения. Приведём подобные.
Получим .
Данное число является иррациональным, так как содержит иррациональное число .
определение, примеры, представления, координатная прямая
Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.
Определение действительных чисел
Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа.
Как дать определение, что такое действительные числа?
Действительные числа — это рациональные и иррациональные числа. Множество действительных чисел обозначается через
Данное определение можно записать иначе с учетом следующего:
- Рациональные числа можно представить в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
- Иррациональные числа представляют собой бесконечные непериодические десятичные дроби.
Действительные числа — числа, которые можно записать в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.
Действительные числа — это любые рациональные и иррациональные числа. Приведем примеры таких чисел: 0; 6; 458; 1863; 0,578; -38; 265; 0,145(3); log512.
Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа.
Нуль является единственным действительным числом, которое не положительно и не отрицательно.
Еще одно название для действительных чисел — вещественные числа. Эти числа позволяют описывать значение непрерывно меняющейся величины без введения эталонного (единичного) значения этой величины.
Координатная прямая и действительные числа
Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.
Представления действительных чисел
Под определение дейситвительных чисел попадают:
- Натуральные числа.
- Целые числа.
- Десятичные дроби.
- Обыкновенные дроби.
- Смешанные числа.
Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.
Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.
Например, значения выражений sin23π·e-285·10log32 и tg676693-8π32 — действительные числа.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Разница между иррациональными и действительными числами
Ключевая разница: Иррациональное число не может быть представлено в виде дроби с ненулевым знаменателем. Это прямо противоположно рациональному числу. Вещественное число — это число, которое может принимать любое значение на числовой прямой. Это могут быть любые рациональные и иррациональные числа.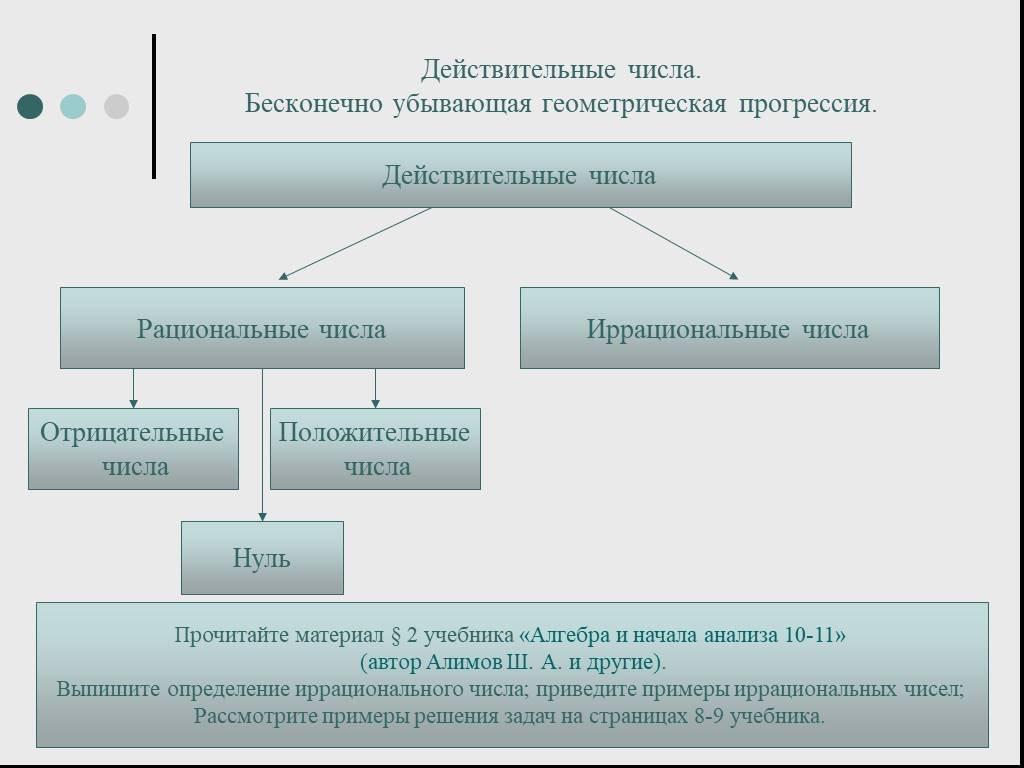
Проще говоря, иррациональные числа — это те действительные числа, которые не могут быть представлены в виде дроби. Иррациональные числа — это просто противоположности рациональных чисел. Другими словами, иррациональные числа можно представить как частное двух целых чисел. Важно отметить, что многие квадратные корни, кубические корни и т. д. попадают в категорию иррациональных чисел. Однако не все корни являются иррациональными числами. Иррациональные числа могут быть представлены как непрерывающиеся, неповторяющиеся десятичные дроби. Следует отметить один важный момент: десятичное расширение иррационального числа не заканчивается и не повторяется (блоками одинаковой длины). Однако он может иметь вид 0,101001000100…
Действительные числа определяют набор значений, лежащих между положительной и отрицательной бесконечностью. Они используются для представления различных типов непрерывных физических величин, таких как расстояние, время и температура. Действительные числа состоят из всех рациональных и иррациональных чисел.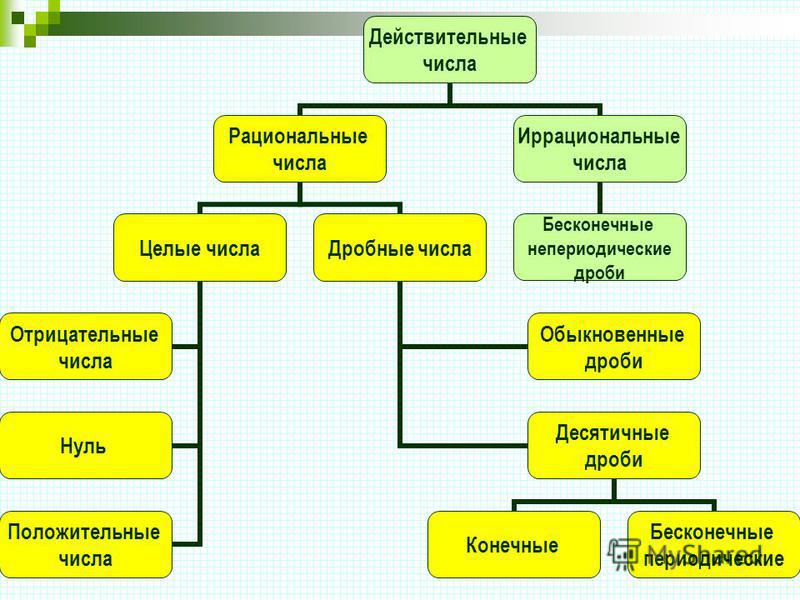
Систему действительных чисел можно далее разделить на множество подмножеств:
Натуральные числа (1, 2, 3,….)
Целые числа (0, 1, 2, 3, 4, 5,…)
Целые числа ( ….., -3, -2, -1, 0, 1, 2, 3,…..)
Действительные числа представляют количество вдоль непрерывной линии, известной как числовая линия. Числа стоят во взаимно однозначном соответствии с непрерывными точками на числовой прямой. Они состоят из целых (0, 1, 3, 9, 26), рациональных (6/9, 78,98) и иррациональных чисел (квадратный корень из 3, пи). Бесконечность не попадает в категорию действительных чисел. Квадратный корень из -1 также не является действительным числом, поэтому его называют мнимым числом. Действительное число может быть представлено как возможно бесконечно длинное и неповторяющееся десятичное число.
Сравнение иррационального и действительного числа:
| Реальный номер | Иррациональное число |
Определение | Вещественное число — это число, которое может принимать любое значение на числовой прямой. | Иррациональное число не может быть представлено в виде дроби с ненулевым знаменателем. |
Номер строки | Можно нанести на числовую прямую. | Может быть нанесен на числовую прямую на основе близости. |
Включает | Сюда входят (но не ограничиваются) положительные и отрицательные числа, целые и рациональные числа, квадратные корни, кубические корни, π (пи) и т. д. |
|
Важные моменты, которые следует помнить |
|
|
Это могут быть любые рациональные и иррациональные числа.
Натуральные, целые, рациональные, иррациональные, вещественные числа и т. д.
Натуральные числа
натуральных (или при подсчете ) чисел равны 1,52,3, и т. д. бесконечно много натуральных чисел. Набор натуральных чисел {1,2,3,4,5,…}, иногда пишется N для краткости.
целые числа являются натуральными числами вместе с 0.
(Примечание: некоторые учебники не согласны и говорят, что натуральные числа включают 0.)
Сумма
любые два натуральных числа также являются натуральным числом (например, 4+2000=2004), а произведение любых двух натуральных чисел
— натуральное число (4×2000=8000). Этот
однако это неверно для вычитания и деления.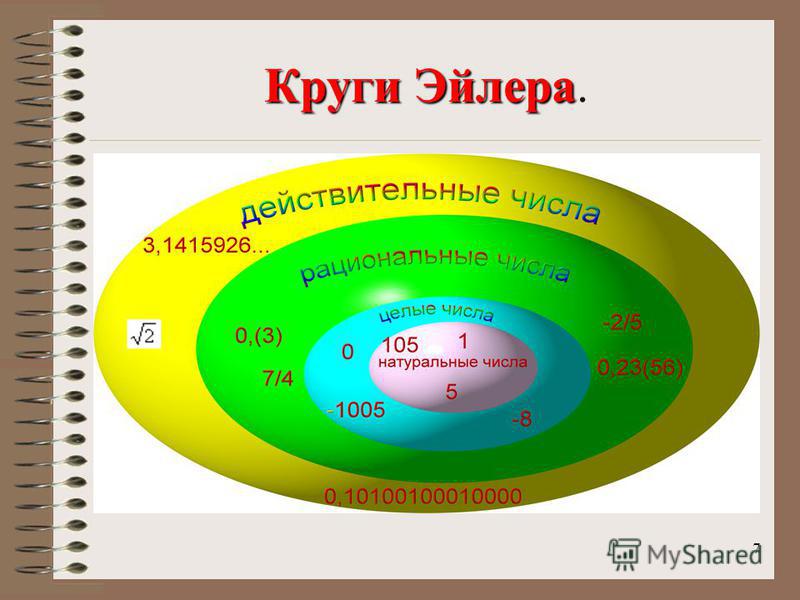
Целые числа
целых числа представляют собой набор действительных чисел, состоящий из натуральных чисел, их аддитивных инверсий и нуля.
{…,−5,−4,−3,−2,−1,0,1,2,3,4,5,…}
Набор целых чисел иногда пишется J или Z для краткости.
сумма, произведение и разность любых двух целых чисел также являются целыми числами. Но это неверно для деления… просто попробуйте 1÷2.
Рациональные числа
рациональных числа те числа, которые могут быть выражены как отношение между два целых числа. Например, дроби 13 и −11118 равны рациональное число. Все целые числа входят в число рациональных, так как любое целое число z может быть записано как отношение z1.
Все десятичные дроби, которые заканчиваются, являются рациональными числами (поскольку 8.27 можно записать как 827100). которые имеют повторяющийся шаблон после некоторого момента, также являются рациональными: например,
0,0833333.
…=112.
Множество рациональных чисел замкнуто относительно всех четырех основных операций, то есть для любых двух рациональных чисел их сумма, разность, произведение и частное также являются рациональными числами (если мы не делим на 0).
Иррациональные числа
Иррациональное число — это число, которое нельзя записать в виде отношения (или дроби). В десятичной форме оно никогда не заканчивается и не повторяется. древние греки обнаружили, что не все числа рациональны; там уравнения, которые нельзя решить, используя отношения целых чисел.
Первое такое уравнение для изучения было 2=x2. Что число, умноженное на себя, равно 2?
2 есть около 1,414, потому что 1,4142=1,999396, что близко к 2. Но вы никогда не попадете точно в квадрат дроби (или десятичная дробь). Квадратный корень из 2 является иррациональным числом, т. десятичный эквивалент продолжается вечно, без повторяющегося шаблона:
2=1.41421356237309…
Другие известные иррациональные числа золотое сечение , число с большим значение для биологии:
1+52=1,61803398874989.
..
π (пи), отношение длины окружности к ее диаметру:
π=3,14159265358979…
и e, самое важное число в исчислении:
e=2,71828182845904…
Иррациональные числа могут быть далее подразделены на алгебраических чисел, которые являются решениями некоторых полиномиальных уравнений (таких как 2 и золотое сечение), и трансцендентных чисел, которые не являются решениями ни одного полиномиального уравнения. π и e оба трансцендентны.
Вещественные числа
Вещественные числа — это набор чисел, содержащий все рациональные числа и все иррациональные числа. Настоящие числа — это «все числа» на числовой прямой. Существует бесконечно много действительных чисел, так же как бесконечно много чисел в каждом из других наборов чисел. Но можно доказать, что бесконечность действительных чисел равна 9.0003 больше бесконечность.
«Меньший»,
или исчисляемых бесконечности целых чисел и
рациональные числа иногда называют ℵ0 (алеф-ноль),
и бесчисленных бесконечности реалов
называется ℵ1 (алеф-один).