Комплексные числа — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Комплексные числа
к.э.н., доцент кафедрыинформационных
технологий ЮРИУ
РАНХиГС
Прокопенко М. В.
2. Содержание
Понятие комплексного числаОперации над комплексными
числами в алгебраической форме
Тригонометрическая и
показательная формы
Возведение комплексных чисел в
степень
3.
 Понятие комплексного числаZ=a+bi – общая форма комплексного
Понятие комплексного числаZ=a+bi – общая форма комплексногочисла
а, b – действительные числа
i – мнимая единица
4. Понятие комплексного числа
а+bi — единое число!5. Понятие комплексного числа
Джероламо Кардано(1501-1576)
Поставил вопрос о
существовании
комплексных чисел
6. Понятие комплексного числа
Иоганн КарлФридрих
Гаусс
(1777-1855)
Ввел понятие
«комплексное
число»
7. Понятие комплексного числа
Уильям РоуэнГамильтон
(1805-1865)
Предложил
стандартную
модель
комплексных чисел
8. Понятие комплексного числа
Комплексная плоскость9. Понятие комплексного числа
Отобразим число Z=4+3i10. Понятие комплексного числа
Множество действительных чисел Rпредставляет собой подмножество
множества комплексных чисел С
R C
11. Понятие комплексного числа
Три формы комплексного числа:алгебраическая;
тригонометрическая;
показательная.

12. Операции над комплексными числами
Операции над комплекснымичислами в алгебраической форме:
сложение;
вычитание;
умножение;
деление.
13. Операции над комплексными числами
Сложение:Действительные и мнимые числа
складываются отдельно
14. Операции над комплексными числами
Вычитание:Действительные и мнимые числа
вычитаются отдельно
15. Операции над комплексными числами
Умножение:Умножение осуществляется по правилам
умножения многочленов;
Квадрат мнимой единицы равен -1
i 1
2
16. Операции над комплексными числами
Умножение:17. Операции над комплексными числами
Деление:Умножение числителя и
знаменателя на сопряженное
знаменателю выражение
18. Операции над комплексными числами
Перевод в алгебраическую форму:19. Тригонометрическая и показательная формы
Любое, кроме нуля, комплексноечисло Z=a=bi можно записать в
тригонометрической форме:
Z Z Cos iSin
20.
 Тригонометрическая и показательная формыZ – модуль комплексного числа;
Тригонометрическая и показательная формыZ – модуль комплексного числа;Z a 2 b2
– аргумент комплексного числа.
b
arg Z arctg
a
21. Тригонометрическая и показательная формы
Z 4 3i22. Тригонометрическая и показательная формы
Формулы аргумента:a > 0 (I и IV четверти)
b
arg Z arctg
a
a < 0, b > 0 (II четверть)
b
arg Z arctg
a
b
a < 0, b < 0 (III четверть) arg Z arctg
a
23. Тригонометрическая и показательная формы
Комплексное число в показательнойформе имеет вид:
Z Ze
i
24. Тригонометрическая и показательная формы
Z 1 3i25. Тригонометрическая и показательная формы
Умножение комплексных чисел втригонометрической и
показательной форме:
Модули перемножаем
Аргументы складываем
26. Тригонометрическая и показательная формы
27. Тригонометрическая и показательная формы
Деление в тригонометрической ипоказательной форме:
Модули делим
Аргументы вычитаем
28.
 Возведение комплексных чисел в степеньФормула Муавра:
Возведение комплексных чисел в степеньФормула Муавра:Z Z Cos( n) iSin ( n)
n
n
Z Z e
n
n
i n
29. Возведение комплексных чисел в степень
Абрахам де Муавр(1667-1754)
30. Возведение комплексных чисел в степень
31. Возведение комплексных чисел в степень
При возведении в степенькомплексного числа в
алгебраической форме необходимо
помнить, что i 2 1,
i 3 i ,
i 1
………
4
32. Возведение в степень комплексного числа
nZ
n
2 k
2 k
Z Cos
iSin
n
n
n
Z n Ze
2 k
n
k 0,1,…, (n 1).
33. Литература
Акимов В.П. Математика для политологов. 2-е изд.,испр. и доп. – М.: МГИМО, 2011.
Грес П.В. Математика для бакалавров.
Универсальный курс для студентов гуманитарных
направлений [Электронный ресурс]: учебное
пособие/ Грес П.В.— Электрон. текстовые
данные.— М.: Логос, 2015.— 288 c.— Режим
доступа: http://www.

ЭБС «IPRbooks»
Ильин В. А. Высшая математика [Текст] : учеб.
для вузов: Рек. Мин. обр. / В. А. Ильин, А. В.
Куркина. — 3-е изд., перераб. и доп. — М. :
Проспект, 2015. — 608 с.
Спасибо за внимание!
English Русский Правила
| Microsoft Learn
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
- Чтение занимает 4 мин
Определяет шаблон complex класса контейнера и его вспомогательные шаблоны.
Требования
Заголовок: <сложный>
Пространство имен: std
Комплексное число — это упорядоченная пара реальных чисел. В чисто геометрических терминах комплексная плоскость является реальной двумерной плоскости. Отличия комплексной плоскости от вещественной состоят в том, что у нее есть дополнительная алгебраическая структура. У этой структуры есть две основные операции.
Добавление, определенное как (a, b) + (c, d) = (ac + ,bd + )
Умножение, определенное как (a, b) * (c, d) = (acbd — , adbc + )
Набор сложных чисел с операциями сложного сложения и сложного умножения — это поле в стандартном алгебраическом смысле:
Операции сложения и умножения коммутативны и ассоциативны, а умножение распределяется над сложением точно так же, как для вещественного сложения и умножения в поле вещественных чисел.

Комплексное число (0, 0) представляет собой аддитивный идентификатор, а число (1, 0) — мультипликативный идентификатор.
Аддитивное обратное для комплексного числа ( a, b) равно (-a, —b), а умножение для всех таких сложных чисел, кроме (0, 0) равно
(a/(a2b2 + ), —b/(a2b2 + ))
Представляя комплексное число z = (a, b) в форме zabi + = , гдеi2 = -1, правила для алгебры набора реальных чисел можно применять к набору сложных чисел и к их компонентам. Например:
(1 + 2i) * (2 + 3i) = 1 * (2 + 3i) + 2i * (2 + 3i) = (2 + 3i) + (4i + 6i2) = (2 – 6) + (3 + 4)i = -4 + 7i
Система сложных чисел — это поле, но это не упорядоченное поле. Нет порядка сложных чисел, так как для поля реальных чисел и его подмножеств, поэтому неравенство не может быть применено к сложным числам, так как они относятся к реальным числам.
Существует три общие формы представления комплексного числа z:
В этих стандартных представлениях комплексных чисел используются следующие термины.
Вещественный компонент арифметического представления или действительная часть a.
Мнимый компонент арифметического представления или мнимая часть b.
Модуль или абсолютное значение комплексного числа r.
Аргумент или угол фазы p в радианах.
Если не указано иное, функции, которые могут возвращать несколько значений, требуются для возврата основного значения аргументов больше -π и меньше или равно +π, чтобы сохранить одно значение. Все углы должны быть выражены в радианах, где в круге есть 2π радианы (360 градусов).
Члены
Функции
| Имя | Описание |
|---|---|
abs | Вычисляет модуль комплексного числа. |
acos | |
acosh | |
arg | Извлекает аргумент из комплексного числа. |
asin | |
asinh | |
atan | |
atanh | |
conj | Возвращает комплексно-сопряженную величину комплексного числа. |
cos | Возвращает косинус комплексного числа. |
cosh | Возвращает гиперболический косинус комплексного числа. |
exp | Возвращает экспоненциальную функцию комплексного числа. |
imag | Извлекает мнимую часть комплексного числа. |
log | Возвращает натуральный логарифм комплексного числа. |
log10 | Возвращает десятичный логарифм комплексного числа. |
norm | Извлекает норму комплексного числа. |
polar | Возвращает комплексное число, соответствующее указанному модулю и аргументу, в декартовой форме. |
pow | Вычисляет комплексное число, получаемое в результате возведения основания (комплексное число) в степень другого комплексного числа. |
proj | |
real | Извлекает вещественную часть комплексного числа. |
sin | Возвращает синус комплексного числа. |
sinh | Возвращает гиперболический синус комплексного числа. |
sqrt | Возвращает квадратный корень комплексного числа. |
tan | Возвращает тангенс комплексного числа. |
| танх | Возвращает гиперболический тангенс комплексного числа. |
Операторы
| Имя | Описание |
|---|---|
operator!= | Проверяет на неравенство два комплексных числа, по крайней мере одно из которых может принадлежать к подмножеству типа для вещественной и мнимой частей. |
operator* | Умножает два комплексных числа, по крайней мере одно из которых может принадлежать к подмножеству типа для вещественной и мнимой частей. |
operator+ | Складывает два комплексных числа, по крайней мере одно из которых может принадлежать к подмножеству типа для вещественной и мнимой частей. |
operator- | Вычитает два комплексных числа, по крайней мере одно из которых может принадлежать к подмножеству типа для вещественной и мнимой частей. |
operator/ | Делит два комплексных числа, по крайней мере одно из которых может принадлежать к подмножеству типа для вещественной и мнимой частей. |
operator<< | Функция шаблона, вставляющая комплексное число в поток вывода. |
operator== | Проверяет на равенство два комплексных числа, по крайней мере одно из которых может принадлежать к подмножеству типа для вещественной и мнимой частей.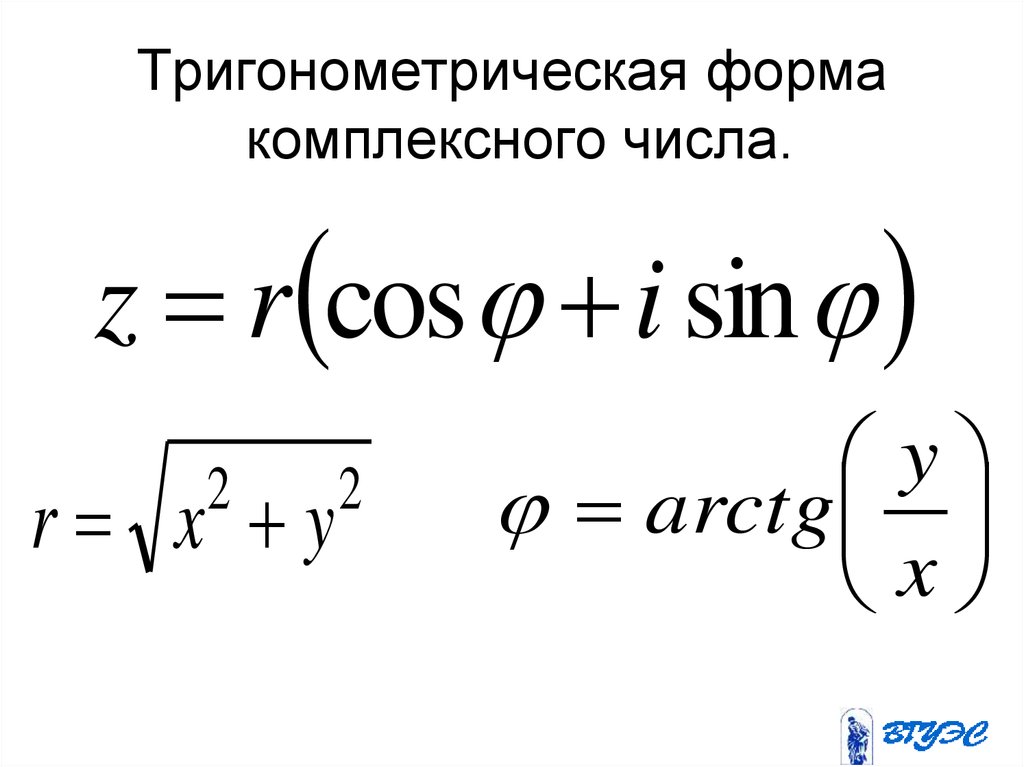 |
operator>> | Функция шаблона, извлекающая комплексное число из входного потока. |
Классы
| name | Описание |
|---|---|
complex<double> | Явно специализированный шаблон класса описывает объект, в котором хранится упорядоченная пара объектов обоих типов double, где первый представляет реальную часть сложного числа, а второй — мнимую часть. |
complex<float> | Явно специализированный шаблон класса описывает объект, в котором хранится упорядоченная пара объектов обоих типов float, где первый представляет реальную часть сложного числа, а второй — мнимую часть. |
complex<long double> | Явно специализированный шаблон класса описывает объект, в котором хранится упорядоченная пара объектов обоих типов long double, где первый представляет реальную часть сложного числа, а второй — мнимую часть. |
complex | Шаблон класса описывает объект, используемый для представления комплексной системы чисел и выполнения сложных арифметических операций. |
Литералы
Сложный <> заголовок определяет следующие пользовательские литералы. Литералы создают комплексное число с реальной частью нуля и мнимой частью, которая имеет значение входного параметра.
| Объявление | Описание |
|---|---|
constexpr complex<long double> operator""il(long double d)constexpr complex<long double> operator""il(unsigned long long d) | Возвращаемый результат: complex<long double>{0.0L, static_cast<long double>(d)} |
constexpr complex<double> operator""i(long double d)constexpr complex<double> operator""i(unsigned long long d) | Возвращает complex<double>{0.. |
constexpr complex<float> operator""if(long double d)constexpr complex<float> operator""if(unsigned long long d) | Возвращает complex<float>{0.0f, static_cast<float>(d)}. |
См. также раздел
Справочник по файлам заголовков
Безопасность потоков в стандартной библиотеке C++
Преобразование комплексных чисел в полярную форму
Пусть r и θ — полярные координаты точки P(x, y), которая соответствует ненулевому комплексному числу z = x + iy . Полярная форма или тригонометрическая форма комплексного числа P:
z = r (cos θ + i sin θ)
Значение «r» представляет абсолютное значение или модуль комплексного числа z .
Угол θ называется аргументом или амплитудой комплексного числа z, обозначаемого θ = arg(z).
Угол θ имеет бесконечно много возможных значений, в том числе отрицательных, отличающихся целыми кратными 2π. Эти значения можно определить из уравнения тангенс θ = y/x
Эти значения можно определить из уравнения тангенс θ = y/x
Чтобы найти главный аргумент комплексного числа, мы можем использовать следующие методы:
1 й квадрант 2 й квадрант 3 й квадрант 4 й 3 квадрант 2 9003 3 квадрант | θ = α θ = π — α θ = — π + α θ = -α |
Капитал А важен здесь для того, чтобы отличать основную стоимость от общей стоимости. Очевидно, что на практике для нахождения главного угла θ обычно вычисляют α = tan −1 |г/х| и скорректируйте проблему квадранта, добавляя или вычитая α с π соответствующим образом
arg z = Arg z + 2nπ, n ∈ z.
Запишите следующие комплексные числа в полярной форме.
Проблема 1:
2 + I 2√3
Решение:
2 + I 2√3 = R (COS θ + I SIN θ)
r = √2 2 + (2√3) 2 r = √(4+12) r = √16 р = 4 | α = тангенс -1 |y/x| α = тангенс -1 (2√3/2) α = тангенс -1 (√3) α = π/3 |
Так как комплексное число 2 + i 2√3 лежит в первом квадранте, имеет главное значение θ = α.
Итак, полярная форма данного комплексного числа:
Задача 2:
3 — i √3
Решение:
3 — i √3 = r (cos θ + i sin θ)
r = √3 2 + (-√3) 2 r = √(9+3) r = √12 r = 2√3 | α = тангенс -1 |y/x| α = tan -1 |-√3/3| α = тангенс -1 (1/√3) α = π/6 |
Поскольку комплексное число 3-i√3 лежит в четвертом квадранте, имеет главное значение θ = -α.
θ = -π/6
3 — i √3 = 2√3 (cos (-π/6) + i sin (-π/6)
3 — i √3 = 2√3 (cos (π/6) — i sin (π/6))
Итак, полярная форма данного комплексного числа:
−2 − i2 = r (cos θ + i sin θ)
r = √(-2) 2 + (-2) 2 r = √(4+4) r = 2√2 | α = тангенс -1 |y/x| α = tan -1 |2/2| α = tan -1 (1) α = π/4 |
Поскольку комплексное число −2 − i2 лежит в третьем квадранте, имеет главное значение θ = -π+α.
θ = -π + π/4
θ = (-4π+π)/4
θ = -3π/4
−2 − i2 = 2√3 (cos ( -3π/4) + i sin ( -3π/4))
Таким образом, полярная форма данного комплексного числа равна
Задача 4:
(i — 1) / [cos (π/3) + i sin (π/3)]
Решение:
= (i — 1) / [cos ( π/3) + i sin (π/3)]
= (i — 1) / [(1/2) + i (√3/2)]
= 2(i — 1) / (1 + i√3)
= (2i — 2) / (1 + i√3)
r = √[(4 + 2√3 + 4 — 2√3)/4]
r = √2
α = тангенс -1 |(√3+1)/(√3-1)|
α = тангенс -1 (5π/12)
тангенс 75 = тангенс (30 + 45)
= (тангенс 30 + тангенс 45)/(1 — тангенс 30 тангенс 45)
= [(1/√3) + 1]/[1 — (1/√3)1]
= (1 + √3)/(√3 — 1)
= (√3 + 1)/(√3 — 1)
(i — 1) / [cos (π/3) + i sin (π/3) ]. материал по математике, пожалуйста, используйте наш пользовательский поиск Google здесь.
Пожалуйста, присылайте свои отзывы на v4formath@gmail. com
com
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Полярная форма комплексных чисел · Алгебра и тригонометрия
Полярная форма комплексных чисел · Алгебра и тригонометрияВ этом разделе вы:
- Нанесете комплексные числа на комплексную плоскость.
- Найдите абсолютное значение комплексного числа.
- Запишите комплексные числа в полярной форме.
- Преобразование комплексного числа из полярной формы в прямоугольную.
- Поиск произведений комплексных чисел в полярной форме.
- Найдите частные комплексных чисел в полярной форме.
- Найдите степени комплексных чисел в полярной форме.
- Найдите корни комплексных чисел в полярной форме.
«Бог создал целые числа; все остальное — дело рук человека». Эта довольно известная цитата немецкого математика девятнадцатого века Леопольда Кронекера закладывает основу для этого раздела о полярной форме комплексного числа. Комплексные числа были изобретены людьми и представляют собой более тысячи лет непрерывных исследований и борьбы таких математиков, как 9.0309 Пифагор , Декарт , Де Муавр, Эйлер , Гаусс и другие. Комплексные числа ответили на вопросы, которые веками озадачивали величайшие умы науки.
Комплексные числа были изобретены людьми и представляют собой более тысячи лет непрерывных исследований и борьбы таких математиков, как 9.0309 Пифагор , Декарт , Де Муавр, Эйлер , Гаусс и другие. Комплексные числа ответили на вопросы, которые веками озадачивали величайшие умы науки.
Впервые мы столкнулись с комплексными числами в книге «Комплексные числа». В этом разделе мы сосредоточимся на механике работы с комплексными числами: переводе комплексных чисел из полярной формы в прямоугольную и обратно, интерпретации комплексных чисел в схеме приложений и применении теоремы Муавра.
Нанесение комплексных чисел на комплексную плоскость
Построение комплексного числа a+bi
аналогично построению действительного числа, за исключением того, что горизонтальная ось представляет действительную часть числа, a,
, а вертикальная ось представляет собой мнимую часть числа, bi.
**Дано комплексное число a+bi,
постройте его в комплексной плоскости.**0338 мнимая ось.
единицы в горизонтальном направлении и
бединиц в вертикальном направлении.
Построение комплексного числа на комплексной плоскости
Построение комплексного числа 2−3i
на комплексной плоскости .
От исходной точки переместитесь на две единицы в положительном горизонтальном направлении и на три единицы в отрицательном вертикальном направлении. См. [ссылка].
Постройте точку 1+5i
на комплексной плоскости.

Нахождение абсолютного значения комплексного числа
Первым шагом к работе с комплексным числом в полярной форме является нахождение абсолютного значения. Абсолютное значение комплексного числа такое же, как его величина , или \|z\|.
Абсолютное значение комплексного числа такое же, как его величина , или \|z\|.
Измеряет расстояние от начала координат до точки на плоскости. Например, график z=2+4i,
в [ссылка], показывает \|z\|.
Абсолютное значение комплексного числа
Учитывая z=x+yi,
комплексное число, абсолютное значение z
определяется как
\|z\|=x2+y2
Это расстояние от начало координат в точку (x,y).
Обратите внимание, что абсолютное значение действительного числа дает расстояние числа от 0, а абсолютное значение комплексного числа дает расстояние числа от начала координат, (0, 0).
Нахождение абсолютного значения комплексного числа с радикалом
Найдите абсолютное значение z=5−i.
Используя формулу, мы имеем
\|z\|=x2+y2\|z\|=(5)2+(−1)2\|z\|=5+1\|z\|= 6
См. [ссылка].
Найдите абсолютное значение комплексного числа z=12−5i.
13
Нахождение абсолютного значения комплексного числа
Дано z=3−4i,
найти \|z\|.
Используя формулу, мы имеем
\|z\|=x2+y2\|z\|=(3)2+(−4)2\|z\|=9+16\|z\|=25\|z\|=5
Абсолютное значение z
равно 5. См. [ссылка].
Дано z=1−7i,
найти \|z\|.
\|z\|=50=52
Запись комплексных чисел в полярной форме
Полярная форма комплексного числа выражает число через угол θ
и его расстояние от начала координат r.
Дан комплексный номер в прямоугольной форме , выраженный как z=x+yi,
мы используем те же формулы преобразования, что и для записи числа в тригонометрической форме:
x=rcos θ y=rsin θ r=x2+y2
Мы рассматриваем эти отношения в [ссылка].
Мы используем термин по модулю для обозначения абсолютного значения комплексного числа или расстояния от начала координат до точки (x,y).
Таким образом, модуль равен r,
. радиус в полярной форме.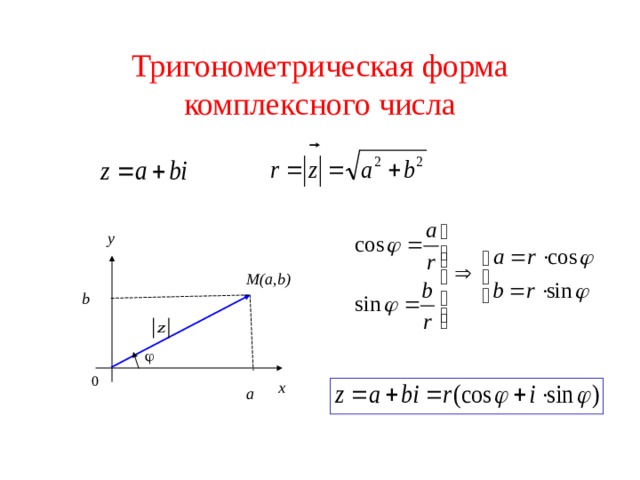 Мы используем θ
Мы используем θ
для указания угла направления (так же, как и с полярными координатами). Подставляя, имеем
z=x+yiz=rcos θ+(rsin θ)iz=r(cos θ+isin θ)
Полярная форма комплексного числа
При записи комплексного числа в полярной форме используются следующие формулы преобразования: yiz=(rcos θ)+i(rsin θ)z=r(cos θ+isin θ)
, где r
— модуль , а θ
— аргумент . Мы часто используем сокращение rcis θ
для представления r(cos θ+isin θ).
Выражение комплексного числа с использованием полярных координат
Выражение комплексного числа 4i
с использованием полярных координат.
На комплексной плоскости число z=4i
совпадает с z=0+4i.
Записав это в полярной форме, мы должны сначала вычислить r
.
r=x2+y2r=02+42r=16r=4
Далее мы смотрим на x.
Если x=rcos θ,
и x=0,
, то θ=π2.
В полярных координатах комплексное число z=0+4i
можно записать как z=4(cos(π2)+isin(π2))
или 4cis( π2).
См. [ссылка].
Выразите z=3i
как r цис θ
в полярной форме.
z=3(cos(π2)+isin(π2))
Нахождение полярной формы комплексного числа
Нахождение полярной формы −4+4i.
Сначала найдите значение r.
r=x2+y2r=(−4)2+(42)r=32r=42
Найти угол θ
по формуле:
cos θ=xrcos θ=−442cos θ=−12 θ=cos−1(−12)=3π4
Таким образом, решение равно (3π42cis).
Запишите z=3+i
в полярной форме.
z=2(cos(π6)+isin(π6))
Преобразование комплексного числа из полярной формы в прямоугольную
Преобразование комплексного числа из полярной формы в прямоугольную зависит от оценки того, что дано, и использования распределительного свойства. Другими словами, учитывая z=r(cos θ+isin θ),
сначала вычислить тригонометрические функции cos θ
и sin θ.
Затем умножьте на r.
Преобразование полярной формы в прямоугольную
Преобразование полярной формы заданного комплексного числа в прямоугольную:
z=12(cos(π6)+isin(π6))
Начнем с вычисления тригонометрических выражений.
cos(π6)=32 and sin(π6)=12
После подстановки комплексное число равно
z=12(32+12i)
Применим свойство распределения:
z=12(32+12i) =(12)32+(12)12i =63+6i
Прямоугольная форма данной точки в комплексной форме равна 63+6i.
Нахождение прямоугольной формы комплексного числа
Нахождение прямоугольной формы комплексного числа при данных r=13
и tan θ=512.
Если tan θ=512,
и tan θ=yx,
, мы сначала определяем r=x2+y2=122+52=13.
Затем мы находим cos θ=xr
и sin θ=yr.
z=13(cos θ+isin θ) =13(1213+513i) =12+5i
Прямоугольная форма данного числа в комплексной форме равна 12+5i.
Преобразование комплексного числа в прямоугольную форму:
z=4(cos11π6+isin11π6)
z=23−2i
Нахождение произведений комплексных чисел в полярной форме
Теперь, когда мы можем преобразовывать комплексные числа в полярную форму, мы научимся выполнять операции над комплексными числами в полярной форме. В оставшейся части этого раздела мы будем работать с формулами, разработанными французским математиком Абрахамом 9.0309 де Муавр (1667-1754). Эти формулы сделали работу с произведениями, частными, степенями и корнями комплексных чисел намного проще, чем кажется. Правила основаны на умножении модулей и добавлении аргументов.
В оставшейся части этого раздела мы будем работать с формулами, разработанными французским математиком Абрахамом 9.0309 де Муавр (1667-1754). Эти формулы сделали работу с произведениями, частными, степенями и корнями комплексных чисел намного проще, чем кажется. Правила основаны на умножении модулей и добавлении аргументов.
Произведения комплексных чисел в полярной форме. =r1r2[cos(θ1+θ2)+isin(θ1+θ2)]z1z2=r1r2cis(θ1+θ2)
Обратите внимание, что произведение требует умножения модулей и сложения углов.
Нахождение произведения двух комплексных чисел в полярной форме +isin(145°)).
Следуйте формуле
z1z2=4⋅2[cos(80°+145°)+isin(80°+145°)]z1z2=8[cos(225°)+isin(225°)]z1z2=8 [cos(5π4)+isin(5π4)]z1z2=8[−22+i(−22)]z1z2=−42−4i2
Нахождение частных комплексных чисел в полярной форме
Частное двух комплексных чисел в полярной форме — это частное двух модулей и разность двух аргументов.
Части комплексных чисел в полярной форме cos(θ1−θ2)+isin(θ1−θ2)], z2≠0z1z2=r1r2cis(θ1−θ2), z2≠0
Обратите внимание, что модули делятся, а углы вычитаются.
Даны два комплексных числа в полярной форме, найдите частное.
- Разделить р1р2.
- Найти θ1−θ2.
- Подставьте результаты в формулу:
z=r(cos θ+isin θ).
Заменить
гс
r1r2,и заменить
θс
θ1−θ2. - Вычислить новые тригонометрические выражения и умножить на р.
Нахождение отношения двух комплексных чисел
Найдите частное z1=2(cos(213°)+isin(213°))
и z2=4(cos(33°)+isin(33°)).
Используя формулу, имеем
z1z2=24[cos(213°-33°)+isin(213°-33°)]z1z2=12[cos(180°)+isin(180°)]z1z2= 12[−1+0i]z1z2=−12+0iz1z2=−12
Найдите произведение и частное z1=23(cos(150°)+isin(150°))
и z2=2(cos(30°)+isin(30°)).
z1z2=−43;z1z2=−32+32i
Нахождение степеней комплексных чисел в полярной форме
Нахождение степеней комплексных чисел значительно упрощается с помощью Теорема де Муавра . В нем говорится, что для положительного целого числа n,zn
В нем говорится, что для положительного целого числа n,zn
находится путем возведения модуля в n-ю
степени и умножение аргумента на n.
Это стандартный метод, используемый в современной математике.
Теорема де Муавра. n
— целое положительное число.
Вычисление выражения с помощью теоремы Муавра
Оцените выражение (1+i)5
, используя теорему Муавра.
Поскольку теорема Муавра применима к комплексным числам, записанным в полярной форме, мы должны сначала записать (1+i)
в полярной форме. Найдем р.
r=x2+y2r=(1)2+(1)2r=2
Затем находим θ.
Использование формулы tan θ=yx
дает
tan θ=11tan θ=1 θ=π4
Используйте теорему де Муавра для вычисления выражения.
(a+bi)n=rn[cos(nθ)+isin(nθ)] (1+i)5=(2)5[cos(5⋅π4)+isin(5⋅π4)] (1+ i)5=42[cos(5π4)+isin(5π4)] (1+i)5=42[−22+i(−22)] (1+i)5=−4−4i
Нахождение корней комплексных чисел в полярной форме
Чтобы найти n -й корень комплексного числа в полярной форме, мы используем n-й
Корневая теорема или Теорема де Муавра и возведите комплексное число в степень с рациональным показателем. Есть несколько способов представить формулу для нахождения n-го
Есть несколько способов представить формулу для нахождения n-го
корня комплексных чисел в полярной форме.
Теорема *n*th о корне
Чтобы найти n-й
корень комплексного числа в полярной форме, используйте формулу, представленную в виде
z1n=r1n[cos(θn+2kπn)+isin(θn+2kπn)]
где k=0, 1, 2, 3, . . . , n−1.
Прибавляем 2kπn
к θn
, чтобы получить периодические корни.
Нахождение *n*го корня комплексного числа
Вычисление кубических корней z=8(cos(2π3)+isin(2π3)).
Имеем
z13=813[cos(2π33+2kπ3)+isin(2π33+2kπ3)]z13=2[cos(2π9+2kπ3)+isin(2π9+2kπ3)]
Будет три корня: k=0, 1, 2.
Когда k=0,
имеем
z13=2(cos(2π9)+isin(2π9))
Когда k=1,
имеем
z13=2[cos(2π9+6π9)+isin(2π9+6π9) ] Добавьте 2(1)π3 к каждому углу. (2π9+12π9)]Добавить 2(2)π3 к каждому углу.z13=2(cos(14π9)+isin(14π9))
Не забудьте найти общий знаменатель, чтобы упростить дроби в подобных ситуациях. Для k=1,
Для k=1,
угловое упрощение равно
2π33+2 (1) π3 = 2π3 (13) +2 (1) π3 (33) = 2π9+6π9 = 8π9
Найдите четыре корня четвертой степени из 16(cos(120°)+isin(120°)).
z0=2(cos(30°)+isin(30°))z1=2(cos(120°)+isin(120°))z2=2(cos(210°)+isin(210°)) z3=2(cos(300°)+isin(300°))
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики работы с полярными формами комплексных чисел.
- Произведение и частное комплексных чисел в тригонометрической форме
- Теорема де Муавра
Ключевые понятия
- Комплексные числа в форме
a+bi
наносятся на комплексную плоскость аналогично тому, как прямоугольные координаты наносятся на прямоугольную плоскость. Пометьте ось x- как реальную ось , а ось y- как воображаемую ось . См. [ссылка].
- Абсолютное значение комплексного числа совпадает с его величиной. Это расстояние от начала до точки:
\|z\|=a2+b2.

См. [ссылка] и [ссылка].
- Чтобы записать комплексные числа в полярной форме, мы используем формулы
х=rcos θ, y=rsin θ,
и
г=х2+у2.Затем
z=r(cos θ+isin θ).См. [ссылка] и [ссылка].
- Чтобы преобразовать полярную форму в прямоугольную, сначала вычислите тригонометрические функции. Затем умножить на
р.
См. [ссылка] и [ссылка].
- Чтобы найти произведение двух комплексных чисел, умножьте два модуля и сложите два угла. Оцените тригонометрические функции и умножьте, используя распределительное свойство. См. [ссылка].
- Чтобы найти частное двух комплексных чисел в полярной форме, найдите частное двух модулей и разность двух углов. См. [ссылка].
- Чтобы найти степень комплексного числа
zn,
поднять
гв степени
п,и умножить
θна
н.См. [ссылка].
- Поиск корней комплексного числа аналогичен возведению комплексного числа в степень, но с использованием рационального показателя степени.
 См. [ссылка].
См. [ссылка].
Секционные упражнения
Устный
Комплексное число a+bi.
Объясните каждую часть.
a — действительная часть, b — мнимая часть и i=−1
Что представляет абсолютное значение комплексного числа?
Как комплексное число преобразуется в полярную форму?
Полярная форма преобразует действительную и мнимую части комплексного числа в полярную форму, используя x=rcosθ
и y=rsinθ.
Как найти произведение двух комплексных чисел?
Что такое теорема Муавра и для чего она используется?
zn=rn(cos(nθ)+isin(nθ))
Используется для упрощения полярной формы, когда число возведено в степень.
Алгебраический
В следующих упражнениях найдите абсолютное значение заданного комплексного числа.
−7+i
52
2−6i
38
2.2−3.1i
14,45
Для следующих упражнений запишите комплексное число в полярной форме.
8−4i
45цис(333,4°)
−12−12i
3+i
2цис(π6)
Для следующих упражнений преобразуйте комплексное число из полярной формы в прямоугольную.
z=7цис(π6)
732+i72
z=2цис(π3)
z=4cis(7π6)
−23−2i
г=7цис(25°)
z=3cis(240°)
−1,5−i332
z=2cis(100°)
Для следующих упражнений найдите z1z2
.в полярной форме.
z1=23cis(116°); z2=2цис(82°)
43цис(198°)
z1=2цис(205°); z2=22цис(118°)
z1=3cis(120°); z2=14цис(60°)
34цис(180°)
z1=3цис(π4); z2=5цис(π6)
z1=5цис(5π8); z2=15цис(π12)
53цис(17π24)
z1=4цис(π2); z2=2цис(π4)
Для следующих упражнений найдите z1z2
.в полярной форме.
z1=21цис(135°); z2=3цис(65°)
7цис(70°)
z1=2цис(90°); z2=2cis(60°)
z1=15cis(120°); z2=3cis(40°)
5cis(80°)
z1=6цис(π3); z2=2цис(π4)
z1=52цис(π); z2=2цис(2π3)
5цис(π3)
z1=2цис(3π5); z2=3цис(π4)
В следующих упражнениях найдите степени каждого комплексного числа в полярной форме.
Найдите z3
, когда z=5cis(45°).
125 цис (135°)
Найдите z4
, когда z=2cis(70°).
Найдите z2
, когда z=3cis(120°).
9цис(240°)
Найдите z2
, когда z=4cis(π4).
Найдите z4
, когда z=cis(3π16).
цис(3π4)
Найдите z3
, когда z=3cis(5π3).
В следующих упражнениях оцените каждый корень.
Вычислите кубический корень из z
, когда z=27cis(240°).
3цис(80°),3цис(200°),3цис(320°)
Вычислите квадратный корень из z
, когда z=16cis(100°).
Вычислите кубический корень из z
, когда z=32cis(2π3).
243цис(2π9),243цис(8π9),243цис(14π9)
Вычислите квадратный корень из z
, когда z=32cis(π).
Вычислите кубический корень из z
, когда z=8cis(7π4).
22цис(7π8),22цис(15π8)
Графический
Для следующих упражнений нанесите комплексное число на комплексную плоскость.
−3−3i

−1−5i

2i

6−2i

1−4i

Технология
Для следующих упражнений найдите все ответы, округленные до сотых.
Используйте функцию прямоугольного преобразования в полярную на графическом калькуляторе, чтобы преобразовать 5+5i
в полярную форму.
Используйте функцию преобразования прямоугольной в полярную на графическом калькуляторе, чтобы изменить 3−2i
в полярную форму.
3,61e−0,59i
Используйте функцию прямоугольного преобразования в полярную на графическом калькуляторе, чтобы преобразовать −3−8i
в полярную форму.
Используйте функцию преобразования полярной формы в прямоугольную на графическом калькуляторе, чтобы преобразовать 4cis(120°)
в прямоугольную форму.
−2+3,46i
Используйте функцию преобразования полярной формы в прямоугольную на графическом калькуляторе, чтобы преобразовать 2cis(45°)
в прямоугольную форму.
Используйте функцию преобразования полярных координат в прямоугольные на графическом калькуляторе, чтобы изменить 5cis(210°)
прямоугольной формы.
−4,33−2,50i
Глоссарий
- аргумент
- угол, связанный с комплексным числом; угол между линией от начала до точки и положительной действительной осью
- Теорема де Муавра Формула
- , используемая для нахождения
nth
степени или n -й корней комплексного числа; утверждает, что для положительного целого числа
n,znнаходится путем возведения модуля в
nthстепень и умножение углов на
п
- модуль
- абсолютное значение комплексного числа или расстояние от начала до точки
(х, у);
также называется амплитудой
- полярная форма комплексного числа
- комплексное число, выраженное через угол
θ
и его расстояние от начала координат
р;можно найти с помощью формул преобразования
х=rcos θ, y=rsin θ,и
г=х2+у2
Эта работа находится под лицензией Creative Commons Attribution 4.
 0 International License.
0 International License.Вы также можете бесплатно скачать на http://cnx.org/contents/[email protected]
Атрибуция:
- По вопросам, касающимся этой лицензии, обращайтесь по адресу [email protected].
- Если вы используете данный учебник в качестве библиографической ссылки, то цитировать его следует следующим образом: Колледж OpenStax, алгебра и тригонометрия. OpenStax CNX. http://cnx.org/contents/[email protected].
- Если вы распространяете этот учебник в печатном формате, вы должны указать на каждой физической странице следующее указание авторства: «Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]».
- Если вы распространяете часть этого учебника, вы должны сохранять при каждом просмотре страницы в цифровом формате (включая, помимо прочего, EPUB, PDF и HTML) и на каждой физической печатной странице следующее указание авторства:
«Скачать бесплатно на http://cnx.



 0, static_cast<double>(d)}
0, static_cast<double>(d)}
 См. [ссылка].
См. [ссылка].