«Ряды» (Задания 1-16 с указанием правильных ответов)
Математика \ Высшая математика
Страницы работы
11 страниц (Word-файл)
Посмотреть все страницы
Скачать файл
Фрагмент текста работы
«Ряды»
Тесты для самопроверки
1. Необходимый признак сходимости ряда.
|
Теорема (необходимый признак сходимости). Если ряд сходится, то . Следствие (достаточное условие расходимости ряда). Если , то ряд расходится. Важно! Если , то вывода о сходимости или расходимости ряда сделать нельзя. |
Задание 1. Среди следующих рядов
Среди следующих рядов
1) ; 2) ; 3) ;
4) ; 5) ; 6) , найдите те, для которых справедливы утверждения:
а) ; б) ;
в) ряд сходится; г) ряд расходится.
Правильные ответы:
|
№ ряда |
1 |
2 |
3 |
4 |
5 |
6 |
|
0 |
0 |
0 |
||||
|
сходится или расходится |
неизвестно |
расходится |
расходится |
неизвестно |
неизвестно |
расходится |
2.
|
Теорема (признак сравнения). Пусть и два знакоположительных ряда таких, что . Тогда, если 1) ряд сходится, то сходится и ряд ; 2) ряд расходится, то расходится и ряд . Важно! При решении использовать: а) ряд Дирихле , который сходится, если и расходится, если ; б) геометрическую прогрессию , которая является сходящимся рядом, если и расходящимся рядом, если . |
Задание 2. Найти верные оценки для :
2.1) ; 2.2) ;
2.3) ; 2.4) ; 2.5) .
Варианты ответов
|
1 |
2 |
3 |
|
|
2. |
|||
|
2.2 |
|||
|
2.3 |
|||
|
2.4 |
|||
|
2. |
Правильные ответы (номера):
|
2.1 |
2.2 |
2.3 |
2.4 |
2.5 |
|
1 |
2 |
2 |
3 |
1 |
Задание 3. Используя признак сравнения, среди рядов, приведенных в задании 2,
найти сходящиеся и расходящиеся.
Используя признак сравнения, среди рядов, приведенных в задании 2,
найти сходящиеся и расходящиеся.
Правильные ответы:
|
сходится |
1, 3, 5 |
|
расходится |
2, 4 |
|
Теорема (предельный признак сравнения). Пусть и два знакоположительных ряда. Если существует конечный, отличный от 0, предел , то ряды сходятся или расходятся одновременно. |
Задание 4. Используя предельный признак сравнения, исследовать на сходимость ряды с общими членами :
4.1) ; 4.2) ;
4.3) ; 4. 4)
.
4)
.
Указание: Использовать для сравнения подходящий ряд Дирихле.
Правильные ответы:
|
№ |
С каким рядом сравнили |
Сходится или расходится |
|
|
4.1 |
сходится |
||
|
4.2 |
расходится |
||
|
4. |
расходится |
||
|
4.4 |
сходится |
|
Теорема (признак сравнения в эквивалентной форме). Пусть ряд с положительными членами и . Тогда при ряд сходится, а при ряд расходится. Важно! При решении нужно использовать таблицу эквивалентных функций:
если — бесконечно малая
функция. А также тот факт, что . |
Задание 5. Используя признак сравнения в эквивалентной форме, найти для и сделать вывод о сходимости следующих рядов:
5.1) ; 5.2) ; 5.3) ; 5.4) ; 5.5) .
Варианты ответов:
1) , сходится; 2) , сходится;
3) , сходится; 4) , расходится;
5) , сходится; 6) , расходится;
7) , расходится; 8) , сходится.
Правильные ответы (номера):
|
|
5.2 |
5.3 |
5.4 |
5. |
|
6 |
5 |
8 |
7 |
4 |
3. Признак Даламбера.
|
Теорема (признак Даламбера). Пусть ряд с положительными членами и существует . Тогда ряд сходится при и расходится при . Важно! Если , то вывода о сходимости ряда сделать нельзя. |
Задание 6. Найти , если
6.1) ; 6.2) ;
6.3) ; 6.4) ;
6.5) ; 6.6) .
Варианты ответов
|
6. |
|||
|
6.2 |
|||
|
6.3 |
|||
|
6.4 |
|||
|
6. |
|||
|
6.6 |
Правильные ответы (номера):
|
6.1 |
6.2 |
6.3 |
6.4 |
6.5 |
6. |
|
2 |
1 |
3 |
1 |
2 |
3 |
Задание 7. Исследовать сходимость рядов из задания 6, вычисляя и применяя признак Даламбера.
Варианты ответов:
7.1) , сходится; 7.2) , расходится;
7.3) , сходится; 7.4) , расходится;
7.5) , сходится; 7.6) , вывод сделать нельзя;
7.7) , расходится; 7.8) , сходится.
Правильные ответы (номера):
|
7. |
7.2 |
7.3 |
7.4 |
7.5 |
7.6 |
|
3 |
5 |
6 |
2 |
1 |
7 |
4. Радикальный признак Коши.
|
Теорема (признак Коши). Пусть ряд с
положительными членами и существует . Важно! Если , то вывода о сходимости ряда сделать нельзя. Важно! и . |
Задание 8. Вычислить и, используя признак Коши, исследовать сходимость следующих рядов:
8.1) ; 8.2) ;
8.3) ; 8.4) ; 8.5) .
Варианты ответов:
8.1) , сходится; 8.2) , расходится;
8.3) , сходится; 8.4) , сходится; 8.5) , сходится;
8.6) , расходится; 8.7) , сходится.
Правильные ответы (номера):
|
8.1 |
8.2 |
8.3 |
8.4 |
8. |
|
6 |
4 |
3 |
2 |
1 |
5. Интегральный признак Коши.
|
Теорема (интегральный признак Коши). Если члены знакоположительного ряда могут быть представлены как числовые значения некоторой монотонно-убывающей на функции так, что , , то: 1) если сходится, то сходится и ряд , 2) если расходится, то расходится и ряд . |
Задание 9. Применить интегральный признак для исследования сходимости рядов:
9.1) ; 9. 2)
;
2)
;
9.3) ; 9.4) .
Указать вид первообразной для и .
Варианты ответов
1) , расходится;
2) , сходится;
3) , сходится;
4) , сходится.
Правильные ответы (номера):
|
9.1 |
9.2 |
9.3 |
9.4 |
|
2 |
4 |
1 |
3 |
6. Знакочередующие ряды. Признак Лейбница. Знакопеременные ряды.
|
Теорема (признак Лейбница). Знакочередующийся ряд сходится, если: 1) последовательность абсолютных величин членов ряда монотонно убывает, т.е. ; 2) общий член ряда стремится к нулю: . При этом сумма S ряда удовлетворяет неравенству: . Важно! Если , то погрешность при этом меньше, чем . Если члены ряда принимают положительные и отрицательные значения, то он называется знакопеременным. Определение. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд , составленный из модулей его членов и условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится. Важно! Для исследования абсолютной сходимости к рядам можно применять все признаки сходимости знакоположительных рядов. Важно! Признак Лейбница — это признак условной сходимости рядов. |
Задание 10. Даны ряды:
Даны ряды:
10.1) ; 10.2) ; 10.3) ;
10.4) ; 10.5) ; 10.6) ;
10.7) ; 10.8) .
Выберите из них те, которые удовлетворяют условиям:
а) знакочередующиеся;
б) знакопеременные;
в) знакоположительные.
Правильные ответы (номера):
|
а |
б |
в |
|
1, 3, 7 |
2, 6, 8 |
4, 5 |
Задание 11. Для знакочередующихся рядов из задания 10 проверить выполнены ли условия признака Лейбница.
Правильные ответы:
1) да; 3) да; 7)
нет.
Задание 12. Из знакочередующихся и знакопеременных рядов задания 10 найти:
а) абсолютно сходящиеся;
б) условно сходящиеся;
в) расходящиеся.
Правильные ответы:
а) абсолютно сходятся: 10.1; 10.2; 10.6;
б) условно сходятся: 10.3;
в) расходятся: 10.7; 10.8.
Задание 13. Вычислить сумму S ряда с точностью:
1) 0,15; 2) 0,02; 3) 0,01.
Сколько n членов ряда при этом надо взять?
Варианты ответов:
1) ; 2) ; 3) .
Правильные ответы (номера):
|
13.1 |
13.2 |
13.3 |
|
3 |
1 |
2 |
7. Степенные ряды.
Степенные ряды.
|
Степенным рядом называется ряд вида (1) или вида , (2) где - постоянное число. |
|
Теорема Абеля. Если степенной ряд (1) сходится при , то он абсолютно сходится при всех х : . Если ряд (1) расходится при , то он расходится при всех х : . Из теоремы Абеля вытекает, что степенной ряд (1)
сходится в интервале (-R, R) и расходится вне этого интервала. Число R
называется радиусом сходимости. При R = 0 ряд (1) сходится в единственной точке
х = 0, при ряд (1) сходится
при . На концах
интервала сходимости, т.е. при вопрос
о сходимости решается для каждого ряда отдельно. Для ряда (2) интервал сходимости имеет вид: . Если , то ряд (2) сходится в точке . Формулы для нахождения радиуса сходимости имеют вид: . |
Задание 14. Даны степенные ряды:
14.1) ; 14.2) ; 14.3) ;
14.4) ; 14.5) ; 14.6) .
Найти: а) радиус сходимости; б) интервал сходимости; в) область сходимости.
Варианты ответов:
а) радиус сходимости:
1) ; 2) ; 3) ; 4) ; 5) ; 6) .
б) интервал сходимости:
1) ; 2) ; 3) точка ; 4) ; 5) ; 6) ; 7) .
в) область сходимости:
1) ; 2) ; 3) ; 4) ; 5) ;
6) ; 7) ; 8) ; 9) точка .
Правильные ответы (номера):
|
14. |
14.2 |
14.3 |
14.4 |
14.5 |
14.6 |
|
|
а |
4 |
2 |
6 |
1 |
6 |
3 |
|
б |
7 |
1 |
5 |
3 |
6 |
4 |
|
в |
1 |
5 |
8 |
9 |
3 |
7 |
8. Применение степенных рядов.
Применение степенных рядов.
Запишите разложения в ряд Тейлора некоторых элементарных функций: .
Задание 15. Зная разложение в степенной ряд элементарных функций, разложить в ряд Маклорена следующие функции:
15.1) ; 15.2) ;
15.3) ; 15.4) .
Варианты ответов:
1) ; 2) ;
3) ; 4) .
Правильные ответы (номера):
|
15.1 |
15.2 |
15.3 |
15.4 |
|
3 |
1 |
2 |
4 |
Задание 16. Найти разложение в ряд первообразных функций
из задания 15,
проинтегрировав соответствующие степенные ряды их в пределах от 0 до х.
Найти разложение в ряд первообразных функций
из задания 15,
проинтегрировав соответствующие степенные ряды их в пределах от 0 до х.
Варианты ответов:
16.1) ;
16.2) ;
16.3) ;
16.4) .
Правильные ответы (номера):
|
16.1 |
16.2 |
16.3 |
16.4 |
|
2 |
4 |
3 |
1 |
Для того, чтобы найти сумму ряда с заданной степенью точности
Похожие материалы
Информация о работе
Скачать файл
Ошибка
Перейти к основному содержанию
Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)
Извините, не удалось найти запрашиваемый Вами файл
Подробнее об этой ошибке
Перейти на.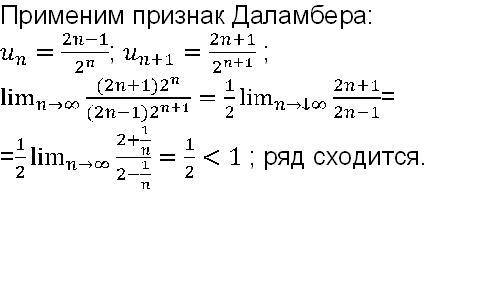 ..
Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ). Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра.
..
Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ). Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра. Линейные операции над векторами»Лекционный материал по теме «Скалярное, векторное и смешанное произведения векторов»Примеры решения задач по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Скалярное, векторное и смешанное произведения векторов»ВЕКТОРНАЯ АЛГЕБРАВекторная алгебра и аналитическая геометрияПрезентация по теме «Векторная алгебра»Векторная алгебра.Аналитическая геометрияТеоретический материал по теме «Метод координат на плоскости и в пространстве»Лекционный материал по теме «Прямая на плоскости»Лекционный материал по теме «Кривые второго порядка»Лекционный материал по теме «Прямая в пространстве»Лекционный материал по теме «Плоскость в пространстве»Лекционный материал по теме «Поверхности второго порядка»Примеры решения задач по теме «Прямая на плоскости»Примеры решения задач по теме «Кривые второго порядка»Примеры решения задач по темам «Прямая и плоскость в пространстве»АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВекторная алгебра и аналитическая геометрияСправочный материал «Прямая на плоскости»Справочный материал «Кривые второго порядка»Справочный материал «Прямая и плоскость в пространстве»Линейная алгебра для экономистовПрезентация по теме «Прямая на плоскости»Презентация по теме «Уравнения плоскости и прямой в пространстве»▶ Виртуальный тренажер «Прямая на плоскости» 👨🎓Введение в анализНачала анализаЛекционный материал по теме «Множества, функции, основные характеристики функций.
Линейные операции над векторами»Лекционный материал по теме «Скалярное, векторное и смешанное произведения векторов»Примеры решения задач по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Скалярное, векторное и смешанное произведения векторов»ВЕКТОРНАЯ АЛГЕБРАВекторная алгебра и аналитическая геометрияПрезентация по теме «Векторная алгебра»Векторная алгебра.Аналитическая геометрияТеоретический материал по теме «Метод координат на плоскости и в пространстве»Лекционный материал по теме «Прямая на плоскости»Лекционный материал по теме «Кривые второго порядка»Лекционный материал по теме «Прямая в пространстве»Лекционный материал по теме «Плоскость в пространстве»Лекционный материал по теме «Поверхности второго порядка»Примеры решения задач по теме «Прямая на плоскости»Примеры решения задач по теме «Кривые второго порядка»Примеры решения задач по темам «Прямая и плоскость в пространстве»АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВекторная алгебра и аналитическая геометрияСправочный материал «Прямая на плоскости»Справочный материал «Кривые второго порядка»Справочный материал «Прямая и плоскость в пространстве»Линейная алгебра для экономистовПрезентация по теме «Прямая на плоскости»Презентация по теме «Уравнения плоскости и прямой в пространстве»▶ Виртуальный тренажер «Прямая на плоскости» 👨🎓Введение в анализНачала анализаЛекционный материал по теме «Множества, функции, основные характеристики функций.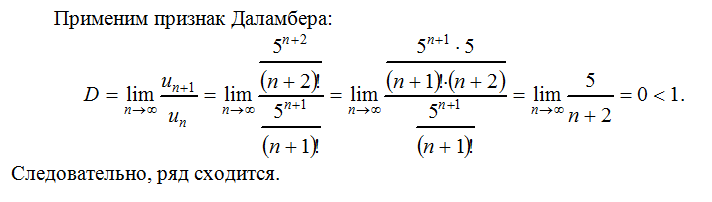 Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления.
Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления. Правила Лопиталя»Лекционный материал по теме «Формулы Тейлора и Маклорена»Лекционный материал по теме «Приложения дифференциального исчисления»Примеры решения задач по теме «Дифференциальное исчисление функций одной переменной»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙТест «Основные правила и формулы дифференцирования»Тест «Дифференциальное исчисление функций одной переменной»Основы дифференцирования. Часть 1Основы дифференцирования. Часть 2Основы дифференцирования. Часть 3Приложения производной Исследование функций, Примеры решения задачПрименение производных при решении экономических задачИнтегральное исчисление функции одной переменнойЛекционный материал по теме «Неопределенный интеграл»Лекционный материал по теме «Определенный интеграл»Практическое занятие 1. Непосредственное интегрирование (неопределённый интеграл)Практическое занятие 2. Интегрирование заменой переменной (неопределённый интеграл)Практическое занятие 3. Интегрирование по частям. Интегрирование выражений, содержащих квадратный многочлен (неопределённый интеграл)Практическое занятие 4.
Правила Лопиталя»Лекционный материал по теме «Формулы Тейлора и Маклорена»Лекционный материал по теме «Приложения дифференциального исчисления»Примеры решения задач по теме «Дифференциальное исчисление функций одной переменной»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙТест «Основные правила и формулы дифференцирования»Тест «Дифференциальное исчисление функций одной переменной»Основы дифференцирования. Часть 1Основы дифференцирования. Часть 2Основы дифференцирования. Часть 3Приложения производной Исследование функций, Примеры решения задачПрименение производных при решении экономических задачИнтегральное исчисление функции одной переменнойЛекционный материал по теме «Неопределенный интеграл»Лекционный материал по теме «Определенный интеграл»Практическое занятие 1. Непосредственное интегрирование (неопределённый интеграл)Практическое занятие 2. Интегрирование заменой переменной (неопределённый интеграл)Практическое занятие 3. Интегрирование по частям. Интегрирование выражений, содержащих квадратный многочлен (неопределённый интеграл)Практическое занятие 4.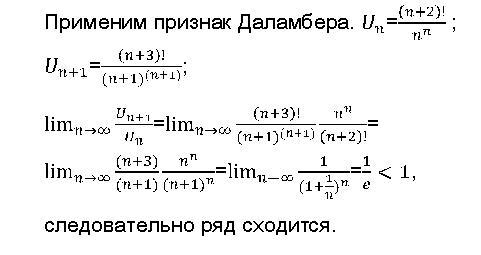 Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1.
Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1. Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий.
Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий.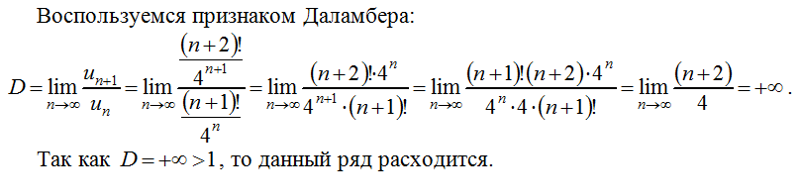 Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности.
Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности. Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика».
Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика». Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа.
Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа. Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)
Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)
 {2n + 1}}} \right)\ ;}}} \] 92}} \право)\;}}} \право| знак равно \mathop {\lim}\limits_{n \to \infty} \left| {\dfrac{{11(n + 1)}}{{(n + 2)49}}} \right| $
{2n + 1}}} \right)\ ;}}} \] 92}} \право)\;}}} \право| знак равно \mathop {\lim}\limits_{n \to \infty} \left| {\dfrac{{11(n + 1)}}{{(n + 2)49}}} \right| $ Разделив числитель и знаменатель на $ n $ для решения предела, мы получим
$ k = \mathop {\lim }\limits_{n \to \infty} \left| {\dfrac{{11\left( {1 + \dfrac{1}{n}} \right)}}{{\left( {1 + \dfrac{2}{n}} \right)49}}} \право| $
Подставив пределы, получим
$ k = \left| {\dfrac{{11(1 + 0)}}{{(1 + 0)49}}} \right| = \dfrac{{11}}{{49}} < 1 $
Так как $ k < 1 $ и мы знаем, что в тесте отношения, если предел оказывается меньше единицы, то ряд сходится. 9{2n + 1}}} \right)\;}}} \] сходится.
Примечание : В этом вопросе мы дали общий термин ряда, так что мы ставим номера терминов, которые мы хотим, и получаем термины напрямую. Но в целом вы будете заниматься реальной серией, так что не бойтесь в это время и сначала найдите общий термин серии, а затем приступайте к тесту.
Примеры испытаний отношений — Статистические инструкции
Расчетные определения >
Содержание:
- Определение соотношения и формула
- Примеры испытаний соотношения
- Родственные термины
Что такое тест соотношения?
Тест отношения говорит вам, сходится ли ряд (т. е. устанавливается на определенное число) или расходится (не устанавливается на определенное число). Этот тест также известен как тест отношения Д’Аламбера (Жан ле Рон д’Аламбер приписывают первую публикацию теста) или как тест отношения Коши 9.0071 . Это основной инструмент для расчета радиуса сходимости.
е. устанавливается на определенное число) или расходится (не устанавливается на определенное число). Этот тест также известен как тест отношения Д’Аламбера (Жан ле Рон д’Аламбер приписывают первую публикацию теста) или как тест отношения Коши 9.0071 . Это основной инструмент для расчета радиуса сходимости.
Проверка соотношения особенно полезна для рядов с факториалами (!). Вы можете использовать тест, когда:
- Каждый термин является действительным числом или комплексным числом и
- a n отлично от нуля, когда n велико.
Для проверки коэффициента необходимо найти предел «L». Как только вы нашли L, вы можете выяснить, сходится ли ряд с или расходится с . Тест соотношения аналогичен тесту сравнения пределов, но используется только тогда, когда сравниваемый ряд равен 1:9.0003
- Если отношение меньше 1, то ряд сходится абсолютно.
- Если отношение больше 1, ряд расходится.

- Если отношение равно 1, то ряд может быть расходящимся, условно сходящимся или абсолютно сходящимся.
Если отношение равно 1, то тест в основном ничего не говорит вам о конвергенции или дивергенции. Причина того, что тест в этом случае неубедителен, заключается в том, что даже два ряда с точно такими же последовательными отношениями могут иметь разные свойства сходимости, когда предел последовательных отношений равен 1. Предел 1 показывает, что члены не ведут себя как геометрический ряд в пределе. Если вы все-таки получили ряд с отношением, равным 1, то выберите другой тест на сходимость.
Формула
Тест отношения представлен алгебраически как:
Приведенная выше формула говорит вам:
- Сформируйте отношение n + 1 /a n ,
- Возьмите абсолютное значение отношения и предела при n → ∞.
- Сравните L с 1 и определите, сходится ряд или расходится.
Пример вопроса: Сходится или расходится следующая последовательность?
Эта последовательность имеет символ суммирования (Σ) и факториал (!). Если вы не уверены, что это такое, вы можете сначала прочитать об обозначении суммирования и факториалах.
Если вы не уверены, что это такое, вы можете сначала прочитать об обозначении суммирования и факториалах.
Шаг 1: Сформируйте коэффициент, следуя формуле.
- Знаменатель (a n ) — исходная последовательность (та, что указана в вопросе).
- В числителе (a n + 1 ) вы добавляете «+1» везде, где видите n.
- Не забудьте добавить символ абсолютного значения.
Если вы не знаете, как это сделать, на следующем рисунке показаны шаги:
Шаг 2. Найдите предел шага 1, когда n стремится к бесконечности (n → ∞). Здесь у вас могут возникнуть трудности, так как это требует некоторых сильных навыков алгебры (на данный момент математические вычисления не нужны!). Вот основные алгебраические шаги:
Что касается предела, обратите внимание, что мы ищем предел, когда n стремится к бесконечности. Чем больше n, тем больше будет знаменатель. Это означает, что он приближается к 2/∞, что по существу равно нулю. Следовательно, предел равен нулю.
Это означает, что он приближается к 2/∞, что по существу равно нулю. Следовательно, предел равен нулю.
Шаг 3: Сравните свой ответ на шаге 2 с ответом на шаг 1 и определите, сходится или расходится ряд. Поскольку предел равен 0, правила проверки отношения говорят, что если отношение меньше 1,, ряд сходится абсолютно .
Тест соотношения
Посмотрите это видео на YouTube.
Связанные термины
- Коэффициент частоты (эпидемиология): сравнивает частоту событий, происходящих в разное время.
- Шкала отношения: шкала измерения, в которой разница между значениями имеет значение, и ноль также имеет значение.
Примеры проверки отношений: Ссылки
[1] Определение интервала сходимости.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Примеры тестов на соотношение» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.

 1
1 5
5

 5
5 1
1 5
5 6
6 1
1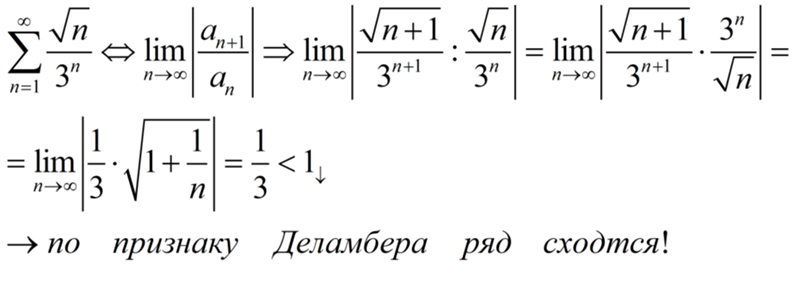 Тогда ряд сходится при и расходится при .
Тогда ряд сходится при и расходится при . 5
5

 1
1