Урок на тему: «Схема исследования функции». | План-конспект урока (алгебра, 10 класс) по теме:
Урок на тему: Схема исследования функции (1 курс, 2 ч)
Цели: повторить схему исследования функции для построения ее графика и рассмотреть исследование функции с помощью производной; упражнять учащихся в исследовании функции с помощью производной и построении графиков функций; развивать навыки исследования функций и построения графиков; закрепить знания нахождения промежутков возрастания и убывания функции, экстремумов функции с помощью производной
Ход урока:
1. Повторение пройденного материала
- Повторить схему исследования функции.
- Исследовать функции на возрастание (убывание) и на экстремум удобно проводить с помпощью производной.
2. Изучение нового материала
- Разобрать по учебнику пример 1. Пояснить осоставление таблицы и построения графика на рис 111.
- Исследовать функцию и построить ее график: у= х4/4-х3/3- х2.

Р е ш е н и е.
1) Область определения — D(y)=R
2) функция не является ни четной, ни нечетной, ни периодической;
3) найдем точки пересечения графика с осью ОХ (т. е. нули функции): х4/4-х3/3- х2=0,
3х4-4х3-12х2=0, х2(3х2-4х-12)=0; х1=0; х2≈ -1,4; х3≈2,8.
Пересечение с осью ОУ: х=0,у=0.
Возьмем также две дополнительные точки: у(1)= — 13/12; у(3)=9/4;
4) находим производную: у’ = х3-х2-2х=х(х2-х-2)=х(х+1)(х-2).
у’=0, х(х+1)(х-2) =0, х=0, х= -1, х=2;
5) найденные критические точки разбивают числовую прямую на четыре промежутка:
(-∞;-1), (-1;0), (0;2), (2;+∞).
Составим таблицу:
х | (-∞;-1) | -1 | (-1;0) | 0 | (0;2) | 2 | (2;+∞) |
f ‘(x) | — | 0 | + | 0 | — | 0 | + |
f(x) | -5/12 | 0 | -8/3 | ||||
убывает | min | возрастает | max | yбывает | min | возрастает |
6) Строим график.
3. Закрепление изученного материала
1. (Устно). Определите по следующим данным характер монотонности функции и указанных промежутках и вид экстремума:
а)
х | (-∞;-1) | -1 | (-1;0) | 0 | (0;+∞) |
f ‘(x) f(x) | — | 0 -4 | + | 0 4,5 | — |
б)
х | (-10;2) | 2 | (2;7) | 7 | (7;10) |
f ‘(x) f(x) | + | 0 5 | — | 0 -3 | — |
в)
х | (-4;0) | 0 | (0;3) | 3 | (3;7) | 7 | (7;+∞) |
f ‘(x) f(x) | + | 0 -3 | — | 0 -4 | + | 0 6 | — |
2. Внесите необходимые данные, при которых в указанных точках функция имела бы заданные виды экстремумов:
Внесите необходимые данные, при которых в указанных точках функция имела бы заданные виды экстремумов:
х | (-7;-2) | -2 | (-2;3,5) | 3,5 | (3,5;+∞) |
f ‘(x) f(x) | 0 max | 0 min |
3. Назовите промежутки возрастания (убывания) и вид каждого из экстермумов функции. Изобразите эскиз графика функции, если, исследуя ее с помощью производной, получили данные:
х | (-∞;-5) | -5 | (-5;0) | 0 | (0;3) | 3 | (3;7) |
f ‘(x) f(x) | + | 0 3 | — | 0 0 | _ | 0 -2 | + |
4. Постройте эскиз графика функции у=ах2, если: а)а>0; б)a
Постройте эскиз графика функции у=ах2, если: а)а>0; б)a
5. Найдите экстремум квадратичной функции у=ах2+bx+c (a≠0), если а)а>0; б)a
6. Изобразите эскиз графика функции у=ах2+bx+c (a≠0), если в левой полуокрестности точки х0 (х0- абсцисса вершины параболы) у’>0, а в правой полуокрестности х0 у’ 0.
7. Определите (с использованием производной) вершину параболы и изобразите эскиз графика функций: а)у=х2-3х+2; б)у= -х2-4х+5; в) у=3х2-х-1; г)у= 2х2+5х-3.
4. Самостоятельная работа (СО)
Карточка — задания №1
Вариант 1. Исследуйте функцию у=х2 +2х-8 с помощью производной и постройте ее график.
П л а н р е ш е н и я:
1)Установите область определения функции.
2) Найдите производную функции.
3) Определите критические точки функции.
4) Определите знак производной в каждом из промежутков, на которые критические точки разбивают область определения.
5) Запишите промежутки возрастания и убывания функции.
6) Найдите точку экстремума функции и значение функции в ней.
7) Постройте график функции.
Карточка- задания№2
Вариант 2. Исследуйте функцию у=х3/9 +х2 с помощью производной и постройте ее график. П л а н р е ш е н и я:
1) Установите область определения функции.
2) Найдите производную функции.
3) Определите критические точки функции.
4) Определите знак производной в каждом из промежутков, на которые критические точки разбивают область определения.
5) Запишите промежутки возрастания и убывания функции.
6) Найдите точку экстремума функции и значение функции в них.
7) Постройте график функции.
Карточка — задания №3
Карточка- задания№2
Вариант 3. Исследуйте функцию у=х2-х3/6 с помощью производной и постройте ее график. П л а н р е ш е н и я:
1) Установите область определения функции.
2) Определите критические точки функции.
3) Определите знак производной в каждом из промежутков, на которые критические точки разбивают область определения.
4) Запишите промежутки возрастания и убывания функции.
5) Найдите точку экстремума функции и значение функции в них.
6) Постройте график функции.
Карточка — задания №4
Вариант 4. Исследуйте функцию у=х4/4-х2 с помощью производной и постройте ее график. П л а н р е ш е н и я:
1) Установите область определения функции.
2) Определите критические точки функции.
3)Определите знак производной в каждом из промежутков, на которые критические точки разбивают область определения.
4) Запишите промежутки возрастания и убывания функции.
5) Найдите точку экстремума функции и значение функции в них.
6) Постройте график функции.
5. Математический диктант:
Вариант 1. Изобразите схематично график непрерывной функции y=f(x), обладающей следующими свойствами:
х | (-∞;-2) | -2 | (-2;1) | 1 | (1;+∞) |
f(x) | 4 max | -3 min |
Вариант 2. Изобразите схематично график непрерывной функции y=f(x), обладающей следующими свойствами:
Изобразите схематично график непрерывной функции y=f(x), обладающей следующими свойствами:
х | (-∞;-3) | -3 | (-3;2) | 2 | (2;+∞) |
f(x) | 6 max | 1 min |
6. Итог урока.
в программе | |
OХ |
Поиск материала «Исследование функций с помощью производной и построение графиков, 65 задач с подробным решением, Каминкова И.В., 2021» для чтения, скачивания и покупки
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Скачать Каминкова И.В. Исследование функций с помощью.
 ..
..Каминкова И.В. Исследование функций с помощью производной и построение графиков. 65 задач с подробным решением. Файл формата pdf. размером 2,55 МБ.
В сборнике представлены 65 задач с подробным решением по теме «Исследование функций с помощью производной и построение графиков». Сборник будет полезен абитуриентам для подготовки к вступительным экзаменам по профильной математике, а также студентам младших курсов при изучении основ математического анализа.
eruditor.io
- Полное исследование функции и построение графика
Примеры решений по исследованию функции. Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении! Задача 1.

www.MatBuro.ru
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- Применение производной к исследованию функции…
Критические точки и экстремумы функции. Достаточное условие существования экстремума. Построение графиков функции с помощью производной. Задачи на экстремумы. Оптимизации. Что такое исследование функции. Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная {рис.
70).
www.evkova.org
- Исследование функции и построение графика функции
5. Промежутки возрастания и убывания функции. Для определения вычисляем первую производную, приравниваем ее к нулю. Полученные нули и точки области определения выносим на числовую прямую. Для каждого интервала определяем знак производной.
Посмотреть подробное решение/ Кликнуть мышкой. Пример исследования функции и построения графика №2. Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
matecos.ru
- Презентация по математике «Построение графика функции…»
НИПКиПРО КАФЕДРА МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ Проект урока по теме: «Построение графика функции методом ее исследования с помощью производной» г.
 Новосибирск 2008.
Новосибирск 2008.Актуальность Данная тема является очень важной и значимой, т. к. в материалах ЕГЭ большое внимание уделяется заданиям, связанным с исследованием функции с помощью графика, с построением графика заданной функции. Успешное изучение этой темы поможет вам хорошо сдать государственный экзамен по математике.
ppt4web.ru
- Открытый урок «Исследование функции с помощью…»
Тема нашего урока «Исследование функции с помощью производной и построение графиков функций». Давайте запишем дату и тему урока в тетрадь. Теме «Исследование функции» уделяется большое внимание в курсе математики, потому, что функция, её график часто встречается в жизни, в профессиональной среде, в работе врачей, юристов и других научных сферах. Одна из основных задач исследования функции – это нахождение промежутков возрастания и убывания.
multiurok.
 ru
ru - Исследование функции. Построение графика. — YouTube
О сервисе Прессе Авторские права Связаться с нами Авторам Рекламодателям Разработчикам Условия использования Конфиденциальность Правила и безопасность Как работает YouTube Тестирование новых функций.
www.youtube.com
- Презентация по математике «Построение графика…»
НИПКиПРО КАФЕДРА МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ Проект урока по теме: «Построение графика функции методом ее исследования с помощью производной» г. Новосибирск 2008.
Цели урока Обобщить и закрепить свои знания и умения при построении графика функции с помощью ее исследования. Применить (ИКТ) новые информационные технологии для проверки результатов построения с помощью программы MathCAD Воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели.
ppt4web.
 ru
ru - Исследование функций с помощью производных
Горизонтальная асимптота является частным случаем наклонной асимптоты: если то наклонная асимптота вырождается в горизонтальную при условии, что Если параметр то горизонтальной асимптоты нет. Полная схема исследования функции с помощью производных.
Пример: Исследовать и построить схематичный график функции. Решение: Используя схему исследования графика функции с помощью производных, найдем: 1. 2. Найдем точки пересечения графика функции с координатными осями.
www.evkova.org
- Открытый урок «Исследование функции с помощью…»
Тема нашего урока «Исследование функции с помощью производной и построение графиков функций». Давайте запишем дату и тему урока в тетрадь. Теме «Исследование функции» уделяется большое внимание в курсе математики, потому, что функция, её график часто встречается в жизни, в профессиональной среде, в работе врачей, юристов и других научных сферах.
 Одна из основных задач исследования функции – это нахождение промежутков возрастания и убывания. Такое исследование легко провести с помощью производной.
Одна из основных задач исследования функции – это нахождение промежутков возрастания и убывания. Такое исследование легко провести с помощью производной.multiurok.ru
- Презентация к практическому занятию «Решение задач по…
Презентация предназначена для сопровождения практического занятия. В презентацию включен теоритический материал и задачи на применение производной к исследованию функций. Рассмотрены алгоритмы исследования функций на монотонность, экстремумы, правило нахождения наибольшего и наименьшего значений функции, схема исследования функции и построения ее графика. Подборка задач включает упражнения на исследование функций по алгоритмам и упражнения в формате ЕГЭ.
kopilkaurokov.ru
- Конспект и презентация к уроку по теме « Исследование…»
Это разработка моего открытого урока в 10 классе по теме «Исследование функции с помощью производной и построение графика».
 Разработка содержит презентацию. Целевая аудитория: для 10 класса.
Разработка содержит презентацию. Целевая аудитория: для 10 класса.В помощь учителю. Уважаемые коллеги! Добавьте свою презентацию на Учительский портал и получите бесплатное свидетельство о публикации методического материала в международном СМИ.
www.uchportal.ru
- Пособие для учащихся Исследование функций по…
Поэтому в таких зданиях, где дан график, сразу же нужно обратить своё внимание в условии на том, что дано: график функции или график производной функции? Если это график производной функции, то рассматривать его нужно как бы «отражение» самой функции, которое просто даёт нам информацию об этой функции. Рассмотрим алгоритм решения задания. Задача. На рисунке изображен график у = f′(х) — производной функции f(х), определенной на интервале (–2;21). Ответим на следующие вопросы
nsportal.ru
- Исследование функций с помощью производной
Лисичкин В.
 Л63 Исследование функций с помощью производной / В. Лисичкин. – М. : Чистые пруды, 2005. – 32 с. (Библиотечка «Первого сентября», серия «Математика»). ISBN 5-9667-0054-0 Данная брошюра написана в соответствии с действующей школьной программой. Пособие может быть использовано для самостоятельного изучения, а также при подготовке к выпускному экзамену в традиционной форме, ЕГЭ и вступительным экзаменам в вузы. Краткие теоретические сведения сопровождаются подробными решениями задач.
Л63 Исследование функций с помощью производной / В. Лисичкин. – М. : Чистые пруды, 2005. – 32 с. (Библиотечка «Первого сентября», серия «Математика»). ISBN 5-9667-0054-0 Данная брошюра написана в соответствии с действующей школьной программой. Пособие может быть использовано для самостоятельного изучения, а также при подготовке к выпускному экзамену в традиционной форме, ЕГЭ и вступительным экзаменам в вузы. Краткие теоретические сведения сопровождаются подробными решениями задач.blog.zabedu.ru
- Презентация к практическому занятию « Решение задач по теме…
Презентация предназначена для сопровождения практического занятия. В презентацию включен теоритический материал и задачи на применение производной к исследованию функций. Рассмотрены алгоритмы исследования функций на монотонность, экстремумы, правило нахождения наибольшего и наименьшего значений функции, схема исследования функции и построения ее графика.
 Подборка задач включает упражнения на исследование функций по алгоритмам и упражнения в формате ЕГЭ.
Подборка задач включает упражнения на исследование функций по алгоритмам и упражнения в формате ЕГЭ.kopilkaurokov.ru
- «Исследование функции с помощью производной…»
использовать производную для изучения свойств функций и построения графиков; применять производную для проведения приближенных вычислений, решать задачи прикладного характера на нахождение наибольшего и наименьшего значения; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
kopilkaurokov.ru
- Презентация «Исследование функции с помощью…»
Используя алгоритмы исследования функций с помощью производной, применить их для решения конкретных задач.
 Формировать глубину и оперативность мышления.
Формировать глубину и оперативность мышления.Задача 6. На рисунке изображен график производной функции f (x), определенной на интервале (—7; 5). Найдите точку экстремума функции f (x) на отрезке [-6; 4]. На этом отрезке производная функции один раз обращается в 0 (в точке -3) и при переходе через эту точку меняет знак, откуда ясно, что точка -3 и есть искомая точка экстремума функции на отрезке.
uchitelya.com
- Конспект и презентация к уроку по теме «Исследование функции…»
Это разработка моего открытого урока в 10 классе по теме «Исследование функции с помощью производной и построение графика». Разработка содержит презентацию. Целевая аудитория: для 10 класса.
В помощь учителю. Уважаемые коллеги! Добавьте свою презентацию на Учительский портал и получите бесплатное свидетельство о публикации методического материала в международном СМИ.
www.uchportal.ru
- Практическая работа «Построение графиков функций.
 ..»
..»Понятие производной — одно из важнейших в математике. С помощью производной, учитывая ее механический смысл (скорость изменения некоторого процесса) и геометрический смысл (угловой коэффициент касательной), можно решать самые разнообразные задачи, относящиеся к любой области человеческой деятельности. В частности, с помощью производных стало возможным подробное исследование функций, более точное построение их графиков, нахождение их наибольших и наименьших значений и т.д.
multiurok.ru
- Полное исследование функции и построение графика
Нахождение области определения. Исследование границ ОДЗ и нахождение вертикальных асимптот. Исследование функции и на четность или нечетность. Нахождение возрастания и убывания, точек экстремума. Нахождение промежутков выпуклости и вогнутости функции и точек перегиба. Нахождение горизонтальных и наклонных асимптот. Вычисление значения функции в промежуточных точках.
 Построение графика. Если в задаче необходимо произвести полное исследование функции f(x)=x24x2−1.
Построение графика. Если в задаче необходимо произвести полное исследование функции f(x)=x24x2−1.Zaochnik.com
- Задачи из сборника Кузнецова Л. А.
Задание 7. Провести полное исследование функции и построить её график. Исследование функции проводится в соответствии с планом полного исследования функции. Посмотрите образец такого исследования с построением графика. Прежде, чем Вы начнёте скачивать свои варианты, попробуйте решить задачу по образцу, приведённому ниже для варианта 3. Часть вариантов заархивированы в формате .rar. Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6.
www.kvadromir.com
- Исследование функции — схема, примеры с решением…
Для построения графика функции у = у{х) выясняют особенности поведения функции. Существенную роль при этом играют характерные точки: концевые точки промежутков задания функции, точки разрыва, стационарные точки и точки недифференцируемости функции и се производной и т.
 д. По этим точкам выделяются участки однообразного поведения функции, а именно: промежутки ее непрерывности; промежутки, на которых у'(х) и y»(x) сохраняют знак, что позволяет изучить характер монотонности функции и направление ее выпуклости.
д. По этим точкам выделяются участки однообразного поведения функции, а именно: промежутки ее непрерывности; промежутки, на которых у'(х) и y»(x) сохраняют знак, что позволяет изучить характер монотонности функции и направление ее выпуклости.www.evkova.org
- Методика исследования функций на примере…
На этом уроке мы рассмотрим методику исследования функции, включающую в себя два этапа: исследование без производной и исследование с помощью производной. Данную методику мы применим для исследования и построения графика функции. Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Производная и интеграл». Введение. Методика исследования функции, построение ее графика, включает в себя 2 этапа: 1. Исследование без производной.
interneturok.ru
- Исследование функций с помощью производных с примерами.
 ..
..Горизонтальная асимптота является частным случаем наклонной асимптоты: если то наклонная асимптота вырождается в горизонтальную при условии, что Если параметр то горизонтальной асимптоты нет. Полная схема исследования функции с помощью производных.
Исследовать и построить схематичный график функции. Решение: Используя схему исследования графика функции с помощью производных, найдем: 1. 2. Найдем точки пересечения графика функции с координатными осями.
www.evkova.org
- Практическая работа «Построение графиков функций при…»
Понятие производной — одно из важнейших в математике. С помощью производной, учитывая ее механический смысл (скорость изменения некоторого процесса) и геометрический смысл (угловой коэффициент касательной), можно решать самые разнообразные задачи, относящиеся к любой области человеческой деятельности. В частности, с помощью производных стало возможным подробное исследование функций, более точное построение их графиков, нахождение их наибольших и наименьших значений и т.
 д.
д.multiurok.ru
- Исследование функций с помощью производной
Лисичкин В. Л63 Исследование функций с помощью производной / В. Лисичкин. – М. : Чистые пруды, 2005. – 32 с. (Библиотечка «Первого сентября», серия «Математика»). ISBN 5-9667-0054-0 Данная брошюра написана в соответствии с действующей школьной программой. Пособие может быть использовано для самостоятельного изучения, а также при подготовке к выпускному экзамену в традиционной форме, ЕГЭ и вступительным экзаменам в вузы. Краткие теоретические сведения сопровождаются подробными решениями задач.
blog.zabedu.ru
- Исследование функции с помощью производной…
Продолжить формировать умения учащихся в исследовании функции (с помощью производной), строить её график; закрепить правила вычисления пределов, понятия асимптоты, их виды и алгоритм их нахождения
Исследование функции с помощью производной и построение её графика Старательность – мать успеха М.
 Сервантес Цель урока : Продолжить усовершенствование умений учащихся в исследовании функции с помощью производной и построение её графика; Повторить всё о асимптотах; Развитие аналитического мышления.
Сервантес Цель урока : Продолжить усовершенствование умений учащихся в исследовании функции с помощью производной и построение её графика; Повторить всё о асимптотах; Развитие аналитического мышления.nsportal.ru
- Презентация «Исследование функции с помощью производной…
2. Способствовать развитию навыков применения теоретических знаний в практической деятельности. 3. Способствовать воспитанию ответственности за качество и результат выполняемой работы на уроке. Задачи: Повторить алгоритм исследования функции на монотонность и экстремумы с помощью производной. Используя алгоритмы исследования функций с помощью производной, применить их для решения конкретных задач. Формировать глубину и оперативность мышления.
uchitelya.com
- Исследование функции — схема, примеры с решением.
 ..
..Для построения графика функции у = у{х) выясняют особенности поведения функции. Существенную роль при этом играют характерные точки: концевые точки промежутков задания функции, точки разрыва, стационарные точки и точки недифференцируемости функции и се производной и т.д. По этим точкам выделяются участки однообразного поведения функции, а именно: промежутки ее непрерывности; промежутки, на которых у'(х) и y»(x) сохраняют знак, что позволяет изучить характер монотонности функции и направление ее выпуклости.
www.evkova.org
- Исследование функции и построение графика…
Схема исследования функции и построение ее графика. График заданной функции можно строить по произвольно взятым точкам. При таком способе можно не обнаружить всех особенностей ее графика. Проведя предварительно исследования, мы ищем характерные для данного графика точки и тем упрощаем решение задачи о построении графика.
 При исследовании функции и построении ее графика целесообразно придерживаться следующей схемы: Первый этап (использование вида заданной функции).
При исследовании функции и построении ее графика целесообразно придерживаться следующей схемы: Первый этап (использование вида заданной функции).natalibrilenova.ru
- Тема: «Исследование функции с помощью производной…»
использовать производную для изучения свойств функций и построения графиков; применять производную для проведения приближенных вычислений, решать задачи прикладного характера на нахождение наибольшего и наименьшего значения; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
kopilkaurokov.ru
- Полное исследование функции и построение графика
Нахождение области определения.
 Исследование границ ОДЗ и нахождение вертикальных асимптот. Исследование функции и на четность или нечетность. Нахождение возрастания и убывания, точек экстремума. Нахождение промежутков выпуклости и вогнутости функции и точек перегиба. Нахождение горизонтальных и наклонных асимптот. Вычисление значения функции в промежуточных точках. Построение графика. Если в задаче необходимо произвести полное исследование функции f(x)=x24x2−1.
Исследование границ ОДЗ и нахождение вертикальных асимптот. Исследование функции и на четность или нечетность. Нахождение возрастания и убывания, точек экстремума. Нахождение промежутков выпуклости и вогнутости функции и точек перегиба. Нахождение горизонтальных и наклонных асимптот. Вычисление значения функции в промежуточных точках. Построение графика. Если в задаче необходимо произвести полное исследование функции f(x)=x24x2−1.Zaochnik.com
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Исследование функций с помощью производной и построение графиков, 65 задач с подробным решением, Каминкова И.В., 2021»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 63 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
Пример 2. Постройте график функции \(y=\frac3x+\frac x3\)
1) Область определения
ОДЗ: \(x\ne 0\)
\(x=0\) — точка разрыва. Исследуем односторонние пределы: \begin{gather*} \lim_{x\rightarrow -0}\left(\frac 3x+\frac x3\right)=\frac{3}{-0}+0=-\infty,\ \ \lim_{x\rightarrow +0}\left(\frac 3x+\frac x3\right)=\frac{3}{+0}+0=+\infty \end{gather*} Пределы не равны и бесконечны. \(x=0\) — точка разрыва 2-го рода.
2) Четность $$ f(-x)=\frac{3}{-x}+\frac{-x}{3}=-\left(\frac 3x+\frac x3\right)=-f(x) $$ Функция нечётная.
Периодов нет. Функция не периодическая.
3) Асимптоты
1. Вертикальная асимптота \(x=0\) – точка разрыва 2-го рода
2. Горизонтальные асимптоты \begin{gather*} b_1=\lim_{x\rightarrow -\infty}\left(\frac 3x+\frac x3\right)=0+(-\infty)=-\infty\\ b_2=\lim_{x\rightarrow +\infty}\left(\frac 3x+\frac x3\right)=0+(+\infty)=+\infty \end{gather*} Пределы бесконечны, горизонтальных асимптот нет.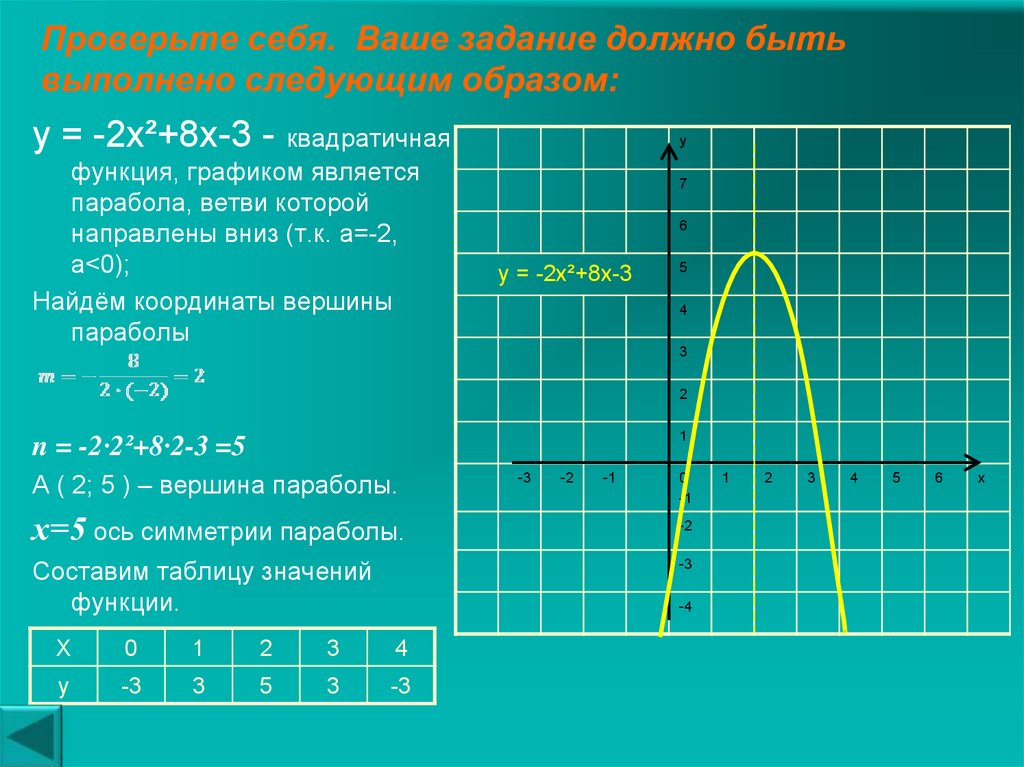 2-4\cdot (-8)=33,\ \ x_{1,2}=\frac{-1\pm \sqrt{33}}{2}= \left[ \begin{array}{l} \approx -3,37\\ \approx 2,37 \end{array} \right.\\ f»(x)=0,\ \text{при}\ x=x_{1,2} \end{gather*} Критические точки 2-го порядка: \(x=\left\{1;\frac{-1\pm \sqrt{33}}{2}\right\}\)
2-4\cdot (-8)=33,\ \ x_{1,2}=\frac{-1\pm \sqrt{33}}{2}= \left[ \begin{array}{l} \approx -3,37\\ \approx 2,37 \end{array} \right.\\ f»(x)=0,\ \text{при}\ x=x_{1,2} \end{gather*} Критические точки 2-го порядка: \(x=\left\{1;\frac{-1\pm \sqrt{33}}{2}\right\}\)
| \(x\) | \((-\infty;x_1)\) | \(x_1\) | \((x_1;1)\) | 1 | \((1;x_2)\) | \(x_2\) | \((x_2;+\infty)\) |
| \(f»(x)\) | <0 | 0 | >0 | \(\varnothing\) | <0 | 0 | >0 |
| \(f(x)\) | \(\cap\) | перегиб | \(\cup\) | \(\varnothing\) | \(\cap\) | перегиб | \(\cup\) |
Функция выпуклая вверх при \(x\in(-\infty;x_1)\cup(1;x_2)\)
Функция выпуклая вниз при \(x\in(x_1;1)\cup (x_2;++\infty)\)
Точки перегиба: $$ \begin{cases} x=\frac{-1-\sqrt{33}}{2}\approx -3,37\\ y\approx 0,51 \end{cases},\ \ \begin{cases} x=\frac{-1+\sqrt{33}}{2}\approx 2,37\\ y\approx 3,62 \end{cases} $$
6) Точки пересечения с осями
Пересечение с OY: \(x=0,\ y=\frac{0^3-4}{(0-1)^3}=4\)
Пересечение с осью OX:
\(\frac{x^3-4}{(x-1)^3}=0\Rightarrow x=\sqrt[3]{4},\ y=0\)
7) График
Чтобы узнать количество корней уравнения \(\frac{x^3-4}{(x-1)^3}=a\), нужно снизу вверх двигать горизонталь \(y=a\) и считать количество точек её пересечения с графиком функции.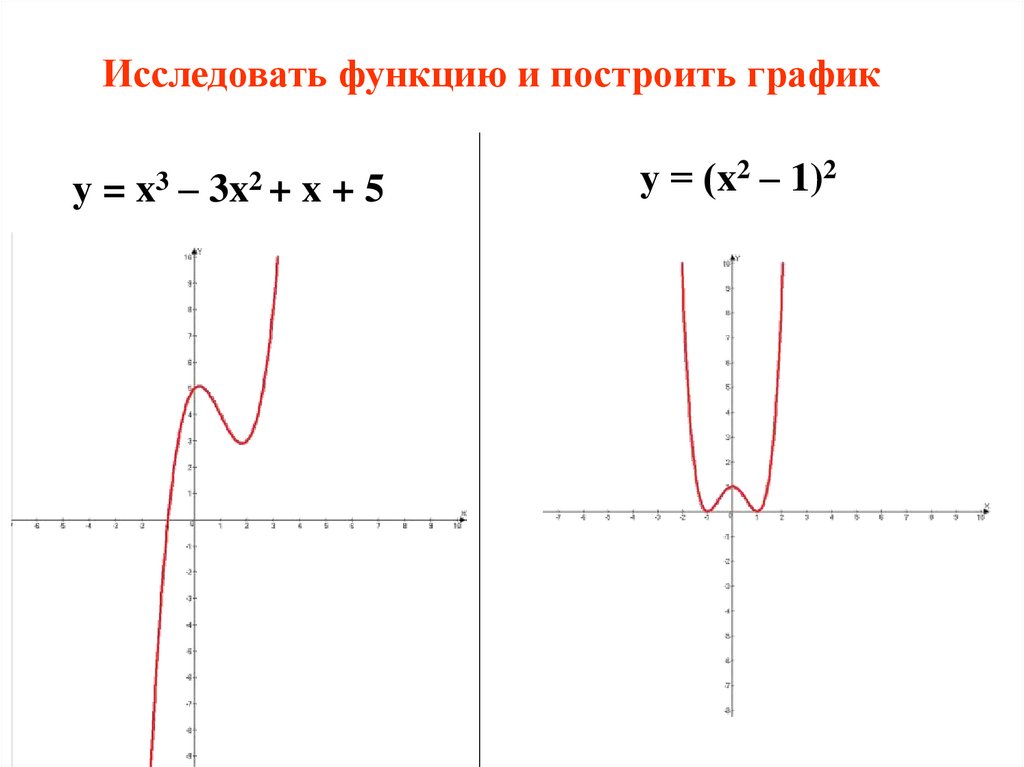 2 2x}{2}=\\ =\frac12\left(1+\frac{1+cos4x}{2}\right)=\frac{3+cos4x}{4} \end{gather*} Функция периодическая с периодом \(T=\frac{2\pi}{4}=\frac \pi 2\)
2 2x}{2}=\\ =\frac12\left(1+\frac{1+cos4x}{2}\right)=\frac{3+cos4x}{4} \end{gather*} Функция периодическая с периодом \(T=\frac{2\pi}{4}=\frac \pi 2\)
Исходя из полученного выражения и применяя правила преобразования графиков тригонометрических функций (см. §8 данного справочника), можно сразу получить результат. $$ y=\frac{3+cos4x}{4}=\frac34+\frac14 cos4x $$ Цепочка преобразований: $$ x \xrightarrow1 4x\xrightarrow2 cos4x \xrightarrow3 \frac14\xrightarrow4 \frac34+\frac14 cos4x $$ Пошагово получаем:
1. Умножение аргумента на 4 приводит к уменьшению периода в 4 раза \(T=\frac\pi 2\)
2. Косинус – функция четная, при \(x=0,\ cos4x=1\), остальные единицы будут через период: \(x=\frac{\pi k}{2},\ cos4x=1\). Соответственно: \(x=\frac\pi 4+\frac{\pi k}{2}0\ ,cos4x=-1\).
Нули функции: \(x=\frac\pi 8+\frac{\pi k}{4},\ cos4x=0\).
3. Умножение на \(\frac14\) уменьшает амплитуду косинусоиды в 4 раза: \(-\frac14\leq\frac14 cos4x\leq \frac14\)
4. Прибавление \(\frac34\) перемещает график на \(\frac34\) вверх: \(\frac12\leq\frac34+\frac14 cos4x\leq 1\)
Получаем график:
Продолжим стандартное исследование функции.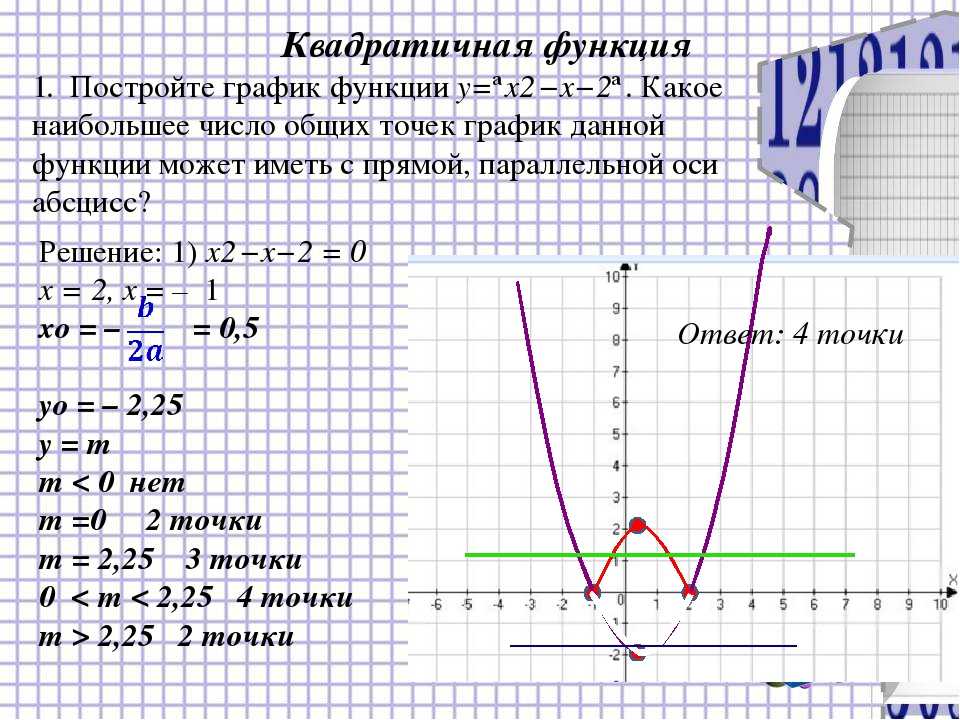 4 x)’=\left(\frac{3+cos4x}{4}\right)’=0-\frac14\cdot 4\cdot sin4x=-sin4x\\ sin4x=0\Rightarrow 4x=\pi k\Rightarrow x=\frac{\pi k}{4} \end{gather*} Критические точки: \(x=\frac{\pi k}{4}\). На периоде \(T=\frac\pi 2\) получаем три точки \(x=\left\{0;\frac\pi 4;\frac\pi 2\right\}\)
4 x)’=\left(\frac{3+cos4x}{4}\right)’=0-\frac14\cdot 4\cdot sin4x=-sin4x\\ sin4x=0\Rightarrow 4x=\pi k\Rightarrow x=\frac{\pi k}{4} \end{gather*} Критические точки: \(x=\frac{\pi k}{4}\). На периоде \(T=\frac\pi 2\) получаем три точки \(x=\left\{0;\frac\pi 4;\frac\pi 2\right\}\)
| \(x\) | 0 | \(\left(0;\frac\pi 4\right)\) | \(\frac\pi 4\) | \(\left(\frac\pi 4;\frac\pi 2\right)\) | \(\frac\pi 2\) |
| \(f'(x)\) | 0 | <0 | 0 | >0 | 0 |
| \(f(x)\) | 1 max | \(\searrow\) | \(\frac12\) min | \(\nearrow\) | 1 max |
Функция убывает при \(x\in\left(\frac{\pi k}{2};\frac\pi 4+\frac{\pi k}{2}\right)\)
Функция возрастает при \(x\in\left(\frac\pi 4+\frac{\pi k}{2};\frac\pi 2+\frac{\pi k}{2}\right)\)
Точки минимума \(x=\frac\pi 4+\frac{\pi k}{2};\ y_{min}=\frac12\)
Точки максимума \(x=\frac{\pi k}{2};\ y_{max}=1\)
5) Вторая производная: \begin{gather*} f»(x)=(-sin4x)’=-4cos4x\\ cos4x=0\Rightarrow 4x=\frac\pi 2+\pi k\Rightarrow x=\frac\pi 8+\frac{\pi k}{4} \end{gather*} Критические точки 2-го порядка: \(x=\frac\pi 8+\frac{\pi k}{4}\).
На периоде \(T=\frac\pi 2\) получаем две точки \(x=\left\{\frac\pi 8;\frac{3\pi}{8}\right\}\)
| \(x\) | \(\left(0;\frac\pi 8\right)\) | \(\frac\pi 8\) | \(\left(\frac\pi 8;\frac{3\pi}{8}\right)\) | \(\frac{3\pi}{8}\) | \(\left(\frac{3\pi}{8};\frac\pi 2\right)\) |
| \(f»(x)\) | <0 | 0 | >0 | 0 | <0 |
| \(f(x)\) | \(\cap\) | перегиб | \(\cup\) | перегиб | \(\cap\) |
Функция выпуклая вниз при \(x\in\left(\frac\pi 8+\frac{\pi k}{2};\frac{3\pi}{8}+\frac{\pi k}{2}\right)\)
Функция выпуклая вверх при \(x\in\left(-\frac\pi 8+\frac{\pi k}{2};\frac\pi 8+\frac{\pi k}{2}\right)\)
Точки перегиба: \( x=\frac\pi 8+\frac{\pi k}{4},\ y=\frac{3+cos4\cdot \left(\frac\pi 8+\frac{\pi k}{4}\right)}{4}=\frac{3+0}{4}=\frac34 \)
6) Точки пересечения с осями
Пересечение с OY: \(x=0,\ y_{max}=1\)
Пересечение с осью OX: т. к. функция ограничена \(\frac12\leq y\leq 1\), пересечений с OX нет.
к. функция ограничена \(\frac12\leq y\leq 1\), пересечений с OX нет.
7) График
График тот же, что и полученный с помощью правил преобразований графиков тригонометрических функций. Добавились только точки перегиба.
Методы построения графиков функций | Обучонок
Автор публикации:
Климов Даниил Сергеевич
ЧПОУ Красноярский кооперативный техникум экономики, коммерции и права
В данном методическом материале по математике на тему «Методы построения графиков функций» дается определение функции, рассматриваются способы задания функций: табличный, словесный, графический и аналитический.
В методическом материале по математике (алгебре) «Методы построения графиков функций» проводится разбор методов построения графиков функций: параллельный перенос, отражение, выполняется построение графиков четной и нечетной функций.
Оглавление
Введение
Глава 1.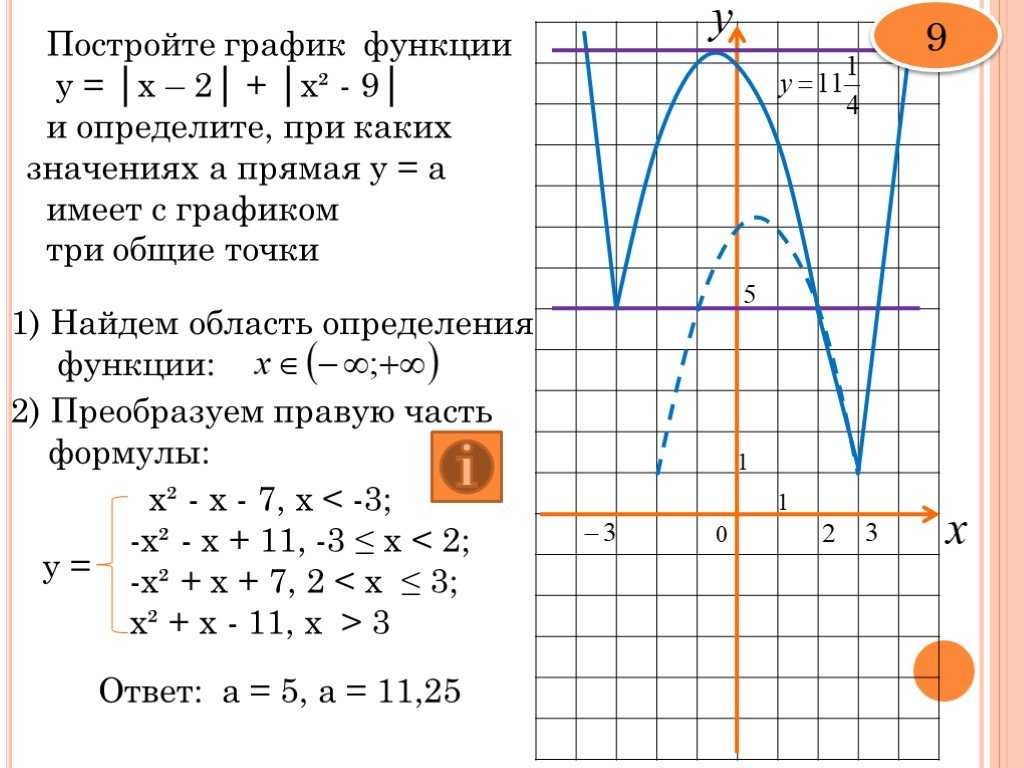 Определение функций.
Определение функций.
Глава 2. Способы задания функций
Глава 3. Методы построения графиков функций
3.1. Параллельный перенос.
3.2. Отражение.
3.3. Построение графиков четной и нечетной функций.
Список источников
Введение
Изучение действий функций и построение их графиков является важным разделом математики.
Свободное владение техникой построения графиков часто помогает решить многие задачи и порой является единственным средством их решения.
Кроме того, умение строить графики функций представляет собой большой самостоятельный интерес.
Глава 1. Определение функций
Величины, участвующие в одном и том же явлении, могут быть взаимосвязаны, так что изменение одних из них влечёт за собой изменение других. Например, увеличение (или уменьшение) радиуса круга ведёт к обязательному увеличению (или уменьшению) его площади.
В таких случаях говорят, что между переменными величинами существует функциональная зависимость, причём одну величину называют функцией, или зависимой переменной (е часто обозначают буквой у), а другую — аргументом, или независимой переменной (её обозначают буквой х).
Функциональную зависимость между х и у принято обозначать символом y=f (x). Если значению х соответствует больше, чем одно значение у, то такая функция называется многозначной.
Переменная величина у есть функция аргумента х, то есть y=f (x), если каждому возможному значению х соответствует одно определённое значение у.
Графиком функции называется совокупность всех точек на плоскости, прямоугольные координаты которых х и у удовлетворяют уравнению y=f (x).
Горизонтальную ось Ох называют осью абсцисс, вертикальную ось Оу — осью ординат.
Графическое изображение функции имеет важное значение для её изучения. На графике функции часто непосредственно видны такие её особенности, которые можно было бы установить лишь путём длительных вычислений. Если между величинами х и у существует функциональная связь, то безразлично, какую из этих величин считать аргументом, а какую — функцией.
Глава 2. Способы задания функций
1). Табличный способ. При этом способе ряд отдельных значений аргумента х1, х2, …, хk и соответствующий ему ряд отдельных значений функции у1, у2, …, уk задаются в виде таблицы.
Несмотря на простоту, такой способ задания функции обладает существенным недостатком, так как не дает полного представления о характере функциональной зависимости между х и у и не является наглядным.
2). Словесный способ. Обычно этот способ задания иллюстрируют примером функции Дирихле у = D (х): если х — рациональное число, то значение функции D (х) равно 1, а если число х — иррациональное, то значение функции D (х) равно нулю.
Таким образом, чтобы найти значение D (x0) при заданном значении х = х0, необходимо каким — либо способом установить, рационально или иррационально число х0.
3). Графический способ. Функциональная зависимость может быть задана с помощью графика функции у = f (x).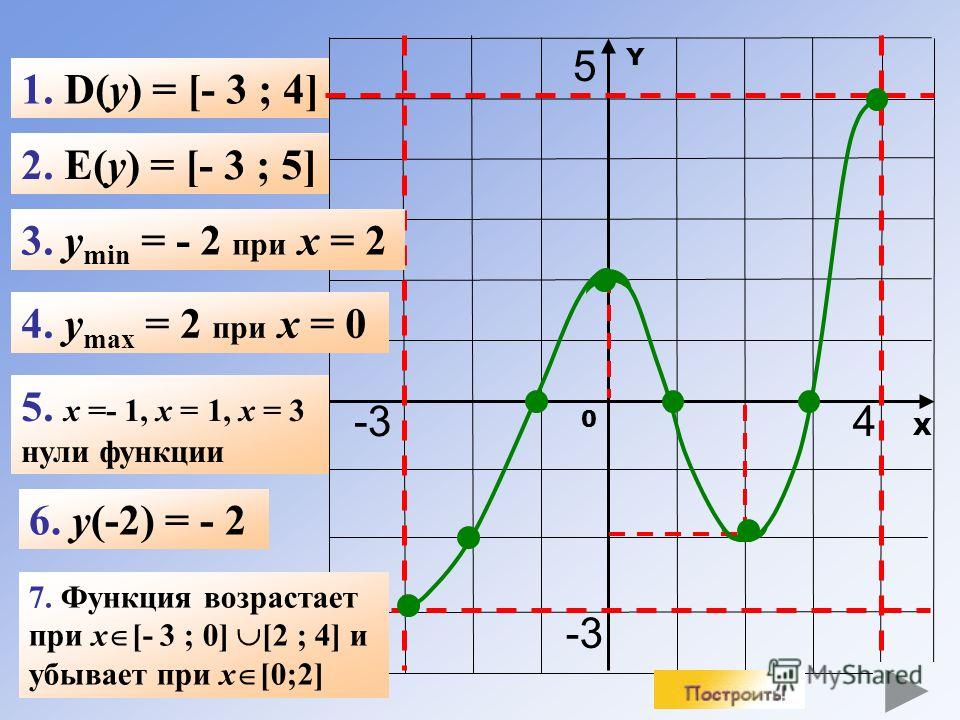
Преимуществом такого способа задания является наглядность, позволяющая установить важные черты поведения функции. Недостаток графического способа заключается в невозможности применения математического аппарата для более детального исследования функции.
4). Аналитический способ. При аналитическом способе задания известна формула, по которой по заданному значению аргумента х можно найти соответствующее значение функции у. В математике чаще всего используется именно аналитический способ задания функций.
Преимуществами такого способа задания являются компактность, возможность подсчета значения у при любом значении х и возможность применения математического аппарата для более детального исследования поведения функции. Однако аналитическому способу задания функции присуща недостаточная наглядность и возможная трудность вычисления значений функции.
Глава 3. Методы построения графиков функций
Исследование функции дает возможность найти область определения и область изменения функции, области ее убывания или возрастания, асимптоты, интервал знакопостоянства и др.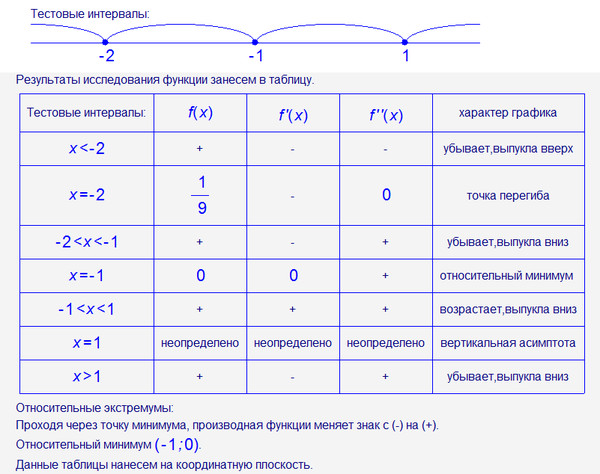
Однако при рассмотрении графиков многих функций часто можно избежать проведения подобного исследования, используя ряд методов, упрощающих аналитическое выражение функции и облегчающих построение графика.
Изложению именно таких методов посвящается эта глава, которая может служить практическим руководством при построении многих функций.
Параллельный перенос
Перенос вдоль оси ординат.
f (x) => f (x) — b
Пусть требуется построить график функции у = f (х) — b. Нетрудно заметить, что ординаты этого графика для всех значений x на ЅbЅ единиц меньше соответствующих ординат графика функций у = f (х) при b>0 и на ЅbЅ единиц больше — при b
Следовательно, график функции у = y (х) — b можно получить параллельным переносом вдоль оси ординат графика функции у = f (х) на ЅbЅ единиц вниз при b>0 или вверх при b
Перемещение графика связано с его перерисовыванием, что бывает затруднительно, особенно в случае сложных графиков. Перенос же графика на ЅbЅ единиц вниз или вверх вдоль оси ординат эквивалентен соответствующему противоположному переносу оси абсцисс настолько же единиц.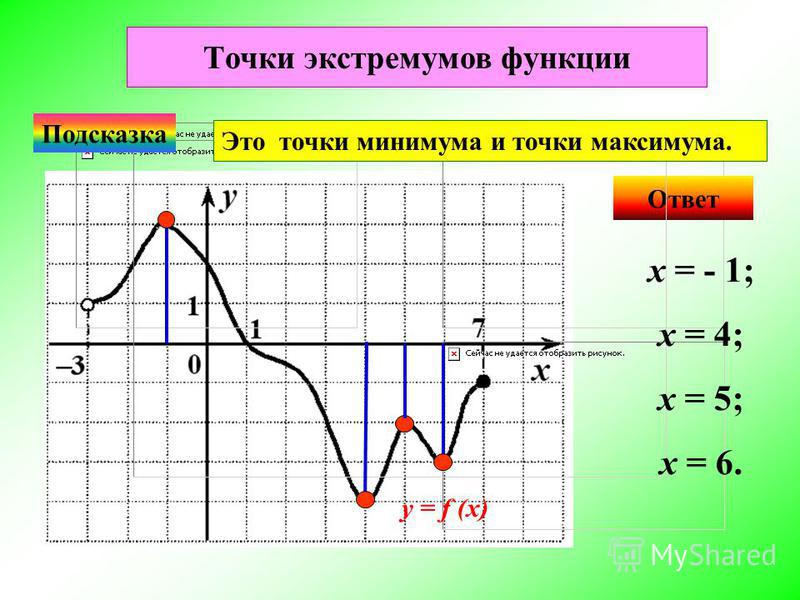
Именно этим способом мы будем пользоваться. Тогда представив исходную функцию в виде у + b = f (х), сформулируем следующее правило.
Для построения графика функции y + b = f (x) следует построить график функции y = f (x) и перенести ось абсцисс на ЅbЅ единиц вверх при b>0 или наЅbЅ единиц вниз при b
Полученный в новой системе координат график является графиком функции y = f (x) — b.
Перенос вдоль оси абсцисс.
f (x) => f (x + a)
Пусть требуется построить график функции у = f (x + a). Рассмотрим функцию y = f (x), которая в некоторой точке x = x1 принимает значение у1 = f (x1).
Очевидно, функция у = f (x + a) примет такое же значение в точке x2, координата которой определяется из равенства x2 + a = x1, т.е. x2 = x1 — a, причем рассматриваемое равенство справедливо для совокупности всех значений из области определения функции.
Следовательно, график функции у = f (x + a) может быть получен параллельным перемещением графика функции y = f (x) вдоль оси абсцисс влево наЅaЅ единиц при a>0 или вправо на ЅaЅ единиц при a
Для построения графика функции y = f (x + a) следует построить график функции y = f (x) и перенести ось ординат на ЅaЅ единиц вправо при a>0 или наЅaЅ единиц влево при a
Отражение
Построение графика функции вида y = f (-x). f (x) => f (-x)
f (x) => f (-x)
Очевидно, что функции y = f (-x) и y = f (x) принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку.
Иначе говоря, ординаты графика функции y = f (-x) в области положительных (отрицательных) значений х будут равны ординатам графика функции y = f (x) при соответствующих по абсолютной величине отрицательных (положительных) значениях х.
Таким образом, получаем следующее правило.
Для построения графика функции y = f (-x) следует построить график функции y = f (x) и отразить его относительно оси ординат. Полученный график является графиком функции y = f (-x)
Построение графика функции вида y = — f (x).
f (x) => — f (x)
Ординаты графика функции y = — f (x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y = f (x) при тех же значениях аргумента.
Таким образом, получаем следующее правило.
Для построения графика функции y = — f (x) следует построить график функции y = f (x) и отразить его относительно оси абсцисс.
Построение графиков четной и нечетной функций.
Как уже отмечалось, для четной функции y = f (x) во всей области изменения ее аргумента справедливо соотношение f (x) = f (-x).
Следовательно, функция такого рода принимает одинаковое значение при всех значениях аргумента, равных по абсолютной величине, но противоположных по знаку. График четной функции симметричен относительно оси ординат.
Для построения графика четной функции y = f (x) следует построить ветвь графика этой функции только в области положительных значений аргумента (хі0). График функции y = f (x) в области отрицательных значений аргумента симметричен построенной ветви относительно оси ординат и получается отражением ее относительно этой оси.
Для нечетной функции y = f (x) в области всех значений аргумента справедливо равенство f (-x) = — f (x).
Таким образом, в области отрицательных значений аргумента ординаты графика нечетной функции равны по величин, но противоположны по знаку ординатам графика той же функции при соответствующих положительных значениях х. График нечетной функции симметричен относительно начала координат.
График нечетной функции симметричен относительно начала координат.
Для построения графика нечетной функции y = f (x) следует построить ветвь графика этой функции только в области положительных значений аргумента (хі0).
График функции y = f (x) в области отрицательных значений аргумента симметричен построенной ветви относительно начала координат и может быть получен отражением этой ветви относительно оси ординат с последующим отражением в области отрицательных значений относительно оси абсцисс.
Список источников
1. Алгебра и начала математического анализа: учебник для 10-11 кл. общеобразовательных учреждений / под редакцией А.Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын, Б. М. Ивлев, С. И. Шварцбурд; 23-изд.-М.: Просвещение, 2014 -384с.
Если страница Вам понравилась, поделитесь в социальных сетях:
6.1 Введение | Функции | Сиявула
6.1 Введение (EMA3Z)
- В этой главе рассматривается понятие функции и представление функций с использованием таблиц, графиков, слов и
формулы.
 Графики с прямыми линиями были рассмотрены в 9 классе и переработаны здесь. Параболы, гиперболы и
здесь вводятся экспоненциальные графики. Также представлены графики для функций синуса, косинуса и тангенса.
здесь.
Графики с прямыми линиями были рассмотрены в 9 классе и переработаны здесь. Параболы, гиперболы и
здесь вводятся экспоненциальные графики. Также представлены графики для функций синуса, косинуса и тангенса.
здесь. - Более формальное определение функции доступно только в 12 классе. На этом уровне учащиеся должны знать термины независимые (входные) и зависимые (выходные) переменные, а также то, как они изменяются.
- Резюме должны быть составлены для каждого типа графика и должны включать эффекты (вертикального растяжения и/или отражение по x) и q (вертикальный сдвиг).
- Помните, что в некоторых практических приложениях графы могут быть дискретными или непрерывными.
- Поощряйте учащихся указывать ограничения, особенно для квадратичных функций.
- Учащиеся должны понимать, что \(y = \sqrt{x}\) не имеет реальных решений для \(x < 0\).
- Рисование графиков основано на знании эффектов \(a\) и \(q\) и использовании их для определения формы
графика.

Инструмент, подобный этому можно использовать для построения графиков для использования в классе. Если вы используете этот инструмент для построения тригонометрических графиков, значения по оси \(x\) не будет в градусах.
Функции — это математические строительные блоки для проектирования машин, предсказания стихийных бедствий, лечения болезней, понимания мировой экономики и поддержания самолетов в воздухе. Функции могут принимать входные данные от многих переменных, но всегда дают один и тот же результат, уникальный для этой функции.
Функции также позволяют нам визуализировать отношения в виде графиков, которые намного легче читать и интерпретировать, чем списки чисел.
Игрок в крикет сталкивается с доставкой. Если игрок в крикет получил удар по своей подушечке ватина и судья считает, что мяч попал бы в пни позади него, ему выдается LBW (нога перед калиткой). На профессиональном уровне игры используется сложное программное обеспечение, чтобы определить, попадет ли мяч в пни. Программное обеспечение использует функции для прогнозирования полета мяча, если бы нога игрока в крикет не находилась в
путь.
Программное обеспечение использует функции для прогнозирования полета мяча, если бы нога игрока в крикет не находилась в
путь.Вот некоторые примеры функций:
Деньги как функция времени. У вас никогда не будет более одной суммы денег в любое время, потому что вы всегда можете добавить все, чтобы получить одну общую сумму. Понимая, как ваши деньги меняются с течением времени, вы можете планировать тратить деньги разумно. Предприятия считают очень полезным построить график своих денег с течением времени, чтобы они могут видеть, когда они тратят слишком много.
Температура как функция различных факторов. Температура — очень сложная функция, потому что она множество входных данных, в том числе: время суток, сезон, количество облаков в небе, сила ветер, где вы находитесь и многое другое. Но важно то, что есть только один температурный выход, когда вы измеряете его в определенном месте.

Местоположение как функция времени. Вы никогда не сможете быть в двух местах одновременно. Если бы вы планировали графики того, где находятся два человека в зависимости от времени, место, где пересекаются линии, означает, что два люди встречаются друг с другом в это время. Эта идея используется в логистике, области математики, которая пытается планировать где люди и предметы для бизнеса.
- Функция
Функция — это математическая связь между двумя переменными, где каждая входная переменная имеет один выход. переменная.
Зависимые и независимые переменные (EMA42)
В функциях переменная \(x\) известна как входная или независимая переменная, потому что ее значение может быть выбрано
свободно. Вычисленная \(y\)-переменная известна как выходная или зависимая переменная, поскольку ее значение зависит от
выбранное входное значение.
Установить обозначение (EMA43)
Примеры:
\(\слева\{х:х\в\mathbb{R},х>0\справа\}\) | Множество всех \(x\)-значений таких, что \(x\) является элементом множества действительных чисел и больше чем \(\text{0}\). |
\(\left\{y:y\in \mathbb{N},3 | Множество всех \(y\)-значений, таких что \(y\) является натуральным числом, больше \(\text{3}\) и меньше или равно \(\text{5}\). |
\(\слева\{z:z\in \mathbb{Z},z\le 100\справа\}\) | Набор всех \(z\)-значений, таких что \(z\) является целым числом и меньше или равно \(\text{100}\). |
Интервальное обозначение (EMA44)
Важно отметить, что это обозначение может использоваться только для представления интервала действительных чисел.
Примеры:
\(\влево(3;11\вправо)\) | Круглые скобки означают, что номер не включен. Этот интервал включает все действительные числа больше, но не равно \(\text{3}\) и меньше, но не равно \(\text{11}\). |
\(\влево(-\infty ;-2\вправо)\) | Круглые скобки всегда используются для положительной и отрицательной бесконечности. В этот интервал входят все действительные числа меньше, но не равны \(-\text{2}\). |
\(\влево[1;9\вправо)\) | Квадратная скобка указывает, что число включено. В этот интервал входят все действительные числа, большие
больше или равно \(\text{1}\) и меньше, но не равно \(\text{9}\). |
Обозначение функций (EMA45)
Это очень удобный способ выражения функции. Другой способ записи \(y=2x+1\) — это \(f(x) = 2x + 1\). Мы говорим «\(f\) из \(x\) равно \(2x + 1\)». Можно использовать любую букву, например \(g(x)\), \(h(x)\), \(р(х)\) и т. д.
Определение выходного значения :
«Найти значение функции для \(x=-3\)» можно записать как: «найти \(f(-3)\)».
Заменить \(x\) на \(-\text{3}\):
\начать{выравнивать*} f(-3) & = 2(-3) + 1 = -5 \\ \поэтому f(-3) & = -5 \конец{выравнивание*}Это означает, что когда \(x = -3\), значение функции равно \(-\text{5}\).
Определение входного значения :
«Найти значение \(x\), которое даст \(y\)-значение \(\text{27}\)» можно записать так: «найти \(x\), если \(f(x)=27\)».

Запишем следующее уравнение и решим относительно \(x\):
\начать{выравнивать*} 2х+1&=27\ \поэтому х = & 13 \конец{выравнивание*}Это означает, что при \(x = 13\) значение функции равно \(\text{27}\).
Представления функций (EMA46)
Функции могут быть выражены разными способами для разных целей.
слов: «Связь между двумя переменными такова, что одна всегда \(\text{5}\) меньше, чем Другой.»
Схема отображения:
Таблица:
Входная переменная \((x)\)
\(-\текст{3}\)
\(\текст{0}\)
\(\текст{5}\)
Выходная переменная \((y)\)
\(-\текст{8}\)
\(-\текст{5}\)
\(\текст{0}\)
Набор упорядоченных пар чисел: \((-3;-8)\), \((0;-5)\), \((5;0)\)
Алгебраическая формула: \(f(x) = x — 5\)
График:
Домен и диапазон (EMA47)
. Область определения функции – это множество всех независимых \(х\)-значений, из которых функция производит одно
\(y\)-значение для каждого \(x\)-значения.
Область определения функции – это множество всех независимых \(х\)-значений, из которых функция производит одно
\(y\)-значение для каждого \(x\)-значения.
Диапазон — это набор всех зависимых \(y\)-значений, которые можно получить, используя независимое \(x\)-значение.
Учебник Упражнение 6.1
\((-\infty;7]\)
\(\left\{x:x\in \mathbb{R},x \le 7\right\}\)
\([-13; 4)\)
\(\left\{x:x\in \mathbb{R}, -13 \le x < 4\right\}\)
\((35;\infty)\)
\(\left\{x:x\in \mathbb{R}, x > 35\right\}\)
\([\frac{3}{4};21)\)
\(\left \{x:x\in \mathbb{R}, \frac{3}{4} \le x < 21\right\}\)
\([-\frac{1}{2};\frac{ 1}{2}]\)
\(\left\{x:x\in \mathbb{R}, -\frac{1}{2} \le x \le \frac{1}{2}\ вправо\}\)
\((-\sqrt{3};\infty)\)
\(\left\{x:x\in \mathbb{R}, x > -\sqrt{3}\right\}\)
\(\left\{p:p\in \mathbb{R}, p \le 6 \right\}\)
\((-\infty;6]\)
\(\left\{ k:k\in \mathbb{R},-5 < k < 5\right\}\)
\((-5;5)\)
\(\left\{x:x\in \mathbb {R},x > \frac{1}{5}\right\}\)
\((\frac{1}{5};\infty)\)
\(\left\{z:z \in \mathbb{R},21 \le x < 41\right\}\)
\([21;41)\)
\[\begin{array}{| л | л | л | л | л | л | л |} \hline х и 1 и 2 и 3 и 4 и 5 и 6\\ \hline у & 5 & 10 & & 20 & & \\ \hline \конец{массив}\]
\[\begin{массив}{| л | л | л | л | л | л | л |} \hline х и 1 и 2 и 3 и 4 и 5 и 6 \\ \hline у и 5 и 10 и 15 и 20 и 25 и 30 \\ \hline \конец{массив}\] \[y = 5x\]
\[\begin{массив}{| л | л | л | л | л | л | л | } \hline х & 1 & & 3 & 4 & & 6 \\ \hline у & 5 & 5 & & & 5 & 5 \\ \hline \конец{массив}\]
\[\begin{массив}{| л | л | л | л | л | л | л |} \hline х и 1 и 2 и 3 и 4 и 5 и 6 \\ \hline у и 5 и 5 и 5 и 5 и 5 и 5 \\ \hline \конец{массив}\] \[y = 5\]
\[\begin{массив}{| л | л | л | л | л | л | л |} \hline х & 2 & & & 8 & 10 & 12 \\ \hline у & 1 & 2 & 3 & & & 6 \\ \hline \конец{массив}\]
\[\begin{массив}{| л | л | л | л | л | л | л |} \hline х и 2 и 4 и 6 и 8 и 10 и 12 \\ \hline у и 1 и 2 и 3 и 4 и 5 и 6 \\ \hline \конец{массив}\] \[y = \frac{1}{2}x\]
\[\begin{array}{| л | л | л | л | л | л | л |} \hline х и 1 и 2 и 3 и 4 и 5 и 6 \\ \hline y & \text{0,1} & \text{0,2} & \text{0,3} & \text{0,4} & \text{0,5} & \text{0,6} \ \ \hline \конец{массив}\]
Обратите внимание, что этот график масштабирован. Каждое значение для \(x\) и \(y\) было умножено на \(\text{10}\).
Этот процесс не меняет функцию, но растягивает график, тем самым делая
его легче читать.
Каждое значение для \(x\) и \(y\) было умножено на \(\text{10}\).
Этот процесс не меняет функцию, но растягивает график, тем самым делая
его легче читать.
\[\begin{массив}{| л | л | л | л | л | л | л |} \hline х и 1 и 2 и 3 и 4 и 5 и 6 \\ \hline у и 5 и 9 и 13 и 17 и 21 и 25 \\ \hline \конец{массив}\]
\(y = \frac{1}{2}x + 2\)
\[\начать{массив}{| л | л | л | л | л | л | л | л |} \hline х и -2 и -1 и 0 и 1 и 2 и 3 и 4 \\ \hline у & 1 & \текст{1,5} & 2 & \текст{2,5} & 3 & \текст{3,5} & 4 \\ \hline \конец{массив}\]
\(у = х — 3\)
\[\начать{массив}{| л | л | л | л | л | л | л |} \hline х и 0 и 1 и 2 и 3 и 4 и 5 \\ \hline у и -3 и -2 и -1 и 0 и 1 и 2 \\ \hline \конец{массив}\] 9{2} + 1 \\ & = 37 \\ \поэтому k(f(6)) & = k(37) \\ к (х) & = 3 \\ k(f(6)) &= 3 \конец{выравнивание*}
Независимо от значения \(x\), вывод всегда равен 3.
Вычислить \(P(8)\)
\begin{align*} P(8) &= \text{13,61}(8) \\ &= \текст{R}\,\текст{108,88} \end{align*}
Вычислить \(D(16)\)
\begin{align*} D(16) &= \text{12,46}(16) \\ &= \текст{R}\,\текст{199,36} \end{align*}
Сколько литров бензина можно купить на \(\text{R}\,\text{300}\)?
\begin{выравнивание*} Р(В) &= 300 \\ \text{13,61}В &= 300 \\ В &= \текст{22 043}\текст{L} \end{align*}
Сколько литров бензина можно купить на \(\text{R}\,\text{275}\)?
\begin{выравнивание*} D(V) &= 275 \\ \text{12,46}В &= 275 \\ В &= \текст{22,071}\текст{L} \end{выравнивание*}
Насколько бензин дороже дизельного топлива? Покажите вам ответ как функцию.
\begin{выравнивание*} P(V) — D(V) &= \text{13,61} V — \text{12,46} V \\ &= \text{1,15}В \end{align*}
После \(\text{6}\) \(\text{s}\) сколько еще мяч должен катиться?
\(\text{7}\) \(\text{m}\)
Каков диапазон функции?
\(\text{0}\) \(\text{m}\) \(\le\) s(t) \(\le\) \(\text{10}\) \(\text{ м}\)
Какова область определения функции и что она представляет?
Домен: \(\text{0}\text{ s} \le t \le \text{20}\text{ s}\).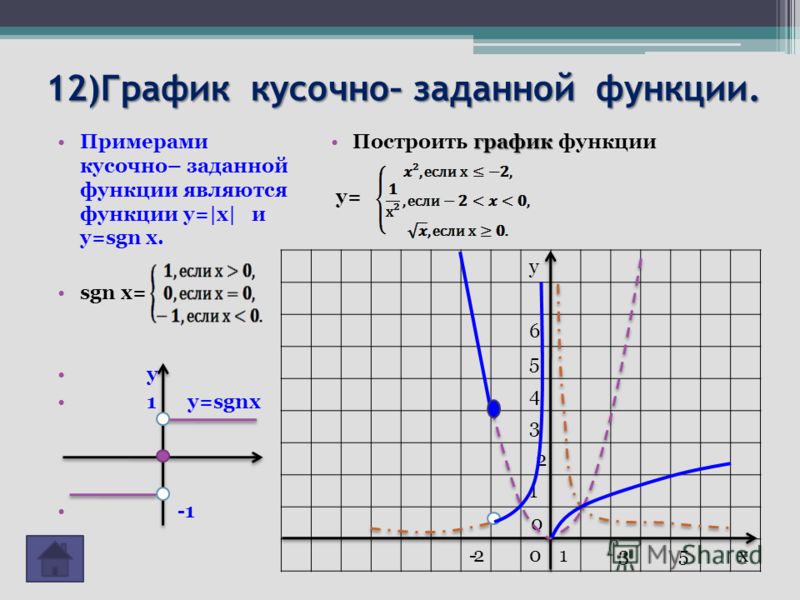 Он представляет собой общее время, затраченное на
добраться до нижней части склона.
Он представляет собой общее время, затраченное на
добраться до нижней части склона.
Какова высота здания, на котором они стояли?
Обе функции имеют максимальное значение \(\text{5}\) \(\text{m}\). Это можно найти, полагая \(x = 0\) в каждой из двух функций и представлен точкой A на графике выше. 92 — 225 &= 0 \\ (х — 15)(х + 15) &= 0\\ \поэтому & х = \текст{15}\текст{м} \конец{выравнивание*}
Темба бросил свой камень \(\text{15}\) \(\text{m}\) прежде, чем он упал на поверхность реки.
Поэтому Темба бросил свой камень \(\text{5}\) \(\text{m}\) дальше, чем Джеймс.
Урок 2 | Функции, графики и особенности | Математика для 9-го класса
Цель
Определение функций и оценка точек в таблицах, графиках и контекстных ситуациях с использованием обозначения функций.
Общие базовые стандарты
Основные стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Ф.
 ИФ.А.1
— Поймите, что функция от одного набора (называемого доменом) к другому набору (называемому диапазоном) присваивает каждому элементу домена ровно один элемент диапазона. Если f — функция, а x — элемент ее области определения, то f(x) обозначает выход f, соответствующий входу x. График f — это график уравнения y = f(x).
ИФ.А.1
— Поймите, что функция от одного набора (называемого доменом) к другому набору (называемому диапазоном) присваивает каждому элементу домена ровно один элемент диапазона. Если f — функция, а x — элемент ее области определения, то f(x) обозначает выход f, соответствующий входу x. График f — это график уравнения y = f(x). Ф.ИФ.А.2 — Используйте нотацию функций, оценивайте функции для входных данных в их доменах и интерпретируйте операторы, использующие нотацию функций, с точки зрения контекста.
Основополагающие стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89508.F.A.1
Критерии успеха
Основные понятия, которые учащиеся должны продемонстрировать или понять для достижения цели урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Определите функции как отношения, в которых каждый вход имеет только один выход в контекстных и неконтекстных ситуациях, представленных в таблицах и графиках.

- Используйте функциональную нотацию для описания функции ситуации, обозначая функцию f. Опишите ввод как $$x$$, вывод как f($$x$$) и координатную точку в функциональном обозначении (например, f(3) = 5 – это координатная точка (3, 5)).
- Вычислите функцию, представленную графически в виде функции.
- Используйте соответствующий язык для представления функций («f of $$x$$») и описывайте ситуацию в терминах независимых переменных (т. е. «Время есть функция расстояния». Представьте это в виде функции, где t — время , а f(t) представляет собой расстояние.)
Советы учителям
Предложения для учителей, которые помогут им провести этот урок стол, прежде чем они смогут полностью получить доступ к этому уроку.

Fishtank Plus
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Проблемы с якорем
Задачи, предназначенные для изучения ключевых моментов урока, и наводящие вопросы, помогающие привлечь внимание учащихся Проблема 1
Ниже приведен пример отношения, которое является функцией , и пример отношения, которое не является функцией .
Каковы определяющие характеристики функции?
ФУНКЦИЯ:
| $$x$$ | $$y$$ |
| 3 | 6 |
| 4 | 6 |
| 5 | 3 |
| 7 | 8 |
НЕ ФУНКЦИЯ:
| $$x$$ | $$y$$ |
| 3 | 5 |
| 4 | 6 |
| 4 | 3 |
| 7 | 8 |
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Проблема 2
Используйте приведенный ниже график, чтобы ответить на следующие вопросы:
Обозначение функции описывает конкретное отношение и подразумевает зависимость переменных.
Общая форма обозначения функций: $${f(x) = y}$$. $$y$$ зависит от $${x }$$.
Часть A:
Функция $$f$$ выше имеет точку $$f(-2) = 1$$. Отметьте эту точку на графике выше.
Часть B:
Найдите значения $$x$$ или $$y$$ на графике, отмеченном обозначением функции ниже.
$$f(-9)=$$
$$f(x)=1$$
$$f(x)=-2$$
$$f(4)=$$
$$g(x)=5$$
$${g(0)=}$$
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Проблема 3
Джон участвовал в забеге, и его тренер замерял его время. Гонку Джона можно описать как расстояние в метрах, $$d$$, как функцию времени в секундах, $$t$$. В середине гонки позицию Джона можно описать как $$d(6)=50$$. Опишите время и расстояние Джона в этот момент.
Опишите время и расстояние Джона в этот момент.
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Набор проблем
Набор предлагаемых ресурсов или типов задач, которые учителя могут превратить в набор задач
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Следующие ресурсы включают проблемы и действия, связанные с целью урок, который можно использовать для создания собственного набора задач.
- Reason and Wonder, «The Date Game», запись в блоге Майкла Фентона.
- Пример задачи: когда $${{f(x)} = {g(x)}}$$? Что такое $${f(x)}$$ на данный момент? Что такое $${g(x)}$$ на данный момент? Что такое $${f(-6)}$$? Каково решение $${g(x)} = 1$$?
- Иллюстративная математика Батат в духовке —
Включите это как продолжение этой проблемы: Напишите это утверждение в обозначении функций: «Температура батата после пребывания в духовке в течение 30 минут составляет 120 градусов.

- Иллюстративная математика Автостоянка
- Mathematics Vision Project: Secondary Mathematics One Модуль 5: Системы уравнений и неравенств — Урок 5.4
- Проект Mathematics Vision: Secondary Mathematics One Модуль 3: Особенности функций — Урок 3.7: Функционировать или не функционировать — практическое задание на понимание
Целевая задача
Задание, которое представляет собой пик мышления урока — мастерство покажет, была ли достигнута цель
А628D5C3-5B97-4E03-B1EC-5AD5C66D8950Проблема 1
Предположим, $$f$$ — функция.
- Если $$10 = f(-4)$$, укажите координаты точки на графике $$f$$.
- Если 6 является решением уравнения $$f(w) = 1$$, укажите точку на графике $$f$$.
Каталожные номера
Illustrative Mathematics Points on a Graph
Points on a Graph , доступ 22 июня 2017 г. , 15:51, лицензирован Illustrative Mathematics в соответствии с CC BY 4.0 или CC BY-NC-SA 4.0. Для получения дополнительной информации обращайтесь в Illustrative Mathematics.
, 15:51, лицензирован Illustrative Mathematics в соответствии с CC BY 4.0 или CC BY-NC-SA 4.0. Для получения дополнительной информации обращайтесь в Illustrative Mathematics.
Проблема 2
Пусть $${f(t)}$$ – количество людей (в миллионах), владеющих сотовыми телефонами через $$t$$ лет после 1990 года. Объясните смысл следующих утверждений.
- $${f(10)=100,3}$$
- $${f(a)=20}$$
- $${f(20)=b}$$
- $$n= {f(t)}$$
Каталожные номера
Illustrative Mathematics Cell Phones
Cell Phones , дата обращения 22 июня 2017 г., 15:53, лицензирована Illustrative Mathematics в соответствии с CC BY 4.0 или CC BY-NC-SA 4.0. Для получения дополнительной информации обращайтесь в Illustrative Mathematics.
значок/стрелка/вправо/крупная копияУрок 1
значок/стрелка/вправо/большойУрок 3
Характеристики функций и их графики
Результаты обучения
- Определить, представляет ли отношение функцию.

- Найти значения функции.
- Определить, является ли функция взаимно однозначной.
- Используйте тест вертикальной линии для определения функций.
- График функций в библиотеке функций.
Реактивный лайнер меняет высоту по мере увеличения расстояния от начальной точки полета. Вес растущего ребенка со временем увеличивается. В каждом случае одна величина зависит от другой. Между двумя величинами существует взаимосвязь, которую мы можем описать, проанализировать и использовать для прогнозирования. В этом разделе мы проанализируем такие отношения.
Характеристики функций
Отношение представляет собой набор упорядоченных пар. Набор первых компонентов каждой упорядоченной пары называется доменом отношения, а набор вторых компонентов каждой упорядоченной пары называется диапазоном отношения. Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел.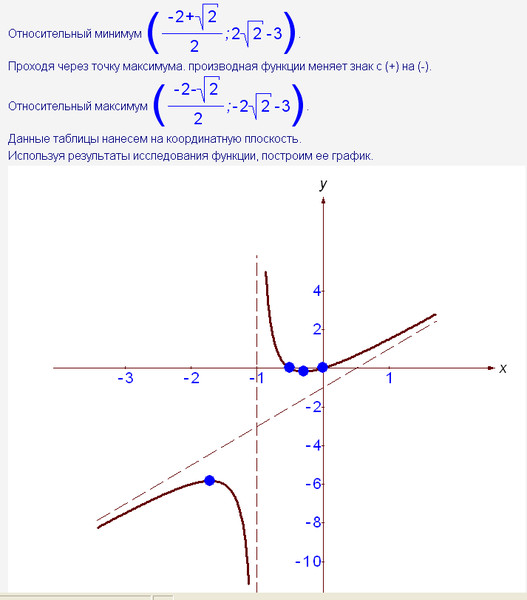 Второе число в каждой паре вдвое больше первого.
Второе число в каждой паре вдвое больше первого.
[латекс] \ влево \ {\ влево (1,2 \ вправо), \ влево (2,4 \ вправо), \ влево (3,6 \ вправо), \ влево (4,8 \ вправо), \ влево (5,10\right)\right\}[/latex]
Домен [latex]\left\{1,2,3,4,5\right\}[/latex]. Диапазон: [латекс]\влево\{2,4,6,8,10\вправо\}[/латекс].
Обратите внимание, что значения в домене также известны как входных значений или значений независимой переменной и часто обозначаются строчной буквой [латекс]х[/латекс]. Значения в этом диапазоне также известны как выход 9.0136 или значения зависимой переменной и часто обозначаются строчной буквой [latex]y[/latex].
Функция [latex]f[/latex] — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене . Другими словами, значения [latex]x[/latex] не используются более одного раза. В нашем примере, который связывает первые пять натуральных чисел с числами, удвоенными их значениями, это отношение является функцией, поскольку каждый элемент в домене [латекс]\лево\{1,2,3,4,5\право\} [/latex], сочетается ровно с одним элементом в диапазоне [latex]\left\{2,4,6,8,10\right\}[/latex].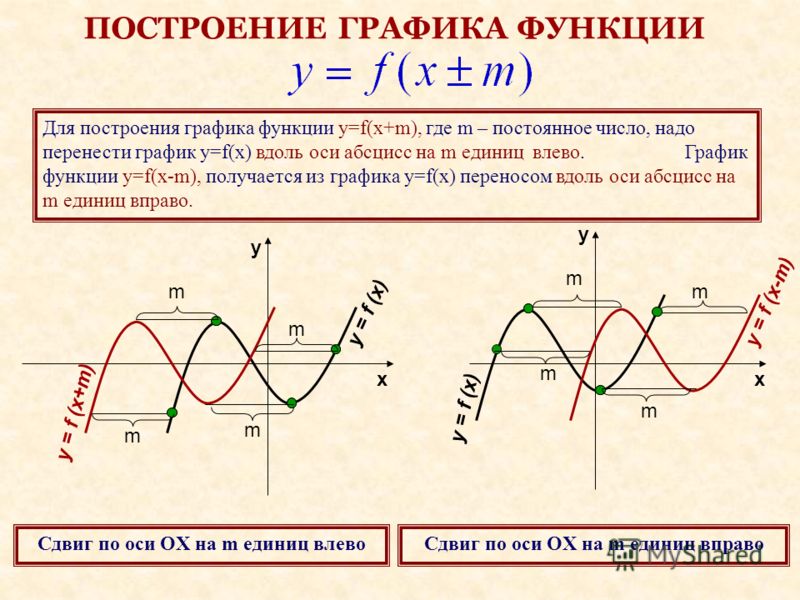
Теперь рассмотрим множество упорядоченных пар, связывающих термины «четный» и «нечетный» с первыми пятью натуральными числами. Это будет выглядеть как
[латекс]\влево\{\влево(\текст{нечетный},1\правый),\влево(\текст{четный},2\правый),\влево(\текст{нечетный}, 3\right),\left(\text{четный},4\right),\left(\text{нечетный},5\right)\right\}[/latex]
Обратите внимание, что каждый элемент в домене, [латекс]\левый\{\текст{четный}\текст{нечетный}\правый\}[/латекс] – это , а не в паре ровно с одним элементом в диапазоне, [латекс]\левый\{1,2, 3,4,5\право\}[/латекс]. Например, термин «нечетный» соответствует трем значениям из домена [латекс]\лево\{1,3,5\право\}[/латекс] , а термин «четный» соответствует двум значениям из диапазона, [латекс]\влево\{2,4\вправо\}[/латекс]. Это нарушает определение функции, поэтому это отношение не является функцией.
На этом изображении сравниваются отношения, которые являются функциями, а не функциями.
(a) Это отношение является функцией, поскольку каждый вход связан с одним выходом. Обратите внимание, что ввод [latex]q[/latex] и [latex]r[/latex] дают вывод [latex]n[/latex]. б) Это отношение также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, потому что ввод [латекс]q[/латекс] связан с двумя разными выходами.
Обратите внимание, что ввод [latex]q[/latex] и [latex]r[/latex] дают вывод [latex]n[/latex]. б) Это отношение также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, потому что ввод [латекс]q[/латекс] связан с двумя разными выходами.
A Общее примечание: функции
Функция представляет собой отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим, что «выход есть функция входа».
Входные значения составляют домен , а выходные значения составляют диапазон .
Как: Имея связь между двумя величинами, определить, является ли связь функцией.- Определите входные значения.
- Определите выходные значения.
- Если каждое входное значение приводит только к одному выходному значению, отношение является функцией.
 Если любое входное значение приводит к двум или более выходам, отношение не является функцией.
Если любое входное значение приводит к двум или более выходам, отношение не является функцией.
Пример: определение того, являются ли прайс-листы меню функциями
Меню кофейни состоит из позиций и их цен.
- Зависит ли цена от товара?
- Является ли предмет функцией цены?
Показать решение
Пример. Определение того, являются ли правила выставления оценок функциями.
В конкретном математическом классе общая оценка в процентах соответствует среднему баллу. Является ли средний балл успеваемости функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице ниже показано возможное правило выставления оценок.
| Процентное содержание | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
|---|---|---|---|---|---|---|---|---|
| Средний балл | 0,0 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
Показать решение
youtube.com/embed/zT69oxcMhPw?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Попробуйте
В таблице ниже перечислены пять величайших бейсболистов всех времен в порядке их ранга.
| Игрок | Ранг |
|---|---|
| Бэйб Рут | 1 |
| Вилли Мейс | 2 |
| Тай Кобб | 3 |
| Уолтер Джонсон | 4 |
| Хэнк Аарон | 5 |
- Зависит ли ранг от имени игрока?
- Зависит ли имя игрока от ранга?
Показать решение
Использование обозначения функций
Как только мы определили, что отношение является функцией, нам нужно отобразить и определить функциональные отношения, чтобы мы могли понять и использовать их, а иногда также чтобы мы могли запрограммировать их в компьютеры.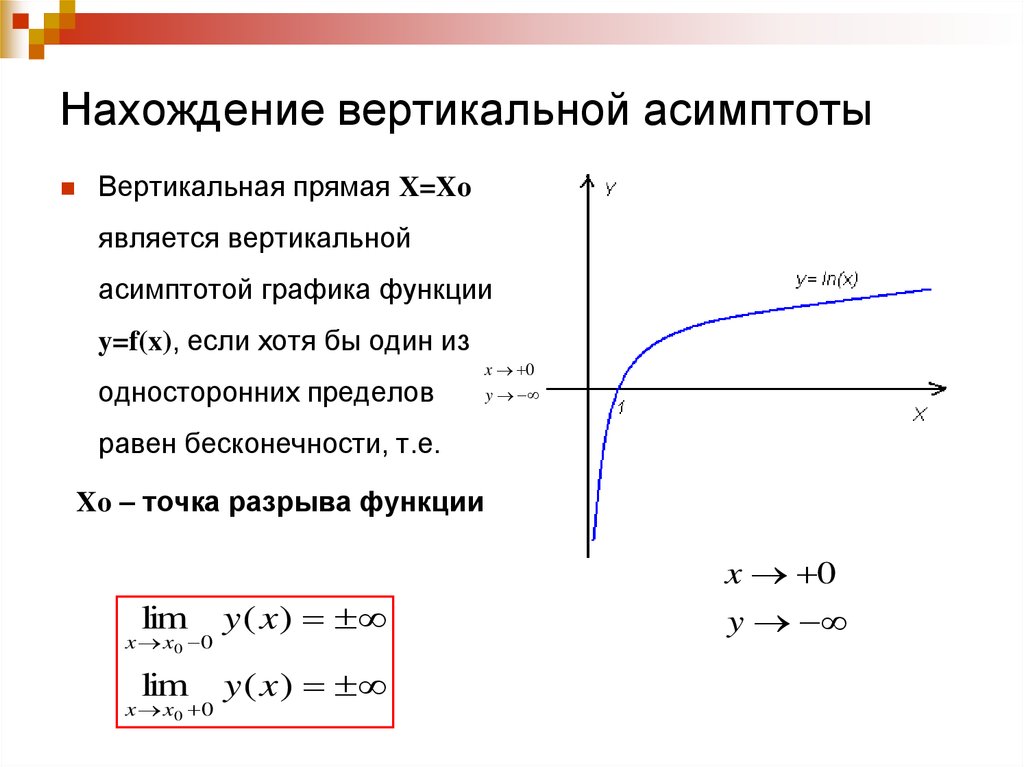 Существуют различные способы представления функций. Стандартное обозначение функции – – это одно из представлений, упрощающее работу с функциями.
Существуют различные способы представления функций. Стандартное обозначение функции – – это одно из представлений, упрощающее работу с функциями.
Чтобы представить «рост является функцией возраста», мы начнем с определения описательных переменных [latex]h[/latex] для роста и [latex]a[/latex] для возраста. Буквы [латекс]f,g[/латекс] и [латекс]ч[/латекс] часто используются для обозначения функций точно так же, как мы используем [латекс]х,у[/латекс] и [латекс]z[/ латекс] для представления чисел и [латекс]А,В[/латекс] и [латекс]С[/латекс] для представления наборов.
[латекс]\begin{align}&h\text{ есть }f\text{ of }a &&\text{Мы называем функцию }f;\text{ высота является функцией возраста}. \\ &h=f\left(a\right) &&\text{Мы используем круглые скобки для обозначения ввода функции}\text{. } \\ &f\left(a\right) &&\text{Назовем функцию }f;\text{ выражение читается как }»f\text{ of }a». \end{align}[/latex]
Помните, мы можем использовать любую букву для названия функции; мы можем использовать обозначение [латекс]ч\влево(а\вправо)[/латекс] , чтобы показать, что [латекс]ч[/латекс] зависит от [латекс]а[/латекс]. Входное значение [latex]a[/latex] должно быть помещено в функцию [latex]h[/latex], чтобы получить выходное значение. Скобки указывают на то, что в функцию вводится возраст; они не указывают на умножение.
Входное значение [latex]a[/latex] должно быть помещено в функцию [latex]h[/latex], чтобы получить выходное значение. Скобки указывают на то, что в функцию вводится возраст; они не указывают на умножение.
Мы также можем задать алгебраическое выражение в качестве входных данных для функции. Например, [латекс]f\влево(а+b\вправо)[/латекс] означает «сначала добавить [латекс]а[/латекс] и [латекс]b[/латекс], и результат будет вводом для функции [латекс]ф[/латекс]». Мы должны выполнять операции в таком порядке, чтобы получить правильный результат.
A Общее примечание: Обозначение функций
Обозначение [latex]y=f\left(x\right)[/latex] определяет функцию с именем [latex]f[/latex]. Это читается как [latex]«y[/latex] является функцией [latex]x.»[/latex] Буква [latex]x[/latex] представляет входное значение или независимую переменную. Буква [latex]y[/latex] или [latex]f\left(x\right)[/latex] представляет выходное значение или зависимую переменную.
Пример: Использование функциональной нотации для дней в месяце
Используйте функциональную нотацию для представления функции, входом которой является название месяца, а выходом — количество дней в этом месяце невисокосного года.
Показать раствор
Пример: интерпретация обозначения функции
Функция [latex]N=f\left(y\right)[/latex] дает количество полицейских, [latex]N[/latex], в городе в год [ латекс]у[/латекс]. Что представляет собой [латекс]f\left(2005\right)=300[/latex]?
Показать решение
Вопросы и ответы
Вместо обозначения, такого как [латекс]у=f\влево(х\вправо)[/латекс], могли бы мы использовать тот же символ для вывода, что и для функции, например [латекс ]y=y\left(x\right)[/latex], что означает « y является функцией x ?»
Да, это часто делается, особенно по прикладным предметам, использующим высшую математику, таким как физика и инженерия. Однако при изучении самой математики нам нравится сохранять различие между такой функцией, как [latex]f[/latex], которая является правилом или процедурой, и выводом [latex]y[/latex], который мы получаем, применяя [latex ]f[/latex] на конкретный ввод [latex]x[/latex]. Вот почему мы обычно используем такие обозначения, как [латекс]y=f\left(x\right),P=W\left(d\right)[/latex] и так далее.
Вот почему мы обычно используем такие обозначения, как [латекс]y=f\left(x\right),P=W\left(d\right)[/latex] и так далее.
Представление функций с помощью таблиц
Обычный метод представления функций — в форме таблицы. В строках или столбцах таблицы отображаются соответствующие входные и выходные значения. В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях в таблице представлены несколько избранных примеров из более полных взаимосвязей.
В таблице ниже перечислены входные числа для каждого месяца (январь = 1, февраль = 2 и т. д.) и выходное значение количества дней в этом месяце. Эта информация представляет собой все, что мы знаем о месяцах и днях для данного года (это не високосный год). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце [latex]f[/latex], где [latex]D=f\left(m\right)[/latex] определяет месяцы целым числом а не по имени.
| Номер месяца, [латекс]м[/латекс] (ввод) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Дней в месяце, [latex]D[/latex] (выход) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
В таблице ниже определяется функция [latex]Q=g\left(n\right)[/latex]. Помните, эта запись говорит нам, что [latex]g[/latex] — это имя функции, которая принимает входные данные [latex]n[/latex] и выдает выходные данные [latex]Q[/latex].
Помните, эта запись говорит нам, что [latex]g[/latex] — это имя функции, которая принимает входные данные [latex]n[/latex] и выдает выходные данные [latex]Q[/latex].
| [латекс]n[/латекс] | 1 | 2 | 3 | 4 | 5 |
| [латекс]Q[/латекс] | 8 | 6 | 7 | 6 | 8 |
В таблице ниже указан возраст детей в годах и их соответствующий рост. В этой таблице представлены лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет собой функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма
| Возраст в годах, [латекс]\текст { }a\text{ }[/latex] (ввод) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Высота в дюймах, [латекс]\текст{ }ч\текст{ }[/латекс] (выход) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |

- Определите входные и выходные значения.
- Проверьте, связано ли каждое входное значение только с одним выходным значением. Если это так, таблица представляет собой функцию.
Пример: определение таблиц, представляющих функции
Какая таблица, A, B или C, представляет функцию (если есть)?
| Стол А | |
|---|---|
| Вход | Выход |
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Таблица B | |
|---|---|
| Вход | Выход |
| –3 | 5 |
| 0 | 1 |
| 4 | 5 |
Показать решение
Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию. Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Когда мы знаем выходное значение и хотим определить входные значения, которые дадут это выходное значение, мы устанавливаем выход равным формуле функции и решить для ввода. Решение может дать более одного решения, потому что разные входные значения могут дать одно и то же выходное значение.
Определить, является ли функция взаимно однозначной
Некоторые функции имеют заданное выходное значение, которое соответствует двум или более входным значениям. Например, на следующем графике акций цена акции составляла 1000 долларов в пять разных дат, а это означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.
Например, на следующем графике акций цена акции составляла 1000 долларов в пять разных дат, а это означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.
Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции однозначными функциями. В качестве примера рассмотрим школу, которая использует только буквенные оценки и десятичные эквиваленты, как указано в
| Буквенная оценка | Средний балл |
|---|---|
| А | 4,0 |
| Б | 3,0 |
| С | 2,0 |
| Д | 1,0 |
Эта система оценивания представляет собой функцию «один к одному», потому что каждая введенная буква дает один конкретный выходной средний балл, а каждый средний балл соответствует одной входной букве.
Чтобы наглядно представить эту концепцию, давайте еще раз взглянем на две простые функции, показанные в (а) и (б) ниже.
Функция в части (a) показывает отношение, которое не является взаимно-однозначным, потому что входные данные [latex]q[/latex] и [latex]r[/latex] дают выходные данные [latex]n[/ латекс]. Функция в части (b) показывает взаимосвязь, которая является взаимно однозначной функцией, поскольку каждый вход связан с одним выходом.
A Общее примечание: Функция «один к одному»
Функция «один к одному» — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.
Пример: определение того, является ли отношение взаимно-однозначной функцией
Является ли площадь круга функцией его радиуса? Если да, то функция один к одному?
Показать раствор
Попробуйте
- Зависит ли баланс от номера банковского счета?
- Является ли номер банковского счета функцией баланса? 9{2}+3x – 4[/latex], оцените каждое из следующих условий.

- [латекс]f\влево(2\вправо)[/латекс]
- [латекс]ф(а)[/латекс]
- [латекс]f(a+h)[/латекс]
- [латекс]\dfrac{f\left(a+h\right)-f\left(a\right)}{h}[/latex]
Показать решение
Попробуйте
Учитывая функцию [латекс]g\left(m\right)=\sqrt{m — 4}[/latex], оцените [латекс]g\left(5\right)[/latex].
Показать раствор
Пример: Решение функций 9{2}+2p[/латекс], найдите [латекс]ч\влево(п\вправо)=3[/латекс].
Показать раствор
Попробуйте
Учитывая функцию [латекс]g\left(m\right)=\sqrt{m — 4}[/latex], решить [латекс]g\left(m\right)=2[ /латекс].

Показать раствор
Вычисление функций, выраженных в формулах
Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения . Если возможно выразить выход функции с помощью формулы с входной величиной, то мы можем определить функцию в алгебраической форме. Например, уравнение [латекс]2n+6p=12[/латекс] выражает функциональную связь между [латекс]n[/латекс] и [латекс]p[/латекс]. Мы можем переписать его, чтобы решить, является ли [latex]p[/latex] функцией [latex]n[/latex].
Как: Дана функция в виде уравнения, напишите ее алгебраическую формулу.
- Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства, а с другой стороны как выражение, включающее только входная переменная.
- Используйте все обычные алгебраические методы для решения уравнений, такие как прибавление или вычитание одной и той же величины из обеих частей или умножение или деление обеих частей уравнения на одну и ту же величину.

Пример: нахождение уравнения функции
Выразите отношение [latex]2n+6p=12[/latex] в виде функции [latex]p=f\left(n\right)[/latex], если возможно .
Показать раствор
Пример: выражение уравнения окружности в виде функции 9{y}[/latex], если мы хотим выразить [latex]y[/latex] как функцию [latex]x[/latex], не существует простой алгебраической формулы, включающей только [latex]x[/latex] что равно [латекс]у[/латекс]. Однако каждый [латекс]x[/латекс] определяет уникальное значение для [латекс]у[/латекс], и существуют математические процедуры, с помощью которых [латекс]у[/латекс] можно найти с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [latex]y[/latex] как функции [latex]x[/latex], даже если формулу нельзя записать явно.

Вычисление функции, заданной в табличной форме
Как мы видели выше, мы можем представлять функции в виде таблиц. И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции, используя таблицы. Например, насколько хорошо наши питомцы помнят приятные воспоминания, которыми мы делимся с ними? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, а бета-рыбка имеет память до 5 месяцев. И если память щенка не превышает 30 секунд, то взрослая собака может помнить 5 минут. Это мизер по сравнению с кошкой, память которой длится 16 часов.
Функцию, связывающую тип питомца с длительностью его памяти, легче визуализировать с помощью таблицы. См. таблицу ниже.
Домашнее животное Объем памяти в часах Щенок 0,008 Взрослая собака 0,083 Кат 16 Золотая рыбка 2160 Бета-рыба 3600 Иногда вычисление функции в виде таблицы может оказаться более полезным, чем использование уравнений.
 Здесь давайте вызовем функцию [latex]P[/latex].
Здесь давайте вызовем функцию [latex]P[/latex].Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию [latex]P[/latex] по входному значению «золотая рыбка». Мы бы написали [латекс]P\влево(\текст{золотая рыбка}\вправо)=2160[/латекс]. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции [latex]P[/latex] кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
Как сделать: Имея функцию, представленную в виде таблицы, определите конкретные выходные и входные значения.
- Найдите заданный вход в строке (или столбце) входных значений.
- Идентифицируйте соответствующее выходное значение в паре с этим входным значением.

- Найдите указанные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда появляется это выходное значение.
- Определите входное значение(я), соответствующее данному выходному значению.
Пример: вычисление и решение табличной функции
Используя приведенную ниже таблицу,
- Вычислите [latex]g\left(3\right)[/latex].
- Решить [латекс]г\влево(п\вправо)=6[/латекс].
[латекс]n[/латекс] 1 2 3 4 5 [латекс]g(n)[/латекс] 8 6 7 6 8 Показать решение
Попробуйте
Используя таблицу из предыдущего примера, вычислите [latex]g\left(1\right)[/latex] .

Показать раствор
Поиск значений функции на графике
Вычисление функции с помощью графика также требует нахождения соответствующего выходного значения для заданного входного значения, только в этом случае мы находим выходное значение, глядя на график. Решение функционального уравнения с использованием графика требует нахождения всех экземпляров заданного выходного значения на графике и наблюдения за соответствующим входным значением (значениями).
Пример: Чтение значений функции из графика
Учитывая приведенный ниже график,
- Вычислить [латекс]f\влево(2\вправо)[/латекс].
- Решить [латекс]f\влево(х\вправо)=4[/латекс].
Показать решение
Попробуйте
Используя график, решите [латекс]f\влево(х\вправо)=1[/латекс].
Показать раствор
Идентификация функций с помощью графиков
Как мы видели в приведенных выше примерах, мы можем представить функцию с помощью графика.
 Графики отображают множество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Графики отображают множество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.Наиболее распространенные графики называют входное значение [латекс]x[/латекс] и выходное значение [латекс]у[/латекс], и мы говорим, что [латекс]у[/латекс] является функцией [латекс]х [/latex], или [latex]y=f\left(x\right)[/latex], когда функция называется [latex]f[/latex]. График функции представляет собой множество всех точек [латекс]\влево(х,у\вправо)[/латекс] на плоскости, удовлетворяющих уравнению [латекс]у=f\влево(х\вправо)[/латекс ]. Если функция определена только для нескольких входных значений, то график функции представляет собой всего несколько точек, где x -координата каждой точки является входным значением, а y -координата каждой точки является соответствующим выходным значением.
 Например, черные точки на графике ниже говорят нам, что [латекс]f\влево(0\вправо)=2[/латекс] и [латекс]f\влево(6\вправо)=1[/латекс ]. Однако множество всех точек [латекс]\влево(х,у\вправо)[/латекс], удовлетворяющих [латекс]у=f\влево(х\вправо)[/латекс], является кривой. Показанная кривая включает [латекс]\влево(0,2\вправо)[/латекс] и [латекс]\влево(6,1\вправо)[/латекс], поскольку кривая проходит через эти точки.
Например, черные точки на графике ниже говорят нам, что [латекс]f\влево(0\вправо)=2[/латекс] и [латекс]f\влево(6\вправо)=1[/латекс ]. Однако множество всех точек [латекс]\влево(х,у\вправо)[/латекс], удовлетворяющих [латекс]у=f\влево(х\вправо)[/латекс], является кривой. Показанная кривая включает [латекс]\влево(0,2\вправо)[/латекс] и [латекс]\влево(6,1\вправо)[/латекс], поскольку кривая проходит через эти точки.Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Вертикальная линия включает все точки с определенным значением [latex]x[/latex]. Значение [latex]y[/latex] точки, в которой вертикальная линия пересекает график, представляет собой результат для этого входного значения [latex]x[/latex]. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, то график , а не определяет функцию, потому что это значение [latex]x[/latex] имеет более одного выхода. Функция имеет только одно выходное значение для каждого входного значения.

Как: Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
- Изучите график, чтобы увидеть, пересекает ли какая-либо вертикальная линия кривую более одного раза.
- Если такая линия есть, то график не представляет функцию.
- Если ни одна вертикальная линия не может пересекать кривую более одного раза, график представляет собой функцию.
Пример: применение теста вертикальной линии
Какой из графиков представляет функцию [latex]y=f\left(x\right)?[/latex]
Показать решение
Попробуйте
Представляет ли график ниже функцию?
Показать раствор
Тест горизонтальной линии
После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — это использовать тест горизонтальной линии .
 Проведите горизонтальные линии через график. Горизонтальная линия включает все точки с определенным значением [latex]y[/latex]. Значение [latex]x[/latex] точки, в которой вертикальная линия пересекает функцию, представляет вход для этого выходного значения [latex]y[/latex]. Если мы можем нарисовать любая горизонтальная линия , которая пересекает график более одного раза, то график , а не представляет собой функцию один к одному, потому что это значение [latex]y[/latex] имеет более одного входа.
Проведите горизонтальные линии через график. Горизонтальная линия включает все точки с определенным значением [latex]y[/latex]. Значение [latex]x[/latex] точки, в которой вертикальная линия пересекает функцию, представляет вход для этого выходного значения [latex]y[/latex]. Если мы можем нарисовать любая горизонтальная линия , которая пересекает график более одного раза, то график , а не представляет собой функцию один к одному, потому что это значение [latex]y[/latex] имеет более одного входа.Как: Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график функцию взаимно однозначного соответствия.
- Изучите график, чтобы увидеть, пересекает ли какая-либо горизонтальная линия кривую более одного раза.
- Если такая строка есть, то функция не является однозначной.
- Если ни одна горизонтальная линия не может пересекать кривую более одного раза, функция является однозначной.
Пример: применение теста горизонтальной линии
Рассмотрим функции (a) и (b), показанные на графиках ниже.

Является ли какая-либо из функций взаимно однозначной?
Показать решение
Идентификация основных функций набора инструментов
В этом тексте мы исследуем функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения задач с ними. При обучении чтению мы начинаем с алфавита. При обучении арифметике мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор элементов стандартного блока. Мы называем их «инструментальными функциями», которые образуют набор основных именованных функций, для которых мы знаем график, формулу и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать [latex]x[/latex] в качестве входной переменной и [latex]y=f\left(x\right)[/latex] в качестве выходной переменной.

Мы будем часто встречаться с этими инструментальными функциями, комбинациями инструментальных функций, их графиками и преобразованиями в этой книге. Будет очень полезно, если мы сможем быстро распознать эти функции инструментария и их функции по имени, формуле, графику и основным свойствам таблицы. Графики и примерные табличные значения прилагаются к каждой функции, показанной ниже.
Функции набора инструментов Имя Функция 9{2}}[/латекс]Квадратный корень [латекс]f\влево(х\вправо)=\sqrt{x}[/латекс] Кубический корень [латекс]f\влево(х\вправо)=\sqrt[3]{х}[/латекс] Попробуйте
Ключевые понятия
- Отношение представляет собой набор упорядоченных пар. Функция — это особый тип отношения, в котором каждое значение домена или входные данные приводят ровно к одному значению диапазона или выходным данным.

- Обозначение функций — это сокращенный метод для связи входных данных с выходными в форме [латекс]у=f\влево(х\вправо)[/латекс].
- В форме таблицы функция может быть представлена строками или столбцами, которые относятся к входным и выходным значениям.
- Чтобы оценить функцию, мы определяем выходное значение для соответствующего входного значения. Алгебраические формы функции можно вычислить, заменив входную переменную заданным значением.
- Чтобы найти конкретное значение функции, мы определяем входные значения, которые дают конкретное выходное значение.
- Алгебраическая форма функции может быть записана из уравнения.
- Входные и выходные значения функции можно определить по таблице.
- Соотношение входных значений с выходными значениями на графике — еще один способ оценки функции.
- Функция является однозначной, если каждое выходное значение соответствует только одному входному значению.
- График представляет собой функцию, если любая вертикальная линия, проведенная на графике, пересекает график не более чем в одной точке.

- График представляет собой взаимно-однозначную функцию, если любая горизонтальная линия, проведенная на графике, пересекает график не более чем в одной точке.
Глоссарий
- зависимая переменная
- выходная переменная
- домен
- набор всех возможных входных значений для отношения
- функция
- отношение, в котором каждое входное значение дает уникальное выходное значение
- проверка горизонтальной линии
- метод проверки того, является ли функция взаимно однозначной, путем определения того, пересекает ли какая-либо горизонтальная линия график более одного раза
- независимая переменная
- входная переменная
- ввод
- каждый объект или значение в домене, связанное с другим объектом или значением отношением, известным как функция
- Функция «один к одному»
- функция, для которой каждое значение вывода связано с уникальным входным значением
- выход
- каждый объект или значение в диапазоне, который создается при вводе входного значения в функцию
- Диапазон
- набор выходных значений, которые являются результатом входных значений в отношении
- отношение
- комплект заказанных пар
- проверка вертикальной линии
- метод проверки того, представляет ли график функцию, путем определения того, пересекает ли график вертикальная линия не более одного раза
3.
 1 Функции и обозначение функций — College Algebra 2e
1 Функции и обозначение функций — College Algebra 2eЦели обучения
В этом разделе вы:
- Определить, представляет ли отношение функцию.
- Найти значение функции.
- Определить, является ли функция взаимно однозначной.
- Используйте тест вертикальной линии для определения функций.
- График функций, перечисленных в библиотеке функций.
Реактивный лайнер меняет высоту по мере увеличения расстояния от начальной точки полета. Вес растущего ребенка со временем увеличивается. В каждом случае одна величина зависит от другой. Между двумя величинами существует взаимосвязь, которую мы можем описать, проанализировать и использовать для прогнозирования. В этом разделе мы проанализируем такие отношения.
Определение того, представляет ли отношение функцию
Отношение представляет собой набор упорядоченных пар. Набор первых компонентов каждой упорядоченной пары называется доменом , а набор вторых компонентов каждой упорядоченной пары называется диапазоном .
 Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.
Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.{(1,2),(2,4),(3,6),(4,8),(5,10)}{(1,2),(2,4),(3,6) ,(4,8),(5,10)}
Домен {1,2,3,4,5}.{1,2,3,4,5}. Диапазон: {2,4,6,8,10}.{2,4,6,8,10}.
Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто обозначается строчной буквой x.x. Каждое значение в диапазоне также известно как выходное значение или зависимая переменная и часто обозначается строчной буквой yy.
Функция ff — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене . Другими словами, значения x не повторяются. В нашем примере, который связывает первые пять натуральных чисел с числами, удвоенными их значениями, это отношение является функцией, поскольку каждый элемент в области значений {1,2,3,4,5},{1,2,3,4,5 }, сочетается ровно с одним элементом в диапазоне {2,4,6,8,10}.
 {2,4,6,8,10}.
{2,4,6,8,10}.Теперь рассмотрим множество упорядоченных пар, связывающих термины «четный» и «нечетный» с первыми пятью натуральными числами. Это выглядело бы как
{(нечетное,1),(четное,2),(нечетное,3),(четное,4),(нечетное,5)}{(нечетное,1),(четное,2),(нечетное,3 ),(четное,4),(нечетное,5)}
Обратите внимание, что каждый элемент в домене {четный, нечетный} {четный, нечетный} равно , а не в паре ровно с одним элементом в диапазоне {1,2,3,4,5}.{1,2,3,4,5}. Например, термин «нечетный» соответствует трем значениям из диапазона {1,3,5}{1,3,5}. а термин «четный» соответствует двум значениям из диапазона {2,4}.{2,4}. Это нарушает определение функции, поэтому это отношение не является функцией.
На рис. 1 сравниваются отношения, которые являются функциями и не функциями.
Рисунок 1 (a) Это отношение является функцией, поскольку каждый вход связан с одним выходом. Обратите внимание, что ввод qq и rr оба дают вывод n.
 n. б) Это отношение также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, поскольку вход qq связан с двумя разными выходами.
n. б) Это отношение также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, поскольку вход qq связан с двумя разными выходами.Функция
Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим, что «выход есть функция входа».
Входные значения составляют домен, а выходные значения составляют диапазон.
Как
Учитывая связь между двумя величинами, определите, является ли связь функцией.
- Определите входные значения.
- Определите выходные значения.
- Если каждое входное значение приводит только к одному выходному значению, классифицируйте отношение как функцию. Если какое-либо входное значение приводит к двум или более выходам, не классифицируйте отношение как функцию.
Пример 1
Определение того, являются ли прайс-листы меню функциями
Меню кофейни, показанное ниже, состоит из элементов и их цен.

ⓐ Зависит ли цена от товара?
ⓑ Является ли предмет функцией цены?Решение
ⓐ Начнем с рассмотрения ввода как пунктов меню. Тогда выходные значения являются ценами.
Каждый пункт в меню имеет только одну цену, поэтому цена зависит от пункта.
ⓑ Два блюда в меню имеют одинаковую цену. Если мы считаем, что цены являются входными значениями, а товары — выходными, то одно и то же входное значение может иметь более одного связанного с ним выхода. См. изображение ниже.
Таким образом, пункт не зависит от цены.Пример 2
Определение того, являются ли правила выставления оценок функциями.
В конкретном математическом классе общая оценка в процентах соответствует среднему баллу. Является ли средний балл успеваемости функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице 1 показано возможное правило выставления оценок.

Процентное содержание 0–56 57–61 62–66 67–71 72–77 78–86 87–91 92–100 Средний балл 0,0 1,0 1,5 2,0 2,5 3,0 3,5 4,0 Стол 1
Решение
Для любого процента полученной оценки существует соответствующий средний балл, поэтому средний балл является функцией процента оценки.
 Другими словами, если мы вводим процентную оценку, на выходе получается определенный средний балл.
Другими словами, если мы вводим процентную оценку, на выходе получается определенный средний балл.В данной системе оценивания существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу. Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.
Попытайся #1
В таблице 2 1 перечислены пять величайших бейсболистов всех времен в порядке их ранга.
Игрок Ранг Бэйб Рут 1 Вилли Мейс 2 Тай Кобб 3 Уолтер Джонсон 4 Хэнк Аарон 5 Стол 2
- ⓐЗависит ли ранг от имени игрока?
- ⓑ Является ли имя игрока функцией ранга?
Использование обозначения функций
Как только мы определили, что отношение является функцией, нам нужно отобразить и определить функциональные отношения, чтобы мы могли понять и использовать их, а иногда также чтобы мы могли запрограммировать их в компьютеры.
 Существуют различные способы представления функций. Стандартная нотация функций — это одно из представлений, упрощающее работу с функциями.
Существуют различные способы представления функций. Стандартная нотация функций — это одно из представлений, упрощающее работу с функциями.Чтобы представить «рост является функцией возраста», мы начнем с определения описательных переменных hh для высоты и аа для возраста. Буквы f,g,f,g и hh часто используются для обозначения функций точно так же, как мы используем x,y,x,y и zz для представления чисел и A,B,A,B, и CC для представления наборов.
его f от a Мы называем функцию f; рост является функцией возраста. h = f (a) Мы используем круглые скобки, чтобы указать вход функции. f(a) Мы называем функцию f; выражение читается как «f of a». Его f of a Мы называем функцию f; высота — это функция возраста. f(a) Мы называем функцию f; выражение читается как «fof a».
Помните, мы можем использовать любую букву для названия функции; обозначение h(a)h(a) показывает нам, что hh зависит от п. в. Чтобы получить результат, необходимо подставить значение aa в функцию hh.
 Скобки указывают на то, что в функцию вводится возраст; они не указывают на умножение.
Скобки указывают на то, что в функцию вводится возраст; они не указывают на умножение.Мы также можем задать алгебраическое выражение в качестве входных данных для функции. Например, f(a+b)f(a+b) означает «сначала добавить к и к , и результатом будет ввод для функции f ». Операции должны выполняться в таком порядке, чтобы получить правильный результат.
Обозначение функции
Обозначение y=f(x)y=f(x) определяет функцию с именем f.f. Это читается как «y«y есть функция x.x». Буква xx представляет входное значение или независимую переменную. Буква y,y или f(x),f(x) представляет собой выходное значение или зависимую переменную.
Пример 3
Использование функциональной нотации для дней в месяце
Используйте функциональную нотацию для представления функции, входом которой является название месяца, а выходом — количество дней в этом месяце.
 Предположим, что домен не включает високосные годы.
Предположим, что домен не включает високосные годы.Решение
Количество дней в месяце зависит от названия месяца, поэтому, если мы назовем функцию f,f, мы напишем days=f(month)days=f(month) или d=f(m).d=f(m). Название месяца является входом для «правила», которое связывает определенное число (выход) с каждым входом.
Рисунок 2
Например, f(март)=31,f(март)=31, потому что в марте 31 день. Обозначение d=f(m)d=f(m) напоминает нам, что количество дней, dd (выход), зависит от названия месяца, mm (вход).
Анализ
Обратите внимание, что входные данные функции не обязательно должны быть числами; входными данными функции могут быть имена людей, метки геометрических объектов или любой другой элемент, определяющий какой-либо вывод. Однако большинство функций, с которыми мы будем работать в этой книге, будут иметь числа в качестве входных и выходных данных.
Пример 4
Обозначение функций интерпретации
Функция N=f(y)N=f(y) дает количество полицейских, N,N, в городе в году y.
 y. Что представляет собой f(2005)=300f(2005)=300?
y. Что представляет собой f(2005)=300f(2005)=300?Решение
Когда мы читаем f(2005)=300,f(2005)=300, мы видим, что входной год — 2005. Выходное значение, количество полицейских (N),(N), равно 300. Помните , N=f(y).N=f(y). Утверждение f(2005)=300f(2005)=300 говорит нам о том, что в 2005 году в городе было 300 полицейских.
Попытайся #2
Используйте функциональные обозначения для выражения веса свиньи в фунтах в зависимости от ее возраста в днях d.d.
вопросы и ответы
Вместо обозначения, такого как y=f(x),y=f(x), можно ли использовать тот же символ для вывода, что и для функции, например y=y(x),y=y( x), что означает « y является функцией x ?»
Да, это часто делается, особенно по прикладным предметам, использующим высшую математику, таким как физика и инженерия.
 Однако при изучении самой математики нам нравится сохранять различие между такими функциями, как f,f, которые являются правилом или процедурой, и выходными данными yy, которые мы получаем, применяя ff к конкретным входным данным x.x. Вот почему мы обычно используем такие обозначения, как y=f(x),P=W(d),y=f(x),P=W(d) и так далее.
Однако при изучении самой математики нам нравится сохранять различие между такими функциями, как f,f, которые являются правилом или процедурой, и выходными данными yy, которые мы получаем, применяя ff к конкретным входным данным x.x. Вот почему мы обычно используем такие обозначения, как y=f(x),P=W(d),y=f(x),P=W(d) и так далее. Представление функций с помощью таблиц
Обычный метод представления функций — в форме таблицы. В строках или столбцах таблицы отображаются соответствующие входные и выходные значения. В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях в таблице представлены несколько избранных примеров из более полных взаимосвязей.
В таблице 3 перечислены введенные номера каждого месяца (январь = 1, февраль = 2 и т. д.) и выходное значение количества дней в этом месяце. Эта информация представляет собой все, что мы знаем о месяцах и днях для данного года (это не високосный год). Обратите внимание, что в этой таблице мы определяем функцию числа дней в месяце ff, где D=f(m)D=f(m) идентифицирует месяцы целым числом, а не именем.

Номер месяца, мм (ввод) 1 2 3 4 5 6 7 8 9 10 11 12 Дней в месяце, ДД (выход) 31 28 31 30 31 30 31 31 30 31 30 31 Стол 3
Таблица 4 определяет функцию Q=g(n).
 Q=g(n). Помните, эта запись говорит нам, что gg — это имя функции, которая принимает входные данные nn и дает выходные данные Q.Q.
Q=g(n). Помните, эта запись говорит нам, что gg — это имя функции, которая принимает входные данные nn и дает выходные данные Q.Q.нн 1 2 3 4 5 QQ 8 6 7 6 8 Стол 4
В таблице 5 указан возраст детей в годах и их соответствующий рост. В этой таблице представлены лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет собой функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма
Возраст в годах, аа (ввод) 5 5 6 7 8 9 10 Высота в дюймах, чч (вывод) 40 42 44 47 50 52 54 Стол 5
Как
Имея таблицу входных и выходных значений, определите, представляет ли таблица функцию.

- Определите входные и выходные значения.
- Проверьте, связано ли каждое входное значение только с одним выходным значением. Если это так, таблица представляет собой функцию.
Пример 5
Идентификация таблиц, представляющих функции
Какая таблица (таблица 6, таблица 7 или таблица 8) представляет функцию (если есть)?
Вход Выход 2 1 5 3 8 6 Стол 6
Вход Выход –3 5 0 1 4 5 Стол 7
Вход Выход 1 0 5 2 5 4 Стол 8
Решение
Таблица 6 и Таблица 7 определяют функции.
 В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица 8 не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям.
В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица 8 не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям.Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функций.
Функция, представленная в Таблице 6, может быть представлена записью
f(2)=1,f(5)=3 и f(8)=6f(2)=1,f(5)=3,и f(8)=6
Аналогично утверждения
g(−3)=5,g(0)=1,g(4)=5g(−3)=5,g(0)=1,g(4)=5
представляют функцию в таблице 7.
Таблица 8 не может быть выражена подобным образом, поскольку она не представляет функцию.
Попытайся #3
Представляет ли таблица 9 функцию?
Вход Выход 1 10 2 100 3 1000 Стол 9
Поиск входных и выходных значений функции
Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оценить функцию.
 Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.Когда мы знаем выходное значение и хотим определить входные значения, которые дадут это выходное значение, мы устанавливаем выход равным формуле функции и решаем для входа. Решение может дать более одного решения, потому что разные входные значения могут дать одно и то же выходное значение.
Вычисление функций в алгебраических формах
Когда у нас есть функция в форме формулы, обычно несложно вычислить функцию. Например, функцию f(x)=5−3x2f(x)=5−3×2 можно вычислить, возведя входное значение в квадрат, умножив его на 3 и вычитая произведение из 5.
Как
Дана формула функции, вычислить.
- Замените входную переменную в формуле предоставленным значением.
- Рассчитать результат.

Пример 6
Оценка функций при определенных значениях
Вычисление f(x)=x2+3x−4f(x)=x2+3x−4 по адресу:
- ⓐ 22
- ⓑ аа
- ⓒ а+ха+ч
- ⓓ Теперь оцените f(a+h)−f(a)hf(a+h)−f(a)h
Решение
Заменить хх в функции с каждым указанным значением.
- ⓐ Поскольку входным значением является число 2, мы можем использовать простую алгебру для упрощения.
f(2)=22+3(2)−4=4+6−4=6f(2)=22+3(2)−4=4+6−4=6
- ⓑ В этом случае входное значение представляет собой букву, поэтому мы не можем еще больше упростить ответ.
f(a)=a2+3a−4f(a)=a2+3a−4
- ⓒ При входном значении a+h,a+h мы должны использовать распределительное свойство.
f(a+h)=(a+h)2+3(a+h)−4=a2+2ah+h3+3a+3h−4f(a+h)=(a+h)2+3( а+h)−4=a2+2ah+h3+3a+3h−4
- ⓓ В этом случае мы применяем входные значения к функции более одного раза, а затем выполняем алгебраические операции над результатом.
 Мы уже нашли это
Мы уже нашли этоf(a+h)=a2+2ah+h3+3a+3h−4f(a+h)=a2+2ah+h3+3a+3h−4
и мы знаем, что
f(a)=a2+3a−4f(a)=a2+3a−4
Теперь объединим результаты и упростим.
f(a+h)−f(a)h=(a2+2ah+h3+3a+3h−4)−(a2+3a−4)h = 2ah+h3+3hh =h(2a+h+3 )hУбрать из h. =2a+h+3Simplify.f(a+h)−f(a)h=(a2+2ah+h3+3a+3h−4)−(a2+3a−4)h =2ah+h3+3hh =h (2a+h+3)hВычтите h. =2a+h+3Упрощение.
Пример 7
Вычисление функций
Учитывая функцию h(p)=p2+2p,h(p)=p2+2p, вычислить h(4).h(4).
Решение
Чтобы вычислить h(4),h(4), мы подставляем значение 4 для входной переменной pp в данной функции.
h(p)=p2+2ph(4)=(4)2+2(4) =16+8 =24h(p)=p2+2ph(4)=(4)2+2(4) = 16+8 =24
Следовательно, при входе 4 на выходе 24.
Попытайся #4
Учитывая функцию g(m)=m−4,g(m)=m−4, вычислить g(5).
 g(5).
g(5).Пример 8
Решающие функции
Для заданной функции h(p)=p2+2p,h(p)=p2+2p найдите h(p)=3.h(p)=3.
Решение
h(p)=3 p2+2p=3Замените исходную функцию h(p)=p2+2p.p2+2p−3=0Вычтите 3 с каждой стороны.(p+3)(p−1)=0Коэффициент. h(p)=3 p2+2p=3Подставить исходную функцию h(p)=p2+2p.p2+2p−3=0Вычесть 3 с каждой стороны.(p+3)(p−1)=0Множитель.
Если (p+3)(p−1)=0, (p+3)(p−1)=0, либо (p+3)=0(p+3)=0, либо (p−1) =0(p−1)=0 (или оба равны 0). Мы установим каждый фактор равным 0 и найдем pp в каждом случае.
(р+3)=0,р=-3(р-1)=0,р=1(р+3)=0,р=-3(р-1)=0,р=1
Это дает нам два решения. Выход h(p)=3h(p)=3, когда на входе либо p=1p=1, либо p=-3.p=-3. Мы также можем проверить с помощью графика, как на рисунке 3. График подтверждает, что h(1)=h(-3)=3h(1)=h(-3)=3 и h(4)=24.h(4) =24.
Рисунок 3
Попытайся #5
Учитывая функцию g(m)=m−4,g(m)=m−4, решить g(m)=2.
 g(m)=2.
g(m)=2.Вычисление функций, выраженных в формулах
Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения. Если возможно выразить выход функции с помощью формулы, включающей входную величину, то мы можем определить функцию в алгебраической форме. Например, уравнение 2n+6p=122n+6p=12 выражает функциональную связь между nn и с.п. Мы можем переписать его, чтобы решить, является ли pp функцией n.n.
Как
Дана функция в виде уравнения, напишите ее алгебраическую формулу.
- Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства, а с другой стороны как выражение, включающее только входную переменную.
- Используйте все обычные алгебраические методы для решения уравнений, такие как прибавление или вычитание одной и той же величины из обеих частей или умножение или деление обеих частей уравнения на одну и ту же величину.

Пример 9
Нахождение уравнения функции
Выразите соотношение 2n+6p=122n+6p=12 в виде функции p=f(n),p=f(n), если возможно.
Решение
Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где pp является функцией n,n, что означает запись в виде p=[выражение, включающее n].p=[выражение, включающее n].
2n+6p=126p=12−2nВычесть 2n из обеих сторон.p=12−2n6Разделить обе стороны на 6 и упростить.p=126−2n6p=2−13n2n+6p=126p=12−2nВычесть 2n из обеих сторон.p= 12−2n6Разделите обе части на 6 и упростите.p=126−2n6p=2−13n
Следовательно, pp как функция nn записывается как
p=f(n)=2−13np=f(n)=2−13n
Анализ
Важно отметить, что не каждое отношение, выраженное уравнением, можно также выразить в виде функции с помощью формулы.
Пример 10
Выражение уравнения окружности в виде функции
Представляет ли уравнение x2+y2=1×2+y2=1 функцию с xx на входе и yy на выходе? Если это так, выразите отношение как функцию y=f(x).
 y=f(x).
y=f(x).Решение
Сначала мы вычитаем x2x2 с обеих сторон.
y2=1−x2y2=1−x2
Теперь попробуем найти yy в этом уравнении.
y=±1−x2=+1−x2and−1−x2y=±1−x2=+1−x2and−1−x2
Мы получаем два выхода, соответствующих одному и тому же входу, поэтому эту связь нельзя представить в виде единственная функция y=f(x).y=f(x).
Попытайся #6
Если x−8y3=0,x−8y3=0, выразить yy как функцию x.x.
вопросы и ответы
Существуют ли отношения, выраженные уравнением, которые представляют функцию, но которые все еще не могут быть представлены алгебраической формулой?
Да, это может случиться. Например, при заданном уравнении x=y+2y,x=y+2y, если мы хотим выразить yy как функцию x,x, не существует простой алгебраической формулы, включающей только xx, равное y.
 y. Однако каждый xx определяет уникальное значение y, y, и существуют математические процедуры, с помощью которых yy можно найти с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для yy как функции x,x, даже если формулу нельзя записать явно.
y. Однако каждый xx определяет уникальное значение y, y, и существуют математические процедуры, с помощью которых yy можно найти с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для yy как функции x,x, даже если формулу нельзя записать явно. Вычисление функции, заданной в табличной форме
Как мы видели выше, мы можем представлять функции в виде таблиц. И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции, используя таблицы. Например, насколько хорошо наши питомцы помнят приятные воспоминания, которыми мы делимся с ними? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, а бета-рыбка имеет память до 5 месяцев. И если память щенка не превышает 30 секунд, то взрослая собака может помнить 5 минут. Это мизер по сравнению с кошкой, память которой длится 16 часов.

Функцию, связывающую тип питомца с длительностью его памяти, легче визуализировать с помощью таблицы. См. Таблицу 10. 2
Домашнее животное Объем памяти в часах Щенок 0,008 Взрослая собака 0,083 Кат 16 Золотая рыбка 2160 Бета-рыба 3600 Стол 10
Иногда вычисление функции в виде таблицы может быть более полезным, чем использование уравнений.
 Здесь назовем функцию P.P.
Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию PP по входному значению «золотая рыбка». Мы бы написали P(золотая рыбка)=2160.P(золотая рыбка)=2160. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции PP кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
Здесь назовем функцию P.P.
Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию PP по входному значению «золотая рыбка». Мы бы написали P(золотая рыбка)=2160.P(золотая рыбка)=2160. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции PP кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.Как
Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения.
- Найдите заданный вход в строке (или столбце) входных значений.
- Идентифицируйте соответствующее выходное значение в паре с этим входным значением.
- Найдите указанные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда появляется это выходное значение.

- Определите входное значение(я), соответствующее данному выходному значению.
Пример 11
Оценка и решение табличной функции
Использование таблицы 11,
ⓐ Вычисление g(3).g(3).
ⓑ Решить g(n)=6.g(n)=6.нн 1 2 3 4 5 г(н)г(н) 8 6 7 6 8 Стол 11
Решение
ⓐ Оценка g(3)g(3) означает определение выходного значения функции gg для входного значения n=3.
 n=3. Выходное значение таблицы, соответствующее n=3n=3, равно 7, поэтому g(3)=7.g(3)=7.
n=3. Выходное значение таблицы, соответствующее n=3n=3, равно 7, поэтому g(3)=7.g(3)=7.
ⓑ Решение g(n)=6g(n)=6 означает определение входных значений n,n, которые дают выходное значение 6. В таблице ниже показаны два решения: 22 и 4.4.пп 1 2 3 4 5 г(н)г(н) 8 6 7 6 8 Когда мы вводим 2 в функцию g,g, наш выход равен 6.
 Когда мы вводим 4 в функцию g,g, наш выход также равен 6.
Когда мы вводим 4 в функцию g,g, наш выход также равен 6.Попытайся #7
Использование таблицы из Оценка и решение табличной функции выше, оцените g(1).g(1).
Поиск значений функции на графике
Вычисление функции с помощью графика также требует нахождения соответствующего выходного значения для заданного входного значения, только в этом случае мы находим выходное значение, глядя на график. Решение функционального уравнения с использованием графика требует нахождения всех экземпляров заданного выходного значения на графике и наблюдения за соответствующим входным значением (значениями).
Пример 12
Чтение значений функции из графика
Учитывая график на рисунке 4,
ⓐ Вычислите f(2).f(2).
ⓑ Решить f(x)=4.f(x)=4.Рисунок 4
Решение
ⓐ Чтобы вычислить f(2),f(2), найдите точку на кривой, где x=2,x=2, затем считайте y -координату этой точки.
 Точка имеет координаты (2,1),(2,1), поэтому f(2)=1.f(2)=1. См. рис. 5.
Точка имеет координаты (2,1),(2,1), поэтому f(2)=1.f(2)=1. См. рис. 5.Рисунок 5
ⓑ Чтобы решить f(x)=4,f(x)=4, мы находим выходное значение 44 по вертикальной оси. Двигаясь горизонтально вдоль линии y=4,y=4, мы находим две точки кривой с выходным значением 4:4:(−1,4)(−1,4) и (3,4).(3,4) ). Эти точки представляют собой два решения f(x)=4:f(x)=4:−1−1 или 3.3. Это означает, что f(-1)=4f(-1)=4 и f(3)=4,f(3)=4, или, когда вход равен -1-1 или 3,3, выход равен 4,4. См. рис. 6.Рисунок 6
Попытайся #8
Используя рисунок 4, решите f(x)=1.f(x)=1.
Определение того, является ли функция взаимно однозначной
Некоторые функции имеют заданное выходное значение, которое соответствует двум или более входным значениям. Например, на биржевой диаграмме, показанной на рисунке в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, а это означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.

Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в таблице 12.
Буквенный класс Средний балл А 4,0 Б 3,0 С 2,0 Д 1,0 Стол 12
Эта система оценивания представляет собой функцию «один к одному», поскольку каждая введенная буква дает один конкретный средний балл успеваемости, а каждая средняя оценка соответствует одной введенной букве.

Чтобы наглядно представить эту концепцию, давайте еще раз взглянем на две простые функции, показанные на рис. 1 (a) и рис. 1 (b) 9.0136 . Функция в части (a) показывает отношение, которое не является взаимно-однозначным, поскольку входные данные qq и rr оба дают выходные данные n.n. Функция в части (b) показывает взаимосвязь, которая является взаимно однозначной функцией, поскольку каждый вход связан с одним выходом.
Функция «один к одному»
Функция «один к одному» — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.
Пример 13
Определение того, является ли отношение взаимно-однозначной функцией
Зависит ли площадь круга от его радиуса? Если да, то функция один к одному?
Решение
Окружность радиуса rr имеет уникальную меру площади, определяемую выражением A=πr2,A=πr2, поэтому для любого входа r,r есть только один выход, A.
 A. Площадь является функцией радиуса r.r.
A. Площадь является функцией радиуса r.r.Если функция является однозначной, выходное значение, площадь, должно соответствовать уникальному входному значению, радиусу. Любая мера площади AA задается формулой A=πr2.A=πr2. Поскольку площади и радиусы — положительные числа, существует ровно одно решение: Aπ.Aπ. Таким образом, площадь круга является взаимно однозначной функцией радиуса круга.
Попытайся #9
- ⓐ Зависит ли баланс от номера банковского счета?
- ⓑ Является ли номер банковского счета функцией баланса?
- ⓒ Является ли баланс однозначной функцией номера банковского счета?
Попытайся #10
Оцените следующее:
ⓐ Если каждый процентный балл, полученный за курс, переводится в одну буквенную оценку, является ли буквенный балл функцией процентного балла?
ⓑ Если да, то является ли функция взаимно однозначной?Использование теста вертикальной линии
Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика.
 Графики отображают большое количество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. По соглашению графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Графики отображают большое количество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. По соглашению графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.Наиболее распространенные графики называют входное значение xx и выходное значение y,y, и мы говорим, что yy является функцией x,x, или y=f(x)y=f(x), когда функция называется f.f. График функции представляет собой набор всех точек (x,y)(x,y) на плоскости, удовлетворяющих уравнению y=f(x).y=f(x). Если функция определена только для нескольких входных значений, то график функции представляет собой всего несколько точек, где x -координата каждой точки является входным значением, а y -координата каждой точки является соответствующим выходным значением. Например, черные точки на графике на рис. 7 говорят нам о том, что f(0)=2f(0)=2 и f(6)=1.
 f(6)=1. Однако множество всех точек (x,y)(x,y), удовлетворяющих y=f(x)y=f(x), является кривой. Показанная кривая включает в себя (0,2)(0,2) и (6,1)(6,1), поскольку кривая проходит через эти точки.
f(6)=1. Однако множество всех точек (x,y)(x,y), удовлетворяющих y=f(x)y=f(x), является кривой. Показанная кривая включает в себя (0,2)(0,2) и (6,1)(6,1), поскольку кривая проходит через эти точки.Рисунок 7
Проверка вертикальной линии может использоваться для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, то график делает , а не определяют функцию, потому что функция имеет только одно выходное значение для каждого входного значения. См. рис. 8.
Рисунок 8
Как
Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
- Изучите график, чтобы увидеть, пересекает ли какая-либо вертикальная линия кривую более одного раза.
- Если такая линия есть, определить, что график не представляет функцию.

Пример 14
Применение теста вертикальной линии
Какой из графиков на рисунке 9 представляет(ют) функцию y=f(x)?y=f(x)?
Рисунок 9
Решение
Если любая вертикальная линия пересекает график более одного раза, отношение, представленное графиком, не является функцией. Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (а) и (б) рисунка 9. Отсюда мы можем сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, так как не более x -значения, вертикальная линия будет пересекать график более чем в одной точке, как показано на рисунке 10.
Рисунок 10
Попытайся #11
Представляет ли график на рисунке 11 функцию?
Рисунок 11
Использование теста горизонтальной линии
После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — использовать тест горизонтальной линии.
 Проведите горизонтальные линии через график. Если любая горизонтальная линия пересекает график более одного раза, то график не представляет однозначной функции.
Проведите горизонтальные линии через график. Если любая горизонтальная линия пересекает график более одного раза, то график не представляет однозначной функции.Как
Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график функцию взаимно однозначного соответствия.
- Изучите график, чтобы увидеть, пересекает ли какая-либо горизонтальная линия кривую более одного раза.
- Если такая строка есть, определить, что функция не является взаимно однозначной.
Пример 15
Применение теста горизонтальной линии
Рассмотрим функции, показанные на рис. 9 (а) и рисунок 9 (б) . Является ли какая-либо из функций взаимно однозначной?
Решение
Функция на рисунке 9 (a) не является однозначной.
 Горизонтальная линия, показанная на рисунке 12, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, пересекающие ее в трех точках).
Горизонтальная линия, показанная на рисунке 12, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, пересекающие ее в трех точках).Рисунок 12
Функция на рис. 9 (b) является однозначной. Любая горизонтальная линия пересекает диагональную линию не более одного раза.
Попытайся #12
Является ли график, показанный на рис. 9, один к одному?
Идентификация функций Basic Toolkit
В этом тексте мы будем изучать функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения задач с ними. При обучении чтению мы начинаем с алфавита. При обучении арифметике мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор элементов стандартного блока. Мы называем их «инструментальными функциями», которые образуют набор основных именованных функций, для которых мы знаем график, формулу и специальные свойства.
 Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать xx в качестве входной переменной и y=f(x)y=f(x) в качестве выходной переменной.
Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать xx в качестве входной переменной и y=f(x)y=f(x) в качестве выходной переменной.Мы будем часто встречаться с этими инструментальными функциями, комбинациями инструментальных функций, их графиками и преобразованиями в этой книге. Будет очень полезно, если мы сможем быстро распознать эти функции инструментария и их функции по имени, формуле, графику и основным свойствам таблицы. Графики и примерные табличные значения прилагаются к каждой функции, показанной в Таблице 13.
Имя Функция График Константа f(x)=c,f(x)=c, где cc — константа Личность е(х)=хf(х)=х Абсолютное значение f(x)=|x|f(x)=|x| Квадратичный е(х)=х2f(х)=х2 Кубический f(x)=x3f(x)=x3 Взаимный f(x)=1xf(x)=1x Обратный квадрат f(x)=1x2f(x)=1×2 Квадратный корень е(х)=хf(х)=х Кубический корень е(х)=х3f(х)=х3 Стол 13
3.
 1 Секционные упражнения
1 Секционные упражненияУстно
1.
В чем разница между отношением и функцией?
2.
В чем разница между вводом и выводом функции?
3.
Почему тест вертикальной линии говорит нам, представляет ли график отношения функцию?
4.
Как определить, является ли отношение однозначной функцией?
5.
Почему тест горизонтальной линии говорит нам, является ли график функции взаимно однозначным?
Алгебраический
В следующих упражнениях определите, представляет ли отношение функцию.
6.
{(а,б),(в,г),(а,в)}{(а,б),(в,г),(а,в)}
7.
{(а,б),(б,в),(в,в)}{(а,б),(б,в),(в,в)}
Для следующих упражнений определите, представляет ли отношение yy как функцию x.
 x.
x.8.
5x+2y=105x+2y=10
9.
у=х2у=х2
10.
х=у2х=у2
11.
3×2+y=143×2+y=14
12.
2х+у2=62х+у2=6
13.
у=-2×2+40xy=-2×2+40x
14.
у=1ху=1х
15.
х=3у+57у-1х=3у+57у-1
16.
х=1-у2х=1-у2
17.
у=3х+57х-1у=3х+57х-1
18.
х2+у2=9х2+у2=9
19.
2ху=12ху=1
20.
х=у3х=у3
21.
у=х3у=х3
22.

у=1-х2у=1-х2
23.
х=±1-ух=±1-у
24.
у=±1-ху=±1-х
25.
у2=х2у2=х2
26.
у3=х2у3=х2
В следующих упражнениях оцените f(−3),f(2),f(−a),−f(a),f(a+h).f(−3),f(2),f( −a),−f(a),f(a+h).
27.
f(x)=2x−5f(x)=2x−5
28.
f(x)=−5×2+2x−1f(x)=−5×2+2x−1
29.
f(x)=2−x+5f(x)=2−x+5
30.
f(x)=6x−15x+2f(x)=6x−15x+2
31.
f(x)=|x−1|−|x+1|f(x)=|x−1|−|x+1|
32.
Учитывая функцию g(x)=5−x2,g(x)=5−x2, вычислить g(x+h)−g(x)h,h≠0.g(x+h)−g( х)ч,ч≠0.
33.
Учитывая функцию g(x)=x2+2x,g(x)=x2+2x, вычислить g(x)−g(a)x−a,x≠a.
 g(x)−g(a)x− а, х ≠ а.
g(x)−g(a)x− а, х ≠ а.34.
Учитывая функцию k(t)=2t−1:k(t)=2t−1:
- ⓐ Оценить k(2).k(2).
- ⓑ Решите k(t)=7.k(t)=7.
35.
Учитывая функцию f(x)=8−3x:f(x)=8−3x:
- ⓐ Вычислить f(−2).f(−2).
- ⓑ Решить f(x)=−1.f(x)=−1.
36.
Учитывая функцию p(c)=c2+c:p(c)=c2+c:
- ⓐ Вычислить p(−3).p(−3).
- ⓑ Решите p(c)=2.p(c)=2.
37.
Учитывая функцию f(x)=x2−3x:f(x)=x2−3x:
- ⓐ Вычислите f(5).f(5).
- ⓑ Решить f(x)=4.f(x)=4.
38.
Учитывая функцию f(x)=x+2:f(x)=x+2:
- ⓐ Вычислить f(7).f(7).
- ⓑ Решить f(x)=4.f(x)=4.
39.

Рассмотрим соотношение 3r+2t=18,3r+2t=18.
- ⓐ Запишите зависимость в виде функции r=f(t).r=f(t).
- ⓑ Вычислить f(−3).f(−3).
- ⓒ Решите f(t)=2.f(t)=2.
Графический
В следующих упражнениях используйте тест вертикальной линии, чтобы определить, какие графики показывают отношения, которые являются функциями.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.

Учитывая следующий график,
- ⓐ Вычислить f(−1).f(−1).
- ⓑ Найдите f(x)=3.f(x)=3.
53.
Учитывая следующий график,
- ⓐ Вычислить f(0).f(0).
- ⓑ Найдите f(x)=−3.f(x)=−3.
54.
Учитывая следующий график,
- ⓐ Вычислите f(4).f(4).
- ⓑ Найдите f(x)=1.f(x)=1.
В следующих упражнениях определите, является ли данный график однозначной функцией.
55.
56.
57.
58.
59.
Числовой
В следующих упражнениях определите, представляет ли отношение функцию.
60.
{(−1,−1),(−2,−2),(−3,−3)}{(−1,−1),(−2,−2),(−3,−3 )}
61.

{(3,4),(4,5),(5,6)}{(3,4),(4,5),(5,6)}
62.
{(2,5),(7,11),(15,8),(7,9)}{(2,5),(7,11),(15,8),(7,9 )}
Для следующих упражнений определите, представляет ли отношение, представленное в виде таблицы, yy как функцию x.x.
63.
хх 5 10 15 гг 3 8 14 64.
хх 5 10 15 г 3 8 8 65.

хх 5 10 10 гг 3 8 14 В следующих упражнениях используйте функцию ff, представленную в таблице ниже.
хх 0 1 2 3 4 5 6 7 8 9 ф(х)ф(х) 74 28 1 53 56 3 36 45 14 47 Таблица 14
66.

Вычислить f(3).f(3).
67.
Решить f(x)=1.f(x)=1.
В следующих упражнениях оцените функцию ff при значениях f(−2),f(−1),f(0),f(1),f(−2),f(−1),f(0 ),f(1) и f(2).f(2).
68.
f(x)=4−2xf(x)=4−2x
69.
f(x)=8−3xf(x)=8−3x
70.
f(x)=8×2−7x+3f(x)=8×2−7x+3
71.
f(x)=3+x+3f(x)=3+x+3
72.
f(x)=x−2x+3f(x)=x−2x+3
73.
f(x)=3xf(x)=3x
Для следующих упражнений оцените выражения для заданных функций f,g,f,g и h:h:
f(x)=3x−2f(x)=3x−2
g(x)=5− x2g(x)=5−x2
h(x)=−2×2+3x−1h(x)=−2×2+3x−174.
3f(1)−4g(−2)3f(1)−4g(−2)
75.

f(73)−h(−2)f(73)−h(−2)
Технология
Для следующих упражнений постройте график y=x2y=x2 в заданной области. Определить соответствующий диапазон. Покажите каждый график.
76.
[−0,1,0,1][−0,1,0,1]
77.
[−10,10][−10,10]
78.
[−100 100][−100 100]
Для следующих упражнений постройте график y=x3y=x3 в заданной области. Определить соответствующий диапазон. Покажите каждый график.
79.
[−0,1,0,1][−0,1,0,1]
80.
[−10,10][−10,10]
81.
[−100 100][−100 100]
Для следующих упражнений постройте график y=xy=x в заданной области. Определить соответствующий диапазон. Покажите каждый график.
82.
[0,0,01][0,0,01]
83.

[0,100][0,100]
84.
[0,10,000][0,10,000]
Для следующих упражнений постройте график y=x3y=x3 в заданной области. Определить соответствующий диапазон. Покажите каждый график.
85.
[−0,001,0,001][−0,001,0,001]
86.
[−1000 1000][−1000 1000]
87.
[−1 000 000,1 000 000][−1 000 000,1 000 000]
Реальные приложения 90 564
88.
Количество мусора, G,G, производимого городом с населением pp, определяется как G=f(p).G=f(p).GG измеряется в тоннах в неделю, а pp измеряется в тысячах люди.
- ⓐ В городе Тола с населением 40 000 человек каждую неделю производится 13 тонн мусора. Выразите эту информацию через функцию f.f.
- ⓑ Объясните значение утверждения f(5)=2.f(5)=2.
89.

Количество кубических ярдов земли, D,D, необходимое для покрытия сада площадью aa квадратных футов, равно D=g(a).D=g(a).
- ⓐ Для сада площадью 5000 футов 2 требуется 50 ярдов 3 земли. Выразите эту информацию через функцию g.g.
- ⓑ Объясните смысл утверждения g(100)=1.g(100)=1.
90.
Пусть f(t)f(t) количество уток в озере через tt лет после 1990 года. Объясните значение каждого утверждения:
- ⓐ f(5)=30f(5)=30
- ⓑ f(10)=40f(10)=40
91.
Пусть h(t)h(t) будет высотой ракеты над землей в футах через tt секунд после запуска. Объясните значение каждого утверждения:
- ⓐ h(1)=200h(1)=200
- ⓑ ч(2)=350ч(2)=350
92.
Покажите, что функция f(x)=3(x−5)2+7f(x)=3(x−5)2+7 равна , а не взаимно однозначно.

графических функций — Как графические функции?
Графические функции — это процесс построения графика (кривой) соответствующей функции. Графики основных функций, таких как линейные, квадратичные, кубические и т. д., довольно просты, графические функции, которые являются сложными, такими как рациональные, логарифмические и т. д., требуют некоторых навыков и некоторых математических понятий для понимания.
Давайте посмотрим процесс графического отображения функций вместе с примерами.
1. Что подразумевается под графическими функциями? 2. Основные графические функции 3. График сложных функций 4. Графические функции с помощью преобразований 5. Часто задаваемые вопросы о графических функциях Что подразумевается под графическими функциями?
Графические функции рисует кривую, представляющую функцию на координатной плоскости.
 Если кривая (график) представляет собой функцию, то каждая точка кривой удовлетворяет уравнению функции. Например, следующий график представляет линейную функцию f(x) = -x+ 2,
Если кривая (график) представляет собой функцию, то каждая точка кривой удовлетворяет уравнению функции. Например, следующий график представляет линейную функцию f(x) = -x+ 2,Возьмем любую точку на этой линии, скажем, (-1, 3). Подставим (-1, 3) = (x, y) (т. е. x = -1 и y = 3) в функцию f(x) = -x + 2 (заметим, что ее можно записать как y = — х + 2). Тогда
3 = -(-1) + 2
3 = 1 + 2
3 = 3, таким образом, (-1, 3) удовлетворяет функции.Таким же образом можно попробовать взять разные точки и проверить, удовлетворяют ли они функции. Каждая точка на линии (обычно называемая «кривой») удовлетворяет этой функции. Рисование таких кривых, представляющих функции, известно как графическое отображение функций.
Основные графические функции
Графики основных функций, таких как линейные функции и квадратичные функции, очень просты. Основная идея графических функций
- Определение формы, если это возможно. Например, если это линейная функция вида f(x) = ax + b, то ее график будет линией; если это квадратичная функция вида f(x) = ax 2 + bx + c, то это парабола.

- найти на нем несколько точек, подставив некоторые случайные значения x и найти соответствующие значения y, подставив каждое значение в функцию.
Вот несколько примеров.
Графики линейных функций
Построим график той же линейной функции, что упоминалась в предыдущем разделе (f(x) = -x + 2). Для этого мы создаем таблицу значений, взяв несколько случайных чисел для x, скажем, x = 0 и x = 1. Затем подставьте каждое из них в y = -x + 2, чтобы вычислить значения y.
х г 0 -0 + 2 = 2 1 -1 + 2 = 1 Таким образом, на прямой есть две точки (0, 2) и (1, 1). Если мы нанесем их на график и соединим их прямой линией (продолжив линию с обеих сторон), мы получим ее график, как показано в предыдущем разделе.
Построение графика квадратичной функции
Для построения графика квадратичной функции мы можем найти на ней несколько случайных точек.
 Но это может не дать идеальной U-образной кривой. Это потому, что для получения идеальной U-образной кривой нам нужно, где она поворачивает. т. е. надо найти его вершину. Найдя вершину, мы можем найти две или три случайные точки с каждой стороны вершины, и они помогут в построении графика функции.
Но это может не дать идеальной U-образной кривой. Это потому, что для получения идеальной U-образной кривой нам нужно, где она поворачивает. т. е. надо найти его вершину. Найдя вершину, мы можем найти две или три случайные точки с каждой стороны вершины, и они помогут в построении графика функции.Пример: График квадратичной функции f(x) = x 2 — 2x + 5.
Решение:
Сравнение с f(x) = ax 2 , a + c + bx = 1, b = -2 и c = 5.
Координата x вершины: h = -b/2a = -(-2)/2(1) = 1.
Ее координата y есть, f(1) = 1 2 — 2(1) + 5 = 4.
Следовательно, вершина (1, 4).
Мы возьмем два случайных числа по обе стороны от 1 (координата x вершины) и создадим таблицу. Затем мы можем вычислить координаты y с помощью функции.
х г -1 (-1) 2 — 2(-1) + 5 = 8 0 0 2 — 2(0) + 5 = 5 Вершина: 1 4 2 2 2 — 2(2) + 5 = 5 3 3 2 — 2(3) + 5 = 8 Теперь мы нанесем точки (-1, 8), (0, 5), (1, 4), (2, 5) и (3, 8) на лист графика, соединим их, и продлите кривую с обеих сторон.

График сложных функций
Графические функции сравнительно просты, если каждый их домен и диапазон представляет собой набор всех действительных чисел. Но это НЕ относится ко всем типам функций. Есть некоторые сложные функции, для которых необходимо учитывать домен, диапазон, асимптоты и дыры при их построении. Самые популярные такие функции:
- Рациональные функции. Его родительская функция имеет форму f(x) = 1/x (которая называется обратной функцией).
- Экспоненциальные функции. Его родительская функция имеет вид f(x) = a x .
- Логарифмические функции. Его родительская функция имеет вид f(x) = log x.
Просто представьте, как выглядят графики родительских функций каждой из этих функций.
В каждом из этих случаев за графические функции , мы выполняем следующие шаги:
- Найдите область определения и диапазон функции и помните об этом при построении кривой.

- Найдите точки пересечения по осям x и y и нанесите их на график.
- Определите отверстия, если они есть.
- Найдите асимптоты (вертикальную, горизонтальную и наклонную) и нарисуйте их пунктирными линиями, чтобы мы могли разбить график по этим линиям и убедиться, что график их не касается.
- Постройте таблицу значений, взяв несколько случайных чисел для x (по обе стороны от точки пересечения x и/или по обе стороны от вертикальной асимптоты), вычислите соответствующие значения y.
- Нанесите точки из таблицы и соедините их, учитывая асимптоты, домен и диапазон.
Давайте посмотрим, как построить график функции в различных случаях, используя описанные выше шаги.
График рациональных функций
Построим график рациональной функции f(x) = (x + 1) / (x — 2). Мы следуем вышеуказанным шагам и рисуем график этой функции.
График экспоненциальных функций
Рассмотрим экспоненциальную функцию f(x) = 2 -x + 2.
 Мы построим ее график, используя те же шаги, что и упомянутые выше.
Мы построим ее график, используя те же шаги, что и упомянутые выше.- Его областью определения является множество всех действительных чисел (R), а его диапазон y > 2. Чтобы узнать, как их найти, нажмите здесь.
- Не имеет вертикальных асимптот. Но у него есть горизонтальная асимптота при y = 2, .
- Он не имеет x-перехватов. Его y-пересечение равно (0, 3).
- Без отверстий.
- У нас нет данных о VA или x-intercept. Пока у нас есть только одно значение (0, 3). Итак, давайте возьмем несколько случайных чисел по обе стороны от x = 0 и составим таблицу.
х г -2 2 -(-2) + 2 = 6 -1 2 -(-1) + 2 = 4 0 3 (г-целое) 1 2 -1 + 2 = 2,5 2 2 -2 + 2 = 2,25 - Нанесем всю информацию на график.

Графики логарифмических функций
Мы построим график логарифмической функции, скажем, f(x) = 2 log 2 x — 2. Теперь мы построим ее график, выполнив действия, описанные ранее.
Точно так же вы можете увидеть, как построить график нелинейных функций, функции тождества, функции модуля, полиномиальной функции, функции нуля, функции наибольшего целого числа, постоянной функции, тригонометрических функций, функции дробной части и т. д., нажав на соответствующие ссылки.
Графические функции с помощью преобразований
Мы можем построить графики функций, применяя преобразования к графикам родительских функций. Вот родительские функции нескольких важных типов функций.
- Линейная функция: f(x) = x
- Квадратичная функция: f(x) = x 2
- Кубические функции: f(x) = x 3
- Функция квадратного корня: f(x) = √x
- Функция кубического корня: f(x) = ∛x
- Функция абсолютного значения: f(x) = |x|
- Обратная функция: f(x) = 1/x
- Экспоненциальная функция: f(x) = a x , 0 < a < 1
- Логарифмическая функция: f(x) = log x
Нам нужно иметь представление о том, как выглядит график каждой из этих родительских функций (нажав на соответствующие ссылки).
 Затем мы можем применить следующие преобразования для построения графика данной функции.
Затем мы можем применить следующие преобразования для построения графика данной функции.Трансформация Изменение графика ф(х) + с Смещает график функции c единиц вверх. ф(х) — с Сдвигает график функции c единиц вниз. ф(х + с) Сдвигает график функции c единиц влево. ф(х — в) Смещает график функции c единиц вправо. -ф(х) Отражает график функции по оси x (в перевернутом виде). ф(-х) Отражает график функции по оси Y (т. е. левая и правая части меняются местами). ф(акс) Горизонтальное расширение с коэффициентом 1/a. а ф(х) Вертикальное расширение в a. Чтобы подробно понять, как построить график функций с помощью преобразований, нажмите здесь.

Важные примечания по графическим функциям:
- f(ax) ≠ a f(x). Оба могут иметь разные значения.
- Значение x, используемое для построения графика любой функции f(x), может быть целым числом, действительным числом или десятичным числом.
- График функции никогда не должен касаться асимптот.
- Не выбирайте значения x в таблице, которых НЕТ в домене функции.
☛ Похожие темы:
- Калькулятор графических функций
- Введение в графику
- Визуализация функций с помощью графиков
Часто задаваемые вопросы о графических функциях
Как графически отображать функции?
Для графических функций нам нужно построить его асимптоты, его точки пересечения x и y, пробелы и несколько точек на нем, построив таблицу значений. Затем просто присоединитесь к точке, не касаясь асимптот и сохраняя примечание области определения и диапазона функции.

Какие этапы построения графика линейной функции?
Шаги построения графика линейной функции приведены ниже:
- Убедитесь, что линейная функция имеет форму y=mx+b.
- Теперь b откладывается по оси Y.
- м переводится в дробь.
- Теперь линия продлевается от b с использованием наклона.
- Линия может быть дополнительно расширена, используя m в качестве направляющего фактора.
Альтернативно:
Любые две точки на линии определяют линию. Итак, чтобы нарисовать линейную функцию, нам нужно всего лишь две точки на ней. Чтобы построить график, просто создайте таблицу значений с двумя столбцами x и y, возьмите несколько случайных чисел для x и вычислите соответствующие значения y, подставив каждое из них в функцию. Затем просто нанесите точки на график, соедините их линией и бесконечно продлите линию с обеих сторон.
Как построить график кусочной функции?
Кусочная функция определяется по-разному (с помощью разных уравнений) на разных интервалах.
 Нам просто нужно рассматривать каждое уравнение как другую функцию в заданной области и отображать ее так же, как мы изображаем нормальную функцию. Чтобы узнать больше о построении графика кусочной функции, нажмите здесь.
Нам просто нужно рассматривать каждое уравнение как другую функцию в заданной области и отображать ее так же, как мы изображаем нормальную функцию. Чтобы узнать больше о построении графика кусочной функции, нажмите здесь.Как идентифицировать функции с помощью графиков?
Вот несколько приемов для определения функций по графикам:
- Если график представляет собой линию, то это линейная функция, имеющая вид f(x) = ax + b.
- Если график имеет форму идеальной буквы U или перевернутой буквы U, то он является квадратичной функцией и имеет вид f(x) = ax 2 + bx + c.
- Если на графике есть две кривые, симметричные относительно наклонной линии, то это рациональная функция, которая обычно имеет вид f(x) = (ax + b) / (cx + d).
- Если график имеет форму V или перевернутой буквы V, то это функция абсолютного значения, имеющая вид f(x) = a |bx + c| + д.
- Если график состоит из нескольких горизонтальных линий, то он представляет собой функцию нижнего или верхнего предела.

- Если график с одной кривой имеет возрастающую или убывающую вертикальную асимптоту, то это логарифмическая функция.
- Если график с одной кривой имеет возрастающую или убывающую горизонтальную асимптоту, то это экспоненциальная функция.
- Если на графике несколько волн, это может быть одна из тригонометрических функций:
Функция синуса
Функция косинуса
Функция тангенса
Функция косеканса
Функция секанса
Функция котангенса
Как узнать, является ли график функцией?
Функция всегда проходит тест вертикальной линии. Чтобы использовать этот тест, просто возьмите вертикальную линию (или просто вертикальную палочку) и проведите ее по графику слева направо по горизонтали. Ни в какой момент времени линия не должна пересекать график более чем в одной точке, чтобы график представлял функцию.
Как использовать график для решения уравнения?
Сначала определите тип функции, взглянув на график.
 Возьмем его общее уравнение. Используйте некоторые точки на графике и общее уравнение, чтобы определить точное уравнение функции.
Возьмем его общее уравнение. Используйте некоторые точки на графике и общее уравнение, чтобы определить точное уравнение функции.Как нарисовать график уравнения?
Чтобы нарисовать график уравнения функции, сделайте следующее:
- Нанесите различные точки уравнения.
- Соедините точки и сформируйте кривую. Полученная таким образом кривая является графиком данного уравнения.
Функции в реальном мире
Когда мы знакомим студентов с функциями, мы обычно воплощаем концепцию в жизнь через идею функциональных машин. Но функции действительно начнут оживать, когда наши ученики найдут применение функциям в реальном мире.
ФУНКЦИОНАЛЬНЫЕ МАШИНЫ
Учащиеся легко понимают идею функциональной машины: поступает ввод; что-то происходит с ним внутри машины; выходит выход. Вводится другой вход; выходит другой выход. Что происходит внутри машины? Если мы знаем правило (или правила) работы машины и входные данные, мы можем предсказать результат.
 Если мы знаем правило(я) и выход, мы можем определить вход. Мы также можем представить, как машина спрашивает: «Каково мое правило?» Если мы изучим входы и выходы, мы сможем выяснить правило или правила загадочной функции.
Если мы знаем правило(я) и выход, мы можем определить вход. Мы также можем представить, как машина спрашивает: «Каково мое правило?» Если мы изучим входы и выходы, мы сможем выяснить правило или правила загадочной функции.Мы можем сделать эту метафору еще более конкретной, установив большую картонную коробку с входными и выходными отверстиями. Один ученик сидит внутри функциональной машины с загадочным правилом функции. Пока другие учащиеся по очереди вводят числа в машину, учащийся внутри коробки отправляет выходные числа через выходную щель. После двух или более входов и выходов класс обычно может понять правило загадочной функции.
ввод
выход
4
12
5
15
«Правило функции: Умножь на 3!»Варианты расширения действия включают:
- Поиск составной функции (включающей 2 или более функциональных правил).

- Включить дроби, десятичные числа и/или отрицательные числа.
- Учитель или учащиеся могут создавать машины функций электронных таблиц, используя функцию формулы.
- Учащиеся могут создавать таблицы функций для решения своих одноклассников с одним или двумя правилами таинственной функции.
ОНЛАЙН-ФУНКЦИОНАЛЬНЫЕ МАШИНЫ
Ряд замечательных онлайн-машин развивает ту же концепцию. Учащиеся могут работать индивидуально, в парах или в классе, чтобы решить головоломки функциональных машин.
- Функциональный автомат математической игровой площадки
Эта машина для угадывания правил функций-загадок позволяет пользователю контролировать максимальное количество вводимых данных с возможностью ручного или компьютерного ввода и 1 или 2 функциональными правилами. Требуется пять входов/выходов, прежде чем он позволит пользователю угадать правило(я) функции.
- Три функциональных автомата на сайте Shodor’s Interactivate включают помощь и уроки для учащихся и учителей:
- Функциональная машина (с 1 правилом)
- Машина положительной линейной функции (с 2 правилами)
- Машина линейных функций (с 2 правилами, включающими положительные и отрицательные целые числа)
- Лаборатория учителей Анненберга Образцы в математике: загадочная операция
Эта сложная функциональная машина принимает пользовательский ввод для двух переменных для получения результата. После изучения ряда пар входных и выходных данных пользователь пытается сделать вывод и применить операцию-загадку, чтобы предсказать результат для пары сгенерированных машиной входных данных. Пример операции-загадки в этой машине: a * (b 1).
После изучения ряда пар входных и выходных данных пользователь пытается сделать вывод и применить операцию-загадку, чтобы предсказать результат для пары сгенерированных машиной входных данных. Пример операции-загадки в этой машине: a * (b 1).
ФУНКЦИИ В РЕАЛЬНОМ МИРЕ
Стандарт NCTM 2 для шаблонов, функций и алгебры предполагает, что учащиеся:
- понимают различные типы шаблонов и функциональных взаимосвязей;
- использовать символические формы для представления и анализа математических ситуаций и структур;
- используют математические модели и анализируют изменения как в реальном, так и в абстрактном контексте.
Обзор стандартов для 3-5 классов предполагает понимание того, что «в« реальном мире »функции являются математическим представлением многих ситуаций ввода-вывода».
По мере того, как мы указываем на функции и используем их в реальных условиях, мы можем попросить наших студентов быть внимательными к другим ситуациям ввода-вывода в реальном мире.
 Вы можете использовать следующие примеры:
Вы можете использовать следующие примеры:
- Автомат с газировкой, закусками или штампами
Пользователь кладет деньги, нажимает определенную кнопку, и определенный предмет падает в выходной слот. (Правило функции — цена продукта. Ввод — это деньги, объединенные с выбранной кнопкой. Выход — товар, иногда доставляемый вместе с монетами в качестве сдачи, если пользователь ввел больше денег, чем требуется по правилу функции.)
- Измерение:
- Мили на галлон
Эффективность автомобиля в милях на галлон бензина является функцией. Если автомобиль обычно получает 20 миль на галлон, и если вы вводите 10 галлонов бензина, он сможет проехать примерно 200 миль. Эффективность автомобиля может зависеть от конструкции автомобиля (включая вес, шины и аэродинамику), скорости, температуры внутри и снаружи автомобиля и других факторов.
- Основы экономики и денежной математики:
- Недельная заработная плата зависит от ставки почасовой оплаты и количества отработанных часов.

- Сложные проценты являются функцией первоначальных инвестиций, процентной ставки и времени.
- Спрос и предложение: по мере роста цены спрос падает.
- Недельная заработная плата зависит от ставки почасовой оплаты и количества отработанных часов.
- Тени
Длина тени зависит от ее высоты и времени суток. Тени можно использовать для определения высоты больших объектов, таких как деревья или здания; то же функциональное правило (соотношение), по которому мы сравниваем длину вертикальной линейки с ее тенью, поможет нам найти неизвестный вход (высоту большого объекта), когда мы измеряем его тень.
- Геометрические узоры
- Многогранники
Изучая взаимосвязь между количеством граней, ребер и вершин различных многогранников, смогут ли учащиеся открыть правило Эйлера? F + V = E + 2 (количество граней плюс количество вершин равняется количеству ребер плюс 2). Например:# сторон
на каждую сторонулица
края
вершины
тетраэдр
3
4
6
4
шестигранник
3
6
9
5
октаэдр
3
8
12
6
декаэдр
3
10
15
7
икосаэдр
3
20
30
12
куб
4
6
12
8
додекаэдр
5
12
30
20
- Маршрутные поезда
Учащиеся могут расположить несколько блоков шаблона в простом дизайне, дать ему имя, найти периметр дизайна (считая стандартное ребро за одну единицу), а затем сделать серию из 2 или 3 повторений этого дизайна и найти периметр.# «кошачьих голов»
периметр
1
7
2
12
3
17
 поезда по мере его роста. Когда они составляют таблицу данных, могут ли они найти правило или правила функции, описывающие взаимосвязь между количеством повторений и периметром поезда?
поезда по мере его роста. Когда они составляют таблицу данных, могут ли они найти правило или правила функции, описывающие взаимосвязь между количеством повторений и периметром поезда?Правило функции: x5+2 (или 5n+2).
- Геометрические узоры в окружающем нас мире
Вы или ваши ученики можете сфотографировать архитектурные детали с повторяющимися узорами и составить таблицу для анализа каждого узора. Например, в показанной здесь кирпичной стене, если каждый кирпич имеет размеры 2 x 8 дюймов, каков периметр ряда кирпичей, расположенных в виде ступенек? Какое функциональное правило описывает эту связь?Количество кирпичей
периметр
1
20
2
32
3
44
Правило функции: x6 + 4 (или 6n + 4).
Как насчет узоров на напольной или настенной плитке? Каково отношение одного цвета к другому цвету? Сколько плиток каждого цвета нам нужно купить, чтобы выложить плиткой комнату заданного размера? Что, если бы мы захотели включить границу заданного цвета? Некоторые из мозаичных полов в Библиотеке Конгресса в Вашингтоне, округ Колумбия, являются великолепными (и сложными) примерами для изучения.
Щелкните здесь, чтобы просмотреть изображения ниже в полном размере.
В большинстве примеров в этой статье используются таблицы данных для анализа функций, но, конечно же, графики являются еще одним эффективным средством представления ситуаций ввода-вывода, включая изменения во времени (независимо от того, является ли скорость изменения постоянной или переменной).
По мере того, как учащиеся начинают использовать функции в реальном мире, будет открываться все больше и больше возможностей, и концепция и ценность функций будут действительно воплощаться в жизнь.

ДОПОЛНИТЕЛЬНЫЙ РЕСУРС
Learning Math: Patterns, Functions, and Algebra
Национальный совет учителей математики. (1998). Принципы и стандарты школьной математики. Рестон, Вирджиния: NCTM
Компания Annenberg Media подготовила прекрасную коллекцию бесплатных потоковых онлайн-видео по запросу для учителей 8-х классов. Темы этой серии включают: алгебраическое мышление, закономерности в контексте, функции и алгоритмы. , пропорциональные рассуждения, линейные функции и наклон, решение уравнений, нелинейные функции и занятия в классе.Об авторе
Венди Петти — создатель отмеченного наградами веб-сайта Math Cats, автор книги «Изучение математики с помощью MicroWorlds EX » и частый докладчик на региональных и национальных конференциях по математике и технологиям.
- Многогранники



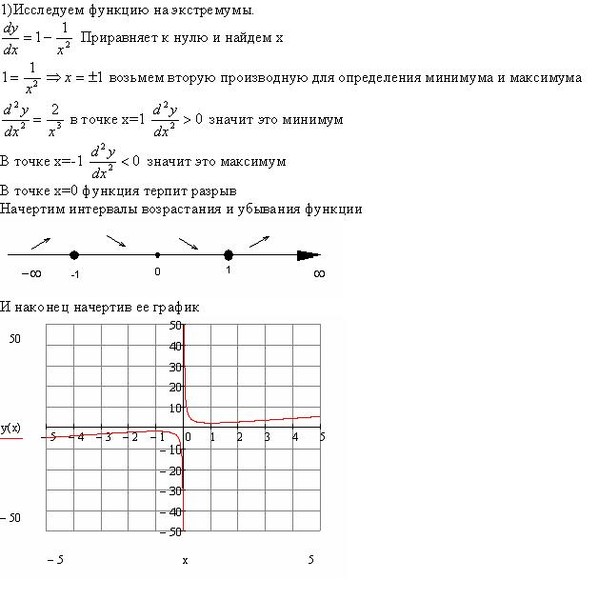 Д. «Информатика и ИКТ» и приложение Power Point, установленное на компьютерах в кабинете информатики;
Д. «Информатика и ИКТ» и приложение Power Point, установленное на компьютерах в кабинете информатики;
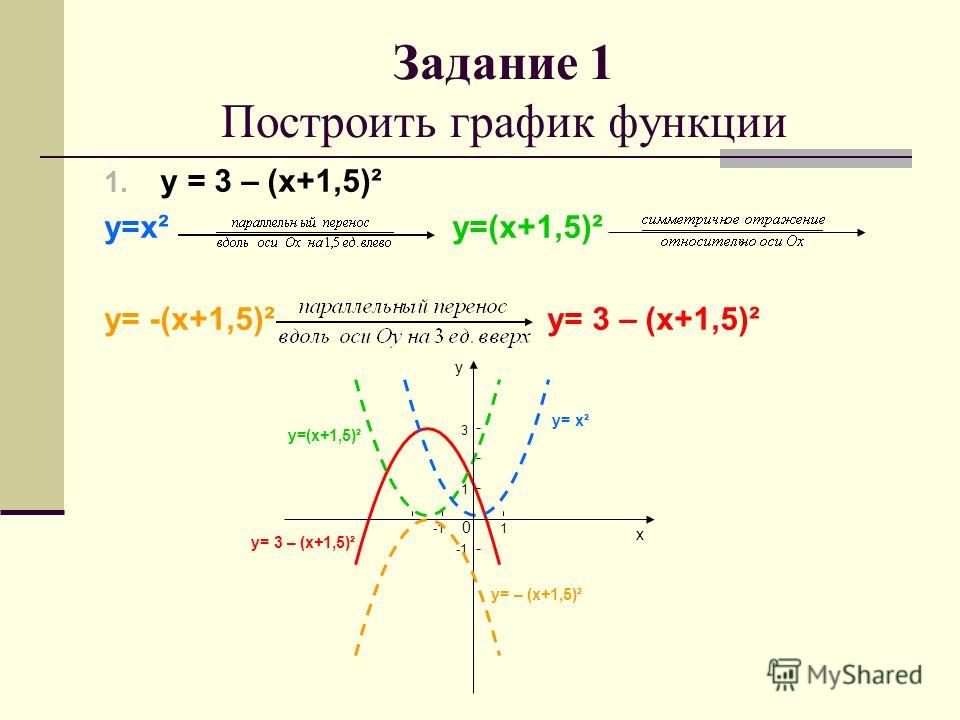

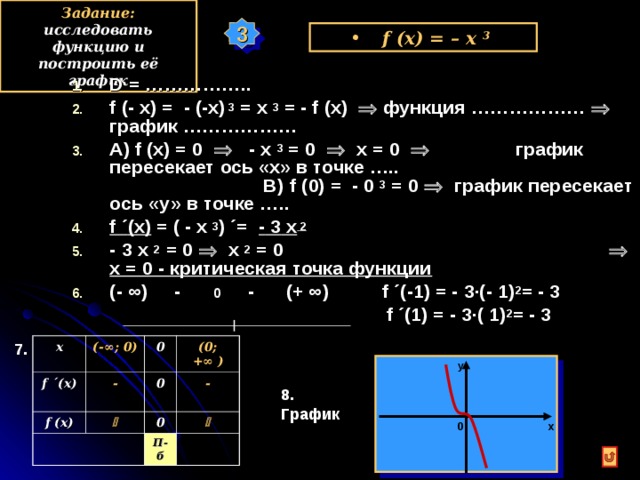


 ..
..

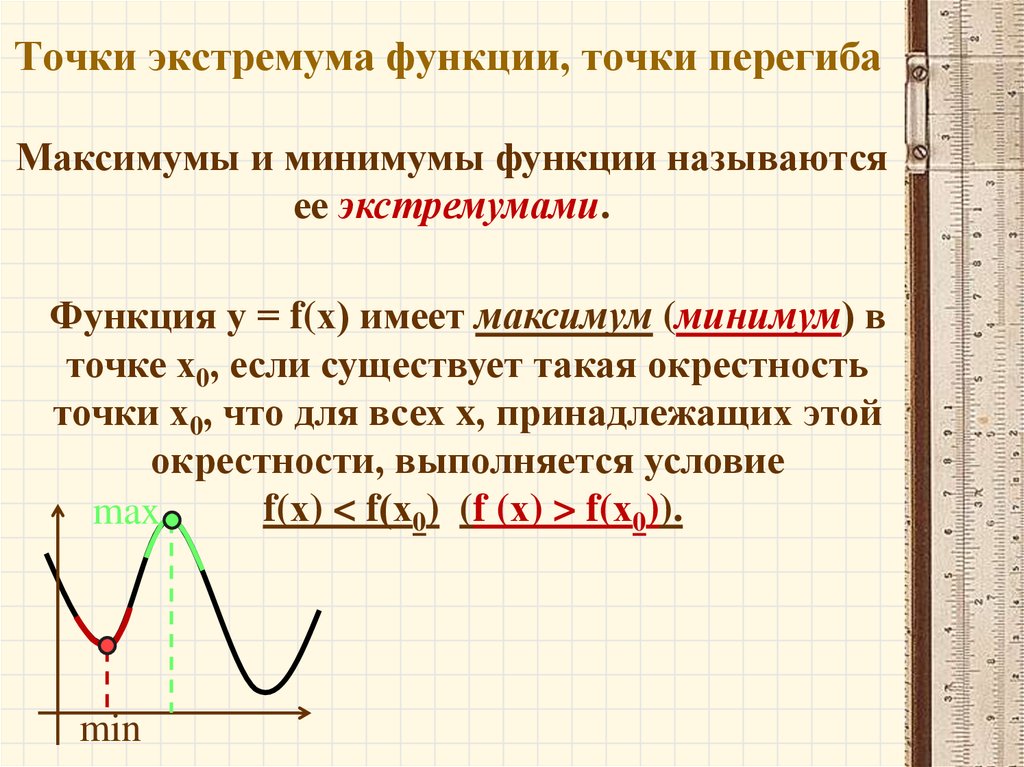 Новосибирск 2008.
Новосибирск 2008.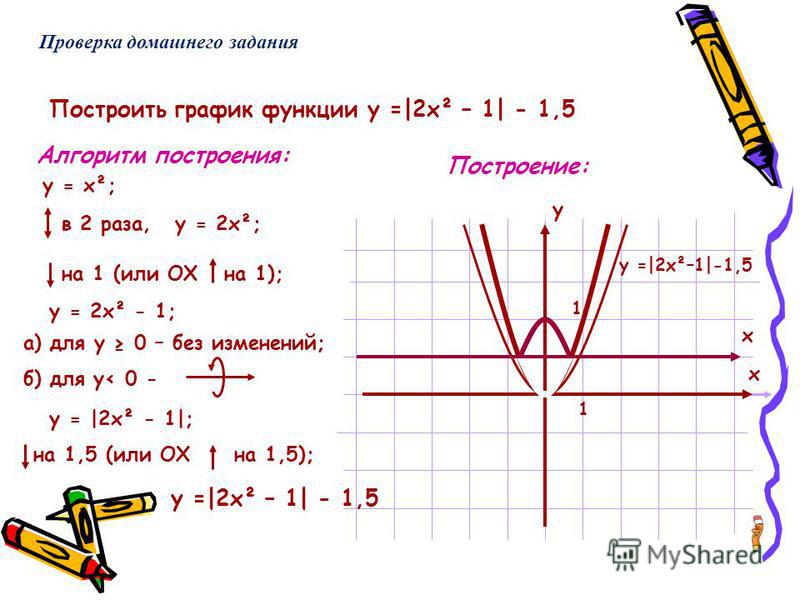 ru
ru ru
ru
 Разработка содержит презентацию. Целевая аудитория: для 10 класса.
Разработка содержит презентацию. Целевая аудитория: для 10 класса. Л63 Исследование функций с помощью производной / В. Лисичкин. – М. : Чистые пруды, 2005. – 32 с. (Библиотечка «Первого сентября», серия «Математика»). ISBN 5-9667-0054-0 Данная брошюра написана в соответствии с действующей школьной программой. Пособие может быть использовано для самостоятельного изучения, а также при подготовке к выпускному экзамену в традиционной форме, ЕГЭ и вступительным экзаменам в вузы. Краткие теоретические сведения сопровождаются подробными решениями задач.
Л63 Исследование функций с помощью производной / В. Лисичкин. – М. : Чистые пруды, 2005. – 32 с. (Библиотечка «Первого сентября», серия «Математика»). ISBN 5-9667-0054-0 Данная брошюра написана в соответствии с действующей школьной программой. Пособие может быть использовано для самостоятельного изучения, а также при подготовке к выпускному экзамену в традиционной форме, ЕГЭ и вступительным экзаменам в вузы. Краткие теоретические сведения сопровождаются подробными решениями задач. Подборка задач включает упражнения на исследование функций по алгоритмам и упражнения в формате ЕГЭ.
Подборка задач включает упражнения на исследование функций по алгоритмам и упражнения в формате ЕГЭ. Формировать глубину и оперативность мышления.
Формировать глубину и оперативность мышления.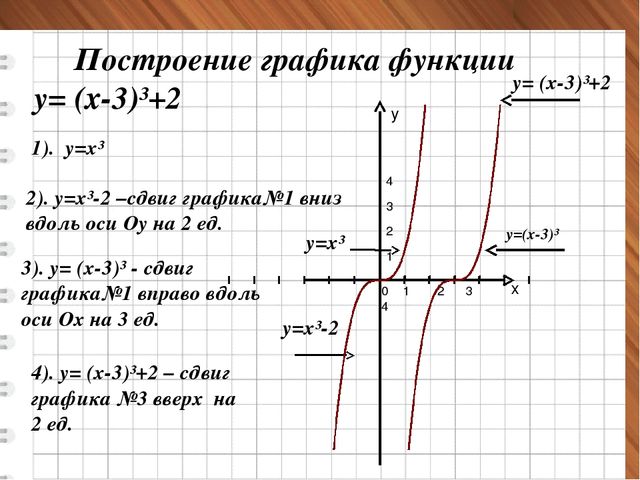 ..»
..» Построение графика. Если в задаче необходимо произвести полное исследование функции f(x)=x24x2−1.
Построение графика. Если в задаче необходимо произвести полное исследование функции f(x)=x24x2−1. д. По этим точкам выделяются участки однообразного поведения функции, а именно: промежутки ее непрерывности; промежутки, на которых у'(х) и y»(x) сохраняют знак, что позволяет изучить характер монотонности функции и направление ее выпуклости.
д. По этим точкам выделяются участки однообразного поведения функции, а именно: промежутки ее непрерывности; промежутки, на которых у'(х) и y»(x) сохраняют знак, что позволяет изучить характер монотонности функции и направление ее выпуклости. ..
.. д.
д. Сервантес Цель урока : Продолжить усовершенствование умений учащихся в исследовании функции с помощью производной и построение её графика; Повторить всё о асимптотах; Развитие аналитического мышления.
Сервантес Цель урока : Продолжить усовершенствование умений учащихся в исследовании функции с помощью производной и построение её графика; Повторить всё о асимптотах; Развитие аналитического мышления. ..
..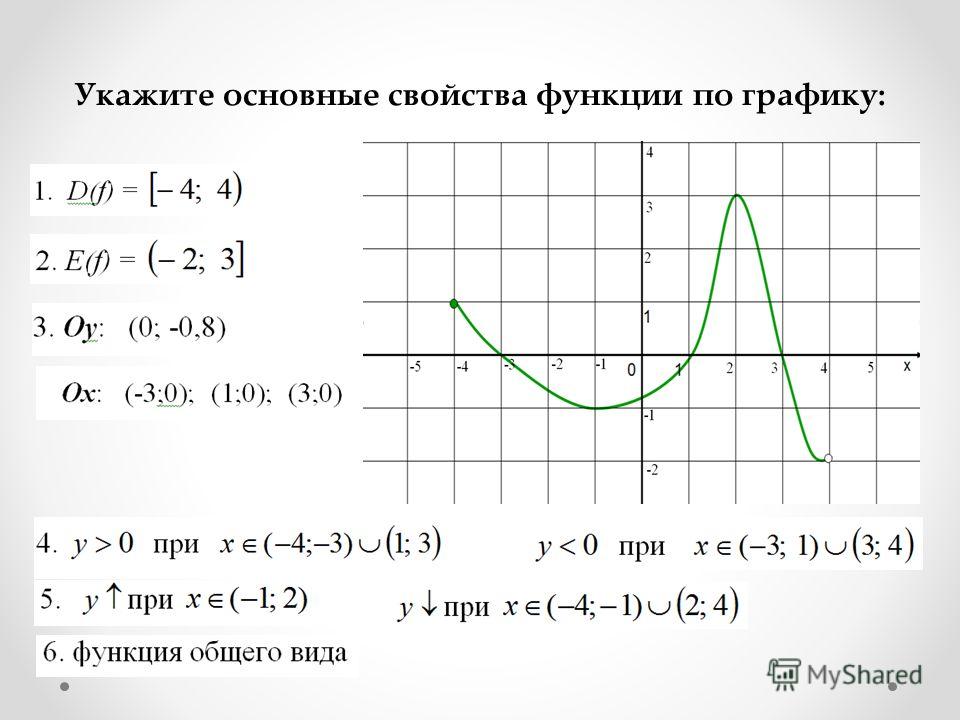 При исследовании функции и построении ее графика целесообразно придерживаться следующей схемы: Первый этап (использование вида заданной функции).
При исследовании функции и построении ее графика целесообразно придерживаться следующей схемы: Первый этап (использование вида заданной функции). Исследование границ ОДЗ и нахождение вертикальных асимптот. Исследование функции и на четность или нечетность. Нахождение возрастания и убывания, точек экстремума. Нахождение промежутков выпуклости и вогнутости функции и точек перегиба. Нахождение горизонтальных и наклонных асимптот. Вычисление значения функции в промежуточных точках. Построение графика. Если в задаче необходимо произвести полное исследование функции f(x)=x24x2−1.
Исследование границ ОДЗ и нахождение вертикальных асимптот. Исследование функции и на четность или нечетность. Нахождение возрастания и убывания, точек экстремума. Нахождение промежутков выпуклости и вогнутости функции и точек перегиба. Нахождение горизонтальных и наклонных асимптот. Вычисление значения функции в промежуточных точках. Построение графика. Если в задаче необходимо произвести полное исследование функции f(x)=x24x2−1. Графики с прямыми линиями были рассмотрены в 9 классе и переработаны здесь. Параболы, гиперболы и
здесь вводятся экспоненциальные графики. Также представлены графики для функций синуса, косинуса и тангенса.
здесь.
Графики с прямыми линиями были рассмотрены в 9 классе и переработаны здесь. Параболы, гиперболы и
здесь вводятся экспоненциальные графики. Также представлены графики для функций синуса, косинуса и тангенса.
здесь.


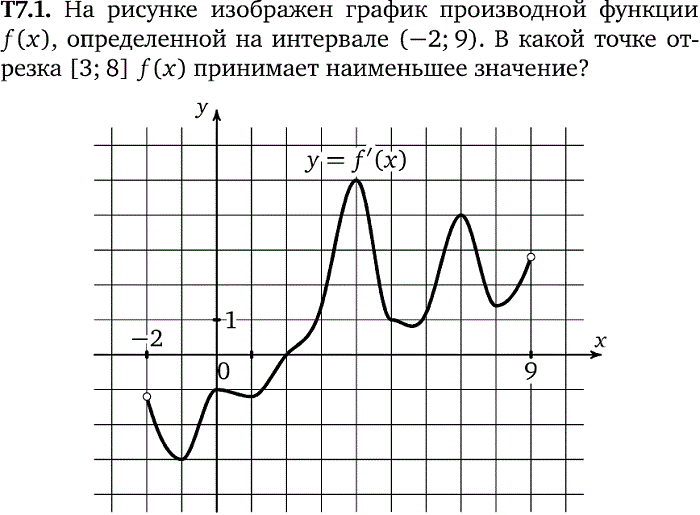
 ИФ.А.1
— Поймите, что функция от одного набора (называемого доменом) к другому набору (называемому диапазоном) присваивает каждому элементу домена ровно один элемент диапазона. Если f — функция, а x — элемент ее области определения, то f(x) обозначает выход f, соответствующий входу x. График f — это график уравнения y = f(x).
ИФ.А.1
— Поймите, что функция от одного набора (называемого доменом) к другому набору (называемому диапазоном) присваивает каждому элементу домена ровно один элемент диапазона. Если f — функция, а x — элемент ее области определения, то f(x) обозначает выход f, соответствующий входу x. График f — это график уравнения y = f(x). 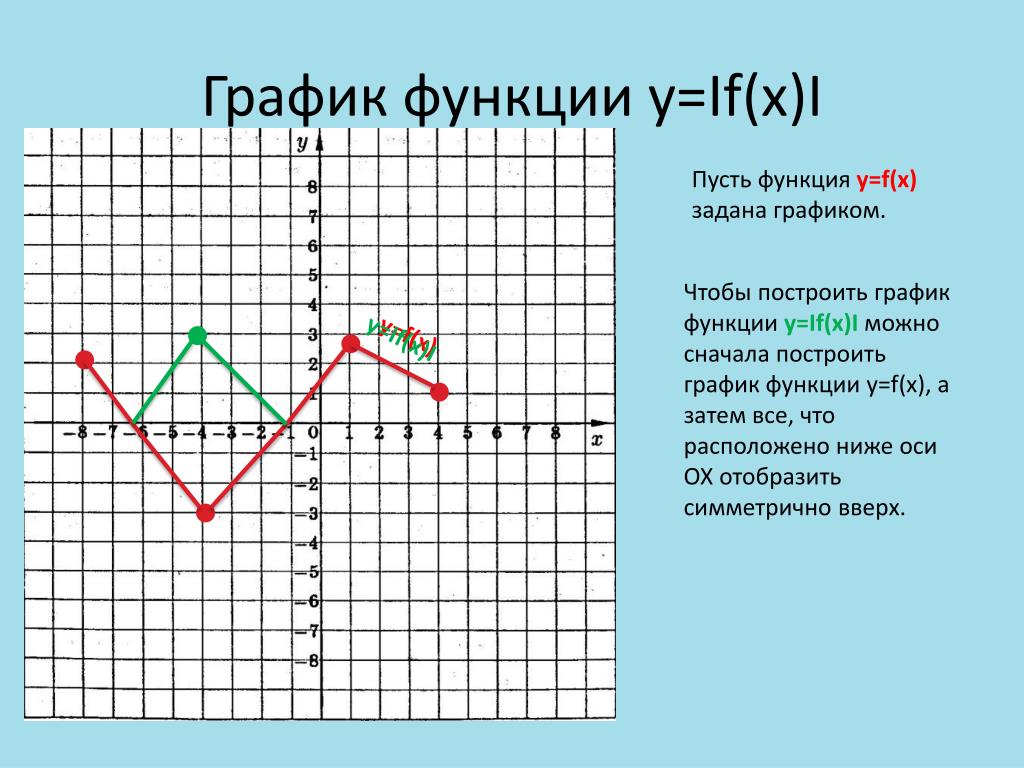


 Если любое входное значение приводит к двум или более выходам, отношение не является функцией.
Если любое входное значение приводит к двум или более выходам, отношение не является функцией.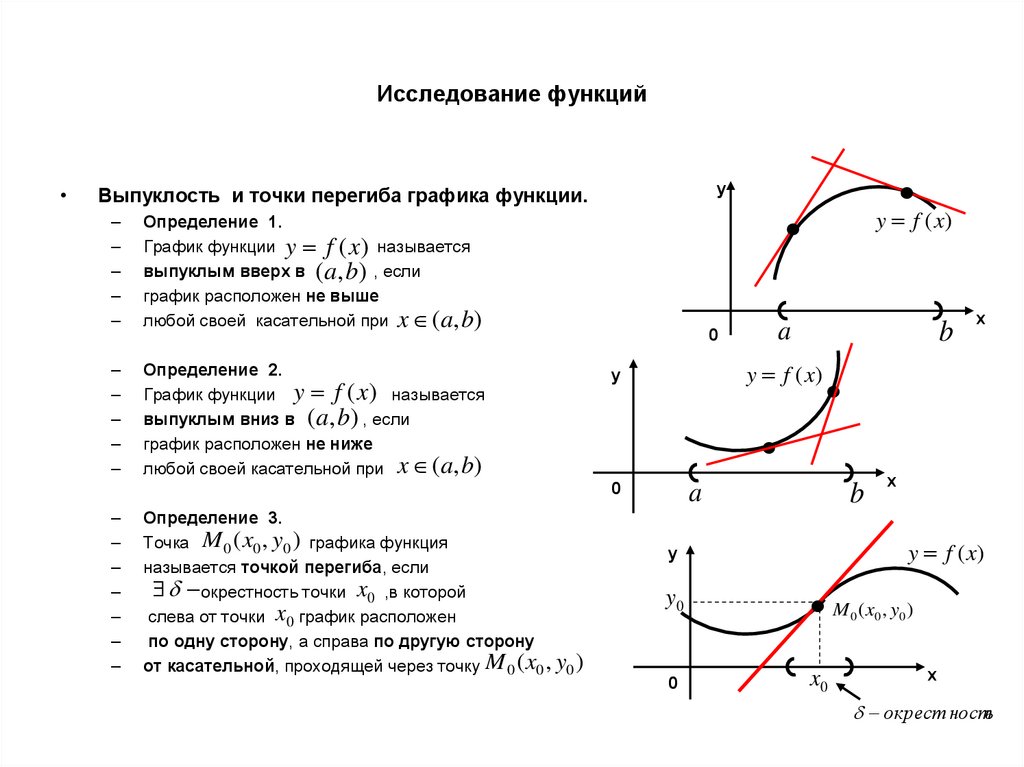



 Здесь давайте вызовем функцию [latex]P[/latex].
Здесь давайте вызовем функцию [latex]P[/latex].

 Графики отображают множество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Графики отображают множество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси. Например, черные точки на графике ниже говорят нам, что [латекс]f\влево(0\вправо)=2[/латекс] и [латекс]f\влево(6\вправо)=1[/латекс ]. Однако множество всех точек [латекс]\влево(х,у\вправо)[/латекс], удовлетворяющих [латекс]у=f\влево(х\вправо)[/латекс], является кривой. Показанная кривая включает [латекс]\влево(0,2\вправо)[/латекс] и [латекс]\влево(6,1\вправо)[/латекс], поскольку кривая проходит через эти точки.
Например, черные точки на графике ниже говорят нам, что [латекс]f\влево(0\вправо)=2[/латекс] и [латекс]f\влево(6\вправо)=1[/латекс ]. Однако множество всех точек [латекс]\влево(х,у\вправо)[/латекс], удовлетворяющих [латекс]у=f\влево(х\вправо)[/латекс], является кривой. Показанная кривая включает [латекс]\влево(0,2\вправо)[/латекс] и [латекс]\влево(6,1\вправо)[/латекс], поскольку кривая проходит через эти точки.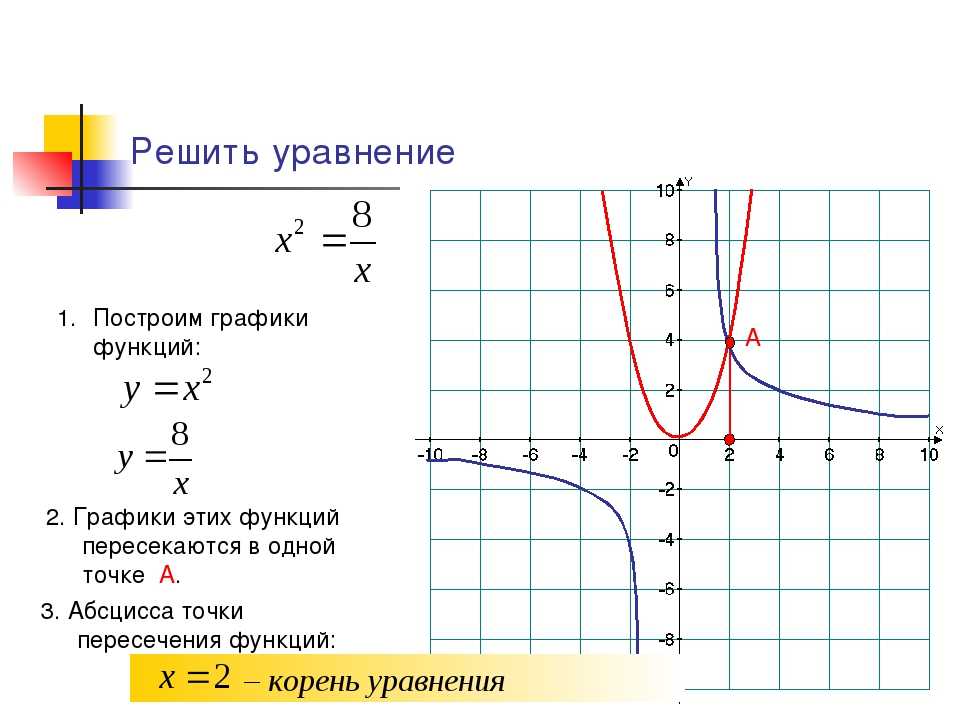
 Проведите горизонтальные линии через график. Горизонтальная линия включает все точки с определенным значением [latex]y[/latex]. Значение [latex]x[/latex] точки, в которой вертикальная линия пересекает функцию, представляет вход для этого выходного значения [latex]y[/latex]. Если мы можем нарисовать любая горизонтальная линия , которая пересекает график более одного раза, то график , а не представляет собой функцию один к одному, потому что это значение [latex]y[/latex] имеет более одного входа.
Проведите горизонтальные линии через график. Горизонтальная линия включает все точки с определенным значением [latex]y[/latex]. Значение [latex]x[/latex] точки, в которой вертикальная линия пересекает функцию, представляет вход для этого выходного значения [latex]y[/latex]. Если мы можем нарисовать любая горизонтальная линия , которая пересекает график более одного раза, то график , а не представляет собой функцию один к одному, потому что это значение [latex]y[/latex] имеет более одного входа.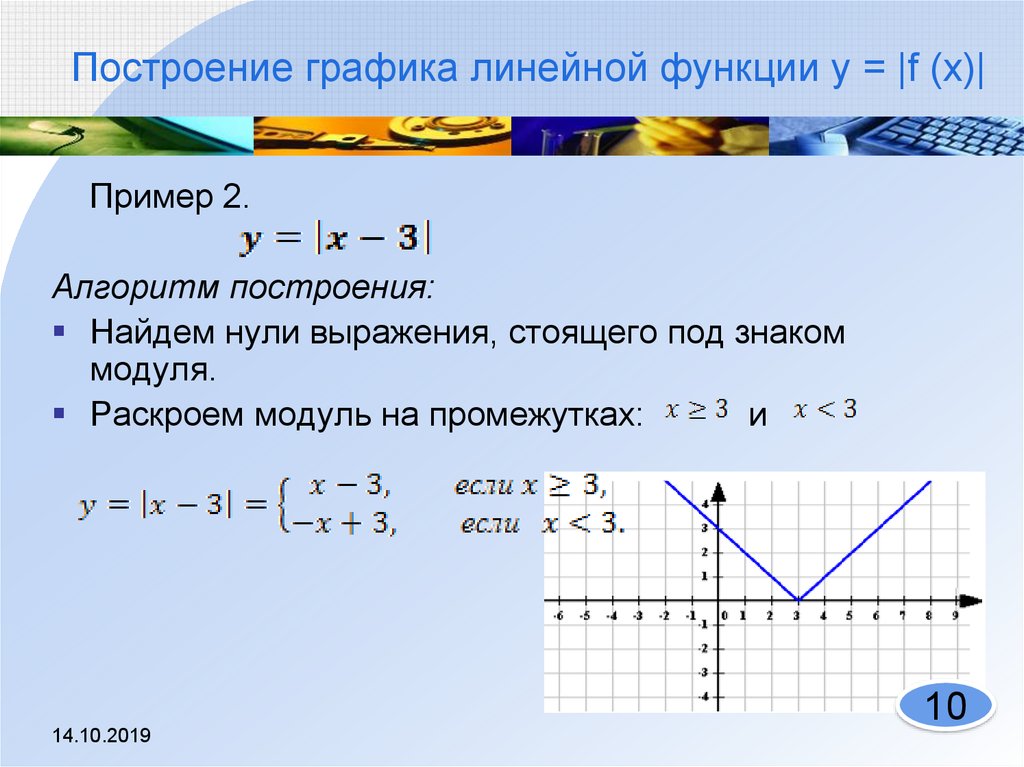



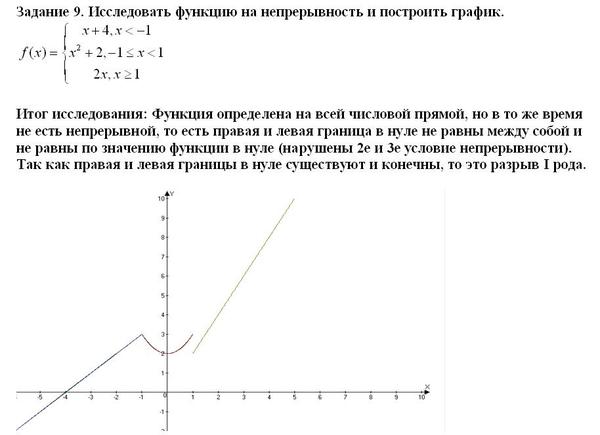 1 Функции и обозначение функций — College Algebra 2e
1 Функции и обозначение функций — College Algebra 2e Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.
Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого. {2,4,6,8,10}.
{2,4,6,8,10}.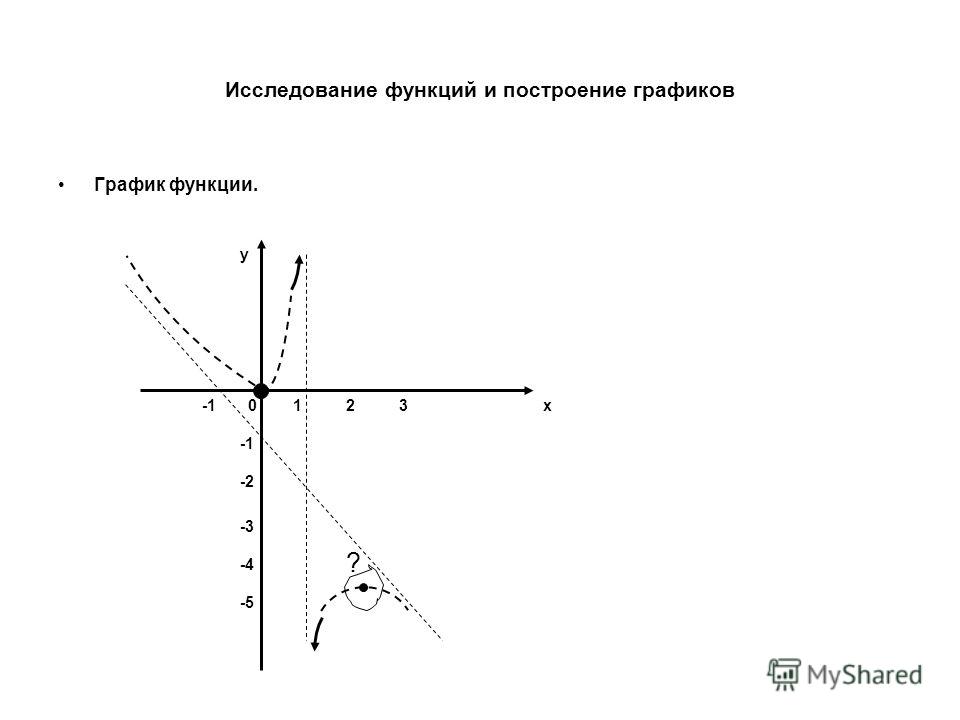 n. б) Это отношение также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, поскольку вход qq связан с двумя разными выходами.
n. б) Это отношение также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, поскольку вход qq связан с двумя разными выходами.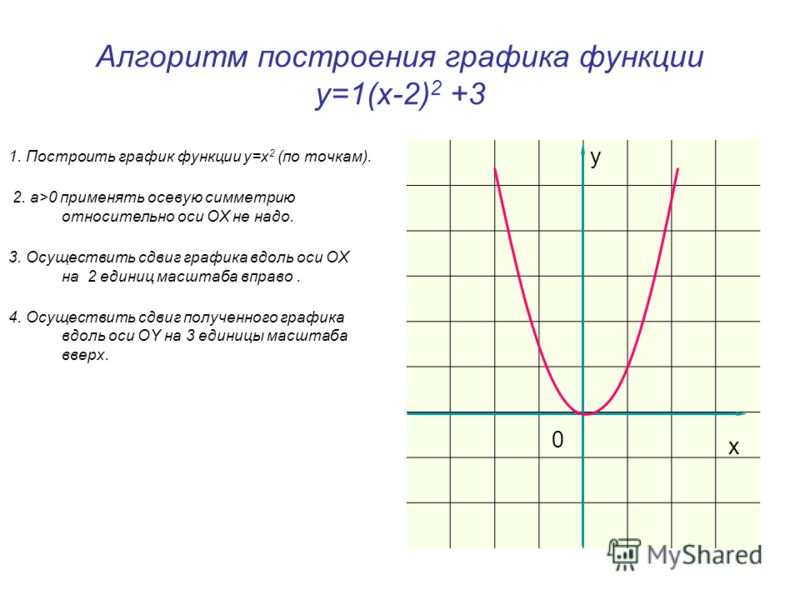

 Другими словами, если мы вводим процентную оценку, на выходе получается определенный средний балл.
Другими словами, если мы вводим процентную оценку, на выходе получается определенный средний балл.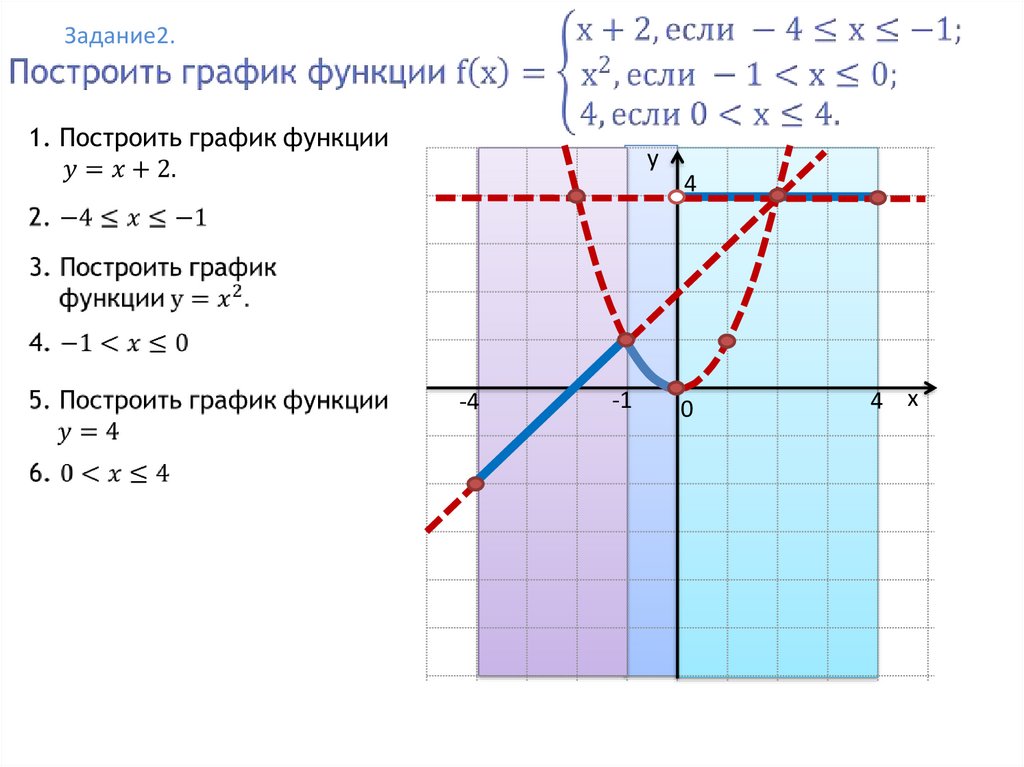 Существуют различные способы представления функций. Стандартная нотация функций — это одно из представлений, упрощающее работу с функциями.
Существуют различные способы представления функций. Стандартная нотация функций — это одно из представлений, упрощающее работу с функциями.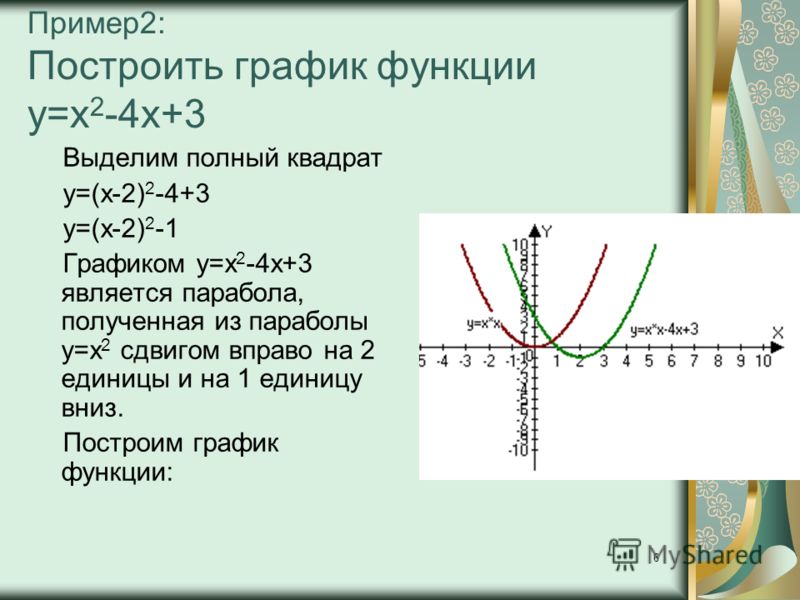 Скобки указывают на то, что в функцию вводится возраст; они не указывают на умножение.
Скобки указывают на то, что в функцию вводится возраст; они не указывают на умножение. Предположим, что домен не включает високосные годы.
Предположим, что домен не включает високосные годы.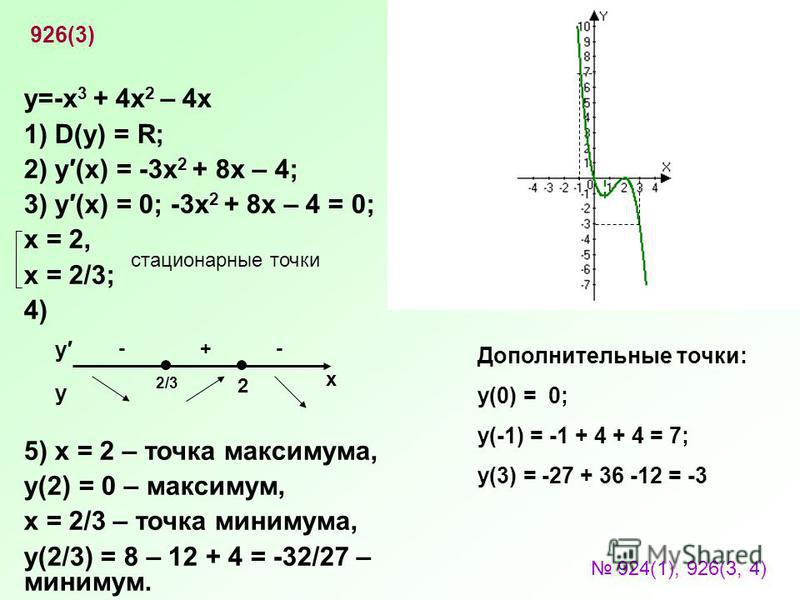 y. Что представляет собой f(2005)=300f(2005)=300?
y. Что представляет собой f(2005)=300f(2005)=300?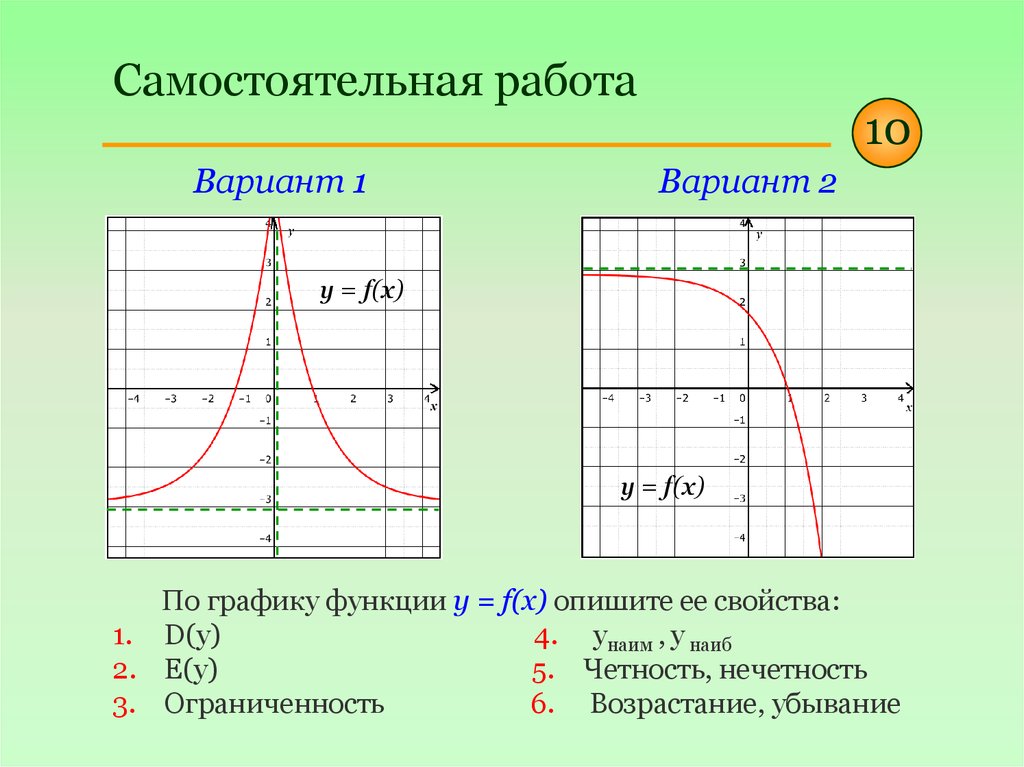 Однако при изучении самой математики нам нравится сохранять различие между такими функциями, как f,f, которые являются правилом или процедурой, и выходными данными yy, которые мы получаем, применяя ff к конкретным входным данным x.x. Вот почему мы обычно используем такие обозначения, как y=f(x),P=W(d),y=f(x),P=W(d) и так далее.
Однако при изучении самой математики нам нравится сохранять различие между такими функциями, как f,f, которые являются правилом или процедурой, и выходными данными yy, которые мы получаем, применяя ff к конкретным входным данным x.x. Вот почему мы обычно используем такие обозначения, как y=f(x),P=W(d),y=f(x),P=W(d) и так далее. 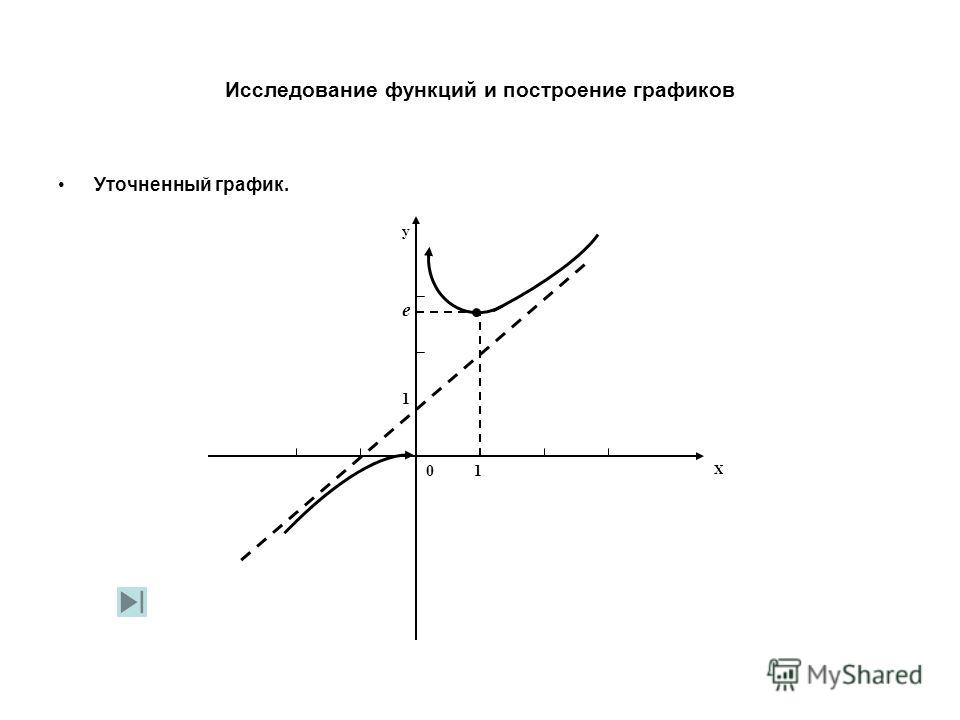
 Q=g(n). Помните, эта запись говорит нам, что gg — это имя функции, которая принимает входные данные nn и дает выходные данные Q.Q.
Q=g(n). Помните, эта запись говорит нам, что gg — это имя функции, которая принимает входные данные nn и дает выходные данные Q.Q.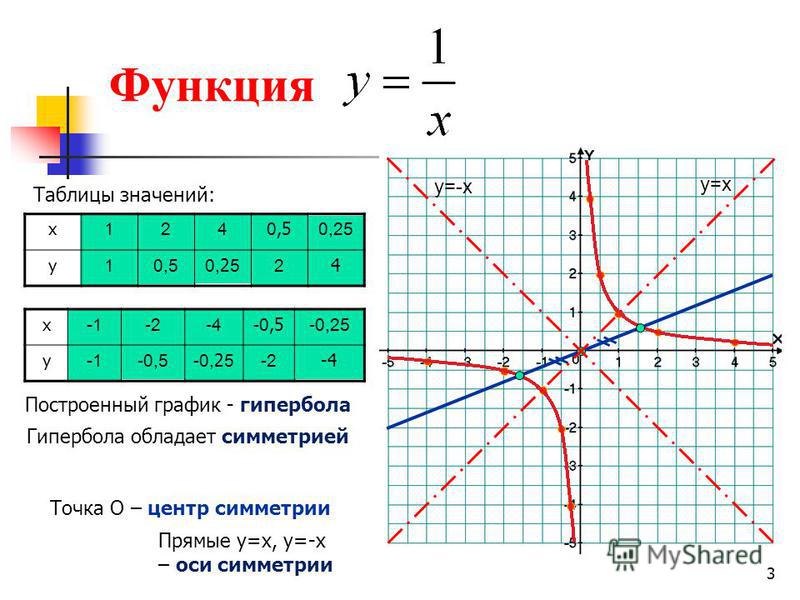
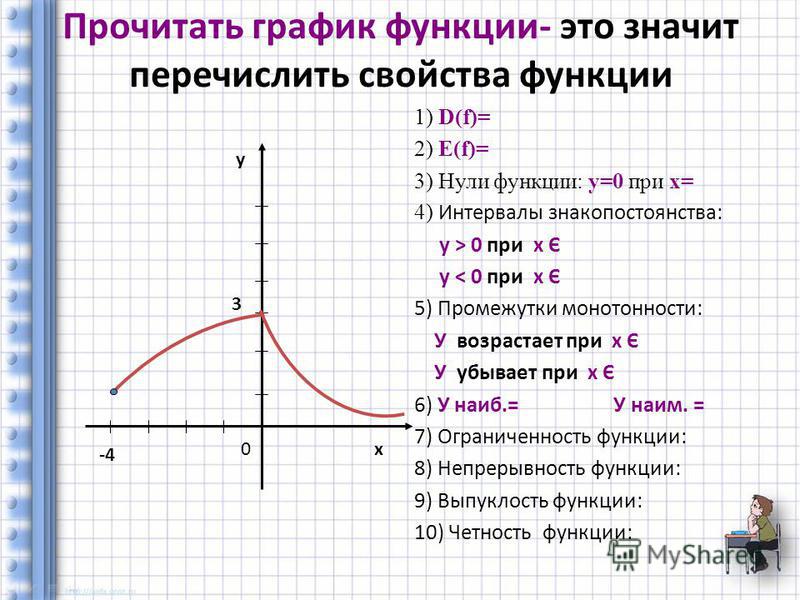 В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица 8 не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям.
В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица 8 не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям.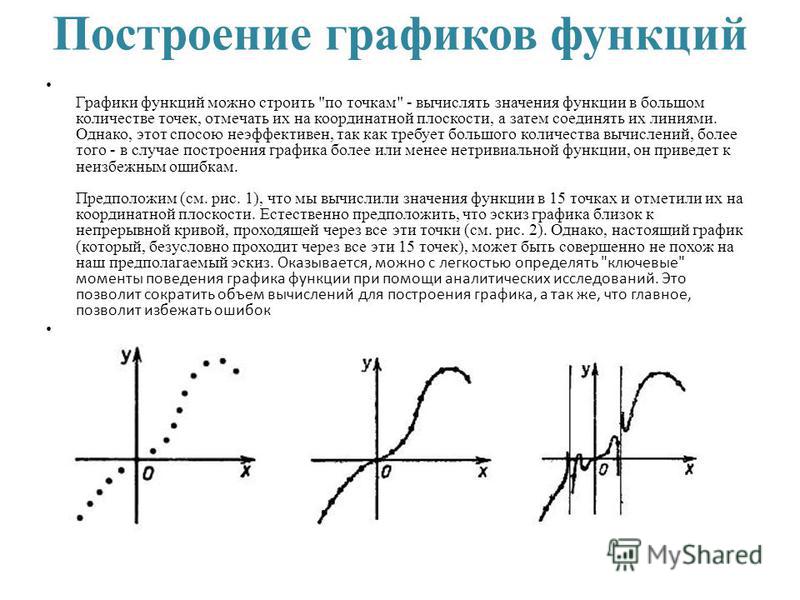 Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Вычисление всегда будет давать один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
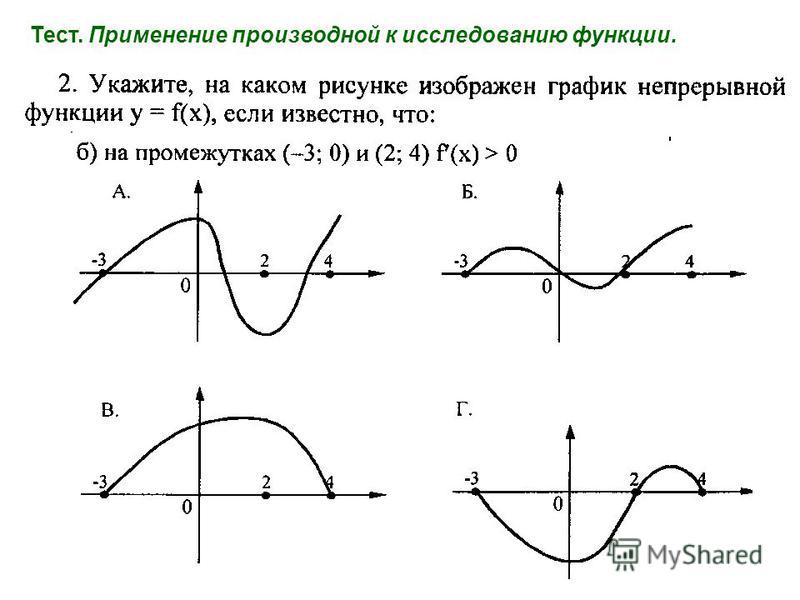 Мы уже нашли это
Мы уже нашли это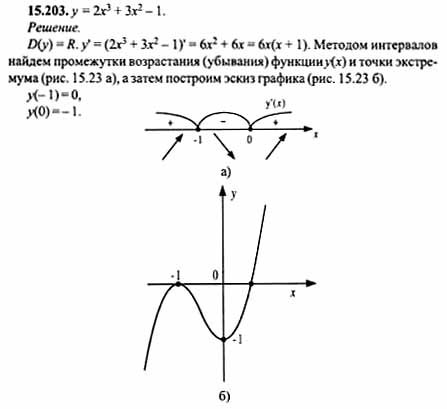 g(5).
g(5).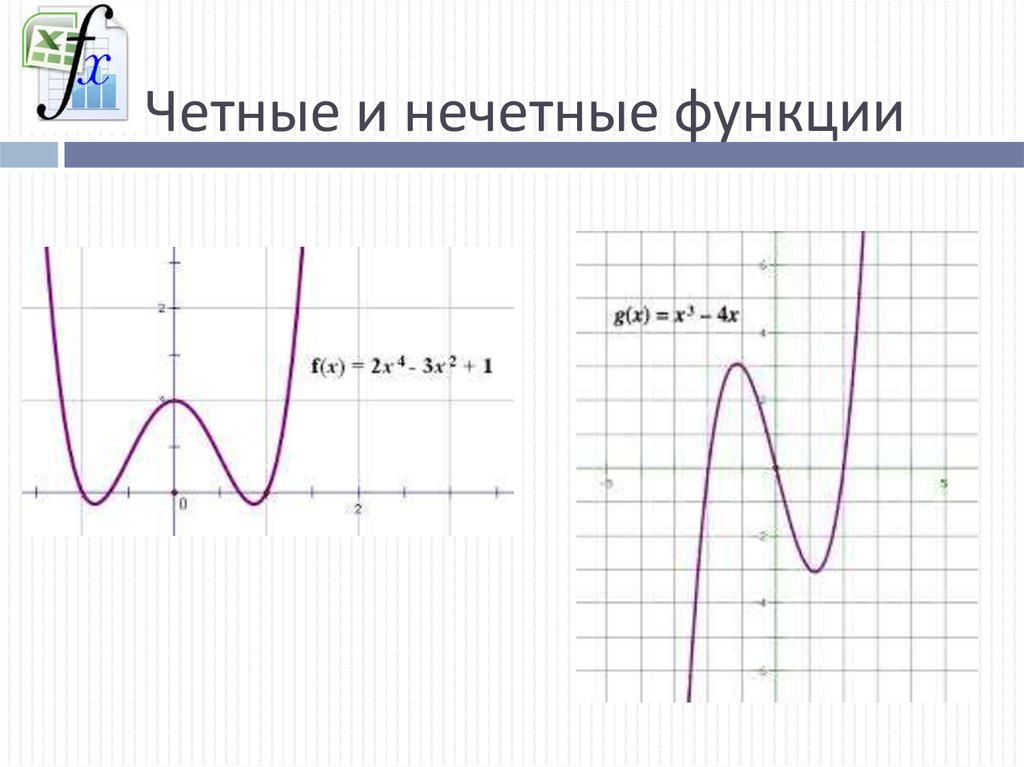 g(m)=2.
g(m)=2.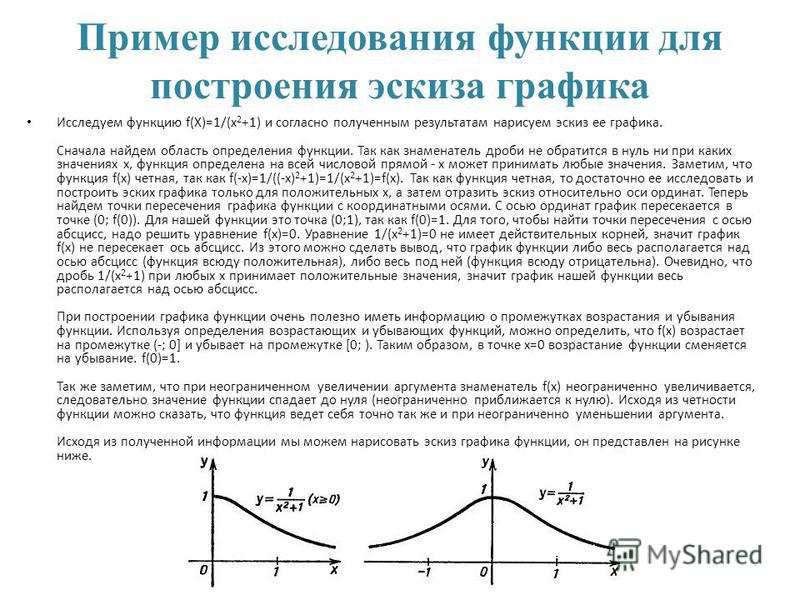
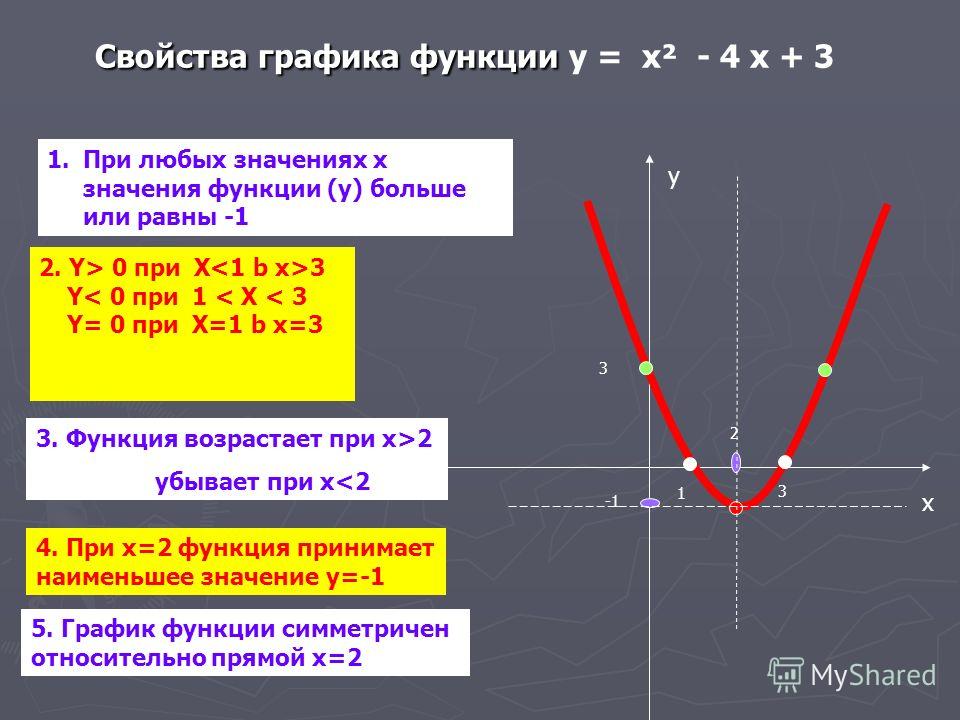 y=f(x).
y=f(x).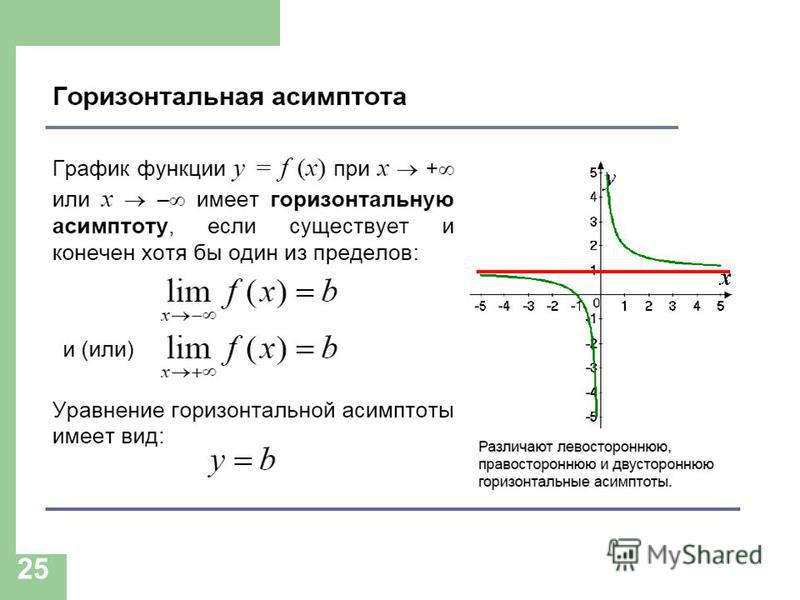 y. Однако каждый xx определяет уникальное значение y, y, и существуют математические процедуры, с помощью которых yy можно найти с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для yy как функции x,x, даже если формулу нельзя записать явно.
y. Однако каждый xx определяет уникальное значение y, y, и существуют математические процедуры, с помощью которых yy можно найти с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для yy как функции x,x, даже если формулу нельзя записать явно. 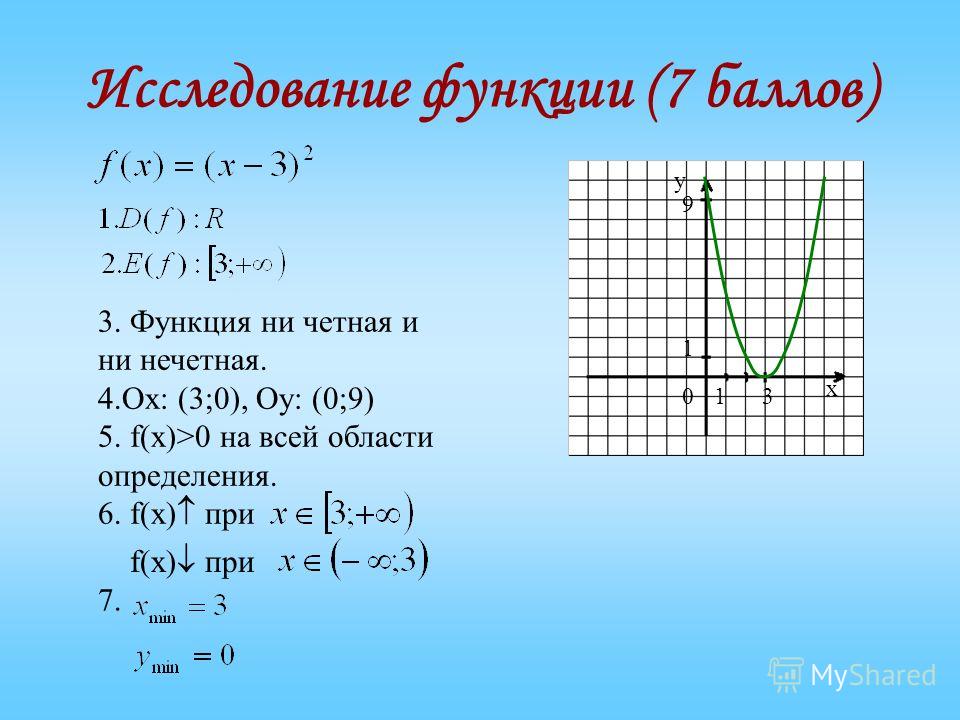
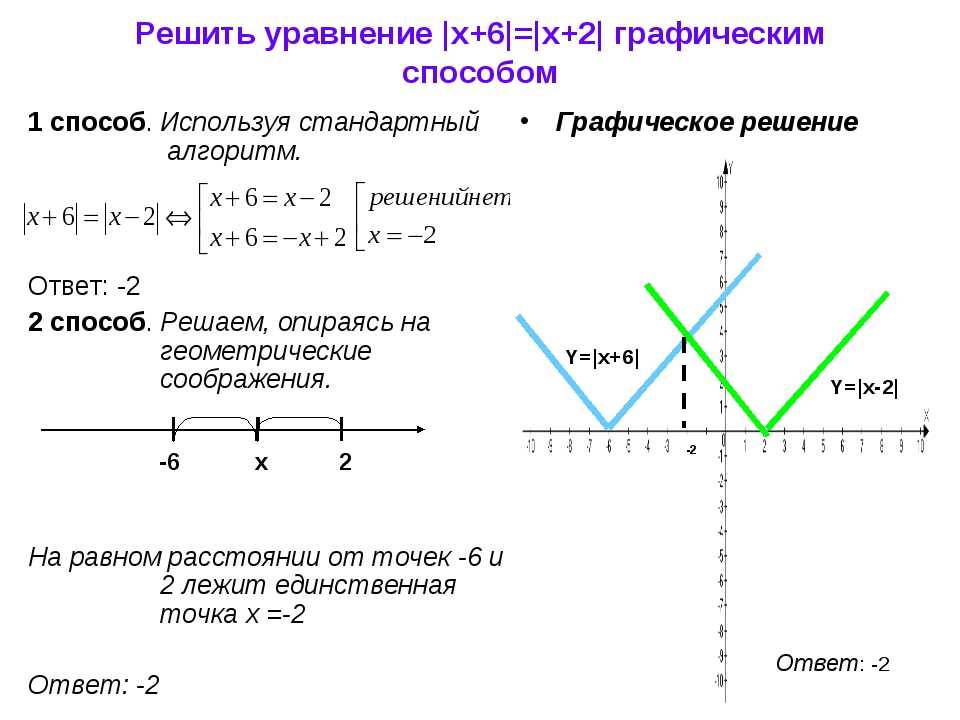 Здесь назовем функцию P.P.
Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию PP по входному значению «золотая рыбка». Мы бы написали P(золотая рыбка)=2160.P(золотая рыбка)=2160. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции PP кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
Здесь назовем функцию P.P.
Домен функции — это тип питомца, а диапазон — действительное число, представляющее количество часов, в течение которых сохраняется память питомца. Мы можем оценить функцию PP по входному значению «золотая рыбка». Мы бы написали P(золотая рыбка)=2160.P(золотая рыбка)=2160. Обратите внимание, что для вычисления функции в форме таблицы мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции PP кажется идеально подходящей для этой функции, в большей степени, чем ее запись в форме абзаца или функции.
 n=3. Выходное значение таблицы, соответствующее n=3n=3, равно 7, поэтому g(3)=7.g(3)=7.
n=3. Выходное значение таблицы, соответствующее n=3n=3, равно 7, поэтому g(3)=7.g(3)=7.  Когда мы вводим 4 в функцию g,g, наш выход также равен 6.
Когда мы вводим 4 в функцию g,g, наш выход также равен 6.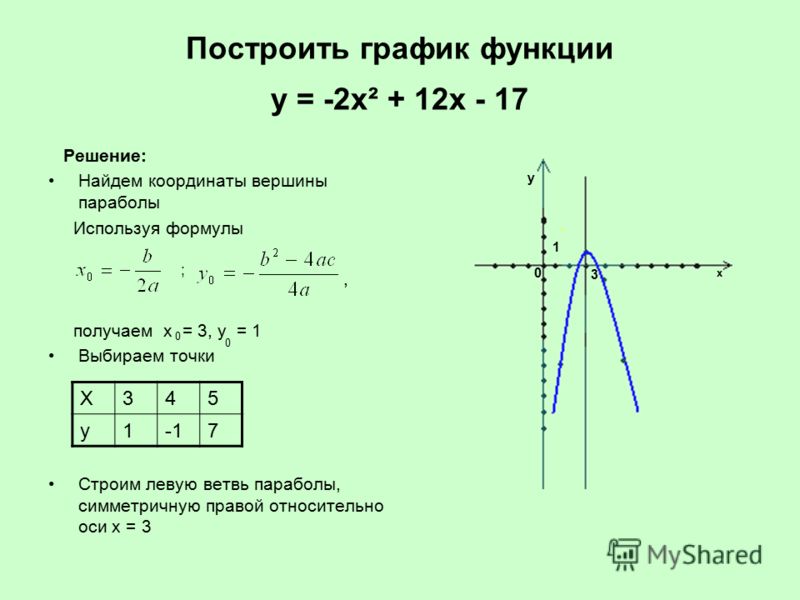 Точка имеет координаты (2,1),(2,1), поэтому f(2)=1.f(2)=1. См. рис. 5.
Точка имеет координаты (2,1),(2,1), поэтому f(2)=1.f(2)=1. См. рис. 5.

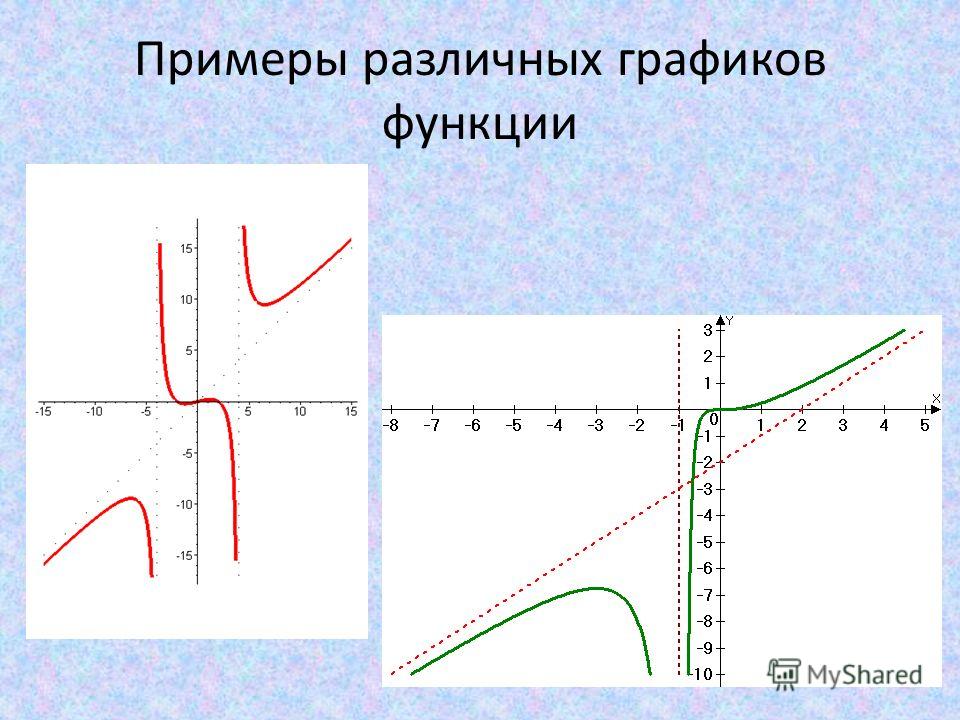 A. Площадь является функцией радиуса r.r.
A. Площадь является функцией радиуса r.r. Графики отображают большое количество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. По соглашению графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Графики отображают большое количество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. По соглашению графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси. f(6)=1. Однако множество всех точек (x,y)(x,y), удовлетворяющих y=f(x)y=f(x), является кривой. Показанная кривая включает в себя (0,2)(0,2) и (6,1)(6,1), поскольку кривая проходит через эти точки.
f(6)=1. Однако множество всех точек (x,y)(x,y), удовлетворяющих y=f(x)y=f(x), является кривой. Показанная кривая включает в себя (0,2)(0,2) и (6,1)(6,1), поскольку кривая проходит через эти точки.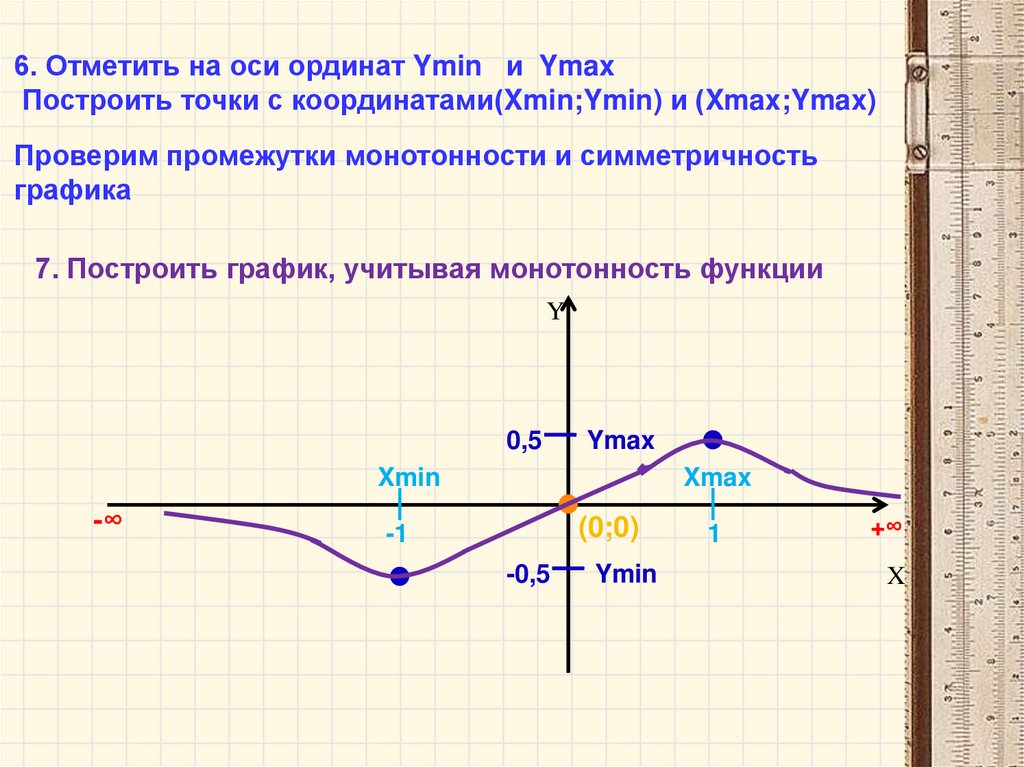
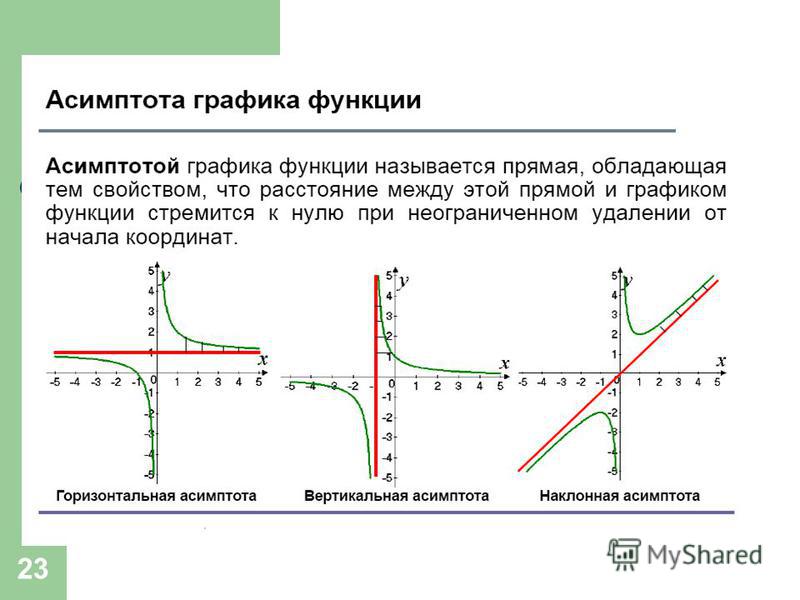 Проведите горизонтальные линии через график. Если любая горизонтальная линия пересекает график более одного раза, то график не представляет однозначной функции.
Проведите горизонтальные линии через график. Если любая горизонтальная линия пересекает график более одного раза, то график не представляет однозначной функции. Горизонтальная линия, показанная на рисунке 12, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, пересекающие ее в трех точках).
Горизонтальная линия, показанная на рисунке 12, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, пересекающие ее в трех точках). Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать xx в качестве входной переменной и y=f(x)y=f(x) в качестве выходной переменной.
Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать xx в качестве входной переменной и y=f(x)y=f(x) в качестве выходной переменной.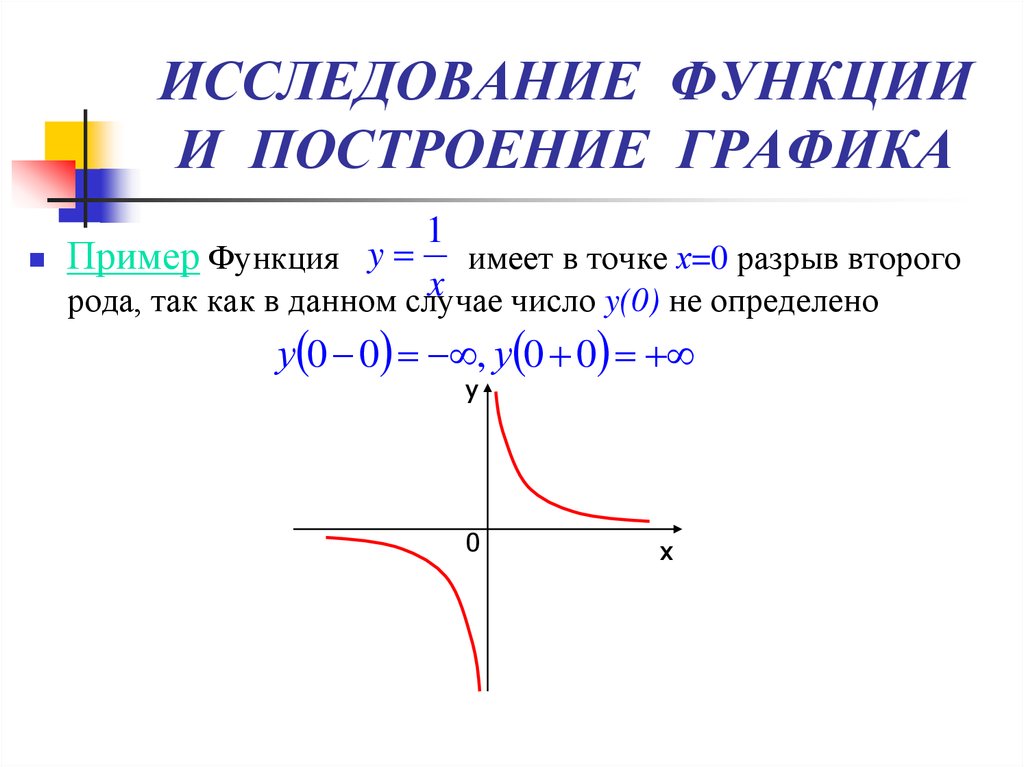 1 Секционные упражнения
1 Секционные упражнения x.
x.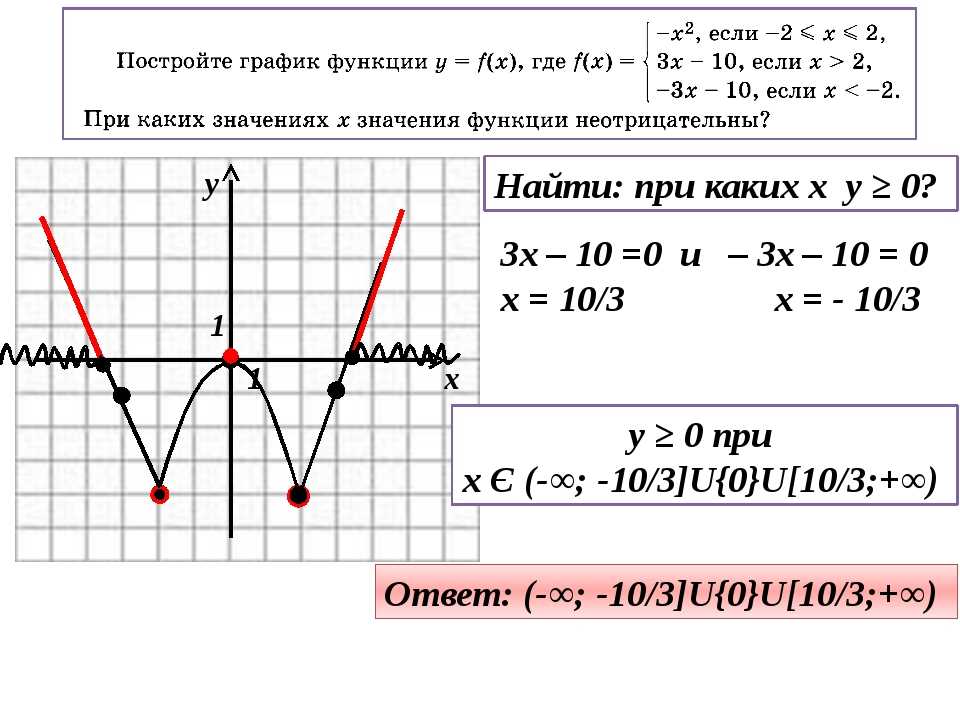
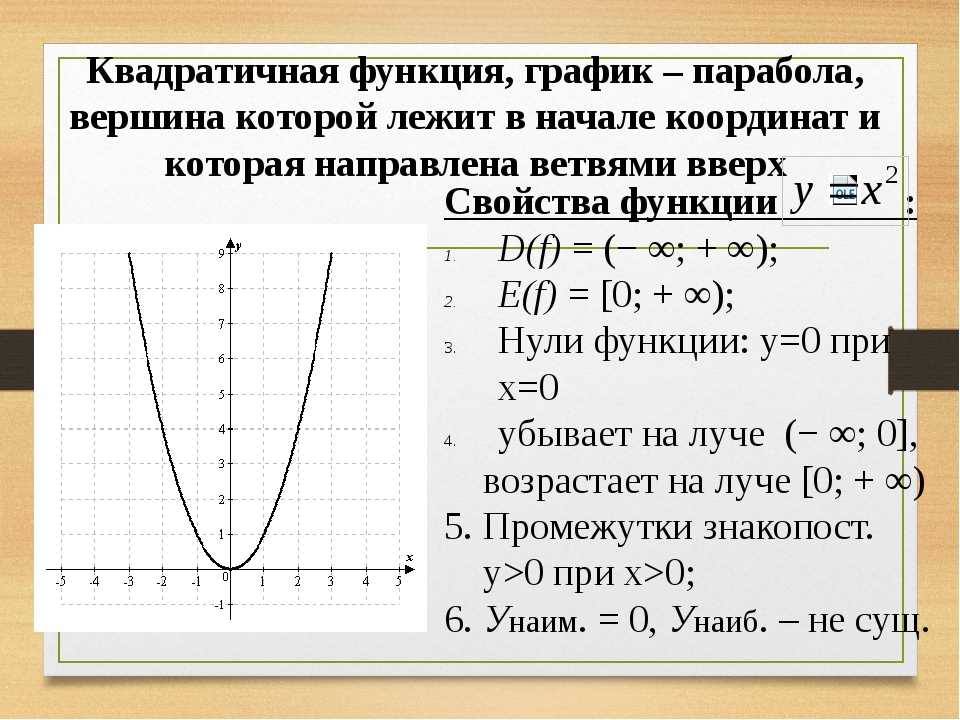 g(x)−g(a)x− а, х ≠ а.
g(x)−g(a)x− а, х ≠ а.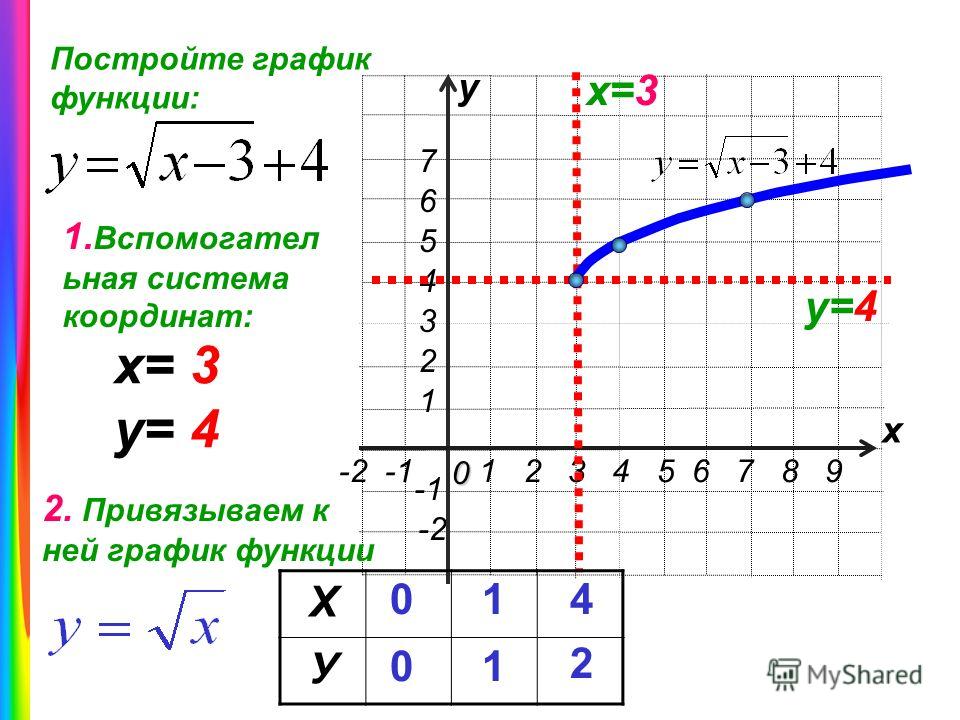

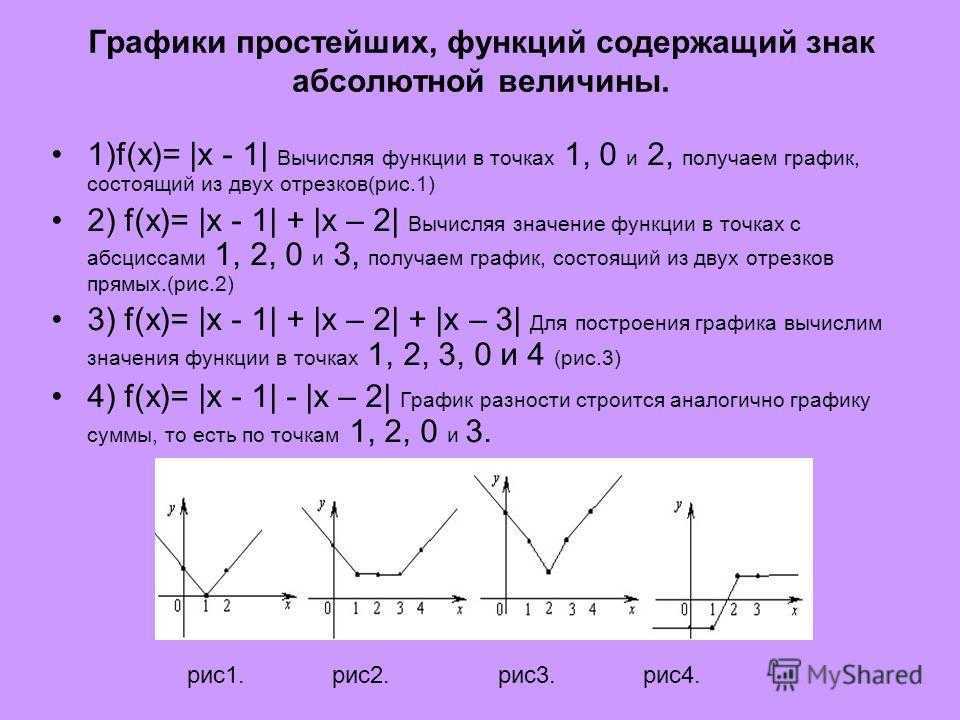






 Если кривая (график) представляет собой функцию, то каждая точка кривой удовлетворяет уравнению функции. Например, следующий график представляет линейную функцию f(x) = -x+ 2,
Если кривая (график) представляет собой функцию, то каждая точка кривой удовлетворяет уравнению функции. Например, следующий график представляет линейную функцию f(x) = -x+ 2,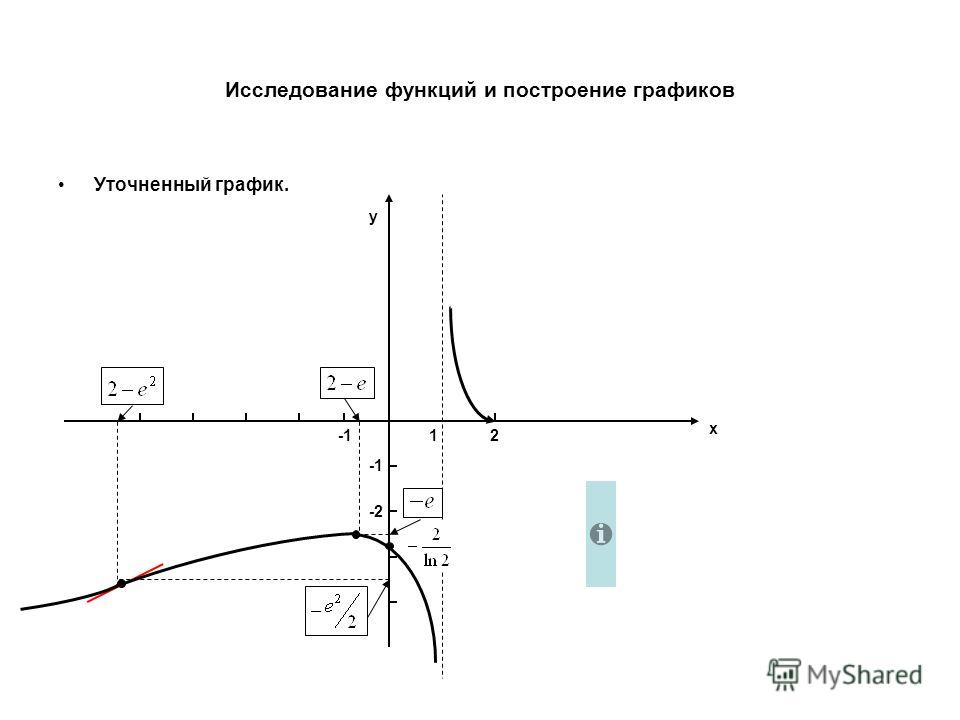
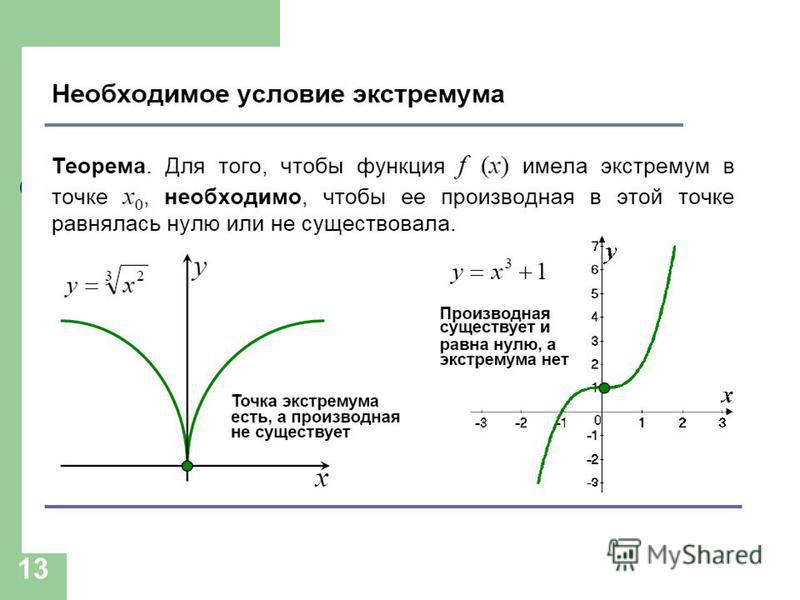 Но это может не дать идеальной U-образной кривой. Это потому, что для получения идеальной U-образной кривой нам нужно, где она поворачивает. т. е. надо найти его вершину. Найдя вершину, мы можем найти две или три случайные точки с каждой стороны вершины, и они помогут в построении графика функции.
Но это может не дать идеальной U-образной кривой. Это потому, что для получения идеальной U-образной кривой нам нужно, где она поворачивает. т. е. надо найти его вершину. Найдя вершину, мы можем найти две или три случайные точки с каждой стороны вершины, и они помогут в построении графика функции.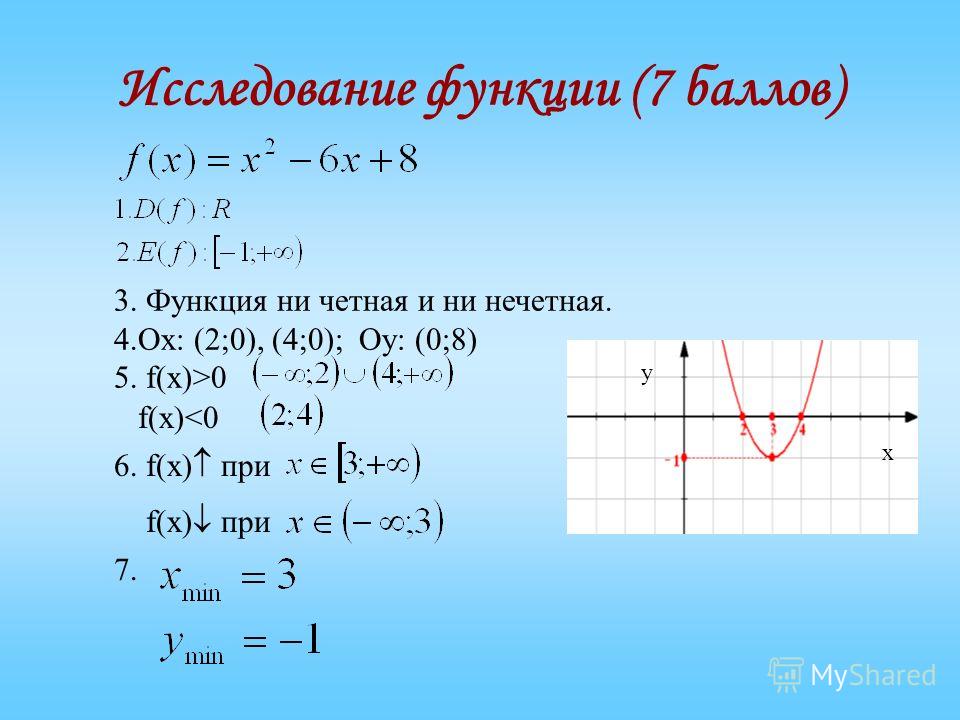
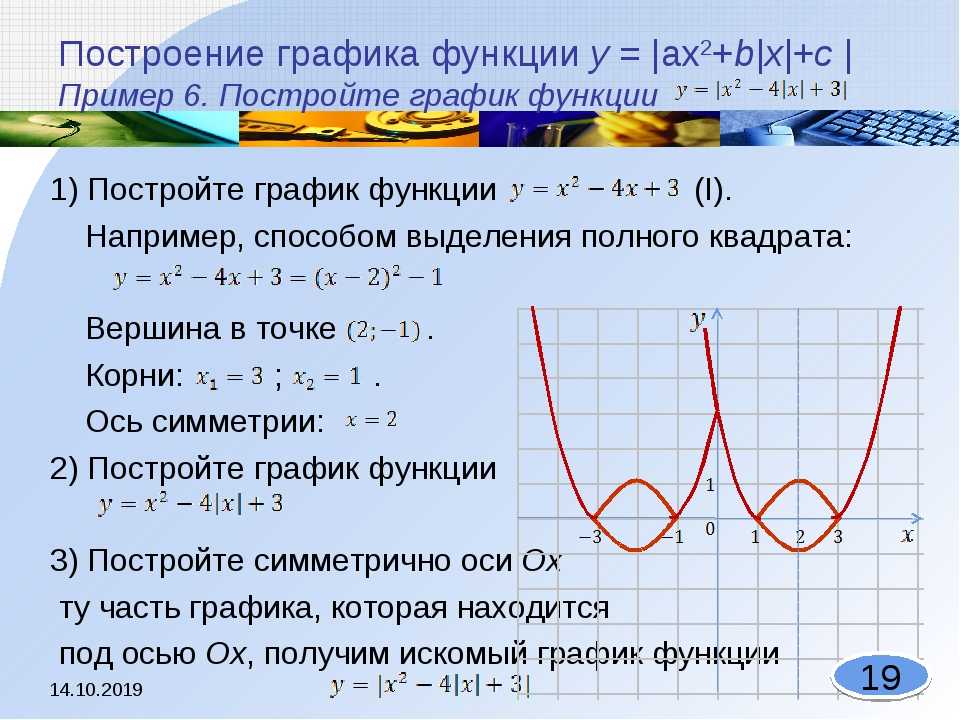
 Мы построим ее график, используя те же шаги, что и упомянутые выше.
Мы построим ее график, используя те же шаги, что и упомянутые выше.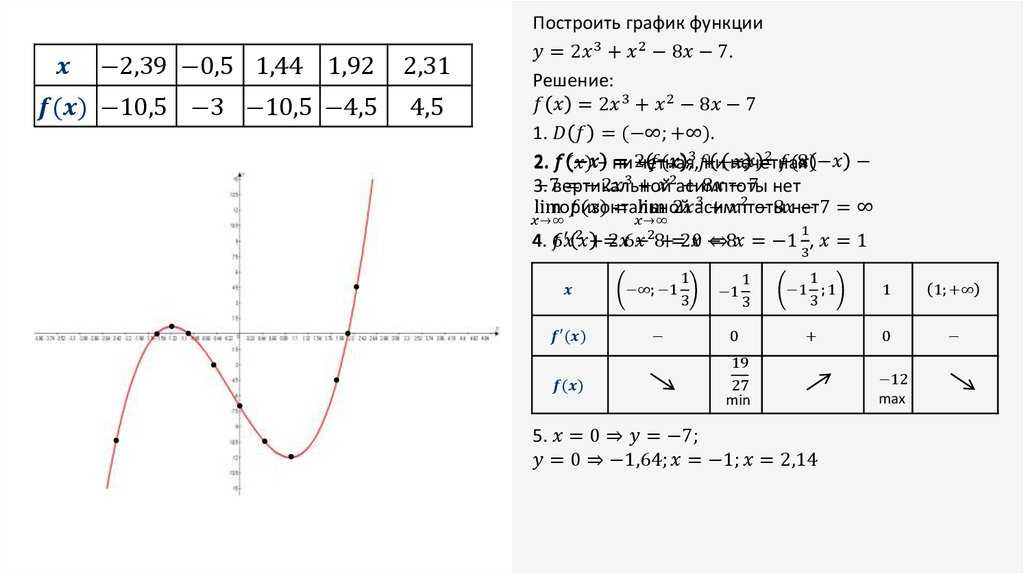
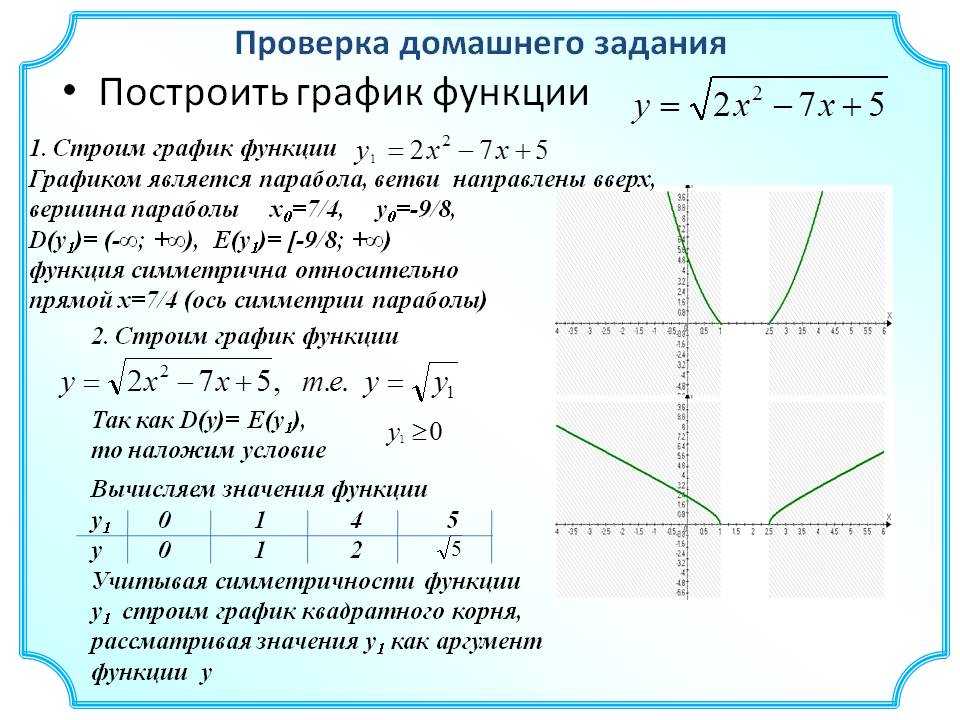 Затем мы можем применить следующие преобразования для построения графика данной функции.
Затем мы можем применить следующие преобразования для построения графика данной функции.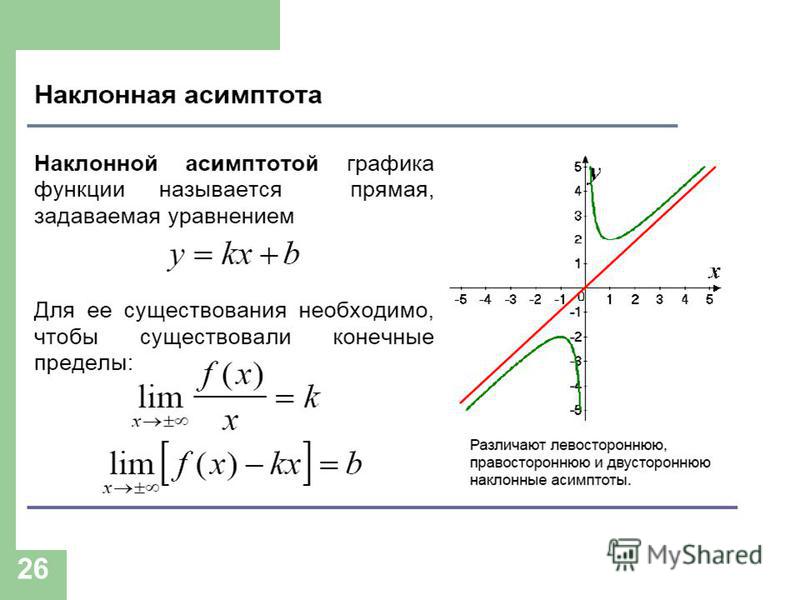
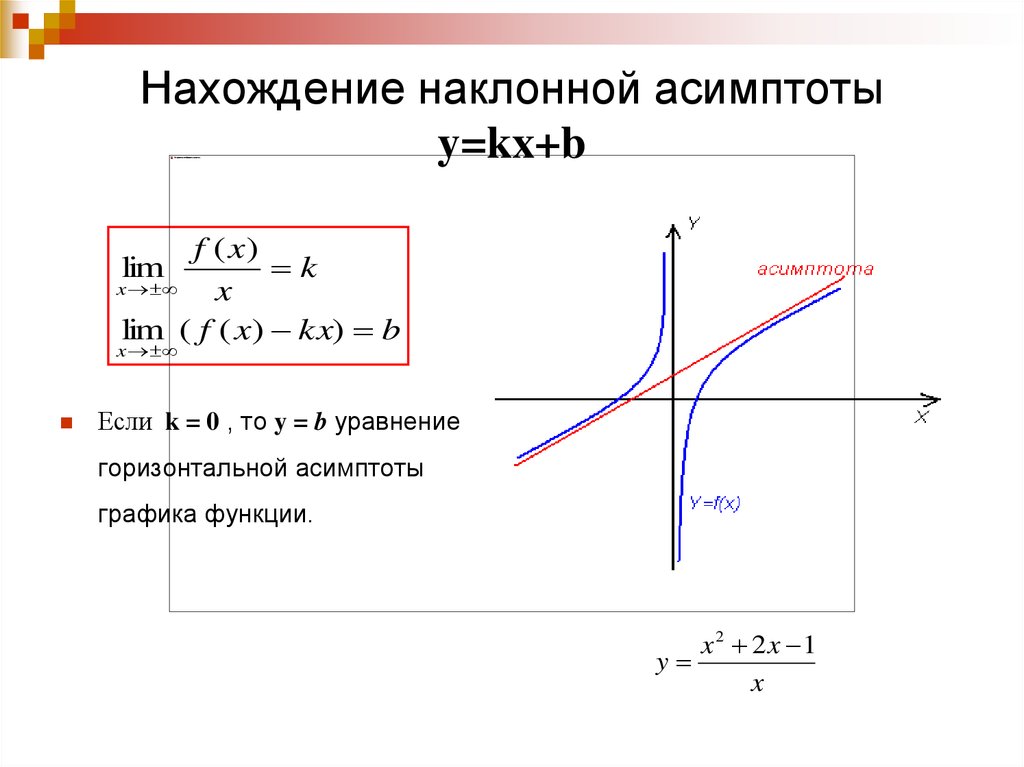
 Нам просто нужно рассматривать каждое уравнение как другую функцию в заданной области и отображать ее так же, как мы изображаем нормальную функцию. Чтобы узнать больше о построении графика кусочной функции, нажмите здесь.
Нам просто нужно рассматривать каждое уравнение как другую функцию в заданной области и отображать ее так же, как мы изображаем нормальную функцию. Чтобы узнать больше о построении графика кусочной функции, нажмите здесь.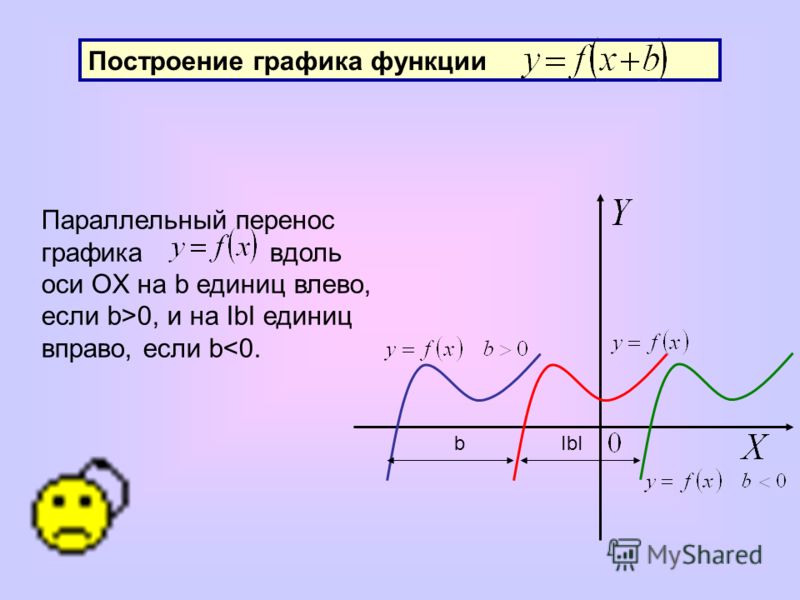
 Возьмем его общее уравнение. Используйте некоторые точки на графике и общее уравнение, чтобы определить точное уравнение функции.
Возьмем его общее уравнение. Используйте некоторые точки на графике и общее уравнение, чтобы определить точное уравнение функции. Если мы знаем правило(я) и выход, мы можем определить вход. Мы также можем представить, как машина спрашивает: «Каково мое правило?» Если мы изучим входы и выходы, мы сможем выяснить правило или правила загадочной функции.
Если мы знаем правило(я) и выход, мы можем определить вход. Мы также можем представить, как машина спрашивает: «Каково мое правило?» Если мы изучим входы и выходы, мы сможем выяснить правило или правила загадочной функции.
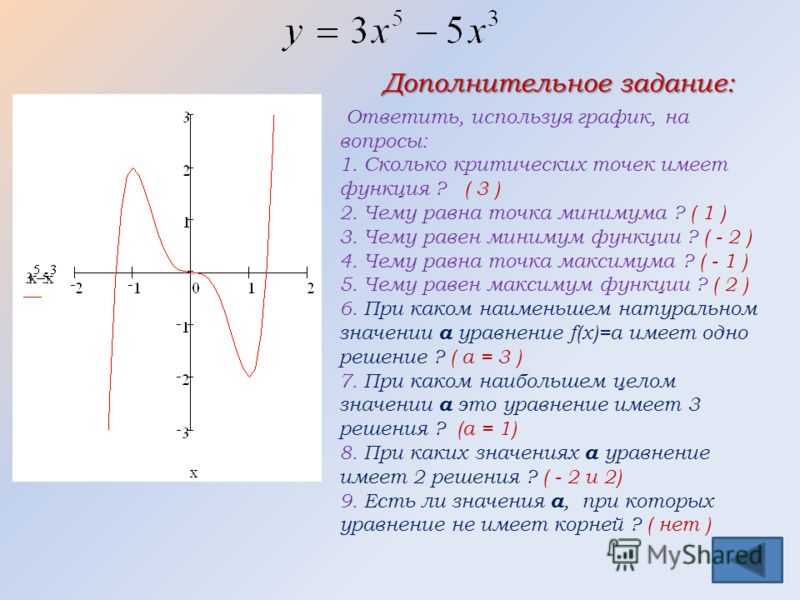 После изучения ряда пар входных и выходных данных пользователь пытается сделать вывод и применить операцию-загадку, чтобы предсказать результат для пары сгенерированных машиной входных данных. Пример операции-загадки в этой машине: a * (b 1).
После изучения ряда пар входных и выходных данных пользователь пытается сделать вывод и применить операцию-загадку, чтобы предсказать результат для пары сгенерированных машиной входных данных. Пример операции-загадки в этой машине: a * (b 1). Вы можете использовать следующие примеры:
Вы можете использовать следующие примеры: 
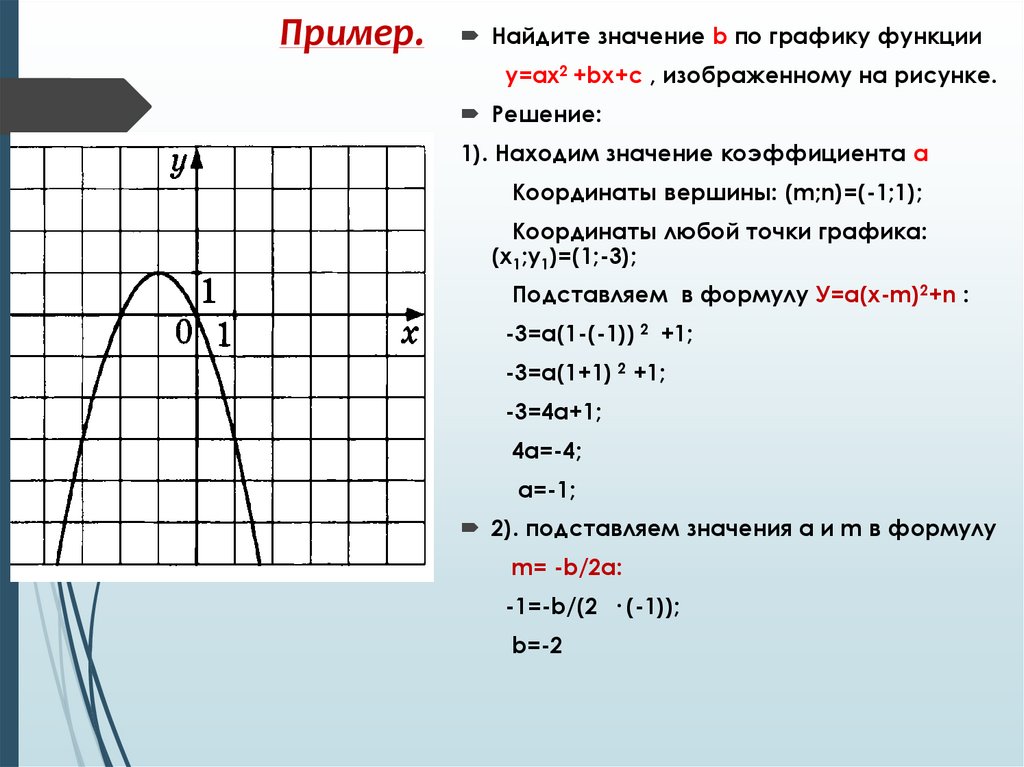 поезда по мере его роста. Когда они составляют таблицу данных, могут ли они найти правило или правила функции, описывающие взаимосвязь между количеством повторений и периметром поезда?
поезда по мере его роста. Когда они составляют таблицу данных, могут ли они найти правило или правила функции, описывающие взаимосвязь между количеством повторений и периметром поезда?

