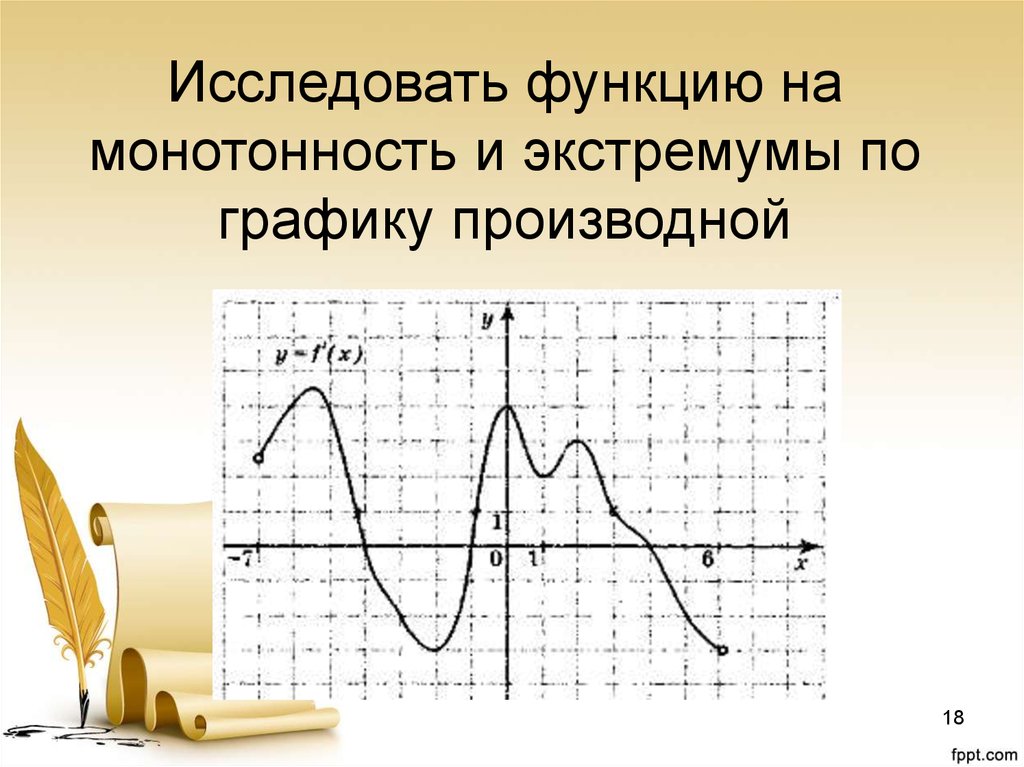
Исследование функции на монотонность и экстремумы
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
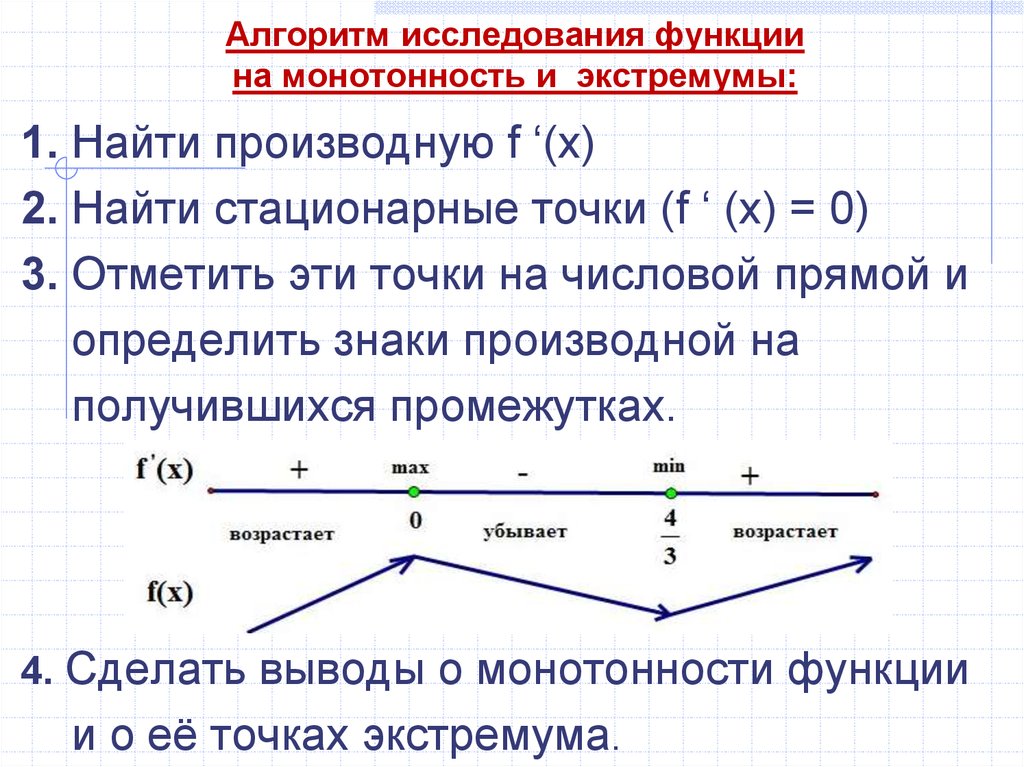
1. Тема: Исследование функции на монотонность и экстремумы. Нахождение наибольшего и наименьшего значения функции на отрезке.
Исследование функциина монотонность и экстремумы.
Нахождение наибольшего и
наименьшего значения функции
на отрезке.
Тема:
• Монотонность функции
• Экстремумы функции
• Наибольшее и наименьшее значение
функции на отрезке
2.
Возрастание и убывание функцииОпр. 1 Функция y=f(x), определяемаяна интервале (a;b), называется
возрастающей на этом интервале,
если из неравенства x2>x1, где x2 и x1
– любые две точки из интервала,
следует неравенство f(x2)>f(x1).
Если обозначить Δx= x2-x1
и Δf= f(x2)-f(x1), то
Δf
____
>0
Δx
Опр. 2 Функция y=f(x), определяемая на
интервале (a;b), называется
убывающей на этом интервале, если
из неравенства x2>x1, следует
неравенство f(x2)<f(x1).
Заметим, что
Δf
____
<0
Δx
4. Теорема 1. (необходимое условие возрастания функции)
Если дифференцируемая в интервале (a;b)функция y=f(x) возрастает, то ее производная
не может быть отрицательной ни в одной точке
этого интервала, т.е. f‘(x)≥0 для a<x<b.
Доказательство: Пусть y=f(x) возрастает на
(a;b), f f ( x x ) f ( x )
0
тогда
x
x
f
lim
Тогда при Δx 0, то x 0 x 0
f
lim
f ( x ), то f ( x ) 0
x 0
x
т.
к.ч.т.д.
5. Теорема 2. (Необходимое условие убывания функции)
Если дифференцируемая в интервале (a;b)функция y=f(x) убывает, то ее производная не
может быть положительной ни в одной точке
этого интервала, т.е. f‘(x)≤ 0 для a <x<b.
6. Теорема 3. (Достаточное условие возрастания функции)
Если непрерывная на [a;b] функция y=f(x) в каждойвнутренней точке имеет положительную производную,
то функция возрастает на [a;b]
Доказательство: Пусть y=f'(x) для всех a <x<b. Рассмотрим
x2>x1 из [a;b].
По теореме Лагранжа f(x2)-f(x1)=(x2-x1) f'(с), где x1≤с<x2,
поэтому
по условию
f'(с)>0
и x2 -x1 >0 имеем f(x2)-f(x1)>0, т.е. из x2>x1 следует
f ( x 2 ) f (возрастает,
x1 )
f(x2) >f(x1), т.f (е.
ч.т.д.
c ) функция
x 2 x1
7. Теорема 4. (Достаточное условие убывания функции)
Если непрерывная на [a;b] функция y=f(x)в каждой внутренней точке имеет
отрицательную производную, то функция
убывает на [a;b].
Пример 1. Найти интервал монотонности
функции
y=x3-3x.
Решение. Находим область определения
функции
D(y)=R
Находим производную
функции
y′=3×2-3
y′>0, если 3×2-3>0
при
x (- ;-1) (1;+ )
y′<0 при x (-1;1)
Ответ:
функция возрастает
на (- ;-1] и на [1;+ ),
функция убывает на [1;1]
9. Точки экстремума и экстремумы функции
Опр. 3 Точка x0 называется точкоймаксимума функции y=f(x), если
существует такая -окрестность точки
x0, что для всех x≠x0 из этой
окрестности выполняется f(x)< f(x0)
Опр. 4 Точка x0 называется точкой
минимума функции y=f(x), если
существует число >0, что для всех
х,удовлетворяющих условию 0<lx-x0l< ,
выполняется f(x)> f(x0)
Точка максимума и точка минимума
называются точками экстремума.
Значение функции в точках экстремума
называется экстремумом функции,
т.е.
fmax=f(xmax) – максимум функции
fmin=f(xmin) – минимум функции.
12. Теорема 5. (Необходимое условие экстремума)
Если дифференциальная функция y=f(x) имеетэкстремум в точке x0, то ее производная в этой точке
равна 0, т.е. f′(x0) =0.
Доказательство: Пусть x0 – точка максимума, тогда в
окрестности точки x0 выполняется f(x0)>f(x), поэтому
f x x f x
f f x0 x f x0
f
0
0
0, если х 0
0, если хи 0
x
x
x
x
f
/
По условию существует производная, которая равна
f x lim
0
Имеем: f’(x0)≤0 при Δx>0 и f’(x0)≥0 при Δx<0,
следовательно f′(x0) =0, ч.т.д.
x 0
x
Обратное утверждение, в общем случае не
верно, т.е. из f′(x0) =0 не следует,что x0 –
точка экстремума.
Геометрический смысл. Если x0 – точка
экстремума и в точке x0 существует
производная, то в точке на графике функции
касательная параллельна оси Оx.
14. Теорема 6. (Достаточное условие экстремума)
Если непрерывная функция y=f(x) дифференцируемав -окружности критической точки х0 и при
переходе через нее (слева направо) f′(x) меняет
знак, то х0 – точка экстремума, причем,
если с «+» на «-», то х0 – точка максимума,
с «-» на «+», то х0 – точка минимума.
Доказательство: Рассмотрим -окр-сть точки х0. Пусть
f′(x) >0 при любых х (х0 — ;х0) и f′(x)<0 при
любых х (х0; х0 + ). Тогда функция f(x)
возрастает на (х0 — ; х0) и убывает на (х0; х0 + ),
следовательно f(x0) – наибольшее значение на
(х0 — ; х0 + ), т.е. f(x) < f(x0) для х (х0 — ; х0)
(х0; х0 + ), следовательно точка х0 – точка
максимума функции, ч.т.д.
15. Пример 2. Найти экстремумы функции
x 3 2y x
Пример 2. Найти экстремумы функции
3
Решение. D(y)=R,
y
1
2
3 2
3 3 x
. y′ =0 при х=8
и y′ не существует при х=0
Поставим эти точки на числовой прямой и
расставим знаки
производной.
xmax=0, xmin=8
ymax=0, ymin=8/3-4=- 4/3
Ответ: уmin=-4/3; ymax=0
16. Теорема 7. (Достаточное условие экстремума,если существует y′′)
Если в точке х0 существует f′(x) и f′(x0)=0, авторая производная не равна 0,т.е. f′′(x0)≠
0, то при f′′(x0)< 0 в точке x0 функция имеет
максимум, а при f′′(x0)> 0 в точке x0
функция имеет минимум.
17. Наибольшее и наименьшее значение функции
Задача: найти наибольшее и наименьшее значениефункции на отрезке [a;b].
1.Функция возрастает на [a;b] 2. Функция убывает на[a;b]
max f(x) =f(b)
max f(x) =f(a)
min f(x) =f(a)
min f(x) =f(b)
[a;b]
[a;b]
[a;b]
[a;b]
3. Функция немонотонна на [a;b]
max f(x) =f(b)
[a;b]
min f(x) =fmin
[a;b]
19. Алгоритм нахождения наибольшего и наименьшего значения функции y=f(x) на отрезке [a;b].
1.2.
3.
4.
Найти f(a)=A и f(b)=B.
Найти нули производной и точки, в которых
производная не существует.
Если найденные точки принадлежат [a;b], то
найти значения функции в этих точках.
Выбрать из всех найденных значений
функции наибольшее и наименьшее.
20. Пример 3. Найти наибольшее и наименьшее значение функции f(x)=3×4+4×3+1 на [-2;1]
Решение: 1.f(-2)=3·16+4·(8)+1=48-32+1=17,f(1)=3+4+1=8.
2.Находим производную
функции f′(x)=12×3+12×2
f′(x)=0 при x=0 [-2;1],
х=-1Є[-2;1].
3. f(0)=1, f(-1)=3-4+1=0.
4. Сравниваем найденные
значения функции,
имеем 0<1<8<17.
Ответ: max f ( x) 17 ; min f ( x) 0
2;1
2;1
21. ПРИМЕНЕНИЕ
Решением задач на нахождение наибольшего инаименьшего значения занимается линейное
программирование.
Задачи: транспортная задача о перевозке груза
с минимальными затратами;
Задача об организации производственного
процесса с целью получения максимальной
прибыли.
22. Пример 4. Из шара радиуса R выточить цилиндр наибольшего объема. Каковы размеры цилиндра?
Пусть х – высота, y –радиус основанияцилиндра.
2
2
4R x
2
4y2+x2=4R2 => y=
4R2 x 2
x
=> V= y x
4
3
x
2
Рассмотрим функциюV( x ) R x
4
2
, x [0;2R]
2R 3
2R 6
x=
— точка максимума => y=
3
3
2R
3
Ответ: размеры цилиндра: высота
,радиус
3
3
English Русский Правила
Исследование функции на монотонность и экстремумы, выпуклость и точки перегиба, вторая производная
- Производная функции и промежутки монотонности
- Критические точки
- Вторая производная, промежутки выпуклости и точки перегиба
- Примеры
п.
1. Производная функции и промежутки монотонностиРассмотрим кусочно-непрерывную функцию: \( y= \begin{cases} x+1,\ \ x\leq 1\\ 2,\ \ 1\lt x\leq 4\\ 6-x,\ \ x\gt 4 \end{cases} \)
Эта функция интересна тем, что имеет промежуток возрастания при \(x\leq 1\), промежуток постоянства при \(1\lt x\leq 4\) и промежуток убывания при \(x\gt 4\).
Посмотрим, как ведет себя производная на каждом из промежутков, используя определение производной (см. §42 данного справочника).
Заметим, что в точках излома x=1 и x=4 функция определена и непрерывна, но её производная не существует.
При \(x\lt 1\): $$ \triangle y=(f(x_0+\triangle x)-f(x_0)=\left((x_0+\triangle x)+1\right)-(x_0+1)=\triangle x $$ Получается, что знаки \(\triangle y\) и \(\triangle x\) всегда совпадают, и их частное \(\frac{\triangle y}{\triangle x}=1\gt 0\) — всегда положительно. Поэтому и производная на промежутке возрастания функции положительна: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x}{\triangle x}=\lim_{\triangle x\rightarrow 0}1=1\gt 0 $$ При \(1\lt x\lt 4\): $$ \triangle y=f(x_0+\triangle x)-f(x_0)=2-2=0 $$ Производная на промежутке постоянства равна нулю: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{0}{\triangle x}=\lim_{\triangle x\rightarrow 0}0=0 $$ При \(x\gt 4\): $$ \triangle y=f(x_0+\triangle x)-f(x_0)=\left(6-(x_0+\triangle x)\right)-(6-x_0)=-\triangle x $$ Знаки \(\triangle y\) и \(\triangle x\) всегда противоположны, и их частное \(\frac{\triangle y}{\triangle x}=-1\lt 0\) — всегда отрицательны.
Напомним, что:
Окрестностью точки \(x_0\) называется любой сколь угодно малый промежуток, для которого \(x_0\) является внутренней точкой.
Точка \(x_0\)является точкой минимума функции \(y=f(x)\), если для всех \(x(x\ne x_0)\) из некоторой окрестности точки \(x_0\) выполняется неравенство \(f(x_0)\lt f(x)\).
Точка \(x_0\) является точкой максимума функции \(y=f(x)\), если для всех \(x(x\ne x_0)\) из некоторой окрестности точки \(x_0\) выполняется неравенство \(f(x_0 )\gt f(x)\).
Все точки минимума и максимума функции \(y=f(x)\) образуют множество точек экстремума данной функции.
| Необходимое условие существования экстремума Точками экстремума функции могут быть только её критические точки. |
Т.е. все критические точки объявляются подозрительными на экстремум.
| Достаточное условие существования экстремума Точка \(x_0\) принадлежит промежутку непрерывности функции \(y=f(x)\) и при подходе к точке \(x_0\) слева и справа производные имеют разные знаки.  3}\) Определить знак производной на промежутке просто: нужно взять любое значение x из промежутка и подставить в производную. При этом не нужно точно считать, сколько получается; главное – понять, какой знак у каждой скобки/множителя. Составим таблицу:
Вывод: п.3. Вторая производная, промежутки выпуклости и точки перегибаПусть функция \(y=f(x)\) является дифференцируемой на промежутке \(x\in(a;b)\), и её производная \(f'(x)\) также является дифференцируемой на этом же промежутке. Кривая \(y=f(x)\) называется выпуклой вверх на интервале \((a;b)\), если все точки, кроме точки касания \(x_0\), лежат под касательной, проведенной через любую точку \(x_0\in(a;b)\). Например:
Внутренние точки области определения функции, в которых вторая производная равна нулю или не существует, называют критическими точками второго порядка.
Т.е. все критические точки второго порядка объявляются подозрительными на перегиб.
Т.е., для всех точек, подозрительных на перегиб, которые лежат в промежутках непрерывности первой производной и для которых вторые производные слева и справа имеют разные знаки, «подозрение подтверждается» — и такие точки признаются точками перегиба. Критические точки: \(x=\left\{\pm2\sqrt{2};\pm 4\right\}\) Составляем таблицу:
Вывод: Пример 2. Монотонность и экстремум функцийЧто такое монотонность и экстремумМонотонность:Характер функции определяется знаком ее производной. Если график функции направлен вверх или вниз, то функция называется монотонной функцией. Если график функции направлен вверх, то она имеет возрастающие значения и называется монотонно возрастающей. Точно так же, если график функции направлен вниз, то он имеет убывающие значения и называется монотонно убывающим. Экстремум:Точки области определения функции, в которых ее график меняет свое направление с восходящего на нисходящее или с нисходящего на восходящее, называются экстремумом. В таких точках производная функции, если она существует, обязательно равна нулю. Монотонные функцииФункция f(x), определенная в области D, называется: i) Монотонно возрастающей: Функция f(x) называется монотонно возрастающей, если x₁ < x₂ и f(x₁) ≤ f(x₂). [Изображение будет загружено в ближайшее время] ii) Монотонно убывающая:Функция называется монотонно убывающей, если x₁ < x₂ и f(x₁) ≥ f(x₂). График монотонной убывающей функции можно представить следующим образом: [Изображение будет загружено в ближайшее время] iii) Строго возрастающая:Функция f(x) называется строго возрастающей функцией в своей области определения, если x₂ > x₁ и f(x₂) > f(x₁) или dy / dx > 0. График строго возрастающей функции можно представить следующим образом: [Изображение будет загружено в ближайшее время] iv) Строго убывающая: Функция f(x) называется строго убывающей функцией в своей области определения, если x₂ > x₁ и f(x₂) < f(x₁) или dy/dx < 0. График строго убывающей функции можно представить следующим образом: [Изображение будет загружено в ближайшее время] Метод проверки монотонности1. Монотонность в точке:Функция f(x ) называется монотонно возрастающей или убывающей в точке x = a своей области определения, если она монотонно возрастает или убывает в интервале (a — h, a + h), где h — малое положительное число. Отсюда можно заметить, что если функция f(x) монотонно возрастает при x = a, то в этой точке касательная к ее графику образует острый угол с осью x, тогда как если функция монотонно убывает, то касательная образует угол с осью x. тупой угол с осью x. Следовательно, f’(a) будет положительным или отрицательным в зависимости от того, монотонно возрастает или убывает f(x) при x = a. Таким образом, при x = a функция f(x) монотонно возрастает, если f’(a) > 0, и монотонно убывает, если f’(a) < 0, 2. Монотонно в интервале:В [a, b] f(x) равно – Монотонно возрастает, если f'(x) ≥ 0 Монотонно убывает, если f'(x) ≤ 0 Постоянно, если f'(x) = 0 Возрастает, если f'(x) > 0 Уменьшается, если f'(x) < 0 В приведенных выше результатах f'(x) не должно быть равно нулю для всех значений x, иначе f(x) будет постоянной функцией. Если в [a, b] f'(x) < 0 хотя бы для одного значения x и f'(x) > 0 хотя бы для одного значения x, то f(x) не будет монотонна по [a, b]. Максимумы и минимумыМаксимумыГоворят, что функция f(x) достигает максимума в точке x = a, если существует окрестность (a — δ , a + δ) такая, что f(x) < f (а) для всех x ∈ (a - δ, a + δ), x ≠ a ⇒ f(x) — f(a) < 0 для всех x ∈ (a - δ, a + δ), x ≠ a В таком случае говорят, что f(x) является максимальным значением f(x) при x = a. МинимумыГоворят, что функция f(x) достигает минимума в точке x = a, если существует окрестность (a — δ, a + δ) такая, что f(x) > f(a) для всех x ∈ (а — δ, а + δ), х ≠ ⇒ f(x) — f(a) > 0 для всех x ∈ (a — δ, a + δ), x ≠ a В таком случае f(x) называется минимальным значением f(x) при x = a. Метод тестирования максимумов и минимумовДля определения экстремальных значений функции f(x) Шаг 1: Положить y = f(x) Шаг 2: Найти dy/dx Шаг 3: Положить dy /dx = 0 и найти x. Шаг 4: Чтобы проверить максимумы или минимумы при x = a, сначала найдите знак f’(x) для значений x чуть меньше a или больше a.
Решенные примеры1. Если f(x) = kx³ — 9x² + 9x + 3 с монотонно возрастает на каждом интервале, то найти значение k.Решение:f'(x) = 3kx² — 18x + 9 f'(x) = 3(kx² — 6x + 3) > 0 ∀ x ∈ R Следовательно, Δ = b² — 4ac < 0, k > 0 36 — 12k < 0 k > 3 2. Решение: Пусть f(x) = x³ — 12x² + 36x + 17. Следовательно, f'(x) = 3x² — 24x + 36 = 0 при x = 2, 6 Опять же, f»(x) = 6x — 24 отрицательно при x = 2 Итак, f(6) = 17, f(2) = 49 В конечных точках f(1) = 42, f(10) = 177. Следовательно, максимальное значение f(x) равно 177. Знаете ли вы
Примечания о монотонности функцииЧто такое монотонностьфункции Монотонность — это неотъемлемая характеристика или свойство функции, с помощью которого мы можем отслеживать поведение и закономерности, демонстрируемые графиком любой функции . y = 3x + 5, y = ex , y = log(x) являются примерами монотонно возрастающей функции, а y = (-x)6 и y = e-x являются примерами монотонно убывающей функции. Как проверить монотонность функции
Функция монотонно возрастает, если первая производная f(x),f1(x) >= 0. Функция монотонно убывает, если первая производная f(x),f1(x) <= 0, Функция монотонно постоянна, если первая производная f(x),f1(x) = 0. Экстремум в функцииЭкстремум: – Экстремум – это точка на графике любой действительной функции, значение функции лежит или минимальное значение функции существует. Если вы подумаете дальше, то поймете, что точки экстремума находятся на значениях домена, и эти точки являются местами, где функция меняет свое направление сверху вниз или снизу вверх. Значение производной этой функции в этой точке будет равно нулю. Три простых случая при экстремуме функции: –
Максимумы и минимумыЛокальный максимум — это точка на графике или кривой, в которой значение функции превышает предельное значение функции. Локальный минимум — это точка на графике или кривой, в которой значение функции ниже предельного значения функции. Глобальный максимум — это точка на графике или кривой, которая является максимальным и самым высоким значением функции среди различного количества критических точек в функции. Глобальный минимум — это точка на графике или кривой, которая является минимальным и наименьшим значением функции среди различного количества критических точек функции. Говорят, что функция f(x) достигает максимума при x = p, если существует соседняя точка в непосредственной близости от других элементов x, так что (p – θ, p + θ). |
4}\)
2\)
График монотонно возрастающей функции можно представить в виде:
Максимальное значение x³ — 12x² + 36x + 17 в интервале [1, 10] равно?
Монотонный смысл любой функции или уравнения означает, что если график возрастает с увеличением значения координаты x, то график будет называться монотонно возрастающим [если x₁ < x₂ & f(x₁) ≤ f(x₂)]. Точно так же, если значение диапазона графика уменьшается с увеличением значений координаты x, то график будет объявлен монотонно убывающим [если x₁ < x₂ & f (x₁) ≥ f (x₂)].
