Исследование функции с модулем на четность: Как исследовать функцию на четность с модулем. Четность и нечетность функций

Простая физика — EASY-PHYSIC

Привет всем посетителям! Сегодня рассматриваем вопрос четности и нечетности функций.

Правило:

Если , то функция четная.

Если , то функция нечетная.

При этом важно, чтобы область определения функции была бы симметричной относительно оси ординат, а при наличии в ней выколотых точек или интервалов они также должны располагаться симметрично.

Алгоритм исследования:

Установить, симметрична ли область определения функции. Если это так, то  найти и сравнить с

Если то функция — четная.
Если , то функция нечетная.

Функция совсем не обязана быть четной или нечетной, она может быть «никакой», несмотря на то, что область определения симметрична.

 

Примеры:

1. Определить, является ли четной функция: .

Область определения этой функции – все действительные числа, то есть она симметрична. Теперь подставим вместо x – (-x) и посмотрим, что получится:

– функция четна.

Надо отметить, что график четной функции симметричен относительно оси ординат, она для него словно зеркало. Поэтому графики таких функций можно строить в правой полуплоскости, а в левую просто отражать.

Верно и следующее:  если функция задана графиком, который симметричен относительно оси ординат, то она четная.

 

2. Определить, является ли четной функция: .

Область определения этой функции может быть найдена из системы неравенств:

Оба неравенства всегда соблюдаются, так как дискриминант обоих трехчленов всегда меньше 0, и ветви парабол направлены вверх – таким образом, мы установили, что область определения симметрична – это вся числовая ось.
Теперь подставим вместо x – (-x): – данная функция нечетна.

График нечетной функции симметричен относительно начала координат, то есть каждой его точке соответствует точка, получить которую можно поворотом на 180 градусов относительно начала координат. Поэтому графики таких функций можно строить в правой полуплоскости, а изображение в левой полуплоскости получить, повернув картинку на 180 градусов.

Верно и следующее:  если функция задана графиком, который симметричен относительно начала координат, то она нечетная.

 

3. Определить, является ли четной функция: .

Область определения может быть найдена из системы неравенств:

Таким образом, область определения симметрична,  и не содержит выколотые точки (1) и (-1).

Подставляем (-х) вместо х:

— исходную функцию не получили, а получили совсем другую — значит, исходная функция не является ни четной, ни нечетной (что и подтверждает график). Мы убедились, что симметрия области определения еще не означает, что функция четная или же нечетная.

 

4. Определить, является ли четной функция: .

 

Область определения – вся числовая ось, кроме 0 – симметричная.

Подставляем (-х) вместо х:

– функция нечетна.

5. Определить, является ли четной функция: .

Область определения – вся числовая ось, кроме точек 3 и (-3) – симметричная.

Подставляем (-х) вместо х:

– функция четная.

 

6. Определить, является ли четной функция: .

 

Область определения – вся числовая ось – симметричная.

Подставляем (-х) вместо х:

– функция четная.

 

7. Определить, является ли четной функция: .

Область определения – вся числовая ось, кроме 0 – симметричная.

Подставляем (-х) вместо х:

– функция нечетная.

Кроме того, здесь мы имеем дело с суммой двух функций.

Правило:

Сумма двух нечётных функций  —  нечётна.

Сумма двух чётных функций  —  чётна.

А вот сумма двух функций разной четности – как правило, ни четна, ни нечетна.

Определим четность этих функций по отдельности.

– функция нечетная.

– функция нечетная.

 

8. Исследуем теперь такую функцию:

 

Одна из них нечётна – это мы только что показали, а вторая?

Область определения функции симметрична, функция нечётна, так как . Тогда по правилу сложение двух нечетных функций даст функцию нечетную.

 

9. Наконец, последняя:

– имеем произведение двух функций.

Правило:

Произведение или частное  двух нечётных функций чётно.

Произведение или частное двух чётных функций чётно.

Произведение или частное нечётной и чётной функций нечётно.

 

Так как обе функции являются чётными, то и их произведение чётно.

Проверим?

Область определения – вся числовая ось. Производим подстановку:

— функция четная.

 

 

 

 

 

 

 

Свойства функций в задачах с параметрами

На этой странице вы узнаете

• Можно ли представить прогресс в виде монотонной функции? 
• Где можно встретить идеальную симметрию?
• Как сломать функцию? 

В восточных боевых искусствах спортсмены разбивают доски руками. А вот плотники для разрезания досок используют пилу, то есть вспомогательный инструмент. Так стоит ли нам справлять с параметрами голыми руками? Или проще взять специальный инструмент? Такая же дилемма может встать и в решении задач с параметром.

Монотонность функции

В математике пилу, разумеется, не используют. Зато мы можем использовать свойства функции, которые и будут нашей опорой при решении задач с параметром. Давайте попробуем собрать свой “ящик с инструментами”. 

Возможно, до детального знакомства с темой, вам захочется вспомнить «Определение и график функции». 

Многим из нас знакома монотонная и скучная работа. Например, удалять с телефона ненужные фотографии или стирать пометки из учебника, прежде чем вернуть его в школьную библиотеку. Приходится повторять одно и то же действие на протяжении всего цикла работы — это утомительно и однообразно.

Монотонная функция так же, как и работа, не меняет своих свойств на всем промежутке. 

Монотонная функция — функция, строго возрастающая или строго убывающая на промежутке.

Разберемся со “строгостью” функций.

Строго возрастающая функция на промежутке — функция, большему значению аргумента которой из промежутка соответствует большее значение функции. 

Иными словами: чем больше х, тем больше у. 

Строго убывающая функция на промежутке — функция, большему значению аргумента которой соответствует меньшее значение функции. 

Или чем больше х, тем меньше у. 

Можно ли представить прогресс в виде монотонной функции? Идеальная картина: чем больше мы работаем, тем лучше наш результат. С каждым днем мы все растем, становимся лучше и избегаем ошибок. То есть наш прогресс — это монотонная функция.  К сожалению, реальность несколько другая. Прогресс никогда не будет монотонной функцией, всегда будут взлеты и падения. Ошибки — неотъемлемая часть обучения, поэтому нельзя бояться неудач. Если представить прогресс человека в виде функции, то она постоянно будет менять промежутки возрастания на промежутки убывания и обратно.

Что еще можно сказать про возрастание функции? Вспомним «Производную», а именно — ее знаки на промежутках возрастания и убывания функции: 

• если производная положительна на некотором промежутке, то функция возрастает на этом промежутке;

• если производная отрицательна на некотором промежутке, то функция убывает на этом промежутке. 

Свойства монотонной функции

Монотонные функции обладают своими свойствами, которые могут пригодиться при решении задач. 

Свойство 1. Монотонная функция принимает свое значение единственный раз. 

Это можно проследить по графику: для каждого значения у будет единственное значение х. 

Свойство 2. Если две функции f(x) и h(x) возрастают на промежутке, то функция y = f(x) + h(x) также будет возрастать. 

Это же свойство будет работать и с убыванием функции. 

Если две функции f(x) и h(x) убывают на промежутке, то функция

y = f(x) + h(x) также будет убывать. 6+2

Заметим, что поскольку  х стоит в четной степени, то какое бы число мы ни подставили в производную, оно будет положительно. Значит, эта функция строго возрастает. 

Шаг 2. Как определить, что решение уравнения будет лежать в заданном отрезке? Решением уравнения будет пересечение функции и оси х. То есть точка этого пересечения должна лежать между −1 и 1 включительно. 

На графике это будет выглядеть так: 

А вот такие случаи нам уже не подходят, поскольку решение уравнения будет лежать за пределами заданного промежутка. 

Шаг 3. При x = — 1 функция отрицательна, а при x = 1 функция будет положительна при любом положении в заданном промежутке. Следовательно, мы можем задать ее положение на графике с помощью значения функции при x = — 1 и x = 1. 

Шаг 4. Получаем два условия, которые должны выполниться одновременно, то есть систему. 

Шаг 5. Решаем первое неравенство системы: 

4*(-1)+2*(-1)+a\leq0

a\leq6

Решаем второе неравенство системы:

4*1+2*1+a\geq0

a\geq-6

Следовательно, условия будут выполняться при

a\in[-6;6]

Ответ:

a\in[-6;6]

Итак, в наш ящик с инструментами отправляется монотонность функции, ее возрастание и убывание.  

Четность функции 

Четной функцией называется такая функция, график которой симметричен относительно оси Оу. 

Для такой функции будет выполняться условие f(x) = f( — x). 

Где можно встретить идеальную симметрию? В природе идеальная симметрия почти не встречается: даже на миллиметр, но одна сторона животного, растения или человека будет отличаться от другой. Идеальная симметрия встречается в математике, в четной функции.  Симметрия часто используется в искусстве и архитектуре для создания гармоничной композиции. Если посмотреть на планы и фасады некоторых храмов и дворцов, созданных много лет назад, то окажется, что части здания располагаются симметрично относительно оси.

Четность функции — это точно не универсальный инструмент, как, например, молоток. Скорее это редкий ключ, который будет большую часть времени просто лежать в ящике, но пригодится в самый ответственный момент.  

Алгоритм применения четности функций при решении задач с параметром  Четность можно применить, когда в функции стоят модули, четные степени, четные корни и другие условия, с которыми минус “не дружит”.  Шаг 1. Перенести все слагаемые в одну сторону и ввести f(x).  Шаг 2. Проверить функцию на четность. Для этого нужно удостовериться, что условие f(x) = f( — x) выполняется.  Четная функция имеет четное количество корней, кроме случая х = 0, когда корень всего один.  Шаг 3. Подставить х = 0.  Шаг 4. Рассмотреть данные значения в зависимости от условия задачи.

Почему функция имеет четное количество корней, кроме случая х = 0? Возьмем зеркало и попробуем подвигать карандаш относительно него. При этом само зеркало будет осью у. 

На какое бы расстояние мы не отодвинули карандаш, в зеркале всегда будет его отражение.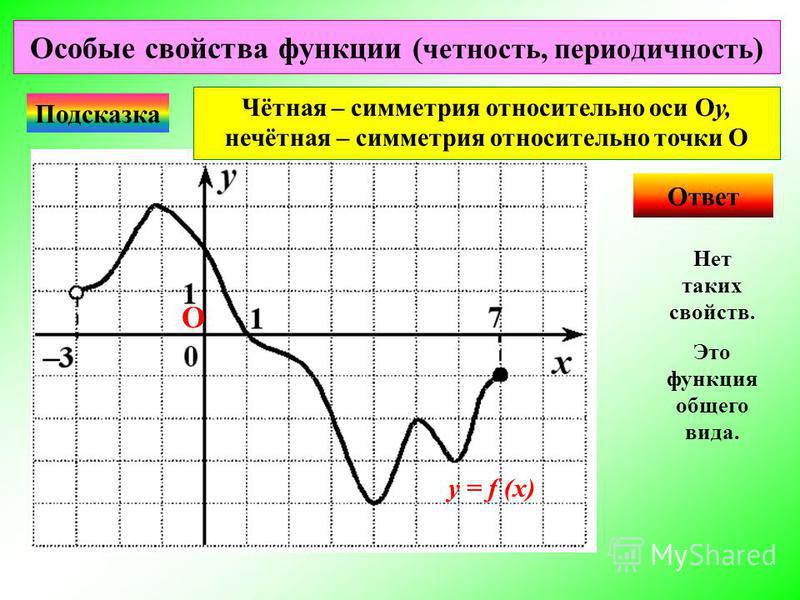 2

— мы получили квадратное уравнение.

Оно задает параболу с ветвями, направленными вниз. Ее вершина будет в точке

x_{в}=-\frac{10}{-2}=5

На графике должно получиться две параболы, которые объединятся в одну фигуру, похожую на горы. Как эти горы могут располагаться относительно друг друга? 

Первая гора может быть выступом для второй горы. То есть одна гора плавно будет перетекать в другую.

Они могут находиться рядом друг с другом, а между ними будет перевал. 

Вторая гора может быть выступом в первой горе. 

Случай, когда горы находятся на разных материках планеты, мы не рассматриваем, поскольку они обязательно должны быть связаны между собой, иначе бы задавались разными функциями. 

Теперь мы можем построить примерные графики функций. При этом в значении a2  будет перелом, поскольку в этой точке происходит переход от первого случая раскрытия модуля ко второму. Эта точка будет называться точкой излома. 

Точка излома — точка, в которой одна функция переходит в другую из-за раскрытия модуля. 2-1>0

(a-1)(a+1)>0

a\in(-\infty;-1)\cup(1;+\infty)

Осталось найти ответ для системы. 

Отсюда

a\in(-\sqrt{5};-1)\cup(1;\sqrt{5})

Ответ:

a\in(-\sqrt{5};-1)\cup(1;\sqrt{5})

Для удобства решения таких заданий мы можем вывести алгоритм.

Алгоритм решения для задач на значение функции  Шаг 1. Раскрыть модули.  Шаг 2. Рассмотреть полученные функции и проанализировать их. Например, если получаются параболы, то нужно определить направление ветвей и положение ветвей.  Шаг 3. Проанализировать точку излома: найти все случаи, где она может находиться в зависимости от значений параметра.  Шаг 4. Найти значения параметра для каждого подходящего случая.

Вот мы и собрали инструменты для решения параметров с помощью свойств функций. В наш ящик вошли:

• монотонность функции;
• возрастание и убывание функции;
• четность функции и ее симметрия;
• область определения и область значений функций;
• наибольшее и наименьшее значение функции и точки экстремума.  

Фактчек

• Монотонная функция — функция, строго возрастающая или строго убывающая на промежутке. Если при решении задач с параметром доказать, что функция монотонно возрастает или монотонно убывает, можно применить свойство производных. Это же свойство можно применить и для доказательства монотонности функции. 
• Производная положительна на промежутках возрастания функции и отрицательна на промежутках убывания. 
• Четной функцией называется такая функция, график которой симметричен относительно оси Оу. Для такой функции будет выполняться условие f(x)=f(-x). Это же условие можно применять для доказательства четности функции. 
• В четной функции всегда будет два решения, кроме случая х = 0. При х = 0 у функции будет единственное решение. 
• Точка излома — точка, в которой одна функция переходит в другую из-за раскрытия модуля. Зная точки излома, можно проанализировать поведение функции. 

Проверь себя

Задание 1.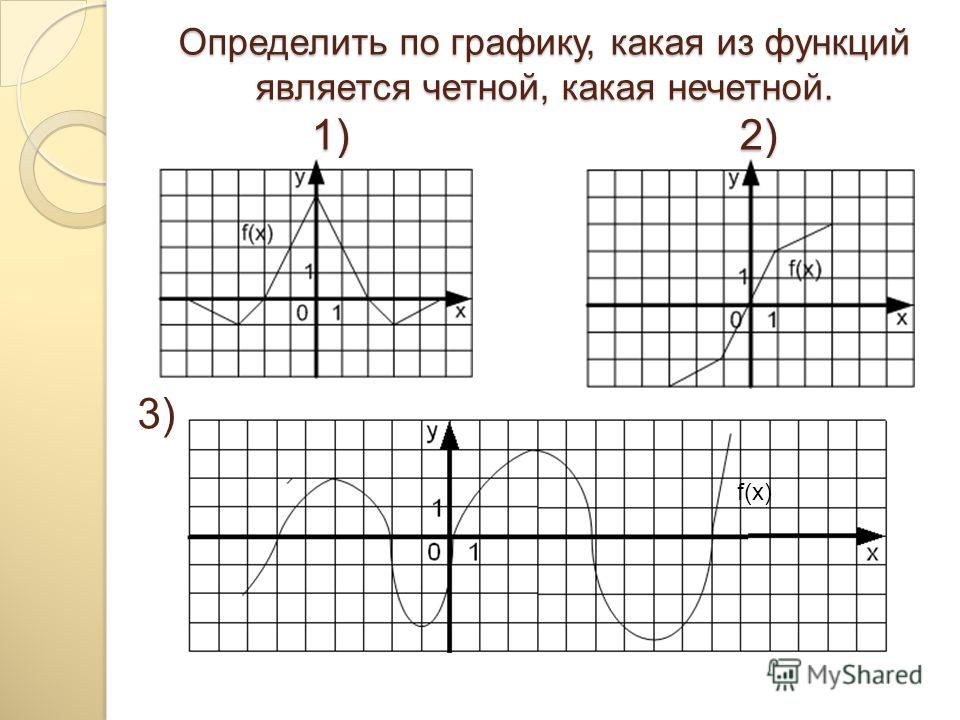  

На заданном промежутке функция монотонно возрастает. Чему будет равна производная функции на этом промежутке? 

1. Производная функции будет отрицательна.
2. Производная функции будет положительна.
3. Производная функции будет равна 0.
4. Невозможно определить производную, не зная функцию. 

Задание 2. 

Выберите верные утверждения для убывающей функции.

1. Чем больше значение х, тем больше значение у.
2. Чем больше значение х, тем меньше значение у.
3. Производная функции положительна.
4. Производная функции отрицательна. 

Задание 3. 

Дана четная функция. Сколько будет решений при х = 0?

1. Четыре решения.
2. Два решения.
3. Одно решение.
4. Решений не будет. 

Задание 4. 

Что такое точка излома? 

1. Точка, в которой одна функция переходит в другую из-за раскрытия модуля.
2. Любая точка на функции, в которой график меняет свое направление.
3. Точки экстремума.
4. Асимптоты функции. 

Ответы: 1. — 2 2. — 24 3. — 3 4. — 1.

Видео с вопросами: Определение четности построенной на графике рациональной функции

Стенограмма видео

Является ли функция, представленная цифрой, четной, нечетной или ни четной, ни нечетной?

Это вопрос о четности функции на графике, и здесь есть три варианта. Функция либо четная, либо нечетная, либо ни то, ни другое. Напомним, что означают термины «четный» и «нечетный» в контексте функций.

Функция 𝑓 от 𝑥 четна, если 𝑓 от минус 𝑥 равно 𝑓 от 𝑥. Это должно выполняться для всех значений 𝑥. Таким образом, 𝑓 отрицательной единицы должно быть 𝑓 единицы, 𝑓 отрицательной семерки должно быть 𝑓 из семи, 𝑓 отрицательной 𝜋 должно быть 𝑓 из 𝜋, и так далее.

Определение нечетной функции очень похоже: функция 𝑓 от 𝑥 нечетна, если 𝑓 от минус 𝑥 равно минус 𝑓 от 𝑥. Таким образом, для нечетной функции 𝑓 отрицательной единицы равно минус 𝑓 единицы, 𝑓 отрицательной семерки равно минус 𝑓 семи, а 𝑓 отрицательной 𝜋 равно минус 𝑓 из 𝜋.

И, в отличие от целых чисел, наша функция 𝑓 от 𝑥 не обязательно должна быть ни четной, ни нечетной; это не может быть ни то, ни другое. Сначала проверим, является ли функция четной. Другими словами, равно ли 𝑓 минус 𝑥 𝑓 из 𝑥 для всех значений 𝑥? Что ж, давайте попробуем значение 𝑥, скажем, единицу, и найдем 𝑓 отрицательной единицы.

Итак, мы смотрим на отрицательную единицу на оси 𝑥, поднимаемся вверх, пока не столкнемся с графиком, и видим, что 𝑓 отрицательной единицы равно единице. Таким образом, чтобы 𝑓 из 𝑥 было четным, 𝑓 из 1 также должно быть равно единице. Мы проходим тот же процесс, чтобы найти 𝑓 единицы, на этот раз спускаясь вниз, пока не попадем на график. И отсчитывая от оси 𝑦, мы заключаем, что 𝑓 единицы равно отрицательной единице. Итак, ясно, что 𝑓 отрицательной единицы не равно 𝑓 единицы, и, следовательно, 𝑓 из 𝑥 не является четным.

Помните, что это не означает, что 𝑓 из 𝑥 нечетно; 𝑓 из 𝑥 не может быть ни четным, ни нечетным. Теперь мы проверяем, является ли 𝑓 из 𝑥 нечетным, поэтому равно ли 𝑓 минус 𝑥 минус 𝑓 из 𝑥 для всех значений 𝑥? Мы можем использовать значения функции, которые мы уже нашли — жалко их терять — и мы можем видеть, что 𝑓 отрицательной единицы равно минус 𝑓 единицы.

В левой части у нас единица, а в правой части минус единица, которая также равна единице. Итак, верно, что 𝑓 отрицательного 𝑥 равно минус 𝑓 числа 𝑥, когда 𝑥 равно хотя бы единице, но недостаточно, чтобы 𝑓 минус 𝑥 было равно минус 𝑓 числа 𝑥 для одного значения 𝑥; это должно быть верно для всех значений 𝑥.

Проверяем другое значение 𝑥, скажем, семь. Хотя трудно прочитать значения 𝑓 отрицательной семерки и 𝑓 семерки, вполне вероятно, что их противоположности 𝑓 отрицательной семерки чуть больше нуля, а 𝑓 семерки чуть меньше нуля. И мы могли бы продолжать пробовать значения 𝑥, пока не убедимся, что 𝑓 из 𝑥 действительно является нечетной функцией.

Здесь мы использовали определение нечетной функции, чтобы показать, что наша функция действительно нечетная, но есть и другой способ сделать это; мы можем использовать свойство нечетных функций. Функция нечетна, если ее график имеет 180-градусную вращательную симметрию относительно начала координат.

Мы видим, что это справедливо и для нашего графика: если мы повернем наш график на 180 градусов вокруг начала координат, мы получим тот же самый график.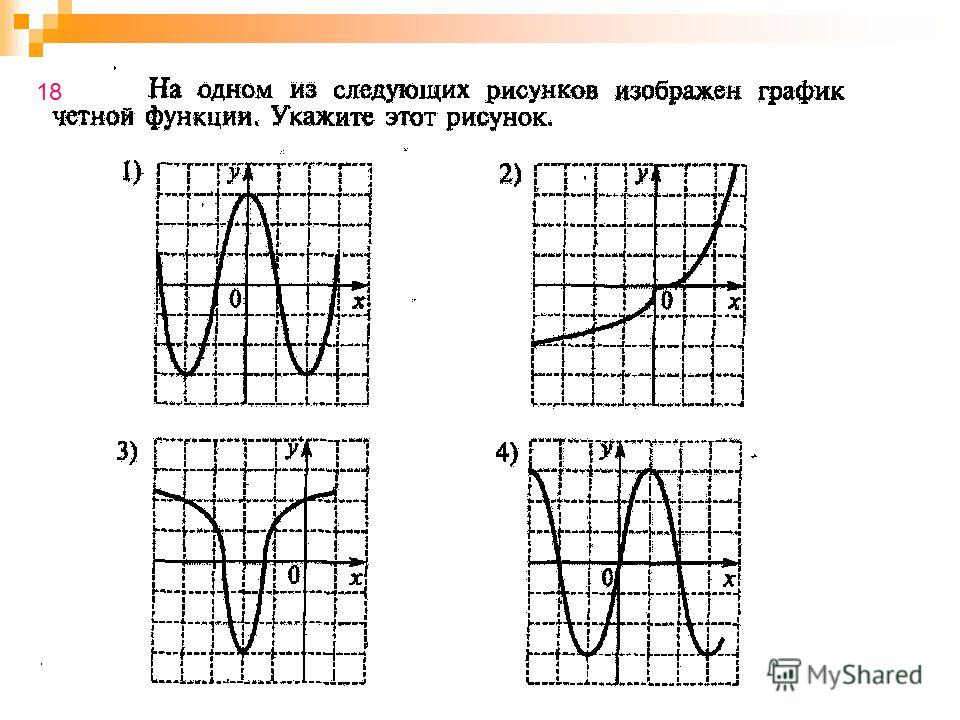 И для четной функции есть соответствующий факт: функция четна, если ее график симметричен относительно оси 𝑦. Поэтому, если вы отразите график четной функции на оси 𝑦, вы получите тот же график.

Глядя на наш график, мы видим, что он несимметричен относительно оси 𝑦, поэтому наша функция не является четной, но, как было сказано ранее, наш график имеет 180-градусную вращательную симметрию относительно начала координат. , наша функция нечетная.

Функция проверки четности целого числа

Задавать вопрос

спросил 1 год, 7 месяцев назад

Изменено 1 год, 7 месяцев назад

Просмотрено 177 раз

$\begingroup$

Существует ли функция f(x), которая определяет, является ли заданное целое число четным или нечетным? Например, если бы x было равно 1237, функция вывела бы 1; и если бы это было 80, это вывело бы 2.