Исследование функций и построение графиков
Опорными точками при исследовании функций и построения их графиков служат характерные точки – точки разрыва, экстремума, перегиба, пересечения с осями координат. С помощью дифференциального исчисления можно установить характерные особенности изменения функций: возрастание и убывание, максимумы и минимумы, направление выпуклости и вогнутости графика, наличие асимптот.
Эскиз графика функции можно (и нужно) набрасывать уже после нахождения асимптот и точек экстремума, а сводную таблицу исследования функции удобно заполнять по ходу исследования.
Обычно используют следующую схему исследования функции.
1. Находят область определения, интервалы непрерывности и точки разрыва функции.
2. Исследуют функцию на чётность или нечётность (осевая или центральная симметрия графика.
3.
Находят асимптоты (вертикальные, горизонтальные или наклонные).
4. Находят и исследуют промежутки возрастания и убывания функции, точки её экстремума.
5. Находят интервалы выпуклости и вогнутости кривой, точки её перегиба.
6. Находят точки пересечения кривой с осями координат, если они существуют.
7. Составляют сводную таблицу исследования.
8. Строят график, учитывая исследование функции, проведённое по вышеописанным пунктам.
Пример. Исследовать функцию
и построить её график.
Решение.
1. Область определения функции – вся числовая прямая. Множеством значений данной функции, как и всякой показательной функции, служит интервал ]0, +∞[. Поэтому график функции расположен выше оси Ox
,2.
Напомним: из школьного курса известно, что функция y = f(x) называется чётной, если
для всех x, принадлежащих области определения функции.
.
График чётной функции симметричен относительно оси Oy, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x; y).
Функция y = f(x) называется нечётной, если
для всех x, принадлежащих области определения функции.
График нечётной функции симметричен относительно начала координат, так как, по определению, вместе с любой своей точкой (x; y) он содержит и точку (-x;
Наша исследуемая функция чётная, так как
её график симметричен относительно оси Oy.
Поэтому исследование можно выполнять только для ]0, +∞[.
3. Вертикальных асимптот у графика нет, поскольку функция непрерывна на всей числовой прямой. Горизонтальной асимптотой является ось Ox, так как
Поскольку кривая имеет двустороннюю горизонтальную асимптоту y = 0, у неё не может быть наклонных асиптот.
4. Находим . Из уравнения имеем .
Так как при переходе через значение x = 0 меняет знак с плюса на минус, то функция в точке x = 0 переходит от возрастания к убыванию, а (0; 1) – точка максимума. Касательная к кривой в этой точке горизонтальна, поскольку .
5. Находим Из уравнения получаем т.е. .
Учитывая чётность функции, исследуем знаки в окрестности только точки .
Следовательно, при x = 1 кривая
меняет выпуклость на вогнутость.
Так как
то
—
точка перегиба кривой. Угловой коэффициент касательной к кривой в этой точке
.
Поэтому в точке перегиба касательная образует с осью Ox тупой угол.
6. График не пересекает оси Ox, поскольку он расположен выше неё. Найдём точки пересечения кривой с осью Oy: полагая x=0, имеем
Тем самым получим точку (0; 1) графика, которая совпадает с точкой максимума.
7. Составим сводную таблицу исследования функции, куда внесём все характерные точки и интервалы между ними. Учитывая чётность функции, получаем следующую таблицу:
Особенности графика | ||||
[-1, 0[ | + | — | Возрастает | Выпуклый |
0 | 0 | — | 1 | (0; 1) – точка максимума |
]0, 1[ | — | — | Убывает | Выпуклый |
1 | — | 0 | — точка перегиба, образует с осью Ox тупой угол | |
]1, +∞[ | — | + | Убывает | Вогнутый |
+∞ | — | + |
| y = 0 – горизонтальная асимптота |
8.
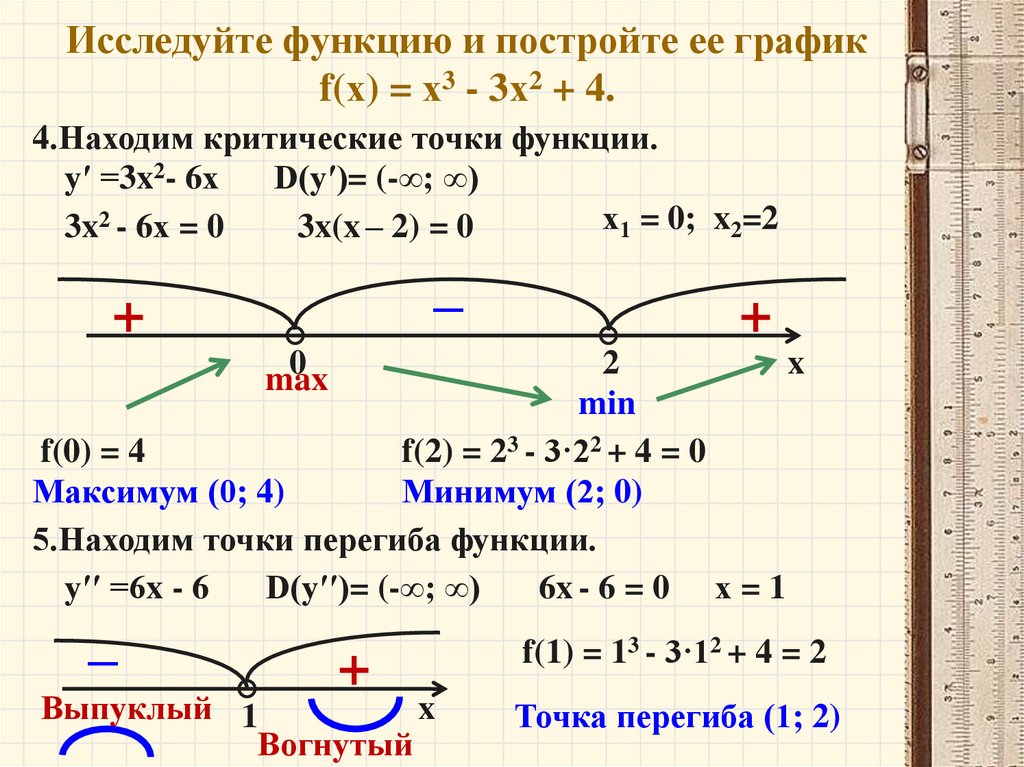Используя результаты исследования, строим график функции (см. рисунок).
| Назад | Листать |
Нет времени вникать в решение? Можно заказать работу!
Пройти тест по теме Производная, дифференциал и их применение
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Уравнение касательной и уравнение нормали к графику функции
- Правило Лопиталя
- Частные производные
- Применение производной к исследованию функций
- Экстремумы функции
- Наименьшее и наибольшее значения функции
- Асимптоты
- Возрастание, убывание и монотонность функции
- Выпуклость и вогнутость графика функции, точки перегиба
- Полное исследование функций и построение графиков
- Функции двух и трёх переменных
- Экстремумы функции двух переменных
- Условные экстремумы и функция Лагранжа
Исследовать функцию и построить график.
Полное исследование функции. Решение задач и контрольных работ по высшей математике онлайн
Краткая теория
Наиболее наглядное представление о ходе изменения функции дает ее график. Поэтому построение графика является заключительным этапом исследования функции, в котором используются все результаты ее исследования.
Схема исследования функции с последующим построением графика такова:
- Исследование области определения функции.
- Исследование функции на четность и нечетность.
- Нахождение точек пересечения графика с осями координат
- Исследование функции на точки разрыва. Нахождение вертикальных асимптот. Нахождение горизонтальных и наклонных асимптот.
- Исследование функции на экстремум и интервалы монотонности функции.
- Исследование функции на интервалы выпуклости и вогнутости графика функции. Нахождение точек перегиба графика функции.
- Построение графика функции.
Полученные данные следует использовать для построения графика функции. Если исследуемая функция является четной или нечетной, то ее достаточно исследовать при неотрицательных значениях аргумента из множества ее задания и принять во внимание, что график четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
Если, например, функция имеет период , то следует построить график на отрезке , а затем продолжить его периодически на всю числовую ось.
Кроме того, если полученных данных окажется недостаточно, то следует, воспользовавшись уравнением , найти дополнительные точки графика, в которых его изменение менее ясно.
Разумеется, в процессе исследования функции не обязательно придерживаться
приведенной схемы, иногда порядок исследования полезно выбрать, исходя из
конкретных особенностей данной функции./ModulBM/ModBM/Praktika/Rechen/pract(IssF_2pr).files/image214.jpg)
Примеры решения задач
Задача 1
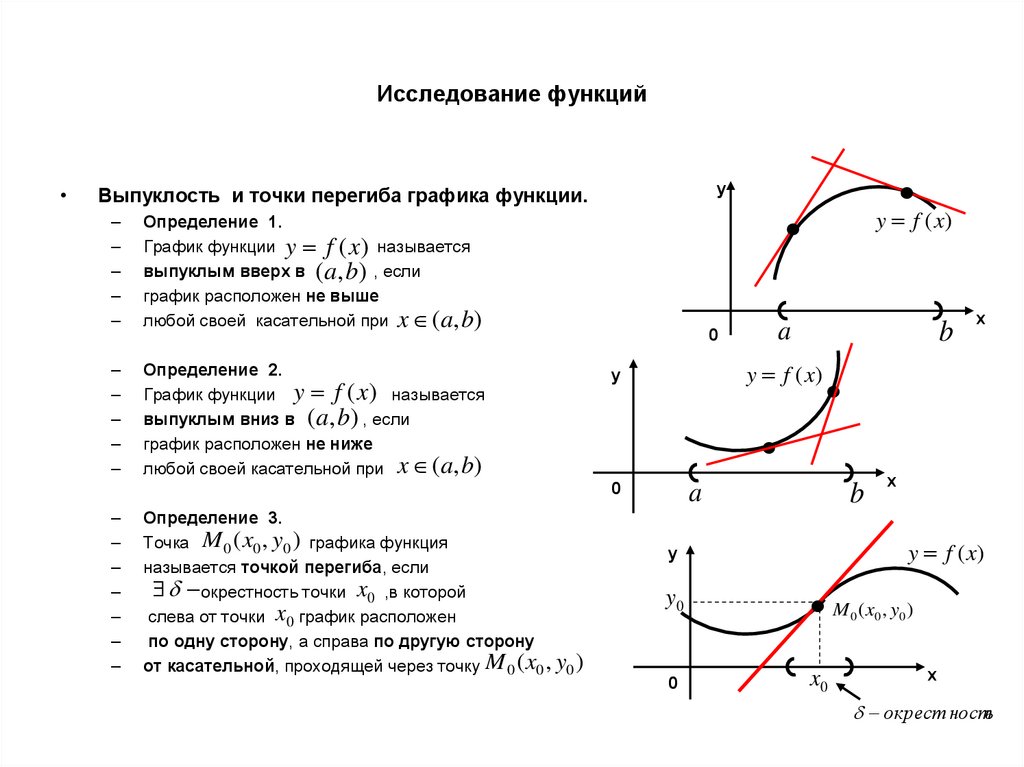
Исследовать функцию и построить ее график:
Решение
1) Область определения функции:
2) Исследуем функцию на четность-нечетность:
Функция является четной
3) Находим точки пересечения с осями координат:
График функции пересекает ось в точках и . Ось график функции не пересекает.
4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
В точке существует разрыв 2-го рода.
Прямая –вертикальная асимптота.
Для нахождения наклонной асимптоты вычисляем пределы:
–горизонтальная асимптота
5) Исследуем функцию на экстремум. Найдем производную функции.
Первая производная на области определения в нуль не обращается
-функция возрастает
-функция убывает
6) Исследуем функцию на интервалы выпуклости и вогнутости.
Вторая производная функции не равна нулю на всей области определения
–график функции вогнутый
– график функции вогнутый
7) График функции имеет вид:
Задача 2
Исследовать функцию и построить ее график:
Решение
1) Область определения функции:
2) Исследуем функцию на четность-нечетность:
Функция является нечетной
3) График функции оси координат не пересекает
4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:
В точке
существует разрыв 2-го рода.
Прямая –вертикальная асимптота.
Для нахождения наклонной асимптоты вычисляем пределы:
–наклонная асимптота
5) Исследуем функцию на экстремум. Найдем производную функции.
Приравняем найденную производную к нулю и решим полученное уравнение:
-функция возрастает
-функция убывает
-функция убывает
-функция возрастает
6) Исследуем функцию на интервалы выпуклости и вогнутости.
Вторая производная функции не равна нулю на всей области определения
–график функции выпуклый
– график функции вогнутый
7) График функции имеет вид:
Задача 3
Исследовать функцию и
построить ее график.
Решение
1) Область определения функции:
2) Исследуем функцию на четность-нечетность:
Функция не обладает свойствами четности — нечетности
3) Находим точки пересечения с осями координат:
График пересекает ось в точке (-0618, 0) и (1.618, 0)
4) Исследуем функцию на непрерывность, точки разрыва, вертикальные и наклонные асимптоты:
Точка является точкой разрыва функции 2-го рода, а прямая -вертикальной асимптотой графика функции.
Точка является точкой разрыва функции 2-го рода, а прямая -вертикальной асимптотой графика функции.
Для нахождения наклонной асимптоты вычисляем пределы:
Прямая –горизонтальная асимптота
5) Исследуем функцию
на экстремум.
Найдем производную функции.
Приравняем найденную производную к нулю и решим полученное уравнение:
Полученное уравнение действительных корней не имеет
– функция убывает
– функция убывает
– функция убывает
6) Исследуем функцию на интервалы выпуклости и вогнутости.
– график функции выпуклый
– график функции вогнутый
– график функции выпуклый
– график функции вогнутый
7) График функции имеет вид:
Графический онлайн-калькулятор Desmos — Freedom Scientific
Графический калькулятор Desmos — это бесплатный математический онлайн-инструмент, широко используемый учителями и учащимися для построения уравнений и изучения математических понятий. Используйте его для построения графиков данных, графических функций, оценки уравнений и создания занятий в классе.
Дополнительную информацию можно найти на странице Learn Desmos .
Desmos доступен с помощью программы чтения с экрана JAWS и может использоваться с обновляемыми дисплеями Брайля. Посетите Desmos Accessibility страница, чтобы узнать о встроенных настройках специальных возможностей и настроить JAWS и Fusion .
Графические функции
Графический калькулятор Desmos представляет собой универсальный инструмент с широкими графическими функциями. Вот несколько примеров задач, которые вы можете выполнить, и шаги для их выполнения. Посетите страницу Learn Desmos Graphing для получения дополнительной информации и ресурсов.
Создание и изучение графика
Для более плавного воспроизведения Desmos предлагает отключить эхо символов и установить режим форм на «полу». Настройки могут измениться с будущими обновлениями JAWS.
Чтобы создать и отследить график, выполните следующие действия:
- Посетите веб-сайт Desmos , затем найдите графический калькулятор .
- Напишите по одному уравнению в каждой строке в соответствующих полях редактирования — «выражение 1», «выражение 2» и т. д. Графики будут немедленно отображены.
- Нажмите ALT+T , затем H , чтобы построить график. Будет воспроизводиться индикатор звуковой дорожки.
- Используйте клавиши со стрелками для изучения графика.
- Нажмите ALT+S для получения сводки по достопримечательностям. Эта сводка доступна как в режиме трассировки, так и вне его.
- Находясь в режиме трассировки, нажмите TAB для навигации по этим точкам интереса. Иногда вам нужно будет нажать SHIFT+TAB , чтобы услышать их.
- Нажмите ESC для выхода из режима трассировки.
Чтобы настроить параметры графика, выполните следующие действия:
- В поле редактирования дважды нажмите TAB , чтобы перейти в меню настроек графика, затем нажмите ПРОБЕЛ , чтобы активировать его.
Доступные настройки:
- Размер дисплея
- Обратный контраст
- Режим Брайля
- Сетка или без сетки
- Сетка или без сетки
- Декартова сетка
- Полярная сетка
- Стрелка
- Номера осей
- Вспомогательные линии сетки
- Показать или скрыть ось X
- Метка оси X
- Минимальный размер оси X
- Те же параметры для оси Y
- Углы в радианах или градусах
Чтобы создать таблицу значений, выполните следующие действия:
- Переход к полям редактирования.
- Дважды нажмите SHIFT+TAB , чтобы перейти к «кнопке редактирования списка выражений», и выполните ее, нажав ПРОБЕЛ . JAWS должен указать, что «режим редактирования списка» включен.
- Нажмите TAB три раза, чтобы найти «преобразовать в таблицу», и нажмите ПРОБЕЛ .
- Нажмите TAB для навигации по значениям таблицы. Не используйте табличные команды.
- Чтобы найти конкретное значение, нажмите TAB или СТРЕЛКА ВНИЗ в строку с пустым полем редактирования и введите значение, которое вы хотите найти. Нажмите TAB, чтобы прослушать полученное значение.
- Чтобы вернуться к графику, нажимайте SHIFT+TAB , пока JAWS не скажет «отменить». Нажмите ПРОБЕЛ , чтобы активировать кнопку.
- Очистите график и все выражения, нажав CTRL+O . Теперь вы готовы начать новый график.
Видеоруководство по созданию и исследованию графика
Экспорт графика
Обмен графиками с коллегами или сверстниками сегодня крайне необходим. Возможность экспортировать четкий график позволяет правильно представить домашнее задание.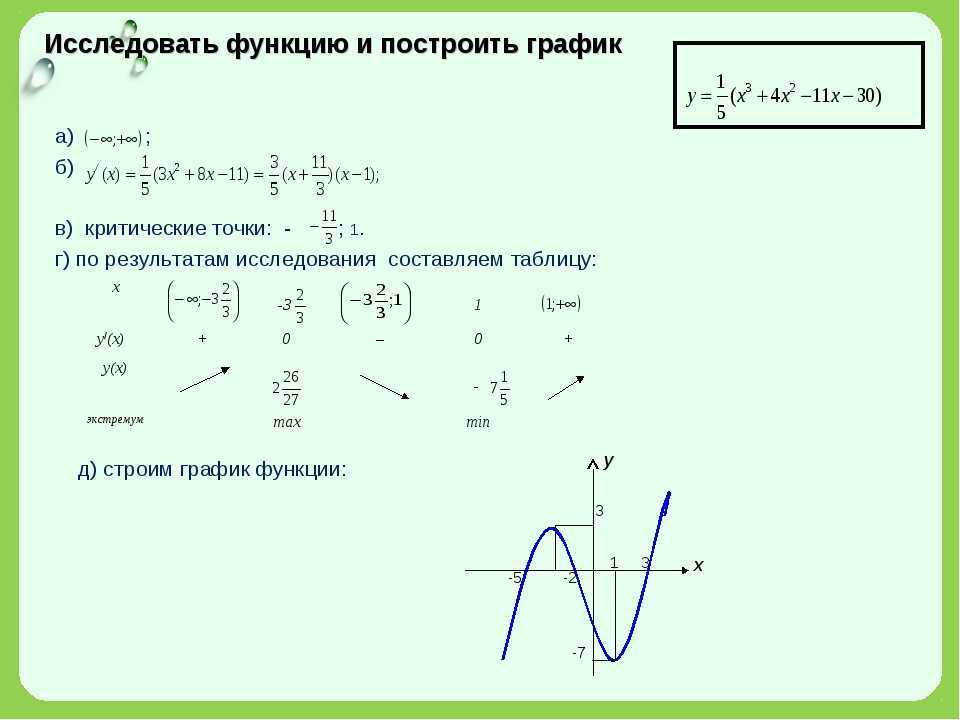
На рабочем месте такое общение повышает вашу способность работать с коллегами, особенно сейчас, когда командная работа так распространена. Общение является ключом к успеху.
После построения графика функции экспортируйте график в Word:
- Нажмите SHIFT+TAB , чтобы найти «поделиться», и нажмите ENTER .
- Несколько раз нажмите клавишу TAB , пока не найдете кнопку «Загрузить».
- Либо нажмите INSERT+F5 , чтобы просмотреть список полей формы, затем нажмите букву I, чтобы найти «загрузку изображения». Дважды нажмите ВВОД . Это поместит фокус рядом с кнопкой «Загрузить» и потребует меньше нажатий клавиши TAB , чтобы найти ее.
- Перейдите к документу Word.
- Вставьте изображение, нажав ALT+N , затем P , затем ENTER .
- Перейдите к адресной строке, нажав ALT+D , и введите первые несколько букв слова «скачать».
- Нажмите СТРЕЛКА ВНИЗ один раз, чтобы найти папку загрузок, и нажмите ENTER .
- Выполните команду «Найти файл», нажав ALT+N , и введите «des», чтобы найти файлы Desmos.
- Нажмите СТРЕЛКА ВНИЗ , пока не найдете нужный файл, затем нажмите ENTER . Фокус будет на графике. Если вы потеряете этот фокус, нажмите CTRL+SHIFT+O , чтобы получить доступ к списку объектов, и выберите график, нажав ENTER .
- Нажмите клавишу ПРИЛОЖЕНИЯ , а затем Z , чтобы перейти на вкладку размера.
- Нажмите ALT+A , чтобы убедиться, что установлен флажок «Блокировать соотношение сторон».
- Нажимайте TAB для навигации по полям, пока не найдете абсолютную высоту и не наберете 2,5
- Нажмите TAB , чтобы перейти к ширине, чтобы убедиться, что она изменилась. Если это не так, снова перейдите к блокировке соотношения сторон, чтобы установить в этом поле правильную ширину и высоту. Нажмите ENTER , чтобы закрыть диалоговое окно.
Если это не так, снова перейдите к блокировке соотношения сторон, чтобы установить в этом поле правильную ширину и высоту. Нажмите ENTER , чтобы закрыть диалоговое окно.
Чтобы добавить и отредактировать замещающий текст, выполните следующие действия:
- Нажмите клавишу ПРИЛОЖЕНИЯ , а затем A , чтобы перейти к полю замещающего текста. Если в этом поле есть текст, нажмите CTRL+A , чтобы выделить текст и либо удалить его, либо ввести новый замещающий текст, чтобы заменить существующий контент.
- Нажмите CTRL+ПРОБЕЛ , а затем C , чтобы закрыть меню навигации. Закрытие меню навигации имеет решающее значение для добавления замещающего текста к изображению. Если вы забудете закрыть меню навигации, у вас возникнут трудности с добавлением замещающего текста к изображению для следующего графика. В этом случае нажмите F6 , чтобы переключиться на панель замещающего текста.
- Нажмите CTRL+END , а затем ENTER , чтобы продолжить запись документа с новой строки.
Видеоруководство по экспорту графика
Быстрый экспорт графика в Word с помощью Print Screen
Print screen работает лучше всего, когда учащийся выполняет домашнюю работу и ему нужно создать много графиков.
После создания графика выполните следующие действия:
- Нажмите PRINT SCREEN , чтобы скопировать график в буфер обмена.
- Перейдите к документу Word.
- Тип «1». (или #, применимый к графику). Введите математическую задачу, затем нажмите ВВОД .
- Вставьте график в Word, нажав CTRL+V .
- Ваш курсор будет помещен в конец вставленного материала. Нажмите SHIFT+СТРЕЛКА ВЛЕВО , чтобы выбрать график. Вы также можете нажать CTRL+SHIFT+O , чтобы перейти к списку объектов и перейти к концу списка, чтобы найти свой график. Оказавшись там, нажмите ENTER .
- Нажмите клавишу ПРИЛОЖЕНИЯ , затем нажмите СТРЕЛКА ВВЕРХ , чтобы найти «размер и положение». Нажмите ВВЕДИТЕ , чтобы выбрать эту опцию. В качестве альтернативы нажмите Z после нажатия клавиши ПРИЛОЖЕНИЯ , чтобы открыть это диалоговое окно.
- Нажмите ALT+A , чтобы убедиться, что установлен флажок «Блокировать соотношение сторон». Нажмите TAB для навигации по полям, чтобы найти абсолютную высоту и введите «2,5», затем нажмите TAB для поля ширины. Убедитесь, что он изменился. Если это не так, снова перейдите к блокировке соотношения сторон, чтобы установить в этом поле правильную ширину и высоту. Нажмите ВВЕДИТЕ , чтобы закрыть диалоговое окно.
Нажмите SHIFT+СТРЕЛКА ВЛЕВО , чтобы выбрать график. Вы также можете нажать CTRL+SHIFT+O , чтобы перейти к списку объектов и перейти к концу списка, чтобы найти свой график. Оказавшись там, нажмите ENTER .
Нажмите ВВЕДИТЕ , чтобы закрыть диалоговое окно.
Чтобы добавить и отредактировать замещающий текст, выполните следующие действия:
- Нажмите клавишу ПРИЛОЖЕНИЯ , а затем A , чтобы перейти к полю замещающего текста. Если в этом поле есть текст, нажмите CTRL+A , чтобы выделить его, и либо удалите текст, либо введите новый замещающий текст, чтобы заменить существующий контент.
- Нажмите CTRL+ПРОБЕЛ , а затем C , чтобы закрыть меню навигации. Закрытие меню навигации имеет решающее значение для добавления замещающего текста к изображению. Если вы забудете закрыть меню навигации, у вас возникнут трудности с добавлением замещающего текста к изображению для следующего графика. Если это произойдет, нажмите F6 для переключения на панель замещающего текста.
- Нажмите CTRL+END , а затем ENTER , чтобы продолжить запись документа с новой строки.
Wolfram|Alpha Примеры: чертежи и графика
Ого! Wolfram|Alpha не работает без JavaScript.
Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.
Примеры для
Графики и графики — это методы визуализации поведения математических функций. Используйте Wolfram|Alpha для построения графиков функций, уравнений и неравенств в одном, двух и трех измерениях. Получите дополнительную перспективу, изучая полярные графики, параметрические графики, контурные графики, графики областей и многие другие типы визуализации интересующих вас функций и уравнений.
Функции
График функции одной переменной в виде кривой на плоскости.
93 t)Укажите диапазон для параметра:
параметрический график (sin 10t, sin 8t), t=0.