Простая физика — EASY-PHYSIC
Привет всем посетителям! Сегодня рассматриваем вопрос четности и нечетности функций.
Правило:
Если , то функция четная.
Если , то функция нечетная.
При этом важно, чтобы область определения функции была бы симметричной относительно оси ординат, а при наличии в ней выколотых точек или интервалов они также должны располагаться симметрично.
Алгоритм исследования:
Установить, симметрична ли область определения функции. Если это так, то найти и сравнить с
Если то функция — четная.
Если , то функция нечетная.
Функция совсем не обязана быть четной или нечетной, она может быть «никакой», несмотря на то, что область определения симметрична.
Примеры:
1. Определить, является ли четной функция: .
Область определения этой функции – все действительные числа, то есть она симметрична. Теперь подставим вместо x – (-x) и посмотрим, что получится:
– функция четна.
Надо отметить, что график четной функции симметричен относительно оси ординат, она для него словно зеркало. Поэтому графики таких функций можно строить в правой полуплоскости, а в левую просто отражать.
Верно и следующее: если функция задана графиком, который симметричен относительно оси ординат, то она четная.
2. Определить, является ли четной функция: .
Область определения этой функции может быть найдена из системы неравенств:
Оба неравенства всегда соблюдаются, так как дискриминант обоих трехчленов всегда меньше 0, и ветви парабол направлены вверх – таким образом, мы установили, что область определения симметрична – это вся числовая ось.
Теперь подставим вместо x – (-x): – данная функция нечетна.
График нечетной функции симметричен относительно начала координат, то есть каждой его точке соответствует точка, получить которую можно поворотом на 180 градусов относительно начала координат. Поэтому графики таких функций можно строить в правой полуплоскости, а изображение в левой полуплоскости получить, повернув картинку на 180 градусов.
Верно и следующее: если функция задана графиком, который симметричен относительно начала координат, то она нечетная.
3. Определить, является ли четной функция: .
Область определения может быть найдена из системы неравенств:
Таким образом, область определения симметрична, и не содержит выколотые точки (1) и (-1).
Подставляем (-х) вместо х:
— исходную функцию не получили, а получили совсем другую — значит, исходная функция не является ни четной, ни нечетной (что и подтверждает график). Мы убедились, что симметрия области определения еще не означает, что функция четная или же нечетная.
4. Определить, является ли четной функция: .
Область определения – вся числовая ось, кроме 0 – симметричная.
Подставляем (-х) вместо х:
– функция нечетна.
5. Определить, является ли четной функция: .
Область определения – вся числовая ось, кроме точек 3 и (-3) – симметричная.
Подставляем (-х) вместо х:
– функция четная.
6. Определить, является ли четной функция: .
Область определения – вся числовая ось – симметричная.
Подставляем (-х) вместо х:
– функция четная.
7. Определить, является ли четной функция: .
Область определения – вся числовая ось, кроме 0 – симметричная.
Подставляем (-х) вместо х:
– функция нечетная.
Кроме того, здесь мы имеем дело с суммой двух функций.
Правило:
Сумма двух нечётных функций — нечётна.
Сумма двух чётных функций — чётна.
А вот сумма двух функций разной четности – как правило, ни четна, ни нечетна.
Определим четность этих функций по отдельности.
– функция нечетная.
– функция нечетная.
8. Исследуем теперь такую функцию:
Одна из них нечётна – это мы только что показали, а вторая?
Область определения функции симметрична, функция нечётна, так как .
Тогда по правилу сложение двух нечетных функций даст функцию нечетную.
9. Наконец, последняя:
– имеем произведение двух функций.
Правило:
Произведение или частное двух нечётных функций чётно.
Произведение или частное двух чётных функций чётно.
Произведение или частное нечётной и чётной функций нечётно.
Так как обе функции являются чётными, то и их произведение чётно.
Проверим?
Область определения – вся числовая ось. Производим подстановку:
— функция четная.
Универсальное решение для изучения проверки битов четности
С увеличением скорости передачи данных и информации по сетевым каналам необходимость проверки целостности полученных данных становится большой проблемой, но для преодоления этой ситуации необходимо используется метод проверки битов четности, который помогает проверить полученные данные на наличие ошибок, а также целостность данных.
В этой статье «Что такое проверка битов четности?» мы рассмотрим все части сетевого метода и его рабочие шаги для решения сетевой проблемы.
Что такое проверка бита четности?
Проверка битов четности — это сетевой метод, предназначенный для обнаружения ошибок и проверки целостности данных, полученных на стороне получателя, стороной отправителя. Метод проверки четности добавляет бит к исходным данным для проверки ошибок на стороне получателя.
В случае повреждения полученных данных принимающая сторона запросит повторную передачу данных со стороны отправителя.
Теперь давайте перейдем к следующей теме этой статьи о проверке четности, т. е. к ключевым атрибутам, связанным с методом.
Ключевые атрибуты проверки четности
При выполнении метода проверки четности для обеспечения точности метода требуется использование нескольких атрибутов, некоторые из которых:
Резервный бит
- Это явно добавленные биты данных в исходные данные для определения ошибки или повреждения на стороне приемника.
- Значение избыточного бита определяется типом метода проверки четности, примененного к данным.
Значение бита четности
- Бит четности — это метод добавления двоичных битов для обеспечения того, чтобы общее количество единиц в исходных данных было либо четным, либо нечетным.
- Используется для обнаружения ошибок в исходных данных на стороне получателя и исправления данных.
Типы битов четности
- Бит четности: в этом типе бита четности общее количество единиц в данных, включая дополнительный бит, должно быть четным.
- Нечетный бит четности: В этом типе значения бита четности общее количество единиц в данных, вызывающих дополнительный бит, должно быть нечетным.
Далее мы рассмотрим решенные примеры с использованием метода проверки на четность, чтобы понять все этапы решения задачи.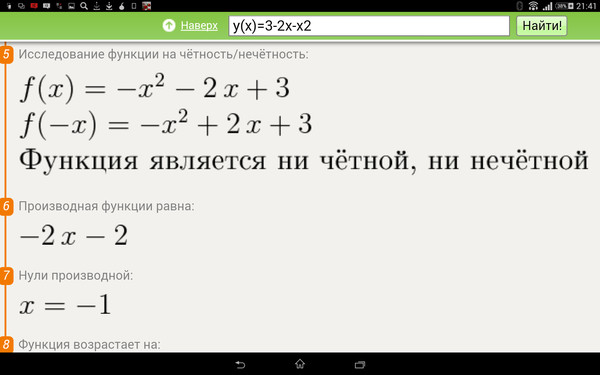
Решенный пример применения проверки четности
Чтобы лучше понять рабочие шаги по устранению ошибки методом проверки четности, рассмотрим следующие примеры:
Q1. Для данного бита данных 101101 примените метод проверки нечетной четности для передачи данных.
- Шаг 1: Подсчитайте количество единиц в исходных данных.
- Шаг 2: В соответствии со значением из шага 1 определите значение бита четности, т. е. 1, чтобы общее количество 1 стало 5 бит.
- Шаг 3: Начать передачу данных на сторону получателя и обсудить все полученные случаи.
Случай 1: Бит данных, полученный при передаче, не содержит ошибок, т. е. полученные данные верны после применения проверки на нечетность.
Случай 2: Бит данных, полученный при передаче, содержит ошибки, т. е. полученные данные повреждены после применения проверки на нечетность.
Случай 3: Бит данных, полученный при передаче, содержит ошибки, т.
е. полученные данные верны после применения проверки на нечетность.
Q2. Для заданного бита данных 110111 примените метод проверки четности для передачи данных.
- Шаг 1: Подсчитайте количество единиц в исходных данных.
> 5 бит - Шаг 2: В соответствии со значением из шага 1 определите значение бита четности, т. е. 1, чтобы общее количество 1 стало равным 6 битам.
- Шаг 3: Начать передачу данных на сторону получателя и обсудить все полученные случаи.
Случай 1: Бит данных, полученный при передаче, не содержит ошибок, т. е. полученные данные верны после применения проверки на четность.
Случай 2: бит данных, полученный при передаче, содержит ошибки, т. е. полученные данные повреждены после применения проверки на четность.
Случай 3: Бит данных, полученный при передаче, содержит ошибки, т. е. полученные данные верны после применения проверки на четность.
На этом мы рассмотрели все важные заголовки для понимания частей и работы метода проверки четности.
Воспользуйтесь возможностью стать частью сообщества профессиональных программ MIT CSAIL и пообщаться со своими коллегами. Посещайте мастер-классы преподавателей Массачусетского технологического института в нашей PGP по кибербезопасности и ускоряйте свою карьеру в области кибербезопасности в кратчайшие сроки!
Заключение
В этой статье «Что такое проверка битов четности?» мы рассмотрели определение и ключевые моменты вместе с тщательно решенными примерами с использованием метода битов четности.
Вы можете обратиться к курсу Simplilearn для экспертов по кибербезопасности, чтобы лучше понять работу сетевых методов. Пройдя этот профессиональный курс, вы лучше разберетесь в терминах, связанных с сетевыми моделями и методами.
Если у вас есть какие-либо вопросы об этой статье «Что такое проверка битов четности?».
Проверить нечетность числа
Является нечетным, онлайн-исчисление
Резюме:
Функция is_odd возвращает значение true, если переданное число нечетное, и значение false в противном случае.
is_odd онлайн
Описание :
Арифметический калькулятор может определить четность целого числа , т.е. проверить, является ли число четным или нечетное .
Целое число является нечетным , если оно не кратно 2. Если целое число не нечетное, то оно четное .
Арифметический калькулятор может проверять нечетность числа. Если число нечетное, функция возвращает
1, иначе возвращает 0.
Например, чтобы проверить, является ли число 11 четным или нечетным 0, введите следующую формулу is_odd(`11`), калькулятор возвращает 1, указывая на то, что 11 — нечетное число.
Например, чтобы проверить, является ли число 0 четным или нечетным 0, введите следующую формулу is_odd(`0`), калькулятор возвращает 0, указывая на то, что 0 не является нечетным числом.
Арифметический калькулятор может проверить, является ли число четным. Через функцию is_odd. Если число четное, калькулятор возвращает 0, что указывает на то, что число не нечетное, а значит, оно четное.
Например, чтобы проверить, является ли число 4 четным, введите следующую формулу is_odd(`4`), калькулятор возвращает 0, что указывает на то, что число не нечетное, т. е. четное.
У калькулятора есть еще одна функция.
проверить, что число четное
.
Синтаксис:
is_odd(число), где число — целое число.
Примеры:
is_odd(`191`), возвращает 0, указывая на то, что число нечетное.
Расчет онлайн с is_odd (четность числа)
См. также
Список связанных калькуляторов:
- Расчет биномиальных коэффициентов: binomial_coefficient. Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел.
- Для подсчета комбинаций: комбинация. Вычислить количество k элементов части множества из n элементов.
- Преобразователь base-n : base_converter. Калькулятор позволяет выполнять десятичные, двоичные, шестнадцатеричные преобразования и, в более общем случае, преобразование в любое основание n от 2 до 36.
- Калькулятор простой факторизации: prime_factorization. Функция prime_factorization используется для онлайн-расчета разложения целого числа на простые множители.
- Калькулятор частного и остатка: euclidean_division. Калькулятор позволяет найти в режиме онлайн частное и остаток при евклидовом делении двух многочленов или двух целых чисел.
- Четность числа: is_odd. Функция Is_odd возвращает true, если переданное число нечетное, иначе false.
- Четность числа: is_even. Функция Is_even возвращает 1, если число четное, иначе 0.
- Калькулятор факториала: факториал. Факториал натурального числа n — это произведение натуральных чисел, меньших или равных n. Калькулятор факториала позволяет найти это число.
- Калькулятор перестановки: перестановка. Подсчитать онлайн количество перестановок набора из n элементов.
- Расчет НОД онлайн: НОД. Калькулятор НОД, который использует алгоритм Евклида для определения шагов вычисления НОД.
- Наименьшее общее кратное: lcm. Калькулятор LCM для расчета наименьшего общего кратного (НОК).
- Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
- Решатель обратного отсчета: arithmetic_solver. Этот решатель обратного отсчета позволяет найти целевое число из набора целых чисел с помощью арифметических операций.
Вычислить онлайн количество расположения p элементов множества из n элементов.
