Свойства углов при параллельных прямых
ТЕОРЕМЫ ОБ УГЛАХ,
ОБРАЗОВАННЫХ ДВУМЯ
ПАРАЛЛЕЛЬНЫМИ
ПРЯМЫМИ
И СЕКУЩЕЙ
22 ЯНВАРЯ 2010Г
Учитель Козина Н.А.
ПОНЯТИЕ ОБРАТНОЙ ТЕОРЕМЫ
ЕСЛИ
Условие
Заключение
ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ,
ТО
ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
ТЕОРЕМа
Свойство
накрест лежащих углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ,
ТО НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ.
Свойство накрест лежащих углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ, ТО НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ.
P
Дано: прямые a ∥ b , секущая MN; 1 и 2 – накрест лежащие;
Доказать: 1 = 2;
M
а
1
2
в
N
Доказательство.
- Допустим, что 1 ≠ 2;
- Отложим от луча MN ∠PMN = 2, так чтобы ∠PMN и 2 были накрест лежащими углами при пересечении прямых MP и b секущей MN;
P
Дано: прямые a ∥ b , секущая MN; 1 и 2 – накрест лежащие;
Доказать: 1 = 2;
M
а
1
2
в
N
Доказательство.
- Допустим, что 1 ≠ 2;
- Отложим от луча MN ∠PMN = 2, так чтобы ∠PMN и 2 были накрест лежащими углами при пересечении прямых MP и b секущей MN;
- По построению эти накрест лежащие углы равны, поэтому MP ∥ b.
P
Дано: прямые a ∥ b , секущая MN; 1 и 2 – накрест лежащие;
Доказать: 1 = 2;
M
а
1
2
в
N
Доказательство.
- По построению эти накрест лежащие углы равны, поэтому MP ∥ b.
- Мы получили, что через точку М проходят 2 прямые параллельные прямой b.
- Но это противоречит аксиоме параллельных прямых.
- Значит, наше допущение неверно и 1 = 2;
следствие
Если прямая перпендикулярна к одной из двух параллельных прямых,
то она перпендикулярна и к другой.
с
Дано: прямые a ∥ b ,
M
c a
Доказать: c b
а
1
2
в
N
Свойство соответственных углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ, ТО СООТВЕТСТВЕННЫЕ УГЛЫ РАВНЫ.
с
1
M
Дано: прямые a ∥ b , секущая MN; 1 и 2 – соответственные;
Доказать: 1 = 2;
а
3
2
в
N
Доказательство.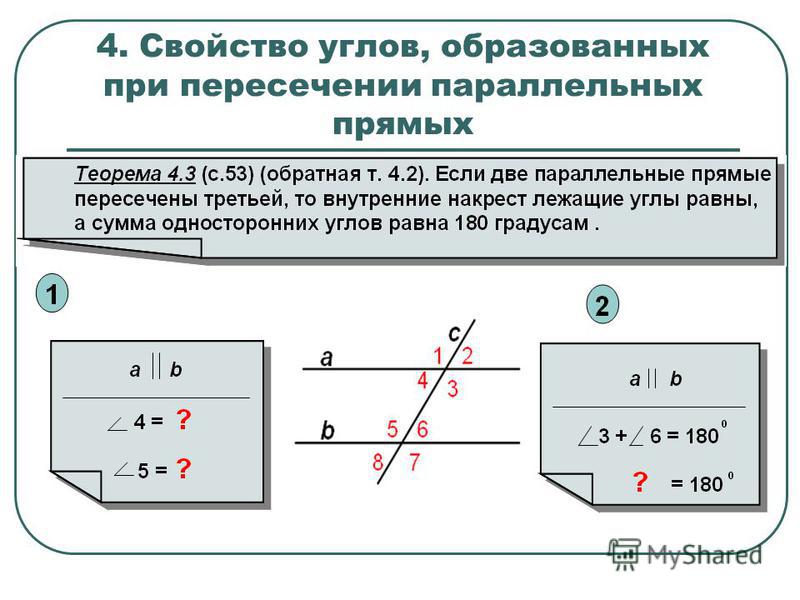
Свойство односторонних углов
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ,
ТО СУММА ОДНОСТОРОННИХ УГЛОВ РАВНА 180⁰.
с
Дано: прямые a ∥ b , секущая MN; 1 и 2 –односторонние;
Доказать:
1 + 2 = 180⁰;
M
а
3
1
2
в
N
Доказательство.
Решение задач
УСТНО
с
4
Дано: прямые a ∥ b ,
1 = 75⁰
Найти: 2, 3, ∠4 .
а
2
3
1
в
Решение задач
УСТНО
с
2
Дано: прямые a ∥ b ,
1 + ∠2 = 160⁰
Найти:

а
4
3
5
1
в
6
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА
ПАРАЛЛЕЛЬНЫХ
ПРЯМЫХ»
- 26 ЯНВАРЯ 2010Г
- Учитель Козина Н.А.
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
УСТНО
ДАНО:
а ║ в, с-секущая, ∠ 1=150˚
Найти:
∠ 2, ∠ 3, ∠ 4, ∠ 5, ∠ 6, ∠ 7, ∠ 8.
1
2
а
3
4
5
6
в
7
8
с
∠ 2=30 ˚, ∠ 3=30 ˚, ∠ 4=150 ˚, ∠ 5=150 ˚,
∠ 6=30 ˚, ∠ 7=30 ˚, ∠8 =150 ˚.
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
УСТНО
По данным рисунка найти:
∠ 1, ∠ 2, ∠ 3, ∠ 4, ∠ 5.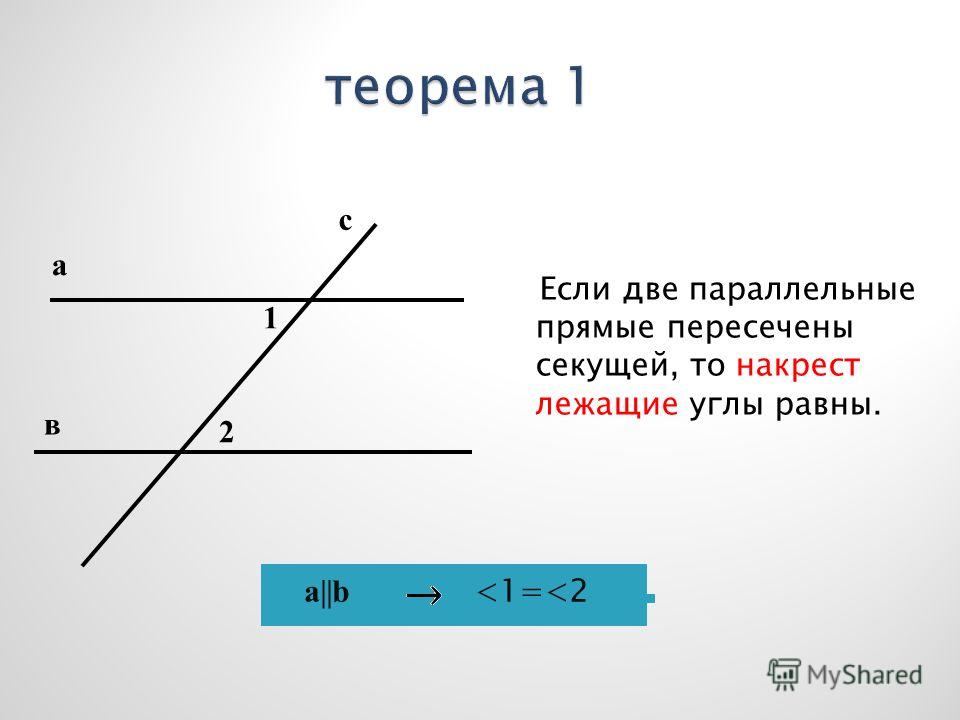
4
73˚
1
3
а
2
107˚
92˚
5
в
∠ 3= 73˚
с
∠ 2=107˚
d
∠ 4=107˚
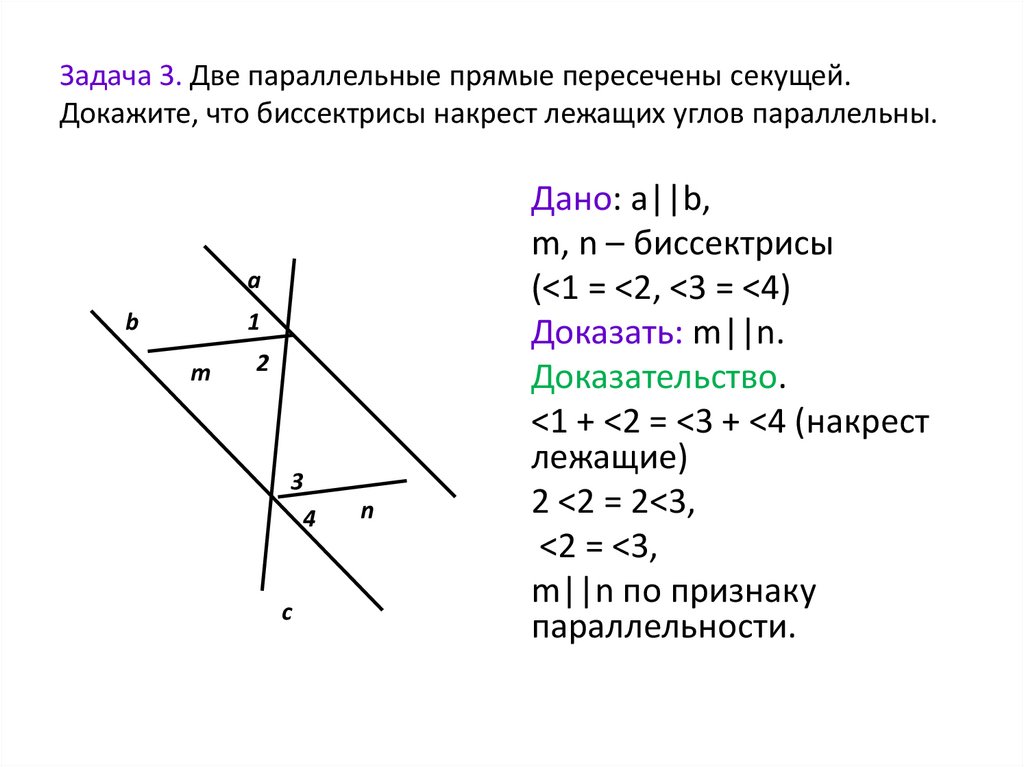
Доказать, что прямые параллельны.
∠ 5=73˚
∠ 1=92˚
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
№ 1
Дано: AE – биссектриса ∠BAD
Найти
∠ ABE, ∠BEA.
E
C
B
50˚
130˚
25˚
A
D
Доказать, что прямые параллельны.
Ответ:∠ BEA =25˚
Ответ:∠ ABE = 130˚,
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
№ 2
70˚
Найти ∠1, ∠2.
K
3
P
70˚
E
M
1
52˚
F
2
Доказать, что прямые параллельны.
∠ 2 =128˚
Ответ:∠ 1= 52˚,
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
№ 3
Найти ∠3
51˚
C
B
4
1
2
129˚
352˚
D
E
A
Доказать, что прямые параллельны.
Ответ:∠ 3 = 76˚,
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
№ 4
A
M
a
1
2
O
3
4
B
b
E
Дано: MO – биссектриса ∠M, EO – биссектриса ∠E,
a ∥ b
Найти ∠MOE
Ответ:∠ MOE = 90˚,
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
САМОСТОЯТЕЛЬНО
№ 5
T
K
N
68˚
1
112˚
4
2
68˚
3
P
M
Доказать, что прямые параллельны.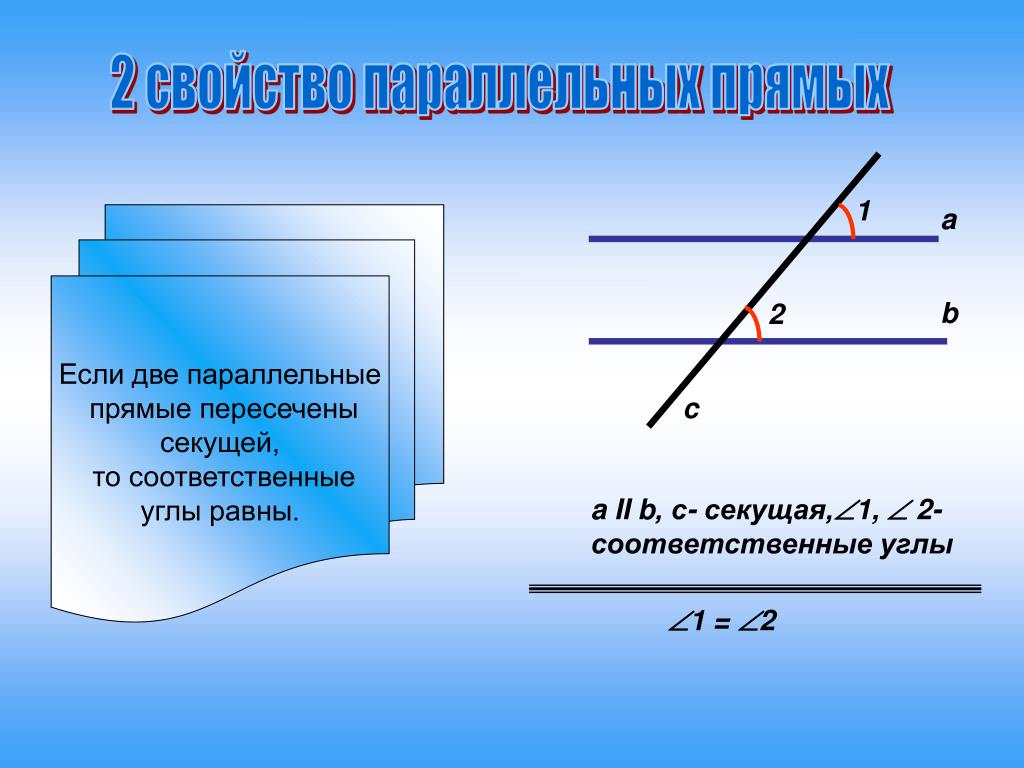
Дано: PT биссектриса ∠MPT
Найти ∠1
Ответ:∠ 1 = 34˚,
РЕШЕНИЕ ЗАДАЧ НА ТЕМУ
«СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ»
ДОМАШНЕЕ ЗАДАНИЕ
№ 208, 210, 211, 212
Урок-практикум по геометрии в 7-м классе «Свойства углов, образованных при пересечении параллельных прямых секущей»
Урок-практикум по геометрии в 7-м классе «Свойства углов, образованных при пересечении параллельных прямых секущей»- Горячева Нина Александровна
Разделы: Математика
Цели урока: (Слайд №1)
Образовательные: закрепление умений использовать знания признаков, свойств углов, образованных при пересечении параллельных прямых секущей, научить видеть различные способы при решении одной задачи.
Воспитательные: воспитание познавательной активности, чувства ответственности, культуры общения.
Развивающие: развитие логического мышления учащихся, внимания, активности, чувство ответственности, самостоятельности, культуры общения.
Тип урока: урок обобщения и систематизации знаний учащихся.
Организационные формы: парная, дифференцированно групповая.
Технология: уровневая дифференциация.
Структура урока:
- вводное слово учителя
- самостоятельная работа групп №2, №3
- актуализация знаний учащихся группы №1
- диктант
- тест
- самостоятельная работа группы №1
- защита у доски работ группами №2, №3
К данному уроку прилагается презентация (Приложение 1)
Ход урока:
Вводное слово учителя
Многие великие люди всех времен и народов говорили о значении математики. Не только ученые — математики, но и поэты, писатели, философы.
Высказывание одного великого мыслителя: «ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства» Леонардо да Винчи (слайд №2).
Не только ученые — математики, но и поэты, писатели, философы.
Высказывание одного великого мыслителя: «ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства» Леонардо да Винчи (слайд №2).
Предметом исследования нашего урока будут углы, образованные при пересечении параллельных прямых секущей. Задачей нашего урока является обобщение и систематизация ваших знаний по данной теме.
В ходе групповой, парной, самопроверки вы еще раз закрепите знания свойств углов, образованных при пересечении параллельных прямых секущей (слайд №3).
Организация работы групп
- класс делится на 3 группы по уровню их обученности
- каждая группа получает определенные задания
- группа №3 — уровень «4-5». Решают по 3 задачи с последующей защитой у доски.
Выполняют в тетрадях и сдают учителю.Задания для групп с уровнем обученности «4-5»
Дано: a и b, c и d;
<2 = 65°, <3 = 115°, <4 = 121°.
Доказать: a || b
Найти: <1В равнобедренных треугольниках ABC и DEF:
<1 = <2
Доказать: AB || CDНа рисунке: MQ = NP
<1 = <2
Доказать: MN || PQ - группа №2 — уровень на «4». Решают 4 задачи по готовым чертежам, по вариантам в парах с последующей защитой у доски, затем обмениваются вариантами и решают самостоятельно до конца урока. Выполняют в тетрадях и сдают учителю.
Решение по готовым чертежам (задания для ребят с уровнем обученности «4»)
Дано: a || b
<1 больше <2 в 5 раз
Найти: <1, <2, <3, <4Дано:m || n
<2 + <8 = 100°
Найти: остальные углыДано: <1 = <2 = <3
Доказать: a || b и m || nДано: <8 = 83°
<2 больше <1 на 14°
Доказать: MN || AB - группа №1 — с низким уровнем обученности.
 С этой группой начинает работать учитель.
С этой группой начинает работать учитель.- Диктант (слайды №4, №5, №6) — 7 мин. Выполняют на отдельных листах. Цель: проверить знания учащихся формулировки теорем, выражающих признаки параллельности прямых, свойств углов, образованных при пересечении секущей двух параллельных прямых, распознавать виды углов по рисунку.
Диктант.
Заполните пропуски в формулировке признаков, свойств углов при пересечении параллельных прямых секущей- Две прямые на плоскости называются параллельными, если они…
- Если две параллельные прямые пересечены третьей, то сумма внутренних…
- Назовите на данном рисунке углы:
- внутренние накрестлежащие…
- соответственные…
- односторонние…
- смежные (две пары)…
- вертикальные (две пары)…
- Если один из внутренних накрестлежащих углов при параллельных прямых и секущей равен 34°
- Если две параллельные прямые пересечены третьей, то соответственные…
- Если один из односторонних углов при параллельных прямых и секущей равен 150°, то другой равен…
- Будут ли прямые параллельными, если односторонние углы равны по 30° и 120°
Ответы к диктанту
- Две прямые на плоскости называются параллельными, если они не пересекаются.

- Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°
-
- 3 и 6; 4 и 5 – накрестлежащие
- 1 и 6; 2 и 5; 3 и 8; 4 и 7 – соответственные
- 3 и 5; 4 и 6 – односторонние
- 1 и 2; 2 и 3 – смежные
- 2 и 4; 1 и 3 – вертикальные
- 34°
- Углы равны
- 30°
- Нет, т.к. их сумма не равна 180°
- Самопроверка с обсуждением неверных ответов (слайд №7) — 5мин. Обмениваются ответами. После выполнения листы сдаются учителю.
- Тест (слайды №8, №9) — 8мин. Выполняют на отдельных листах Цель: проверить их умения объяснять по рисунку, какие углы являются накрест лежащими, соответственными, односторонними. Уметь применять признаки, свойства углов при решении задач (с учащимися работает ассистент-старшеклассник, а учитель работает с группой №2).

Тест
Выберите правильный ответ:
1. Прямые a и b — параллельные, с-секущая. <7 и <1- соответственные
- односторонние
- накрестлежащие
2. Дано: <8 = 35°. Найти: <1
- не знаю
- <1 = 145°
- <1 = 35°
3. Дано: m || n, <3 + <5 = 260°. Найти: <3
- <3 = 50°
- <3 = 130°
- не знаю
4. Параллельны ли прямые a и b, если (см.
 рисунок)
рисунок)
- да
- не знаю
- нет
Ответы к тесту:
-
<7 и <1 (см. рис.)
- соответственные
- односторонние
- накрестлежащие
- <8 = 35°. Найти: <1
- не знаю
- 145°
- 35°
- m || n, <3 + <5 = 260°. Найти: <3
- <3 = 50°
- <3 = 130°
- не знаю
- Будет ли a и b, если (см. рис.)
- да
- не знаю
- нет
- самопроверка с обсуждением (слайды №10, №11) — 5 мин.
 После выполнения листы сдаются учителю.
После выполнения листы сдаются учителю.
- самостоятельная работа — 15мин. Выполняется в рабочих тетрадях, затем сдаются на проверку (в это время учитель работает с группой №3).
Самостоятельная работа
Вариант 1 Дано: a || b, c — секущая
<3 = 138°
Найти: <1, <2, <3Дано: p ? m, p ? n
<2 = 40°, <7 = 40°
Доказать : a || bВариант 2 Дано: m || n, p — секущая
<1 = 34°
Найти: <2, <3, <4Дано: c ? a, c ? b
<8 = 120°, <1 = 60°
Доказать : a || b
- Диктант (слайды №4, №5, №6) — 7 мин. Выполняют на отдельных листах. Цель: проверить знания учащихся формулировки теорем, выражающих признаки параллельности прямых, свойств углов, образованных при пересечении секущей двух параллельных прямых, распознавать виды углов по рисунку.
Параллельные линии – определение, свойства и примеры
При работе с параллельными линиями важно знать их определение и свойства. Давайте продолжим и начнем с его определения.
Параллельные прямые — это прямые, лежащие в одной плоскости, но никогда не пересекающиеся.
Понимание того, что такое параллельные линии, может помочь нам найти недостающие углы, найти неизвестные значения и даже узнать, что они представляют в координатной геометрии.
Так как параллельные прямые используются в разных разделах математики, нам необходимо освоить их уже сейчас.
Что такое параллельные линии?
Параллельные линии — это равноудаленные линии (линии, имеющие одинаковое расстояние друг от друга), которые никогда не пересекутся.
Вот несколько примеров параллельных линий в разных направлениях : по горизонтали, диагонали и вертикали.
Еще один важный факт о параллельных линиях: они имеют одно и то же направление .
Какие есть реальные примеры параллельных линий?
- Дороги и пути: противоположные пути и дороги будут иметь одно направление, но они никогда не пересекутся в одной точке.
- Линии на блокноте: все линии находятся в одной плоскости, но они никогда не пересекутся.
- Пешеходные переходы: все нарисованные линии проходят в одном направлении и по дороге, но эти линии никогда не пересекутся.
Как мы используем параллельные линии в координатной геометрии?
- Когда графики двух линейных уравнений параллельны в координатной геометрии, два уравнения не имеют общего решения .
- наклона двух параллельных прямых равны в координатной геометрии.
Мы узнаем об этом больше в координатной геометрии, а пока давайте сосредоточимся на свойствах параллельных линий и их использовании для решения задач.
Как доказать, что прямые параллельны?
Можно использовать несколько геометрических соотношений , чтобы доказать, что две прямые параллельны.
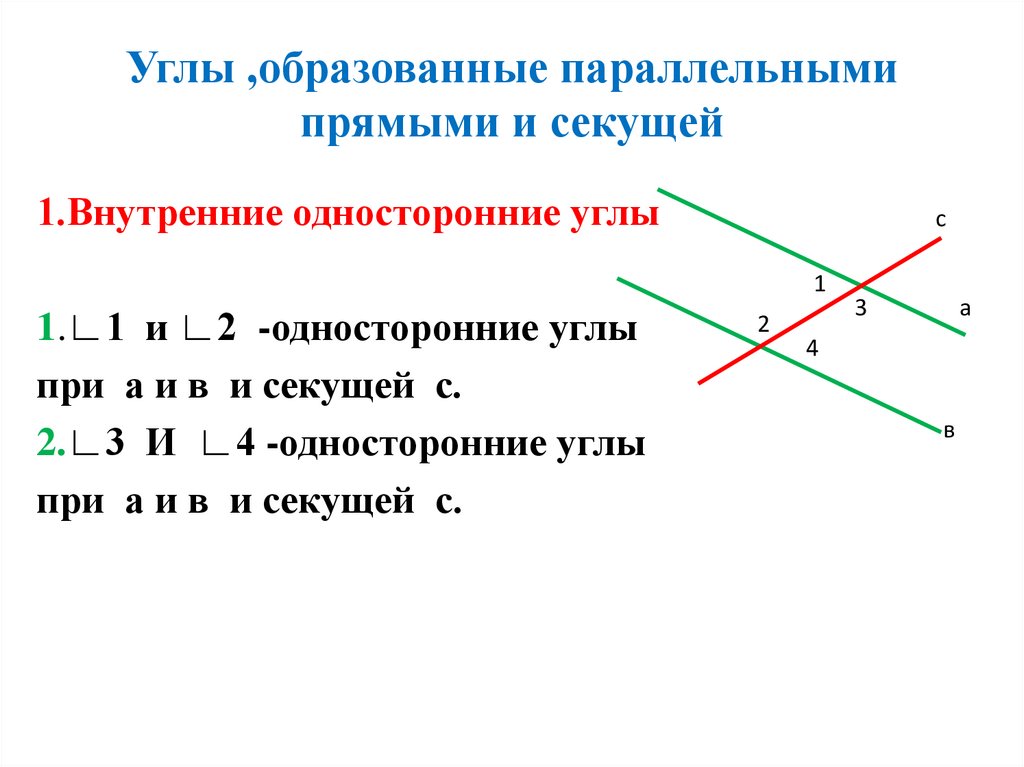
Прежде чем мы начнем, давайте рассмотрим определение поперечных линий.
Поперечные линии — это линии, которые пересекают две или более линий .
На изображении справа показано, как поперечная линия пересекает пару параллельных линий .
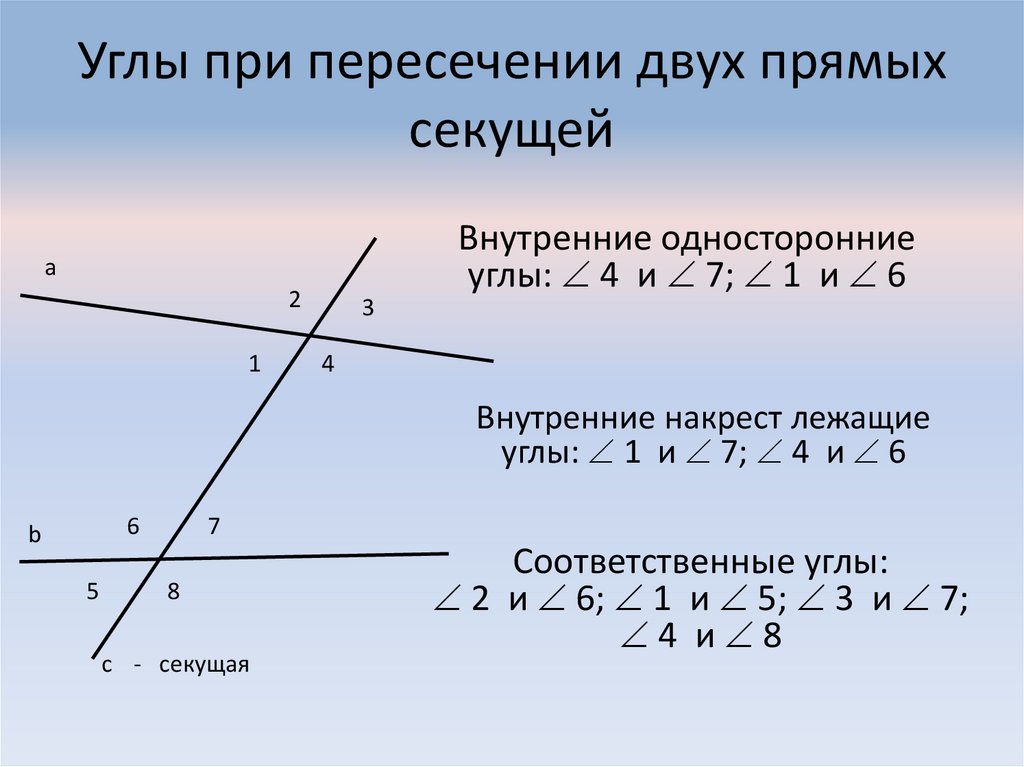
Когда поперечная линия пересекает пару параллельных прямых, образуются разные пары углов. Эти различные типы углов используются для доказательства того, параллельны ли две прямые друг к другу.
В следующем разделе вы узнаете, что такое следующие углы и их свойства:
- Соответствующие углы
- Чередующиеся внутренние углы
- Чередующиеся внешние углы
- Последовательные внутренние углы 90 2 параллельны поперечная линия пересекает две прямые, свойства, приведенные ниже, помогут нам определить, параллельны ли прямые.

1. Две линии, пересеченные поперечной линией, параллельны, когда соответствующие углы равны .
Две пары углов, показанные выше, являются примерами соответствующих углов. В общем случае это углы, находящиеся в взаимном положении и лежащие вдоль одной и той же стороны.
2. Две прямые, пересеченные поперечной линией, параллельны, если внутренних угла равны .
Альтернативные внутренние углы — это пара углов, находящихся на внутренней стороне, но лежащих друг напротив друга.
3. Две прямые, пересеченные поперечной линией, параллельны, если 9{\circ}}$.
Последовательные внешние углы — это последовательные углы, имеющие одну и ту же внешнюю сторону вдоль линии.
Резюме определения параллельных линий
Подведем итог тому, что мы уже узнали о параллельных линиях:
- они компланарны
- они равноудалены
- они никогда не пересекутся
Следующие свойства помогут нам определить и покажите, что две прямые параллельны .

1. Соответственные углы равны. 9{\circ}$
Давайте попробуем ответить на приведенные ниже примеры, используя определения и свойства, которые мы только что изучили.
Пример 1
Какой из следующих терминов не описывает пару параллельных прямых?
а. Некомпланарные
б. Копланарный
c. Равноудаленная
d. В одном направлении
Решение
Вернемся к определению параллельных линий: это линии в одной плоскости, находящиеся на одном расстоянии, но никогда не пересекающиеся. Это показывает, что параллельные линии никогда не бывают некомпланарными .
Пример 2
Какой из следующих реальных примеров не представляет пару параллельных прямых?
а. Стрелки часов
b. Стеклоочистители
c. Лестница и перила
d. Вертикальные струны сетки теннисной ракетки
Решение
Варианты в б , в , и d — это объекты, которые имеют одни и те же направления, но никогда не встретятся.
 Все они лежат в одной плоскости (т. е. струны лежат в одной плоскости сетки).
Все они лежат в одной плоскости (т. е. струны лежат в одной плоскости сетки).Однако стрелки часов встречаются в центре часов, поэтому пара параллельных линий никогда не будет их изображать.
Следовательно, правильный ответ а.
Пример 3
Параллельны ли две прямые, пересеченные поперечной линией? Какое свойство вы можете использовать, чтобы обосновать свой ответ? 9{\circ}}$.
Пример 5
Если две прямые параллельны и пересекаются поперечной линией, какова стоимость $x$ ?
Решение
Так как прямые параллельны и $\boldsymbol{\angle B}$ и $\boldsymbol{\angle C}$ являются соответствующими углами, то $\boldsymbol{\angle B = \angle С}$ .
Приравняйте их два выражения, чтобы найти $x$.
$60 = 2x + 8$
Изолируйте $2x$ в левой части уравнения.
$2x = 60 – 8$
$2x = 52$
Разделите обе части уравнения на $2$, чтобы найти $x$.

$x = 26$
Это означает, что $\boldsymbol{x = 26}$.
Пример 6
, если ♂ WTTS и ↑яув являются дополнительными (они имеют сумму 180 ° ), показывают, что WX и YZ — это параллельные линии и . .
Решение
Углы $\угол WTS$ 9{\circ}$
Сложите два выражения, чтобы упростить левую часть уравнения.
$x + 48 + 3x – 120 = 180$
$4x – 72 = 180$
Добавьте 72$ к обеим частям уравнения, чтобы выделить $4x$.
$4x = 252$
Разделите обе части уравнения на $4$, чтобы найти $x$.
$x = 63$
Подставьте это значение $x$ в выражение для $\angle EFA$, чтобы найти его фактическую меру.
$\begin{align}3x – 120 &= 3(63) – 120\\ &=69{\circ}$ представляют собой пару альтернативных внешних углов и равны.

Напомним, что две прямые параллельны, если их пара альтернативных внешних углов равны. Следовательно, $\overline{AB}$ и $\overline{CD}$ — параллельные прямые.
Теперь, когда мы показали, что прямые параллельны, альтернативных внутренних угла равны.
Поперечное — углы и параллельные линии
Овладейте семью столпами школьного успеха
Улучшить свои оценки и снизить стресс
Pre-Algebra/Expractions, уравнения, Percasions
Pre-Algebra/FRACES, Appraction, Appraction, Appraction, Appraction, Appraction, Appraction, Appraction, Appraction, Appraction, Appraction, Appraction, Appraction, Appraction, Appractions
, Appraction, уравнения
.
 Радикалы
Радикалы Математические калькуляторы
Геометрия/фигуры
Геометрия/SAT
Геометрия/плоскость
Геометрия/базовые науки
19
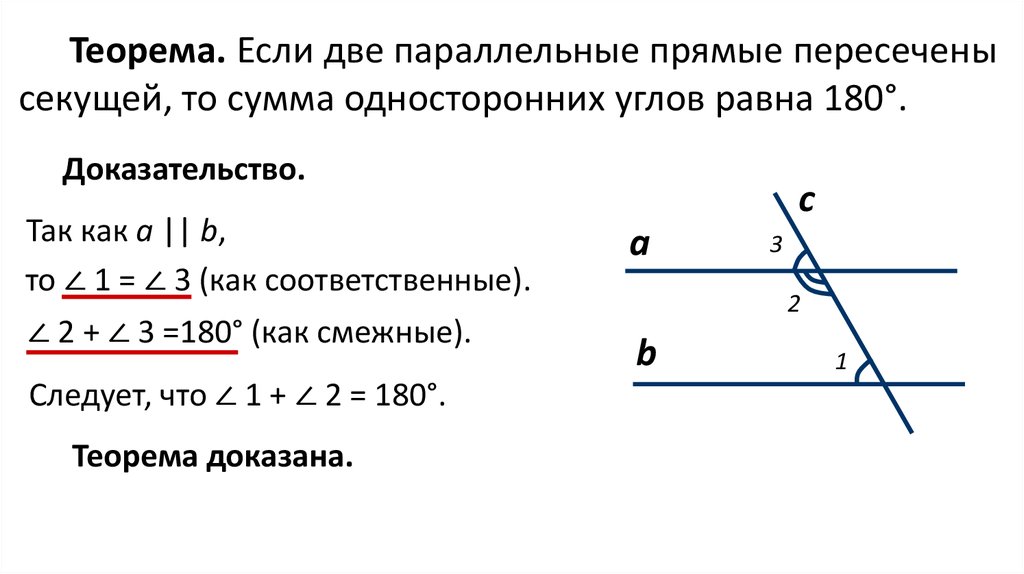
1Теорема : если две параллельные прямые пересечены секущей, внутренние углы равны.
Теорема : Если две прямые пересечены секущей и внутренние углы равны, то прямые параллельны.
Теорема : Если две параллельные прямые пересечены секущей, то противоположные внешние углы равны.
Теорема : Если две прямые пересечены секущей и противоположные внешние углы равны, то прямые параллельны.
Теоремы, связанные с углами, образованными секущей
Добро пожаловать в MooMooMath. Сегодня мы поговорим о параллельных прямых, пересекаемых секущими. Прежде всего, у нас есть две параллельные линии здесь. Линия M и линия N, они нарисованы синим цветом и параллельны друг другу, что означает, что они не касаются друг друга.
 Затем у нас есть эта зеленая линия, и мы назовем ее линией L, и это то, что мы назовем секущей. Это прямая, пересекающая обе параллельные прямые. Теперь он может создать несколько взаимосвязей углов. В этом видео речь пойдет только об одном из этих отношений. Скажем, нам дан этот угол (указывает на угол вверху), а первый угол равен 70 градусам, и я обозначу угол 70 градусов. Мы можем вычислить угол 2 и угол 3. Угол 2 является вертикальным углом к углу один, а это означает, что мера второго угла также равна 70 градусам, потому что вертикальные углы конгруэнтны друг другу. Теперь давайте посмотрим на угол три. Угол три представляет собой линейную пару с углом два. Мы знаем, что мера длины линий в сумме составляет 180, поэтому, если этот угол равен 70, угол три будет дополнительным, поэтому возьмите 180 и вычтите 70, и это будет равно 110 градусам. Таким образом, третий угол будет равен 110 градусам. Угол 1 и угол три являются дополнительными, углы два и три также являются дополнительными, потому что углы 1 и угол 2 конгруэнтны друг другу, поэтому надеюсь, что это видео было полезным.
Затем у нас есть эта зеленая линия, и мы назовем ее линией L, и это то, что мы назовем секущей. Это прямая, пересекающая обе параллельные прямые. Теперь он может создать несколько взаимосвязей углов. В этом видео речь пойдет только об одном из этих отношений. Скажем, нам дан этот угол (указывает на угол вверху), а первый угол равен 70 градусам, и я обозначу угол 70 градусов. Мы можем вычислить угол 2 и угол 3. Угол 2 является вертикальным углом к углу один, а это означает, что мера второго угла также равна 70 градусам, потому что вертикальные углы конгруэнтны друг другу. Теперь давайте посмотрим на угол три. Угол три представляет собой линейную пару с углом два. Мы знаем, что мера длины линий в сумме составляет 180, поэтому, если этот угол равен 70, угол три будет дополнительным, поэтому возьмите 180 и вычтите 70, и это будет равно 110 градусам. Таким образом, третий угол будет равен 110 градусам. Угол 1 и угол три являются дополнительными, углы два и три также являются дополнительными, потому что углы 1 и угол 2 конгруэнтны друг другу, поэтому надеюсь, что это видео было полезным.
Углы < 1 и < 3 и < 2 и < 4 являются вертикальными углами.
Угловые меры этих углов равны.
На этом рисунке углы < 1 и < 4 и < 2 и < 3 являются линейными парами. Угловая мера линейных пар равна 180 градусам.
Интерьер
Exterior
Exterior
In this example < 2 and < 6 and < 5 and < 3 are alternate interior angles
In this example < 1 и < 8 и
< 4 и < 7 являются альтернативными внешними углами
<6<и В этом примере,0178 3 and< 8, < 1 and < 5, and < 2 and< 7 are corresponding anglesTransversal
Transversal Angles
Вертикальные углы расположены друг напротив друга при пересечении двух прямых.
 Вертикальные углы равны. Их называют вертикальными углами, потому что они имеют одну и ту же вершину 9.0179 .
Вертикальные углы равны. Их называют вертикальными углами, потому что они имеют одну и ту же вершину 9.0179 . Какими свойствами обладают в геометрии углы, образованные секущими? Секущей называют прямую, пересекающую две или более прямых, которые могут быть параллельны. Трансверсаль образует несколько углов. Этим углам даны «имена», которые описывают их расположение и свойства. Ниже приводится список имен с иллюстрациями, описывающими углы, образуемые секущими, а также несколько теорем.
Три термина, которые помогут вам понять углы, связанные с секущими.
Интерьер означает между строк.
Внешний означает за пределами линий.
Альтернативный означает на противоположных сторонах поперечной.
Линейные Пары углов расположены на соответствующих сторонах секущей. Они могут быть как внутренними, так и внешними углами. Угловая мера линейных пар составляет 180°, поэтому они являются дополнительными.



 С этой группой начинает работать учитель.
С этой группой начинает работать учитель.

 рисунок)
рисунок)
 После выполнения листы сдаются учителю.
После выполнения листы сдаются учителю.
 Все они лежат в одной плоскости (т. е. струны лежат в одной плоскости сетки).
Все они лежат в одной плоскости (т. е. струны лежат в одной плоскости сетки).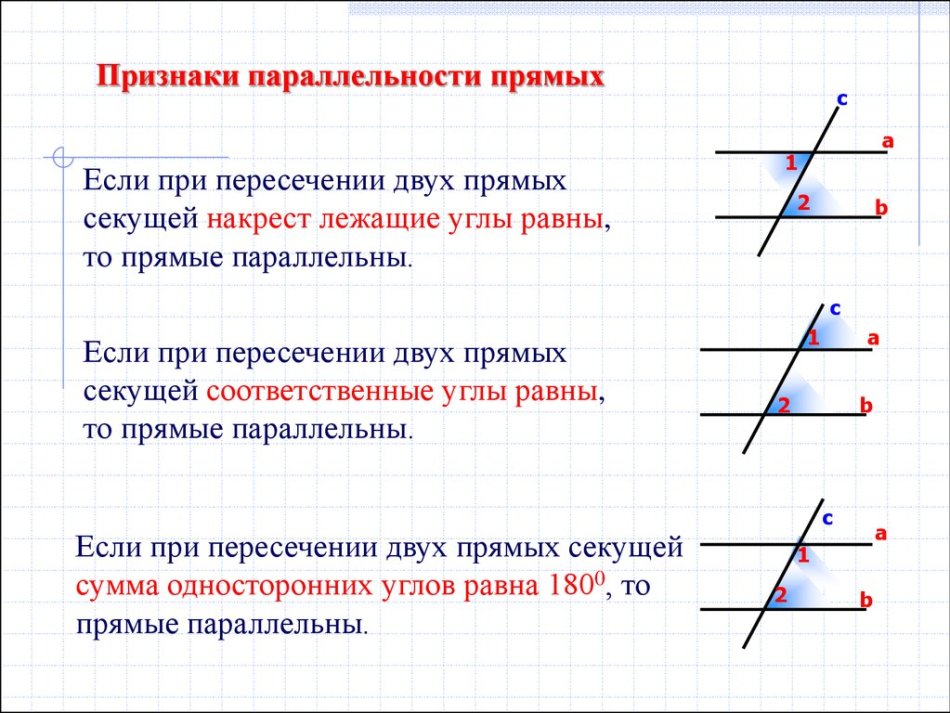

 Радикалы
Радикалы 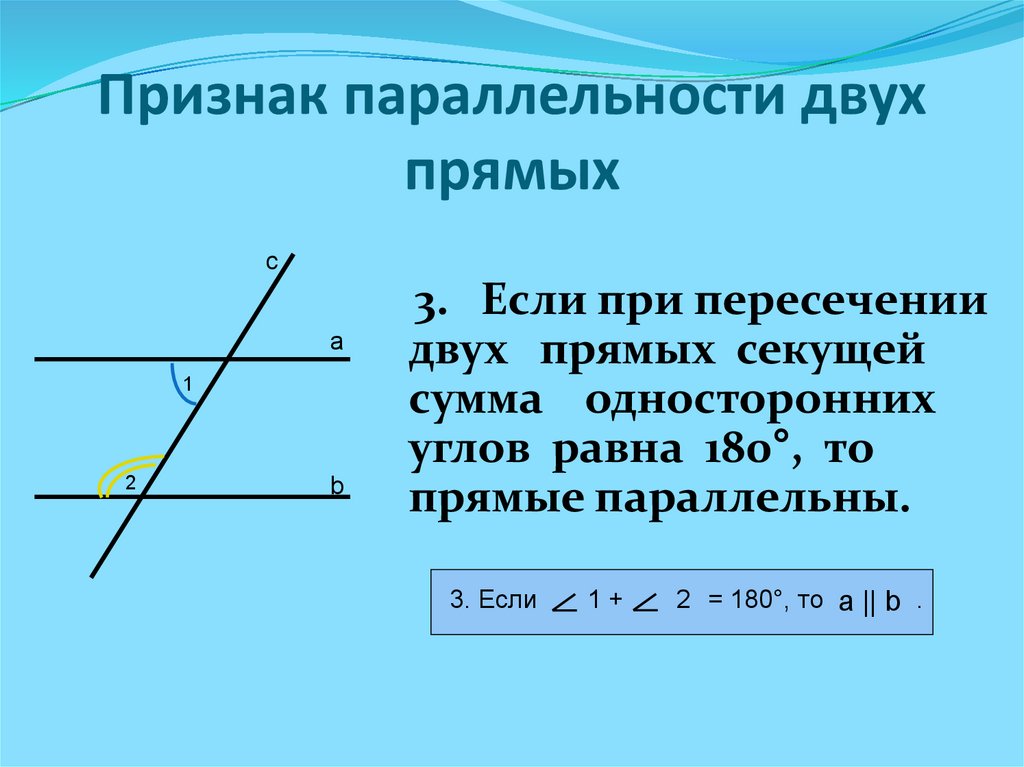 Затем у нас есть эта зеленая линия, и мы назовем ее линией L, и это то, что мы назовем секущей. Это прямая, пересекающая обе параллельные прямые. Теперь он может создать несколько взаимосвязей углов. В этом видео речь пойдет только об одном из этих отношений. Скажем, нам дан этот угол (указывает на угол вверху), а первый угол равен 70 градусам, и я обозначу угол 70 градусов. Мы можем вычислить угол 2 и угол 3. Угол 2 является вертикальным углом к углу один, а это означает, что мера второго угла также равна 70 градусам, потому что вертикальные углы конгруэнтны друг другу. Теперь давайте посмотрим на угол три. Угол три представляет собой линейную пару с углом два. Мы знаем, что мера длины линий в сумме составляет 180, поэтому, если этот угол равен 70, угол три будет дополнительным, поэтому возьмите 180 и вычтите 70, и это будет равно 110 градусам. Таким образом, третий угол будет равен 110 градусам. Угол 1 и угол три являются дополнительными, углы два и три также являются дополнительными, потому что углы 1 и угол 2 конгруэнтны друг другу, поэтому надеюсь, что это видео было полезным.
Затем у нас есть эта зеленая линия, и мы назовем ее линией L, и это то, что мы назовем секущей. Это прямая, пересекающая обе параллельные прямые. Теперь он может создать несколько взаимосвязей углов. В этом видео речь пойдет только об одном из этих отношений. Скажем, нам дан этот угол (указывает на угол вверху), а первый угол равен 70 градусам, и я обозначу угол 70 градусов. Мы можем вычислить угол 2 и угол 3. Угол 2 является вертикальным углом к углу один, а это означает, что мера второго угла также равна 70 градусам, потому что вертикальные углы конгруэнтны друг другу. Теперь давайте посмотрим на угол три. Угол три представляет собой линейную пару с углом два. Мы знаем, что мера длины линий в сумме составляет 180, поэтому, если этот угол равен 70, угол три будет дополнительным, поэтому возьмите 180 и вычтите 70, и это будет равно 110 градусам. Таким образом, третий угол будет равен 110 градусам. Угол 1 и угол три являются дополнительными, углы два и три также являются дополнительными, потому что углы 1 и угол 2 конгруэнтны друг другу, поэтому надеюсь, что это видео было полезным.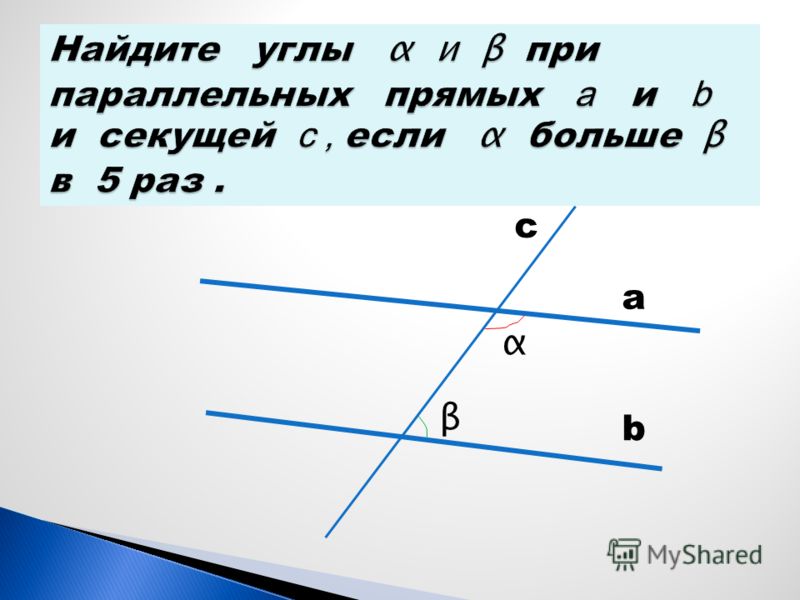
 Вертикальные углы равны. Их называют вертикальными углами, потому что они имеют одну и ту же вершину 9.0179 .
Вертикальные углы равны. Их называют вертикальными углами, потому что они имеют одну и ту же вершину 9.0179 . 