Исследовать функцию: Исследование функции и построение графика функции

Исследовать функцию и построить график.

Пример 1:

Исследовать функцию и построить ее график.

Решение от преподавателя:

1) Область определения функции х – любое.
2) Четность или нечетность функции. 

y(-x) = y(x), четная функция 
3) Точки пересечения кривой с осями координат. 
Пересечение с осью 0Y 

Пересечение с осью 0X 
y=0 

x₁ = 1, x₂ = -1 
4) Исследование на экстремум. 
1. Находим интервалы возрастания и убывания. Первая производная. 

=  

 

Находим нули функции. Для этого приравниваем производную к нулю 
x = 0 
Откуда: 
x₁ = 0 

(-∞ ;0)	(0; +∞)
f'(x) > 0	f'(x)
функция возрастает	функция убывает

В окрестности точки x = 0 производная функции меняет знак с (+) на (-). Следовательно, точка x = 0 — точка максимума. Y_max=1
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная. 

или 

Находим корни уравнения. Для этого полученную функцию приравняем к нулю. 

Откуда точки перегиба: 

 

 

f»(x) > 0	f»(x)	f»(x) > 0
функция вогнута	функция выпукла	функция вогнута

5) Асимптоты кривой. 

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. 2+20 
1. Находим интервалы возрастания и убывания. Первая производная. 
f'(x) = 3x²+6x 
или 
f'(x)=3x(x+2) 
Находим нули функции. Для этого приравниваем производную к нулю 
x(x+2) = 0 
Откуда: 
x₁ = 0 
x₂ = -2 

 

 

 

(-∞ ;-2)	(-2; 0)	(0; +∞)
f'(x) > 0	f'(x)	f'(x) > 0
функция возрастает	функция убывает	функция возрастает

В окрестности точки x = -2 производная функции меняет знак с (+) на (-). Следовательно, точка x = -2 — точка максимума. В окрестности точки x = 0 производная функции меняет знак с (-) на (+). Следовательно, точка x = 0 — точка минимума.  
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная. 
f»(x) = 6x+6 
Находим корни уравнения. Для этого полученную функцию приравняем к нулю. 
6x+6 = 0 
Откуда точки перегиба: 
x₁ = -1 

(-∞ ;-1)	(-1; +∞)
f»(x)	f»(x) > 0
функция выпукла	функция вогнута

6) Асимптоты кривой. 
y = x³+3x²+20 
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: 

Находим коэффициент k: 

Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует. 

Пример 3:

Исследовать функцию и построить график:

Решение от преподавателя:

1. Находим область определения D(x) функции: определена на всей числовой оси.

2.Асимптоты:

Вертикальных асимптот нет.

Находим наклонную асимптоту:

следовательно график функции не имеет наклонных асимптот.

Горизонтальная асимптота y=0.

3. Функция обладает свойствами четности, а, следовательно, график функции симметричен относительно оси OX.

4.Точек пересечения с осями координат: x=0, y=2.

5.Находим точки экстремума и интервалы монотонности, точки перегиба и интервалы выпуклости и вогнутости.

Первая производная функции:

Вторая производная функции:

Точек перегиба график функции не имеет.

На интервале  – функция возрастает.

На интервале   – функция убывает.

Точка максимума:

Функция выпуклая вверх на интервале:

Функция вогнута вниз на интервалах:

 6. Изображаем график функции:

 

 

Пример 4:

Решение от преподавателя:

Пример 5:

Исследовать функцию у = 15х² – 2х³ – 36х и построить ее график.

Решение от преподавателя:

1) Область определения функции

2) Четность или нечетность функции. 
y(-x)=2x³+15x²+36x y(x)
Функция общего вида 
3) Точки пересечения кривой с осями координат. 
Пересечение с осью 0Y            x=0, y=0 
Пересечение с осью 0X            y=0 
15x²-2x³-36x=0, x = 0 
5) Исследование на экстремум. 
y = -2x³+15x²— 36x 
1. Находим интервалы возрастания и убывания. Первая производная. 
f'(x) = -6x²+30x-36 
Находим нули функции. Для этого приравниваем производную к нулю 
-6x²+30x-36 = 0    или    x²+5x-6 = 0 
Откуда: 
x₁ = 2 
x₂ = 3 

(-∞ ;2)	(2; 3)	(3; +∞)
f'(x)	f'(x) > 0	f'(x)
функция убывает	функция возрастает	функция убывает

В окрестности точки x = 2 производная функции меняет знак с (-) на (+). Следовательно, точка x = 2 — точка минимума. 

В окрестности точки x = 3 производная функции меняет знак с (+) на (-). Следовательно, точка x = 3 — точка максимума. 

Y_min=y(2)=-28,     Y_max=y(3)=-27

2. Найдем интервалы выпуклости и вогнутости функции.

 Вторая производная    f»(x) = -12x+30 
Находим корни уравнения. Для этого полученную функцию приравняем к нулю. 
-12x+30 = 0 
Откуда точки перегиба: 
x₁ = 5/2    y(5/2)=-27,5

(-∞ ;5/2)	(5/2; +∞)
f»(x) > 0	f»(x)
функция вогнута	функция выпукла
6) Асимптоты кривой.   y = 15x2-2x3-36x  Уравнения наклонных асимптот обычно ищут в виде                                          y = kx + b. Находим коэффициент k:  Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.

Пример 6:

Методами дифференциального исчисления исследовать функцию y = f(x). Построить график этой функции, используя результаты исследования.

Решение от преподавателя:

1) Область определения функции. Точки разрыва функции. 

Все действительные числа кроме х = 2
2) Четность или нечетность функции. 

Функция общего вида 
3) Периодичность функции. 
4) Точки пересечения кривой с осями координат. 
Пересечение с осью 0Y 
x=0, y=0 
Пересечение с осью 0X 
y=0 

x = 0, x = 0 
5) Исследование на экстремум. 2)/(x-2) 
Найдем точки разрыва функции. 
x₁ = 2 
1. Находим интервалы возрастания и убывания. Первая производная. 

или 

Находим нули функции. Для этого приравниваем производную к нулю 
-2x²+8x-6 = 0 
Откуда: 
x₁ = 1 
x₂ = 3 

(-∞ ;1)	(1; 2)	(2; 3)	(3; +∞)
f'(x)	f'(x) > 0	f'(x) > 0	f'(x)
функция убывает	функция возрастает	функция возрастает	функция убывает

В окрестности точки x = 1 производная функции меняет знак с (-) на (+).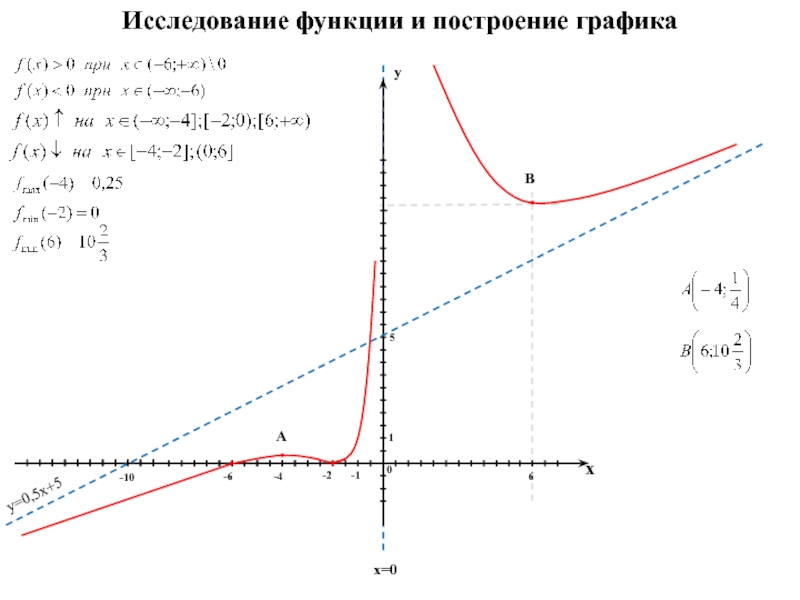 Следовательно, точка x = 1 — точка минимума. В окрестности точки x = 3 производная функции меняет знак с (+) на (-). Следовательно, точка x = 3 — точка максимума. 
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная. 

или 

Находим корни уравнения. Для этого полученную функцию приравняем к нулю. 

Для данного уравнения корней нет. 

(-∞ ;2)	(2; +∞)
f»(x) > 0	f»(x)
функция вогнута	функция выпукла

6) Асимптоты кривой. 

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: 

Находим коэффициент k: 


Находим коэффициент b: 


Получаем уравнение наклонной асимптоты: 
y = -2x-1 
Найдем вертикальные асимптоты. Для этого определим точки разрыва: 
x₁ = 2 
Находим переделы в точке x=2 


x₁ = 2 — точка разрыва II рода и является вертикальной асимптотой. 

Пример 7:

Исследовать функцию и построить ее график.

Решение от преподавателя:

 

Пример 8:

Исследовать функцию и построить её схематический график.

Решение от преподавателя:

Пример 9:

Исследовать заданную функцию и начертить ее график.

Решение от преподавателя:

Пример 10:

Провести полное исследование функции и построить график.

Решение от преподавателя:

1) Область определения функции.  
2) Четность или нечетность функции. 

y(-x) = -y(x), нечетная функция 
3) Точки пересечения кривой с осями координат. 
Пересечение с осью 0Y 
Нет пересечений. 
Пересечение с осью 0X 
y=0 

4) Исследование на экстремум.  
1. Находим интервалы возрастания и убывания. Первая производная. 

Находим нули функции. Для этого приравниваем производную к нулю 
x²+3 = 0 
Для данного уравнения корней нет. 

(-∞ ;0)	(0; +∞)
f'(x) > 0	f'(x) > 0
функция возрастает	функция возрастает

2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная. 

Находим корни уравнения. Для этого полученную функцию приравняем к нулю. 

Для данного уравнения корней нет. 

(-∞ ;0)	(0; +∞)
f»(x) > 0	f»(x)
функция вогнута	функция выпукла

6) Асимптоты кривой.  

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: 

Находим коэффициент k: 


Находим коэффициент b: 


Получаем уравнение наклонной асимптоты: 
y = x 
Найдем вертикальные асимптоты. Для этого определим точки разрыва: 
x₁ = 0 
Находим переделы в точке x=0 


x₁ = 0 — точка разрыва II рода и является вертикальной асимптотой. 

Пример 11:

Провести полное исследование и построить график функции .

Найти наибольшее и наименьшее значения функции на отрезке .

Решение от преподавателя:

График:

Пример 12:

Провести полное исследование функции

Решение от преподавателя:

Пример 13:

Провести полное исследование и построить график функции .

Решение от преподавателя:

Пример 14:

Исследовать функцию и построить график:

Решение от преподавателя:

 

Пример 15:

Провести полное исследование и построить график функции. Найти наибольшее и наименьшее значения функции на отрезке

 

Решение от преподавателя:

Пример 16:

Исследовать функцию  и построить ее график.

Решение от преподавателя:

Пример 17:

Провести полное исследование и построить график функции.

Решение от преподавателя:

Пример 18:

Исследовать данную функцию и построить график:

Решение от преподавателя:

1) Область определения функции – множество всех действительных чисел: .

2) Чётность и нечётность функции:

Функция не обладает свойствами чётности или нечётности. Следовательно, график функции не будет симметричен ни относительно оси Oy, ни относительно начала координат.

3) Периодичности функции.

Функция непериодическая, так как является многочленом.

4) Непрерывность функции.

На всей области определения функция непрерывна как многочлен.

5) Интервалы монотонности и точки экстремума.

Вычислим производную функции и найдём критические точки.

 Точки  — критические.

Они делят область определения функции на интервалы:

Определим знак производной на каждом из интервалов:

 .

Следовательно, на интервале  функция возрастает;

.

Следовательно, на интервале  функция убывает;

.

Следовательно, на интервале  функция возрастает;

При переходе через точку производная меняет свой знак с плюса на минус. Следовательно, — точка максимума функции. При переходе через точку производная меняет свой знак с минуса  на плюс. Следовательно, — точка минимума функции.

6) Интервалы выпуклости, вогнутости и точки перегиба.

Найдём производную второго порядка от функции

7) Точки пересечения графика с осями координат.

8) График функции. 

Пример 19:

Исследовать функцию и построить график: 

Решение от преподавателя:

Пример 20:

Для данной функции  требуется:

а) найти точки разрыва;

б) найти скачок функции в каждой точке разрыва;

в) сделать чертеж.

Решение от преподавателя:

При х=0

Разрыва нет

При х=2

Разрыв есть

Определяем пределы слева и справа от данной точки

Т. к. оба пределы конечны, но равны между собой, то получили точку разрыва 1-го рода – точку скачка

Скачок функции составляет 8-3=5 единиц

 

Пример 21:

Исследовать функцию и построить график

y = 2x·lnx

Решение от преподавателя:

1. Область определения —  точек разрыва нет.

2. Область значений — .

3. функция общего вида, пересекает оси координат в точке (1, 0).

4. интервалы монотонности:

Корень х=1\е, это минимум. Функция убывает на участке (0, 1\е) и возрастает на остальной области определения.

5. интервалы выпуклости, вогнутости.

Корней нет – нет и точек перегиба.

Вторая производная положительна на всей области определения (x>0) – функция вогнутая.

6. Асимптоты.

Вертикальных –нет.

Поскольку

, горизонтальной асимптоты нет.

Проверим, есть ли наклонная асимптота вида y=kx+b.

Найдем , наклонной также нет.

7. строим график:

 

Пример 22:

Исследовать функцию и построить ее график:

 

Решение от преподавателя:

\

Пример 23:

Исследовать функция  и построить её график.

Решение от преподавателя:

Пример 24:

Исследовать функцию и построить график:

y= 

Решение от преподавателя:

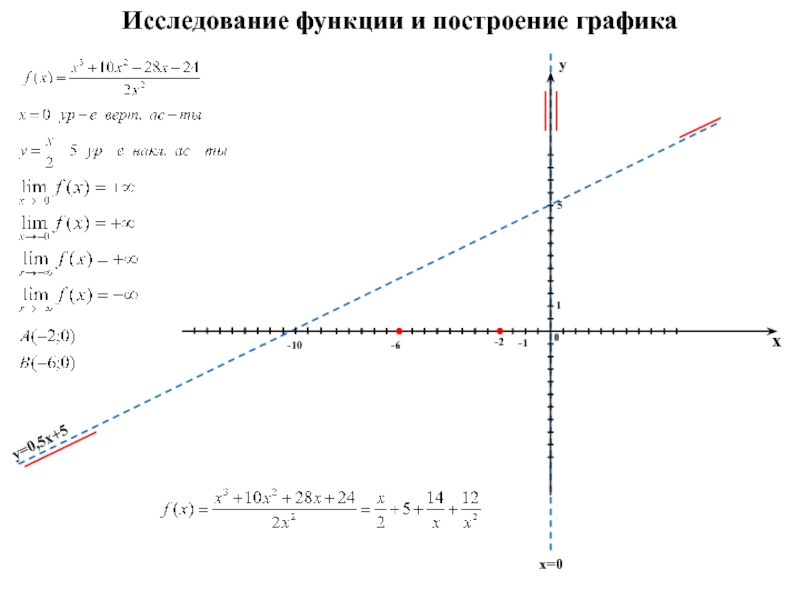
1) Область определения функции   x€(-∞,-4)Ù(-4,+∞)

2) Четность или нечетность функции. 

y(-x)≠y(x),   y(-x)≠ — y(x),  
Функция общего вида 

3) Точки пересечения кривой с осями координат. 
Пересечение с осью 0Y 

Пересечение с осью 0X: y=0 

4) Исследование на экстремум. 
Найдем точки разрыва функции. 
x₁ = -4 
1. Находим интервалы возрастания и убывания. Первая производная. 
 

Находим нули функции. Для этого приравниваем производную к нулю 

x²+8x+15 = 0 

Откуда: 

x₁ = -5 x₂ = -3 

(-∞ ;-5)	(-5; -4)	(-4; -3)	(-3; +∞)
f'(x) > 0	f'(x)	f'(x)	f'(x) > 0
функция возрастает	функция убывает	функция убывает	функция возрастает

В окрестности точки x = -5 производная функции меняет знак с (+) на (-). Следовательно, точка x = -5 — точка максимума.

Y_max = y(-5) = -10

В окрестности точки x = -3 производная функции меняет знак с (-) на (+). Следовательно, точка x = -3 — точка минимума. 

Y_min = y(-3) = -6
2. Найдем интервалы выпуклости и вогнутости функции.

Вторая производная. 
 

Находим корни уравнения. Для этого полученную функцию приравняем к нулю. 

Для данного уравнения корней нет. 

(-∞ ;-4)	(-4; +∞)
f»(x)	f»(x) > 0
функция выпукла	функция вогнута

5) Асимптоты кривой. 

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: 

Находим коэффициент k: 

Находим коэффициент b: 


Получаем уравнение наклонной асимптоты: 
y = x-4 
Найдем вертикальные асимптоты. Для этого определим точки разрыва: 
x₁ = -4 
Находим переделы в точке x=-4 


x₁ = -4 — точка разрыва II рода и является вертикальной асимптотой. 

№ 31.3 ГДЗ Алгебра 10-11 класс Мордкович. Помогите исследовать функцию и построить ее график – Рамблер/класс

№ 31.3 ГДЗ Алгебра 10-11 класс Мордкович. Помогите исследовать функцию и построить ее график – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Исследуйте функцию и постройте ее график:
а) у = 3х² — 4х + 5;
б) у = 3 + 2х — х²;
в) у = 7 — х — 2х²;
г) у = 5х² — 15х — 4.

 

ответы

Держи все решения:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

9 класс

похожие вопросы 5

Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра

10. При каких значениях р уравнение  -х 2 + 6х — 2 = р:
а)    не имеет корней;
б)    имеет один корень; (Подробнее…)

ГДЗМордкович А.Г.Алгебра8 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

ГДЗ Тема 21 Физика 7-9 класс А. В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Какой был проходной балл в вузы в 2017 году?

Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)

Поступление11 классЕГЭНовости

исследовать

исследовать

Роланд Крассер

14.01.2023

Пакет Explore упрощает исследовательский анализ данных (EDA). Получать более быстрое понимание с меньшим количеством кода!

Пакет можно использовать тремя способами:

• Интерактивное исследование данных

  (одновариантный, бивариат, мультивариат)

• Создание автоматического отчета с одной строкой код. Цель может быть бинарной, категориальной или числовой.

• Исследование вручную с помощью легко запоминающегося набора аккуратных функций. Вводит четыре основных глагола. explore() для графического исследования переменной или таблицы, описать() для описания переменной или таблицы, объясните_дерево() для создания простого дерева решений, которое объясняет цель. report() для создания автоматизированного отчет обо всех переменных.

исследовать пакет на Github: https://github.com/rolkra/explore

Поскольку функции исследования хорошо вписываются в tidyverse, мы загружаем dplyr-пакет.

библиотека

 (dplyr)
библиотека (исследовать) 

Интерактивное исследование данных

Исследуйте свой набор данных (в данном случае набор данных радужной оболочки глаза) в одной строке код:

 explore(iris) 

Запускается блестящее приложение, вы можете проверить отдельные переменные, исследовать их отношение к цели (бинарное / категориальное / числовое), расти дерево решений или создать полностью автоматизированный отчет обо всех переменных с несколько «щелчков мыши».

Вы можете выбрать каждую переменную, содержащуюся в качестве цели, которая является двоичной. (0/1, FALSE/TRUE или «нет»/«да»), категориальный или числовой.

Переменные отчета

Создайте отчет в формате HTML обо всех переменных с помощью одной строки кода:

 # отчет обо всех переменных
iris %>% report(output_file = "report.html", output_dir = tempdir()) 

Или вы можете просто добавить цель и создать отчет. В этом случае мы используйте бинарную цель, но категориальная или числовая цель будет работать как хорошо.

 # отчет обо всех переменных и их связи с бинарной целью
iris$is_versicolor <- ifelse(iris$Species == "разноцветный", 1, 0)
ирис %>%
  отчет (выходной_файл = "отчет.html",
         выходной_каталог = временный_каталог(),
         target = is_versicolor) 

Если вы используете бинарную цель, параметр split = FALSE (или targetpct = TRUE) даст вам другое представление на данные.

Вырастить дерево решений

Вырастите дерево решений с помощью одной строки кода:

 iris %>%объяснение_дерева(цель = виды) 

Вы также можете вырастить дерево решений с помощью бинарной цели.

 iris$is_versicolor <- ifelse(iris$Species == "versicolor", 1, 0)
ирис %>
 % select(-Species) %>%объяснение_дерева(цель = is_versicolor) 

Или с использованием числового целевого значения. Синтаксис остается прежним.

 ирис %>% объясните_дерево (цель = чашелистик.Длина) 

Вы можете управлять ростом дерева с помощью параметров maxdepth , minsplit и cp .

Исследуйте набор данных

Исследуйте свою таблицу с помощью одной строки кода, чтобы узнать, какой тип содержащиеся в нем переменные.

 iris %>% explore_tbl() 

Вы также можете использовать описать_tbl(), если вам нужны только основные факты без визуализации.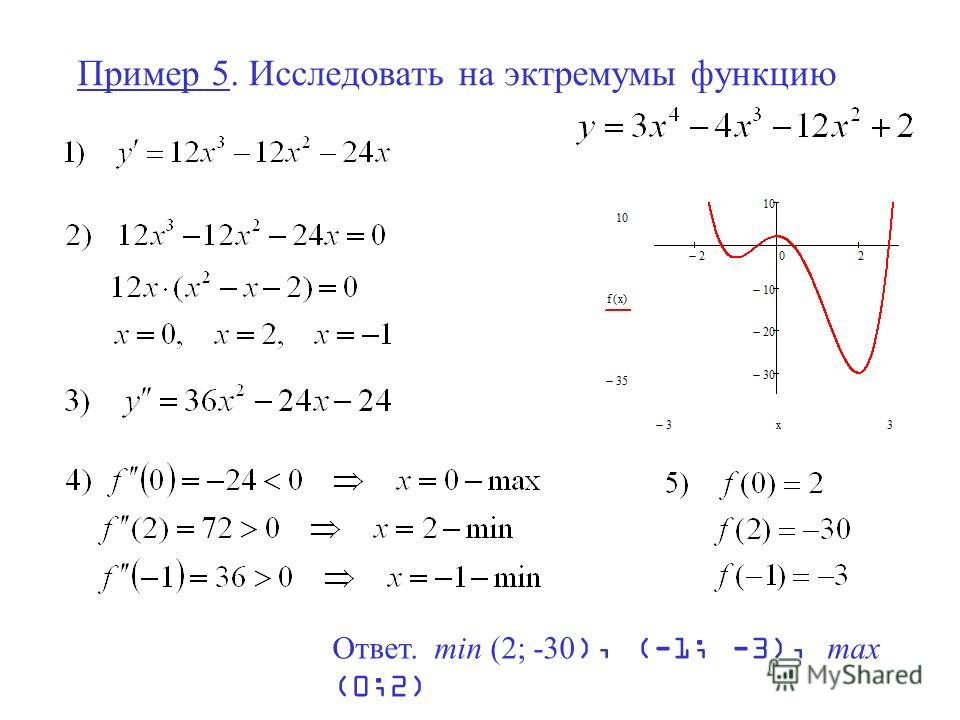

 ирис %>% description_tbl()
#> 150 наблюдений с 6 переменными
#> 0 наблюдений, содержащих пропущенные значения (NA)
#> 0 переменных, содержащих пропущенные значения (NA)
#> 0 переменных без дисперсии 

Исследование переменных

Исследование переменной с помощью одной строки кода. Вам не нужно заботиться о том, переменная является числовой или категориальной.

 Ирис %>% исследовать(Виды) 

 Ирис %>% исследовать(Длина чашелистиков) 

Исследуйте переменные с целью

Исследуйте переменную и ее связь с бинарной целью с помощью одного строка кода. Вам не нужно заботиться о том, является ли переменная числовой или категоричный.

 радужная оболочка %>% explore(Sepal.Length, target = is_versicolor) 

Использование split = FALSE изменит график на %target:

 радужная оболочка %>% explore(Sepal.Length, target = is_versicolor, split = FALSE) 

Цель может иметь более двух уровней:

 радужная оболочка %>% explore(Sepal. Length, target = Species) 

Или цель может быть даже числовой:

 радужная оболочка %>
  % исследовать (Длина чашелистика, цель = Длина лепестка) 

Исследуйте несколько переменных

 диафрагма %>%
  select(Sepal.Length, Sepal.Width) %>%
  explore_all() 

 ирис %>%
  select(Sepal.Length, Sepal.Width, is_versicolor) %>%
  explore_all(target = is_versicolor) 

 радужная оболочка %>%
  select(Sepal.Length, Sepal.Width, is_versicolor) %>%
  explore_all(target = is_versicolor, split = FALSE) 

 радужная оболочка %>%
  select(Sepal.Length, Sepal.Width, Species) %>%
  explore_all (цель = виды) 

 ирис %>%
  select(Sepal.Length, Sepal.Width, Petal.Length) %>%
  explore_all(target = Petal.Length) 

 data(iris) 

Чтобы использовать большое количество переменных с explore_all() в RMarkdown-File, необходимо установить осмысленную рис. ширину и рис.высота в утиль. Функция total_fig_height() помогает автоматически установить fig.height:

fig.height=total_fig_height(радужная оболочка)

 диафрагма %>%
  исследовать_все() 

Если вы используете цель: fig.height=total_fig_height(iris, var_name_target = "Species")

 iris %>% explore_all(target = Species) 

Вы можете управлять total_fig_height() параметрами ncols (количество столбцы участков) и размер (высота 1 участка)

Исследование корреляции между двумя переменными

Исследование корреляции между двумя переменными с помощью одной строки кода:

 радужная оболочка %>% explore(Sepal.Length, Petal.Length) 

Вы также можете добавить цель:

 Радужная оболочка %>% исследовать (Длина чашелистиков, Длина лепестков, цель = Виды) 

Другие параметры

Если вы используете Исследовать для изучения переменной и хотите установить более низкое и верхние пределы значений, вы можете использовать min_val

и max_val параметров. Все значения ниже min_val будут установлены на мин_знач. Все значения выше max_val будут установлены на max_val.

 диафрагма %>% исследовать (Sepal.Length, min_val = 4,5, max_val = 7) 

исследовать по умолчанию использует автомасштабирование. Чтобы деактивировать его, используйте параметр auto_scale = FALSE

 диафрагма %>% explore(Sepal.Length, auto_scale = FALSE) 

Описание данных

Опишите свои данные одной строкой кода:

 радужная оболочка %>% описать()
#> # Буквы: 5 × 8
#> тип переменной na na_pct уникальный минимум средний максимум
#>        
#> 1 Чашелистик.Длина dbl 0 0 35 4,3 5,84 7,9#> 2 Сепал.Ширина dbl 0 0 23 2 3.06 4.4
#> 3 Лепесток.Длина dbl 0 0 43 1 3,76 6,9
#> 4 Лепесток.Ширина dbl 0 0 22 0.1 1.2 2.5
#>  5 Species fct 0 0 3 NA NA NA 

Результатом является кадр данных, где каждая строка является переменной вашего данные. Вы можете использовать фильтр от dplyr для быстрой проверки:

 # показать все переменные, которые содержат менее 5 уникальных значений
ирис %>% описать() %>% фильтр(уникальный < 5)
#> # Блокнот: 1 × 8
#> тип переменной na na_pct уникальный минимум средний максимум
#>        
#> 1 Виды fct 0 0 3 NA NA NA 

 # показать все переменные, содержащие значения NA
ирис %>% описать() %>% фильтр(нет > 0)
#> # Буквы: 0 × 8
#> # … с 8 переменными: переменная , тип , na , na_pct ,
#> # unique , min , mean , max  

Вы также можете использовать описать для описания переменных. Ты не нужно заботиться о том, является ли переменная числовой или категориальной. Выход это текст.

 # описать числовую переменную
ирис %>% описать (виды)
#> переменная = виды
#> тип = фактор
#> нет данных = 0 из 150 (0%)
#> уникальный = 3
#> сетоса = 50 (33,3%)
#> лишай = 50 (33,3%)
#> virginica = 50 (33,3%) 

 # описать категориальную переменную
ирис %>% описать (Sepal. Length)
#> переменная = Sepal.Length
#> тип = двойной
#> нет данных = 0 из 150 (0%)
#> уникальный = 35
#> мин|макс = 4,3 | 7,9#> q05|q95 = 4,6 | 7,255
#> q25|q75 = 5,1 | 6.4
#> медиана = 5,8
#> среднее значение = 5,843333 

Создать данные

Используйте один из подготовленных наборов данных для изучения:

• create_data_app()
• create_data_buy()
• Create_data_churn()
• create_data_person()
• create_data_unfair()
• create_data_random()

 # создать набор данных и описать его
данные <- create_data_app(obs = 100)
описать (данные)
#> # Таблица: 7 × 8
#> тип переменной na na_pct уникальный минимум средний максимум
#>        
#> 1 os chr 0 0 3 NA NA NA
#> 2 бесплатно int 0 0 2 0 0.62 1
#> 3 загрузки int 0 0 99 255 6704. 18386
#> 4 рейтинг dbl 0 0 5 1 3,44 5
#> 5 тип chr 0 0 10 NA NA NA
#> 6 обновлений dbl 0 0 72 1 45,6 99
#> 7 screen_sizes dbl 0 0 5 1 2. 61 5 

 # создать набор данных и описать его
данные <- create_data_random (obs = 100, vars = 5)
описать (данные)
#> # Таблица: 7 × 8
#> тип переменной na na_pct уникальный минимум средний максимум
#>        
#> 1 идентификатор int 0 0 100 1 50,5 100
#> 2 target_ind int 0 0 2 0 0,53 1
#> 3 var_1 int 0 0 61 1 51.4 99
#> 4 var_2 целое 0 0 63 1 48,6 98
#> 5 var_3 int 0 0 62 1 49,2 100
#> 6 var_4 int 0 0 68 0 48,6 100
#> 7 var_5 int 0 0 64 2 51.9 99 

Вы можете создать свой собственный набор случайных данных, используя create_data_empty() и add_var_randm_*() functions:

 # создать набор данных и описать его
данные <- create_data_empty(obs = 1000) %>%
  add_var_random_01 ("цель") %>%
  add_var_random_dbl("возраст", min_val = 18, max_val = 80) %>%
  add_var_random_cat ("пол",
                     кошка = с ("мужчина", "женщина", "другое"),
                     вероятность = c(0,4, 0,4, 0,2)) %>%
  add_var_random_starsign() %>%
  add_var_random_moon()
описать (данные)
#> # Буквы: 5 × 8
#> тип переменной na na_pct уникальный минимум средний максимум
#>        
#> 1 цель int 0 0 2 0 0. 51 1
#> 2 возраст дбл 0 0 1000 18,1 48,980,0
#> 3 пол chr 0 0 3 NA NA NA
#> 4 random_starsign chr 0 0 12 NA NA NA
#> 5 random_moon chr 0 0 4 NA NA NA 

 data %>% select(random_starsign, random_moon) %>% explore_all() 

Словарь данных

Создать словарь данных набора данных (файл Markdown data_dict.md)

 диафрагма %>% data_dict_md(output_dir = tempdir()) 

Добавить заголовок, подробные описания и изменить имя файла по умолчанию

 описание <- data.frame(
                  переменная = с ("Виды"),
                  description = c("Виды цветка ириса"))
data_dict_md (радужная оболочка,
             title = "набор данных цветов ириса",
             описание = описание,
             output_file = "data_dict_iris.md",
             выходной_каталог = временный_каталог()) 

Базовая очистка данных

Для очистки переменной можно использовать чистая_вар . С одной линией кода вы можете переименовать переменную, заменить NA-значения и установить минимум и максимальное значение.

 ирис %>%
  clean_var(Sepal.Длина,
            мин_знач = 4,5,
            макс_значение = 7,0,
            п = 5,8,
            имя = "sepal_length") %>%
  описывать()
#> # Буквы: 5 × 8
#> тип переменной na na_pct уникальный минимум средний максимум
#>        
#> 1 sepal_length dbl 0 0 26 4,5 5,81 7
#> 2 Сепал.Ширина dbl 0 0 23 2 3.06 4.4
#> 3 Лепесток.Длина dbl 0 0 43 1 3,76 6,9#> 4 Лепесток.Ширина dbl 0 0 22 0.1 1.2 2.5
#> 5 Виды fct 0 0 3 NA NA NA 

Создать блокнот

Создайте шаблон RMarkdown для изучения собственных данных. Установить output_dir (существующий файл может быть перезаписан)

 create_notebook_explore(
  выходной_каталог = временный_каталог(),
  output_file = "notebook-explore.Rmd") 

Четыре полезные функции для изучения данных в Python | Садрак Пьер, доктор философии.

Садрак Пьер, доктор философии.

·

Подписаться

Опубликовано в

·

5 мин чтения

·

9 января 2020 г.

В процессе исследования data Я часто ловлю себя на том, что повторно определяю подобную логику Python для выполнения простых аналитические задачи. Например, я часто рассчитываю среднее значение и стандартное отклонение числового столбца для определенных категорий данных. Я также часто анализирую частоту категориальных значений в данных. Чтобы сэкономить время, я написал несколько функций, которые позволяют мне выполнять этот тип анализа, не переписывая много кода.

В этом посте я расскажу о четырех полезных функциях, которые я часто использую на этапе исследовательского анализа данных при построении модели. Затем я покажу, как мы можем использовать эти функции для изучения набора данных Wine Reviews . Набор данных можно найти здесь. Папка содержит три файла .csv. Я буду использовать файл под названием «winemag-data_first150k.csv».

Начнем!

1. СЧЕТЧИК

Первая функция, которую я буду обсуждать, позволяет нам посмотреть, как часто категориальные значения появляются в наборе данных. Он принимает в качестве входных данных фрейм данных, имя столбца и лимит. При вызове он выводит словарь категориальных значений и частоту их появления:

 def return_counter(data_frame, column_name, limit): 
 from collections import Counter print(dict(Counter(data_frame[column_name].values).most_common(limit))) 

Давайте напечатаем первые пять строк набора данных:

 import pandas as pd 
 df = pd.read_csv('winemag-data_first150k.csv') 
 print(df.head()) 

Мы видим, что есть несколько категориальных столбцов. Давайте применим нашу функцию к столбцу «страна» и ограничим наши результаты пятью наиболее распространенными странами:

 return_counter(df, 'country', 5) 

Мы видим, что большинство записей о винах соответствуют винам, произведенным в США.

Давайте применим нашу функцию к столбцу «разнообразие»:

 return_counter(df, 'разнообразие', 5) 

Большинство вин — Шардоне и Пино Нуар. Это полезно в качестве быстрого теста, чтобы увидеть, есть ли какой-либо значительный дисбаланс в данных, что часто является важным моментом, когда дело доходит до построения модели.

2. ОБЩАЯ СТАТИСТИКА

Следующая функция представляет собой сводную статистическую функцию (немного похожую на df.describe()). Эта функция принимает фрейм данных, категориальный столбец и числовой столбец. Среднее значение и стандартное отклонение числового столбца для каждой категории хранятся во фрейме данных, а фрейм данных сортируется в порядке убывания в соответствии со средним значением. Это полезно, если вы хотите быстро увидеть, имеют ли определенные категории более высокие или более низкие значения среднего и/или стандартного отклонения для определенного числового столбца.

 def return_statistics(data_frame, categorical_column, numeric_column): 
 mean = [] 
 std = [] 
 field = [] 
 for i in set(list(data_frame[categorical_column].values)): 
 new_data = data_frame[data_frame [categorical_column] == i] 
 field.append(i) 
 mean.append(new_data[numerical_column].mean()) 
 std.append(new_data[numerical_column]. std()) 
 df = pd.DataFrame({ '{}'.format(categorical_column): field, 'mean {}'.format(numerical_column): mean, 'std in {}'.format(numerical_column): std}) 
 df.sort_values('mean {}'.format(numerical_column), inplace = True, восходящий = False) 
 df.dropna(inplace = True) 
 return df 

Мы можем просмотреть сводную статистику для «разновидностей» и 'prices':

 stats = return_statistics(df, 'разновидности', 'цены') 
 print(stats.head()) 

Самая высокая средняя цена сорта Muscadel.

То же самое можно сделать для стран:

 stats = return_statistics(df, ‘countries’, ‘prices’) 
 print(stats.head()) 

В Англии самая высокая средняя цена.

3. КОРОБОЧНАЯ ДИАГРАММА

Следующая функция — это функция блочной диаграммы. Мы используем ящичные диаграммы для визуализации распределения числовых значений на основе минимума, максимума, медианы, первого квартиля и третьего квартиля. Если вы не знакомы с ними, взгляните на статью Понимание Boxplots.

Подобно функции сводной статистики, эта функция берет фрейм данных, столбец категорий и числовой столбец и отображает диаграммы для наиболее распространенных категорий на основе ограничения:

 def get_boxplot_of_categories(data_frame, categorical_column, numeric_column, limit): 
 импортировать seaborn как sns 
 импортировать matplotlib.pyplot как plt 
 keys = [] 
 for i in dict(Counter(df[categorical_column].values).most_common(limit )): 
 keys.append(i) 
 print(keys) 
 df_new = df[df[categorical_column].isin(keys)] 
 sns.boxplot(x = df_new[categorical_column], y = df_new[numerical_column]) 
 

Давайте создадим диаграммы для цен на вино в 5 наиболее часто встречающихся странах:

 get_boxplot_of_categories(df, 'country', 'price', 5) 

Как мы видим, во всех пяти категориях стран цены на вина имеют значительные отклонения. Мы можем сделать то же самое для «разнообразия». Я ограничил значения категорий тремя странами для лучшей визуализации:

 get_boxplot_of_categories(df, 'разнообразие', 'цена', 3) 

4. SCATTERPLOT

Последняя функция — это функция диаграммы рассеяния. Эта функция принимает фрейм данных, категориальный столбец, категориальное значение и два числовых столбца в качестве входных данных и отображает диаграмму рассеяния:

 def get_scatter_plot_category (data_frame, categorical_column, categorical_value, числовой_column_one, числовой_column_two): 
 импортировать matplotlib.pyplot как plt 
 импортировать seaborn как snsdf_new = data_frame[data_frame[categorical_column] == categorical_value] 
 sns.set() 
 plt.scatter( x= df_new[numerical_column_one], y = df_new[numerical_column_two]) 
 plt.xlabel(numerical_column_one) 
 plt.ylabel(numerical_column_two) 

Let's generate a scatterplot of points vs price for wines in the US:

 get_scatter_plot_category(df, 'country', 'US', 'points', 'price') 

Кажется, существует небольшая положительная связь между ценой и начисленными баллами. Я остановлюсь здесь, но, пожалуйста, не стесняйтесь экспериментировать с данными и программировать самостоятельно.