Из диаметра длина окружности: Длина окружности. Площадь круга — урок. Математика, 6 класс.

6 класс. Математика. Длина окружности. Площадь круга — Длина окружности. Площадь круга

Комментарии преподавателя

Рас­смот­рим чер­теж. Перед нами окруж­ность с цен­тром в точке О и от­ре­зок АВ, ко­то­рый со­еди­ня­ет две точки окруж­но­сти и про­хо­дит через ее центр. Мы пом­ним, что  он на­зы­ва­ет­ся диа­метр. Длину окруж­но­сти при­ня­то обо­зна­чать бук­вой С, а длину диа­мет­ра бук­вой d.

 

Чтобы уяс­нить смысл по­ня­тия длина окруж­но­сти, вы­пол­ним мыс­лен­ный экс­пе­ри­мент. Пред­ставь­те себе окруж­ность, из­го­тов­лен­ную из тон­кой про­во­ло­ки. Если раз­ре­зать про­во­ло­ку и вы­пря­мить ее, то длина вы­прям­лен­но­го куска про­во­ло­ки и будет дли­ной окруж­но­сти.

От­но­ше­ние длины окруж­но­сти к ее диа­мет­ру – число по­сто­ян­ное. Этот факт был об­на­ру­жен экс­пе­ри­мен­таль­но. Еще егип­тяне за­ме­ти­ли, если де­лить длину окруж­но­сти на ее диа­метр, то все­гда по­лу­ча­ет­ся одно и то же число. В Древ­нем Егип­те ду­ма­ли, что это число – три, то есть длина окруж­но­сти в три раза боль­ше диа­мет­ра. Затем люди нашли более точ­ное зна­че­ние для этого от­но­ше­ния: или . В этом слу­чае длина окруж­но­сти в  раза боль­ше диа­мет­ра. Позд­нее вы­яс­ни­лось, что   — это до­ста­точ­но точ­ное, но все-та­ки при­бли­зи­тель­ное зна­че­ние. Более того, по­тре­бо­ва­лось вве­сти осо­бое число – число π. Итак, вер­ным яв­ля­ет­ся утвер­жде­ние: «длина окруж­но­сти в π раз боль­ше диа­мет­ра»

Мы знаем, что диа­метр в два раза боль­ше ра­ди­у­са, тогда у нас по­яв­ля­ет­ся фор­му­ла:

Если ра­ди­ус умно­жить на два и на π, то мы по­лу­чим длину окруж­но­сти.

В гру­бом  при­бли­же­нии число π равно трем.

С точ­но­стью до сотых: π = 3,14.

С точ­но­стью до де­ся­ти­ты­сяч­ных: π = 3,1416

Можно за­пи­сать при­бли­жен­ное зна­че­ние числа π с точ­но­стью до мил­ли­он­ных, до мил­ли­ард­ных, но за­пи­сать, чему точно равно число π с по­мо­щью цифр нель­зя! Ока­за­лось, что это число нель­зя вы­ра­зить обык­но­вен­ной дро­бью. По­это­му в фор­му­лах ис­поль­зу­ют букву π, а для прак­ти­че­ских вы­чис­ле­ний при­бли­жен­ное зна­че­ние.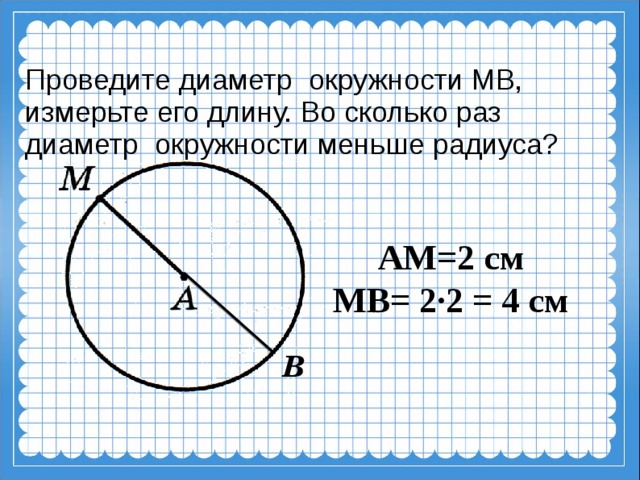

Окруж­ность арены во всех цир­ках мира имеет длину 40,8 м. Най­ди­те диа­метр арены, если  .

За­пи­шем фор­му­лу и под­ста­вим из­вест­ные зна­че­ния букв. Вме­сто π мы под­ста­ви­ли его при­бли­жен­ное зна­че­ние, по­это­му мы за­ме­ни­ли знак равно, ко­то­рый был в фор­му­ле, на знак при­бли­жен­но равно. Вы­пол­нив неслож­ные пре­об­ра­зо­ва­ния, по­лу­чим, что диа­метр  при­бли­зи­тель­но равен   13,6м.   

За­ме­тим, что три – это гру­бое при­бли­же­ние числа π. По­про­бу­ем в рас­смот­рен­ной за­да­че под­ста­вить более точ­ное зна­че­ние. Пусть .

Тогда, чтобы найти диа­метр, нужно раз­де­лить  40,8 на 3,14. Вы­пол­ним де­ле­ние. Можно, на­при­мер, вос­поль­зо­вать­ся каль­ку­ля­то­ром. По­лу­чим, что диа­метр со­став­ля­ет 12,99м.

Видно, что ошиб­ка со­ста­ви­ла 61 см. Это зна­чи­тель­ная ошиб­ка. Если вме­сто числа π под­ста­вить его зна­че­ние с точ­но­стью до де­ся­ти­ты­сяч­ных, то вновь по­лу­чен­ный ре­зуль­тат будет от­ли­чать­ся от преды­ду­ще­го на 7 мм. Раз­ни­ца в 7мм для дан­ной за­да­чи несу­ще­ствен­на.

Вывод: В рас­смот­рен­ной за­да­че оп­ти­маль­ным было зна­че­ние π с точ­но­стью до сотых. Такую точ­ность ис­поль­зу­ют при ре­ше­нии боль­шин­ства прак­ти­че­ских задач.

Для вы­во­да этой фор­му­лы наших ма­те­ма­ти­че­ских зна­ний пока недо­ста­точ­но. По­это­му мы огра­ни­чим­ся неко­то­ры­ми рас­суж­де­ни­я­ми на эту тему, а для ре­ше­ния задач будем ис­поль­зо­вать го­то­вую фор­му­лу. Как по­лу­ча­ют эту фор­му­лу, вы узна­е­те в стар­ших клас­сах. Рас­смот­рим чер­теж.

Перед нами круг с цен­тром в точке О и два квад­ра­та АВСD   и EFKM. Ра­ди­ус круга равен r, по­это­му длина сто­ро­ны боль­ше­го квад­ра­та равна 2r, а его пло­щадь равна . Ма­лень­кий квад­рат сво­и­ми диа­го­на­ля­ми раз­би­ва­ет­ся на че­ты­ре рав­ных пря­мо­уголь­ных тре­уголь­ни­ка. Пло­щадь каж­до­го та­ко­го тре­уголь­ни­ка . Зна­чит, пло­щадь ма­лень­ко­го квад­ра­та . Ясно, что пло­щадь круга боль­ше пло­ща­ди ма­лень­ко­го квад­ра­та и мень­ше пло­ща­ди боль­шо­го квад­ра­та. Можно ска­зать, что пло­щадь круга при­мер­но равна .  На уро­ках ма­те­ма­ти­ки в стар­ших клас­сах будет до­ка­за­но, что .

Диа­метр круга равен 14 см. най­ди­те его пло­щадь, если .

Сна­ча­ла най­дем ра­ди­ус круга. Для этого раз­де­лим диа­метр по­по­лам. По­лу­чим, что ра­ди­ус равен 7см. Под­ста­вим в фор­му­лу вме­сто букв их зна­че­ния. Со­кра­тим по­лу­чен­ную дробь на 7. Итак, пло­щадь круга при­мер­но равна 154  .

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/otnosheniya-i-proporcii/dlina-okruzhnosti-ploschad-kruga?seconds=0&chapter_id=341

источник видео — http://www.youtube.com/watch?v=S5oVau-eyrs

источник видео — http://www.youtube.com/watch?v=XtRa6BudCTo

источник видео — http://www.youtube.com/watch?v=r7Zsq89ClDI

источник теста — http://testedu.ru/test/matematika/6-klass/masshtab-dlina-okruzhnosti-i-ploshhad-kruga.html

источник презентации — http://ppt4web.ru/matematika/dlina-okruzhnosti-i-ploshhad-kruga0. html

Тема урока: «Длина окружности»

• Ильина Наталия Кирилловна, учитель математики

Разделы: Математика, Конкурс «Презентация к уроку»

---

Презентация к уроку

Загрузить презентацию (68 кБ)

---

Учебно-методическое обеспечение: Н.Я. Виленкин, В.И. Жохов и др. Математика-6, «Мнемозина» 2007.

Цели урока:

• Выведение формулы длины окружности круга опытным путём, показать применение формул при решении задач;
• Знакомство с числом π, расширение понятия множества чисел;
• Прививать интерес к математике, развивать культуру вычисления, воспитывать аккуратность.

Тип урока: изучения нового материала.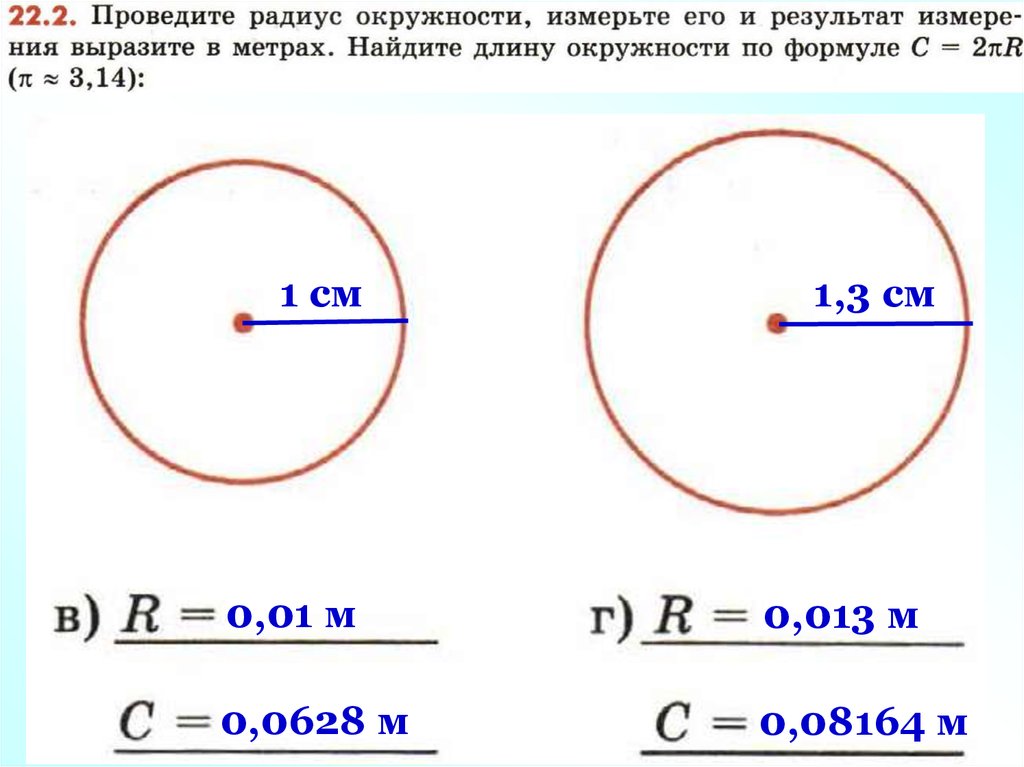

Оборудование: компьютер, проектор, раздаточный материал.

Ход урока

I. Организационный момент

Проверка готовности учащихся к работе.

Сегодня на уроке мы выведем формулы длины окружности, познакомимся с древнейшим числом π, будем учиться видеть красоту чертежей . А вы покажите аккуратность и точность пользования измерительными приборами. Для успешной работы нам с вами нужно повторить некоторые геометрические фигуры и понятия, вспомнить правила округления десятичных дробей, выполнить умножения и деления десятичных дробей.

II. Актуализация опорных знаний

1. Вычислите:

5², r x r, (⅓)², 6² (Слайд №1)

2,1 ×5		0,7 ×15		1,53÷10
0,6×0,3		3,2 ×2,5		0,64÷0,2
0,12×10		9,6÷1,6		2,2÷0,11
3,2 ×2,1		3,5 ×2		8,4÷100

2. Округлите число 3,14159265. Сформулируйте правило для округления десятичных дробей.

(Слайд №2)

а. до десятых;
б. до тысячных;
в. до сотых;
г. до десятых;
д. до целых.

3. а) Какая фигура изображена на рисунке 1? (Окружность — замкнутая линия, все точки которой равноудалены от одной точки.)

б) Как называется точка О? (Центр окружности.) (Слайд №3)

в)Чем является отрезок BD? (

Диаметр.)

г) Что называется диаметром окружности? (Диаметр — это отрезок, соединяющий две точки окружности и проходящий через центр.)

д) Назовите все радиусы, изображённые на рисунке 1.

е) Что называется радиусом окружности? (Радиус окружности — отрезок, соединяющий центр окружности с какой-либо точкой окружности.)

ж) Какая фигура изображена на рисунке 2?

з) Каким отрезком на чертеже изображена хорда?

и) Какой отрезок называется хордой?

к) Каким соотношением взаимосвязаны между собой диаметр и радиус окружности? (D = 2R)

III. Формулировка темы урока

1) Исследовательская работа

Приведите примеры, где в жизни мы встречаемся с формами, дающими представление об окружности? (Длина окружности, которую описывает конец стрелки Кремлёвских курантов, длина земного экватора, длина арены цирка и т.д.) Перед нами встала задача как измерить длину окружности, если сама окружность-кривая линия, а единицы измерения длины-отрезок.

Для проведения работы используются круги красного и жёлтого цвета разных диаметров, сделанные из плотного картона (два на одну парту), работу выполняют в парах. Рассмотрим два способа измерения длины окружности.

Способ 1. В тетради начертите прямую линию. Поставьте круг красного цвета ребром на лист бумаги, где начерчена прямая линия. Отметьте на прямой и на окружности точку их касания А. Затем плавно катите круг по прямой до тех пор, пока отмеченная точка А на окружности не окажется на прямой в точке В. Отрезок АВ тогда будет равен длине окружности.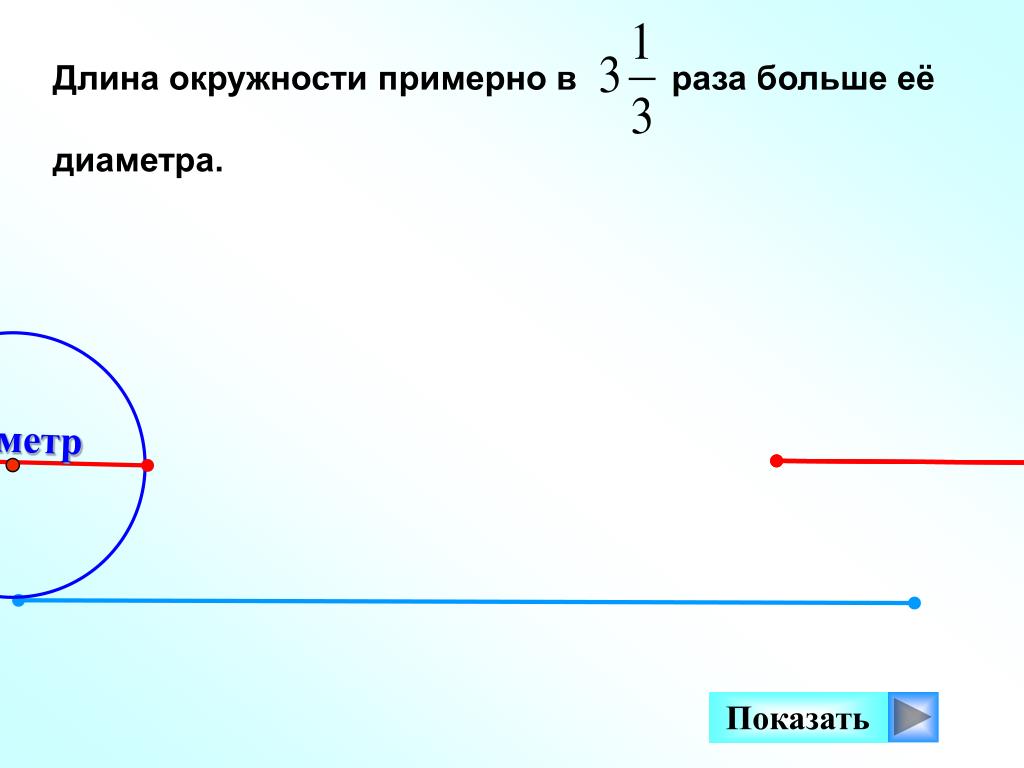 Тем самым мы измерим длину окружности.

(Слайд №4)

• Измерьте длину окружности и запишите в таблицу.
• Измерьте диаметр окружности и результат запишите в таблицу.
• Найдите отношение длины окружности к диаметру, ответ округлите до сотых.

	С	D	C ⁄D
Окружность красного цвета
Окружность жёлтого цвета

Способ 2.

Возьмите второй круг (жёлтого цвета). Оберните круг верёвочкой по окружности так, чтобы конец верёвочки совпал с началом в одной и той же точке окружности. Затем растяните эту верёвочку и измерьте её длину. Длина верёвочки будет равна длине окружности.

1) Измерьте длину окружности и запишите в таблицу.

2) Измерьте диаметр окружности, и результат измерения запишите в таблицу.

3) Найдите отношение длины окружности к диаметру, ответ округлите до сотых.

— Какие результаты вы получили? (Близкие к 3.) А ведь окружности были различными и длину мы находили разными способами.

— Отношение длины окружности к её диаметру-величина постоянная. Она не зависит от диаметра окружности. Для обозначения используют греческую букву π.

(С ⁄D=π)

— Число π = 3,141592653589… — это бесконечная десятичная дробь.

2) Исторические сведения

Многие математики пытались доказать, что отношение С ⁄D есть число постоянное, не зависящее от размеров окружности, и найти более точное значение этого отношения.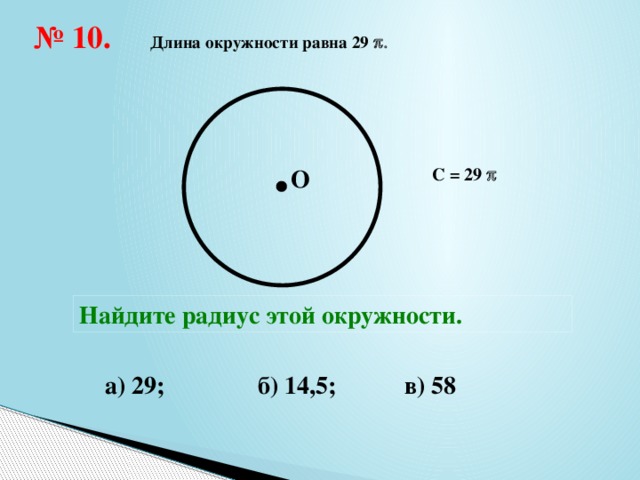

Впервые это удалось сделать древнегреческому математику Архимеду. Архимед установил, что отношение длины окружности к диаметру есть величина постоянная, и нашёл довольно точное значение этого отношения. Это отношение стали обозначать греческой буквой П- первой буквой греческого слова «периферия»-круг. Архимед родился в 287-м году до н. э. в Сиракузах (Сицилия) и на 75-м году своей жизни был убит римским воином при взятии римлянами города Сиракуз в 212 году до н. э. Во время осады Сиракуз римлянами Архимед руководил обороной города, изобрёл много различных механизмов, которые успешно использовались в этой обороне. Так, согласно легенде он с помощью системы зеркал поджигал подходящие к городу морские суда римлян. Но силы римлян превосходили силы горожан, и город был взят. В день взятия города Архимед сидел около своего дома и чертил на земле какие-то фигуры. Погружённый в свои расчёты, решал какую-то задачу, он не заметил, как ворвались в город римские войны, начавшие поголовное избиение жителей. И подбежавшего к нему воина он просил только об одном: «Не трогай моих чертежей». Гибель Архимеда так описывается в одном из стихотворений:

Он был, задумчив и спокоен,
Загадкой круга увлечён…
Над ним невежественный воин
Взмахнул разбойничьим мечом.

Чертил мыслитель с вдохновеньем,
Сдавил лишь сердце тяжкий груз:
«Ужель гореть моим твореньям
Среди развалин Сиракуз?»

И думал Архимед: «Поникну ль
Я головой на смех врагу?»
Рукою твёрдой взял он циркуль,
Провёл последнюю дугу.

Уж пыль клубится над дорогой,
То в рабство путь, в ярмо цепей.
«Убей меня, но лишь не трогай,
О, варвар, этих чертежей!»

Прошли столетий вереницы,
Научный подвиг не забыт.
Никто не знает, кто убийца,
Но знают все, кто был убит!

3) Итак, вернёмся к полученной закономерности С ⁄D = π, тогда С = πD или С = 2πR, где С- длина окружности, R-радиус окружности, D-диаметр окружности.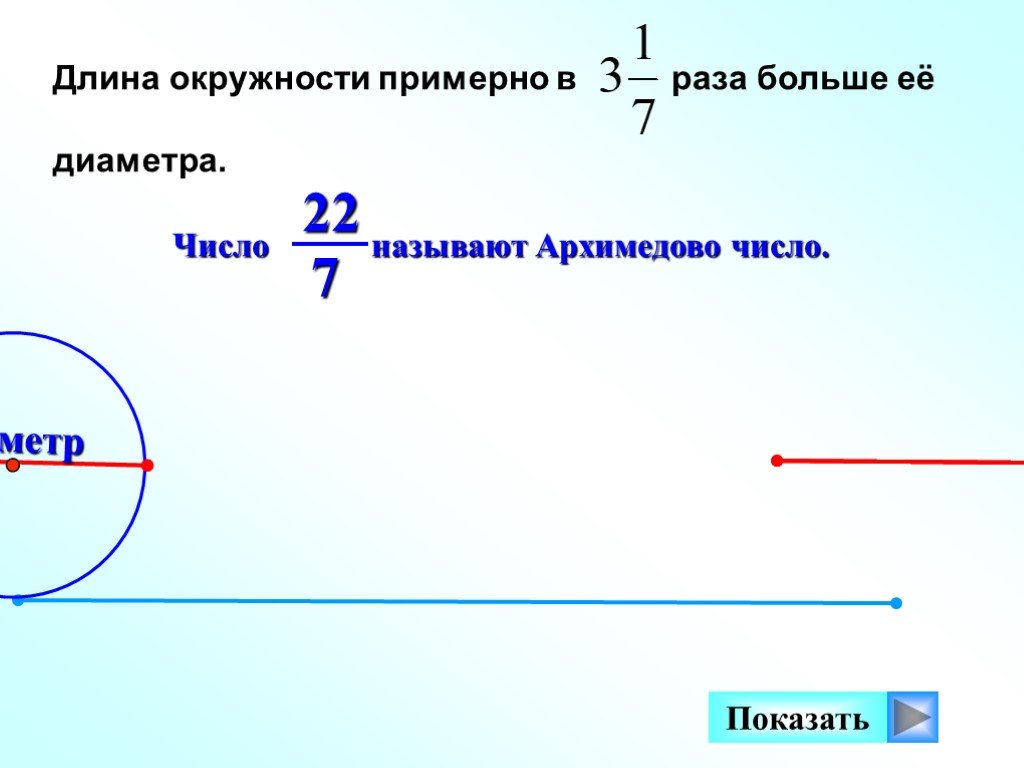

IV. Закрепление изученного материала

№ 841 (1) , 849 (1) , 851

V. Подведение итогов урока

Домашнее задание: § 24, № 841(2), 849(2), 868.

чему равна окружность круга диаметром 1,3м?

Вот ответ на вопросы типа: как найти периметр круга диаметром 1,3 м?

Круговой калькулятор

Радиус (г): или Диаметр (d): или Площадь (А): Единица длины: полегадафутыярдмильмиллиметрсантиметрметрметркилометр

Длина окружности диаметром 1,3 равна 4,084 (*)

Изображение круга = 0,65d = 1,3C = 4,08 С = 2·π·r С = π·d С = √4·π·A π = 3,1415 A = площадь круга C = длина окружности или периметр r = радиус , d = диаметр

Окружность цикла в пересчете на радиуса : Окружность = 2·π·r = 2·3,14·0,65 = 4,09 (*) В пересчете на диаметр : Окружность = π·d = 3,14·1,3 = 4. 08 (*) По площади : Окружность C = √4·π·А = √4·π·1,33 = 4,09 (*) (*) 4,084 м точно или ограничено точностью этого калькулятора (13 знаков после запятой). Примечание: для простоты указанные выше операции были округлены до 2 знаков после запятой, а число π округлено до 3,14. Длина окружности 4,084 метра равна: 0.004084 kilometers (km) 408.4 centimeters (cm) 4084 millimeters (mm) 0.00253768 miles (mi) 4.46632 yards (yd) 13.399 feet (ft) 160.787 inches (in)

Используйте этот калькулятор длины окружности выше, чтобы найти периметр круга, зная его диаметр или другие параметры.

Формула для расчета длины окружности

Вот три способа нахождения длины окружности или периметра круга:

Формула длины окружности через радиус

C = 2·π·r

Формула длины окружности через диаметр

C = π·d

Формула длины окружности через площадь

C = √4·π·A

Вопросы, на которые может ответить этот калькулятор:

• Как найти периметр круга с радиусом 0,65 м?
• Круг имеет диаметр 1,3 м. Какова его окружность?
• Если площадь круга равна 1,327 кв. Каков его периметр?

Examples of Circumference of a Circle Solutions

• Circunference with diameter 9.31 cm
• Circunference with diameter 4.42 meters
• Circunference with radius 2.5 m

• Circunference with diameter 6.86
• Circunference with area 2.5 pi cm
• Окружность диаметром 2,46 дюйма

• Окружность диаметром 6,11 дюйма
• Окружность диаметром 1273 фута
• Окружность радиусом 12 единиц

Отказ от ответственности

Мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, но ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. . Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.

Как вычислить диаметр по окружности?

7

7 ответов

Кэти Гарри ответила

Формула для нахождения длины окружности:
Длина окружности = 2(pi x r)
Где r — радиус.
Теперь число пи всегда принимается равным 3,14. Если у нас есть значение длины окружности, мы можем найти значение радиуса.

Что такое химия

Включите JavaScript

Что такое химия

Предположим, длина окружности равна х. Следовательно, чтобы найти радиус:

C = 2(Pi.r)
x = 2(3.14.r)
x = 6,28 (2r)
x = 12,56r
r = x/12,56

Теперь диаметр равен всегда вдвое больше длины радиуса. Следовательно, любой ответ, который вы получите для радиуса, вам просто нужно умножить на 2, чтобы получить значение для диаметра.
В этом случае:
Диаметр = 2xr
Диаметр = 2(x/12,56)

Давайте сделаем это с реальным числом. Предположим, что окружность равна 20 см, радиус будет:
20 = 2 (Pi.r)
20 = 2 (3,14r)
20 = 6,28r
r = 20/6,28
r = 3,19 см

поблагодарил автора.

брякнул это.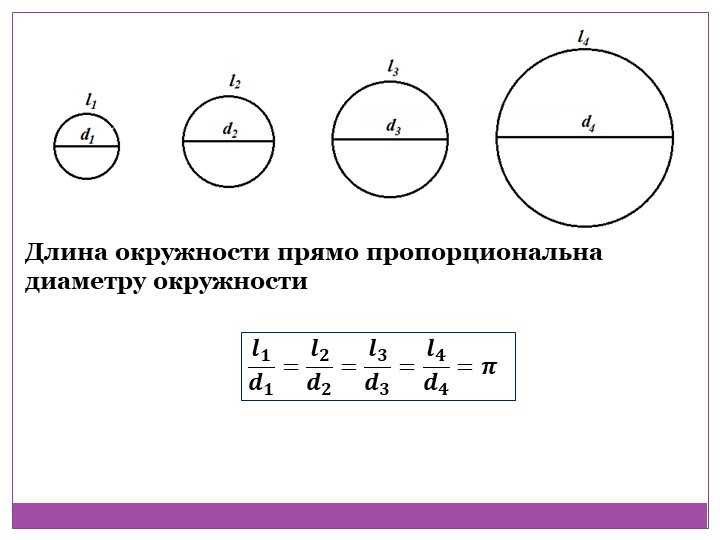

Анонимный ответил

Диаметр x Пи = окружность

диаметр = окружность / Пи

Пи = 3,141592654

7 1/2 / 3,141592654 =

поблагодарил автора.

брякнул это.

Анонимный ответил

У меня размер окружности 28 1/2 дюйма и мне нужно знать такой же диаметр

поблагодарил автора.

брякнул это.

Аноним ответил

Окружность зеркала 185см
найди диаметр зеркала

поблагодарил автора.

брякнул это.

Анонимный пользователь ответил

Диаметр = окружность/пи

пи = 3,14 или 22/7

Окружность 1: c1= 7 1/2 = 15/2 2

D1=c1/pi

= (15/2) / (22/7)
= 15/2 x 7/22
= 105/44
= 2,386 дюйма
 
D2 = c2/pi
= (29/2) / (22/7)
= 29/2 x 7/22
= 203 / 44
= 4,614 дюйма.