КОМПЛЕКСНЫЕ ЧИСЛА
Комплексные числа
Комплексные числа. Комплексным числом z называется выражение вида z=х+iу, где х и у — действительные числа, a i — так называемая мнимая единица, i2=-1. Если x=0, то число 0+iy=iy называется чисто мнимым; если у=0, то число х+i0=х отождествляется с действительным числом х. Число х называется действительной частью комплексного числа z и обозначается х=Re z, а у — мнимой частью z, у = Im z. Два комплексных числа z1=x1+iy1 и z2=х2+iy2 называются равными (z1=z2) тогда и только тогда, когда равны их действительные части и равны их мнимые части: х1=х2, y1=у2. В частности, комплексное число z=х+iy равно нулю тогда и только тогда, когда х=у=0. Два комплексных числа z=х+iy и z=х-iy, отличающиеся лишь знаком мнимой части, называются сопряженными.
Их изображение на комплексной плоскости. Всякое комплексное число z=x+iy можно изобразить точкой М(х;у) плоскости ОXY такой, что х=Rez, у=Imz. И, наоборот, каждую точку М(х;у) координатной плоскости можно рассматривать как образ комплексного числа z=х+iy
Модуль и аргумент комплексного числа. Комплексное число z=х+iy можно задавать с помощью радиус-вектора r=ОМ=(х;у). Длина вектора r, изображающего комплексное число z, называется модулем этого числа и обозначается |z| или r.
Величина угла между положительным направлением действительной оси и вектором r, изображающим комплексное число, называется аргументом этого комплексного числа, обозначается Argz или φ.
Аргумент комплексного числа z=0 не определен. Аргумент комплексного числа z≠0 — величина многозначная и определяется с точностью до слагаемого 2πk
Алгебраическая, тригонометрическая, показательная формы записи комплексного числа. в виде z=х+iy называют алгебраической формой комплексного числа.
запись комплексного числа называется тригонометрической формой.z=rcosφ+irsinφ или z=r(cosφ+isinφ)___( при переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента комплексного числа z, т. е. считать φ=argz.)
комплексное число z=r(cosφ+isiπφ) можно записать в так называемой показательной (или экспоненциальной) форме z=rеiφ, где r=|z| — модуль комплексного числа, а угол φ=Argz=argz+2kp
Операции над комплексными числами. Суммой двух комплексных чисел z1=х1+iy1 и z2=х2+iy2 называется комплексное число, определяемое равенством
z1+z2=(x1+x2)+i(y1+y2). Сложение комплексных чисел обладает переместителъным (коммутативным) и сочетательным (ассоциативным) свойствами:
z1+z2=z2+z1
(z1+z2)+z3=z1+(z2+z3).
Разностью двух комплексных чисел z1 и z2 называется такое комплексное число z, которое, будучи сложенным с z2, дает число zl т. е. z=z1-z2, если z+z2=z1.
Если z1=x1+iy1, z2=x2+iy2, то из этого определения легко получить z:
z=z1-z2=(x1-x2)+i(y1-y2).
модуль разности двух комплексных чисел равен расстоянию d между точками, изображающими эти числа на плоскости
Произведением к омплексных чисел z1 =х1 +iy1 и z2=х2+iy2 называется комплексное число, определяемое равенством
z=z1 z2 =(x1 x2- у1 у2)+i(x1 y2+y1x 2 )
z1=r1(cosφ1+isinφ1) и z2=r2(cosφ2+isinφ2)= z1z2=r1r2(cos(φ1+φ2)+isin(φ1+φ2)).
Деление:
Для тригонометрической формы комплексного числа формула деления имеет вид
Корнем n-й степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ωn=z, т. е., если ωn= z.
Решение уравнений с комплексными числами. Рассмотрим сначала простейшее квадратное уравнение
Z2 = a,
где а — заданное число,
z — неизвестное.
На множестве действительных чисел это уравнение:
1) имеет один корень z = 0, если а = 0;
2) имеет два действительных корня z1,2 = , если а>0;3) не имеет действительных корней, если а<0.
На множестве комплексных чисел это уравнение всегда имеет кореньВОТ ТУТ НЕ УВЕРЕНА!!НУЖНО ДОПИСАТЬ!!!
Формула Муавра zn=(r(cosφ+isinφ))n=rn(cosnφ+isinnφ).
studfiles.net
Изображение комплексных чисел. Модуль и аргумент комплексного числа
Рассмотрим на плоскости декартову прямоугольную систему координат . Каждому комплексному числу можно сопоставить точку с координатами , и наоборот, каждой точке с координатами можно сопоставить комплексное число . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью
Пример.Изобразим на комплексной плоскости числа :
Рис. 9. Изображение комплексных чисел точками плоскости
Однако чаще комплексные числа изображают в виде вектора с началом в точке , а именно, комплексное число изображается радиус-вектором точки с координатами . В этом случае изображение комплексных чисел из предыдущего примера будет таким:
Рис. 10. Изображение комплексных чисел векторами
Отметим, что изображением суммы двух комплексных чисел является вектор, равный сумме векторов, изображающих числа и . Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие (рис. 11).
Рис. 11. Изображение суммы комплексных чисел
Пусть комплексное число изображается радиус-вектором. Тогда длина этого вектора называется модулем числа и обозначается . Из рисунка 12 очевидно, что .
Рис. 12.Модуль и аргумент
Угол, образованный радиус-вектором числа с осью , называется аргументом числа и обозначается . Аргумент числа определяется не однозначно, а с точностью до числа, кратного . Однако, обычно аргумент указывают в диапазоне от до или в диапазоне от до . Кроме того у числа аргумент не определен.
На рис. 9 равен углу . Из того же рисунка очевидно, что .
С помощью этого соотношения можно находить аргумент комплексного числа:
или ,
причем первая формула действует, если изображение числа находится в первой или четвертой четверти, а вторая, если — во второй или третьей. Если , то комплексное число изображается вектором на оси и его аргумент равен или .
Тригонометрическая форма комплексного числа
Пусть . Положим . Из рисунка 9 очевидно, что .
Тогда . Это выражение запишем в виде
.
Пример.Запишите в тригонометрической форме числа .
Решение. Находим модуль, аргумент, а затем выписываем тригонометрическую форму:
.
Для возведения комплексного числа в степень , где — натуральное число применяется формула Муавра
.
Пример.Вычислите , если .
Решение. Находим тригонометрическую форму числа :
, .
По формуле Муавра
.
Переходим к алгебраической форме, вычисляя косинус и синус: .
Ответ. .
cyberpedia.su
4.5. Изображение синусоидальных функций времени векторами и комплексными числами на комплексной плоскости
Расчёт цепей переменного тока облегчается, если изображать синусоидально изменяющиеся токи и напряжения, ЭДС и т. д. векторами или комплексными числами.На рис. 4.6 показана комплексная плоскость, на которой можно изобразить комплексные числа. Комплексное число имеет действительную (вещественную) и мнимую части. По оси абсцисс комплексной плоскости будем откладывать действительную часть комплексного числа, а по оси ординат – мнимую часть. На положительной полуоси действительных значений ставим +1, а на положительной полуоси мнимых значений — + j
Из курса математики известна формула Эйлера
где е – основание натуральных логарифмов. Комплексное число еja изображают на комплексной плоскости вектором, составляющим угол
Действительно . Проекция функцииеja на ось + 1 равна cos a, а на ось + j равна sin a. Если вместо функции еja взять функцию Imеja,
то
На
комплексной плоскости эта функция так
же, как и функция еja, изобразится вектором, направленным под
углом а к оси +1, но величина вектора (модуль)
будет в Im раз больше (рис. 4.7). Угол а может быть любым. Комплексное число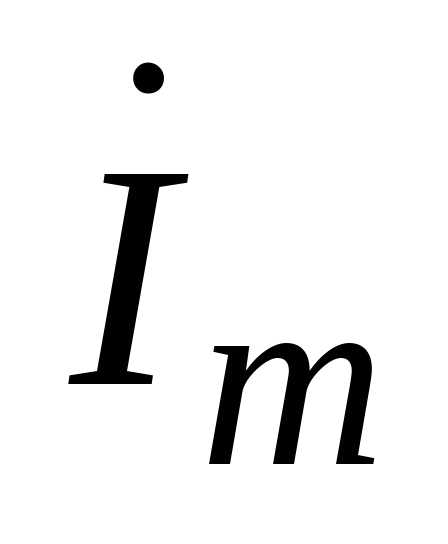 
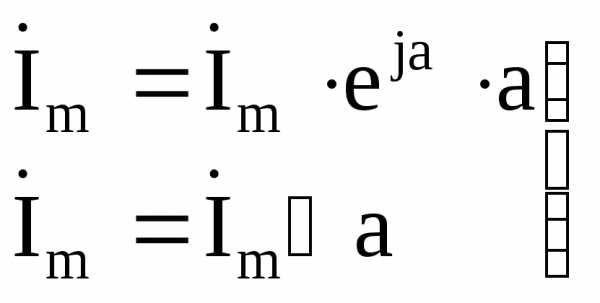–показательная
форма записи;
–тригонометрическая форма записи;
– алгебраическая форма записи,
где 
–проекция вектора Im на действительную ось; 
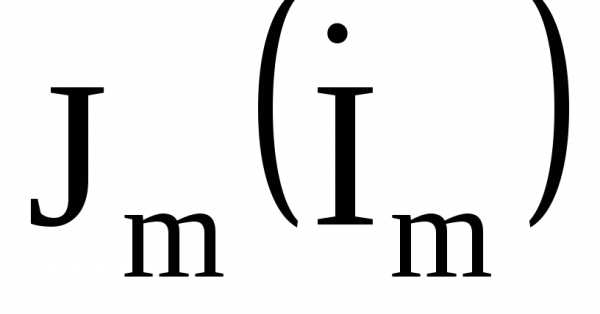– проекция
вектора Im на мнимую ось.
Положим, что а = t + , т. е. угол а изменяется прямо пропорционально времени. Тогда (рис. 4.7)
Слагаемое
представляет собой действительную
часть (Re) выражения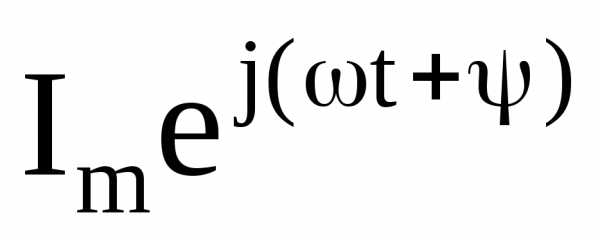 
а
функция
есть коэффициент при мнимой части(Jm) выражения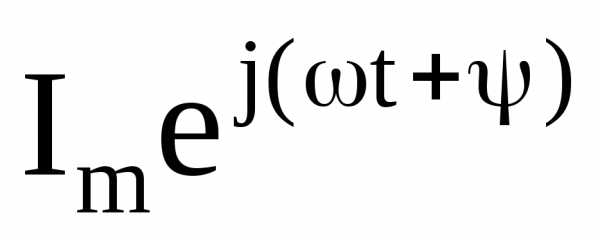 
,
т. е.
Иными
словами току i соответствует комплекс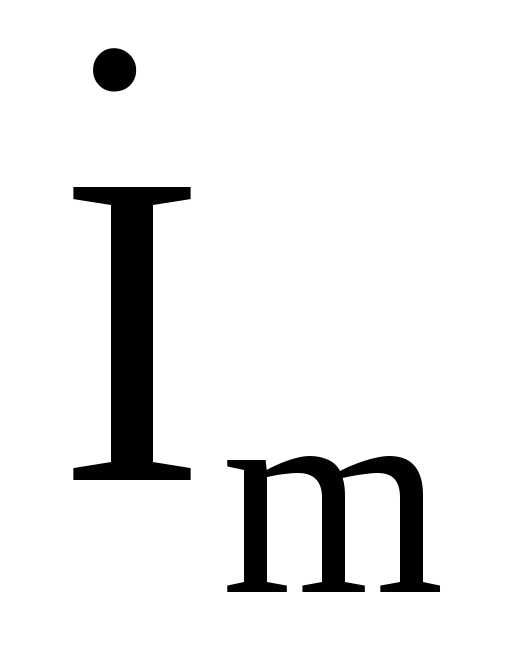 
,
т. е.
Таким
образом синусоидально изменяющийся
ток i(t) можно представить как проекцию
вращающегося со скоростью вектора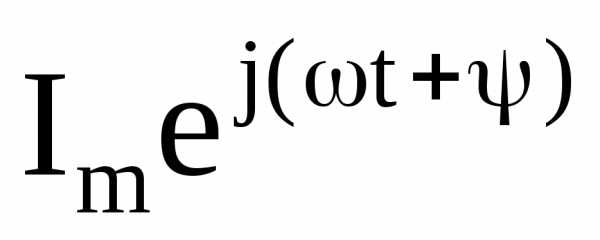 
на ось +j.
Заметим также, что
Две комплексные величины, имеющие равные модули и равные, но противоположные
по знаку аргументы, называют сопряженными и обозначаются в виде комплекса со звездоч
кой (см. рис. 4.8).
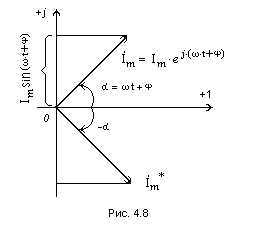
С целью единообразия принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для момента времени t = 0, т. е. t = 0. При этом вектор
равен
где
— комплексная величина; модуль ее равена угол, под которым вектор
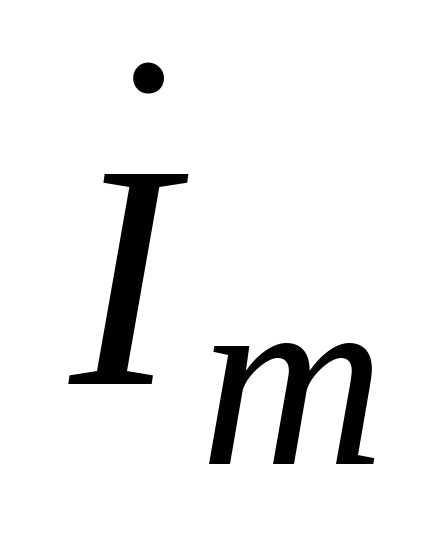(Проведен к оси +1 на комплексной плоскости,
равен начальной фазе; – является аргументом комплексного
числа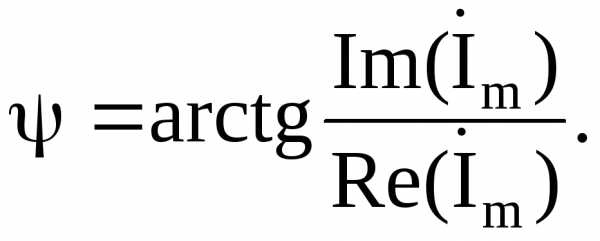
Величину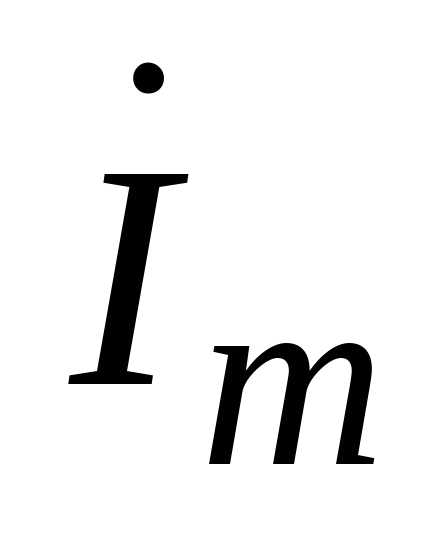 
называют комплексной амплитудой токаi.
Рассмотрим два числовых примера на переход от мгновенного значения тока к комплексной амплитуде и от комплексной амплитуды к мгновенному значению.
Пример 4.1. Дано: ток i = l,0 sin (t + 120°)A. Записать выражение комплексной амплитуды этого тока и построить её на комплексной плоскости.
studfiles.net
Изображение комплексных чисел радиус-векторами координатной плоскости
⇐ ПредыдущаяСтр 5 из 8Следующая ⇒
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x, y).
Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy — мнимой осью.
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z.
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z.
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента, обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ, то мы можем найти вещественную и мнимую части по формулам
| (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y, то модуль этого числа, конечно же, определяется по формуле
| (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Тригонометрическая форма записи комплексного числа
Из формулы (3) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r (cos φ + i sin φ) , | (5) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству
r > 0.
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа.
Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера:
| cos φ + i sin φ = e iφ. | (6) |
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству
r > 0.
Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа.
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
cos φ + i sin φ,
или, что то же самое, числа e iφ, при любом значении φ равен 1.
Вопросы для самоконтроля:
Комплексные числа.
Формы записи и изображение комплексных чисел.
Тема 3.2 Действия над комплексными числами
Сложение, умножение, деление комплексных чисел. Возведение комплексного числа в степень. Извлечение корня n-ой степени из комплексного числа.
Методические указания
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел и записанных в экспоненциальной форме, осуществляется по формулам
Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Рекомендуемые страницы:
lektsia.com