Изобразить на комплексной плоскости неравенство онлайн: Решение неравенств с модулем онлайн · Как пользоваться Контрольная Работа РУ

Теория комплексных чисел. Геометрическая интерпретация комплексного числа. (Тема 3)

Похожие презентации:

Теория комплексных чисел. Показательная форма комплексного числа. (Тема 4)

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

Комплексные числа

1. Теория комплексных чисел

2. Геометрическая интерпретация комплексного числа XVIII-XIX вв

• Г.Вессель, Ж.Арган, К. Гаусс
z=a+bi
у-мнимая ось
М(a,b)
b
0
a
х-действительная ось
К.Гаусс

3. 1. Изобразить на комплексной плоскости следующие числа:

у
z1 3 2 i
2
z5
0
z 2 z1
z 3 z1
z 4 Re z1
z 5 Im z1
-3
3
х
z4
-2

4. Модуль комплексного числа

• Модулем комплексного числа
z=a+bi
называется длина вектора z
:
у-мнимая ось
М(a,b)
b
z a 2 b2
r z
0
a
х-действительная ось

5.

2. Найти модуль комплексного числа:z a 2 b2
z1 2 i
z 2 2 6 5i
z1 2 2 1 4 1 5
2
z2
2 6
2
5 2 24 25 49 7
z3 i
z3 0 2 12 1 1
z 4 4
z4
4 2 0 2
16 4

6. Аргумент комплексного числа

• Аргументом комплексного числа называется угол ,
который образует вектор OM с положительным
направлением оси абсцисс.
=arg z
у-мнимая ось
М(a,b)
b
z
0
х-действительная ось
a

7. Аргумент определяется неоднозначно

z 1 i
у
у
у
1
1
1
2
1
0
1
1
4
х
0
1
х
9
2 2
4
4
3
0
3
1
4
х
2
7
4
Любые два аргумента комплексного числа отличаются друг
от друга слагаемым, кратным 2π.
Для нашего примера: k 2 k , k Z
4

8. 3. Найти аргументы комплексного числа:

z2 1
z1 i
у
arg z1
0
3
2 k , k Z
2
arg z2 0 2 k , k Z
у
х
0
1
х
-1
z3 1 3 i
tan
3
1
у
-1
0
3
х
3
3
3
4
3
arg z3
4
2 k , k Z
3

9.

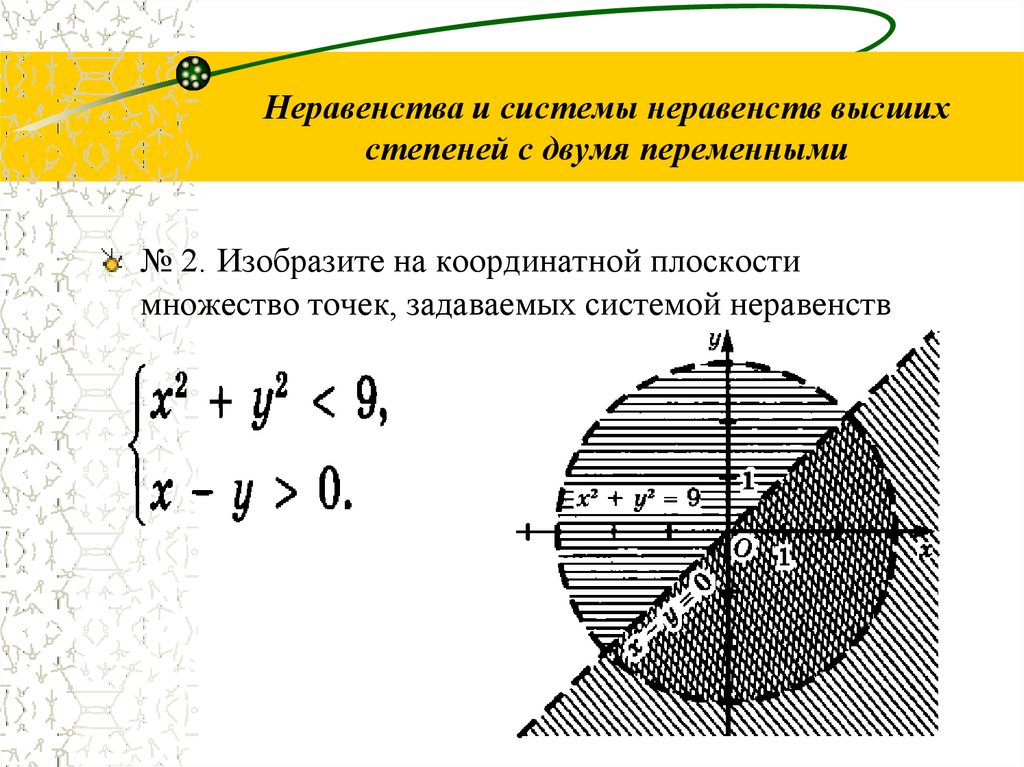4.Найти модуль и аргумент комплексного числа:3 i17
z
18
i
z
tan
3
2
b
a
3 i
3 i
1
12 3 1 4 2
1
3
5
6
6
у
1
6
3
0
х
5
arg z
2 k , k Z
6

10. Тригонометрическая форма комплексного числа

2
2
r z a b
z a bi
у
М(a,b)
b
z
a
cos
r a r cos
b b r sin
sin
r
0
a
х
z a bi r (cos i sin )

11. 5.Записать число в тригонометрической форме:

5.Записать число z 2 2 3 i
тригонометрической форме:
r z
2
2
2 3
2
2 3
-2
0
4 12 16 4
a 2
1
cos
2
r
4
2
3
b 2 3
3
sin
r
4
2
у
в
х
2
2
z 2 2 3 i 4 cos
i sin
3
3

12. 6. Записать число в алгебраической форме:

z 2 cos i sin
6
6
6. Записать число
в алгебраической форме:
z 2 cos i sin 2 cos i sin
6
6
6
6
3 1
2
i 3 i
2
2

13.

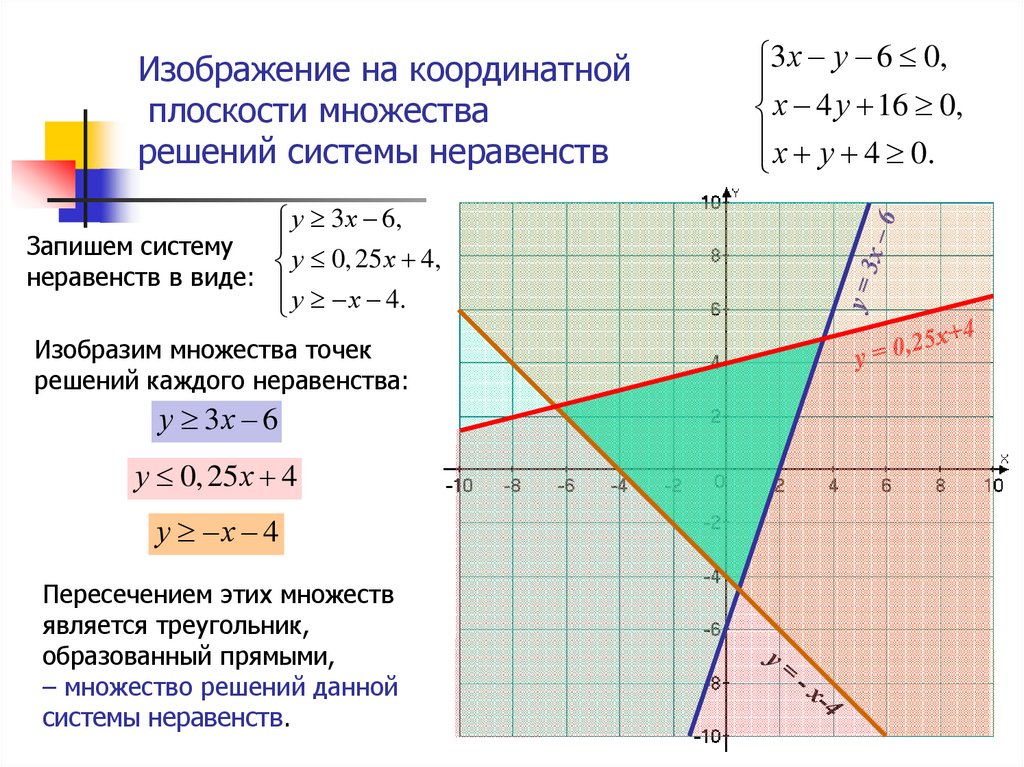7. Записать число в алгебраической форме:25
25
z 2 cos
i sin
3
3
7. Записать число
в алгебраической форме:
25 24
8 2 4
3
3
3
3
3
z 2 cos 2 4 i sin 2 4 2 cos i sin
3
3
3
3
1
3
1 i 3
2 i
2
2

14. Действия над комплексными числами в тригонометрической форме Умножение комплексных чисел.

• Пусть
z1 r1 cos 1 i sin 1
z2 r2 cos 2 i sin 2
z1z 2 r1r2 cos 1 i sin 1 cos 2 i sin 2
r1r2 cos 1 cos 2 i sin 1 cos 2 i sin 2 cos 1 i 2 sin 1 sin 2
r1r2 cos 1 cos 2 sin 1 sin 2 i sin 1 cos 2 cos 1 sin 2
r1r2 cos 1 2 i sin 1 2
z1z2 r1r2 cos 1 2 i sin 1 2

15. 8. Найти произведение комплексных чисел:

z1
7
cos 950 i sin 950
2
u
z2 2 cos 650 i sin 650
7
z1 z 2 2 cos 950 650 i sin 950 650
2
7 cos 950 650 i sin 950 650 7 cos 300 i sin 300
3 1 7 3 7
7
i
i
2
2
2 2
Деление комплексных чисел.
z1 r1 cos 1 i sin 1 r1 cos 1 i sin 1 cos 2 i sin 2
z 2 r2 cos 2 i sin 2 r2 cos 2 i sin 2 cos 2 i sin 2
r1 cos 1 cos 2 i sin 1 cos 2 i sin 2 cos 1 i 2 sin 1 sin 2
2
2
r2
cos 2 i sin 2
r1 cos 1 cos 2 sin 1 sin 2 i sin 1 cos 2 cos 1 sin 2
2
2
cos 2 sin 2
r2
r1
cos 1 2 i sin 1 2
r2
z1 r1
cos 1 2 i sin 1 2
z2 r2

17. 9. Найти частное комплексных чисел:

2
z1 cos1500 i sin 1500
3
u
z 2 2 cos 900 i sin 900
z1 2 1 cos1500 i sin 1500 1
0
0
0
0
cos
150
90
i
sin
150
90
0
0
z 2 3 2 cos 90 i sin 90
3
1
1 1
3 1
3
0
0
cos 60 i sin 60
i
i
3
3 2 2 6 6

18. 10. Записать в тригонометрической форме комплексное число:

cos i sin
3
3
z
i 1
3 i
• Пусть
z1 cos
3
i sin
3
z2 3 i
z3 i 1 1 i
Запишем каждое из чисел в тригонометрической форме.
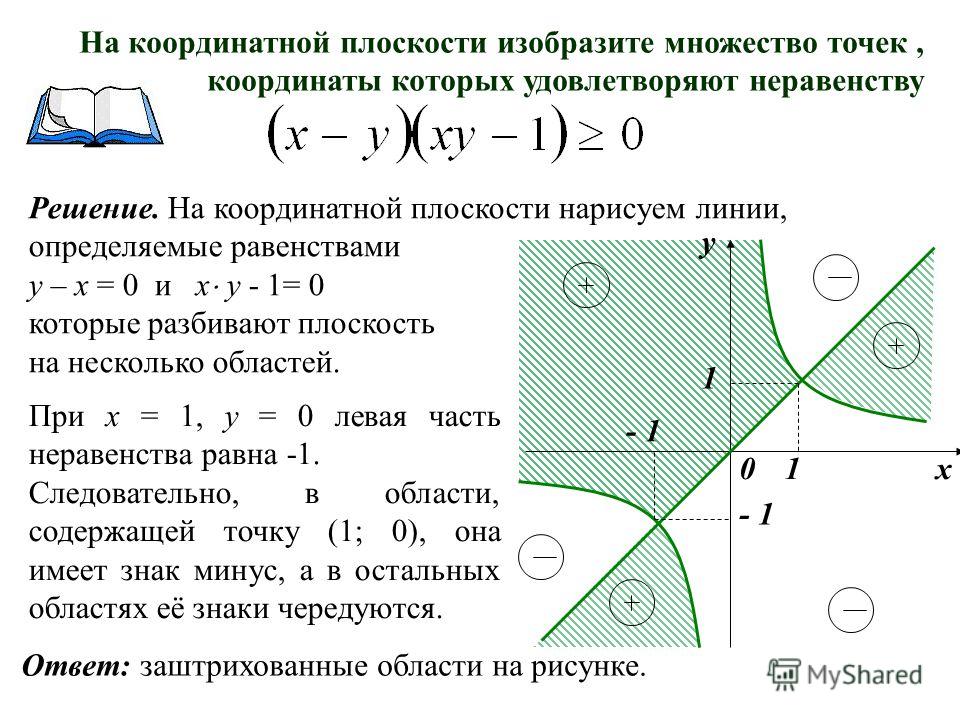
z1 cos i sin cos i sin
3
3
3
3
z2 3 i
r z
3 1
2
2
3 1 2
a
3
cos
r
2
6
b 1
sin
r 2
у
1
0
3
х
z 3 i 2 cos i sin
6
6
z3 1 i
1 2 12
r z
2
a 1
cos
r
3
2
b
1
4
sin
r
2
у
1
-1
0
х
3
3
z 1 i 2 cos
i sin
4
4
cos
i
sin
3
3
z
i 1
3 i cos i sin 2 cos i sin
6
6
3
3
3
3
2 cos
i sin
4
4
11
2 3
3
11
cos
i sin
2 cos
i sin
2 3 6 4
3 6 4
12
12

23. Действия над комплексными числами в тригонометрической форме. Возведение в степень.

z r cos i sin
• Пусть
z r cos n i sin n — формула Муавра
n
n
11. Возвести в четвертую степень комплексное
число:
z 2 cos i sin
3
3
4
4
z 2 cos 4 i sin 4 16 cos
i sin
3
3
3
3
4
4

24.

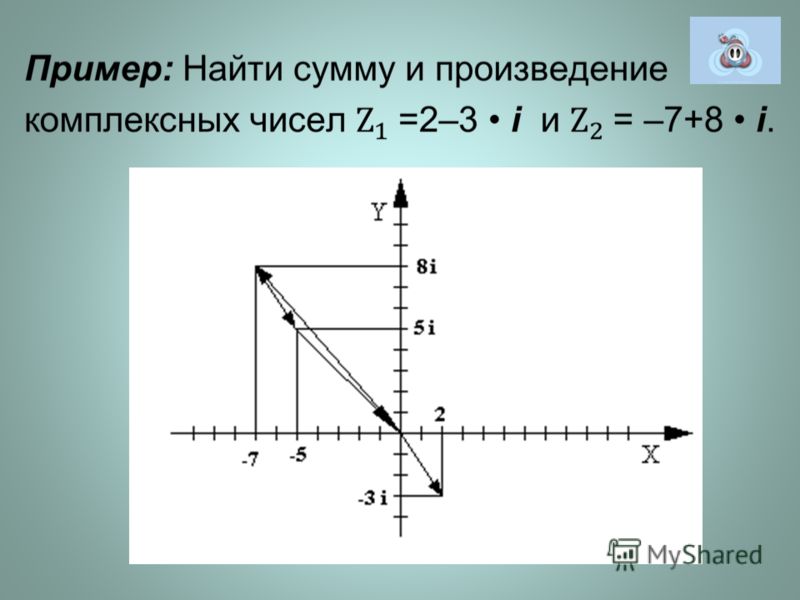12. Возвести в степень комплексное число и записать результат в алгебраической форме:18
2 i
z
2 i 2
Пусть
z1 2i
z2 2 i 2
Запишем каждое из чисел в тригонометрической форме.
z1 2i
r z 02 22 2
у
2
х
z2 2 i 2
r z
у
0
2 2
2
2
2 2 2
3
4
2
2
2
z 2i 2 cos i sin
2
2
0
х
3
3
z 2 i 2 2 cos
i sin
4
4

26. Разделим одно число на другое в тригонометрической форме:

2 cos i sin
z1
2i
2
2
3
3
cos i sin
3
3
z2 2 i 2
2 4
2 4
2 cos
i sin
4
4
cos i sin
4
4
18
А теперь возведём в степень:
18
2 i
z
2 i 2
cos i sin cos 18 i sin 18
4
4
4
4
9
9
cos
i sin
2
2

27. Теперь можно результат записать в алгебраической форме:

Теперь
можно
результат
алгебраической форме:
записать
в
9
9
9
9
z cos
i sin
i sin
cos
2
2
2
2
9 8
4 2 2
2
2
2
2
2
cos 2 2 i sin 2 2 cos i sin
2
2
2
2
0 i

28.

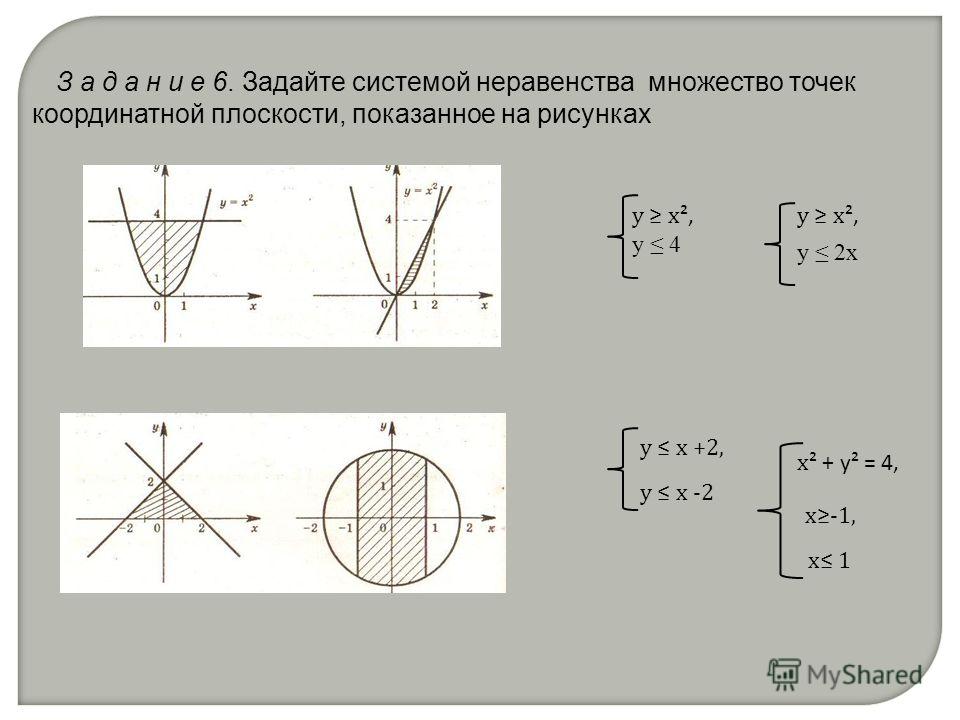Действия над комплексными числами в тригонометрической форме. Извлечение корня.• Пусть
z r cos i sin
Корнем n-ой степени из числа z (n∈N, n≥2) называется
такое комплексное число u, для которого справедливо
n
u
z
равенство
Корень n-ой степени из комплексного числа z имеет ровно n
значений, которые находятся по формуле:
n
2 k
2 k
z n r (cos i sin ) n r cos
i sin
, k 0,1,2,…, n 1
n
n

29. 13. Найти все значения корня:

6
1
z 1
Пусть
Запишем данное число в тригонометрической форме:
у
r z 12 02 1
0
1
0
х
z 1 cos 0 i sin 0
6
0 2 k
0 2 k
k
k
1 cos 0 i sin 0 cos
i sin
cos i sin
6
6
3
3
6
k 0,1,2,3,4,5
k 0 : u0 cos 0 i sin 0 1
1
3
k 1 : u1 cos i sin
i
3
3 2 2
2
2
1
3
k 2 : u2 cos
i sin
i
3
3
2 2
k 3 : u3 cos i sin 1
4
4
1
3
k 4 : u4 cos
i sin
i
3
3
2 2
5
5 1
3
k 5 : u5 cos
i sin
i
3
3 2 2
у
u2
u1
u3
u0
u4
u5
х
z 1 i 3 0
5
14. Решить уравнение:
z5 1 i 3 z 5 1 i 3
Пусть
z 1 i 3
Запишем данное число в тригонометрической форме:
r z 1
2
у
3 1 2
a
r
b
sin
r
cos
3
0
3
2
1
х
z 1 i 3 2 cos i sin
3
3
1
2
3
3
2
2
k
2
k
5
1 i 3 5 2 cos i sin 5 2 cos 3
i sin 3
3
3
5
5
2 k
2 k
2 cos
i sin
, k 0,1,2,3,4
5
5
15
15
5
2 k
2 k
z 2 cos
i sin
, k 0,1,2,3,4
5
5
15
15
5
k 0 : u0 2 cos i sin
15
15
7
7
5
k 1 : u1 2 cos
i sin
15
15
5
13
13
k 2 : u2 2 cos
i sin
15
15
19
19
k 3 : u3 5 2 cos
i sin
15
15
у
u1
u2
5
25
25
k 4 : u4 5 2 cos
i sin
15
15
u0
u3
u4
х
15. Сделать действия в тригонометрической
форме и ответ записать в алгебраической форме:
7
7
1) 2 cos
i sin
6
6
11
11
2) 3 cos
i sin
3
3
3
Ответ.
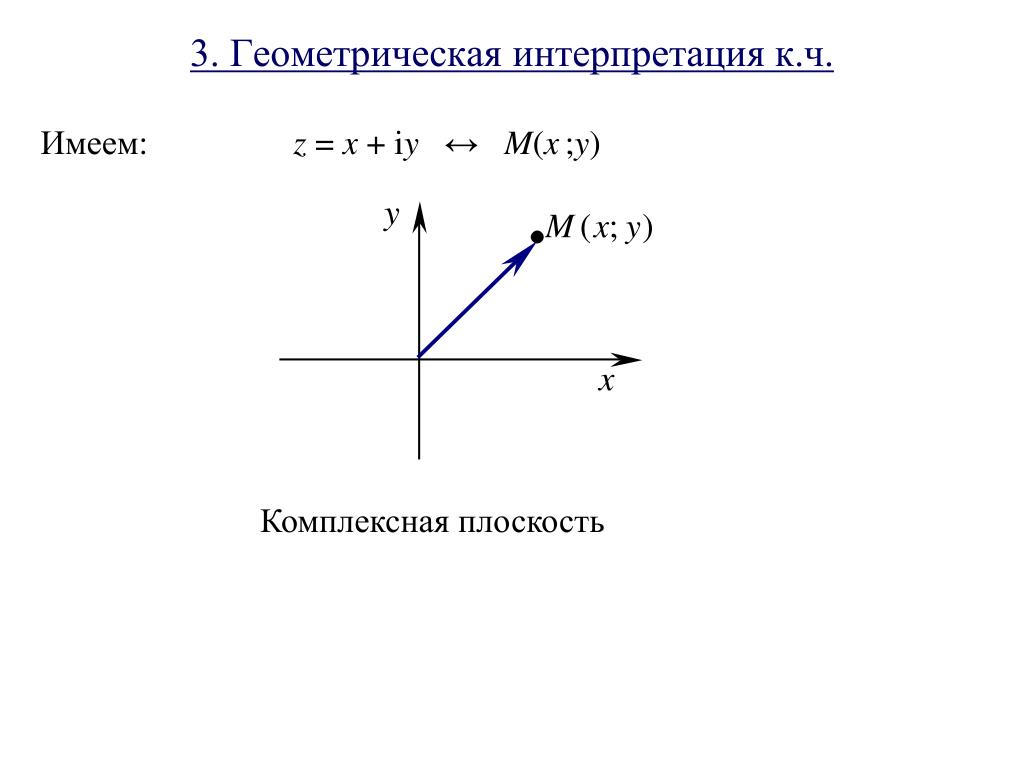
2
0 8i
Ответ. 9 9 3 i
2
2
16. Сделать действия над комплексными числами
и ответ записать в тригонометрической форме:
1)
2 cos 400 i sin 400
3 cos 600 i sin 600
Ответ.
2) 2 cos 300 i sin 300 3 cos 700 i sin 700
Ответ.
2
cos 200 i sin 200
3
2 3 cos1000 i sin 1000
17. Представить числа в тригонометрической
форме:
1
3
1) z
i
5 5
3 1
2) z
i
6 6
Ответ.
Ответ.
2
2
2
i sin
cos
5
3
3
1
7
7
i sin
cos
3
6
6
18. Найти z1 z2 ,
форме для чисел
z1
в
z2
1
3
z1
i
5 5
u
тригонометрической
3 1
z2
i
6 6
2
11
11
cos
i
sin
15
6
6
Ответ.
z1 z 2
Ответ.
z1 6
cos i sin
z2 5 2
2
z1
z2
7
19. Найти
в тригонометрической
форме и результат представить в алгебраической
форме, если
1
3
z1
i
5 5
7
Ответ.
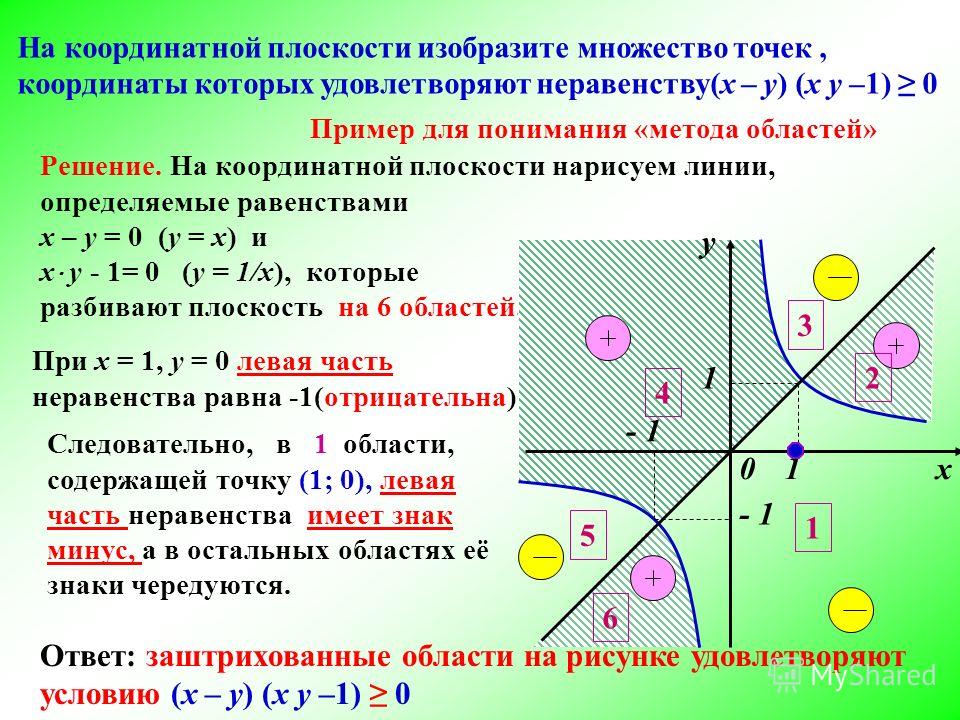
u
3 1
z2
i
6 6
z1
67 3
3
7 cos
i sin
5 2
2
z2
67
0 7 i
5
20. Найти все значения корня:
Ответ.
2
2
u0 3 4 cos
i sin
9
9
8
8
3
u1 4 cos
i sin
9
9
14
14
u 2 3 4 cos
i sin
9
9
3
2 2 3i

English     Русский Правила

04. Множества точек на комплексной плоскости. задание геометрических мест

При решении геометрических задач используется геометрический смысл модуля комплексного числа, его аргумента, геометрический смысл введенных алгебраических операций и пр. Приведем конкретные примеры.

Пример 1. Какое множество точек на плоскости (z) определяется условием

Решение. Имеем и, стало быть, . По условию или . Последнее неравенство определяет множество точек в первом и третьем квадрантах, соответственно над и под гиперболой (см. рис.6).

Пример 2. Какое множество точек на плоскости (Z) определяется условием ?

Решение. Комплексное число изображается вектором, началом которого является точка –1+I и концом – точка z. Угол между этим вектором и осью Ox есть , и он меняется в пределах от до . Следовательно, данное неравенство определяет угол между прямыми, выходящими из точки –1+

I и образующими с осью Ox углы в и
(рис.7).

Пример 3. Какая кривая задается уравнением , где C и A – действительные положительные числа, причем A >C.

Решение. Модуль Есть расстояние между точками Z и – C; — расстояние между точками Z и C. По условию сумма расстояний от точки Z до двух данных точек —C и C есть величина постоянная. Значит, точка Z лежит на эллипсе. Уравнение этого эллипса имеет вид , где
(рис.8).

Пример 4. Какая кривая определяется уравнением ?

Решение. Имеем (см.(1.9)) . По условию или — это окружность (рис.9).

Пример 5. Написать в комплексной форме уравнение прямой .

Решение. Подставляя X и Y по формуле (1.9) в уравнение прямой, получим , или . Обозначив , получим уравнение: — уравнение прямой в комплексной форме.

Задачи для самостоятельного решения

1. Доказать следующие соотношения:

А) ; б) ; в) ; г) .

2. Найти:

А) ; б) ; в) ; г) ; д) .

3. Найти действительные решения уравнений:

А) ;

Б) , где A, B – заданные действительные числа, ;

В) .

4. Представить комплексное число в алгебраической форме.

5. Вычислить (X— действительное число).

6. Выделить X и Y через U и V (X,…,V – действительные числа), если .

7. Найти все числа, удовлетворяющие условию .

8. Решить системы уравнений:

А) б)

В) г)

9. Найти модуль и главное значение аргумента комплексного числа.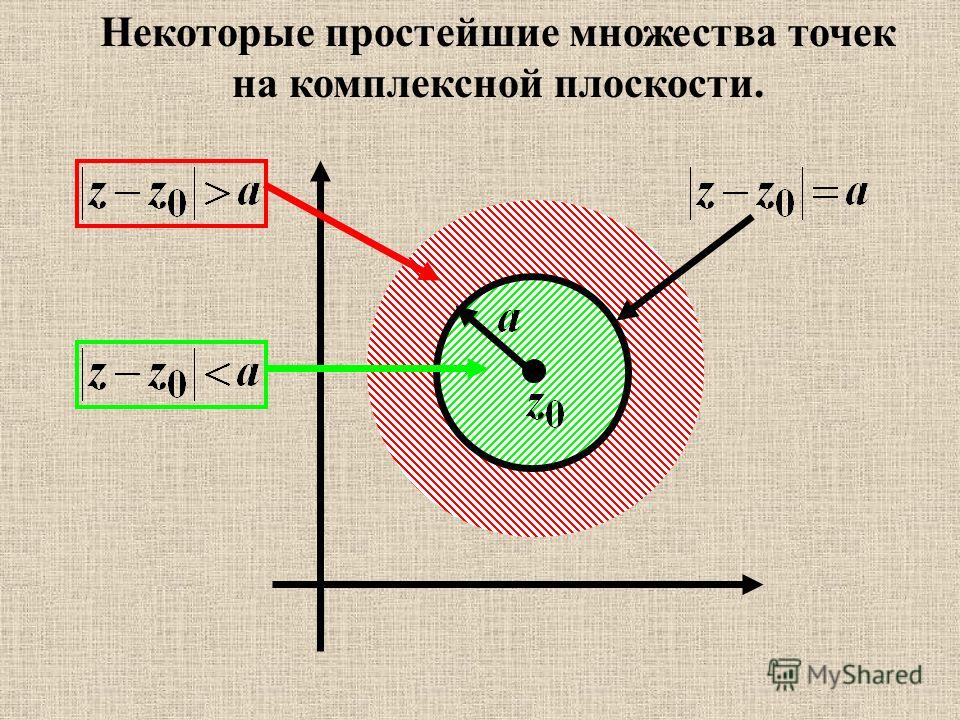 Записать число в тригонометрической и показательной формах:

А) –2; б) 2I; в) ; г) –Z — I; д) 4-3I; е)
ж) ; з) ;

И) .

10. Вычислить:

А) ; б) ; в) ; г) ;

Д) .

11. Найти все значения корней:

А) ; б) ; в) ; г) ; д) ; е) ;

Ж) ; з) ; и); к) ; л) ; м) .

12. Решить квадратные уравнения:

А) ; б) ;

В) .

13. Решить уравнения:

А); б) ; в) ;

Г) ; д) .

14. Найти множества точек на плоскости (Z), определяемые заданными условиями:

А) ; б) ; в) ; г) ;

Д) ; е) ; ж) ;

з) .

15. Какие линии определяются следующими уравнениями:

А) ; б) ; в) ;

Г) ; д) ; е) ; ж) .

16. Написать в комплексной форме уравнение следующих линий:

А) координатных осей Ox и Oy; б) прямой Y = X; в) прямой , — действительные числа; г) гиперболы ; д) окружности .

< Предыдущая		Следующая >

численных методов.

Как изобразить неравенство на реальной/мнимой плоскости?

Задай вопрос

спросил 6 лет, 7 месяцев назад

Изменено 6 лет, 7 месяцев назад

Просмотрено 256 раз

$\begingroup$ 92$, который иногда помогает построить график неравенства, преобразуя неравенство в формулу окружности в начале координат $(h, k)$ с радиусом $r$.

Но я не могу преобразовать приведенное выше неравенство RK2 в формулу окружности, а также не могу правильно получить мнимую часть, если воспользуюсь методом «приравнять к равенству» (хотя я знаю, что $-2< Re{\{z \}} < 0$).

• неравенство
• численные-методы
• устойчивость-в-одах

$\endgroup$

$\begingroup$

Хорошо, ответы Эрика Стаки и Моргана Роджерса указывают на замену $z$ на $x+iy$. Проблема в том, что на экзаменах нет компьютера, чтобы построить неравенство, полученное через $x$ и $y$.

Ниже приведен подход, который я узнал из http://www.math.ubc.ca/~peirce/M405_607E_Lecture%2018.pdf, который я нашел наиболее подходящим подходом, когда вы находитесь в экзаменационной комнате:

Сначала установите неравенство на функция G такая, что: 92}{2}$

Для устойчивости требуется $|G(z)| < 1$.

Решите $z$ через $G$:

$z = -1 \pm \sqrt{2G-1}$

Теперь мы можем приступить к построению графика $z$. Сначала предположим, что $G$ — это окружность радиуса 1 в начале координат реальной/мнимой плоскости. Затем мы масштабируем $G$ на два и получаем $2G$, затем смещаем круг влево и получаем $2G-1$ и так далее, пока не получим $-1 \pm \sqrt{2G-1}$ .

Процесс показан с пошаговой конформной картой в http://www.math.ubc.ca/~peirce/M405_607E_Lecture%2018.pdf 9{2}}{2})} — 1= 0.$$ Я думаю, что если вы хотите решить эту проблему, вы должны просмотреть $z = x+y\mathrm{i}$ и относиться к ней как к уравнению с двумя переменными. Это дает (после того, как вы избавитесь от квадратного корня) уравнение 4-й степени относительно $x$ и $y$.

$\endgroup$

1

$\begingroup$

Начало и конец истории здесь таковы: установить $z=x+iy$ и преобразовать в неравенство двух переменных. Нет особенно веских причин полагать, что ваш домен должен быть чем-то красивым, вроде круга. 92$ и $x$, с границами $-2x\pm2\sqrt{-x(x+2)}$. Поскольку оценки должны быть действительными, мы восстанавливаем уже обнаруженное вами неравенство в действительной части.

В качестве альтернативы вы можете оставить его в виде $x$ и $y$; что, вероятно, является лучшей формой для помещения его в автоматизированное графическое устройство. Похоже, вам это понадобится (или много терпения, проб и ошибок), так как описываемая область не так красива аналитически.

$\endgroup$

2

Искусство решения проблем

Комплексные числа возникают, когда мы пытаемся решить такие уравнения, как .

Содержание

• 1 Производная
• 2 Формальное определение
• 3 детали
• 4 Операции
  • 4.1 Примеры
• 5 Альтернативные формы
• 6 тем
• 7 Проблемы
  • 7.1 Введение
  • 7.2 Промежуточный уровень
  • 7.3 Олимпиада
• 8 См. также

Вывод

Мы знаем (из тривиального неравенства), что квадрат действительного числа не может быть отрицательным, поэтому это уравнение не имеет решений в действительных числах. Однако можно определить число , такое, что . Если мы добавим это новое число к действительным числам, у нас будут решения для . Оказывается, в системе, полученной в результате этого добавления, мы можем не только найти решения, но теперь мы можем найти всех решений каждый полином . (Подробнее см. в Фундаментальной теореме алгебры.)

Формальное определение

Теперь мы готовы к более формальному определению. Комплексное число — это число вида где и — мнимая единица. Множество комплексных чисел обозначается . Множество комплексных чисел содержит множество действительных чисел, так как .

Части

Каждое комплексное число имеет действительную часть обозначенную или и мнимую часть обозначается или . Обратите внимание, что мнимая часть комплексного числа действительна: например, . Итак, если , мы можем написать . ( и традиционно используются вместо и в качестве переменных при работе с комплексными числами, в то время как и (а часто также и ) используются для представления действительных значений, таких как действительная и мнимая части комплексных чисел. Это математическое соглашение часто нарушается, когда оно неудобно, поэтому при работе с комплексными числами убедитесь, что вы знаете, из каких множеств берутся переменные.)

Как видите, комплексные числа позволяют снять ограничение из домена функции (хотя необходимы некоторые дополнительные соображения).

Операции

Сложение и вычитание комплексных чисел подобны выполнению тех же операций с полиномами — сложите действительные части, а затем сложите мнимые части.

Умножение также похоже на выполнение тех же операций с многочленами — используйте распределительное свойство и применяйте . Однако для деления знаменатель должен быть действительным числом; это делается путем умножения комплексного сопряжения, где знак мнимой части меняется местами. Комплексно-сопряженный обозначается .

Абсолютное значение (или модуль, или величина) комплексного числа — это расстояние от комплексного числа до начала координат. Он обозначается .

Аргументом комплексного числа является угол, образованный между прямой, проведенной от комплексного числа к началу координат, и положительной действительной осью на плоскости комплексных координат. Он обозначается .

Примеры

Если и ,

• ,

Альтернативные формы

В дополнение к стандартной форме комплексные числа могут быть выражены в двух других формах.