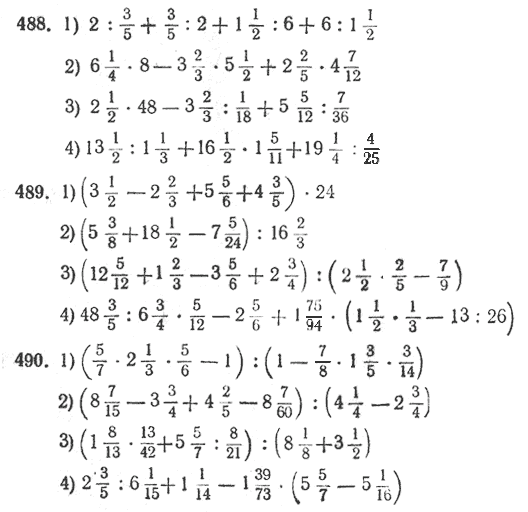Примеры на действия с дробями 6 класс: сокращение, вычитание, умножение, деление, сравнение. В этой статье мы представим вам пошаговую инструкцию, как решать примеры с дробями для 6 класса.

Умножение обыкновенных дробей – примеры, правило (6 класс, математика)

4

Средняя оценка: 4

Всего получено оценок: 323.

4

Средняя оценка: 4

Всего получено оценок: 323.

Умножение обыкновенных дробей – это самое простое действие с дробями, которое себе можно представить в 6 классе. Разберем в подробности все особенности этого действия.

Что такое дробь?

Дробью называют часть единицы, которую используют для вычислений. То есть, целое разделили на какое-то количество частей, причем некоторое количество таких частей были взяты и использованы для вычислений.

Для того, чтобы пользоваться таким числом нужно знать, на сколько частей поделили единицу и сколько таких частей взяли для расчета.

Поэтому дробь записывается с помощью черты. Число под чертой называется знаменатель. Именно оно обозначает количество частей, на которое поделили целое. Над чертой записывается знаменатель. Это количество частей, которые были взяты для расчета.

Выделяют несколько видов дробей:

• Правильная дробь. Эту дробь также называют обыкновенной. Это число, у которого числитель меньше знаменателя.
• Неправильная дробь. Это дробь, у которой числитель больше знаменателя.
• Смешанное число. Это дробь, которая имеет две части: целую и дробную. Смешанные числа стараются не использовать при расчетах. Куда чаще неправильную дробь преобразуют в смешанное число, чтобы записать результат. Записывать ответ в виде неправильной дроби считается некрасивым.
• Десятичная дробь. Это дробь, записанная в строку с помощью разделительной запятой. Количество знаков после запятой равняется степени 10, которая находится в условном знаменателе дроби.

Смешанным числом может быть как обыкновенная, так и десятичная дробь. Но нельзя называть какую-либо десятичную дробь правильной или неправильной. Это другой подвид чисел. Все дроби вместе принадлежат к подмножеству рациональных чисел и называются дробно-рациональными числами.

Умножение дробей

Умножать дроби достаточно просто. Для этого числитель умножается на числитель, а знаменатель на знаменатель – правило достаточно простое. Объясним, почему умножение выполняется именно так. Для этого нужно сказать, что дробь считается незавершенной операцией деления. То есть любое дробное число можно заменить на деление. Это выглядит так:

${3\over{5}}=3:5$

Тогда умножение дробей можно записать так:

${3\over{5}}*{4\over{8}}= (3:5)*(4:8)$ – а при умножении таких скобок можно умножить отдельно делители и делимые не меняя конечного результата. Тогда:

$(3:5)*(4:8)=(3*4):(5*8)=15:32$ – завершать операцию деления нам не нужно, просто вернем числу вид дроби.

$15:35={15\over{32}}$ – если пропустить все промежуточные действия, то получится, что действия выполняются точно так же, как в правиле. То есть числитель умножается на числитель, а знаменатель на знаменатель.

Что мы узнали?

Мы поговорили о дробях. Вспомнили все виды дробей и их особенности. Рассказали все об умножении обыкновенных дробей. Сказали, почему это действие производится именно в таком порядке. Все объяснения подтвердили примером умножения обыкновенных дробей.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Баха Кабиров

  5/5

• Мурад Абакаров

  5/5

• Матвей Лопатин

  5/5

• Гена Горбаленко

  4/5

• Топ-Ташер Фри-Фаер

  5/5

Оценка статьи

4

Средняя оценка: 4

Всего получено оценок: 323.

---

А какая ваша оценка?

Открытый урок по математике для обучающихся с ОВЗ по теме «Действия с дробями» (6 класс)

Государственное казенное общеобразовательное учреждение

Владимирской области «Лухтоновская специальная (коррекционная) общеобразовательная школа-интернат»

 

Методическая разработка открытого урока по математике в 6 классе для обучающихся с ОВЗ

по теме «Действия с дробями»

 

Составитель:

Никитина Надежда Николаевна,

учитель математики,

высшая квалификационная категория

 

2022 год

Аннотация

Методическая разработка посвящается активизации познавателного интереса учеников среднего школьного возраста с нарушением интеллекта на уроках математики через игру.

Раскрывает следующие вопросы:

— как с помощью применённых учителем методов и форм обучения можно провести урок в интересной для учеников форме;

— облегчить ученикам восприятие, осмысление, запоминание учебного материала, выработать умение его применять сначала в аналогичной, а затем в новой ситуации.

 

Введение

К моменту изучения долей, а затем и обыкновенных дробей у школьников с нарушением интеллекта имеется уже жизненный опыт в образовании и наблюдении целых предметов или величин. Однако, при изучении дробей ученики встречаются с новыми свойствами дробных чисел, значительно отличающих их от натуральных чисел: название, запись, возможность выполнение преобразований над дробями, которые изменят вид дроби, но дробь остаётся равной данной. На примере изучения дробей учитель имеет возможность показать то общее, что свойственно всем числам, и то особенное, что свойственно только дробным числам. Перед учащимися возникают проблемы при изучении дробей. Потому, учителю нужно обратить внимание на практическую направленность урока, на применение дидактических игр, активизируя познавательный интерес, опираясь на жизненный опыт учеников.

 

Методические рекомендации по проведению урока

Для проведения урока необходимы технические средства: компьютер с мультимедийным проектором, презентация «Действия с дробями.

Оборудование: дидактическая игрушка мяч, карточки с числами от 0 до 9, игра «Действия и знаки», «Название компонентов действий», карточки для групп, компьютеры, образец решения примеров.

 

План урока

 

Тема урока: «Действия с дробями»

Тип урока: комбинированный (повторение ранее полученных знаний, сообщение новых знаний, первичное их закрепление, формирование умений и навыков).

 

Цель урока: воспроизвести математические знания учащихся, уточняя, обобщая и систематизируя основные понятия и действия с дробями и смешанными числами и научить решать примеры вида

2 —

Задачи:

коррекционные:

— коррекция и развитие аналетико-синтетической деятельности при работе с дробями и смешанными числами;

развивающие:

— работать над развитием наблюдательности, внимания, речи при использовании дидактического материала;

— работать над формированием логического мышления, умения находить причинные связи;

воспитательные:

— воспитание умения применять полученные знания на практике, повышение мотивации к математике через использование компьютера;

— воспитание умения слушать и вступать в диалог и стремления к достижению положительного интереса.

Формы учебной деятельности учащихся: фронтальная работа, статичные пары, группы, индивидуальная работа.

Метод: диалог.

Структура урока

№	Этап урока	Время
1	Орг. момент. Тема и цель урока	2 минуты
2	Проверка домашнего задания	3 минуты
3	Устный счёт	6 минут
4	Повторение, работа с компьютерами	8 минут
5	Физкультминутка	1 минут
6	Объяснение нового материала	5 минут
7	Первичное закрепление новых знаний	12 минут
8	Домашнее задание	2 минуты
9	Итоги урока	1 минута

 

Конспект урока «Действия с дробями»

 

1. Организационный момент

Учитель:

Посмотрите, все ль в порядке:

Книга, ручка и тетрадка

Прозвенел уже звонок,

Начинается урок!

Вопрос: « О чем я не сказала, но у вас на парте это есть? (дневник)».

Отчет дежурного.

Запись числа, классной работы и темы урока в тетрадях.

2. Проверка домашнего задания

Вопрос: «В каком примере у вас поучился ответ: 5 ,1, , 2 , ?

Какие примеры не были названы? (задание на дом было: + ; — ; 4 + 2 ; + 5; 8 — 4 ; 1 — ; 7 — ).

3. Устный счет

Нам игру пора начать,

Пришло время вычислять.

И на нетрудные вопросы

Вы ответ сумейте дать.

Игра в мяч. Устный счет в пределах 20 на «+» и «-».

Работа с карточками от 0 до 9 на знание таблицы умножения и деления.

Игра в группах.

Задание : повторите действия, знаки и название компонентов действий (пример: «+» — «сложение», «-» — «вычитание» и т. д.; «первое слагаемое», «второе слагаемое», «сумма»).

Задание : на карточке записаны дроби, назовите их и составьте 2 примера на сложение «+» и вычитание «-». Сделайте вывод (дроби: ; ; ; 7 ).

4. Повторение. Работа с компьютером

Учитель:

Чтобы спорилось трудное дело,

Чтобы в жизни не знать неудач,

Мы с тобой отправляемся смело

В мир загадок и сложных задач.

Задание:

+ = — = + = 2 + =

 

4 + = 5 — 1 = 1 — = 4 — =

 

Ответы: ; ; 4 ; 1; ; ; ; .

Задание: соедините примеры с ответами с помощью курсора на экране.

Задача

Масса дыни кг, арбуза кг. Сравните массы арбуза и дыни.

Решение:

1й способ. Сколько весят дыня и арбуз вместе?

кг + кг = кг = кг.

2й способ. На сколько арбуз тяжелее дыни? кг — кг = кг.

Задание: выберите правильный способ решения и отметьте его.

5. Физкультминутка

6. Объяснение нового материала

Учитель: Учитесь думать, объяснять

Учитесь мыслить, рассуждать.

Ведь в математике, друзья,

Без логики никак нельзя!

 

Рассматриваем образец решения примеров.

2 — = 1 — = 1 = 1

Из можно вычесть ? Нет.

Что делать? Нужно из 2 целых занять 1! А это , т.к. у нас знаменатель 4. К прибавляем , получится .

Практическая работа

 

 

 

 

 

7. Первичное закрепление новых знаний

Работа с учебником – стр. 122 № 456

Выполнение решения примеров по образцу

8. Домашнее задание

Учитель:

Кто ничего не замечает,

Тот ничего не изучает.

Кто ничего не изучает,

Тот вечно хнычет и скучает.

 

Домашнее задание (работа с дневником):

Таблица умножения и деления – повторить.

№ 246, с. 78 – работа с перфокартой (рабочая тетрадь по математике для 6го класса).

9. Итоги урока. Оценки за урок.

 

Литература:

1. Капустина Г. М., Перова М. Н., Математика 6 класс, Учебник для специальных (коррекционных) образовательных учреждений 8 вида.

2. Перова М. Н., Яковлева И. М., Рабочая тетрадь 6 кл. Математика.

3. Перова М. Н., Методика преподавания математики в коррекционной школе, Москва, Владос, 2001.

 

 

Самоанализ урока:

Вид урока: комбинированный (повторение ранее полученных знаний, сообщение новых знаний, первичное их закрепление, формирование умений и навыков).

Все этапы урока подчинены основной дидактической цели и включает в себя следующие этапы:

Организация учащихся на урок;

Проверка домашнего задания;

Устный счет;

Актуализация знаний к новой теме, повторение;

Физминутка

Объяснение нового материала;

Коррекция и первичное закрепление знаний;

Задание на дом;

Подведение итогов урока.

На уроке я пыталась работать с элементами интерактивного обучения, основанного на диалоге с учениками через доступные средства и методы (наглядные, словесные, практические).

Присутствовала социальная активность учеников (учащиеся не равнодушны к тому, что происходит вокруг, отвечают на вопросы, ищут пути решения и т.д.) и умственная активность (познавательная) – сами ищут решения, работают с заданиями.

Осуществлялись следующие принципы:

-опора на опыт учащихся;

-через использование интерактивных методов;

-взаимодействие видов активности.

Учитель выступал в роли консультанта – фасилитатора (помощника), создающего условия для самореализации личности, побуждая к решению проблем.

Метод: диалог.

Формы: фронтальная работа, статичные пары, группы, индивидуальная работа.

Рабочие листы дробей

Фракции (базовые)

Печатные дроби и рабочие листы; Манипулятивные дробные полоски, распечатываемые дробные пиццы, игра на запоминание и многое другое.

Равнозначные дроби и упрощение

На этой странице представлены рабочие листы и упражнения для обучения учащихся работе с эквивалентными дробями и приведению дробей к простейшим терминам.

Сравнение и упорядочивание дробей

Сравните и упорядочите пары дробей с помощью этих карточек с заданиями, заданий учебного центра и рабочих листов.

Дроби в числовых рядах

Все эти рабочие листы содержат дроби в числовых рядах.

Дробные части множества

Скачать и распечатать задания по вычислению дробных частей множества. (пример: что такое 3/4 от 24?)

Смешанные числа и неправильные дроби

Печатные формы со смешанными числами; Включает в себя основные смешанные числа, а также сложение и вычитание смешанных чисел.

Взаимные дроби

Распечатайте рабочие листы для изучения обратных дробей.

Операции с дробями

Сложение дробей

Практика сложения и вычитания дробей (с одинаковыми и разными знаменателями) и смешанных чисел.

Вычитание дробей

Потренируйтесь вычитать дроби и смешанные числа с помощью этих печатных форм. Включает подобные и неодинаковые знаменатели.

Умножение дробей

Умножение дробей и смешанных чисел. Включает текстовые задачи, а также рабочие листы с моделями и иллюстрациями.

Деление дробей

С помощью этих рабочих листов ваши ученики могут попрактиковаться в делении дробей и смешанных чисел.

Дополнительные дроби

Дробные полосы и круги

На этой странице можно распечатать дробные полоски, дробные круги, дробные пиццы и другие инструменты для манипулирования дробями.

Дроби: только половинки и четверти (очень простые)

Эти очень простые рабочие листы дробей охватывают только половинки и четверти (четверти).

Наименьшие общие знаменатели — LCD

Найдите наименьшие общие знаменатели для данных пар дробей.

См. также:

Десятичные дроби

Узнайте об основных десятичных дробях, десятичных разрядах, сравнении и упорядочении десятичных дробей, округлении десятичных дробей, а также сложении, вычитании, умножении и делении десятичных дробей.

Проценты

Узнайте о процентах, таких как преобразование десятичных знаков и дробей в проценты и текстовые задачи, связанные с процентами.

Соотношения

Потренируйтесь сравнивать две величины с отношениями. Посмотрите на картинки и определите соотношения предметов.

Дроби во 2-м классе (6–7 лет)

Существует множество повседневных способов помочь вашему ребенку понять дроби. Вот лишь несколько идей.

 

1. Изучение долей количества

Попробуйте разделить объекты поровну, чтобы найти доли количества. Вы можете сделать это, используя предметы в доме — например, виноград, пуговицы, бусы или кусочки сушеных макарон… варианты безграничны!

• • Половинки . Найдите 12 предметов одного типа и попросите ребенка найти половину. Спросите их, сколько предметов в каждой группе, и помогите им понять, что половина от 12 — это 6, потому что в каждой группе по 6 предметов.
  • Четверти . Изучив половинки, вы сможете найти четверть из 12 объектов. Покажите ребенку, что вы можете сделать это, разделив предметы на четыре равные группы или найдя половину и еще раз половину.
  • Третьи . Теперь посмотрите, сможет ли ваш ребенок разделить предметы на три равные группы. Сколько в каждой группе? Попробуйте найти три четверти, а затем две трети из 12 предметов.

Проверьте, понимает ли ваш ребенок, что две четверти равны половине, а четыре четверти равны целому числу. Помогите им понять, что нахождение половины эквивалентно делению на 2, нахождение четверти эквивалентно делению на 4, а нахождение трети эквивалентно делению на 3.

 

2. Дроби фигур

Если вашему ребенку нравится рисовать и делать поделки, используйте бумагу, ручки и ножницы, чтобы показать ему, как работают дроби. Вместе нарисуйте простые фигуры, такие как квадраты, треугольники или круги. Вам нужно будет убедиться, что они достаточно ровные и точные — в этом может помочь рисование.

Вырежьте фигуры, а затем сложите их, чтобы получить половинки, трети и четверти фигур. Можно ли сложить фигуру на две, три или четыре равные части? Есть много способов использовать эти фигуры для изучения дробей. Например:

Покажите ребенку квадрат и спросите, как он найдет половину фигуры. Они могут сложить фигуру пополам, чтобы увидеть, есть ли две равные части. Попросите их показать вам одну половину. Какой формы половинка?

 

Определите, сколькими способами фигуру можно сложить пополам. Например, вы можете сложить квадрат по диагонали, чтобы получились треугольные фигуры. Найдите разные способы сделать четверть фигуры или треть фигуры.

3. Запись дробей

Помогите ребенку научиться записывать дроби, используя математические символы. Число внизу называется знаменателем, а число вверху называется числителем. Знаменатель говорит нам, на сколько равных частей мы делим. Числитель говорит нам, сколько равных частей мы ищем.

Вы можете сыграть в игру, в которой дети сопоставят написанную дробь с изображением дроби. Например:

¼ =

4. Дроби как самостоятельные числа

Ваш ребенок должен понимать, что дробь также является самостоятельным числом. Вы можете помочь своему ребенку с этой концепцией, используя числовые линии.

Вы можете показать ребенку числовой ряд, как показано ниже. Попросите их показать, где на числовой прямой будет половина. Помогите им понять, что половинка находится точно посередине между 0 и 1.

Точно так же ваш ребенок должен уметь находить четверть, три четверти и треть на числовой прямой, как показано ниже:

5. Счет дробными шагами

Поощряйте ребенка начинать считать пополам, четвертям и третям, используя в качестве помощи предметы и числовые линии. Например, разрежьте кусочки фруктов на три равные части и сосчитайте на треть: ⅓, ⅔, 1, 1 ⅓, 1 ⅔ и так далее.

Это укрепит идею о том, что дроби — это числа, и покажет, как в сумме они могут составлять более единицы.

No related posts.