«Кривые второго порядка». Уравнение окружности. Часть 1
Высшая математика / Практикум по аналитической геометрии
Задача №1. Определить центр и радиус окружности, заданной уравнением х²+у²-2х+4y-20=0.
Решение. Так как в заданном уравнении коэффициенты при х² и у² равны между собой и отсутствует член с произведением координат, го заданное уравнение действительно представляет собой уравнение окружности. Чтобы определить координаты центра и радиус окружности, необходимо уравнение привести к каноническому виду:
(х²-2х)+(y²+4у)=20, (x²-2х+1)+(у²+4х+4)=25, (x-1)²+(y+2)²=25.
Координаты центра и радиус окружности можно найти, не приводя данное уравнение к каноническому виду,
Рис.1
достаточно сравнить данное уравнение с уравнением окружности в общем виде:
Ответ: (1, —2), R = 5.
Задача №2. Составить уравнение окружности, проходя¬щей через точки А (—1;1) и В (1;-3), если центр ее лежит на прямой 2х-у+1=0.
Решение. Каноническое уравнение окружности:
(x-a)²+(y-b)² = r².
Так как окружность проходит через точки А и B, то координаты этих точек должны удовлетворять уравнению окружности. Имеем два уравнения:
(-1-а)² + (1-b)²=r², (1-а)² + (-3-b)² = r².
Если центр окружности лежит на прямой 2х-у+1=0, то координаты центра также должны удовлетворить уравнению прямой.
Имеем третье уравнение: 2а-b+1=0.
Рис.2
Решим систему уравнений:
Таким образом, координаты центра окружности найдены:
Чтобы определить г², получим: г² = 1+2а+5а²,
Уравнение окружности:
Ответ: 9х² + 9y² + 24x + 30у — 31 =0.
Задача №3.
Составить уравнение окружности, если ее центр находится в точке С(5;4) и окружность отсекает от прямой х+2у-3=0 хорду, длина которой равна 8.
Решение. Искомое уравнение будет иметь вид:
(x-5)²+(у-4)²=r².
Определим расстояние центра С от данной прямой:
Так как радиус, перпендикулярный к хорде, делит ее пополам, то половина хорды будет равна 4 единицам.
Рис.3
По теореме Пифагора имеем:
г²=4²+CD²=16+20=36, r² = 36, r = 6.
Уравнение окружности: (х -5)²+(у — 4)² = 36.
Ответ: (х -5)²+(у — 4)² = 36.
Задача №4. Составить уравнение окружности, касающейся двух параллельных прямых 2х+у-5=0 и 2х+y+15=0, причем одной из них — в точке А(2; 1).
Решение. Определим диаметр окружности, для чего используем формулу расстояния точки от прямой
Уравнение прямой 2x+y+15=0, точка А(2; 1)
Воспользовавшись координатами точки A, можем составить такое уравнение:
(2 — а)²+(1 — b)² = 20.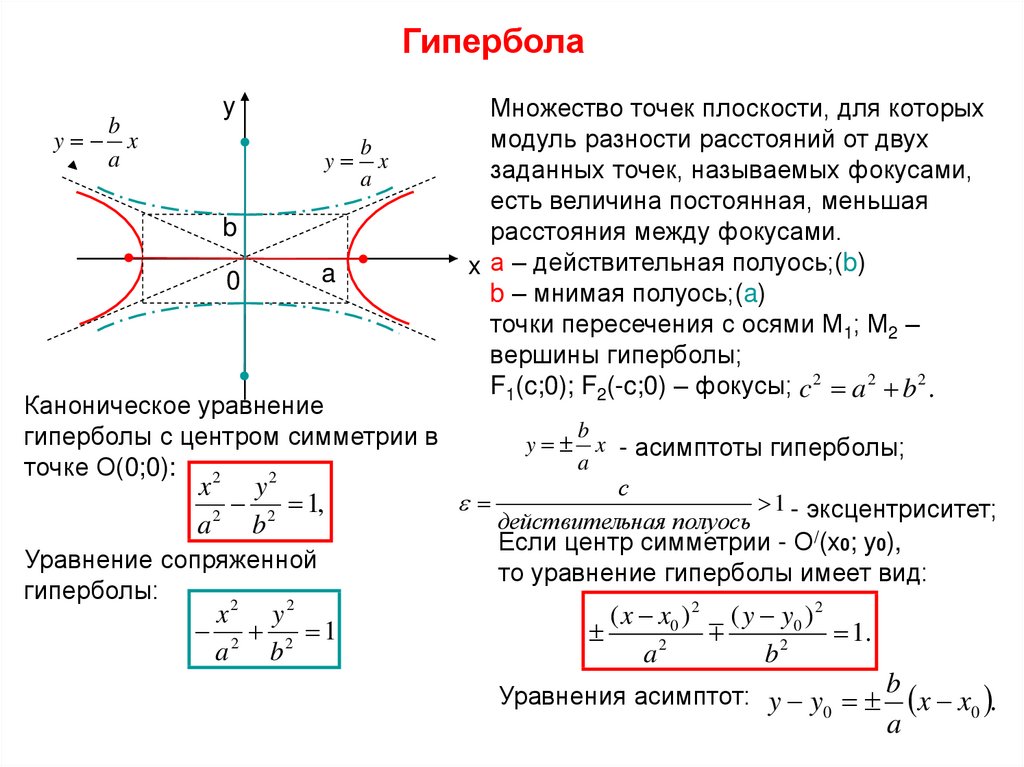
Второе уравнение с неизвестными а и b получим, определив расстояние точки С от первой прямой
Поскольку точка С лежит по одну сторону от прямой
Рис. 4
вместе с началом координат, то расстояние АС
Решая полученную систему уравнений, найдем а=-2; b=-1.
Эту задачу рекомендуем решить самостоятельно другим способом.
Указания. Составить уравнение перпендикуляра А В к данным прямым и найти координаты точки В.
Ответ: (x+2)²+(у + 1)²=20.
Открытое образование — Линейная алгебра и аналитическая геометрия для инженеров и исследователей
«Линейная алгебра и аналитическая геометрия» является составной частью дисциплины «Математика», читаемой для всех инженерных и экономических направлений НИТУ «МИСиС».
Данный онлайн-курс является базовым для естественно-научного образования.
Курс разработан НИТУ «МИСиС».
- About
- Format
- Information resources
- Requirements
- Course program
- Education results
- Formed competencies
- Education directions
About
Курс «Линейная алгебра и аналитическая геометрия» является базовой составляющей в образовании современного инженера. Включает в себя следующие разделы: векторная алгебра, прямая на плоскости, прямая и плоскость в пространстве, кривые и поверхности второго порядка, определители и матрицы, системы линейных уравнений, линейные операторы и квадратичные формы.
Цель курса:
— научить анализировать геометрические объекты с помощью методов и понятий векторной алгебры и аналитической геометрии;
-научить исследовать системы линейных алгебраических уравнений методами линейной алгебры;
-научить оперировать основными понятиями линейной алгебры и использовать методы линейной алгебры при построении и анализе математических моделей, необходимых для решения технологических, производственных и экономико-организационных задач.
Format
В состав курса входят видео-лекции продолжительностью 6-10 минут, материалы для самостоятельного изучения пользователями, анимационные ролики с инфографикой.
Разделы курса завершаются тестами на понимание материала (10-15 вопросов).
1. Ильин В.А., Позняк Э.Г., Аналитическая геометрия, М., «Наука», 1981.- 232с
2. Ильин В.А., Позняк Э.Г., Линейная алгебра. — М., «Наука», 1978.- 294с
3. Сборник задач по математике для ВТУЗов. Линейная алгебра и основы математического анализа.
(Под редакцией Ефимова А.В., Демидовича Б.П.), М.,Наука, 1986, 464с., с илл.
4. Клетеник Д.В., Сборник задач по аналитической геометрии. -М., «Наука», 1969.- 240с.
5. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А., Сборник задач по аналитической геометрии и линейной алгебре, М., — «Наука», 1987.- 495с.
Requirements
Для полноценного освоения учебного материала по дисциплине студент должен использовать знания, полученные предварительно в объеме, предусмотренном программами общего среднего образования.
Course program
Неделя 1
Раздел 1.
1.1.Вводный урок. Предмет аналитической геометрии. Линейные пространства.
1.2. Предмет аналитической геометрии. Геометрические векторы. Общие понятия. Коллинеарные и компланарные векторы. Орт вектора.
1.3. Линейные операции над векторами
1.4. Понятие о линейном пространстве. Примеры линейных пространств.
1.5. Линейная зависимость и независимость векторов. Свойства линейно зависимых и независимых систем элементов линейного пространства.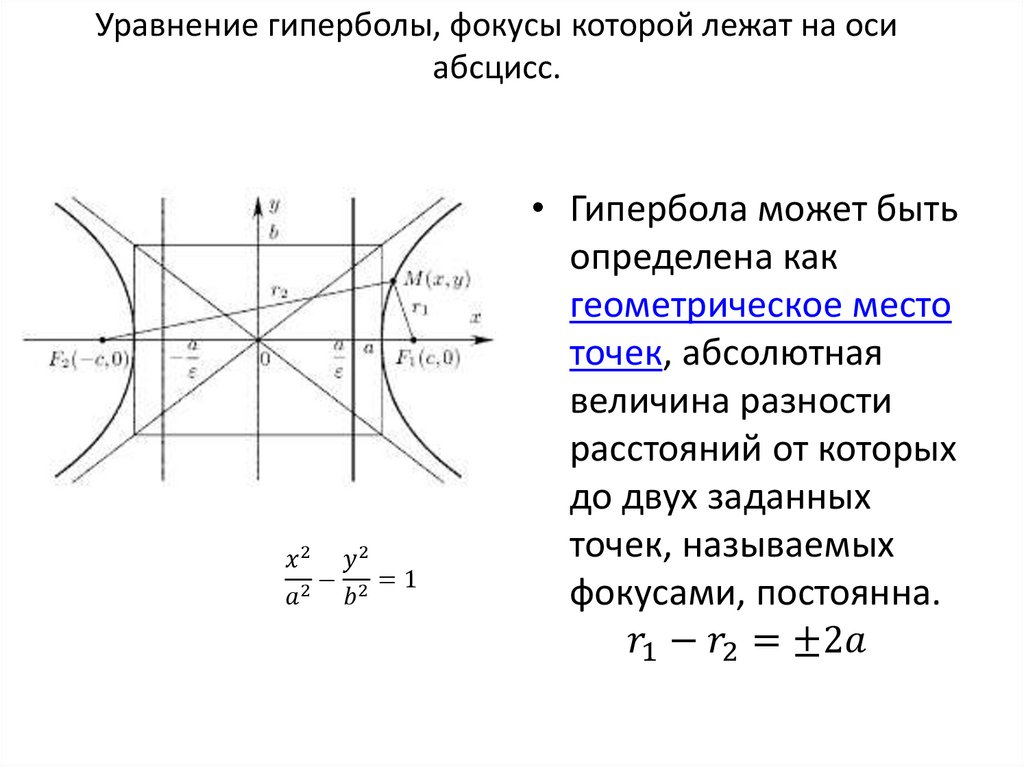
1.6. Базис в линейном пространстве. Размерность линейного пространства. Единственность разложения вектора по базису.
1.7. Координаты вектора. Линейные операции в координатной форме.
Неделя 2
Раздел 2. Векторная алгебра. Часть 1.
2.1. Проекция вектора на вектор. Свойства проекций. Ортогональная проекция вектора на ось. Ортогональная проекция вектора на плоскость
2.2. Базис в множестве геометрических векторов. Координаты вектора.
2.3. Декартова прямоугольная система координат (Д.П.С.К).
2.4. Действия над векторами, заданными в Д.П.С.К. Условие коллинеарности двух векторов. Деление отрезка в данном отношении.
2.5. Скалярное произведение векторов, его свойства.
2.6. Связь с ортогональной проекцией вектора на ось. Применение скалярного произведения в физике.
Неделя 3
Раздел 2. Векторная алгебра. Часть 2.
2.7. Определители второго и третьего порядков, их свойства.
2.8. Правые и левые тройки векторов.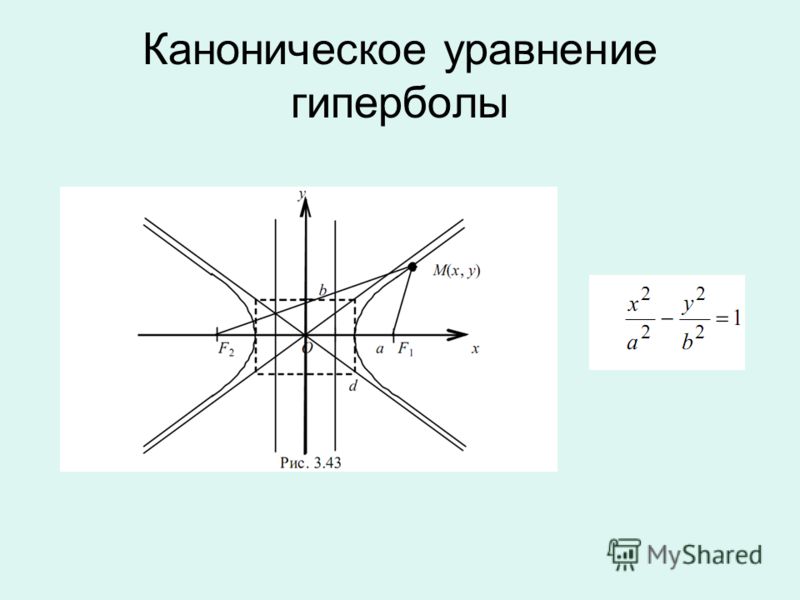
2.9. Векторное произведения векторов, его свойства, координатное представление.
2.10. Смешанное произведения векторов, его свойства, координатное представление.
2.11. Применение скалярного, смешанного и векторного произведения в физике и механике.
Неделя 4
Раздел 3. Прямая на плоскости, прямая и плоскость в пространстве
3.1 Прямая на плоскости как алгебраическая кривая первого порядка. Основные виды уравнений прямой на плоскости.
3.2. Взаимное расположение прямых на плоскости Угол между прямыми на плоскости Расстояние от точки до прямой на плоскости
3.3 Плоскость как алгебраическая поверхность первого порядка. Основные виды уравнений плоскости.
3.4. Взаимное расположение плоскостей Угол между плоскостями Расстояние от точки до плоскости.
3.5. Прямая в пространстве. Основные способы задания прямой в пространстве.
3.6. Взаимное расположение двух прямых в пространстве. Угол между прямыми в пространстве
3.7. Расстояние от точки до прямой в пространстве.
Расстояние между скрещивающимися прямыми в пространстве.
3.8. Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.
Неделя 5
Раздел 4. Кривые второго порядка.
4.1. Общее уравнение алгебраической кривой второго порядка. Параллельный перенос системы координат. Классификация кривых 2-го порядка.
4.2. Приведение к каноническому виду уравнений алгебраических кривых второго порядка, не содержащих произведения переменных
4.3. Эллипс, каноническое уравнение, основные параметры, фокальное свойство.
4.4. Директориальное свойство эллипса.
4.5. Касательная к эллипсу, оптическое свойство эллипса.
4.6. Примеры решения задач по теме “эллипс” (урок с практической частью).
4.7. Гипербола, каноническое уравнение, основные параметры, фокальное свойство.
4.8. Директориальное свойство гиперболы.
4.9. Асимптоты гиперболы. Касательная к гиперболе. Оптическое свойство гиперболы.
4.10. Примеры решения задач по теме “гипербола” (урок с практической частью).
4.11. Парабола, каноническое уравнение, основные параметры, директориальное свойство параболы.
4.12. Касательная к параболе, оптическое свойство параболы.
4.13. Примеры решения задач по теме “парабола” (урок с практической частью).
Неделя 6
Раздел 5. Поверхности второго порядка
5.1. Общее уравнение алгебраической поверхности второго порядка. Эллипсоид, основные свойства и построение по сечениям, параллельным координатным плоскостям.
5.2. Однополостный и двуполостный гиперболоиды. Их основные свойства и построение по сечениям, параллельным координатным плоскостям.
5.3. Конус второго порядка, эллиптический параболоид. Их основные свойства и построение по сечениям, параллельным координатным плоскостям.
5.4. Гиперболический параболоид. Цилиндрические поверхности второго порядка. Их основные свойства и построение по сечениям, параллельным координатным плоскостям.
5.5. Приведение к каноническому виду уравнений поверхностей, не содержащих произведений переменных.
Примеры решения задач по теме “поверхности второго порядка” (урок с практической частью).
Неделя 7.
Раздел 6. Определители и матрицы. Часть 1.
6.1. Матрицы и действия над ними: линейные операции и умножение матриц.
6.2. Умножение матриц как преобразование строк и столбцов. Транспонирование.
6.3. Специальные типы матриц.
6.4. Ориентированная площадь на плоскости.
6.5. Ориентированный объём в пространстве.
6.6. n-мерный ориентированный объём.
6.7. Перестановки и их чётность.
6.8. Формула для ориентированного объёма и определитель.
6.9. Полилинейные кососимметричные функции.
6.10. Композиции перестановок и обратные перестановки.
Неделя 8.
Раздел 6. Определители и матрицы. Часть 2.
6.11. Свойства определителя.
6.12. Определитель произведения матриц.
6.13. Формулы Крамера и ориентированный объём.
6.14. Определитель специального вида.
6.15. Миноры и алгебраические дополнения.
Разложение определителя.
6.16. Биортогональная система к системе строк/столбцов. Обратная матрица.
6.17. Ранг матрицы и базисный минор.
6.18. Свойства ранга матрицы.
6.19. Ориентированный объём повёрнутого куба.
6.20. Связь ориентированного объёма и обычного.
Неделя 9
Раздел 7. Системы линейных алгебраических уравнений и матричные уравнения.
7.1. Матричные уравнения.
7.2. Системы линейных алгебраических уравнений.
7.3. Правило Крамера решения систем линейных уравнений.
7.4. Условие существования решений систем линейных уравнений (теорема Кронекера-Капелли). Решение систем линейных уравнений методом последовательного исключения неизвестных (метод Гаусса).
7.5. Фундаментальная система решений. Свойства общего решения однородной системы линейных уравнений.
7.6. Свойства общего решения неоднородной системы линейных уравнений. Структура общего решения неоднородной системы линейных уравнений.
Неделя 10
Раздел 8.
Линейные операторы
8.1. Линейные операторы. Примеры линейных операторов. Действия над линейными операторами. Пространство линейных операторов.
8.2. Матрица линейного оператора.
8.3. Примеры матриц линейных операторов. Оператор поворота.
8.4. Координаты вектора в новом базисе. Преобразование матрицы линейного оператора при переходе к новому базису.
8.5. Обратный оператор. Ядро, образ и ранг линейного оператора.
8.6. Собственные значения и собственные векторы линейного оператора. Характеристический многочлен.
8.7. Нахождение собственных чисел и собственных векторов линейного оператора.
8.8. Алгебраическая и геометрическая кратность собственных значений.
8.9. Линейная независимость векторов, отвечающих различным собственным значениям.
8.10. Приведение матрицы линейного оператора к диагональному виду. Теорема о матрице линейного оператора в базисе из собственных векторов
Неделя 11.
Раздел 9. Самосопряженные линейные операторы
9.
1. Евклидово пространство. Скалярное произведение.
9.2. Норма. Теорема Пифагора.
9.3. Неравенство Коши–Буняковского и неравенство треугольника.
9.4. Ортонормированный базис конечномерного евклидова пространства. Разложение произвольного вектора по ортогональному базису.
9.5.Теорема о существовании в евклидовом пространстве ортонормированного базиса. Процесс ортогонализации Грама–Шмидта.
9.6. Ортогональные операторы.
9.7. Сопряженные линейные операторы в евклидовом пространстве. Самосопряженные операторы.
9.8. Свойства собственных значений и собственных векторов самосопряженного оператора. Диагональный вид самосопряженного оператора. Спектральное разложение самосопряженного оператора
9.9* Комплексные числа
9.10* Доказательство теоремы о вещественности собственных значений самосопряженного оператора
9.11* Доказательство теоремы о приведении самосопряженного оператора к диагональному виду
* – бонусные (дополнительные) темы
Неделя 12
Раздел 10.
Билинейные и квадратичные формы.
10.1. Линейные функционалы.
10.2. Билинейные формы. Соответствие между билинейными формами и линейными операторами. Матрица билинейной формы и её изменение при замене базиса..
10.3. Симметричные и кососимметричные билинейные формы. Разложение формы на симметричную и кососимметричную.
10.4. Квадратичные формы. Соответствие между квадратичными и билинейными формами. Матрица квадратичной формы.
10.5. Закон инерции.
10.6. Приведение квадратичной формы к каноническому виду.
10.7. Метод Якоби.
10.8. Критерий Сильвестра.
10.9. Приведение квадратичной формы к каноническому виду в евклидовом пространстве ортогональными преобразованиями.
10.10. Приведение уравнения линии второго порядка к каноническому виду с помощью поворота.
Education results
В результате освоения курса
обучающиеся будут:
–выполнять операции над векторами, матрицами, операторами, элементами линейных пространств, а также находить собственные векторы линейных операторов и приводить матрицу симметрического линейного оператора и матрицу квадратичной формы к диагональному виду, по общему уравнению определять типы алгебраических кривых и алгебраических поверхностей второго порядка;
— использовать методы аналитической геометрии и линейной алгебры для решения геометрических задач на плоскости и в пространстве, а также для выяснения взаимного расположения двух прямых, двух плоскостей, прямой и плоскости в пространстве;
— решать матричные уравнения и исследовать системы линейных алгебраических уравнений;
— применять теорию линейных операторов для приведения к каноническому виду общих уравнений кривых и поверхностей второго порядка, а также теорию квадратичных форм к исследованию экстремальных свойств функций нескольких переменных;
– применять аппарат векторной алгебры для решения задач физики.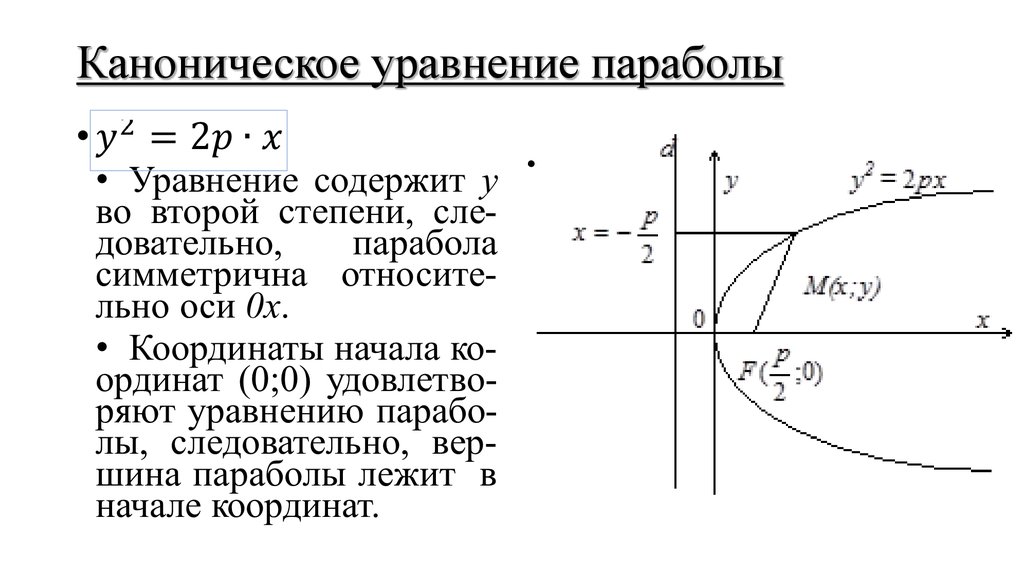
Formed competencies
Освоение курса направлено на получение [базового уровня]*) следующих универсальных (УК) и общепрофессиональных (ОПК) компетенций.
УК:
-использовать основные законы аналитической геометрии и линейной алгебры при решении практических задач, анализировать практические ситуации, выделять базовые составляющие задачи, подбирать варианты решения и разрабатывать алгоритмы решения практической задачи.
ОПК
— способность применять знание фундаментальной математики и естественно-научных дисциплин при решении задач в области естественных наук и инженерной практике
Education directions
01.03.04 Прикладная математика
03.04.02 Физика
09.03.01 Информатика и вычислительная техника
09.03.02 Информационные системы и технологии
09.03.03 Прикладная информатика
11.04.04 Электроника и наноэлектроника
15.03.02 Технологические машины и оборудование
21.
05.04 Горное дело
21.05.05 Физические процессы горного или нефтегазового производства
22.03.02 Металлургия
22.04.01 Материаловедение и технологии материалов
23.05.01 Наземные транспортно-технологические средства
28.04.01 Нанотехнологии и микросистемная техника
38.03.01 Экономика
38.03.02 Менеджмент
Курс может быть включен в бакалаврскую программу обучения онлайн-образования. Курс может быть включен в программу обучения специалиста. Курс может быть использован как курс ДПО.2}{9} = 1 $$
и систему координат необходимо повернуть на угол равный
$$ \арктан{3} $$
и начало новой системы координат необходимо перенести в точку $O'(-1,2)$. Я проверил это в программе Mathematica®, поэтому думаю, что можно с уверенностью предположить, что в учебнике нет ошибок.
А теперь о самой проблеме. Я рассчитал угол поворота по формуле из моего учебника. Это (вышеприведенное выражение является примером многочлена для объяснения таких индексов, как $a,b,c$ и т. д.) 92 $$
Оставшаяся часть:
$$ -12х-26у+11=\ -12(\cos{\alpha}*x’ — \sin{\alpha}*y’) — 26(\sin{\alpha}*x’ + \cos{\alpha}*y’) + 11 = \ \ -12\cos{\alpha}*x’ + 12\sin{\alpha}*y’ -26\sin{\alpha}*x’ — 26\cos{\alpha}*y’ + 11 = \\ (-12\cos{\alpha} — 26\sin{\alpha})*x’ + (12\sin{\alpha} — 26\cos{\alpha})*y’ + 11 = \\ 2((-6\cos{\alpha} — 13\sin{\alpha}))*x’ + 2(6\sin{\alpha} — 13\cos{\alpha})*y’ + 11 $$
Итак, теперь эта кривая имеет следующее уравнение в повернутой системе координат (позвольте мне использовать $x$ и $y$ вместо $x’$ и $y’$): 92 + 2dx + 2ey + g = 0 $$
Тогда в моем учебнике утверждается, что это уравнение можно еще уменьшить, переместив начало системы координат в точку $O(-\frac{d}{a}, -\frac{e}{c })$
И это место, где я не могу получить правильный ответ (то есть $O(-1,2)$), потому что вместо этого $-\frac{d}{a}$ дает мне 1,58114 из -1, и эта $-\frac{e}{c}$ дает 1,58114 вместо 2.
Я проверил это в Mathematica.
Может ли кто-нибудь объяснить мне, где я ошибаюсь, пожалуйста?
Заранее спасибо.
Формы квадратных уравнений: пояснения, советы и примеры
Хотите понять различные формы квадратных уравнений? Ниже читайте объяснение трех основных форм квадратичных чисел (стандартная форма, факторизованная форма и вершинная форма), примеры каждой формы, а также стратегии преобразования между различными квадратичными формами.
Ваше путешествие по математике завело вас далеко. Было время, когда слова «переменная» и «уравнение» были всего лишь понятиями, которые вы когда-нибудь поймете. Навыки, которые вы тогда развили, дали вам основу для использования математики для решения простых задач. Затем вы углубились в переменные и неизвестные значения. Вы победили, решая уравнения на значение x. Вы можете создавать и интерпретировать графики уравнений.
Теперь мы открываем новый инструмент: квадратика ! Квадратные уравнения могут казаться разными, пугающими, захватывающими или всеми вышеперечисленными.
Независимо от того, как вы себя чувствуете, приступая к изучению квадратных уравнений, знайте, что вы тоже можете справиться с этим. Вы выходите на новый уровень математического понимания и новый мир реальных жизненных ситуаций для моделирования. Давайте начнем!
Что мы рассматриваем
Три формы квадратных уравнений
Существуют три широко используемые формы квадратных уравнений: 92+k
Каждая квадратичная форма выглядит уникально, что позволяет легче решать различные задачи в одной форме, чем в другой. Мы раскроем особенности каждой формы и способы переключения между формами.
Вернуться к оглавлению
Почему существуют формы квадратных уравнений?
Каждая форма квадратного уравнения имеет определенные преимущества. Признание преимуществ каждой отдельной формы может облегчить понимание и решение различных ситуаций. 92+bx+c
Преимущества стандартной формы включают быстрое определение конечного поведения функции и определение значений a, b и c.
конечное поведение функции определяется старшим коэффициентом и степенью функции. Степень квадратного уравнения всегда равна двум. Старший коэффициент квадратного уравнения всегда представляет собой член а, если он записан в стандартной форме.
Если значение a положительное, парабола раскрывается, то есть функция возрастает влево и вправо. Если значение a отрицательно, парабола раскрывается вниз, то есть функция падает влево и падает вправо. 92+2x+1
Примечание : отрицательное значение, степень 2, парабола открывается «вниз»
Одним из методов решения квадратного уравнения является использование квадратной формулы . Для этого мы должны определить значения a, b и c. Чтобы узнать больше об этом, прочитайте нашу подробную обзорную статью о квадратичной формуле.
Что говорит вам
факторизованная форма квадратного числа? Теперь давайте рассмотрим, почему факторизованная форма полезна.
Чтобы получить факторизованную форму, мы делаем именно то, на что это похоже: мы факторизуем уравнение из стандартной формы.
| Факторизованная форма квадратного уравнения : y=a(x-r_1)(x-r_2) |
В факторизованной форме квадратного уравнения мы также можем определить конечное поведение, используя значение а. Хотя степень не так легко определить, мы знаем, что есть только два фактора, делающих степень второй. Конечное поведение следует тем же правилам, которые описаны выше.
Дополнительным преимуществом факторизованной формы является идентификация нулей или пересечений x функции. Значение r_1 и значение r_2 оба являются нулями (также называемыми «решениями») квадратичной функции.
y= — (x + 2)(x — 3)
Нули: x = -2 \text{ и } x= 3
Следует отметить, что не все квадратичные уравнения имеют «действительные» нули (некоторые квадратичные уравнения требуют в качестве нулей мнимых чисел), поэтому факторизованная форма не всегда применима.
О чем говорит форма вершины
квадратного числа?Наконец, у нас есть формы вершины квадратного числа. Помните, вершина — это точка пересечения оси симметрии с параболой. Это также самая нижняя точка параболы, раскрывающейся вверх, или наивысшая точка параболы, раскрывающейся вниз. 92+7х-9
… имеет стандартную форму и говорит нам, что a=3, b=7 и c=-9.
Что такое факторизованная форма квадратного числа?| Факторированная форма квадратичного уравнения: Y = A (X-R_1) (X-R_2) |
в Форма , мы можем увидеть Zeros, также называемые также называемыми x- перехваты, это r_1 и r_2. Нашими переменными остаются x и y, а a — коэффициент.
В факторизованном уравнении:
92+16…который находится в форме вершины, вершина (2,16) и значение a равно -2.
Преобразование между формами квадратных уравнений
Часто нам требуется много различной информации о квадратных уравнениях.
Может быть полезно увидеть одно и то же квадратное уравнение в нескольких формах. Точно так же, как хамелеон может менять цвет в различных ситуациях, мы можем изменять формы квадратичных уравнений в соответствии со своими потребностями.
Изменяйте формы квадратика, как хамелеон!
Способность быстро и точно переключаться между формами позволяет нам хорошо понимать квадратное уравнение и легко находить необходимую информацию. Например, вас могут попросить определить нули квадратного уравнения, заданного в стандартной форме. Чтобы идентифицировать нули, мы сначала должны преобразовать уравнение в факторизованную форму.
Вернуться к оглавлению
Преобразование стандартной формы в факторизованную
Начнем с уравнения: 92+5х-24. Давайте вспомним, как выглядит факторизованная форма:
| Факторированная форма квадратного уравнения: y=a(x-r_1)(x-r_2) |
2 Исследуйте школы Альберта 60 0 лицензий
2!
Чтобы разложить выражение на множители, мы должны определить множители -24, сумма которых равна 5.
Мы можем перечислить множители -24 и их суммы:
у=(х-3)(х+8)
Для определения нулей приравняем уравнение к нулю . Затем мы можем решить, установив каждый множитель равным нулю:
(x-3)(x+8)=0
х-3=0
х=3
х+8=0
х=-8
Следовательно, нули функции равны 3 и -8. Окончательная факторизованная форма уравнения:
y=(x-3)(x+8)
Чтобы узнать больше об этом подходе, прочитайте нашу статью о решении квадратных уравнений с помощью факторинга.
Преобразование из квадратичной формы в стандартную форму довольно распространено, поэтому вы также можете посмотреть это полезное видео для другого примера.
Вернуться к оглавлению
Преобразование факторизованной формы в стандартную
Чтобы преобразовать уравнение из факторизованной формы в стандартную форму, достаточно просто умножить коэффициенты. Например, изменим квадратное уравнение:
y=(3x-2)(-x+7)
… к стандартной форме. Мы будем использовать двойное распределение, чтобы перемножить коэффициенты (3x-2) и (-x+7). 92+28х+88.
Вернуться к оглавлению
Практика с формами квадратичных чисел
Для некоторых практических вопросов, касающихся форм квадратичных чисел, ознакомьтесь с практическим курсом Albert’s Algebra 1! Все вопросы Альберта включают объяснения решений и способы избежать распространенных ошибок.
Кроме того, лицензированные преподаватели Альберта могут назначить учащимся этот короткий тематический тест по алгебре 1, посвященный вершинам, корням и различным формам квадратичных уравнений.