Обратная пропорциональность. Гипербола | ЮКлэва
Сейчас мы будем говорить об обратной пропорциональности, или другими словами об обратной зависимости, как о функции.
Мы закрепим понятие функции и научимся работать с коэффициентами и графиками.
А еще мы разберем несколько примеров построения графика функции — гиперболы.
Начнём!
Обратная пропорциональность — коротко о главном
Определение:
Функция, описывающая обратную пропорциональность, – это функция вида \( \displaystyle y=\frac{k}{x-a}+b \), где \( k\ne 0\), \( x\ne 0\) и \( x\ne а\)
По-другому эту функцию называют обратной зависимостью.
Область определения и область значений функции:
\( D\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\) или, что то же самое, \( D\left( y \right)=\mathbb{R}\backslash \left\{ 0 \right\}\)
\( E\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\) или \( E\left( y \right)=\mathbb{R}\backslash \left\{ 0 \right\}\).
График обратной пропорциональности (зависимости) – гипербола.
Коэффициент \( \displaystyle k\)
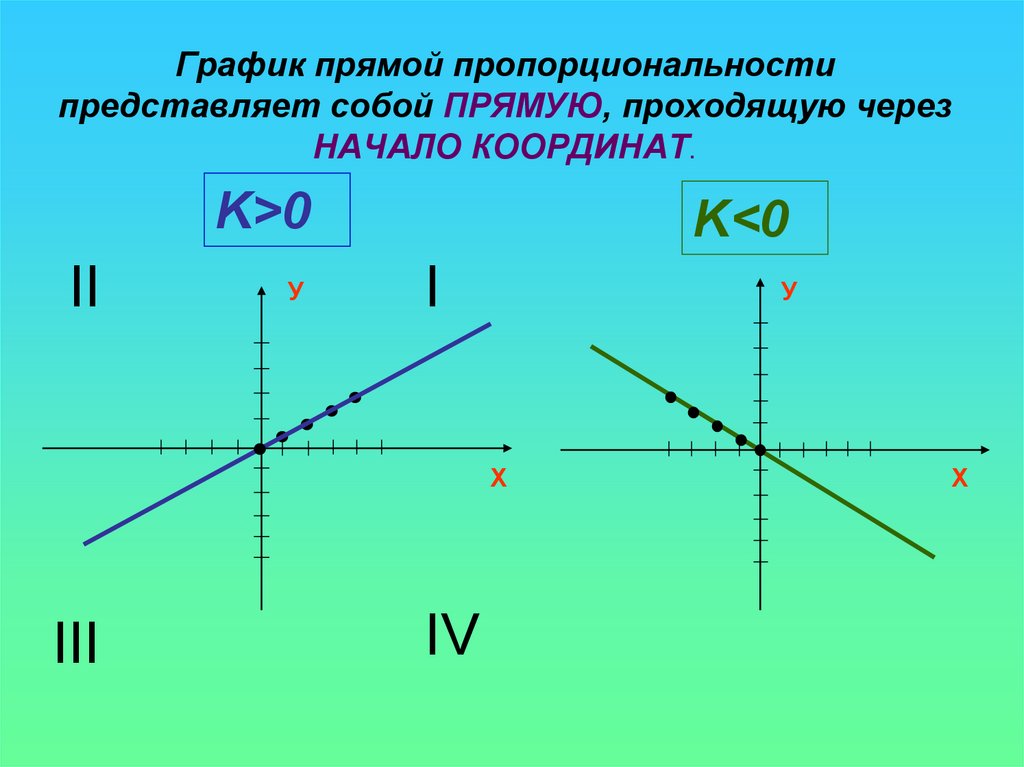
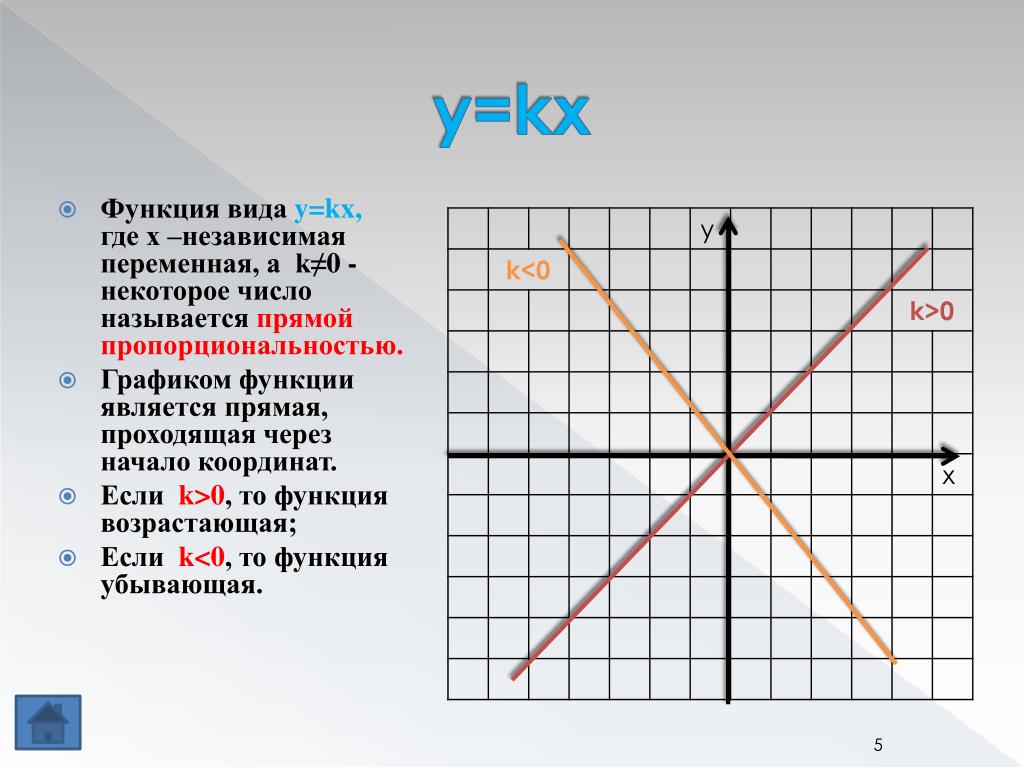
\( \displaystyle k\) – отвечает за «пологость» и направление графика. Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).
Знак коэффициента \( \displaystyle k\) влияет на то, в каких четвертях расположен график:
если \( \displaystyle k>0\), то ветви гиперболы расположены в \( \displaystyle I\) и \( \displaystyle III\) четвертях;
если \( \displaystyle k<0\), то во \( \displaystyle II\) и \( \displaystyle IV\).
Коэффициент \( \displaystyle a\)
Если внимательно посмотреть на знаменатель, видим, что \( \displaystyle a\) – это такое число, которому не может равняться \( \displaystyle x\).
То есть \( x=a\) – это вертикальная асимптота, то есть вертикаль, к которой стремится график функции
Коэффициент \( b\)
Число \( b\) отвечает за смещение графика функции вверх на величину \( b\), если \( b>0\), и смещение вниз, если \( b<0\).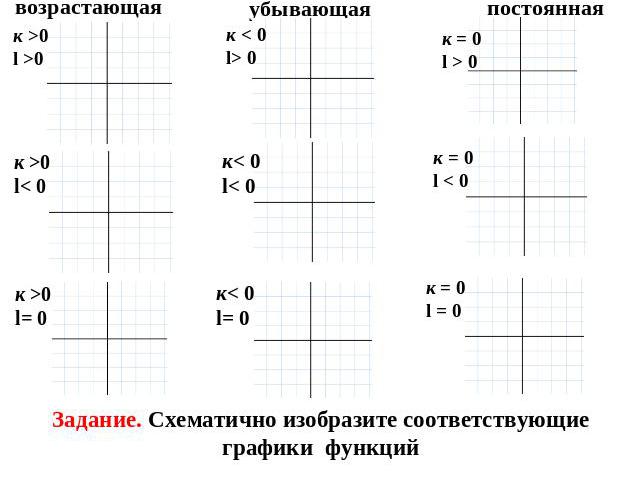
Следовательно, \( y=b\) – это горизонтальная асимптота.
Алгоритм построения графика функции \( \displaystyle y=\frac{k}{x-a}+b\)
- Определяем коэффициенты \( \displaystyle k\), \( \displaystyle a\) и \( \displaystyle b\).
- Строим график функции \( \displaystyle y=\frac{k}{x}\) (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).
- График должен быть сдвинут вправо на \( \displaystyle a\). Но проще двигать не график, а оси, так что ось \( \displaystyle Oy\) сдвигаем влево на \( \displaystyle a\).
- График должен быть сдвинут вверх на \( \displaystyle b\). Но проще двигать не график, а оси, так что ось \( \displaystyle Ox\) сдвигаем вниз на \( \displaystyle b\).
- Старые оси (прямые, которые служили нам осями в пункте 2) оставляем в виде пунктирных линий. Это теперь просто вертикальная и горизонтальная асимптоты.
Что такое функция
Ты помнишь, что функция – это определенного рода зависимость?
Если ты еще не читал тему «Функции», настоятельно рекомендую бросить все и прочитать, ведь нельзя изучать какую-либо конкретную функцию, не понимая, что это такое – функция.
Также очень полезно перед началом этой темы освоить две более простые функции: линейную и квадратичную.
Там ты закрепишь понятие функции и научишься работать с коэффициентами и графиками.
Ну и на всякий случай немного повторим…
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Что значит «допустимому значению»?
Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции»!
Все дело в понятии «область определения»: для некоторых функций не все аргументы можно подставить в зависимость. Например, для функции \( y=\sqrt{x}\) отрицательные значения аргумента \( x\) – недопустимы.
Например, для функции \( y=\sqrt{x}\) отрицательные значения аргумента \( x\) – недопустимы.
Функция, описывающая обратную зависимость
Это функция вида \( \displaystyle y=\frac{k}{x}\), где \( k\ne 0\).
По-другому ее называют обратной пропорциональностью: увеличение аргумента вызывает пропорциональное уменьшение функции.
Давай определим область определения. Чему может быть равен \( x\)? Или, по-другому, чему он не может быть равен?
Единственное число, на которое нельзя делить – это \( 0\), поэтому \( x\ne 0\):
\( D\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\)
или, что то же самое,
\( D\left( y \right)=\mathbb{R}\backslash \left\{ 0 \right\}\)
Такая запись означает, что \( x\) может быть любым числом, кроме \( 0\).
- Знак «\( \mathbb{R}\)» обозначает множество действительных чисел, то есть всех возможных чисел.
- Знаком «\( \backslash \)» обозначается исключение чего-нибудь из этого множества (аналог знака «минус»).

- Число \( 0\) в фигурных скобках означает просто число \( 0\).
Получается, что из всех возможных чисел мы исключаем \( 0\)).
Множество значений функции, оказывается, точно такое же: ведь если \( k\ne 0\), то на что бы мы его не делили, \( 0\) не получится:
\( E\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\) или \( E\left( y \right)=\mathbb{R}\backslash \left\{ 0 \right\}\).
Также возможны некоторые вариации формулы \( y=\frac{k}{x}\). Например, \( y=\frac{k}{x+a}\) – это тоже функция, описывающая обратную зависимость.
Определи самостоятельно область определения и область значений этой функции. Должно получиться:
- \( D\left( y \right)=\left( -\infty ;-a \right)\cup \left( -a;+\infty \right)\)
- \( E\left( y \right)=\left( -\infty ;0 \right)\cup \left( 0;+\infty \right)\).
 {2}}-25}=\frac{x-5}{\left( x-5 \right)\left( x+5 \right)}=\frac{1}{x+5},\text{ }x\ne 5\).
{2}}-25}=\frac{x-5}{\left( x-5 \right)\left( x+5 \right)}=\frac{1}{x+5},\text{ }x\ne 5\).Действительно, мы получили обратную зависимость, но с оговоркой: \( x\ne 5\).
Почему так? А потому, что выражение \( \left( x-5 \right)\) было в исходном выражении в знаменателе, поэтому если мы возьмём значение \( x=5\) и подставим его в исходную функцию (а ведь именно её нам нужно исследовать), то что мы получим?
Ноль, делённый на ноль. Но ведь на ноль нельзя делить ничего, даже другой ноль. Поэтому \( x\) никак не может быть равен \( 5\).
Но почему тогда мы также не пишем \( x\ne -5\)? Оно ведь тоже в знаменателе!
А всё потому, что оно как было в знаменателе, так там и осталось, следовательно мы и так видим, что такое значение икса невозможно.
А поэтому — зачем лишний раз писать? Да-да, математики — народ ленивый, без надобности напрягаться не станут:)
Вот еще пример: \( \displaystyle y=\frac{x+2}{x-3}\).
Тут сложнее: ведь числитель и знаменатель теперь уж точно не сокращаются. Но все-же мы можем попробовать:
Но все-же мы можем попробовать:
\( \displaystyle y=\frac{x+2}{x-3}=\frac{x-3+3+2}{x-3}=\frac{\left( x-3 \right)+5}{x-3}\)
Ты понял, что я сделал? В числителе я добавил и вычел одно и то же число (\( 3\)), таким образом я вроде бы ничего не изменил, но теперь в числителе есть часть, равная знаменателю.
Теперь я почленно поделю, то есть разобью эту дробь на сумму двух дробей:
\( \displaystyle y=\frac{\left( x-3 \right)+5}{x-3}=\frac{x-3}{x-3}+\frac{5}{x-3}\)
(и правда, если привести то что у меня получилось к общему знаменателю, получится как-раз наша начальная дробь):
\( \displaystyle y=\underbrace{\left( \frac{x-3}{x-3} \right)}_{=1}+\frac{5}{x-3}=1+\frac{5}{x-3}.\)
Ух ты! Снова получается обратная пропорциональность, только теперь к ней еще прибавляется число \( \displaystyle 1\).
Этот метод нам очень пригодится позже при построении графиков.
Решения
Пример 1
\( \displaystyle y=1-\frac{3}{x+2}\)
Пример 2
Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»). {2}}+4{x}-5=\left( x+5 \right)\left( x-1 \right)\), следовательно:
{2}}+4{x}-5=\left( x+5 \right)\left( x-1 \right)\), следовательно:
\( \displaystyle y=\frac{x+5}{\left( x+5 \right)\left( x-1 \right)}=\frac{1}{x-1},\text{ }x\ne -5\)
Пример 3
Ты уже попробовал решить сам? В чем загвоздка?
Наверняка в том, что в числителе у нас \( \displaystyle 2x\), а в знаменателе – просто \( \displaystyle x\).
Это не беда. Нам нужно будет сократить на \( \displaystyle \left( x+2 \right)\), поэтому в числителе следует вынести \( \displaystyle 2\) за скобки (чтобы в скобках \( \displaystyle x\) получился уже без коэффициента):
\( \displaystyle y=\frac{2{x}-3}{x+1}=\frac{2\left( x-\frac{3}{2} \right)}{x+1}=2\cdot \frac{x-1,5}{x+1}=2\cdot \frac{x+1-1-1,5}{x+1}=…\) дальше сам.
Ответ: \( \displaystyle y=2-\frac{5}{x+1}\).
График обратной пропорциональности
Как всегда, начнем с самого простого случая: \( \displaystyle y=\frac{1}{x}\).
Составим таблицу.
Таблица обратной пропорциональности (зависимости)
| \( \displaystyle \mathbf{x}\) | \( \displaystyle -3\) | \( \displaystyle -2\) | \( \displaystyle -1\) | \( \displaystyle -0,5\) | \( \displaystyle 0,5\) | \( \displaystyle 1\) | \( \displaystyle 2\) | \( \displaystyle 3\) | \( \displaystyle 4\) |
| \( \displaystyle \mathbf{y}\) | \( \displaystyle -\frac{1}{3}\) | \( \displaystyle -\frac{1}{2}\) | \( \displaystyle -1\) | \( \displaystyle -2\) | \( \displaystyle 2\) | \( \displaystyle \;1\) | \( \displaystyle \frac{1}{2}\) | \( \displaystyle \frac{1}{3}\) | \( \displaystyle \frac{1}{4}\) |
Нарисуем точки на координатной плоскости:
Теперь их надо плавно соединить, но как?
Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии.
Это график гиперболы и выглядит он так:
Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом.
Каждая из них стремится своими концами приблизиться к осям \( \displaystyle Ox\) и \( \displaystyle Oy\), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина:
Оно и понятно: так как \( \displaystyle x\ne 0\), график не может пересекать ось \( \displaystyle Oy\). Но и \( \displaystyle y\ne 0\), так что график никогда не коснется и оси \( \displaystyle Ox\).
Ну что же, теперь посмотрим на что влияют коэффициенты.
На что влияют коэффициенты
Рассмотрим такие функции:
\( \displaystyle y=\frac{1}{x};\text{ }y=\frac{2}{x};\text{ }y=\frac{4}{x};\text{ }y=-\frac{1}{x};\text{ }y=-\frac{3}{x}\):
Ух ты, какая красота!
Все графики построены разными цветами, чтобы легче было их друг от друга отличать.
Итак, на что обратим внимание в первую очередь?
Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси \( \displaystyle Ox\).
Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.
А что, если функция выглядит сложнее, например, \( \displaystyle y=\frac{1}{x-1}+2\)?
В этом случае гипербола будет точно такой же, как обычная \( \displaystyle y=\frac{1}{x}\), только она немного сместится. Давай думать, куда?
Чему теперь не может быть равен \( x\)? Правильно, \( x\ne 1\). Значит, график никогда не достигнет прямой \( x=1\).
А чему не может быть равен \( y\)? Теперь \( y\ne 2\). Значит, теперь график будет стремиться к прямой \( y=2\), но никогда ее не пересечет.
Итак, теперь прямые \( x=1\) и \( y=2\) выполняют ту же роль, которую выполняют координатные оси для функции \( \displaystyle y=\frac{1}{x}\).
Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):
Более подробно о том, как строятся такие графики, мы выучим чуть позже.
А теперь попробуй решить несколько примеров для закрепления.
Обратная пропорциональность в жизни
Где же нам встречается такая функция на практике? Примеров множество. Самый распространенный – это движение: чем больше скорость, с которой мы движемся, тем меньшее время нам потребуется, чтобы преодолеть одно и то же расстояние.
И правда, вспомним формулу скорости: \( \displaystyle v=\frac{S}{t}\), где \( v\) – скорость, \( t\) – время в пути, \( S\) – расстояние (путь).
Отсюда можно выразить время: \( \displaystyle t=\frac{S}{v}\)
Пример:
Человек едет на работу со средней скоростью \( 40\) км/ч, и доезжает за \( 1\) час. Сколько минут он потратит на эту же дорогу, если будет ехать со скоростью \( 60\) км/ч?
Решение:
Вообще, такие задачи ты уже решал в 5 и 6 классе. Ты составлял пропорцию:
Ты составлял пропорцию:
\( \displaystyle 60\) км/ч – \( 60\) мин.
\( \displaystyle 60\) км/ч – \( x\) мин.
Далее ты определял, что это обратная пропорциональность, так как чем больше скорость, тем меньше время. Значит, чтобы решить эту пропорцию, нужно поделить числа «крест-накрест»:
\( \displaystyle \frac{40}{x}=\frac{60}{60}\text{ }\Rightarrow \text{ }x=40\)(мин).
То есть понятие обратной пропорциональности тебе уже точно знакомо. Вот и вспомнили. А теперь то же самое, только по-взрослому: через функцию.
Функция (то есть зависимость) времени в минутах от скорости:
\( \displaystyle t\left( v \right)=\frac{S}{v}\).
Известно, что \( t\left( 40 \right)=60\), тогда:
\( \frac{S}{40}=60\text{ }\Rightarrow \text{ }S=40\cdot 60=2400\).
Нужно найти \( t\left( 60 \right)\):
\( \displaystyle t\left( 60 \right)=\frac{2400}{60}=40\) (мин).
Теперь придумай сам несколько примеров из жизни, в которых присутствует обратная пропорциональность.
Придумал? Молодец, если да. Удачи!
Принципы построения графика обратной пропорциональности (гиперболы)
Теперь давай научимся строить простейшую гиперболу – \( \displaystyle y=\frac{k}{x}\).
Достаточно помнить, как она выглядит, и тогда нам хватит всего трех-четырех точек.
Например, построим гиперболу \( \displaystyle y=\frac{3}{x}\).
Составим таблицу из \( 4\) точек, которые принадлежат одной ветке (например, правой):
| \( x\) | \( \frac{1}{2}\) | \( \displaystyle 1\) | \( \displaystyle 3\) | \( \displaystyle 6\) |
| \( y\) | \( \displaystyle 6\) | \( \displaystyle 3\) | \( \displaystyle 1\) | \( \frac{1}{2}\) |
Отмечаем точки на рисунке:
Проводим через них плавную линию, которая краями приближается к осям:
Это одна ветвь гиперболы
Проверить правильность построения этой кривой можно так: она должна быть симметрична относительно биссектрисы угла между осями координат:
Отлично, осталось вспомнить, что собой представляет вторая ветвь?
Это точно такая же кривая, расположенная симметрично относительно начала координат. То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы.
То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы.
Вот:
Еще один полезный факт.
Посмотри на красные точки на графике. Видно, что их абсцисса совпадает с ординатой. Так вот, эти абсцисса с ординатой равны \( \sqrt{k}\) для правой ветви гиперболы, и \( -\sqrt{k}\) для левой.
Для функций, у которых \( k\) – точный квадрат (например, \( 1\), \( 4\) или \( \displaystyle \frac{1}{4}\)), эту точку, относительно которой ветвь гиперболы симметрична, будет очень легко поставить.
В этом случае достаточно даже трех точек, чтобы построить график.
Например, построим график функции \( \displaystyle y=\frac{4}{x}\)
Как и в прошлый раз, начнем с правой ветви.
Точка симметрии: \( \displaystyle x=y=2\). Выберем еще одну точку, например, \( \displaystyle x=1\), \( \displaystyle y=4\). У третьей точки координаты будут наоборот: \( \displaystyle x=4\), \( \displaystyle y=1\).
Рисуем:
И теперь симметрично отображаем эту ветвь в третью координатную четверть:
Теперь выясним, что будет, если \( \displaystyle k<0\)?
Очень просто: если есть график функции с таким же по величине, но положительным \( \displaystyle k\), то нужно просто отразить его относительно оси \( \displaystyle Ox\)
То есть правая ветвь теперь будет ниже оси \( \displaystyle Ox\) (в \( \displaystyle IV\) четверти), а левая – выше (в \( \displaystyle III\) четверти).
Принцип построения же останется прежним:
Ну что же, осталось объединить все то, что мы уже выяснили в один алгоритм:
Алгоритм построения гиперболы
Алгоритм построения графика функции \( \displaystyle y=\frac{k}{x-a}+b\)
- Определяем коэффициенты \( \displaystyle k\), \( \displaystyle a\) и \( \displaystyle b\).
- Строим график функции \( \displaystyle y=\frac{k}{x}\) (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).
 {2}}-4{x}-15}=1-\frac{1}{2x+3}=\frac{-\frac{1}{2}}{x+\frac{3}{2}}+1,\text{ }x\ne \frac{5}{2}\).
{2}}-4{x}-15}=1-\frac{1}{2x+3}=\frac{-\frac{1}{2}}{x+\frac{3}{2}}+1,\text{ }x\ne \frac{5}{2}\).\( \displaystyle k=-\frac{1}{2}\), \( \displaystyle a=-\frac{3}{2}\), \( b=1\), выколотая точка \( \displaystyle x\ne \frac{5}{2}\):
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики.
На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).
Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.

Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Требования к средствам учета электроэнергии
Для учета электрической энергии используются приборы учета, типы которых утверждены федеральным органом исполнительной власти по техническому регулированию и метрологии и внесены в государственный реестр средств измерений.
Технические параметры и метрологические характеристики счётчиков электрической энергии должны соответствовать требованиям ГОСТ 52320-2005 Часть 11 «Счетчики электрической энергии», ГОСТ Р 52323-2005 Часть 22 «Статические счетчики активной энергии классов точности 0,2S и 0,5S», ГОСТ Р 52322-2005 Часть 21 «Статические счетчики ивной энергии классов точности 1 и 2» (для реактивной энергии — ГОСТ Р 52425−2005 «Статические счетчики реактивной энергии»).

Основным техническим параметром электросчетчика является «класс точности», который указывает на уровень погрешности измерений прибора. Классы точности приборов учета определяются в соответствии с техническими регламентами и иными обязательными требованиями, установленными для классификации средств измерений.
Требования к приборам учета электрической энергии, потребляемой юридическими лицами:
1. В зависимости от значения максимальной мощности (указанной в акте разграничения) и уровня напряжения на месте установки измерительного комплекса класс точности прибора учёта должен быть:
· Для точек присоединения к объектам электросетевого хозяйства напряжением 35 кВ и ниже с максимальной мощностью (согласно акту разграничения) менее 670 кВт — счетчики класса точности не менее 1,0.
· Для точек присоединения к объектам электросетевого хозяйства напряжением 110 кВ и выше класса точности не менее 0,5S.

Для учета электрической энергии, потребляемой потребителями с максимальной мощностью не менее 670 кВт, подлежат использованию счетчики, позволяющие измерять почасовые объемы потребления электрической энергии, класса точности не менее 0,5S, обеспечивающие хранение данных о почасовых объемах потребления электрической энергии за последние 90 дней и более или включенные в систему учета.
(основание п. 139 ПП РФ №442 от 04.05.2012)
2. На винтах, крепящих корпус счётчика должна быть пломба с клеймом госповерителя (основание п. 1.5.13 ПУЭ).
3. На крышке клеммной колодки счётчика должна быть пломба энергоснабжающей организации (основание п. 1.5.13 ПУЭ).
4. Прибор учёта должен быть допущен в эксплуатацию в установленном порядке (основание п. 137 ПП РФ №442 от 04.05.2012).
5. Собственник прибора учёта обязан:
· обеспечить эксплуатацию прибора учёта;
· обеспечить сохранность и целостность прибора учёта, а также пломб и (или) знаков визуального контроля;
· обеспечить снятие и хранение показаний прибора учёта;
· обеспечить своевременную замену прибора учёта;
(основание п.
 145 ПП РФ №442 от 04.05.2012).
145 ПП РФ №442 от 04.05.2012).6.Энергоснабжающая организация должна пломбировать:
клеммники трансформаторов тока;
крышки переходных коробок, где имеются цепи к электросчетчикам;
токовые цепи расчетных счетчиков в случаях, когда к трансформаторам тока совместно со счетчиками присоединены электроизмерительные приборы и устройства защиты;
испытательные коробки с зажимами для шунтирования вторичных обмоток трансформаторов тока и места соединения цепей напряжения при отключении расчетных счетчиков для их замены или поверки;решетки и дверцы камер, где установлены трансформаторы тока;
решетки или дверцы камер, где установлены предохранители на стороне высокого и низкого напряжения трансформаторов напряжения, к которым присоединены расчетные счетчики;
приспособления на рукоятках приводов разъединителей трансформаторов напряжения, к которым присоединены расчетные счетчики.
Во вторичных цепях трансформаторов напряжения, к которым подсоединены расчетные счетчики, установка предохранителей без контроля за их целостностью с действием на сигнал не допускается.

Поверенные расчетные счетчики должны иметь на креплении кожухов пломбы организации, производившей поверку, а на крышке колодки зажимов счетчика пломбу энергоснабжающей организации.
Для защиты от несанкционированного доступа электроизмерительных приборов, коммутационных аппаратов и разъемных соединений электрических цепей в цепях учета должно производиться их маркирование специальными знаками визуального контроля в соответствии с установленными требованиями.
(Основание – п. 2.11.18 Правил технической эксплуатации электроустановок потребителей)
Требования к учету электрической энергии с применением измерительных трансформаторов:
Измерительные трансформаторы тока по техническим требованиям должны соответствовать ГОСТ 7746-2001 («Трансформаторы тока. Общие технические условия»).
1. Класс точности измерительных трансформаторов, используемых в измерительных комплексах для установки (подключения) приборов учета, должен быть не ниже 0,5.
 (основание п. 139 ПП РФ №442 от 04.05.2012).
(основание п. 139 ПП РФ №442 от 04.05.2012).2. Допускается применение трансформаторов тока с завышенным коэффициентом трансформации (по условиям электродинамической и термической стойкости или защиты шин), если при максимальной нагрузке присоединения ток во вторичной обмотке трансформатора тока будет составлять не менее 40% номинального тока счетчика, а при минимальной рабочей нагрузке — не менее 5% (основание п. 1.5.17 ПУЭ).
3. Присоединение токовых обмоток счетчиков к вторичным обмоткам трансформаторов тока следует проводить, отдельно от цепей защиты и совместно с электроизмерительными приборами (основание п. 1.5.18 ПУЭ).
4. Использование промежуточных трансформаторов тока для включения расчетных счетчиков запрещается (основание п. 1.5.18 ПУЭ).
5. Нагрузка вторичных обмоток измерительных трансформаторов, к которым присоединяются счетчики, не должна превышать номинальных значений (основание п.
 1.5.19 ПУЭ).
1.5.19 ПУЭ).6. Сечение и длина проводов и кабелей в цепях напряжения расчетных счетчиков должны выбираться такими, чтобы потери напряжения в этих цепях составляли не более 0,25 % номинального напряжения при питании от трансформаторов напряжения класса точности 0,5. Для обеспечения этого требования допускается применение отдельных кабелей от трансформаторов напряжения до счетчиков (основание п. 1.5.19 ПУЭ).
7. Измерительные трансформаторы напряжения по техническим характеристикам должны соответствовать ГОСТ 1983-2001 («Трансформаторы напряжения. Общие технические условия»).
Требования к приборам учета электрической энергии, потребляемой гражданами (физическими лицами):
1. Счётчики должны иметь класс точности не менее 2,0 (основание п. 138 ПП РФ №442 от 04.05.2012).
2. На винтах, крепящих корпус счётчика должна быть пломба с клеймом госповерителя (основание п. 1.5.13 ПУЭ).
3. На крышке клеммной колодки счётчика должна быть пломба энергоснабжающей организации (основание п.
 1.5.13 ПУЭ).
1.5.13 ПУЭ).4. К использованию допускаются приборы учета утвержденного типа и прошедшие поверку в соответствии с требованиями законодательства Российской Федерации об обеспечении единства измерений (основание п. 80 ПП РФ №354 от 06.05.2011г.).
5. Оснащение жилого или нежилого помещения приборами учета, ввод установленных приборов учета в эксплуатацию, их надлежащая техническая эксплуатация, сохранность и своевременная замена должны быть обеспечены собственником жилого или нежилого помещения.
Ввод установленного прибора учета в эксплуатацию, то есть документальное оформление прибора учета в качестве прибора учета, по показаниям которого осуществляется расчет размера платы за коммунальные услуги, осуществляется исполнителем в том числе на основании заявки собственника жилого или нежилого помещения, поданной исполнителю. (основание п. 81 ПП РФ №354 от 06.05.2011г.).
6. Эксплуатация, ремонт и замена приборов учета осуществляются в соответствии с технической документацией.
 Поверка приборов учета осуществляется в соответствии с положениями законодательства Российской Федерации об обеспечении единства измерений (основание п. 81(10) ПП РФ №354 от 06.05.2011г.).
Поверка приборов учета осуществляется в соответствии с положениями законодательства Российской Федерации об обеспечении единства измерений (основание п. 81(10) ПП РФ №354 от 06.05.2011г.).7. Прибор учета должен быть защищен от несанкционированного вмешательства в его работу (основание п. 81(11) ПП РФ №354 от 06.05.2011г.).
Минеральные вещества | Tervisliku toitumise informatsioon
В человеческом организме установлено наличие более 70 химических элементов. Достоверно установлена потребность в более чем 20 биоэлементах. Для обеспечения достаточного количества этих элементов крайне важно, чтобы питание было разнообразным.
Встречающиеся в организме минеральные вещества можно условно разделить на две группы:
- Содержание макроэлементов в организме составляет более 0,01%. Ими являются фосфор (P), кальций (Ca), натрий (Na), калий (K), магний (Mg), сера (S), хлор (Cl) (см Таблица 1).
- Содержание микроэлементов – менее 0,01%, у некоторых даже 0,00001.

Потребность в некоторых микроэлементах установлена, это железо (Fe), цинк (Zn), медь (Cu), йод (I), селен (Se) , марганец (Mn), молибден (Mo), фтор (F), хром (Cr), кобальт (Co), кремний (Si), ванадий (V), бор (B), никель (Ni), мышьяк (As) и олово (Sn).
Помимо них в организме обнаружен целый ряд элементов, функция которых пока не ясна, их появление в организме может быть обусловлено загрязнением окружающей среды и частым соприкосновением с ними. Например, люди, работающие в теплицах, постоянно контактируют с химическими веществами, различные элементы могут быть признаком разного рода заболеваний. В числе таких элементов алюминий (Al), стронций (Sr), барий (Ba), рубидий (Rb), палладий (Pd), бром (Br).
В организм могут попадать и тяжелые, т.е. ядовитые металлы, такие как кадмий (Cd), ртуть (Hg) или свинец (Pb).
Минеральные вещества в нашем организме являются важными компонентами скелета, биологических жидкостей и энзимов и способствуют передаче нервных импульсов.

Люди и животные получают различные биологические элементы из пищи, воды и окружающего воздуха, самостоятельно синтезировать минеральные вещества живые организмы не могут. В растениях минеральные вещества накапливаются из почвы, и их количество зависит от места произрастания и наличия удобрений. В питьевой воде также имеются минеральные вещества, и их содержание зависит от места, откуда получают воду.
Несмотря на то, что человек нуждается в небольших количествах минеральных веществ (макроэлементов в миллиграммах и граммах, микроэлементов – в милли- и микрограммах), в его организме, тем не менее, отсутствуют достаточные запасы минеральных веществ, чтобы нормально перенести их долговременный дефицит. Потребность в минеральных веществах зависит также от возраста, пола и прочих обстоятельств (см Таблица 2). Например, повышенная потребность в железе у женщин связана с менструациями и беременностью, а спортсменам требуется больше натрия, потому что он интенсивно выводится с потом.

Чрезмерные количества минеральных веществ могут привести к сбоям в работе организма, потому что, будучи компонентами биоактивных соединений, они оказывают влияние на регуляторные функции. Получать чрезмерные количества минеральных веществ (за исключением натрия) с пищей практически невозможно, однако это может произойти при чрезмерном употреблении биологически активных добавок и обогащенных минеральными веществами продуктов.
Усвоению минеральных веществ могут препятствовать:
- злоупотребление кофе,
- употребление алкоголя,
- курение,
- некоторые лекарства,
- некоторые противозачаточные таблетки,
- определенные вещества, встречающиеся в некоторых продуктах, например, в ревене и шпинате.
Потери минеральных веществ при тепловой обработке продуктов питания значительно меньше, чем потери витаминов. Однако при рафинировании или очистке часть минеральных веществ удаляется. Поэтому важно есть больше цельнозерновых и нерафинированных продуктов.
 Минеральные вещества могут образовывать соединения с другими веществами, содержащимися в продуктах питания (например, с оксалатами в ревене), в результате чего организм не может их усвоить.
Минеральные вещества могут образовывать соединения с другими веществами, содержащимися в продуктах питания (например, с оксалатами в ревене), в результате чего организм не может их усвоить.Таблица 1
Названия и источники важнейших минеральных веществ
Обозначение
Название
Лучшие источники *
Макроэлементы
Na
натрий
поваренная соль (NaCl), готовая еда, сыр, ржаной хлеб, консервы, мясные продукты, оливки, картофельные чипсы
K
калий
растительные продукты: сушеные фрукты и ягоды, орехи, семена, топинамбур, картофель, редис, капуста, зеленые овощи, мука «Кама», свёкла, банан, ржаной хлеб, смородина, томаты
Ca
кальций
молоко и молочные продукты (особенно сыр), миндаль, орехи, семена, рыба (с костями), шпинат
Mg
магний
орехи, семена, мука «Кама», ржаной хлеб, шпинат, бобовые, греча, цельнозерновые продукты, свинина, говядина и курятина, банан, брокколи
P
фосфор
семена, орехи, молочные продукты (особенно сыр), печень, птица, говядина, ржаной хлеб, рыба, цельнозерновые продукты, бобовые
S
сера
продукты с белками, содержащими аминокислоты метионин (зерновые, орехи) и цистеин (мясо, рыба, соевые бобы, зерновые)
Cl
хлор
поваренная соль
Микроэлементы
Fe
железо
печень, кровяная колбаса, семечки, яйца, изюм, ржаной хлеб, нежирная говядина и свинина, цельнозерновые продукты, греча, клубника
Zn
цинк
печень, мясо, мука «Кама», семена, орехи, сыр, ржаной хлеб, бобовые, дары моря (крабы, салака), цельнозерновые продукты, яйца
Cu
медь
печень, какао-порошок, мясо, бобовые, цельнозерновые продукты, семена, орехи, греча, ржаной хлеб, лосось, авокадо, свёкла, дары моря
I
йод
йодированная соль, рыба и другие дары моря, сыр, яйца, некоторые виды ржаного хлеба и йогурта
Se
селен
арахис, печень, рыба и дары моря, семена подсолнечника, мясо
* Количество, содержащееся в 100 г продукта, покрывает не менее 10% суточной потребности взрослой женщины
Таблица 2
Рекомендуемые в зависимости от возраста суточные нормы потребления важнейших минеральных веществ
Возраст
Натрий, мг
Кальций, мг
Калий, г
Магний, мг
Железо, мг
Цинк, мг
Медь, мг
Йод, мкг
Селен, мкг
Дети
6–11 месяцев
до 650
550
1,1
80
8
5
0,3
60
15
12–23 месяца
до 830
600
1,4
85
8
6
0,3
90
25
2–5 лет
до 1580
600
1,8
120
8
6
0,4
90
30
6–9 лет
до 1580
700
2
200
9
7
0,5
120
30
Женщины
10–13 лет
до 2400
900
2,9
300
11
8
0,7
150
40
14–17 лет
до 2400
900
3,1
320
15
9
0,9
150
50
18–30 лет
до 2400
900
3,1
320
15
9
0,9
150
50
31–60 лет
до 2400
800
3,1
320
15
9
0,9
150
50
61–74 лет
до 2400
800
3,1
320
10
9
0,9
150
50
> 75 лет
до 2400
800
3,1
320
10
9
0,9
150
50
Беременные
до 2400
900
3,1
360
15
10
1
175
60
Кормящие матери
до 2400
900
3,1
360
15
11
1,3
200
60
Мужчины
10–13 лет
до 2400
900
3,3
300
11
11
0,7
150
40
14–17 лет
до 2400
900
3,5
380
11
12
0,9
150
60
18–30 лет
до 2400
900
3,5
380
10
9
0,9
150
60
31–60 лет
до 2400
800
3,5
380
10
9
0,9
150
60
61–74 лет
до 2400
800
3,5
380
10
10
0,9
150
60
> 75 лет
до 2400
800
3,5
380
10
10
0,9
150
60
* Для 18–20-летних рекомендуемая суточная доза составляет 900 мг кальция и 700 мг фосфора.

** Потребность в железе зависит от потери железа при менструациях. Для женщин в постменопаузе рекомендуемая дневная доза железа составляет 10 мг.
*** Для достижения сбалансированного содержания железа во время беременности в организме женщины должны иметься запасы железа как минимум на 500 мг больше, чем до беременности. В двух последних триместрах беременности, в зависимости от уровня железа в организме, может потребоваться дополнительный прием железа.
**** На самом деле, селена можно потреблять больше указанной в таблице рекомендованной дозы, поскольку селен по-разному всасывается из разных источников и происходит постоянное обеднение им поверхности, т.е. таблицы питательной ценности продуктов «не поспевают» за истинным положением дел (в них зачастую указываются значения больше реальных).Максимальные разовые безопасные дозы минеральных веществ и пищевых добавок:
Минеральное вещество Доза Кальций (мг) 2500 Фосфор (мг) 3000 Калий (мг) 3,7* Железо (мг) 60 Цинк (мг) 25 Медь (мг) 5 Йод (мкг) 600 Селен (мкг) 300 * Только из биоактивных добавок или обогащенной пищи
Экзотермический против эндотермического и K
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1347
- K c — константа равновесия (для концентраций)
- [A], [B], [C], [D] — концентрации
- a, b, c и d — стехиометрические коэффициенты сбалансированного уравнения
- Если K=1, то ни реагенты, ни продукты не являются предпочтительными. Обратите внимание, что это не то же самое, что предпочтение отдается обоим.
- Если в реакции преобладают реагенты, то К < 1. Чем меньше значение К, тем больше реакция будет клониться влево.
- 0,20 M \(\ce{h3}\),
- 0,10 М \(\ce{NO}\),
- 0,20 М \(\ce{h3O}\) и
- 0,10M \(\ce{N2}\).

- 92 }\\[4pt] &= 10 \end{align*}\]
- Ответить
Поскольку \(K_c = 10 > 1\), реакция идет в пользу продуктов.
- Ответ
Поскольку значение K уменьшается с повышением температуры, реакция является экзотермической.
- Ответ
В начальной реакции выделяется отрицательная энергия, поэтому реакция экзотермическая.
 Однако повышение температуры позволяет системе поглощать энергию и, таким образом, способствует эндотермической реакции; равновесие сместится влево.
Однако повышение температуры позволяет системе поглощать энергию и, таким образом, способствует эндотермической реакции; равновесие сместится влево.- Элисон Сэлмон, Никита Патель (UCD), Дипак Наллур (UCD)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Лицензия
- СС BY
- Показать страницу TOC
- № на стр.
- Теги
- Температурная зависимость константы равновесия
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 142272
- Знать взаимосвязь между свободной энергией и константой равновесия.
- Ответить
2,2 × 10 12
- \([{\textrm N_2}]\) = 2,00 М,
- \([{\textrm H_2}]\) = 7,00 М,
- \([{\textrm{NH}_3}]\) = 0,021 М,
- и Т = 100°С.

- Используя значение ΔG°, рассчитайте значение K с помощью уравнения \(\ref{18.36b}\)
- Подставьте значения K и Q в уравнение \(\ref{18.37}\), чтобы получить ΔG для реакции в нестандартных условиях. 9{4}} \)
\(=-77\textrm{ kJ}_2\)Поскольку ΔG < 0 и K > Q, реакция идет самопроизвольно в прямом направлении, как написано. Другими словами, чтобы достичь равновесия, реакция должна идти вправо.
Упражнение \(\PageIndex{2}\)
Рассчитайте ΔG для реакции \(N_{2g} + O_{2(g)} \rightleftharpoons 2NO_{g}\) в условиях: T = 423 K, [\(NO\)] = 0,0100 М, [\(O_2\)] = 0,200 М и [\(N_2\)] = 1,00 × 10 -4 М.
 Значение ΔG° для этой реакции равно + 22,7 кДж. В каком направлении пойдет реакция, чтобы достичь равновесия?
Значение ΔG° для этой реакции равно + 22,7 кДж. В каком направлении пойдет реакция, чтобы достичь равновесия?- Ответить
ΔG = +28,3 кДж; реакция несамопроизвольна вправо, как написано, поэтому реакция пойдет влево, чтобы достичь равновесия. Это можно проверить тем, что K < Q.
Зависимость константы равновесия от температуры
Тот факт, что ΔG° и K связаны, дает нам другое объяснение того, почему константы равновесия зависят от температуры. Эта взаимосвязь явно показана в уравнении \(\ref{18.36b}\), которое можно изменить следующим образом: 9\circ}{R} \label{18.40}\]
Предполагая, что ΔH° и ΔS° не зависят от температуры, для экзотермической реакции (ΔH° < 0) величина K уменьшается с повышением температуры, тогда как для эндотермической реакции (ΔH° > 0) величина K увеличивается с ростом температуры. Количественная зависимость, выраженная в уравнении \(\ref{18.40}\), согласуется с качественными прогнозами, сделанными с применением принципа Ле Шателье.
 Поскольку в экзотермической реакции выделяется тепло, добавление тепла (за счет повышения температуры) сдвинет равновесие влево в пользу реагентов и уменьшит величину K. И наоборот, поскольку тепло расходуется в эндотермической реакции, добавление тепла сместит равновесие равновесие вправо, в пользу продуктов и увеличения величины K. Уравнение \(\ref{18.40}\) также показывает, что величина ΔH ° определяет, насколько быстро K изменяется в зависимости от температуры. Напротив, величина и знак ΔS° влияют на величину K, но не на ее температурную зависимость.
Поскольку в экзотермической реакции выделяется тепло, добавление тепла (за счет повышения температуры) сдвинет равновесие влево в пользу реагентов и уменьшит величину K. И наоборот, поскольку тепло расходуется в эндотермической реакции, добавление тепла сместит равновесие равновесие вправо, в пользу продуктов и увеличения величины K. Уравнение \(\ref{18.40}\) также показывает, что величина ΔH ° определяет, насколько быстро K изменяется в зависимости от температуры. Напротив, величина и знак ΔS° влияют на величину K, но не на ее температурную зависимость.Если мы знаем значение K при данной температуре и значение ΔH° для реакции, мы можем оценить значение K при любой другой температуре, даже при отсутствии информации о ΔS°. Предположим, например, что K 1 и K 2 — константы равновесия реакции при температурах T 1 и T 2 соответственно. Применение уравнения \(\ref{18.40}\) дает следующее соотношение для каждой температуры:
\[\begin{align}\ln K_1&=\dfrac{-\Delta H^\circ}{RT_1}+\dfrac{ \Дельта S^\circ}{R} 9\circ}{R}\left(\dfrac{1}{T_1}-\dfrac{1}{T_2}\right) \label{18.
 41}\]
41}\]Таким образом, рассчитывая ΔH° из табличных энтальпий образования и измеряя константы равновесия при одной температуре (K 1 ) позволяют вычислить значение константы равновесия при любой другой температуре (K 2 ), предполагая, что ΔH° и ΔS° не зависят от температуры.
Резюме
И K, и ΔG° можно использовать для прогнозирования соотношения продуктов и реагентов в равновесии для данной реакции. ΔG° связано с K уравнением \(ΔG°= −RT\ln K \).
- Если ΔG° < 0, то K > 1, и в равновесии продукты имеют преимущество перед реагентами.
- Если ΔG° > 0, то K < 1, и реагенты имеют преимущество перед продуктами, находящимися в равновесии.
- Если ΔG° = 0, то K = 1, и количество продуктов будет примерно равно количеству реагентов в равновесии. Это редкое явление для химических реакций.
Если система не находится в равновесии, ΔG и Q можно использовать, чтобы сказать нам, в каком направлении должна идти реакция, чтобы достичь равновесия.
 ΔG связано с Q уравнением \(ΔG= RT\ln \dfrac{Q}{K} \).
ΔG связано с Q уравнением \(ΔG= RT\ln \dfrac{Q}{K} \).- Если ΔG < 0, то K > Q, и для достижения равновесия реакция должна идти вправо.
- Если ΔG > 0, то K < Q, и для достижения равновесия реакция должна идти влево.
- Если ΔG = 0, то K = Q и реакция находится в равновесии.
Мы можем использовать измеренную константу равновесия K при одной температуре вместе с ΔH° для оценки константы равновесия реакции при любой другой температуре.
Авторы
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать страницу TOC
- № на стр.

- Метки
- источник-хим-47055
Конические сечения и стандартные формы уравнений
Горячая математикаА коническое сечение является пересечением плоскости и двойной правой окружности конус . Изменяя угол и место пересечения, мы можем создавать различные типы коник. Существует четыре основных типа: круги , эллипсы , гиперболы а также параболы . Ни одно из пересечений не будет проходить через вершины конуса.
Если прямой круговой конус разрезается плоскостью, перпендикулярной оси конуса, пересечение представляет собой окружность. Если плоскость пересекает одну из частей конуса и его ось, но не перпендикулярна оси, то пересечение будет эллипсом. Чтобы образовалась парабола, пересекающая плоскость должна быть параллельна одной стороне конуса и должна пересекать одну часть двойного конуса.
 И, наконец, для создания гиперболы плоскость пересекает обе части конуса. Для этого наклон пересекающейся плоскости должен быть больше, чем у конуса.
И, наконец, для создания гиперболы плоскость пересекает обе части конуса. Для этого наклон пересекающейся плоскости должен быть больше, чем у конуса.Общее уравнение для любого конического сечения:
А Икс 2 + Б Икс у + С у 2 + Д Икс + Е у + Ф знак равно 0 куда А , Б , С , Д , Е а также Ф являются константами.
При изменении значений некоторых констант изменится и форма соответствующей коники. Важно знать различия в уравнениях, чтобы помочь быстро определить тип коники, представленной данным уравнением.
Если Б 2 − 4 А С меньше нуля, то если коника существует, то это будет либо окружность, либо эллипс.
Если Б 2 − 4 А С равна нулю, то если коника существует, то это будет парабола.
Если Б 2 − 4 А С больше нуля, то если коника существует, то это будет гипербола.СТАНДАРТНЫЕ ФОРМЫ УРАВНЕНИЙ КОНИЧЕСКИХ СЕЧЕНИЙ:
Круг ( Икс − час ) 2 + ( у − к ) 2 знак равно р 2 Центр ( час , к ) .

Радиус р .
Эллипс с горизонтальной большой осью ( Икс − час ) 2 а 2 + ( у − к ) 2 б 2 знак равно 1 Центр ( час , к ) .
Длина большой оси 2 а .
Длина малой оси 2 б .
Расстояние между центром и любым фокусом с с
с 2 знак равно а 2 − б 2 , а > б > 0 .
Эллипс с вертикальной большой осью ( Икс − час ) 2 б 2 + ( у − к ) 2 а 2 знак равно 1 Центр ( час , к ) .
Длина большой оси 2 а .
Длина малой оси 2 б .
Расстояние между центром и любым фокусом с с
с 2 знак равно а 2 − б 2 , а > б > 0 .
Гипербола с горизонтальной поперечной осью ( Икс − час ) 2 а 2 − ( у − к ) 2 б 2 знак равно 1 Центр ( час , к ) .
Расстояние между вершинами равно 2 а .
Расстояние между фокусами 2 с .
с 2 знак равно а 2 + б 2Гипербола с вертикальной поперечной осью ( у − к ) 2 а 2 − ( Икс − час ) 2 б 2 знак равно 1 Центр ( час , к ) .

Расстояние между вершинами равно 2 а .
Расстояние между фокусами 2 с .
с 2 знак равно а 2 + б 2Парабола с горизонтальной осью ( у − к ) 2 знак равно 4 п ( Икс − час ) ,
п ≠ 0
Вершина ( час , к ) .

Фокус есть ( час + п , к ) .
Directrix это линия
Икс знак равно час − п
Ось это линия у знак равно кПарабола с вертикальной осью ( Икс − час ) 2 знак равно 4 п ( у − к ) ,
п ≠ 0
Вершина ( час , к ) .

Фокус есть ( час , к + п ) .
Directrix это линия
у знак равно к − п .
Ось это линия Икс знак равно часРешение систем уравнений
Вы должны быть знакомы с решение системы линейных уравнений . Геометрически это дает точку (точки) пересечения двух или более прямых линий. Точно так же решения системы квадратных уравнений давали бы точки пересечения двух или более коник.
Алгебраически система квадратных уравнений может быть решена с помощью устранение или же замена как и в случае линейных систем.
Пример:
Решите систему уравнений.

Икс 2 + 4 у 2 знак равно 16 Икс 2 + у 2 знак равно 9
Коэффициент Икс 2 одинаково для обоих уравнений. Итак, вычтем второе уравнение из первого, чтобы исключить переменную Икс . Вы получаете:
3 у 2 знак равно 7
Решение для у :
3 у 2 3 знак равно 7 3 у 2 знак равно 7 3 у знак равно ± 7 3
Используйте значение у оценить Икс .

Икс 2 + 7 3 знак равно 9 Икс 2 знак равно 9 − 7 3 знак равно 20 3 Икс знак равно ± 20 3
Следовательно, решения ( + 20 3 , + 7 3 ) , ( + 20 3 , − 7 3 ) , ( − 20 3 , + 7 3 ) а также ( − 20 3 , − 7 3 ) .

Экзотермическая реакция происходит, когда температура системы повышается из-за выделения тепла. Это тепло выделяется в окружающую среду, что приводит к общему отрицательному количеству теплоты реакции (\(q_{rxn} <0\)). эндотермическая реакция происходит, когда температура изолированной системы снижается, в то время как окружающая среда неизолированной системы нагревается. Эндотермические реакции приводят к общей положительной теплоте реакции (\(q_{rxn} > 0\)).
Это тепло выделяется в окружающую среду, что приводит к общему отрицательному количеству теплоты реакции (\(q_{rxn} <0\)). эндотермическая реакция происходит, когда температура изолированной системы снижается, в то время как окружающая среда неизолированной системы нагревается. Эндотермические реакции приводят к общей положительной теплоте реакции (\(q_{rxn} > 0\)).
Экзотермические и эндотермические реакции вызывают различия в уровнях энергии и, следовательно, различия в энтальпии (\(ΔH\)), сумме всех потенциальных и кинетических энергий. ΔH определяется системой, а не окружающей средой в реакции. Система, которая выделяет тепла в окружающую среду, экзотермическая реакция, имеет отрицательную ΔH условно, потому что энтальпия продуктов ниже, чем энтальпия реагентов системы.
\[ \ce{C(т) + O2(г) -> CO2(г)} \tag{ΔH = –393,5 кДж} \]
\[\ce{ h3(г) + 1/2 O2(г) -> h3O(ж)} \tag{ΔH = –285,8 кДж} \]
Энтальпии этих реакций на меньше, чем на нуля, и, следовательно, являются экзотермическими реакциями. Система реагентов, которая поглощает тепла из окружающей среды в эндотермической реакции имеет положительное \(ΔH\), так как энтальпия продуктов выше, чем энтальпия реагентов системы.
Система реагентов, которая поглощает тепла из окружающей среды в эндотермической реакции имеет положительное \(ΔH\), так как энтальпия продуктов выше, чем энтальпия реагентов системы.
\[ \ce{N2(г) + O2(г) -> 2NO(г)} \tag{ΔH = +180,5 кДж > 0}\]
\[ \ce{ C(s) + 2S(s) -> CS2(l)} \tag{ΔH = +92,0 кДж > 0}\]
Поскольку энтальпии этих реакций в раз больше нуля, , они являются эндотермическими реакциями.
Константа равновесия
Константа равновесия (\(K_c\)) определяет соотношение между концентрациями химических веществ, участвующих в реакции, при равновесии. Принцип Ле Шателье гласит, что если на равновесную реакцию оказывается воздействие, такое как изменение температуры, давления или концентрации, реакция смещается, чтобы восстановить равновесие. Для экзотермических и эндотермических реакций этим дополнительным напряжением является изменение температуры. Константа равновесия показывает, насколько далеко продвинется реакция при определенной температуре, путем определения отношения продуктов к реакциям с использованием равновесных концентраций. 9b} \label{Equation:Kc}\]
9b} \label{Equation:Kc}\]
где
| Экзотермические реакции | Эндотермические реакции |
|---|---|
| Если K c уменьшается с повышением температуры, то реакция сдвигается влево. | Если K c увеличивается с повышением температуры, то реакция на сдвигается вправо. |
| Если K c увеличивается с понижением температуры, то реакция на сдвигается вправо. | Если K c уменьшается с понижением температуры, то реакция на сдвигается влево. |
Если в реакции преобладают продукты, значение K больше 1. Чем больше значение K, тем больше реакция будет стремиться вправо и, следовательно, к завершению.
Пример \(\PageIndex{1}\) : Процесс Габера
Предположим, что следующая реакция находится в равновесии и что концентрация N 2 равна 2 М, концентрация H 2 93} \\[4pt] &= \dfrac{9}{128} \\[4pt] &= 0,07 \end{align*}\]
Упражнение \(\PageIndex{1}\)
Определить \( K_c\) для следующей химической реакции в равновесии, если молярные концентрации молекул равны:
\[\ce{2h3(g) + 2NO(g) <=> 2h3O(g) + N2(g)} \номер\]
Упражнение \(\PageIndex{2}\)
В предыдущем уравнении равновесие благоприятствует продуктам или реагентам?
Упражнение \(\PageIndex{3}\)
В следующей реакции температура повышается, а значение \(K_ c\) уменьшается с 0,75 до 0,55. Это экзотермическая или эндотермическая реакция?
\[\ce{N_2 (г) + 3H_2 <=>2NH_3 (г) } \номер\]
Упражнение \(\PageIndex{4}\)
В следующей реакции, в каком направлении сместится равновесие, если произойдет повышение температуры и задана энтальпия реакции так, что \(ΔH\) равно -92,5 кДж?
\[\ce{PCl3(g) + Cl2(g) <=> PCl_5(g)} \nonumber\]
Авторы и ссылки
7.
 11 Свободная энергия Гиббса и равновесие
11 Свободная энергия Гиббса и равновесиеРазвитие навыков
Мы определили три критерия того, будет ли данная реакция протекать спонтанно (т. е. двигаться в прямом направлении, как написано, для достижения равновесия): ΔS univ > 0, ΔG sys < 0 и относительная величина зависимости отношения реакции Q от константы равновесия K. Напомним, что если K > Q, то реакция протекает самопроизвольно вправо, как написано, что приводит к чистому превращению реагентов в продукты. И наоборот, если K < Q, то реакция протекает самопроизвольно влево, как написано, что приводит к чистому превращению продуктов в реагенты. Если K = Q, то система находится в равновесии и никакой реакции не происходит. Таблица \(\PageIndex{1}\) суммирует эти критерии и их относительные значения для спонтанных, неспонтанных и равновесных процессов.
Если K = Q, то система находится в равновесии и никакой реакции не происходит. Таблица \(\PageIndex{1}\) суммирует эти критерии и их относительные значения для спонтанных, неспонтанных и равновесных процессов.
| Самопроизвольное | Равновесие | Несамопроизвольное* |
|---|---|---|
| *Спонтанно в обратном направлении. | ||
| ΔS унив > 0 | ΔS унив = 0 | ΔS универсальный < 0 |
| «> ΔG сис < 0 | ΔG сис = 0 | ΔG сис > 0 |
| К > Q | К = Q | К < Q |
Поскольку все три критерия оценивают одно и то же — спонтанность процесса, — было бы действительно удивительно, если бы они не были связаны между собой. В этом разделе мы исследуем взаимосвязь между изменением свободной энергии реакции (ΔG) и мгновенным коэффициентом реакции (Q). Для этого сначала выявим связь между стандартным изменением свободной энергии реакции (ΔG°) и константой равновесия (K). 9\circ+RT\ln Q \label{18. 35}\]
35}\]
, где ΔG° указывает, что все реагенты и продукты находятся в своих стандартных состояниях. Для системы в равновесии (\(K = Q\)), и, как вы узнали из этой главы, ΔG = 0 для системы в равновесии. Следовательно, мы можем описать связь между ΔG° и K следующим образом: {18.36b}\]
Если объединить уравнения \(\ref{18.35}\) и \(\ref{18.36b}\), получится уравнение
\[ΔG= RT\ln \dfrac{Q}{K} \label{18.37}\]
Если продукты и реагенты находятся в своих стандартных состояниях и ΔG° < 0, то K > 1 и продукты предпочтение отдается реагентам, находящимся в равновесии. И наоборот, если ΔG ° > 0, то K < 1, и реагенты имеют преимущество перед продуктами в состоянии равновесия. Если ΔG° = 0, то \(K = 1\), и ни реагенты, ни продукты не благоприятствуют равновесию.
Для процесса, благоприятствующего продукту, при стандартных условиях \(K\) больше 1,
Пример \(\PageIndex{1}\)
Рассчитайте K для реакции O 2 с N 2 с образованием NO при 423 K: \[N_{2(g)}+O_{2( g)} \rightleftharpoons 2NO_{(g)} \nonumber\] ΔG° для этой реакции составляет +22,7 кДж/моль N 2 .
Дано : ΔG° и температура
Запрошено : K
Стратегия:
Подставьте значения для ΔG° и T (в градусах Кельвина) в уравнение 3 (6} ref18. рассчитать К, константу равновесия образования монооксида азота. 9{-3}\end{align}\)
Таким образом, константа равновесия для образования монооксида азота при комнатной температуре меньше 1. При равновесии реакция протекает с преимуществом по реагентам.
Упражнение \(\PageIndex{1}\)
Рассчитайте K для реакции NO с O 2 с получением NO 2 при 25°C. ΔG° для этой реакции составляет -70,5 кДж/моль O 2 .
Пример \(\PageIndex{2}\)
ΔG° равно −32,7 кДж/моль N 2 для реакции при 100 o C
\[N_{2(g)}+3H_{ 2(g)} \rightleftharpoons 2NH_{3(g)} \nonumber\]
Рассчитайте ΔG для той же реакции при следующих нестандартных условиях:
В каком направлении должна протекать реакция, чтобы достичь равновесия?
Дано : сбалансированное химическое уравнение, молярность каждого вида, температура и ΔG°
Запрошено : направление, в котором реакция будет протекать для достижения равновесия заданные значения, рассчитать Q.

 {2}}-4{x}-15}=1-\frac{1}{2x+3}=\frac{-\frac{1}{2}}{x+\frac{3}{2}}+1,\text{ }x\ne \frac{5}{2}\).
{2}}-4{x}-15}=1-\frac{1}{2x+3}=\frac{-\frac{1}{2}}{x+\frac{3}{2}}+1,\text{ }x\ne \frac{5}{2}\).

 145 ПП РФ №442 от 04.05.2012).
145 ПП РФ №442 от 04.05.2012).
 (основание п. 139 ПП РФ №442 от 04.05.2012).
(основание п. 139 ПП РФ №442 от 04.05.2012). 1.5.19 ПУЭ).
1.5.19 ПУЭ). 1.5.13 ПУЭ).
1.5.13 ПУЭ). Поверка приборов учета осуществляется в соответствии с положениями законодательства Российской Федерации об обеспечении единства измерений (основание п. 81(10) ПП РФ №354 от 06.05.2011г.).
Поверка приборов учета осуществляется в соответствии с положениями законодательства Российской Федерации об обеспечении единства измерений (основание п. 81(10) ПП РФ №354 от 06.05.2011г.).

 Минеральные вещества могут образовывать соединения с другими веществами, содержащимися в продуктах питания (например, с оксалатами в ревене), в результате чего организм не может их усвоить.
Минеральные вещества могут образовывать соединения с другими веществами, содержащимися в продуктах питания (например, с оксалатами в ревене), в результате чего организм не может их усвоить.
 Однако повышение температуры позволяет системе поглощать энергию и, таким образом, способствует эндотермической реакции; равновесие сместится влево.
Однако повышение температуры позволяет системе поглощать энергию и, таким образом, способствует эндотермической реакции; равновесие сместится влево.
 Значение ΔG° для этой реакции равно + 22,7 кДж. В каком направлении пойдет реакция, чтобы достичь равновесия?
Значение ΔG° для этой реакции равно + 22,7 кДж. В каком направлении пойдет реакция, чтобы достичь равновесия? Поскольку в экзотермической реакции выделяется тепло, добавление тепла (за счет повышения температуры) сдвинет равновесие влево в пользу реагентов и уменьшит величину K. И наоборот, поскольку тепло расходуется в эндотермической реакции, добавление тепла сместит равновесие равновесие вправо, в пользу продуктов и увеличения величины K. Уравнение \(\ref{18.40}\) также показывает, что величина ΔH ° определяет, насколько быстро K изменяется в зависимости от температуры. Напротив, величина и знак ΔS° влияют на величину K, но не на ее температурную зависимость.
Поскольку в экзотермической реакции выделяется тепло, добавление тепла (за счет повышения температуры) сдвинет равновесие влево в пользу реагентов и уменьшит величину K. И наоборот, поскольку тепло расходуется в эндотермической реакции, добавление тепла сместит равновесие равновесие вправо, в пользу продуктов и увеличения величины K. Уравнение \(\ref{18.40}\) также показывает, что величина ΔH ° определяет, насколько быстро K изменяется в зависимости от температуры. Напротив, величина и знак ΔS° влияют на величину K, но не на ее температурную зависимость. 41}\]
41}\] ΔG связано с Q уравнением \(ΔG= RT\ln \dfrac{Q}{K} \).
ΔG связано с Q уравнением \(ΔG= RT\ln \dfrac{Q}{K} \).
 И, наконец, для создания гиперболы плоскость пересекает обе части конуса. Для этого наклон пересекающейся плоскости должен быть больше, чем у конуса.
И, наконец, для создания гиперболы плоскость пересекает обе части конуса. Для этого наклон пересекающейся плоскости должен быть больше, чем у конуса.