Производная tgx 1: Найти производную f(x)= 1/tgx — ответ на Uchi.ru

2+1)/sin x 3)f(x)=ctg… — Учеба и наука

Лучший ответ по мнению автора

30. 10.16 Лучший ответ по мнению автора

Другие ответы

30. 10.16

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Галина Владимировна Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Имеется два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. 2

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.

Пользуйтесь нашим приложением

Смысл первой производной. Производная функции

Приведем сводную таблицу для удобства и наглядности при изучении темы.

Константа y = C Степенная функция y = x p (x p) » = p · x p — 1	Показательная функция y = a x (a x) » = a x · ln a В частности, при a = e имеем y = e x (e x) » = e x
Логарифмическая функция (log a x) » = 1 x · ln a В частности, при a = e имеем y = ln x (ln x) » = 1 x	Тригонометрические функции (sin x) » = cos x (cos x) » = — sin x (t g x) » = 1 cos 2 x (c t g x) » = — 1 sin 2 x
Обратные тригонометрические функции (a r c sin x) » = 1 1 — x 2 (a r c cos x) » = — 1 1 — x 2 (a r c t g x) » = 1 1 + x 2 (a r c c t g x) » = — 1 1 + x 2	Гиперболические функции (s h x) » = c h x (c h x) » = s h x (t h x) » = 1 c h 2 x (c t h x) » = — 1 s h 2 x

Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.

Производная постоянной

Доказательство 1

Для того, чтобы вывести данную формулу, возьмем за основу определение производной функции в точке. Используем x 0 = x , где x принимает значение любого действительного числа, или, иначе говоря, x является любым числом из области определения функции f (x) = C . Составим запись предела отношения приращения функции к приращению аргумента при ∆ x → 0:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C — C ∆ x = lim ∆ x → 0 0 ∆ x = 0

Обратите внимание, что под знак предела попадает выражение 0 ∆ x . Оно не есть неопределенность «ноль делить на ноль», поскольку в числителе записана не бесконечно малая величина, а именно нуль. Иначе говоря, приращение постоянной функции всегда есть нуль.

Итак, производная постоянной функции f (x) = C равна нулю на всей области определения.

Пример 1

Даны постоянные функции:

f 1 (x) = 3 , f 2 (x) = a , a ∈ R , f 3 (x) = 4 . 13 7 22 , f 4 (x) = 0 , f 5 (x) = — 8 7

Решение

Опишем заданные условия. В первой функции мы видим производную натурального числа 3 . В следующем примере необходимо брать производную от а , где а — любое действительное число. Третий пример задает нам производную иррационального числа 4 . 13 7 22 , четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби — 8 7 .

Ответ: производные заданных функций есть нуль при любом действительном x (на всей области определения)

f 1 » (x) = (3) » = 0 , f 2 » (x) = (a) » = 0 , a ∈ R , f 3 » (x) = 4 . 13 7 22 » = 0 , f 4 » (x) = 0 » = 0 , f 5 » (x) = — 8 7 » = 0

Производная степенной функции

Переходим к степенной функции и формуле ее производной, имеющей вид: (x p) » = p · x p — 1 , где показатель степени p является любым действительным числом.

Доказательство 2

Приведем доказательство формулы, когда показатель степени – натуральное число: p = 1 , 2 , 3 , …

Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:

(x p) » = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p — x p ∆ x

Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:

(x + ∆ x) p — x p = C p 0 + x p + C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p — x p = = C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p

Таким образом:

(x p) » = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p — x p ∆ x = = lim ∆ x → 0 (C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 · x p — 1 + C p 2 · x p — 2 · ∆ x + . . . + C p p — 1 · x · (∆ x) p — 2 + C p p · (∆ x) p — 1) = = C p 1 · x p — 1 + 0 + 0 + . . . + 0 = p ! 1 ! · (p — 1) ! · x p — 1 = p · x p — 1

Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.

Доказательство 3

Чтобы привести доказательство для случая, когда p — любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.

Рассмотрим два случая: когда x положительны и когда x отрицательны.

Итак, x > 0 . Тогда: x p > 0 . Логарифмируем равенство y = x p по основанию e и применим свойство логарифма:

y = x p ln y = ln x p ln y = p · ln x

На данном этапе получили неявно заданную функцию. Определим ее производную:

(ln y) » = (p · ln x) 1 y · y » = p · 1 x ⇒ y » = p · y x = p · x p x = p · x p — 1

Теперь рассматриваем случай, когда x – отрицательное число.

Если показатель p есть четное число, то степенная функция определяется и при x

Тогда x p

Если p есть нечетное число, тогда степенная функция определена и при x

y » (x) = (- (- x) p) » = — ((- x) p) » = — p · (- x) p — 1 · (- x) » = = p · (- x) p — 1 = p · x p — 1

Последний переход возможен в силу того, что если p — нечетное число, то p — 1 либо четное число, либо нуль (при p = 1), поэтому, при отрицательных x верно равенство (- x) p — 1 = x p — 1 .

Итак, мы доказали формулу производной степенной функции при любом действительном p .

Пример 2

Даны функции:

f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 — 1 4 , f 3 (x) = 1 x log 7 12

Определите их производные.

Решение

Часть заданных функций преобразуем в табличный вид y = x p , опираясь на свойства степени, а затем используем формулу:

f 1 (x) = 1 x 2 3 = x — 2 3 ⇒ f 1 » (x) = — 2 3 · x — 2 3 — 1 = — 2 3 · x — 5 3 f 2 » (x) = x 2 — 1 4 = 2 — 1 4 · x 2 — 1 4 — 1 = 2 — 1 4 · x 2 — 5 4 f 3 (x) = 1 x log 7 12 = x — log 7 12 ⇒ f 3 » (x) = — log 7 12 · x — log 7 12 — 1 = — log 7 12 · x — log 7 12 — log 7 7 = — log 7 12 · x — log 7 84

Производная показательной функции

Доказательство 4

Выведем формулу производной, взяв за основу определение:

(a x) » = lim ∆ x → 0 a x + ∆ x — a x ∆ x = lim ∆ x → 0 a x (a ∆ x — 1) ∆ x = a x · lim ∆ x → 0 a ∆ x — 1 ∆ x = 0 0

Мы получили неопределенность. Чтобы раскрыть ее, запишем новую переменную z = a ∆ x — 1 (z → 0 при ∆ x → 0). В таком случае a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Для последнего перехода использована формула перехода к новому основанию логарифма.

Осуществим подстановку в исходный предел:

(a x) » = a x · lim ∆ x → 0 a ∆ x — 1 ∆ x = a x · ln a · lim ∆ x → 0 1 1 z · ln (z + 1) = = a x · ln a · lim ∆ x → 0 1 ln (z + 1) 1 z = a x · ln a · 1 ln lim ∆ x → 0 (z + 1) 1 z

Вспомним второй замечательный предел и тогда получим формулу производной показательной функции:

(a x) » = a x · ln a · 1 ln lim z → 0 (z + 1) 1 z = a x · ln a · 1 ln e = a x · ln a

Пример 3

Даны показательные функции:

f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x

Необходимо найти их производные.

Решение

Используем формулу производной показательной функции и свойства логарифма:

f 1 » (x) = 2 3 x » = 2 3 x · ln 2 3 = 2 3 x · (ln 2 — ln 3) f 2 » (x) = 5 3 x » = 5 3 x · ln 5 1 3 = 1 3 · 5 3 x · ln 5 f 3 » (x) = 1 (e) x » = 1 e x » = 1 e x · ln 1 e = 1 e x · ln e — 1 = — 1 e x

Производная логарифмической функции

Доказательство 5

Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значениях основания а логарифма. Опираясь на определение производной, получим:

(log a x) » = lim ∆ x → 0 log a (x + ∆ x) — log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x · log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x · x x = lim ∆ x → 0 1 x · log a 1 + ∆ x x x ∆ x = = 1 x · log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x · log a e = 1 x · ln e ln a = 1 x · ln a

Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифма. Равенство lim ∆ x → 0 1 + ∆ x x x ∆ x = e является верным в соответствии со вторым замечательным пределом.

Пример 4

Заданы логарифмические функции:

f 1 (x) = log ln 3 x , f 2 (x) = ln x

Необходимо вычислить их производные.

Решение

Применим выведенную формулу:

f 1 » (x) = (log ln 3 x) » = 1 x · ln (ln 3) ; f 2 » (x) = (ln x) » = 1 x · ln e = 1 x

Итак, производная натурального логарифма есть единица, деленная на x .

Производные тригонометрических функций

Доказательство 6

Используем некоторые тригонометрические формулы и первый замечательный предел, чтобы вывести формулу производной тригонометрической функции.

Согласно определению производной функции синуса, получим:

(sin x) » = lim ∆ x → 0 sin (x + ∆ x) — sin x ∆ x

Формула разности синусов позволит нам произвести следующие действия:

(sin x) » = lim ∆ x → 0 sin (x + ∆ x) — sin x ∆ x = = lim ∆ x → 0 2 · sin x + ∆ x — x 2 · cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 · cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Наконец, используем первый замечательный предел:

sin » x = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Итак, производной функции sin x будет cos x .

Совершенно также докажем формулу производной косинуса:

cos » x = lim ∆ x → 0 cos (x + ∆ x) — cos x ∆ x = = lim ∆ x → 0 — 2 · sin x + ∆ x — x 2 · sin x + ∆ x + x 2 ∆ x = = — lim ∆ x → 0 sin ∆ x 2 · sin x + ∆ x 2 ∆ x 2 = = — sin x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = — sin x

Т.е. производной функции cos x будет – sin x .

Формулы производных тангенса и котангенса выведем на основе правил дифференцирования:

t g » x = sin x cos x » = sin » x · cos x — sin x · cos » x cos 2 x = = cos x · cos x — sin x · (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g » x = cos x sin x » = cos » x · sin x — cos x · sin » x sin 2 x = = — sin x · sin x — cos x · cos x sin 2 x = — sin 2 x + cos 2 x sin 2 x = — 1 sin 2 x

Производные обратных тригонометрических функций

Раздел о производной обратных функций дает исчерпывающую информацию о доказательстве формул производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому дублировать материал здесь не будем.

Производные гиперболических функций

Доказательство 7

Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:

s h » x = e x — e — x 2 » = 1 2 e x » — e — x » = = 1 2 e x — — e — x = e x + e — x 2 = c h x c h » x = e x + e — x 2 » = 1 2 e x » + e — x » = = 1 2 e x + — e — x = e x — e — x 2 = s h x t h » x = s h x c h x » = s h » x · c h x — s h x · c h » x c h 2 x = c h 2 x — s h 2 x c h 2 x = 1 c h 2 x c t h » x = c h x s h x » = c h » x · s h x — c h x · s h » x s h 2 x = s h 2 x — c h 2 x s h 2 x = — 1 s h 2 x

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Можно выносить за знак производной :

(af(x)» =af » (x).

Например :

Производная алгебраической суммы нескольких функций (взятых в неизменном числе) равна алгебраической сумме их производных :

(f 1 (x) + f 2 (x) — f 3 (x))» = f 1 » (x) + f 2 » (x) — f 3 » (x).

Например :

(0,3 х 2 — 2 х + 0,8)» = (0,3 х 2)» — (2 х)» + (0,8)» = 0,6 х — 2 (производная последнего слагаемого уравнения равна нулю).

Если производная функции g отлична от нуля, то отношение f/g также имеет конечную производную . Данное свойство можно записать в виде:

.

Пусть функции y = f(x) и y = g(x) имеют конечные производные в точке x 0 . Тогда функции f ± g и f · g также имеют конечные производные в этой точке . Тогда получим:

(f ± g) ′ = f ′ ± g ′,

(f · g) ′ = f ′ · g + f · g ′.

Производная сложной функции.

Пусть функция y = f(x) имеет конечную производную в точке x 0 , функция z = s(y) имеет конечную производную в точке y 0 = f(x 0).

Тогда сложная функция z = s (f(x)) также имеет конечную производную в этой точке. Сказанное можно записать в виде:

.

Производная обратной функции.

Пусть функция y = f(x) имеет обратную функцию x = g(y) на некотором интервале (a, b) и существует отличная от нуля конечная производная этой функции в точке x 0 , принадлежащая области определения , т. е. x 0 ∈ (a, b).

Тогда обратная функция имеет производную в точке y 0 = f(x 0):

.

Производная неявной функции.

Если функция y = f(x) задана неявно уравнением F(x, y(x)) = 0, то её производная находится из условия:

.

Говорят, что функция y = f(x) задана неявно , если она тождественно удовлетворяет соотношению:

где F(x, y) — некоторая функция двух аргументов.

Производная функции, заданной параметрически.

Если функция y = f(x) задана параметрическим образом с помощью рассмотренной

Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна . Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.

Запомним определение:

Производная — это скорость изменения функции.

На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.

Вот другой пример.

Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная , — разная. Что касается Матвея — у его дохода производная вообще отрицательна.

Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?

На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти с помощью графика.

Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной .

Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :

Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .

Есть и другое важное соотношение. Вспомним, что прямая задается уравнением

Величина в этом уравнении называется угловым коэффициентом прямой . Она равна тангенсу угла наклона прямой к оси .

.

Мы получаем, что

Запомним эту формулу. Она выражает геометрический смысл производной.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу угла наклона касательной.

Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.

Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол с положительным направлением оси .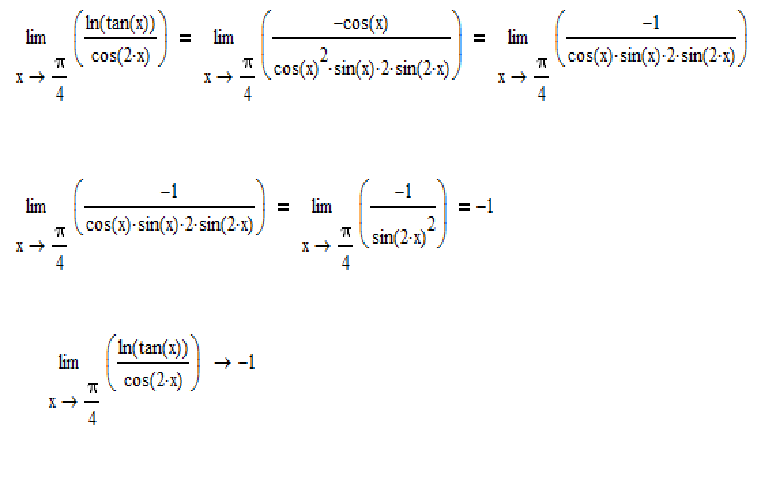 Значит, в точке производная положительна.

В точке наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.

Вот что получается:

Если функция возрастает, ее производная положительна.

Если убывает, ее производная отрицательна.

А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».

В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».

Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.

Если производная положительна, то функция возрастает.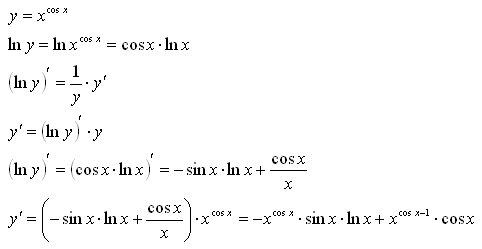

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

	возрастает	точка максимума	убывает	точка минимума	возрастает
+	0	—	0	+

Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.

Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :

В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.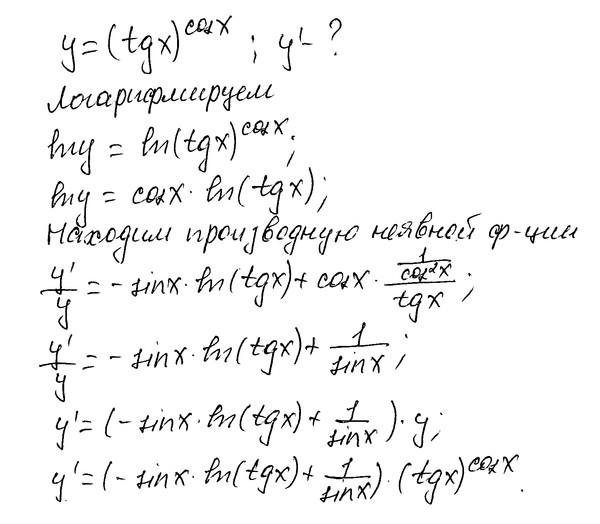

Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Геометрический и физический смысл производной

Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

Значение первой производной.

Производная функции

Вот сводная таблица для удобства и наглядности при изучении темы.

Константа y=C Степенная функция y = x p (х р)» = р х р — 1	Экспоненциальная функция y = x (а х)» = а х пер а В частности, когда a = e , мы имеем y = e x (е х)» = е х
логарифмическая функция (log a x) » = 1 x ln a В частности, когда a = e , мы имеем y = log x (ln x)» = 1 x	Тригонометрические функции (sin x) «= cos x (cos x)» = — sin x (t g x) » = 1 cos 2 x (c t g x)» = — 1 sin 2 x
Обратные тригонометрические функции (a r c sin x) » = 1 1 — x 2 (a r c cos x) » = — 1 1 — x 2 (ar c t g x)» = 1 1 + x 2 (a r c c t g x) » = — 1 1 + x 2	Гиперболические функции (s h x) » = c h x (c h x) » = s h x (t h x)» = 1 c h 2 x (c t h x) » = — 1 s h 2 x

Проанализируем, как были получены формулы указанной таблицы, или, другими словами, докажем вывод формул производных для каждого вида функции.

Производная постоянной

Доказательство 1

Чтобы вывести эту формулу, возьмем за основу определение производной функции в точке. Мы используем х 0 = х, где х принимает значение любого действительного числа, или, другими словами, х — любое число из области определения функции f(x) = C. Запишем предел отношения приращения функции к приращению аргумента как ∆ x → 0:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C — C ∆ x = lim ∆ x → 0 0 ∆ x = 0

Обратите внимание, что выражение 0 ∆ x попадает под знак предела. Это не неопределенность «ноль разделить на ноль», так как в числителе стоит не бесконечно малая величина, а ноль. Другими словами, приращение постоянной функции всегда равно нулю.

Итак, производная постоянной функции f(x) = C равна нулю во всей области определения.

Пример 1

Даны постоянные функции:

f 1 (x) = 3 , f 2 (x) = a , a ∈ R , f 3 (x) = 4 . 13 7 22 , f 4 (x) = 0 , f 5 (x) = — 8 7

Решение

Опишем данные условия. В первой функции мы видим производную от натурального числа 3. В следующем примере нужно взять производную от a , где a — любое действительное число. Третий пример дает нам производную от иррационального числа 4. 13 7 22 , четвертая — производная от нуля (ноль — целое число). Наконец, в пятом случае имеем производную рациональной дроби — 8 7 .

Ответ: производные данных функций равны нулю для любых действительных x (по всей области определения)

f 1 «(x) = (3)» = 0 , f 2 «(x) = (a) » = 0 , a ∈ R , f 3 » (x) = 4 . 13 7 22 » = 0 , f 4 » (x) = 0 » = 0 , f 5 » (x) = — 8 7 » = 0

Производная степенной функции

Обратимся к степенной функции и формуле ее производной, которая имеет вид: (x p)» = p x p — 1, где показатель степени p — любое действительное число.

Доказательство 2

Вот доказательство формулы, когда показатель степени — натуральное число: p = 1 , 2 , 3 , …

Опять опираемся на определение производной, запишем предел отношения приращения степенной функции к приращению аргумента:

(x p) » = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p — x p ∆ x

Для упрощения выражения в числителе воспользуемся биномом Ньютона формула:

(x + ∆x) p — x p = C p 0 + x p + C p 1 x p — 1 ∆ x + C p 2 x p — 2 (∆ x) 2 + .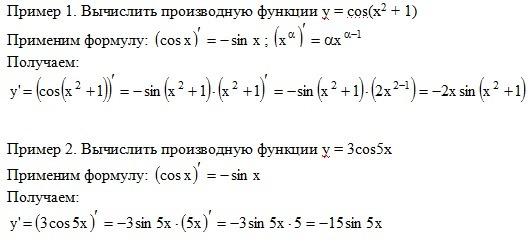 . . + + C p p — 1 x (∆ x) p — 1 + C p p (∆ x) p — x p = = C p 1 x p — 1 ∆ x + C p 2 x p — 2 (∆ x) 2 +… + C p p — 1 x (∆ x) p — 1 + C p p (∆ x) p

Таким образом:

(x p) » = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x ) p — x p ∆ x = = lim ∆ x → 0 (C p 1 x p — 1 ∆ x + C p 2 x p — 2 (∆ x) 2 + . . . + C p p — 1 x (∆ x) p — 1 + C p p (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 x p — 1 + C p 2 x p — 2 ∆ x + . . . + C p p — 1 x (∆ x) p — 2 + C p p (∆ x) p — 1) = = C p 1 x p — 1 + 0 + 0 + . . . + 0 = р! 1! (р — 1)! х р — 1 = р х р — 1

Итак, мы доказали формулу производной степенной функции, когда показатель степени является натуральным числом.

Доказательство 3

Чтобы привести доказательство для случая, когда p- любое действительное число, отличное от нуля, воспользуемся логарифмической производной (здесь следует понимать отличие производной от логарифмической функции). Для более полного понимания желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной комплексной функции.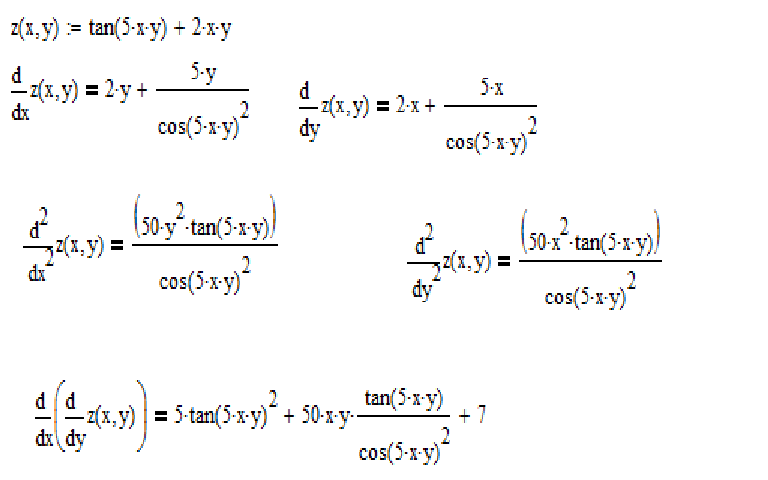

Рассмотрим два случая: когда x положительное и когда x отрицательное.

Так х > 0 . Тогда: х р > 0 . Логарифмируем равенство y = x p по основанию e и применяем свойство логарифма:

y = x p ln y = ln x p ln y = p ln x

На этом этапе неявно определенная функция имеет было получено. Определим его производную:

(ln y) » = (p ln x) 1 y y » = p 1 x ⇒ y » = p y x = p x p x = p x p — 1

Теперь рассмотрим случай, когда х- отрицательное число.

Если показатель p четное число, то степенная функция также определена для x

Затем ХР

Если p является нечетным числом, то степенная функция определяется для x

у «(х) = (- (- х) р) » = — ((- х) р)» = — р (- х) р — 1 (- х) » = = р ( — x) p — 1 = p x p — 1

Последний переход возможен потому, что если p нечетное число, то p — 1 либо четное число, либо ноль (при p = 1), поэтому для отрицательных x справедливо равенство (- x) p — 1 = x p — 1.

Итак, мы доказали формулу производной степенной функции для любого действительного p.

Пример 2

Даны функции:

f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 — 1 4 , f 3 (x) = 1 x log 7 12

Определите их производные .

Раствор

Преобразуем часть заданных функций в табличный вид y = x p , исходя из свойств степени, а затем воспользуемся формулой:

f 1 (х) = 1 х 2 3 = х — 2 3 ⇒ f 1 «(х) = — 2 3 х — 2 3 — 1 = — 2 3 х — 5 3 ф 2″( х) = х 2 — 1 4 = 2 — 1 4 х 2 — 1 4 — 1 = 2 — 1 4 х 2 — 5 4 f 3 (х) = 1 х log 7 12 = х — log 7 12 ⇒ f 3 «( x) = — log 7 12 x — log 7 12 — 1 = — log 7 12 x — log 7 12 — log 7 7 = — log 7 12 x — log 7 84

Производная показательной функции

Доказательство 4

Выведем формулу для производной, исходя из определения:

(а х)» = lim ∆ х → 0 а х + ∆ х — а х ∆ х = lim ∆ х → 0 а х (а ∆ х — 1) ∆ x = a x lim ∆ x → 0 a ∆ x — 1 ∆ x = 0 0

У нас неопределенность. Чтобы расширить его, мы пишем новую переменную z = a ∆ x — 1 (z → 0 при ∆ x → 0). В этом случае a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Для последнего перехода используется формула перехода к новому основанию логарифма.

Сделаем замену в исходном пределе:

(a x) » = a x lim ∆ x → 0 a ∆ x — 1 ∆ x = a x ln a lim ∆ x → 0 1 1 z ln (z + 1) = = a x ln a lim ∆ x → 0 1 ln (z + 1) 1 z = a x ln a 1 ln lim ∆ x → 0 (z + 1) 1 z

Вспомним второй чудесный предел и тогда получим формулу производной экспоненциальной функции:

(a x) » = a x ln a 1 ln lim z → 0 (z + 1) 1 z = a x ln a 1 ln e = a x ln a

Пример 3

Показательные функции даны:

f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x

Нужно найти их производные

Решение

Используем формулу производной показательной функции и свойства логарифма:

f 1 «(x) = 2 3 x» = 2 3 x ln 2 3 = 2 3 x (ln 2 — ln 3) f 2 «(x) = 5 3 x» = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 «(x) = 1 (e) x» = 1 e x » = 1 e x ln 1 e = 1 e x ln e — 1 = — 1 e x

Производная логарифмической функции

Доказательство 5

Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значений основания а логарифма, основанное на определении производной , получаем:

(log a x) » = lim ∆ x → 0 log a (x + ∆ x) — log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x x x = lim ∆ x → 0 1 x log a 1 + ∆ x x x ∆ x = = 1 x log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x log a e = 1 x ln e ln a = 1 x ln a

Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифмичности Равенство lim ∆ x → 0 1 + ∆ x x x ∆ x = e верно в соответствии со вторым замечательным пределом9.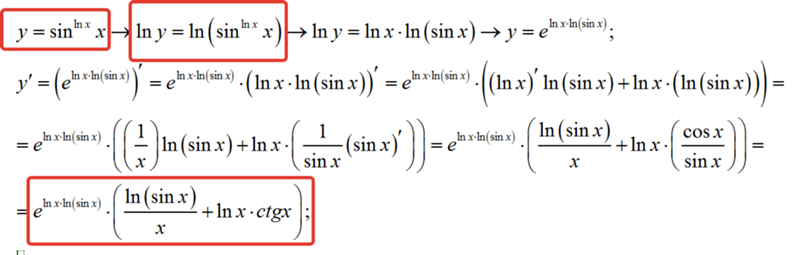 0907

Пример 4

Даны логарифмические функции:

f 1 (x) = log log 3 x , f 2 (x) = log x

Необходимо вычислить их производные.

Раствор

Применим полученную формулу:

f 1 «(x) = (log ln 3 x)» = 1 x ln (ln 3) ; f 2 «(x) = (ln x)» = 1 x ln e = 1 x

Значит, производная натурального логарифма равна единице, деленной на x .

Производные тригонометрических функций

Доказательство 6

Мы используем некоторые тригонометрические формулы и первый чудесный предел, чтобы вывести формулу для производной тригонометрической функции.

Согласно определению производной функции синуса получаем:

(sin x)» = lim ∆ x → 0 sin (x + ∆ x) — sin x ∆ x

Формула разности синусов позволит нам выполнить следующие действия:

(sin x)» = lim ∆ x → 0 sin (x + ∆ x) — sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x — x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Наконец, воспользуемся первым чудесным пределом:

sin»x = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Итак, производная функции sin x будет быть cos x .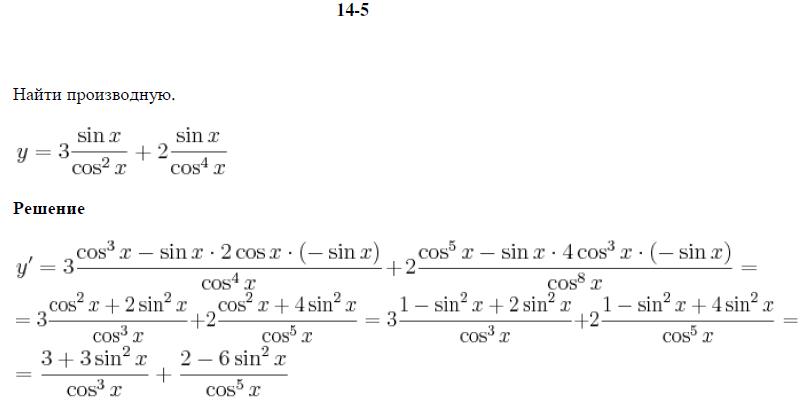

Таким же образом докажем и формулу для производной косинуса: x → 0 — 2 sin x + ∆ x — x 2 sin x + ∆ x + x 2 ∆ x = = — lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = — sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = — sin x

Тех. производная функции cos x будет – sin x .

Выводим формулы производных тангенса и котангенса исходя из правил дифференцирования:

t g»x = sin x cos x» = sin»x cos x — sin x cos» x cos 2 x = = cos x cos x — sin x (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g «x = cos x sin x» = cos «x sin x — cos x sin» x sin 2 x = = — sin x sin x — cos x cos x sin 2 x = — sin 2 x + cos 2 x sin 2 x = — 1 sin 2 x

Производные обратных тригонометрических функций

Раздел о производных обратных функций содержит исчерпывающую информацию о доказательстве формул для производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому мы не будем дублировать здесь материал.

Производные гиперболических функций

Доказательство 7

Мы можем вывести формулы для производных гиперболического синуса, косинуса, тангенса и котангенса, используя правило дифференцирования и формулу для производной показательной функции:

s h «x = e x — e — x 2» = 1 2 e x «- e — x» == 1 2 e x — — e — x = e x + e — x 2 = c h x c h «x = e x + e — x 2» = 1 2 e x «+ e — x» == 1 2 e x + — e — x = e x — e — x 2 = s h x t h «x = s h x c h x» = s h «x c h x — s h x c h» x c h 2 x = c h 2 x — s h 2 x c h 2 x = 1 c h 2 x c t h «x = c h x s h x» = c h «x s h x — c h x s h «x s h 2 x = s h 2 x — c h 2 x s h 2 x = — 1 s h 2 x

Если вы заметили ошибку в текст, выделите его и нажмите Ctrl+Enter

Можно убрать из знака производная :

(af(x)»=af» (x).

Например :

Производная алгебраической суммы нескольких функций (взятых в постоянное число) равна алгебраической сумме их производных :

(f 1 (x) + f 2 (x) — f 3 (x))» = f 1 «(x) + f 2» (x) — f 3 «(x).

Например, :

(0,3 x 2 — 2 x + 0,8) «= (0,3 x 2)» — (2 x) «+ (0,8)» = 0,6 x — 2 ( производная последний член 9уравнение 0914 равно нулю).

Если производная функции g отлична от нуля, то отношение f/g также имеет окончательную производную . Это свойство может быть записано как:

.

Пусть функций y = f(x) и y = g(x) имеют конечных производных в точке x 0 . Тогда функций f ± g и f g также имеют конечных производных в этой точке . Тогда получаем:

(f ± g) ′ = f ′ ± g ′,

(f g) ′ = f ′ g + f g ′.

Производная сложной функции.

Пусть функция y = f(x) имеет конечных производных в точке x 0 , функция z = s(y) имеет конечную производную в точке y 0 = f(x 0).

Тогда комплексная функция z = s (f(x)) также имеет в этой точке конечную производную. Это можно записать в виде:

.

Производная обратной функции.

Пусть функция y = f(x) имеет обратную функцию x = g(y) на некоторых интервал (a, b) и существует ненулевая окончательная производная этой функции в точке x 0 , которая принадлежит областям , т. е. x 0 ∈ (a, b).

Тогда обратная функция Она имеет производную в точке y 0 = f(x 0):

.

Производная неявной функции.

Если функция y = f(x) определена неявно уравнением F(x, y(x)) = 0, то ее производная находится из условия:

.

Говорят, что функция y = f(x) задана неявно , Если она тождественно удовлетворяет соотношению:

где F(x, y) — некоторая функция двух аргументов.

Производная функции, заданной параметрически.

Если функция y = f(x) задана параметрически с использованием рассматриваемого

Производная функции — одна из самых сложных тем школьной программы. Не каждый выпускник ответит на вопрос, что такое производная.

В этой статье просто и понятно объясняется, что такое дериватив и зачем он нужен. . Мы не будем сейчас стремиться к математической строгости изложения. Самое главное понять смысл.

Давайте вспомним определение:

Производная это скорость изменения функции.

На рисунке показаны графики трех функций. Как вы думаете, какой из них растет быстрее?

Ответ очевиден — третий. У него самая высокая скорость изменения, то есть самая большая производная.

Вот еще один пример.

Костя, Гриша и Матвей устроились на работу одновременно. Посмотрим, как изменился их доход в течение года:

На графике сразу все видно, правда? Доход Кости увеличился более чем в два раза за полгода. И доходы Гриши тоже увеличились, но совсем чуть-чуть. И доход Мэтью уменьшился до нуля. Исходные условия те же, но скорость изменения функции, т.е. производной , — разная. Что касается Матвея, то производная от его дохода вообще отрицательна.

Интуитивно мы можем легко оценить скорость изменения функции. Но как мы это делаем?

На самом деле мы смотрим на то, насколько круто график функции идет вверх (или вниз). Другими словами, как быстро изменяется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной, т. е. изменяться быстрее или медленнее.

Производная функции обозначается .

Покажем, как найти по графику.

Нарисован график некоторой функции. Отметьте на нем точку с абсциссой. Проведите касательную к графику функции в этой точке. Мы хотим оценить, насколько круто идет вверх график функции. Удобным значением для этого является тангенс наклона касательной .

Производная функции в точке равна тангенсу наклона касательной к графику функции в этой точке.

Обратите внимание — в качестве угла наклона касательной берем угол между касательной и положительным направлением оси.

Иногда студенты спрашивают, что является касательной к графику функции. Это прямая, имеющая единственную общую точку с графиком на этом участке, причем, как показано на нашем рисунке. Похоже на касательную к окружности.

Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника:

Мы нашли производную по графику, даже не зная формулы функции. Такие задачи часто встречаются на ЕГЭ по математике под номером.

Есть еще одна важная корреляция. Напомним, что прямая задается уравнением

Величина в этом уравнении называется наклоном прямой . Он равен тангенсу угла наклона прямой к оси.

.

Получаем, что

Давайте запомним эту формулу. Он выражает геометрический смысл производной.

Производная функции в точке равна наклону касательной, проведенной к графику функции в этой точке.

Другими словами, производная равна тангенсу наклона тангенса.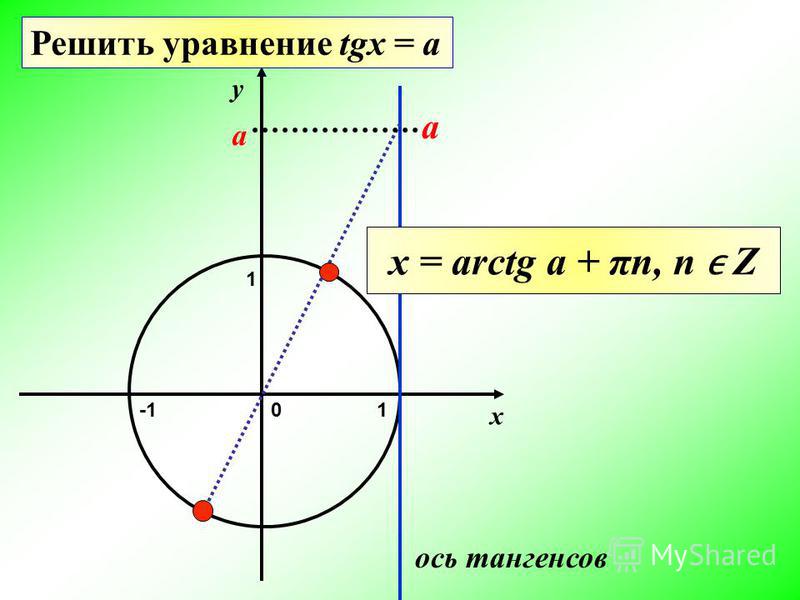

Мы уже говорили, что одна и та же функция может иметь разные производные в разных точках. Давайте посмотрим, как производная связана с поведением функции.

Нарисуем график некоторой функции. Пусть эта функция в одних областях возрастает, а в других убывает, причем с разной скоростью. И пусть эта функция имеет точки максимума и минимума.

В какой-то момент функция увеличивается. Касательная к графику, проведенная в точке, образует острый угол с положительным направлением оси. Значит, производная в этой точке положительна.

В данный момент наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси. Так как тангенс тупого угла отрицателен, то и производная в этой точке отрицательна.

Вот что происходит:

Если функция возрастает, то ее производная положительна.

Если он убывает, его производная отрицательна.

А что будет в максимальной и минимальной точках? Мы видим, что в (точке максимума) и (точке минимума) касательная горизонтальна. Следовательно, тангенс наклона касательной в этих точках равен нулю, и производная тоже равна нулю.

Точка является максимальной точкой. В этот момент увеличение функции сменяется уменьшением. Следовательно, знак производной меняется в точке с «плюс» на «минус».

В точке — точке минимума — производная также равна нулю, но ее знак меняется с «минус» на «плюс».

Вывод: с помощью производной можно узнать все, что нас интересует о поведении функции.

Если производная положительна, то функция возрастает.

Если производная отрицательна, то функция убывает.

В точке максимума производная равна нулю и меняет знак с плюса на минус.

В точке минимума производная также равна нулю и меняет знак с минуса на плюс.

Запишем эти выводы в виде таблицы:

	увеличивает	максимальная точка	уменьшение	минимальная точка	увеличивает
+	0	—	0	+

Сделаем два небольших уточнения.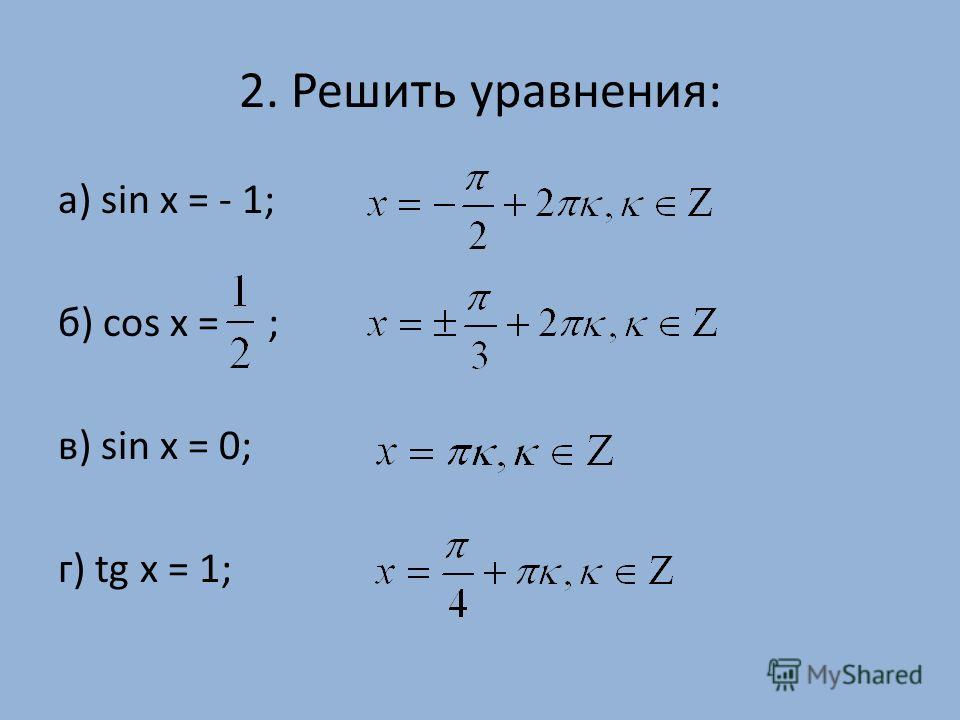 Один из них понадобится вам при решении экзаменационных задач. Другой — на первом курсе, с более серьезным изучением функций и производных.

Возможен случай, когда производная функции в какой-то точке равна нулю, но функция не имеет в этой точке ни максимума, ни минимума. Это так называемые :

В точке касательная к графику горизонтальна и производная равна нулю. Однако до точки функция возрастала, а после точки продолжает увеличиваться. Знак производной не меняется — он как и был, так и остался положительным.

Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда невозможно провести касательную в данной точке.

Но как найти производную, если функция задана не графиком, а формулой? В данном случае применяется

Совершенно невозможно решать физические задачи или примеры по математике без знания производной и способов ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как вычислить производную функции? Все эти вопросы можно объединить в один: как понять производную?

Геометрический и физический смысл производной

Пусть есть функция f(x) , заданные через некоторый интервал (a,b) . Точки x и x0 принадлежат этому интервалу. При изменении x изменяется и сама функция. Изменение аргумента — разница его значений x-x0 . Эта разница записывается как дельта x и называется приращением аргумента. Изменением или приращением функции называется разница между значениями функции в двух точках. Производное определение:

Производной функции в точке называется предел отношения приращения функции в данной точке к приращению аргумента при стремлении последнего к нулю.

Иначе можно записать так:

Какой смысл находить такой предел? Но какой:

производная функции в точке равна тангенсу угла между осью ОХ и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, со школьной скамьи всем известно, что скорость — это частный путь. х=f(t) и время т . Средняя скорость за определенный период времени:

Узнать скорость движения в момент времени t0 нужно рассчитать лимит:

Правило первое: вынести константу

Константу можно вынести из знака производной. Более того, это необходимо сделать. При решении примеров по математике берите за правило — если можете упростить выражение, то обязательно упростите .

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же верно и для производной разности функций.

Мы не будем приводить доказательство этой теоремы, а рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производная функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В приведенном выше примере мы сталкиваемся с выражением:

В этом случае промежуточный аргумент равен 8x в пятой степени. Для того чтобы вычислить производную от такого выражения, сначала рассмотрим производную внешней функции по промежуточному аргументу, а затем умножим на производную самого промежуточного аргумента по независимой переменной.

Четвертое правило: производная от частного двух функций

Формула для определения производной частного двух функций:

Мы попытались рассказать о производных для чайников на пустом месте. Эта тема не так проста, как кажется, поэтому будьте осторожны: в примерах часто встречаются подводные камни, поэтому будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обращаться в студенческую службу. В короткие сроки мы поможем вам решить самые сложные контрольные и разобраться с задачами, даже если вы никогда раньше не имели дела с расчетом производных.

Производная и ее свойства. Производная функции

Совершенно невозможно решать физические задачи или примеры по математике без знания производной и способов ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы решили посвятить сегодняшнюю статью. Что такое производная, в чем ее физический и геометрический смысл, как вычислить производную функции? Все эти вопросы можно объединить в один: как понять производную?

Геометрический и физический смысл производной

Пусть есть функция f(x) , заданные через некоторый интервал (a,b) . Точки x и x0 принадлежат этому интервалу. При изменении x изменяется и сама функция. Изменение аргумента — разница его значений x-x0 . Эта разница записывается как дельта x и называется приращением аргумента. Изменением или приращением функции называется разница между значениями функции в двух точках. Производное определение:

Производной функции в точке называется предел отношения приращения функции в данной точке к приращению аргумента при стремлении последнего к нулю.

Иначе можно записать так:

Какой смысл находить такой предел? Но какой:

производная функции в точке равна тангенсу угла между осью ОХ и касательной к графику функции в данной точке.

производная физического значения: производная пути по времени равна скорости прямолинейного движения.

Действительно, со школьной скамьи всем известно, что скорость — это частный путь.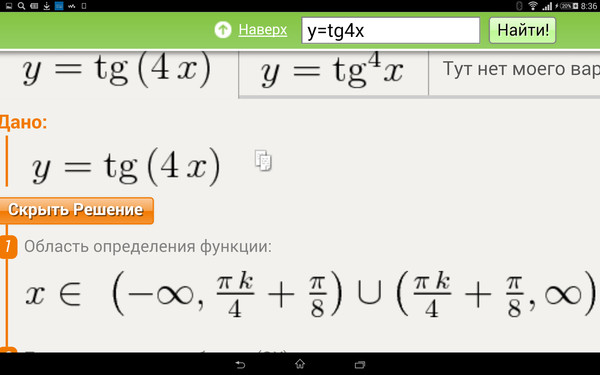 х=f(t) и время т . Средняя скорость за определенный период времени:

Узнать скорость движения в момент времени t0 нужно рассчитать лимит:

Правило первое: вынести константу

Константу можно вынести из знака производной. Более того, это необходимо сделать. При решении примеров по математике берите за правило — если можете упростить выражение, то обязательно упростите .

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же верно и для производной разности функций.

Мы не будем приводить доказательство этой теоремы, а рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производная функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В приведенном выше примере мы сталкиваемся с выражением:

В этом случае промежуточный аргумент равен 8x в пятой степени. Для того чтобы вычислить производную от такого выражения, сначала рассмотрим производную внешней функции по промежуточному аргументу, а затем умножим на производную самого промежуточного аргумента по независимой переменной.

Четвертое правило: производная от частного двух функций

Формула для определения производной частного двух функций:

Мы попытались рассказать о производных для чайников на пустом месте. Эта тема не так проста, как кажется, поэтому будьте осторожны: в примерах часто встречаются подводные камни, поэтому будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обращаться в студенческую службу. В короткие сроки мы поможем вам решить самые сложные контрольные и разобраться с задачами, даже если вы никогда раньше не имели дела с расчетом производных.

ПЕРВАЯ ПРОИЗВОДНАЯ

ПЕРВАЯ ПРОИЗВОДНАЯ

(первая производная) Скорость роста значения функции при росте ее аргумента в некоторой точке, если сама функция определена в этой точке. На графике первая производная функции показывает угол ее наклона. Если a y=f(x), его первая производная в точке x0 является пределом, к которому f(x0+а)–f(x0)/а as a стремится к бесконечно малому значению. Первую производную можно обозначить dy/dx или y´(x). Функция y(x) имеет постоянное значение в точке x0, , если dy/dx в точке x0 равно нулю. Первая производная, равная нулю, является необходимым, но недостаточным условием достижения функцией максимума или минимума в данной точке.

Эконом. Словарь. — М.: «ИНФРА-М», Издательство «Весь Мир». Дж. Блэк. Общая редакция: д.э.н. Осадчая И.М. 2000 г. .

Экономический словарь. 2000 г. .

Смотреть что такое «ПЕРВАЯ ПРОИЗВОДНАЯ» в других словарях:

— (производная) Скорость увеличения значения функции при увеличении её аргумента в какой-то точке, если сама функция определена в этой точке. На графике первая производная функции показывает угол ее наклона. Если y = f(x), его первая производная в точке… … Экономический словарь

У этого термина есть и другие значения, см. Производное. Иллюстрация понятия производного производного … Википедия

Производная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Он определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел… … Википедия

Краевая задача специального вида; состоит в том, чтобы найти в области D переменных x=(x1,…,xn).решения дифференциального уравнения(1) четного порядка 2m относительно заданных значений всех производных порядка не выше m на границе S области D (или ее части) … Математическая энциклопедия

— (вторая производная) Первая производная от первой производной функции. Первая производная измеряет наклон функции; вторая производная измеряет, как наклон изменяется с увеличением аргумента. Вторая производная от y = f(x)… … Экономический словарь

Эта статья или раздел нуждается в доработке. Пожалуйста, доработайте статью в соответствии с правилами написания статей. Дробное про … Википедия

— (перекрестная частная производная) Влияние изменения одного аргумента функции от двух или более переменных на производную этой функции, взятую по отношению к другому аргументу. Если y = f(x,z), то ее производная, или первая производная функции y по аргументу x, равна… … Экономический словарь

аналог скорости точки — Первая производная движения точки по обобщенной координате механизма…

аналог угловой скорости звена — Первая производная угла поворота звена по обобщенной координате механизма … Политехнический терминологический толковый словарь

обобщенная скорость механизма — Первая производная обобщенной координаты механизма по времени … Политехнический терминологический толковый словарь

Книги

• Сборник задач по дифференциальной геометрии и топологии, Мищенко А. С.
• Мои научные статьи Книга 3. Метод матрицы плотности в квантовых теориях лазера, произвольный атом, Бондарев Борис Владимирович. В данной книге рассматриваются опубликованные научные статьи, в которых методом матриц плотности излагаются новые квантовые теории лазера, произвольного атома и затухающего квантового осциллятора.…

Приведем сводную таблицу для удобства и наглядности при изучении темы .

Константа y=C Степенная функция y = x p (х р)» = р х р — 1	Экспоненциальная функция y = x (а х)» = а х пер а В частности, когда a = e , мы имеем y = e x (е х)» = е х
логарифмическая функция (log a x) » = 1 x ln a В частности, когда a = e , мы имеем y = log x (ln x)» = 1 x	Тригонометрические функции (sin x) «= cos x (cos x)» = — sin x (t g x) » = 1 cos 2 x (c t g x)» = — 1 sin 2 x
Обратные тригонометрические функции (a r c sin x) » = 1 1 — x 2 (a r c cos x) » = — 1 1 — x 2 (ar c t g x)» = 1 1 + x 2 (a r c c t g x) » = — 1 1 + x 2	Гиперболические функции (s h x) » = c h x (c h x) » = s h x (t h x)» = 1 c h 2 x (c t h x) » = — 1 s h 2 x

Проанализируем, как были получены формулы указанной таблицы, или, другими словами, докажем вывод формул производных для каждого вида функции.

Производная постоянной

Доказательство 1

Для вывода этой формулы возьмем за основу определение производной функции в точке. Мы используем x 0 = x, где x принимает значение любого действительного числа, или, другими словами, x — это любое число из области определения функции f(x) = C . Запишем предел отношения приращения функции к приращению аргумента как ∆ x → 0:

lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C — C ∆ x = lim ∆ х → 0 0 ∆ х = 0

Обратите внимание, что выражение 0 ∆ x попадает под знак предела. Это не неопределенность «ноль разделить на ноль», так как в числителе стоит не бесконечно малая величина, а ноль. Другими словами, приращение постоянной функции всегда равно нулю.

Итак, производная постоянной функции f(x) = C равна нулю во всей области определения.

Пример 1

Даны постоянные функции:

f 1 (x) = 3 , f 2 (x) = a , a ∈ R , f 3 (x) = 4 . 13 7 22 , f 4 (х) = 0 , f 5 (х) = — 8 7

Раствор

Опишем данные условия. В первой функции мы видим производную от натурального числа 3. В следующем примере нужно взять производную от через , где через — любое действительное число. Третий пример дает нам производную от иррационального числа 4. 13 7 22 , четвертая — производная от нуля (ноль — целое число). Наконец, в пятом случае имеем производную рациональную дробь — 8 7 .

Ответ: производные данных функций равны нулю для любых действительных х (во всей области определения)

f 1 «(x) = (3)» = 0 , f 2 «(x) = (a) » = 0 , a ∈ R , f 3 » (x) = 4 . 13 7 22 » = 0 , f 4 » (x) = 0 » = 0 , f 5 » (x) = — 8 7 » = 0

Производная степенной функции

Обратимся к степенной функции и формуле ее производной, которая имеет вид: (x p) » = p x p — 1, где показатель степени p — любое действительное число.

Доказательство 2

Вот доказательство формулы, когда показатель степени является натуральным числом: p = 1 , 2 , 3 , …

Опять же, мы полагаемся на определение производной. Запишем предел отношения приращения степенной функции к приращению аргумента: x) p — x p ∆ x

Для упрощения выражения в числителе воспользуемся биномиальной формулой Ньютона:

(x + ∆ x) p — x p = C p 0 + x p + C p 1 x p — 1 ∆ x + C p 2 x p — 2 (∆ x) 2 +… + + C p p — 1 x (∆ x) p — 1 + C p p (∆ x) p — x p = = C p 1 x p — 1 ∆ x + C p 2 x p — 2 (∆ x) 2 +… + C p p — 1 x (∆ x) p — 1 + C p p (∆ x) p

Таким образом:

(x p) » = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p — x p ∆ x = = lim ∆ x → 0 (C p 1 x p — 1 ∆ x + C p 2 x p — 2 (∆ x) 2 + … + C p p — 1 x (∆ x) p — 1 + C p p (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 x p — 1 + C p 2 x p — 2 ∆ x + . . . + C p p — 1 x (∆ x) p — 2 + C p p (∆ x) p — 1) = = C p 1 x p — 1 + 0 + 0 +… + 0 = p!1!(p — 1)! x p — 1 = p x p — 1

Итак, мы доказали формулу производной степенной функции при показатель степени — натуральное число

Доказательство 3

Чтобы привести доказательство для случая, когда p- любое действительное число, отличное от нуля, воспользуемся логарифмической производной (здесь следует понимать отличие производной от логарифмической функции).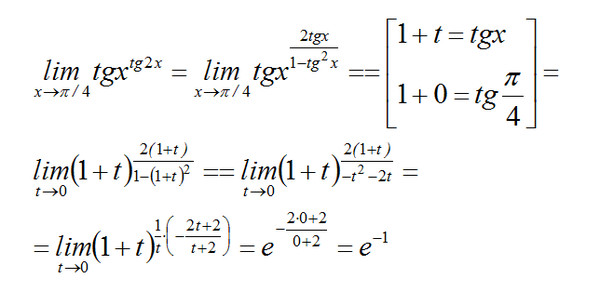 Для более полного понимания желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной комплексной функции.

Рассмотрим два случая: когда x положительный, а когда x отрицательный.

Так х > 0 . Тогда: х р > 0 . Логарифмируем равенство y = x p по основанию e и применяем свойство логарифма:

y = x p ln y = ln x p ln y = p ln x

На этом этапе неявно определенная функция имеет было получено. Определим его производную:

(ln y) » = (p ln x) 1 y y » = p 1 x ⇒ y » = p y x = p x p x = p x p — 1

Теперь рассмотрим случай, когда x- отрицательное число.

Если показатель p четное число, то степенная функция также определена для x

Затем ХР

Если p является нечетным числом, то степенная функция определяется для x

у «(х) = (- (- х) р) » = — ((- х) р)» = — р (- х) р — 1 (- х) » = = р ( — х) р — 1 = р х р — 1

Последний переход возможен потому, что если р — нечетное число, то р — 1 либо четное число, либо ноль (при р = 1), следовательно, для отрицательных x справедливо равенство (- x) p — 1 = x p — 1.

Итак, мы доказали формулу производной степенной функции для любого действительного p.

Пример 2

Даны функции:

f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 — 1 4 , f 3 (x) = 1 x log 7 12

Определите их производные .

Раствор

Преобразуем часть заданных функций в табличный вид y = x p , исходя из свойств степени, а затем воспользуемся формулой:

f 1 (х) = 1 х 2 3 = х — 2 3 ⇒ f 1 «(х) = — 2 3 х — 2 3 — 1 = — 2 3 х — 5 3 ф 2″( х) = х 2 — 1 4 = 2 — 1 4 х 2 — 1 4 — 1 = 2 — 1 4 х 2 — 5 4 f 3 (х) = 1 х log 7 12 = х — log 7 12 ⇒ f 3 «( x) = — log 7 12 x — log 7 12 — 1 = — log 7 12 x — log 7 12 — log 7 7 = — log 7 12 x — log 7 84

Производная показательной функции

Доказательство 4

Выведем формулу для производной, исходя из определения:

(а х)» = lim ∆ х → 0 а х + ∆ х — а х ∆ х = lim ∆ х → 0 а х (а ∆ х — 1) ∆ x = a x lim ∆ x → 0 a ∆ x — 1 ∆ x = 0 0

У нас неопределенность. Чтобы расширить его, мы пишем новую переменную z = a ∆ x — 1 (z → 0 при ∆ x → 0). В этом случае a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Для последнего перехода используется формула перехода к новому основанию логарифма.

Сделаем замену в исходном пределе:

(a x) » = a x lim ∆ x → 0 a ∆ x — 1 ∆ x = a x ln a lim ∆ x → 0 1 1 z ln (z + 1) = = a x ln a lim ∆ x → 0 1 ln (z + 1) 1 z = a x ln a 1 ln lim ∆ x → 0 (z + 1) 1 z

Вспомним второй чудесный предел и тогда получим экспоненциальную функцию формулы производной:

(a x) » = a x ln a 1 ln lim z → 0 (z + 1) 1 z = a x ln a 1 ln e = a x ln a

Пример 3

Даны экспоненциальные функции:

f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x

We нужно найти их производные

Решение

Используем формулу производной показательной функции и свойства логарифма:

f 1 «(x) = 2 3 x» = 2 3 x ln 2 3 = 2 3 x (ln 2 — ln 3) f 2 «(x) = 5 3 x» = 5 3 x ln 5 1 3 = 1 3 5 3 x ln 5 f 3 «(x) = 1 (e) x» = 1 e x » = 1 e x ln 1 e = 1 e x ln e — 1 = — 1 e x

Производная логарифмической функции

Proof 5

Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значений оснований логарифма. На основании определения производной получаем:

(log a x) » = lim ∆ x → 0 log a (x + ∆ x) — log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x x x = lim ∆ x → 0 1 x log a 1 + ∆ x x x ∆ x = = 1 x log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x log a e = 1 x ln e ln a = 1 x ln a

Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифмичности Равенство lim ∆ x → 0 1 + ∆ x x x ∆ x = e верно в соответствии со вторым замечательным пределом9.0907

Пример 4

Даны логарифмические функции:

f 1 (x) = log log 3 x , f 2 (x) = log x

Необходимо вычислить их производные.

Раствор

Применим полученную формулу:

f 1 «(x) = (log ln 3 x)» = 1 x ln (ln 3) ; f 2 «(x) = (ln x)» = 1 x ln e = 1 x

Значит, производная натурального логарифма равна единице, деленной на x .

Производные тригонометрических функций

Доказательство 6

Мы используем некоторые тригонометрические формулы и первый чудесный предел, чтобы вывести формулу для производной тригонометрической функции.

Согласно определению производной функции синуса получаем:

(sin x)» = lim ∆ x → 0 sin (x + ∆ x) — sin x ∆ x

Формула разности синусов позволит нам выполнить следующие действия:

(sin x)» = lim ∆ x → 0 sin (x + ∆ x) — sin x ∆ x = = lim ∆ x → 0 2 sin x + ∆ x — x 2 cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2

Наконец, воспользуемся первым чудесным пределом:

sin»x = cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x

Итак, производная функции sin x будет быть cos x .

Таким же образом докажем и формулу для производной косинуса: x → 0 — 2 sin x + ∆ x — x 2 sin x + ∆ x + x 2 ∆ x = = — lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 = = — sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = — sin x

Тех. производная функция cos x будет равна – sin x .

Выводим формулы производных тангенса и котангенса исходя из правил дифференцирования:

t g»x = sin x cos x» = sin»x cos x — sin x cos» x cos 2 x = = cos x cos x — sin x (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g «x = cos x sin x» = cos «x sin x — cos x sin» x sin 2 x = = — sin x sin x — cos x cos x sin 2 x = — sin 2 x + cos 2 x sin 2 x = — 1 sin 2 x

Производные обратных тригонометрических функций

Раздел о производных обратных функций содержит исчерпывающую информацию о доказательстве формул для производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому мы не будем дублировать здесь материал.

Производные гиперболических функций

Доказательство 7

Мы можем вывести формулы для производных гиперболического синуса, косинуса, тангенса и котангенса, используя правило дифференцирования и формулу для производной показательной функции:

s h «x = e x — e — x 2» = 1 2 e x «- e — x» == 1 2 e x — — e — x = e x + e — x 2 = c h x c h «x = e x + e — x 2» = 1 2 e x «+ e — x» == 1 2 e x + — e — x = e x — e — x 2 = s h x t h «x = s h x c h x» = s h «x c h x — s h x c h» x c h 2 x = c h 2 x — s h 2 x c h 2 x = 1 c h 2 x c t h «x = c h x s h x» = c h «x s h x — c h x s h «x s h 2 x = s h 2 x — c h 2 x s h 2 x = — 1 s h 2 x

Если вы заметили ошибку в текст, выделите его и нажмите Ctrl+Enter

Абсолютно невозможно решать физические задачи или примеры по математике без знания производной и методов ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы решили посвятить сегодняшнюю статью.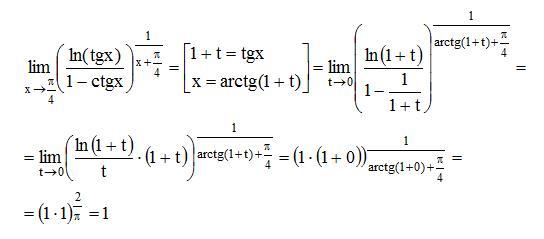 Что такое производная, каков ее физический и геометрический смысл, как вычислить производную функции? Все эти вопросы можно объединить в один: как понять производную?

Геометрический и физический смысл производной

Пусть есть функция f(x) , заданные через некоторый интервал (a,b) . Точки x и x0 принадлежат этому интервалу. При изменении x изменяется и сама функция. Изменение аргумента — разница его значений x-x0 . Эта разница записывается как дельта x и называется приращением аргумента. Изменением или приращением функции называется разница между значениями функции в двух точках. Производное определение:

Производной функции в точке называется предел отношения приращения функции в данной точке к приращению аргумента при стремлении последнего к нулю.

Иначе можно записать так:

Какой смысл находить такой предел? Но какой:

производная функции в точке равна тангенсу угла между осью ОХ и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, со школьной скамьи всем известно, что скорость — это частный путь. х=f(t) и время т . Средняя скорость за определенный период времени:

Узнать скорость движения в момент времени t0 нужно рассчитать лимит:

Правило первое: вынести константу

Константу можно вынести из знака производной. Более того, это необходимо сделать. При решении примеров по математике берите за правило — если можете упростить выражение, то обязательно упростите .

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же верно и для производной разности функций.

Мы не будем приводить доказательство этой теоремы, а рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производная функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В приведенном выше примере мы сталкиваемся с выражением:

В этом случае промежуточный аргумент равен 8x в пятой степени. Для того чтобы вычислить производную от такого выражения, сначала рассмотрим производную внешней функции по промежуточному аргументу, а затем умножим на производную самого промежуточного аргумента по независимой переменной.

Четвертое правило: производная от частного двух функций

Формула для определения производной частного двух функций:

Мы попытались рассказать о производных для чайников на пустом месте. Эта тема не так проста, как кажется, поэтому будьте осторожны: в примерах часто встречаются подводные камни, поэтому будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обращаться в студенческую службу. В короткие сроки мы поможем вам решить самые сложные контрольные и разобраться с задачами, даже если вы никогда раньше не имели дела с расчетом производных.

Можно вывести из знака производная :

(af(x)»=af» (x).

Например :

постоянное число) равно алгебраической сумме их производных :

(f 1 (x) + f 2 (x) — f 3 (x))» = f 1 «(x) + f 2» (x ) — f 3 «(x).

Например, :

(0,3 х 2 — 2 х + 0,8) «= (0,3 х 2)» — (2 х) «+ (0,8)» = 0,6 х — 2 ( производная последний член уравнение равно нулю).

Если производная функции g отлична от нуля, то отношение f/g также имеет окончательную производную . Это свойство может быть записано как:

.

Пусть функций y = f(x) и y = g(x) имеют конечных производных в точке x 0 . Тогда функций f ± g и f g также имеют конечных производных в этой точке . Тогда получаем:

(f±g)′ = f′±g′,

(ж г) ′ = ж ′ г + ж г ′.

Производная сложной функции.

Пусть функция y = f(x) имеет конечных производных в точке x 0 , функция z = s(y) имеет конечную производную в точке y 0 = f(x 0).

Тогда комплексная функция z = s (f(x)) также имеет в этой точке конечную производную. Это можно записать в виде:

.

Производная обратной функции.

Пусть функция y = f(x) имеет обратная функция x = g(y) на некотором интервале (a, b) и существует ненулевая окончательная производная этой функции в точке x 0 , которая принадлежит областям , т. е. x 0 ∈ (a , б).

Тогда обратная функция Она имеет производную в точке y 0 = f(x 0):

.

No related posts.