| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | cos(150 град. ) | ||
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.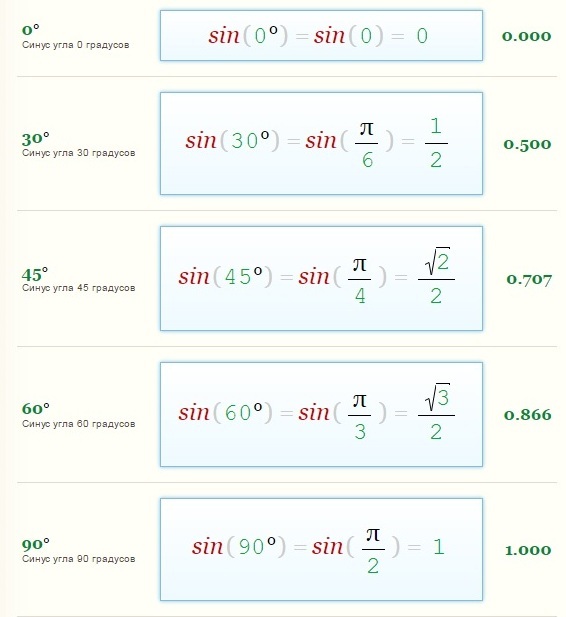 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | ||
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.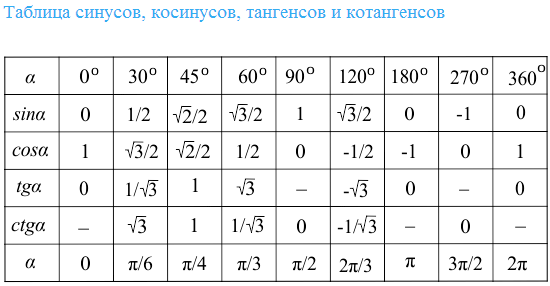 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град.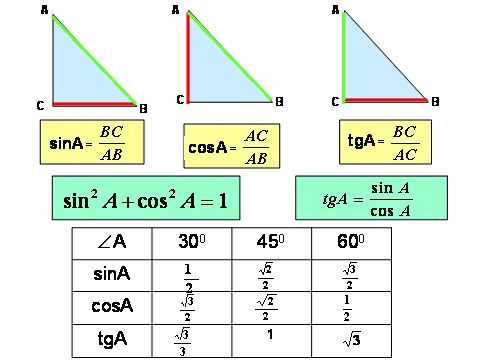 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
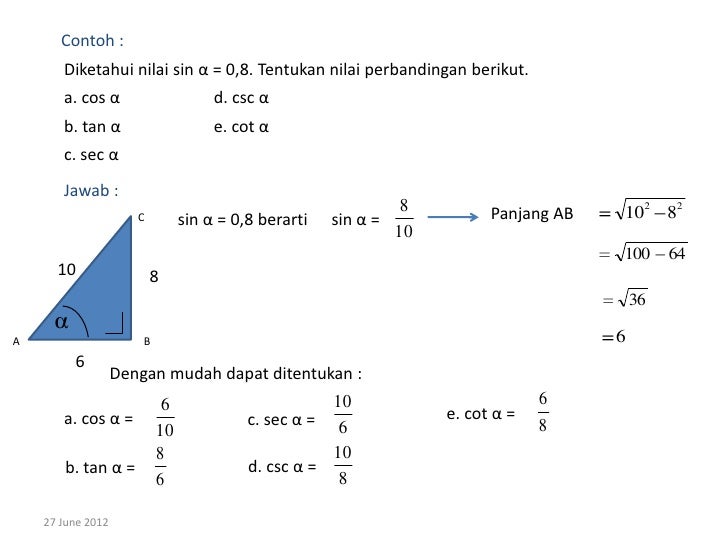
Найдите тангенс альфа если синус
Получи беслпатные курсы подготовки к ЕГЭ и ОГЭ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2012-10-03
В данной статье мы с вами разберём некоторые задачи связанные с выражениями. Задания данной группы довольно разнообразны. Если вы запомнили свойства степеней, корней и логарифмов, знаете основные формулы тригонометрии, и постоянно практикуетесь, то большинство задач для вас никакого труда не представят.
Задания данной группы довольно разнообразны. Если вы запомнили свойства степеней, корней и логарифмов, знаете основные формулы тригонометрии, и постоянно практикуетесь, то большинство задач для вас никакого труда не представят.
Относительную сложность могут вызывать следующие:
— преобразования буквенных иррациональных выражений
— вычисление значений тригонометрических выражений
— преобразования тригонометрических выражений
Если перечислить все группы задач, то они довольно разнообразны.
Они включают в себя: ПОКАЗАТЬ/СКРЫТЬ
Здесь мы с вами разберём задачи на вычисление значений тригонометрических выражений. Конечно, все их в одной статье разобрать невозможно. Но мы обязательно разберём и другие примеры, не пропустите!
Итак, что обязательно вы должны знать и всегда помнить? Это знаки тригонометрических функций в четвертях. ЭТО ВАЖНО!!!
Как осознать эту информацию и понять следствием чего она является – об этом будет отдельная статья (если вы это знаете, то прекрасно). Пока предлагаю пока просто запомнить:
Пока предлагаю пока просто запомнить:
Основное тригонометрическое тождество:
Формулы тангенса и котангенса:
Выполняются элементарные алгебраические преобразования:
1. Числитель и знаменатель дроби можем умножать и делить на одно и тоже число.
2. Левую и правую часть уравнения можем умножать и делить на одно и тоже число.
В представленных ниже заданиях используется основное тригонометрическое тождество и формула тангенса.
Найдите тангенс альфа, если
В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:
Косинус угла нам известен. Из формулы основного тригонометрического тождества мы можем найти значение синуса. Затем подставить их в формулу тангенса.
Теперь ВАЖНЫЙ момент: необходимо определить знак синуса для интервала (3Пи/2;2Пи). Это интервал от 270 до 360 градусов (четвёртая четверть). Как переводить радианы в градусы можно посмотреть здесь.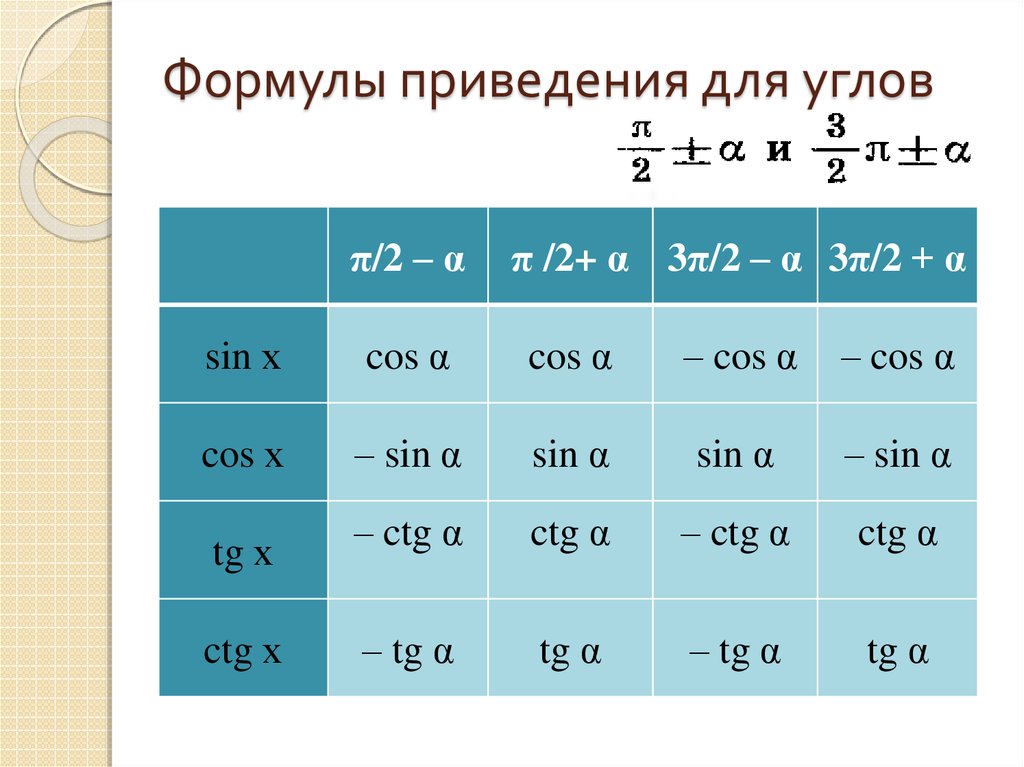 Значение синуса в этой четверти отрицательное, поэтому:
Значение синуса в этой четверти отрицательное, поэтому:
Таким образом:
Ответ: – 0,5
Найдите tg α, если
В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:
Cинус угла нам известен. Из формулы основного тригонометрического тождества мы можем найти значение косинуса. Затем подставить их в формулу тангенса.
Определяем знак косинуса для интервала (Пи/2;Пи). Это интервал от 90 до 180 градусов (вторая четверть). Значение косинуса в этой четверти отрицательное (смотрите эскиз). Поэтому
Таким образом:
Ответ: – 0,25
Найдите 5·cos α, если синус альфа
Необходимо найти косинус угла. Из формулы основного тригонометрического тождества следует, что cos2x = 1– sin2x и
Определим знак косинуса. Угол принадлежит интервалу (3Пи/2;2Пи).
Это интервал от 270 до 360 градусов (четвёртая четверть).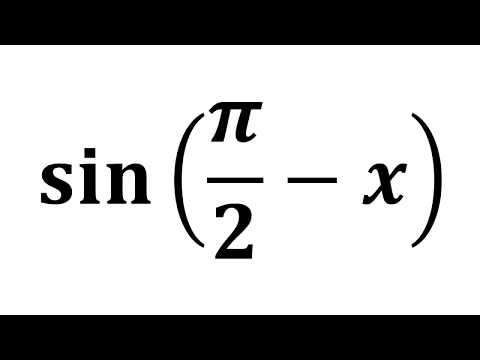 Значение косинуса в этой четверти положительное, поэтому:
Значение косинуса в этой четверти положительное, поэтому:
Таким образом, 5·cos α = 5∙0,7 = 3,5
Ответ: 3,5
Найдите 0,1·sin α, если
Необходимо найти синус угла. Из формулы основного тригонометрического тождества следует, что sin2x = 1– cos2x и
Определим знак синуса. Угол принадлежит интервалу (0; Пи/2).
Это интервал от 0 до 90 градусов (первая четверть). Значение синуса в этой четверти положительное, поэтому:
Таким образом 0,1·sin α = 0,1∙0,3 = 0,03
Ответ: 0,03
Общая рекомендация для следующих данных примеров! Если требуется найти тангенс аргумента (квадрат тангенса), то осуществляем деление на косинус (квадрат косинуса). Если требуется найти котангенс аргумента (квадрат котангенса), то осуществляем деление на синус (квадрат синуса). Примеры:
65217. Найдите tg2 α, если 3sin2 α + 8 cos2 α = 7
Требуется найти квадрат тангенса. Разделим обе части уравнения на cos2 α, получим:
Разделим обе части уравнения на cos2 α, получим:
Второй способ:
Далее по формуле основного тригонометрического тождества можно найти квадрат синуса и используя формулу тангенса вычислить уже его квадрат:
Ответ: 0, 25
65269. Найдите
Преобразуем данное выражение так, чтобы в числителе и знаменателе был тангенс. Разделим числитель и знаменатель на cos α, получим:
Ответ: – 0,5
65273. Найдите
Здесь дано значение тангенса. Необходимо сделать так, чтобы в выражении у нас был тангенс. Вынесем cosα за скобки в числителе и знаменателе (или разделим числитель и знаменатель на cosα), получим:
Подставим значение тангенса данное в условии, получим:
*Косинус у нас сократился.
Ответ: 4
65363. Найдите tg α, если
В левой части в числителе и знаменателе вынесем cosα за скобки, получим:
Ответ: 0,4
65423. Найдите tg α, если
Найдите tg α, если
Умножим обе части уравнения на 4 (2sinα+cosα+1)
Ответ: –1,9
26775. Найдите tg α, если
Посмотреть решение
26776. Найдите tg α, если
Посмотреть решение
26777. Найдите 3cos α, если
Посмотреть решение
26778. Найдите 5sin α, если
Посмотреть решение
26787. Найдите tg2 α, если
Посмотреть решение
26788. Найдите
Посмотреть решение
26789. Найдите
Посмотреть решение
26790. Найдите tg α, если
Посмотреть решение
26791. Найдите tg α, если
Посмотреть решение
Подведём итог, для решения подобных примеров вы:
1. Должны знать на зубок основные формулы тригонометрии.
2. Не забывать определять знак (+ или -) для тригонометрических функций в четвертях. Потерянный знак на экзамене – это ошибка и потерянный бал, будьте внимательны!!!
Надеюсь, что материал был для вас полезен.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Преобразование выражений | ЕГЭ-№6Тригонометрия
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Чему равен косинус альфа формула. Уравнение sin x = a
На этой странице вы найдете все основные тригонометрические формулы, которые помогут вам решать многие упражнения, значительно упростив само выражение.
Тригонометрические формулы — математические равенства для тригонометрических функций, которые выполняются при всех допустимых значениях аргумента.
Формулами задаются соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом, котангенсом.
Синус угла – это координата y точки (ордината) на единичной окружности. Косинус угла – это координата x точки (абсцисса).
Тангенс и котангенс – это, соответственно, соотношения синуса к косинусу и наоборот.
`sin \ \alpha, \ cos \ \alpha`
`tg \ \alpha=\frac{sin\ \alpha}{cos \ \alpha},` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
И две, которые используются реже – секанс, косеканс. Они обозначают соотношения 1 к косинусу и синусу.
`sec \ \alpha=\frac{1}{cos\ \alpha},` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac{1}{sin \ \alpha},` ` \alpha\ne\pi+\pi n,\ n \in Z`
Из определений тригонометрических функций видно, какие знаки они имеют в каждой четверти. Знак функции зависит только от того, в какой из четвертей располагается аргумент.
При изменении знака аргумента с «+» на «-» только функция косинус не меняет своего значения. Она называется четной. 2 \alpha,` ` \alpha\ne\pi n, \ n \in Z`
2 \alpha,` ` \alpha\ne\pi n, \ n \in Z`
Формулы суммы и разности углов тригонометрических функций
Формулы сложения и вычитания аргументов выражают тригонометрические функции суммы или разности двух углов через тригонометрические функции этих углов.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac{tg \ \alpha+tg \ \beta}{1-tg \ \alpha\ tg \ \beta}`
`tg(\alpha-\beta)=\frac{tg \ \alpha-tg \ \beta}{1+tg \ \alpha \ tg \ \beta}`
`ctg(\alpha+\beta)=\frac{ctg \ \alpha \ ctg \ \beta-1}{ctg \ \beta+ctg \ \alpha}`
`ctg(\alpha-\beta)=\frac{ctg \ \alpha\ ctg \ \beta+1}{ctg \ \beta-ctg \ \alpha}`
Формулы двойного угла
`sin \ 2\alpha=2 \ sin \ \alpha \ cos \ \alpha=` `\frac {2 \ tg \ \alpha}{1+tg^2 \alpha}=\frac {2 \ ctg \ \alpha}{1+ctg^2 \alpha}=` `\frac 2{tg \ \alpha+ctg \ \alpha}`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \ sin^2 \alpha=2 \ cos^2 \alpha-1=` `\frac{1-tg^2\alpha}{1+tg^2\alpha}=\frac{ctg^2\alpha-1}{ctg^2\alpha+1}=` `\frac{ctg \ \alpha-tg \ \alpha}{ctg \ \alpha+tg \ \alpha}`
`tg \ 2\alpha=\frac{2 \ tg \ \alpha}{1-tg^2 \alpha}=` `\frac{2 \ ctg \ \alpha}{ctg^2 \alpha-1}=` `\frac 2{ \ ctg \ \alpha-tg \ \alpha}`
`ctg \ 2\alpha=\frac{ctg^2 \alpha-1}{2 \ ctg \ \alpha}=` `\frac { \ ctg \ \alpha-tg \ \alpha}2`
Формулы тройного угла
`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac{3 \ tg \ \alpha-tg^3 \alpha}{1-3 \ tg^2 \alpha}`
`ctg \ 3\alpha=\frac{ctg^3 \alpha-3 \ ctg \ \alpha}{3 \ ctg^2 \alpha-1}`
Формулы половинного угла
`sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`
`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`
`tg \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}=` `\frac {sin \ \alpha}{1+cos \ \alpha}=\frac {1-cos \ \alpha}{sin \ \alpha}`
`ctg \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}=` `\frac {sin \ \alpha}{1-cos \ \alpha}=\frac {1+cos \ \alpha}{sin \ \alpha}`
Формулы половинных, двойных и тройных аргументов выражают функции `sin, \ cos, \ tg, \ ctg` этих аргументов (`\frac{\alpha}2, \ 2\alpha, \ 3\alpha,… `) через эти ж функции аргумента `\alpha`. 4 \alpha=\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`
4 \alpha=\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`
Формулы суммы и разности тригонометрических функций
Формулы являют собой преобразования суммы и разности тригонометрических функций разных аргументов в произведение.
`sin \ \alpha+sin \ \beta=` `2 \ sin \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`sin \ \alpha-sin \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2`
`cos \ \alpha+cos \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2=` `2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\beta-\alpha}2`
`tg \ \alpha \pm tg \ \beta=\frac{sin(\alpha \pm \beta)}{cos \ \alpha \ cos \ \beta}`
`ctg \ \alpha \pm ctg \ \beta=\frac{sin(\beta \pm \alpha)}{sin \ \alpha \ sin \ \beta}`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac{cos(\alpha \mp \beta)}{cos \ \alpha \ sin \ \beta}`
Здесь происходит преобразование сложения и вычитаний функций одного аргумента в произведение. 2 (\frac {\pi} 4-\frac{\alpha}2)`
2 (\frac {\pi} 4-\frac{\alpha}2)`
`1 \pm tg \ \alpha=\frac{sin(\frac{\pi}4 \pm \alpha)}{cos \frac{\pi}4 \ cos \ \alpha}=` `\frac{\sqrt{2} sin(\frac{\pi}4 \pm \alpha)}{cos \ \alpha}`
`1 \pm tg \ \alpha \ tg \ \beta=\frac{cos(\alpha \mp \beta)}{cos \ \alpha \ cos \ \beta};` ` \ ctg \ \alpha \ ctg \ \beta \pm 1=\frac{cos(\alpha \mp \beta)}{sin \ \alpha \ sin \ \beta}`
Формулы преобразования произведений функций
Формулы преобразования произведения тригонометрических функций с аргументами `\alpha` и `\beta` в сумму (разность) этих аргументов.
`sin \ \alpha \ sin \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}`
`sin\alpha \ cos\beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}`
`cos \ \alpha \ cos \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}`
`tg \ \alpha \ tg \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)} =` `\frac{tg \ \alpha + tg \ \beta}{ctg \ \alpha + ctg \ \beta}`
`ctg \ \alpha \ ctg \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)} =` `\frac{ctg \ \alpha + ctg \ \beta}{tg \ \alpha + tg \ \beta}`
`tg \ \alpha \ ctg \ \beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}`
Универсальная тригонометрическая подстановка
Эти формулы выражают тригонометрические функции через тангенс половинного угла. 2 \alpha}}=\frac 1{tg \ \alpha}`
2 \alpha}}=\frac 1{tg \ \alpha}`
Тригонометрия в буквальном смысле переводится, как «измерение треугольников». Она начинает изучаться еще в школе, и продолжается более детально в ВУЗах. Поэтому основные формулы по тригонометрии нужны, начиная еще с 10 класса, а также для сдачи ЕГЭ. Они обозначают связи между функциями, а поскольку этих связей много, то и самых формул есть немало. Запомнить их все нелегко, да и не надо – при необходимости их все можно вывести.
Тригонометрические формулы применяются в интегральном исчислении, а также при тригонометрических упрощениях, вычислениях, преобразованиях.
В тригонометрии многие формулы легче вывести, чем вызубрить. Косинус двойного угла — замечательная формула! Она позволяет получить формулы понижения степени и формулы половинного угла.
Итак, нам нужны косинус двойного угла и тригонометрическая единица:
Они даже похожи: в формуле косинуса двойного угла — разность квадратов косинуса и синуса, а в тригонометрической единице — их сумма. Если из тригонометрической единицы выразить косинус:
Если из тригонометрической единицы выразить косинус:
и подставить его в косинус двойного угла, то получим:
Это — еще одна формула косинуса двойного угла:
Эта формула — ключ к получению формулы понижения степени:
Итак, формула понижения степени синуса:
Если в ней угол альфа заменить на половинный угол альфа пополам, а двойной угол два альфа — на угол альфа, то получим формулу половинного угла для синуса:
Теперь из тригонометрической единицы выразим синус:
Подставим это выражение в формулу косинуса двойного угла:
Получили еще одну формулу косинуса двойного угла:
Эта формула — ключ к нахождению формулы понижения степени косинуса и половинного угла для косинуса.
Таким образом, формула понижения степени косинуса:
Если в ней заменить α на α/2, а 2α — на α, то получим формулу половинного аргумента для косинуса:
Так как тангенс — отношение синуса к косинусу то формула для тангенса:
Котангенс — отношение косинуса к синусу. Поэтому формула для котангенса:
Поэтому формула для котангенса:
Конечно, в процессе упрощения тригонометрических выражений формулы половинного угла или понижения степени нет смысла каждый раз выводить. Гораздо проще перед собой положить листик с формулами. И упрощение продвинется быстрее, и зрительная память включится на запоминание.
Но несколько раз вывести эти формулы все же стоит. Тогда вы будете абсолютно уверены в том, что на экзамене, когда нет возможности воспользоваться шпаргалкой, вы без труда их получите, если возникнет необходимость.
Задание .
Найти значение х при .
Решение.
Найти значение аргумента функции , при котором он равен какому-либо значению, означает определить, при каких аргументах значение синуса будет именно таким, как указано в условии.
В данном случае нам нужно выяснить, при каких значениях значение синуса будет равным 1/2. Это можно сделать несколькими способами.
Например, использовать , по которому определить при каких значениях х функция синус будет равна 1/2.
Другим способом является использование . Напомню, что значения синусов лежат на оси Оу.
Самым распространенным способом является обращение к , особенно если речь идет о таких стандартных для этой функции значениях, как 1/2.
Во всех случаях не стоит забывать об одном из важнейших свойств синуса — о его периоде.
Найдем в таблице значение 1/2 для синуса и посмотрим какие аргументы ему соответствуют. Интересующие нас аргументы равны Пи / 6 и 5Пи / 6.
Запишем все корни, которые удовлетворяют заданное уравнение. Для этого записываем интересующий нас неизвестный аргумент х и одно из значений аргумента, полученное из таблицы, то есть Пи / 6. Запишем для него, учитывая период синуса, все значения аргумента:
Возьмем второе значение, и проделаем те же шаги, что и в предыдущем случае:
Полным решением исходного уравнения будет:
и
q может принимать значение любого целого числа.
Простейшие тригонометрические тождества
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств .
См. также доказательство правильности преобразования простейших тригонометрических тождеств .
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса .
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).
Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
Как видно, косинус и секанс является четной функцией , синус, тангенс и котангенс — нечетные функции .
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.
Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла ) в одинарный происходит по следующим правилам:
Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.
Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции (sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .Данные формулы называются формулами универсальной тригонометрической подстановки . Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.
Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.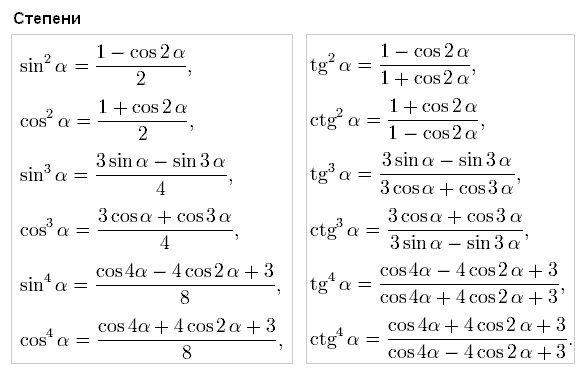
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:
Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:
В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.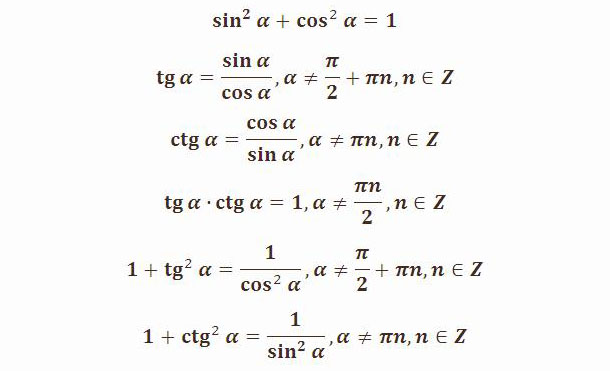
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
абс | Вычисляет абсолютное значение каждого элемента в |
абсолютный | Псевдоним для |
акос | Вычисляет арккосинус каждого элемента в |
арккос | Псевдоним для |
акош | Возвращает новый тензор с обратным гиперболическим косинусом элементов |
арккош | Псевдоним для |
добавить | Добавляет |
addcdiv | Выполняет поэлементное деление |
аддкмуль | Выполняет поэлементное умножение |
уголок | Вычисляет поэлементный угол (в радианах) заданного |
как | Возвращает новый тензор с арксинусом элементов |
угловой синус | Псевдоним для |
асинх | Возвращает новый тензор с обратным гиперболическим синусом элементов |
угловой синус | Псевдоним для |
атан | Возвращает новый тензор с арктангенсом элементов |
арктан | Псевдоним для |
атанх | Возвращает новый тензор с аркгиперболическим тангенсом элементов |
арктанг | Псевдоним для |
атан2 | Поэлементный арктангенс inputi/otheri\text{input}_{i} / \text{other}_{i}inputi/otheri с учетом квадранта. |
арктанг2 | Псевдоним для |
побитовое_не | Вычисляет побитовое НЕ заданного входного тензора. |
побитовое_и | Вычисляет побитовое И для |
побитовое_или | Вычисляет побитовое ИЛИ для |
побитовое_исключение | Вычисляет побитовое XOR для |
bitwise_left_shift | Вычисляет арифметический сдвиг влево |
побитовый_правый_сдвиг | Вычисляет арифметический сдвиг вправо ввода |
потолок | Возвращает новый тензор с ceil элементов |
зажим | Захватывает все элементы в |
зажим | Псевдоним для |
conj_physical | Вычисляет поэлементное сопряжение заданного |
копия | Создайте новый тензор с плавающей запятой с величиной |
| Возвращает новый тензор с косинусом элементов |
кош | Возвращает новый тензор с гиперболическим косинусом элементов |
град2рад | Возвращает новый тензор с каждым из элементов |
раздел | Делит каждый элемент ввода |
разделить | Псевдоним для |
дигамма | Псевдоним для |
| Псевдоним для |
erfc | Псевдоним для |
ерфинв | Псевдоним для |
эксп | Возвращает новый тензор с экспонентой элементов входного тензора |
exp2 | Псевдоним для |
опыт1 | Псевдоним для |
fake_quantize_per_channel_affine | Возвращает новый тензор с данными в |
fake_quantize_per_tensor_affine | Возвращает новый тензор с данными в |
исправить | Псевдоним для |
float_power | Возводит |
этаж | Возвращает новый тензор с полом элементов |
пол_раздел | |
Фмод | Применяет C++ std::fmod по записи. |
трещина | Вычисляет дробную часть каждого элемента в |
частота 9n \rightarrow \mathbb{R}g:Rn→R в одном или нескольких измерениях с использованием метода центральных разностей второго порядка точности. | |
изображение | Возвращает новый тензор, содержащий мнимые значения собственного тензора |
лдэксп | Умножает |
лерп | Выполняет линейную интерполяцию двух тензоров |
лгамма | Вычисляет натуральный логарифм абсолютного значения гамма-функции на входе |
журнал | Возвращает новый тензор с натуральным логарифмом элементов |
лог10 | Возвращает новый тензор с логарифмом по основанию 10 элементов |
log1p | Возвращает новый тензор с натуральным логарифмом (1 + |
журнал2 | Возвращает новый тензор с логарифмом по основанию 2 элементов |
logaddexp | Логарифм суммы возведений в степень входных данных. |
logaddexp2 | Логарифм суммы возведений в степень входных данных по основанию 2. |
логический_и | Вычисляет поэлементное логическое И заданных входных тензоров. |
логическое_не | Вычисляет поэлементное логическое НЕ заданного входного тензора. |
логический_или | Вычисляет поэлементное логическое ИЛИ заданных входных тензоров. |
логический_xor | Вычисляет поэлементное логическое XOR для заданных входных тензоров. |
логит | Псевдоним для |
гипотетический | Зная катеты прямоугольного треугольника, верните его гипотенузу. |
i0 | Псевдоним для |
игамма | Псевдоним для |
игаммак | Псевдоним для |
мул | Умножает |
умножить | Псевдоним для |
мвлгамма | Псевдоним для |
nan_to_num | Заменяет |
отрицательный | Возвращает новый тензор с отрицательным значением элементов |
отрицательный | Псевдоним для |
следующий за | Возвращает следующее значение с плавающей запятой после |
полигамма | Псевдоним для |
положительный | Возвращает |
мощность | Принимает степень каждого элемента в |
quantized_batch_norm | Применяет пакетную нормализацию к четырехмерному (NCHW) квантованному тензору. |
Quantized_max_pool1d | Применяет одномерное максимальное объединение к входному квантованному тензору, состоящему из нескольких входных плоскостей. |
Quantized_max_pool2d | Применяет двухмерное максимальное объединение к входному квантованному тензору, состоящему из нескольких входных плоскостей. |
рад2град | Возвращает новый тензор с каждым из элементов |
реальный | Возвращает новый тензор, содержащий действительные значения тензора |
взаимное | Возвращает новый тензор с обратной величиной элементов |
остаток | Вычисляет операцию модуля Python по записи. |
круглый | Элементы ввода |
корп | Возвращает новый тензор с обратной величиной квадратного корня каждого из элементов |
сигмовидная | Псевдоним для |
знак | Возвращает новый тензор со знаками элементов |
знак | Эта функция является расширением torch.sign() для сложных тензоров. |
знаковый бит | Проверяет, установлен ли бит знака каждого элемента |
грех | Возвращает новый тензор с синусом элементов |
синк | Псевдоним для |
синх | Возвращает новый тензор с гиперболическим синусом элементов |
кв | Возвращает новый тензор с квадратным корнем элементов из |
квадратный | Возвращает новый тензор с квадратом элементов |
суб | Вычитает |
вычесть | Псевдоним для |
желтовато-коричневый | Возвращает новый тензор с тангенсом элементов |
танх | Возвращает новый тензор с гиперболическим тангенсом элементов |
true_divide | Псевдоним для |
ствол | Возвращает новый тензор с усеченными целочисленными значениями элементов |
xlogy | Псевдоним для |
Samacheer Kalvi 12th Math Solutions Chapter 6 Applications of Vector Algebra Ex 6.1 — Samacheer Kalvi
14 ноября 2019 г. 19 февраля 2021 г. / By Прасанна
Вы можете загрузить Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Совет штата Тамилнаду поможет вам пересмотреть полную программу и получить больше баллов на экзаменах.
Вопрос 1.
Докажите векторным методом, что если провести прямую из центра окружности окружности в середину хорды, то эта прямая перпендикулярна хорде.
Решение:
Пусть «С» будет серединой хорды АВ.
Возьмем «О» в центре окружности.
Так как OA = OB (Radii)
Вопрос 2.
Докажите векторным методом, что медиана основания равнобедренного треугольника перпендикулярна основанию.
Решение:
Пусть OAB — равнобедренный треугольник с OA = OB
Пусть OC будет медианой основания AB
C будет серединой AB
Возьмем O за начало отсчета.
Вопрос 3.
Докажите методом векторов, что угол, лежащий в полуокружности, прямой.
Решение:
Пусть AB — диаметр окружности с центром «O».
Пусть P — любая точка полуокружности.
Это дает ∠APB = 90°. Отсюда и результат.
Вопрос 4.
Докажите векторным методом, что диагонали ромба делятся пополам под прямым углом.
Решение:
Пусть ABCD — ромб
Вопрос 5.
Используя векторный метод, докажите, что если диагонали параллелограмма равны, то он является прямоугольником.
Решение:
Пусть ABCD — параллелограмм.
Доказать, что ABCD — прямоугольник, если диагонали равны.
\(\overrightarrow{\mathrm{AB}}\) ⊥ r в \(\overrightarrow{\mathrm{BC}}\)
⇒ ABCD — прямоугольник.
Вопрос 6.
Докажите векторным методом, что площадь четырехугольника ABCD с диагоналями AC и BD равна \(\frac{1}{2}|\overrightarrow{\mathrm{AC}} \times \overrightarrow{\mathrm {БД}}|\)
Решение:
Площадь вектора четырехугольника ABCD = {Площадь вектора ∆ABC} + {Площадь вектора ∆ACD}
Вопрос 7.
Докажите векторным методом, что параллелограммы на одном основании и между одинаковыми параллелями равны в области.
Решение:
Пусть ABCD и ABC'D' — два параллелограмма между параллелями с одинаковым основанием
Чтобы доказать: Площадь ABCD = площади ABC'D'
Вопрос 8.
Если G — центр тяжести AABC, докажите это.
(площадь ∆GAB) = (площадь ∆GBC) = (площадь ∆GAC) = \(\frac{1}{3}\) [площадь ∆ABC]
Решение:
Аналогично можно доказать
Площадь ∆GBC = Площадь ∆GAC = \(\frac{1}{3}\) [Площадь ∆ABC]
Вопрос 9.
Используя векторный метод, докажите, что cos(α – β) = cos α cos β + sin α sin β.
Решение:
Из (1) и (2) получаем
cos(α + β) = cos α cos β + sin α sin β
Вопрос 10.
Докажите векторным методом, что sin(α + β) = sin α cos β + cos α sin β.
Решение:
Возьмем две точки A и B на единичной окружности с центром в точке O, так что \(|\overrightarrow{\mathrm{OA}}|=|\overrightarrow{\mathrm{OB}}|\) = 1
Из (1) и (2) получаем
sin (α + β) = sin α cos β + cos α sin β
Вопрос 11.
Частица, на которую действуют постоянные силы \(8 \ vec{i}+2 \vec{j}-6 \vec{k}\) и \(\overrightarrow{6 i}+2 \vec{j}-2 \vec{k}\) смещается от точки (1, 2, 3) до точки (5, 4, 1). Найдите полную работу сил.
Решение:
Из (1) и (2) получаем
Работа силы = \(\overrightarrow{\mathrm{F}} \cdot \vec{d}\) = 56 + 8 + 16 = 80 единиц.
Вопрос 12.
Силы величины \(5 \sqrt{2}\) и \(10 \sqrt{2}\) единиц, действующие в направлениях \((3 \vec{i}+4 \vec{j }+5 \vec{k})\) и \((10 \vec{i}+6 \vec{j}-8 \vec{k})\) соответственно действуют на частицу, смещенную от точка с вектором положения \((4 \vec{i}-3 \vec{j}-2 \vec{k})\) в точку с вектором положения \((\overrightarrow{6 i}+\vec{j }-3 \vec{k})\). Найдите работу, совершенную силами.
Решение:
Вопрос 13.
Найдите модуль и направление косинусов крутящего момента силы, представленной \(3 \vec{i}+4 \vec{j}-5 \vec{k}\ ) относительно точки с вектором положения \(2 \vec{i}-3 \vec{j}+4 \vec{k}\), действующим через точку, вектор положения которой равен \(\overrightarrow{4 i}+2 \ vec{j}-3 \vec{k}\).
Решение:
Вопрос 14.
Найдите момент равнодействующей трех сил, представленных \(-3 \vec{i}+6 \vec{j}-3 \vec{k}\), \( \overrightarrow{4 i}-10 \vec{j}+12 \vec{k}\) и \(\overrightarrow{4 i}+7 \vec{j}\), действующие в точке с позиционным вектором \(8 \vec{i}-\overrightarrow{6} \vec{j}-4 \vec{k}\), относительно точки с вектором положения \(18 \vec{i}+3 \vec{j}-9\vec{k}\)
Решение:
Samacheer Kalvi 12th Math Solutions Chapter 6 Applications Vector Algebra Ex 6.1 Дополнительные задачи
Вопрос 1.
Работа силы \(\overrightarrow{\mathrm{F }}=a \vec{i}+\vec{j}+\vec{k}\) при перемещении точки приложения из (1, 1, 1) в (2, 2, 2) по прямой равно дано 5 ед. Найдите значение а.
Решение:
Вопрос 2.
Если векторы положения трех точек A, B и C равны соответственно и \(7(\vec{i}+\vec{k})\). Найдите \(\overrightarrow{\mathrm{AB}} \times \overrightarrow{\mathrm{AC}}\). Интерпретируйте результат геометрически.
Решение:
Вопрос 3.
В точке (1, -1, -1, 2). Найдите момент силы относительно точки (2, -1, 3).
Решение:
Вопрос 4.
Покажите, что площадь параллелограмма с диагоналями равна \(5 \sqrt{3}\)
Решение:
SPY: что ждет рынок после преодоления июньских минимумов? (NYSEARCA:SPY)
- Сегодняшний рынок
27 сентября 2022 г. 14:20 ETSPDR S&P 500 Trust ETF (SPY)AMZN, IJH, IJR, MSFT, NTSX, PFFD, PSLDX, RIVN, SCZ, TSLA, TYA, VEA, VYMI, ACTV, AFMC, AFSM, AMER, ARKK, AVUV, BAPR, BAUG, BBMC, BBSC, BFOR, BFTR, BJUL, BJUN, BKMC, BKSE, BMAR, BMAY, BOCT, BOSS, BOUT, BUFF, BUL, CALF, CATH, CBSE, CSA, CSB, CSD, CSF, CSML, CSTNL, CWS, CZA, DDIV, DEEP, DES, DEUS, DFAS, DGRS, DIA, DIV, DJD, DON, DSPC, DVLU, DWAS, DWMC, EES, EFIV, EPS, EQAL, ESML, ETHO, EWMC, EWSC, EZM, FAB, FAD, FDM, FFTY, FLQM, FLQS, FNDA, FNK, FNX, FNY, FOVL, FRTY, FSMD, FTA, FTDS, FYC, FYT, FYX, GLRY, GSSC, HAIL, HIBL, HIBS, HLGE, HOMZ, HSMV, IJJ, IJK, IJS, IJT, IMCB, IMCG, IMCV, IPO, ISCB, ISCG, ISCV, ISMD, IUSS, IVDG, IVE, IVOG, IVOO, IVOV, IVV, IVW, IWC, IWM, IWN, IWO, IWP, IWR, IWS, IYY, JDIV, JHMM, JHSC, JPME, JPSE, JSMD, JSML, KAPR, KJAN, KJUL, KNG, KOMP, KSCD, LSAT, MDY, MDYG, МДЫВ, МГМТ, МИД, МИДЭ, НАПР, НЯН, НОБЛ, НУМГ, НУМВ, НУСК, НВК, ОМФС, ОНЭО, ОНЭК, ОНЭВ, ОНЕЙ, ОСКВ, ОУСМ, ОВС, ПАМК, ПАПР, ПАУГ, ПБП, П BSM, PEXL, PEY, PJAN, PJUN, PLTL, PRFZ, PSC, PTMC, PUTW, PWC, PY, QDIV, QMOM, QQC, QQD, QQEW, QQQ, QQQA, QQQE, QQQJ, QQQM, QQQN, QQXT, QTEC, QVAL, QVML, QVMM, QVMS, QYLD, QYLG, REGL, RFG, RFV, RNMC, RNSC, ROSC35 Комментарии
Логан Кейн
18,47 тыс. подписчиков
подписчиков
Резюме
- Цены были слишком высокими в 2021 году из-за потока стимулов, бесплатных денег и посткоронавирусного менталитета YOLO.
- Акции в настоящее время приближаются к моей оценке справедливой стоимости примерно в 3300 по S&P 500, но могут упасть ниже этой отметки из-за принудительной продажи.
- Учитывая быстрое повышение ставок ФРС, вскоре ожидается, что наличными будет выплачиваться около 4%. Это вознаграждает терпеливых инвесторов, которые удерживают часть денег от акций.
- Какие действия предпринять и что купить, если рынки продолжат падать.
GibsonPictures/E+ via Getty Images
Акции упали с середины августа, при этом широкий индекс S&P 500 (NYSEARCA:SPY) закрылся примерно на 24% за год по состоянию на вчерашний день. Распродажу часто связывают с продолжающейся борьбой ФРС с инфляцией, поскольку наличные ставки приближаются к 4%, а 30-летние фиксированные ипотечные кредиты приближаются к 7%. Послание ФРС было ясным, что она не будет менять политику/снижать ставки в ответ на падение фондового рынка, надеюсь, извлекая уроки из неудавшихся полумер 19-го созыва.70-х и начала 1980-х годов. После того, как все лето поступали необъяснимо огромные ставки на то, что ФРС снизит ставки до нуля и допустит рост инфляции, рынок, похоже, протрезвел, и летнее ралли сошло на нет. Сейчас акции находятся примерно в диапазоне своих июньских минимумов, и очевидный вопрос заключается в том, что, вероятно, произойдет дальше.
Послание ФРС было ясным, что она не будет менять политику/снижать ставки в ответ на падение фондового рынка, надеюсь, извлекая уроки из неудавшихся полумер 19-го созыва.70-х и начала 1980-х годов. После того, как все лето поступали необъяснимо огромные ставки на то, что ФРС снизит ставки до нуля и допустит рост инфляции, рынок, похоже, протрезвел, и летнее ралли сошло на нет. Сейчас акции находятся примерно в диапазоне своих июньских минимумов, и очевидный вопрос заключается в том, что, вероятно, произойдет дальше.
S&P — самый популярный индекс среди розничных инвесторов и 401 000 счетов, но если его крупнейшие технологические холдинги с мегакапитализацией будут получать непропорционально большие суммы спекулятивных денег во время огромных взлетов и падений, я думаю, что лично я предпочел бы иметь небольшие… капитализации (IJR) и средней капитализации (IJH) в качестве основы моего портфеля. Пища для размышлений!
Пища для размышлений!
Почему вы платите 50-кратную прибыль за акции технологических компаний с мега-капитализацией, когда наличные платят 4%?
Современная портфельная теория говорит нам, что как рациональные инвесторы мы должны выбирать инвестиции, способные приносить необходимую нам прибыль с минимальным риском. С другой стороны, мы можем выбрать, на какой риск пойти, и максимизировать прибыль, которую мы получим от этого. Современная портфельная теория вызывает много критики, но этот момент довольно очевиден: инвесторы должны оценивать свои доходы по тому, как они работают по сравнению с безрисковыми казначейскими векселями, и не должны платить большие суммы, чтобы получить доход, который можно получить с риском. бесплатные казначейские обязательства.
На момент моего написания сегодня вы можете получать 3,35% годовых по 3-месячным казначейским векселям, 3,99% годовых по 6-месячным казначейским векселям и 4,16% годовых по 1-летним казначейским векселям. Или вы можете заплатить 50-кратную ожидаемую прибыль за 2023 год для Amazon (AMZN) и не получать дивидендов.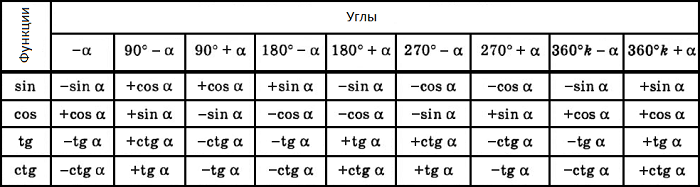 Amazon-быки скажут вам, что они могут быстро увеличить прибыль от облака, но в последнее время им удалось потерять кучу денег, инвестируя в Rivian (RIVN), и в этом году они не получили прибыль. Что касается электромобилей, то Tesla (TSLA) также торгуется с прибылью в 48 раз больше, чем в 2023 году, при условии, что они работают идеально.
Amazon-быки скажут вам, что они могут быстро увеличить прибыль от облака, но в последнее время им удалось потерять кучу денег, инвестируя в Rivian (RIVN), и в этом году они не получили прибыль. Что касается электромобилей, то Tesla (TSLA) также торгуется с прибылью в 48 раз больше, чем в 2023 году, при условии, что они работают идеально.
Быки Microsoft (MSFT), вероятно, скажут вам, что они могут съесть обед Amazon в облачных вычислениях. MSFT также торгует оценкой прибыли 23x 2023, и это единственная компания, которую я упомянул, которая имеет более высокую доходность, чем однолетнее казначейство. Все эти компании конкурируют друг с другом, и многие из них оцениваются так, как будто они собираются отобрать долю рынка у конкурентов, хотя на самом деле это игра с нулевой суммой, поэтому кто-то должен потерять долю рынка. Это означает, что рынок в целом по-прежнему переоценен. И по этим пунктам состояние всех этих акций связано с макроэкономической средой, тогда как, если вы вкладываете немного денег в казначейские облигации, вы получаете возврат, несмотря ни на что, основная сумма плюс проценты (я думаю, если не произойдет апокалипсис).
Очевидный результат состоит в том, что крупные инвесторы не желают платить такую же высокую цену за акции, как в прошлом году, теперь, когда у них есть альтернатива.
S&P 500 PE Ratio (Yardeni Research)
Для акций мультипликаторы от 15x до 18x считаются соответствующими долгосрочной ожидаемой доходности от 9,5% до 10,5% годовых. Когда акции действительно дешевые, как в период с 2008 по 2012 год, вы можете заработать больше, а когда они дорогие, как в 2021 году, вы, как правило, зарабатываете намного меньше. Вот долгосрочный график для иллюстрации.
Коэффициенты P/E S&P 500 (Yardeni Research)
Видите, насколько дорогими были акции в конце 1990-х? Это совпало с ужасной долгосрочной доходностью. Несмотря на неудачное время, инвесторы, купившие акции в 2007 году, получили справедливые цены, что привело к более быстрому восстановлению и более высокой долгосрочной доходности.
Исключительно на основе соотношения цена/прибыль S&P 500 выглядит здесь довольно неплохо при примерно 16-кратном доходе, а компании со средней и малой капитализацией выглядят еще лучше.
Однако проблема, конечно же, в заработке. Неустойчивость и возможный разворот роста прибыли являются основной причиной, по которой я считаю, что акции еще нельзя покупать и что инвесторам следует дождаться еще 10%-го снижения, чтобы начать покупать. С импульсом, сильно направленным против акций, это кажется более вероятным, чем нет.
Рост прибыли является структурной проблемой в мире с ростом ставок (и налогов)
2021 год был лучшим годом для корпоративной прибыли S&P 500 на уровне 209 долларов на единицу индекса, но начало 2022 года сдуло даже 2021 год. Второй квартал 2022 года (апрель-июнь) стал лучшим кварталом для корпоративной прибыли. Потребители, которым надоели 2 года самоизоляции, перешли на YOLO, тратя деньги на путешествия, рестораны и покупки. Однако под капотом уровень жизни более или менее неуклонно снижался с 2021 года, поскольку инфляция опережает доходы потребителей.
В моей последней части макроса я выделил интересный документ из ФРС.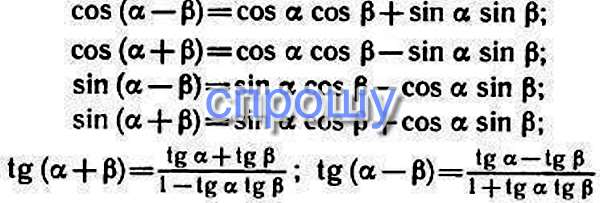 В документе показано, что прибыль до вычета процентов и налогов росла с поправкой на инфляцию на 3,6% в год с 2004 года для фирм S&P 500. Однако при снижении налогов и более низких ставок чистая прибыль ежегодно росла на 5,4% больше, чем инфляция (из-за более низких ставок и более низких налогов). Цены на акции росли еще быстрее, превышая инфляцию на 5,9% в год (за это время инфляция составила около 2,5%).
В документе показано, что прибыль до вычета процентов и налогов росла с поправкой на инфляцию на 3,6% в год с 2004 года для фирм S&P 500. Однако при снижении налогов и более низких ставок чистая прибыль ежегодно росла на 5,4% больше, чем инфляция (из-за более низких ставок и более низких налогов). Цены на акции росли еще быстрее, превышая инфляцию на 5,9% в год (за это время инфляция составила около 2,5%).
Это предварительный расчет, но если вы дефлятируете доходность S&P 500 на сумму, на которую помогли снижение подоходного налога и снижение процентной ставки за последние 17 лет, индекс будет только около 3300, а не достигнув почти 4800 в январе. Интересно, что это согласуется с моей собственной нисходящей оценкой рынков. И если вы сделаете прогнозы будущих доходов до вычета процентов и налогов, но превратите их во встречный, а не попутный ветер, долгосрочная картина доходов будет еще более мрачной, потенциально подразумевая справедливую стоимость акций в нижней части типичного 15-летнего диапазона. -18-кратный диапазон, помимо того, что сами доходы ниже.
-18-кратный диапазон, помимо того, что сами доходы ниже.
Все это структурные проблемы с инвестированием в акции, но это еще не принимает во внимание, какой циклический спад мы могли бы увидеть без стимулов, наводняющих экономику. Он также не принимает во внимание вызовы, которые нездоровое и быстро стареющее население создаст для экономики и правительства. Как только сбережения потребителей, накопленные в эпоху пандемии, закончатся, у корпораций останется не так много рычагов для роста прибыли. Имейте это в виду, когда увидите, что прогноз средней прибыли на 2022 год составляет примерно 224 доллара на акцию, а на 2023 год — примерно 242 доллара на акцию. До дурацкой стимулирующей экономики 2021 года предыдущий исторический максимум составлял 163 доллара в 2019 году.. Эти прогнозные оценки прибыли просто не будут реализованы. Я предполагаю, что совокупная прибыль за 2022 и 2023 годы составит 390 долларов за оба года (чуть меньше 200 долларов в год), в зависимости от того, когда рецессия ударит в полную силу.
Суть в том, что если убрать все эти безумные стимулы, необоснованное снижение налогов и снижающиеся процентные ставки за последние 20 лет, акции еще не станут супердешевыми, даже если они упали на 20% с лишним за год.
Акции могут не перестать падать по справедливой стоимости: раскручивание Bezzle
Если вы посмотрите на исторические графики коэффициентов PE, вы заметите, что, как правило, акции не просто колеблются между переоценкой и справедливой стоимостью. На самом деле акции имеют тенденцию падать намного ниже их справедливой стоимости на медвежьем рынке, иногда в течение многих лет.
Почему так?
Одно из наиболее практически полезных понятий в экономике называется «беззл». Bezzle относится к преступлению растраты, уникальному среди преступлений тем, что украденные деньги временно существуют дважды. Например, если я владелец среднего бизнеса и думаю, что в прошлом году получил миллион долларов прибыли, но на самом деле мой контролер присвоил 250 000 долларов, то фиктивная прибыль для нас обоих составит 1,25 миллиона долларов.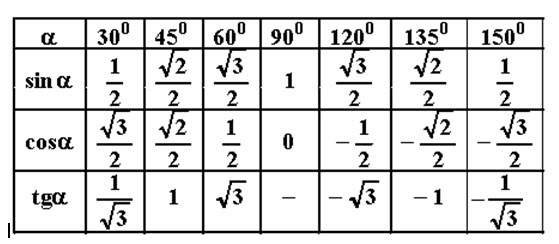 Думаю, я заработал миллион долларов, а мой контроллер прикарманил 250 тысяч. Однако со временем деньги не могут существовать в двух местах одновременно, и в конце концов их обнаруживают. Когда это происходит, я зарабатываю 750 000 долларов за год, потому что мне приходится списывать убытки, в то время как мой корпоративный контролер зарабатывает 0 долларов вместо 250 000 долларов, будь то в тюрьме или в бегах. Когда это обнаруживается, наш совокупный «доход» уменьшается в два раза по сравнению с хищениями. Подобные ситуации могут происходить и на рынках.
Думаю, я заработал миллион долларов, а мой контроллер прикарманил 250 тысяч. Однако со временем деньги не могут существовать в двух местах одновременно, и в конце концов их обнаруживают. Когда это происходит, я зарабатываю 750 000 долларов за год, потому что мне приходится списывать убытки, в то время как мой корпоративный контролер зарабатывает 0 долларов вместо 250 000 долларов, будь то в тюрьме или в бегах. Когда это обнаруживается, наш совокупный «доход» уменьшается в два раза по сравнению с хищениями. Подобные ситуации могут происходить и на рынках.
1. Неправильное инвестирование
2021 год, скорее всего, войдет в историю как год наихудших инвестиций. IPO 2021 года были сильно завышены, но IPO бледнели по сравнению с бумом SPAC, когда сотни компаний стали публичными, большинство из которых не имели реальных шансов на успех в бизнесе. Стоимость капитала для бизнеса была настолько низкой в 2021 году, что предприятия, которые никогда не получат финансирование в условиях свободного рынка, столкнулись с огромным притоком денежных средств.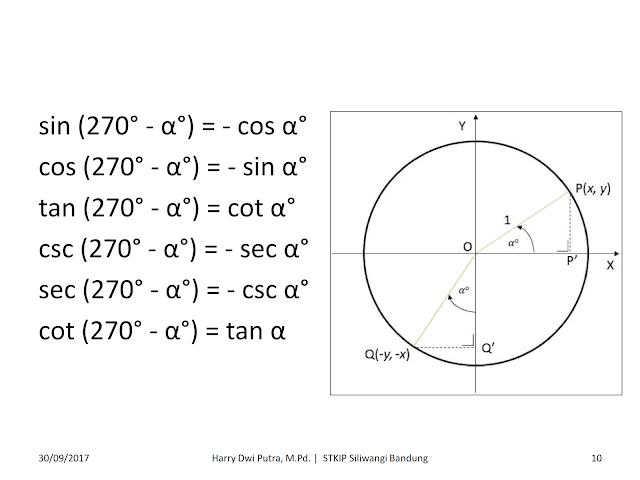 Я имел несчастье купить пару из них, хотя я избежал большей части худшего.
Я имел несчастье купить пару из них, хотя я избежал большей части худшего.
- Исследование космоса? Почему бы и нет!
- Недифференцированные компании по производству электромобилей? Проверять.
- Альткойны и NFT? Проверять.
- Потеря денег Концепции Силиконовой долины с названиями из одного слова? Проверять.
- Каннабис и азартные игры? Проверьте (хотя здесь некоторые хорошие компании вышли на биржу по завышенным ценам и с плохим капиталом).
Суть игры заключалась в том, что рост доходов был важнее всего, а получение прибыли в большинстве случаев не имело значения, потому что можно было брать взаймы бесконечные суммы денег бесплатно или привлекать в качестве капитала при огромных объемах продаж. Такие безумные компании, к счастью, исключены из индексов S&P (чтобы попасть в них, нужно зарабатывать деньги), но они занимают место в портфелях инвесторов. Итак, как вы думаете, что инвесторы собираются получить наличными теперь, когда их SPAC разорены? Они коснутся своих индексных фондов. И говоря об индексных фондах, управляющие активами, которые получают оплату в виде процента от AUM (1% для большинства финансовых консультантов, но 2% и 20% от прибыли для хедж-фондов), получали огромную прибыль в течение многих лет на основе завышенной рыночной стоимости — и теперь они быстро меняются.
И говоря об индексных фондах, управляющие активами, которые получают оплату в виде процента от AUM (1% для большинства финансовых консультантов, но 2% и 20% от прибыли для хедж-фондов), получали огромную прибыль в течение многих лет на основе завышенной рыночной стоимости — и теперь они быстро меняются.
Многие инвесторы крупно выиграли в 2021 году. Многие из этих же инвесторов развернулись и понесли большие убытки в 2022 году. Они заплатили правительству США сотни миллиардов налогов на прирост капитала больше, чем обычно, но из-за того, как налоговая система работает, они не получат возмещения, потому что потери в основном в последующие годы.
Неправильное инвестирование глубоко проникло в экономику не только потому, что убыточные компании присоединились к вакханалии, но и потому, что низкие процентные ставки поощряли все виды потребительских расходов и займов. Если стоимость вашего дома в Остине, штат Техас, за год выросла на 250 тысяч долларов, почему бы не взять HELOC, чтобы купить новую лодку и пару F-150? Почему бы не купить пальто Loro Piana за 5000 долларов? Или заплатить 1500 долларов за перелет в Майами, чтобы повеселиться на выходных?
Население США почти не выросло после COVID, но мы начали строительство миллионов домов, многие из которых были некачественными из-за проблем с цепочкой поставок в 2021 году. Кто купит эти миллионы домов по свободной рыночной ставке 7%, а не по сильно субсидируемой ставке 3%? Хороший вопрос.
Кто купит эти миллионы домов по свободной рыночной ставке 7%, а не по сильно субсидируемой ставке 3%? Хороший вопрос.
Это только то, о чем мы знаем. Скорее всего, следующий Enron и следующий Madoff все еще скрываются там, ожидая, когда их обнаружат, когда ликвидность упадет настолько низко, что они не смогут поддерживать свои уловки. Я предполагаю, что, возможно, 5% из 100 ведущих компаний в Америке и во всем мире будут разоблачены как мошенники — мы пока не знаем, кто именно, но это происходит при каждом серьезном спаде. И я не удивлюсь, увидев, что Интерпол работает сверхурочно, пытаясь поймать больше крипто-беглецов, которые якобы сбежали с деньгами инвесторов.
2. Бум раннего выхода на пенсию
Ну, во-первых, еще около 3 миллионов человек посмотрели на свой собственный капитал во время COVID и решили, что с них достаточно работы. В этом чувстве нет ничего плохого, но время оказалось выбрано очень неудачным, поскольку акции рухнули в 2022 году.
Риск последовательности доходности — жестокая хозяйка.
Bloomberg
Но что произойдет, если акции упадут на 40% по сравнению с тем, когда они были выведены из обращения, или даже на 50%, как это было в 2000-2002 или 2008 году? Миллионы людей, которых вынудили выйти на пенсию из-за высоких цен на активы, затем были бы вынуждены неоднократно продавать в условиях рыночного разгрома, чтобы оплатить расходы на проживание. Неясно, что произойдет в будущем, но существует риск того, что многие достаточно богатые люди могут столкнуться с тем, что их пенсионные счета постепенно обнулятся из-за чрезмерного использования заемных средств и недостаточного финансирования. Пенсионеры, как правило, являются вынужденными продавцами акций, и их сейчас гораздо больше, чем было раньше. Эти 3 миллиона новоиспеченных пенсионеров будут оказывать постоянное понижательное давление на активы, если они останутся на пенсии. В противном случае, единственный способ получить деньги на жизнь — это вернуться к работе.
3. Чрезмерное использование заемных средств
Низкие процентные ставки побуждали людей использовать все виды заемных средств.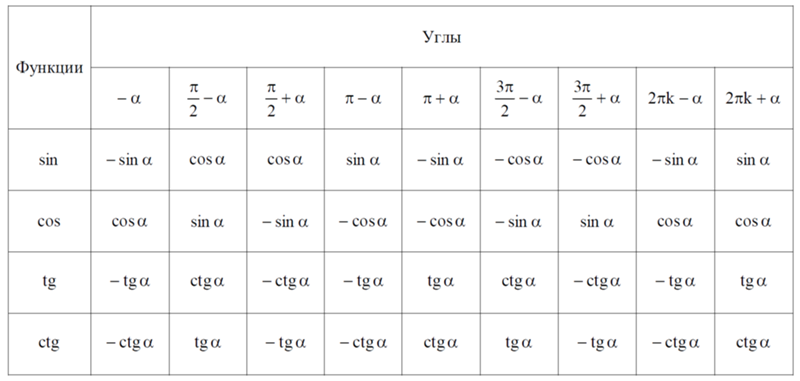 Это не грех, и занимать деньги для разумных долгосрочных инвестиций — разумная стратегия. Проблемы возникают, когда взаимодействуют леверидж и неэффективные инвестиции, или когда макросреда меняется настолько решительно, что вы застреваете в плохой ситуации.
Это не грех, и занимать деньги для разумных долгосрочных инвестиций — разумная стратегия. Проблемы возникают, когда взаимодействуют леверидж и неэффективные инвестиции, или когда макросреда меняется настолько решительно, что вы застреваете в плохой ситуации.
Компании, выпустившие бросовые облигации в 2021 году, сошли с рук убийство благодаря ставкам, которые они платят, и риску, который они представляют, но что произойдет через два-три года, когда эти облигации нужно будет пролонгировать? Будет много компаний-зомби, которые обанкротятся в 2023 и 2024 годах.0013
И, конечно же, маржинальный долг, который по последним подсчетам составил немногим менее 700 миллиардов долларов. Это не так много по сравнению со стоимостью акций, достигнув пика около 2% от общей рыночной стоимости в начале этого года, но это потенциальный источник принудительных продаж, поскольку акции падают.
Жилищный бум, вызванный пандемией, побудил людей покупать большие дома далеко от центра города. Но что произойдет, если счет за электроэнергию для этого дома удвоится? Если покупателям нужен доход обоих супругов, чтобы соответствовать требованиям, что произойдет, если один из супругов потеряет работу? Это в два раза выше вероятности того, что один человек потеряет работу, превратив двойной доход из источника силы в источник слабости. Это операционный рычаг, еще одна неочевидная форма рычага.
Но что произойдет, если счет за электроэнергию для этого дома удвоится? Если покупателям нужен доход обоих супругов, чтобы соответствовать требованиям, что произойдет, если один из супругов потеряет работу? Это в два раза выше вероятности того, что один человек потеряет работу, превратив двойной доход из источника силы в источник слабости. Это операционный рычаг, еще одна неочевидная форма рычага.
Много ли у банков было проблемных кредитов в 2021 и начале 2022 года? Если цены на жилье упали на 5-10% уже с мая на десятках рынков, а многие первоначальные взносы составляют всего 10%, то это проблема для этого поколения кредитов. Согласитесь, кредиты 2019 года выглядят хорошо из-за огромных запасов капитала и низких платежей, но я чувствую, что рынок жилья вернется к равновесию, то есть рухнет, поскольку миллионы завершенных домов наводнят рынок без спроса на их поддержку. .
Куда S&P 500, вероятно, пойдет дальше
Импульс фондового рынка снижается. Многие покупатели справедливо предпочитают зарабатывать 4% наличными, а не бросать кости на акциях, а отказ от чрезмерного использования заемных средств и неэффективных инвестиций означает, что многие люди, вероятно, продолжат продавать на падающем рынке, потому что им это необходимо.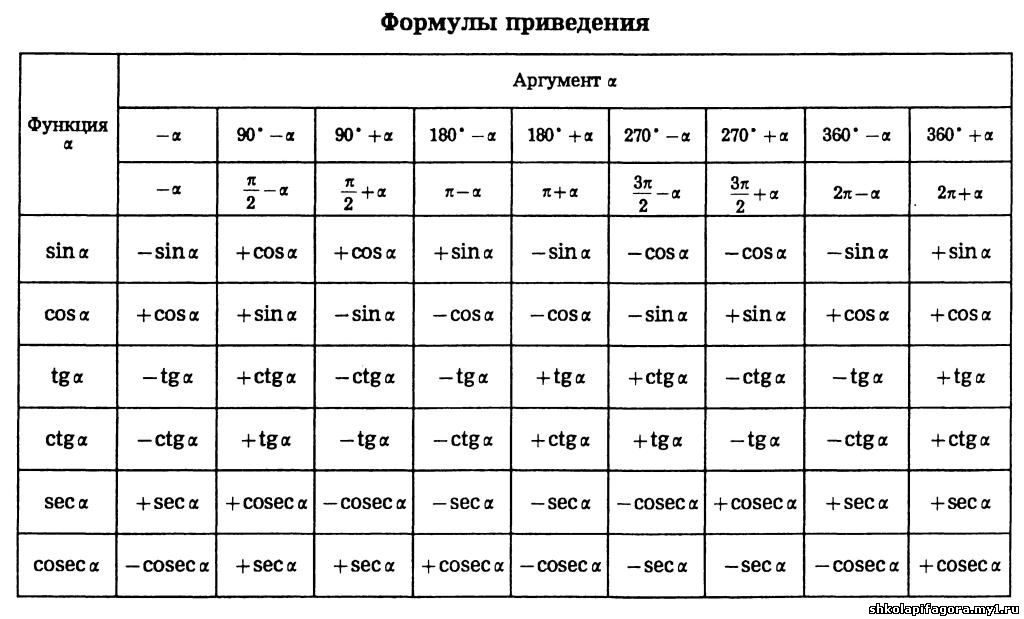
Итак, когда в дело вступят покупатели? Несмотря на то, что акции компаний с большой капитализацией сейчас торгуются с доходом менее 16x, акции все еще немного высоки из-за жестких встречных ветров, столкнувшихся с прибылью в ближайшие несколько лет. Весьма вероятно, что крупные институциональные инвесторы имеют цифры, подобные тем, которые мы получили здесь, а это означает, что они начнут покупать на S&P 500 на уровне около 33009.0013
Несмотря на это, количество структурно вынужденных продавцов означает, что рынки, скорее всего, не опустятся вниз по справедливой стоимости, а несколько упадут. Если бы мне пришлось угадывать, S&P 500 достигнет дна где-то около 2800 где-то весной, но впоследствии к концу года подскочит выше 3000. 3300 — это справедливая стоимость — мы можем попытаться снизить количество принудительных продаж или лишения капитала, которые произойдут в 2023 году, но если вы можете покупать активы по хорошим ценам, вы должны постоянно делать это, даже если они могут немного упасть в цене. цена.
цена.
2800 — чистое предположение, основанное на истории. 2800 поместит нас примерно на уровень, на котором акции были летом 2019 года, когда началось безумие с точки зрения оценок, поэтому, хотя они сильно упали в цене, на самом деле это не так уж и далеко во времени. С более жесткими деньгами условия для роста в реальной экономике постепенно будут создаваться, поскольку капитал и рабочая сила будут оттягиваться от спекулятивного бизнеса к областям роста, таким как автоматизация, устойчивая энергетика и другие технологии, повышающие производительность.
Ключевые выводы
- Пузырь всего лопнул. Большинство людей будут вести свою повседневную жизнь, не зная и не заботясь о них, но если вы инвестор, вам будет трудно отключиться. К сожалению, если вы переплатили за что-то в 2021 году (я делал это несколько раз на акциях), сейчас вы мало что можете с этим поделать, кроме как переждать.
- У рынка сильный импульс, идущий против него, и S&P 500 все еще торгуется выше моей оценки справедливой стоимости в районе 3300.
 Я бы дождался еще некоторого снижения, чтобы начать активно покупать. В то же время вы можете заработать 3-4% наличными.
Я бы дождался еще некоторого снижения, чтобы начать активно покупать. В то же время вы можете заработать 3-4% наличными. - У акций все еще есть некоторые структурные проблемы, но более низкая цена в долгосрочной перспективе адекватно компенсирует вам риск, который вы принимаете, покупая их.
- Инвесторам следует пересмотреть свои портфели на предмет возможностей фиксации налоговых убытков по текущим ценам. Таблицы корреляции очень полезны в этом случае и могут помочь инвесторам отсрочить налоги, сохраняя при этом желаемый доступ к акциям. Если вы сомневаетесь, проконсультируйтесь с вашим CPA.
- Как только акции достигают справедливой стоимости, лучшими покупками, вероятно, будут акции компаний США с малой капитализацией (IJR), компаний США со средней капитализацией (IJH), привилегированных акций (PFFD), международных компаний с малой капитализацией (SCZ), международных компаний (VEA), международная высокодивидендная (VYMI). Для стратегии с более высоким октановым числом для инвесторов с длительными временными горизонтами есть несколько хороших игр с использованием заемных средств, таких как 9.
 0 акций/60 облигаций (NTSX) и 100 акций/100 облигаций (PSLDX). Мне также нравятся казначейские фонды с кредитным плечом (TYA), если ставки продолжают расти. Вы можете начать покупать некоторые из них сейчас, но не торопитесь и оставьте немного сухого порошка.
0 акций/60 облигаций (NTSX) и 100 акций/100 облигаций (PSLDX). Мне также нравятся казначейские фонды с кредитным плечом (TYA), если ставки продолжают расти. Вы можете начать покупать некоторые из них сейчас, но не торопитесь и оставьте немного сухого порошка. - Также будут некоторые возможности приобрести акции голубых фишек роста, такие как Microsoft и Google (GOOG) (GOOGL), если они сильно пострадают от продажи ETF.
- Тот факт, что вы покупаете активы ниже справедливой стоимости, не означает, что они не будут падать еще больше на импульсе. По этой причине я бы не рекомендовал никому идти ва-банк, основываясь на том, что рынок достиг определенной ценовой цели, если только цены не обрушатся по-настоящему. С этой точки зрения усреднение долларовой стоимости является разумной стратегией на рынках с высокой волатильностью/падением.
Эта статья была написана пользователем
Logan Kane
18,47 тыс. подписчиков
Автор и предприниматель. Мои статьи обычно охватывают портфельную стратегию, стоимостное инвестирование и поведенческие финансы.

 acosh()
acosh()  asin()
asin()  atan2()
atan2() 
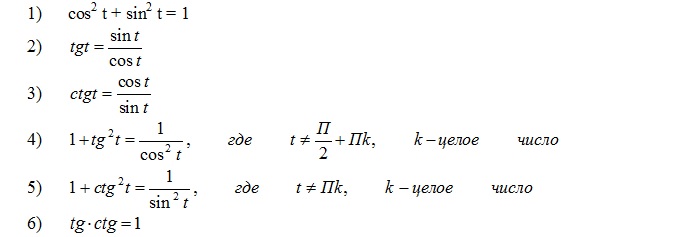



 special.gammainc()
special.gammainc()  neg()
neg() 


 Я бы дождался еще некоторого снижения, чтобы начать активно покупать. В то же время вы можете заработать 3-4% наличными.
Я бы дождался еще некоторого снижения, чтобы начать активно покупать. В то же время вы можете заработать 3-4% наличными. 0 акций/60 облигаций (NTSX) и 100 акций/100 облигаций (PSLDX). Мне также нравятся казначейские фонды с кредитным плечом (TYA), если ставки продолжают расти. Вы можете начать покупать некоторые из них сейчас, но не торопитесь и оставьте немного сухого порошка.
0 акций/60 облигаций (NTSX) и 100 акций/100 облигаций (PSLDX). Мне также нравятся казначейские фонды с кредитным плечом (TYA), если ставки продолжают расти. Вы можете начать покупать некоторые из них сейчас, но не торопитесь и оставьте немного сухого порошка.