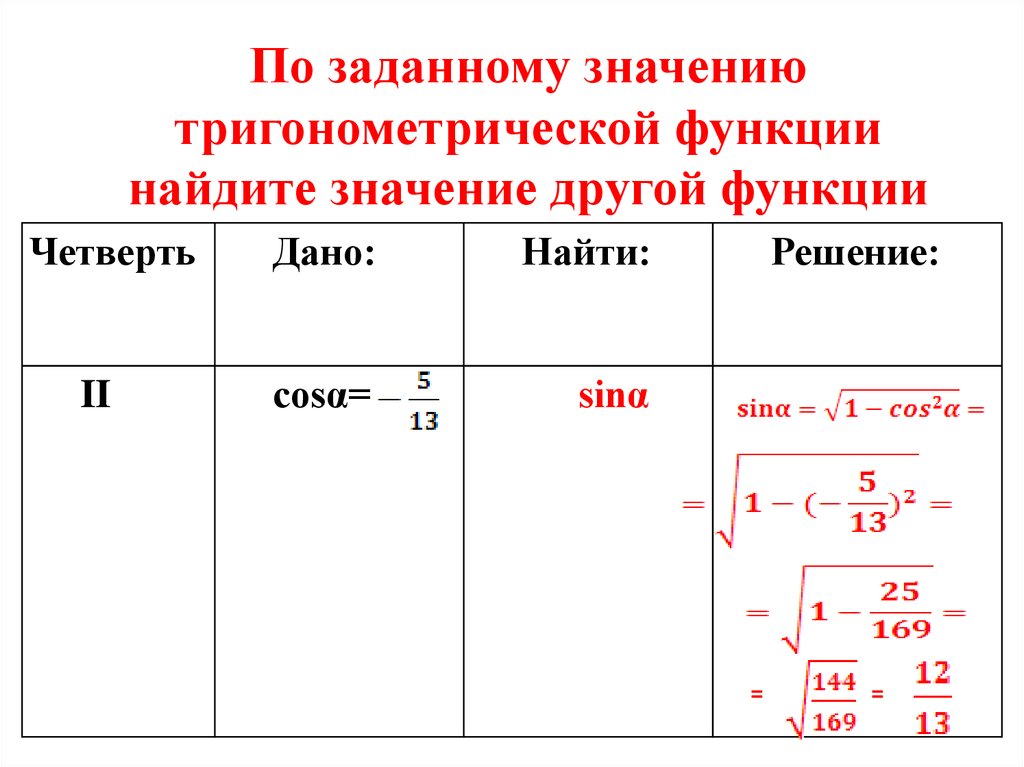
Как легко и быстро запомнить формулы?
Сегодня очень многие школьники и студенты испытывают сложности с тем, чтобы запомнить важные формулы.
Порой это приводит к стрессам, нервным срывам, которые приводят к потере сна и проблемам со здоровьем, что отразится на состоянии человека в более взрослом возрасте. Но из данной статьи вы узнаете, как заполнить формулы и не забыть их в самый ответственный момент.
С чего следует начать?- В первую очередь вам нужно максимально расслабиться. Школьные формулы по физике и математике ни в коем случае нельзя учить в состоянии стресса. Та же физика требует максимальной концентрации.
- Также удовлетворите все свои потребности. Невозможно что-либо запоминать на голодный желудок, если вы хотите спать и так далее.
1) Вам следует сесть перед формулой и «просканировать» ее глазами примерно 10-15 минут.
Многие люди совершают одну и ту же ошибку. Они просто смотрят на формулу 5-10 секунд, им становится лениво, они считают, что они ее уже запомнили. Но через час-два или даже на следующее утро они осознают, что вся важная информация улетучилась. Так что тщательно сканируйте все глазами.
2) А после этого возьмите лист бумаги А4 и самостоятельно напишите только что запомненную формулу. Пишите ее до тех пор, пока на листке не останется свободного места.
ВАЖНО: Старайтесь как можно меньше подглядывать. Если вы не чувствуете уверенности, то повторите все с самого начала.
Те же тригонометрические формулы и сокращенного умножения, а также приведения знаменателей отличаются своей сложностью, а вот в физике все относительно легко. Здесь можно ориентироваться на переменные. Просто отбросьте единицы измерения и посмотрите, верная ли переменная у вас осталась.
ВАЖНО! Обязательно вникните в условие формулы. Это ведь не просто набор переменных, а какое-то действие, которое должно приводить к определенному результату. Самый простой пример — формула свободного падения. Она показывает, что, чем больше сила, тем больше и ускорение.
Если и данные советы вам не помогли, через час-два вы все равно забываете все, то остается только один выход.
3) Просто запишите все важные формулы на листочек. И перед контрольной работой или зачетом просто пробежитесь по ним глазами.
4) Если у вас есть несколько дней, то распечатайте их на большом ватмане и повесьте на видном месте. Когда у вас будет свободная минутка, вы сможете снова и снова обращать на них свое внимание и освежать информацию в памяти.
Что можно сказать в заключении?Сегодня количество учителей, заставляющих запоминать формулы, становится все меньше и меньше.
Связано это с тем, что во многих тестах они уже есть. Так что лучше предварительно все же обговорить с преподавателем, что вам не следует запоминать, а на чем сконцентрировать свое внимание.
Также можно придумать с одноклассниками или членами семьи какую-нибудь забавную игру или лотерею, как-то связанную со школьной программой. В такой разряженной обстановке запоминается все гораздо лучше.
«Как выучить всю тригонометрию за неделю?» — Яндекс Кью
Популярное
Сообщества
ОбразованиеЛайфхак
Вячеслав Дятлов
·
3,6 K
Ответить1УточнитьАлен Мухамеджанов
9
Школьник, недоученый, атеист, не знаю куда валить после 11 · 18 окт 2018
Вообще можно выучить тригонометрию и за 3 дня, но потребуется быть крайне усердным.
Будем исходить из того, что есть: 7 дней и нулевые познания в таком сложном разделе, как тригонометрия. Каждый день НЕОБХОДИМА ПРАКТИКА!
День 1. Изучаем основные тригонометрические тождества (по тригонометру, он будет нашим главным помощником) и, конечно же, практикуемся. Выучим значения тригонометрических функций с аргументами 0, 30, 45, 60, 90 градусов. Изучим понятие, что такое «радианы».
День 2. Познакомимся с выражением наших 4 основных функций (синус, косинус, тангенс и котангенс). Подробнее познакомимся с графиком и свойствами каждой из них: область определения( D ), область значений( E ), четность, периодичность. Научимся строить их график.
День 3. Изучим правило приведения функций.
День 4. Выучим формулы суммы и разности аргументов функций. Выучим формулы кратных (половинных, двойных, тройных) аргументов, т.к эти две темы идут смежно.
День 5. Выучим формулы суммы и разности самих функций. Также научимся обратной операции, а именно сумма и разность самих функций будет давать в результате произведение, а мы это произведение превратим в сумму, или разность.
День 6. Познакомимся с обратными тригонометрическими функциями. Также выучим их свойства: D(y) , E(y) , характер монотонности, четность, нули и асимптоты. Научимся строить их график простых и обратных функций.
День 7. Настал «День Х». В этот день мы ускоряем темп: повторяем все изученное в обобщающей теме «Решение тригонометрических уравнений и неравенств» и надеемся не забыть все изученное. Напоследок стоит сказать, что я автор собственной методики «ЕНТ за месяц», поэтому за более подробными ответами стоит обращаться ко мне лично в ВК https://vk.com/phantom_al
Комментировать ответ…Комментировать…
Первый
Картышов Сергей
папа · 17 февр 2021
если даже это и можно сделать , я уверен что это будут только основные понятия, не дающие возможность четко решать более сложные задания , так как практику за неделю занятий получить не возможно и удерживать эти знания будет довольно сложно
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Предварительное исчисление алгебры— Как запомнить тригонометрические тождества?
Задать вопрос
спросил
Изменено 8 лет, 5 месяцев назад
Просмотрено 31к раз
$\begingroup$
Я застрял, пытаясь запомнить тождества триггеров, и, как я ни пытался, я просто не могу их запомнить (особенно формулы сумма-произведение и произведение-сумма).
Есть предложения?
Спасибо.
РЕДАКТИРОВАТЬ: Пройден тест, благодаря вашим хорошим предложениям. Спасибо вам всем!
- алгебра-предварительное исчисление
- тригонометрия
$\endgroup$
3
$\begingroup$
Честно говоря, я всегда забывал все свои триггерные тождества, пока не выучил комплексные числа. Предполагая, что вы не хотите туда идти, постарайтесь быть максимально эффективным. Я говорю своим ученикам запомнить эти как минимум :
$$ \cos(A\pm B) = \cos(A)\cos(B)\mp \sin(A)\sin(B)\\ \sin(A\pm B) = \sin(A)\cos(B)\pm \cos(A)\sin(B) $$
Где `$\mp$’ означает перевернуть знак, т.е. $A+B$ внутри становится $-$ снаружи. Затем вы можете получить множество других тождеств, просто добавляя или вычитая их! Например, правило произведения на сумму для косинуса получается из сложения формул для $\cos(A+B)$ и $\cos(A-B)$, а правило произведения на сумму для sin получается их вычитанием.
2\theta = \cos\theta\cos\theta — \sin\theta\sin\theta$$
напоминает мне, что
$$\cos(A+B) = \cos A\cos B — \sin A\sin B$$$\endgroup$
Предварительное исчисление по алгебре — Как запомнить тригонометрические тождества
Для чего это стоит:
Я просто запомнил одно тождество Пифагора и одно тождество суммы. Многие другие (помимо очевидных: обратную, периодичность и пифагоровость) можно вывести начиная с одной из формул суммы.
Итак, вы можете просто запомнить, как их получить. Конечно, в тестовом сценарии это может привести к потере драгоценного времени…
Взаимные тождества
Взаимные тождества следуют из определений тригонометрических функций.
$$\выравнивание { \sec\theta&= {1\over \cos\theta} \qquad \tan\theta= {\sin\theta\over \cos\theta} \cr \csc\theta&= {1\over \sin\theta} \qquad \cot\theta= {1\over \tan\theta} \cr } $$
Соотношения периодичности
Соотношения периодичности легко следуют из рассмотрения
прилежащие углы на единичной окружности.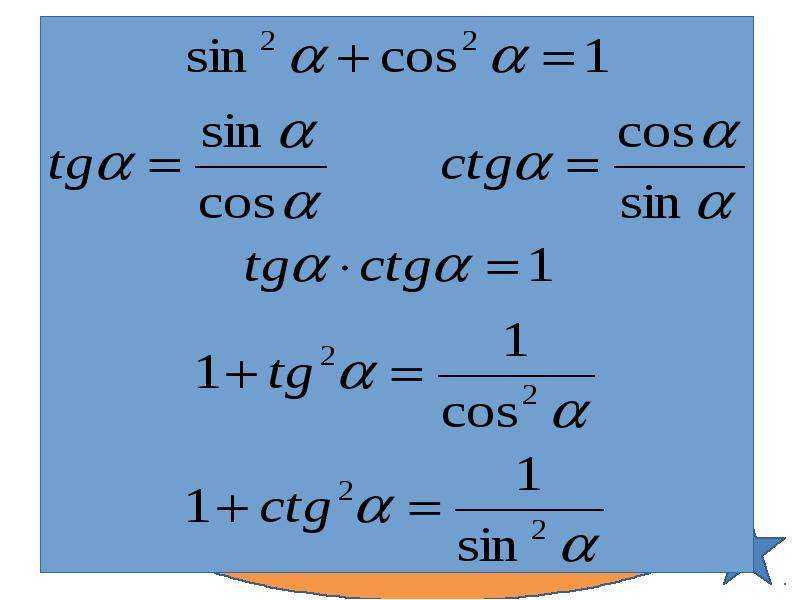
$$\def\ts{}\eqalign { \sin(\theta)&= \sin(\theta \pm2k\pi) \qquad \csc(\theta)= \csc(\theta \pm2k\pi) \cr \cos(\theta)&= \cos(\theta \pm2k\pi) \qquad \sec(\theta)= \sec(\theta \pm2k\pi)\cr \tan(\theta)&= \tan(\theta \pm k\pi)\phantom{2} \qquad \cot(\theta)= \cot(\theta \pm k \pi) \cr } $$
$$\выравнивание { \sin(\theta)&= — \sin(\theta -\pi) \qquad \csc(\theta)= — \csc(\theta -\pi) \cr \cos(\theta)&= — \cos(\theta -\pi) \qquad \sec(\theta)= — \sec(\theta -\pi) \cr \tan(\theta)&= — \tan(\theta -\ts{\pi\over2}) \qquad \kern-3pt \cot(\theta)= — \cot(\theta -\ts{\pi\ более2}) \cr } $$ 92\тета} $$
Формулы суммы и разности
Запомните первую формулу суммы и разности. Второе можно вывести из первого, используя тот факт, что $\sin$ — нечетная функция.
Затем можно вывести два последних тождества суммы, используя первые два и тот факт, что $\cos(\theta-\pi/2)=\sin\theta$.
$$\выравнивание{ \cos(x+y)&=\cosx\cosy-\sinx\siny\cr \cos(xy)&=\cosx\cosy+\sinx\siny\cr \sin(x+y)&=\sinx\cosy+\siny\cosx\cr \sin(xy)&=\sinx\cosy-\siny\cosx\cr } $$ 92\тета\кр } $$
Формулы половинного угла
Формулы половинного угла для $\sin$ и $\cos$ затем получаются из формулы двойного угла для $\cos$ путем записи, например, $\cos\theta =\cos(2\cdot{\theta\over2})$
Здесь формула $\tan$ может быть легко получена из двух других.