По отношению к другому отрезку, исходный направленный отрезок может быть сонаправленным a b , то есть направления совпадают, между ними угол 0°, и противонаправленным a b , то есть направления противоположны, между ними угол 180°.
Коллинеарные векторы – это векторы, лежащие на параллельных прямых или на одной прямой.
Компланарные векторы – это векторы, лежащие в параллельных плоскостях или в одной плоскости.
Условие равенства двух a =b заключается в их коллинеарности и сонаправленности a b , равенстве длин |a |=|b |.
Как умножить вектор на число
Что значит умножить вектор на число? Это значит получить другой вектор, коллинеарный данному, сонаправленный с ним при положительном числе >0 или противонаправленный с ним при <0, модуль которого равен произведению модуля заданного вектора и модуля .
Чтобы умножить вектор на число необходимо воспользоваться формулами:
b =a и |b |=|a |||
где a – исходный вектор, – число, не равное 0, b – полученный при умножении вектор.
Чтобы умножить число на координаты вектора необходимо воспользоваться формулой:
a =(x,y)
где x и y – координаты исходного вектора.
Примеры задач
Задача 1: Упростить выражение 2(a -b )-3(c +a )+4(a +c ) и найти w , если a =(1;3)(2;7), b =(4;8)(6;5), c =(2;4)(1;9).
Решение: 2(a -b )-3(c +a )+4(b -c ) = 2a -2b -3c -3a +4b —4c =-a +2b -7c .
x_wн=-x_aн+2x_bн-7x_cн=-1+24-72=-1+8-14=-7;
x_wк=-x_aк+2x_bк-7x_cк=-2+26-71=-2+12-7=3;
y_wн=-y_aн+2y_bн-7y_cн=-3+28-74=-3+16-28=-15;
y_wк=-y_aк+2y_bк-7y_cк=-7+25-79=-7+10-63=-60;
Ответ: w =(-7;-15)(3;-60).
Задача 2: На рисунке графически изображены два вектора, определить на какое был умножен a для получения b .
Решение:
a имеет координаты: x_aн=1; x_aк=2;y_aн=2; y_aк=4;
b имеет координаты: x_bн=3; x_bк=6;y_bн=6; y_bк=12.
Возьмем координаты начала и конца b разделим на a :
=x_bнx_aн=31=3.
Аналогично и с другими координатами.
Ответ: =3.
Задача 3: Получить b , зная a =(1;4)(3;9) и =5.
Решение:
x_bн=x_aн =15=5;
x_bк=x_aк =35=15;
y_bн=y_aн =45=20;
y_bк=y_aк =95=45.
Ответ: b =(5;20)(15;45).
Рисунок 2 – графическое изображение a (фиолетовым цветом) и b (синим цветом).
Произведение вектора на число / Векторы / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Векторы
- Произведение вектора на число
Определение
Произведением ненулевого вектора на число называется такой вектор , длина которого равна , причём векторы и сонаправлены при 0 и противоположно направлены при 0. Произведением нулевого вектора на любое число считается нулевой вектор. |
Произведение вектора на число обозначается так:
Из определения следует, что:
- произведение любого вектора на число нуль есть нулевой вектор;
- для любого числа и любого вектора векторы и коллинеарны.
Основные свойства умножения вектора на число:
Для любых чисел , и любых векторов , справедливы равенства: 10. () = () (сочетательный закон). 20. ( + ) = + (первый распределительный закон). 30. ( + ) = + (второй распределительный закон). |
Замечание
Рассмотренные нами свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях.
Например, выражение = 2( — ) + ( + ) — 3( — + ) можно преобразовать так:
= 2 — 2 + + — 3 + 3 — 3= — 5 + 4.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Сумма двух векторов
Законы сложения векторов. Правило параллелограмма
Сумма нескольких векторов
Вычитание векторов
Применение векторов к решению задач
Средняя линия трапеции
Векторы
Правило встречается в следующих упражнениях:
7 класс
Задание 775, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 781, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 804, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 805, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 806, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 903, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1074, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Умножение вектора на скаляр – примеры и практические приложения
Задумывались ли вы когда-нибудь, что такое вектор и что можно сделать с векторами? Если да, то ответы на все ваши вопросы о векторах можно найти в этой статье.
Физическая величина — это та величина, которую можно физически измерить с помощью научного прибора. Однако такие величины, как голод, любовь, депрессия, гнев и т. д., не могут быть охарактеризованы как физические величины, потому что их нельзя измерить вручную. Физическая величина, которая имеет только величину, называется скалярной величиной. Скалярная величина не зависит от направления. Физическая величина, которая имеет как величину, так и направление, называется векторной величиной. Скаляры представлены отрезками прямых линий без каких-либо наконечников стрелок, тогда как векторы представлены прямыми линиями со стрелкой в одной из конечных точек, указывающей направление вектора.
Умножение векторов
Правила умножения векторов — одно из самых простых и интересных понятий в математике. Умножение векторов — это нахождение произведения любых двух векторов либо как скаляра, либо как вектора. Умножение векторов может быть выполнено в двух формах, а именно скалярное произведение и векторное произведение.
Если вектор умножается на скаляр, это означает, что величина вектора умножается на число.
Умножение векторов на скаляры
Хотя векторы и скаляры представляют разные разновидности физических величин, иногда необходимо, чтобы они взаимодействовали. Добавление скаляра к векторной величине крайне невозможно из-за их различий в размерностях. Однако векторную величину можно умножить на скаляр. В то же время обратное этому невозможно. то есть скаляр никогда не может быть умножен на вектор.
При умножении векторов на скаляры одинаковые величины подвергаются арифметическому умножению. т. е. величина векторов умножается на величину скалярных величин. Произведение, полученное путем умножения векторов на скаляры, является вектором. Вектор произведения имеет то же направление, что и вектор, умноженный на скаляр, и его величина увеличивается во столько же раз, сколько произведение умноженных величин вектора и скаляра.
Пример правил умножения на скалярный вектор
Пример умножения на скалярный вектор 1
Рассмотрим некоторый вектор, скажем, вектор «a» умножается на скаляр, величина которого равна 0,25.
В этом случае вектор произведения — это вектор, представляющий вектор, направление которого совпадает с направлением вектора «а», а величина в 1/4 раза больше, чем у вектора «а» (поскольку 0,25 представляет 1/4).
Умножение скалярного вектора Пример 2
Сила физической величины является векторной величиной. Совершаемая работа зависит как от величины, так и от направления, в котором сила приложена к объекту. Эта сила на самом деле является произведением вектора на скалярную величину согласно второму закону Ньютона о линейном движении. Сила задается как: F = m x aВ приведенном выше уравнении «a» обозначает ускорение, которое является векторной величиной, а «m» обозначает массу объекта, которая является скалярной. Таким образом, это один из примеров в физике для умножение векторов на скаляры.
Умножение скалярного вектора Пример 3
Пусть любое чисто безразмерное арифметическое число принимается в качестве скалярной величины.
При умножении векторов на этот скаляр полученное произведение представляет собой масштабированную версию исходного вектора. Предположим, что число, рассматриваемое как скаляр, равно 3, тогда вектор, умноженный на этот скаляр, дает вектор произведения, который в три раза больше исходного вектора.
(Изображение будет загружено в ближайшее время)
Практические приложения умножения векторов на скаляры
Умножение векторов на скаляры находит широкое применение в физике. Многие единицы СИ векторных величин являются произведениями вектора и скаляров. Например, единицей скорости в системе СИ является метр в секунду. Скорость является векторной величиной. Это получается путем умножения двух скалярных величин: длины и времени на единичный вектор в определенном направлении. В математике и физике есть много других случаев, когда используется векторное умножение на скаляр.
Интересные факты о правилах умножения векторов
Вектор можно умножить на скаляр.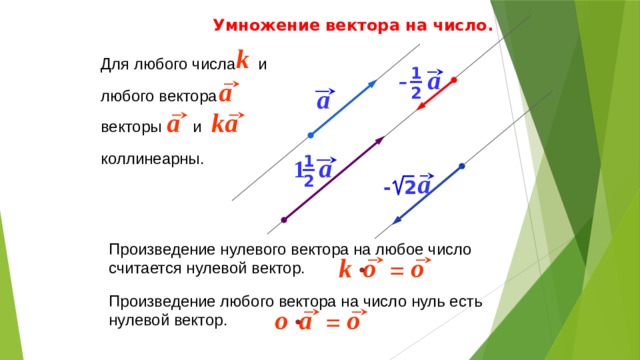
Но скалярную величину нельзя умножить на вектор.
Когда вектор умножается на скаляр, получается вектор с тем же направлением, но с увеличенной величиной
Умножение векторной и скалярной величин и направление.
Умножение вектора
Существует два типа умножения векторов
Скалярное умножение и векторное умножение
Скалярное умножение числа — это умножение вектора на скаляр, и его следует отличать от внутреннего произведения двух векторов.
В математике умножение векторов — это метод, используемый для умножения двух или более векторов. Он также определяется как произведение первого вектора на второй вектор. Существует два вида умножения векторов. Один из них — это скалярное умножение, которое также называется скалярным произведением, а другой — векторное умножение, которое называется перекрестным произведением.
Величина вектора
Какова величина вектора?
Вектор – это величина, имеющая как величину, так и направление.
Если вы хотите найти величину вектора, вы должны сначала вычислить длину вектора. Такие величины, как сила, скорость, импульс, перемещение и т. д., являются векторными величинами. Такие величины, как объем, скорость, температура и т. д., являются скалярными величинами. Скалярные величины имеют только величину и не имеют направления, но векторные величины имеют и величину, и направление.
(Изображение будет загружено в ближайшее время)
Можно рассчитать длину заданного вектора, и это поможет рассчитать величину вектора. Длина вектора — это расстояние между начальной и конечной точками вектора.
Разница между скаляром и вектором
Скаляр и вектор кажутся похожими терминами, но между ними есть разница. Обе величины используются для представления движения объекта.
Скалярная величина отличается от векторной величины направлением. У скаляров нет направления, а у векторов есть. Следовательно, из-за этого Из-за этой характеристики скалярная величина является одномерной, тогда как векторная величина является многомерной.
Now, we will look at some more differences between scalar and vector quantities:
Differences between Scalar and Vector Quantities
Scalar | Vector |
Scalar quantities have только величина | Векторные величины имеют как величину, так и направление |
Скалярные величины одномерны | Векторные величины являются многомерными скалярными величинами |
Скалярные величины изменяются с изменением в направлении и магнитуде | |
. | Существует другой набор правил, используемых для векторных величин |
Одно скалярное число может делить другое скалярное число | One vector quantity cannot divide another vector quantity |
Examples of scalar quantity include speed, distance, time, etc | Examples of vector quantity include velocity, acceleration, etc. |
Умножение или деление вектора на скаляр
Скалярные и векторные величины — это только два вида величин. Если мы хотим измерить какое-либо количество, есть два способа измерения: либо только по величине, либо по величине и направлению. Если величина имеет только величину, она называется скалярной величиной. Если величина имеет как величину, так и направление, она называется векторной величиной. В этой статье будет рассмотрено умножение или деление вектора на скаляр.
Если есть скаляр и вектор, их произведение будет обозначаться как а.
В зависимости от значения (положительного или отрицательного) новый вектор a будет иметь то же направление, что и вектор a, либо противоположное.
Величина нового вектора a равна произведению скалярной величины на величину вектора. a = a
Если = 1a, то a = a = 1aa = 1
Однако при условии, что вектор a равен 0.
Следовательно, a не должен быть нулевым вектором, чтобы вышеуказанное условие выполнялось.
Распределительные законы для сложения и умножения вектора на скаляр- b) = ka + kb
Единичный вектор в направлении вектора a = 1a a = 15 (i – 2j) = 15i – 25j
Новый вектор величины 7, направленный в направлении вектора a is
7 a = 7 (15i – 25j) = 75i – 145j
Как умножить вектор на скаляр?
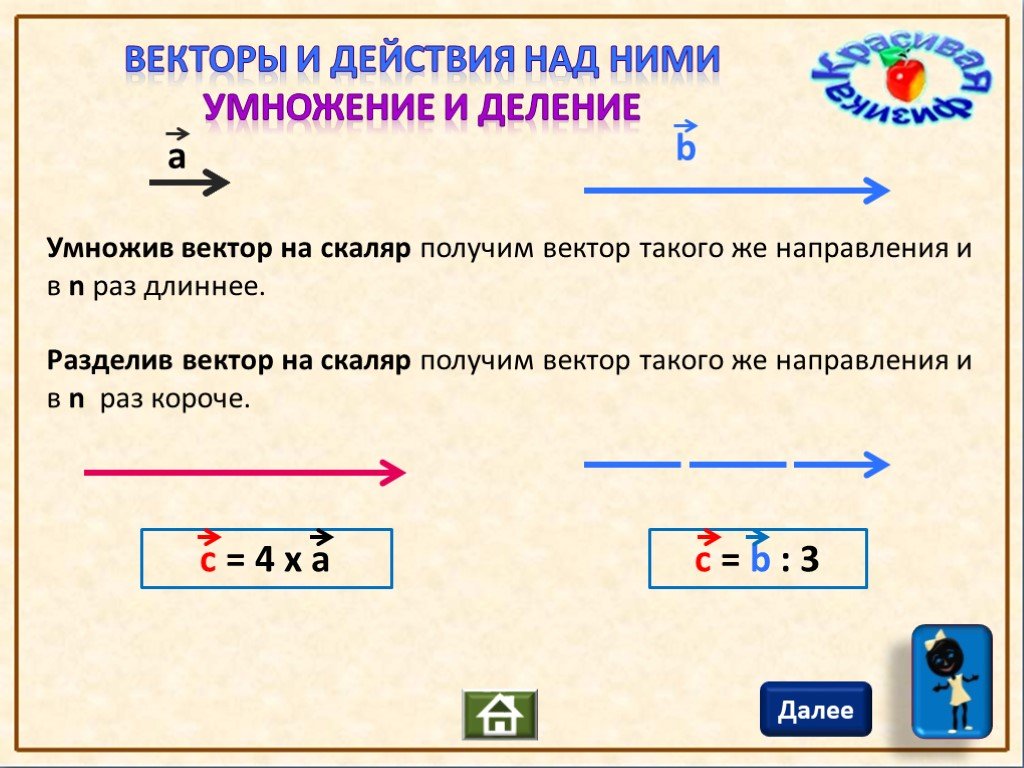
Умножить вектор на скаляр очень просто; умножьте величины вектора на скаляр.
Когда мы умножаем вектор A на действительное число k, мы получаем другой вектор A’. Величина A’ в k раз больше величины A. Если она положительна, направление A’ совпадает с направлением A .
Результирующий новый вектор будет иметь то же направление.
Например, пусть c = ⟨8⟩.
Найдите 7с.
Найдите 7с.7C = 7⟨8⟩
= ⟨7 (8)⟩
= ⟨56⟩
Скалярные кратные вектор
, когда вектор умножается на шкалу, магнитный изменения.
Направление скалярного множителя остается таким же, как и у входного вектора.
Либо скаляр равен нулю, либо вектор равен нулю, если скаляр, кратный вектору, равен нулю.
Таблица умножения вектора на вещественное число с другим коэффициентом:
Коэффициенты | Оригинальный вектор | Продукт вектора после размножения | Продукт вектора после размножения | Продукт вектора. чем 0 | A | λA | То же, что и A | ||
– λ меньше 0 | A | λA | Opposite to A | ||||||
λ equal to 0 | A | 0 = null vector | None. |
Исходное и конечное положение одинаковые.В общем случае умножение действительного числа r на вектор A дает этот результат. Это даст нам что-то в том же направлении, что и раньше, но в r раз больше исходной величины. r A имеет две составляющие: r Ax и r Ay с точки зрения составляющих.
Если r равно -1, результирующий вектор будет указывать в противоположном направлении, если A истинно.
Пример умножения или деления вектора на скаляр
Сила — это векторная величина в физическом мире. Количество выполненной работы определяется величиной и направлением силы, приложенной к предмету. Согласно второму закону линейного движения Ньютона эта сила является произведением вектора на скалярное число.
Сила следующая:
m x a = F.
В приведенном выше уравнении a — это ускорение объекта, которое является векторной величиной, а m обозначает массу объекта, которая является скалярной величиной.