| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.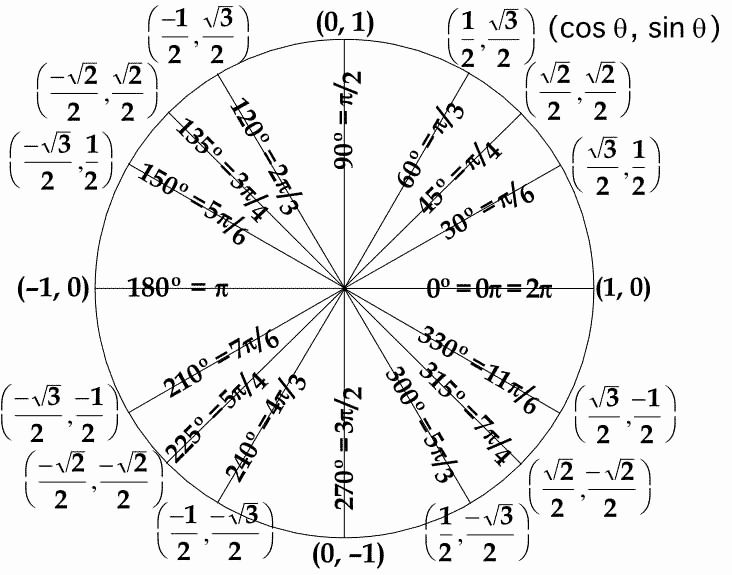 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.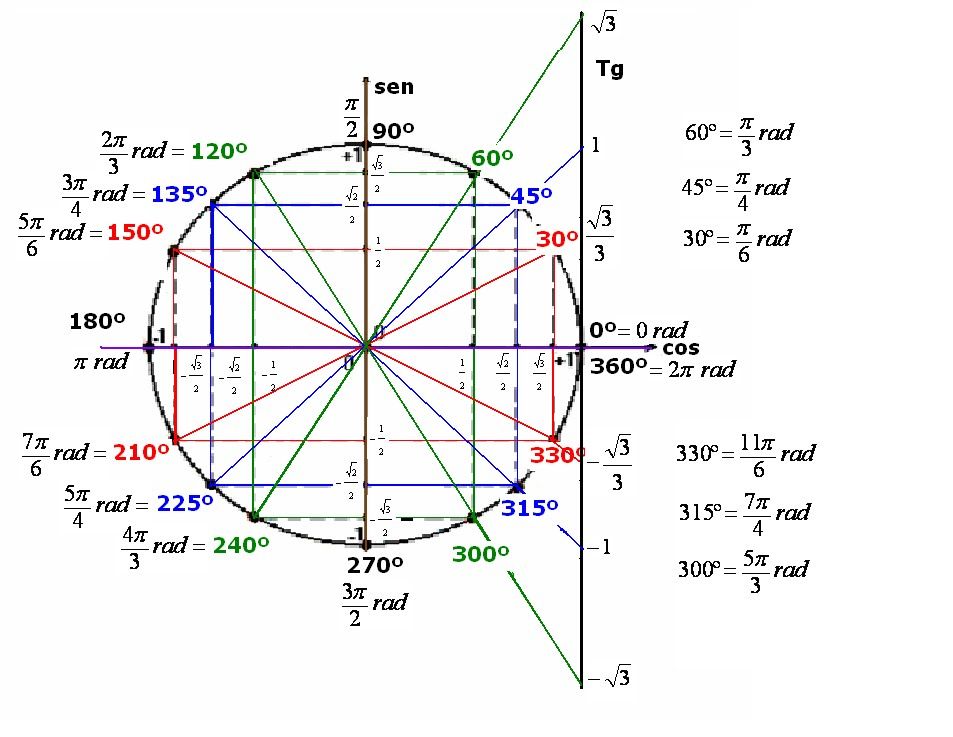 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.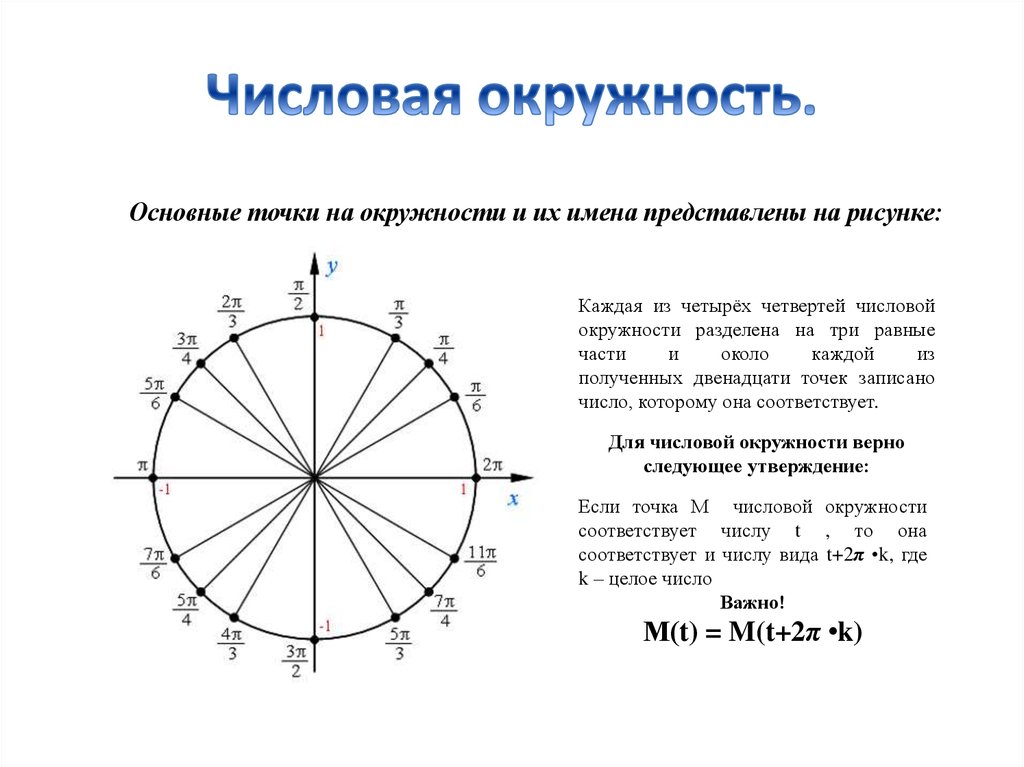 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град.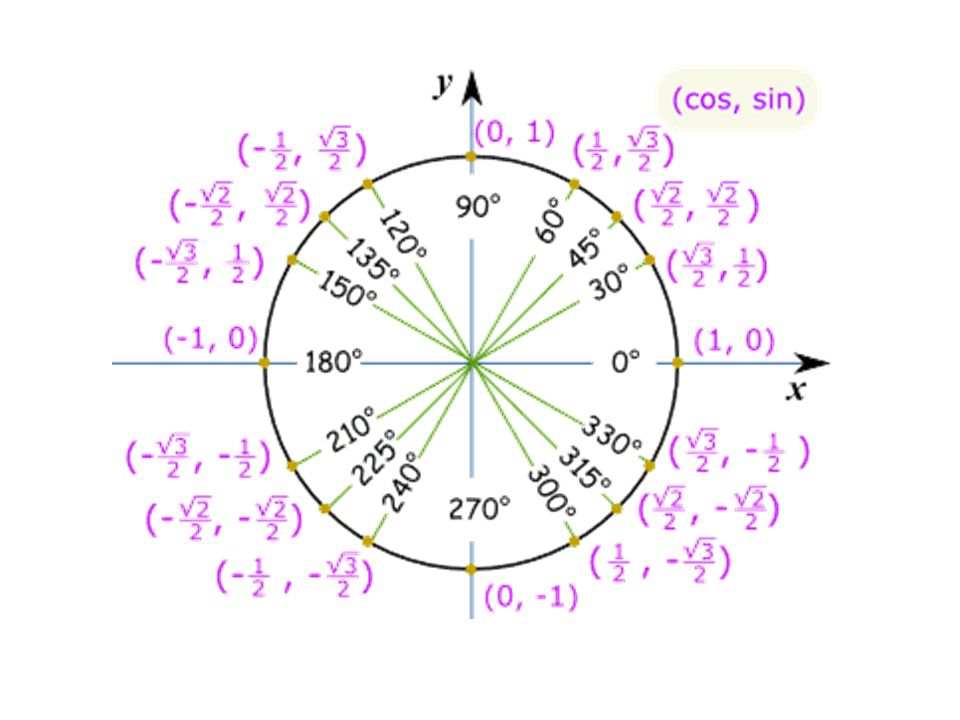 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Как никогда не путать табличные значения синусов и косинусов Секрет моей классной
Единственный в мире Музей Смайликов | Скачать 259.
|
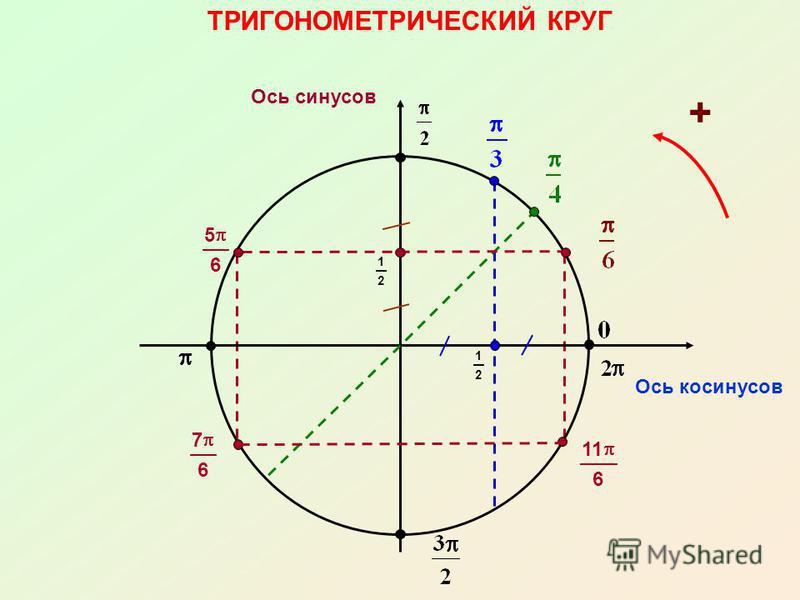
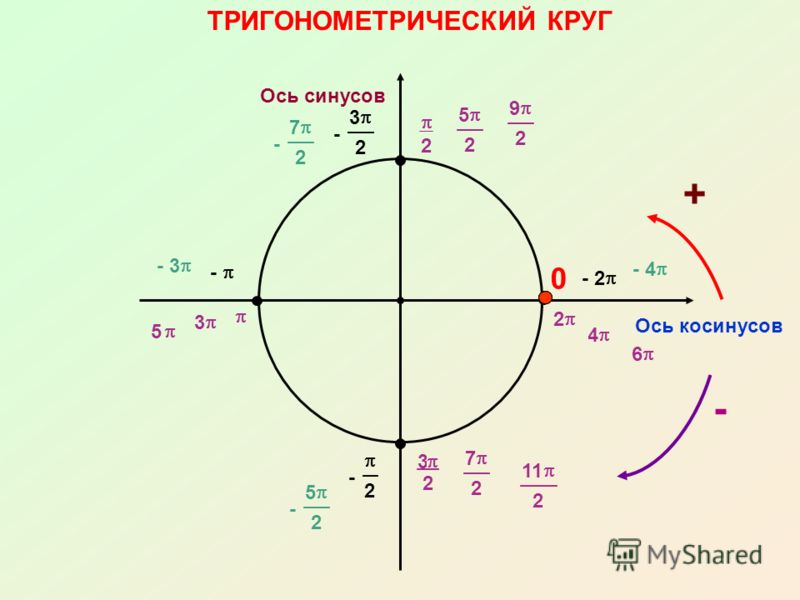
С этим файлом связано 1 файл(ов). Среди них: Проблемы социального обеспечения граждан РФ (доработка).pdf. Подборка по базе: классный час Ты помни, никогда не забывай.docx, Пр.р. Графические и табличные модели.docx, Урок Поповой Л.В. Табличные модели.pptx, Урок Поповой Л.В. Табличные модели.docx, То, что никогда не понадобится.docx, Не тот велик кто никогда не падал.docx, ЗАДАНИЕ Табличные данные.doc, Сегодня как никогда особую остроту приобретает этическая проблем, 12 причин никогда не сдаваться. 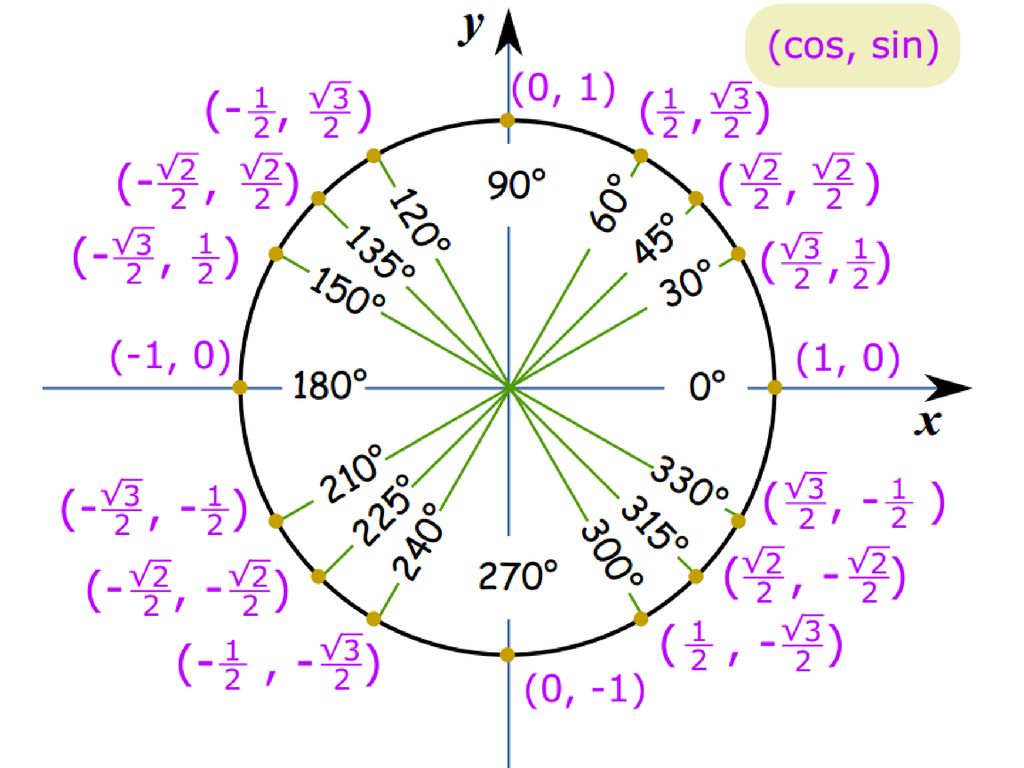 pdf pdfКак никогда не путать табличные значения синусов и косинусов? Секрет моей классной… 17 октября 2020 Вчера помогала сыну разобраться с задачей из ОГЭ по математике и поняла, что он «плавает» в табличных значениях тригонометрических функций. Объяснила ему, как их запомнить так, чтобы больше никогда не ошибиться. Для начала рисуем единичную окружность, откладываем нужный угол, получаем точку А при пересечении с окружностью. Вспоминаем, что синус — это ордината точки А (координата по оси OY), а косинус — абсцисса точки А (координата по оси OX). Наша замечательная классная руководительница, которая вела у нас математику, учила нас запоминать так: Противоположности притягиваются. Сиииинус (произносим писклявым голоском) — звучит так мяяягко, а с ним в паре орррдинаааата (басом) — звучит жестко… Кооосинус (басом) — звучит твердо, а с ним в паре абсциииисса (пискляво) — звучит мяяягко. Вот так запомнить — даже во сне уже не перепутаешь. Проверено! Обычно ни у кого нет проблем запомнить, что вся эта таблица синусов-косинусов крутится вокруг трех чисел: Осталось только понять, какое из этих чисел чему соответствует. На всякий случай вспомним, что корень из одного, это все равно, что один, тогда наши волшебные числа имеют вид: Ну и тут уж совсем очевидно, что И теперь, когда нам нужно сообразить, чему, например, равен синус угла в тридцать градусов, мы на полях тетради рисуем маленькую единичную окружность (от руки, разумеется, без всяких линеек и циркулей), откладываем там углы 30, 45, 60. Видим, что ордината (басом) у угла 30 градусов самая маленькая, значит, синус (пискляво) равен самой маленькой из этих трех величин — одной второй. А абсцисса (пискляво) у этого угла сама большая, значит, косинус (басом) равен самой большой величине — корню из трех на два (простите, что числа пишу словами, в Дзен сложно вставлять формулы в текст). По единичной окружности сразу видно, что синус угла 30 градусов равен синусу угла 150 градусов, потому что ординаты у них одинаковые. А вот косинус 150-ти равен самому большому, но отрицательному числу — минус корень из трех на два… Так, пользуясь притяжением противоположностей и единичной окружностью, Вы никогда не перепутаете табличные значения синусов и косинусов! Осталось вспомнить, что тангенс — синус деленный на косинус, а котангенс — наоборот, косинус на синус. И, вспомнив значения синуса и косинуса, легко вычислить тангенс и котангенс. Так что их тоже не забудете. Поначалу, я помню, что эти единичные окружности я прямо рисовала в тетради на полях постоянно, чтобы наглядно все было. А потом в этом отпала необходимость: картинка у меня просто возникала перед мысленным взором. Надеюсь, этот пост кому-нибудь окажется полезным 🙂 Ставьте лайки, и пишите, если нашли неточности… 22 дня Нас ещё научили, как запомнить, кто из них кто.
20 дней Я запомнил так: cos – косить, косят по горизонтали, sin – значит по вертикали! 21 день Синус противолежащий катет, косинус прилежащий. 17 дней Синус угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Чем это отношение больше, тем больше наклон. Это отношение изменяется от нуля до единицы. Ноль – это горизонтально, единица – вертикально. |
Рисунок 1: Singapore Flyer — самое высокое колесо обозрения в мире. (кредит: «Vibin JK»/Flickr)
Хотите острых ощущений? Тогда подумайте о поездке на Singapore Flyer, самом высоком в мире колесе обозрения. Расположенное в Сингапуре колесо обозрения поднимается на высоту 541 фут — чуть больше десятой мили! Описанное как колесо обозрения, всадники наслаждаются захватывающими видами, путешествуя от земли к вершине и снова спускаясь по повторяющейся схеме. В этом разделе мы рассмотрим этот тип вращательного движения по окружности. Для этого нам нужно сначала определить тип круга, а затем поместить этот круг в систему координат. Тогда мы можем обсудить круговое движение в терминах пар координат.
Расположенное в Сингапуре колесо обозрения поднимается на высоту 541 фут — чуть больше десятой мили! Описанное как колесо обозрения, всадники наслаждаются захватывающими видами, путешествуя от земли к вершине и снова спускаясь по повторяющейся схеме. В этом разделе мы рассмотрим этот тип вращательного движения по окружности. Для этого нам нужно сначала определить тип круга, а затем поместить этот круг в систему координат. Тогда мы можем обсудить круговое движение в терминах пар координат.
Нахождение значений функции для синуса и косинуса
Чтобы определить наши тригонометрические функции, мы начнем с рисования единичной окружности с центром в начале координат и радиусом 1, как показано на рисунке 2. Угол (в радианах), который [ latex]t[/latex] образует дугу длины [latex]s.[/latex] Используя формулу [latex]s=rt,[/latex] и зная, что [latex]r=1,[/latex] мы видим, что для единичного круга [латекс]s=t.[/латекс]
Напомним, что x- и y- 9Оси 0026 делят координатную плоскость на четыре четверти, называемые квадрантами.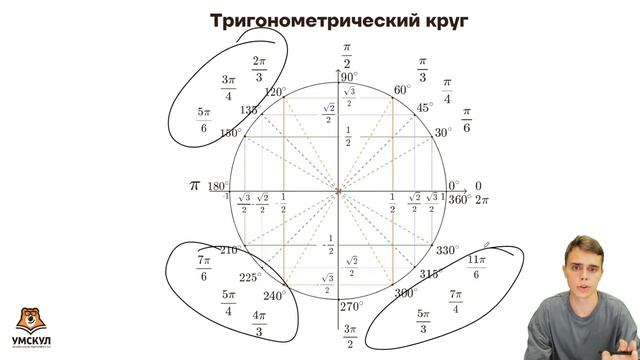 Мы помечаем эти квадранты, чтобы имитировать направление положительного угла. Четыре квадранта обозначены I, II, III и IV.
Мы помечаем эти квадранты, чтобы имитировать направление положительного угла. Четыре квадранта обозначены I, II, III и IV.
Для любого угла [латекс]t,[/латекс] мы можем пометить пересечение конечной стороны и единичной окружности его координатами [латекс]\влево(х,у\вправо).[/латекс] Рассмотрим угол угол, лежащий в первой четверти. Мы можем провести перпендикулярную линию к оси X, чтобы создать прямоугольный треугольник. Стороны прямоугольного треугольника будут равны х и у. Если мы воспользуемся правыми тригонометрическими определениями из раздела 3.1, то увидим, что [латекс]\mathrm{cos}\left(t\right)=\frac{x}{1}[/latex] и [latex]\mathrm{ sin}\left(t\right)=\frac{y}{1}.[/latex] Это означает [латекс]\left(x,\text{ }y\right)\text{ }=\text{ } \left(\mathrm{cos}\left(t\right),\text{ }\mathrm{sin}\left(t\right)\right).[/latex]
. /latex] и радиус [latex]1[/latex] . В единичном круге длина пересекаемой дуги равна радианной мере центрального угла [latex]t\text{.}[/latex]
Пусть [latex]\left(x,y\right)[ /latex] — конечная точка единичной окружности дуги длины дуги [latex]t. [/latex] Координаты [latex]\left(x,y\right)[/latex] этой точки можно описать как функции угла [latex]t[/latex], где:
[/latex] Координаты [latex]\left(x,y\right)[/latex] этой точки можно описать как функции угла [latex]t[/latex], где:
[латекс]\mathrm{cos}\left(t\right)=x[/latex] и
[латекс]\mathrm{sin}\left(t\right)=y.[/latex]
Обратите внимание, что это определение позволяет нам использовать неострые углы или, другими словами, углы в стандартном положении, конечная сторона которых не находится в первом квадранте.
Теперь, когда мы пометили нашу единичную окружность, мы можем узнать, как координаты [латекс]\влево(х,у\вправо)[/латекс] соотносятся с длиной дуги и углом. Функция синуса связывает действительное число [латекс]t[/латекс] с y -координата точки пересечения соответствующего угла с единичной окружностью. Точнее, синус угла [latex]t[/latex] равен y -значению конечной точки на единичной окружности дуги длины [latex]t.[/latex] На рисунке 3 синус равно [latex]y.[/latex] Как и все функции, функция синуса имеет вход и выход. Его вход является мерой угла; его вывод — y -координата соответствующей точки на единичной окружности. {2}.[/latex] Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
{2}.[/latex] Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
Как
Дана точка P [латекс]\влево(х,у\вправо)[/латекс] на единичной окружности, соответствующая углу [латекс]t,[/латекс] найдите синус и косинус.
- Синус [latex]t[/latex] равен y -координате точки [latex]P:\mathrm{sin}\left(t\right)=y.[/latex]
- Косинус [latex]t[/latex] равен x -координате точки [latex]P: \text{cos}\left(t\right)=x.[/latex]
Пример 1. Нахождение значений функции для синуса и косинуса
Точка [latex]P[/latex] — это точка на единичной окружности, соответствующая углу [latex]t,[/latex], как показано на рис. 4. Найти [латекс]\mathrm{cos}\left(t\right)[/latex] и [latex]\mathrm{sin}\left(t\right).[/latex]
Рисунок 4: График окружность с углом t, радиусом 1 и конечной стороной, пересекающей окружность в заданной точке
Показать решение
Попробуйте #1
Некоторый угол [latex]t[/latex] соответствует точке на единичной окружности в точке [latex]\left(-\frac{\sqrt[\leftroot{1}\uproot{2 } ]{2}}{2},\frac{\sqrt[\leftroot{1}\uproot{2} ]{2}}{2}\right)[/latex], как показано на рис.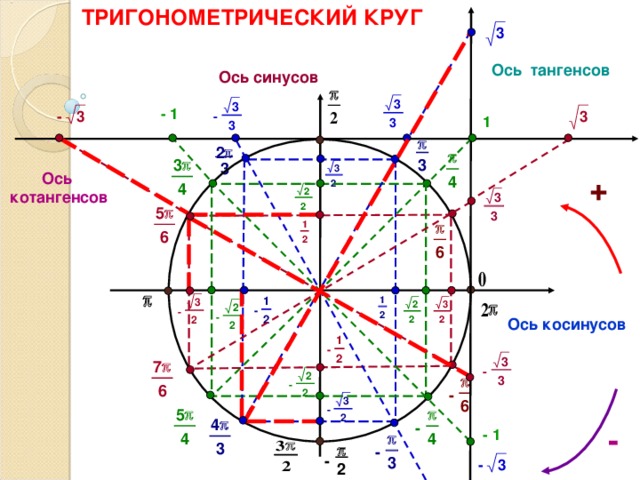 5. Найдите [латекс ]\mathrm{cos}\left(t\right)[/latex] и [latex]\mathrm{sin}\left(t\right).[/latex]
5. Найдите [латекс ]\mathrm{cos}\left(t\right)[/latex] и [latex]\mathrm{sin}\left(t\right).[/latex]
Рис. 5: График окружности с углом t, радиусом 1 и конечной стороной, пересекающей окружность в заданной точке.
Показать решение
Нахождение синусов и косинусов углов на оси
Для четырехугольных углов соответствующая точка на единичной окружности приходится на x- или y -оси. В этом случае мы можем легко вычислить косинус и синус по значениям [latex]x[/latex] и [latex]y.[/latex]
9{2}\left(t\right)=1,[/latex] известен как Пифагорейская идентичность . См. рис. 7.Рис. 7
Мы можем использовать тождество Пифагора, чтобы найти косинус угла, если нам известен синус, или наоборот. Однако, поскольку уравнение дает два решения, нам нужно дополнительное знание угла, чтобы выбрать решение с правильным знаком. Если мы знаем квадрант, в котором находится угол, мы можем легко выбрать правильное решение.
Определение
9{2}\left(t\right)=1.[/latex]How To
Зная синус некоторого угла [latex]t[/latex] и его положение в квадранте, найдите косинус [latex] t.[/latex]
- Подставить известное значение [latex]\mathrm{sin}\left(t\right)[/latex] в тождество Пифагора.
- Решите для [латекс]\mathrm{cos}\left(t\right).[/latex]
- Выберите решение с соответствующим знаком для значений x в квадранте, где находится [латекс]t[/латекс].
Пример 3. Нахождение косинуса по синусу или синуса по косинусу
If [latex]\mathrm{sin}\left(t\right)=\frac{3}{7}[/latex] and [ латекс]t[/латекс] находится во втором квадранте, найдите [латекс]\mathrm{cos}\left(t\right).[/латекс]
Показать решение
Попробуйте #3
Если [latex]\mathrm{cos}\left(t\right)=\frac{24}{25}[/latex] и [latex]t[/latex] находится в четвертом квадрант, найдите [latex]\text{sin}\left(t\right).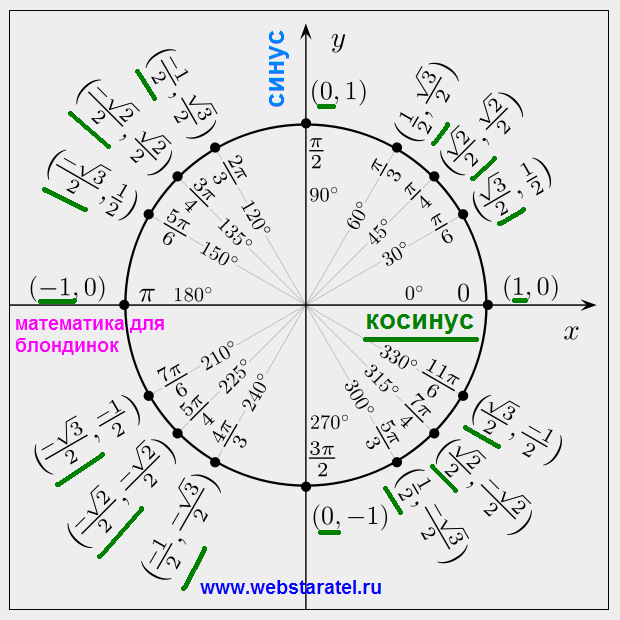 [/latex]
[/latex]
Показать решение
Нахождение синусов и косинусов специальных углов
Мы уже изучили некоторые свойства специальных углов, например, преобразование радианов в градусы. В разделе 3.1 мы также вычислили синусы и косинусы специальных углов, используя тождество Пифагора и наши знания о треугольниках.
Нахождение синусов и косинусов углов 45° и углов 30° и 60°
Мы уже нашли значения косинусов и синусов для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. Рисунок 9суммирует эти значения.
| Уголок | 0 | [латекс]\frac{\pi }{6},[/латекс] или 30° | [латекс]\frac{\pi }{4},[/латекс] или 45° | [латекс]\frac{\pi }{3},[/латекс] или 60° | [латекс]\frac{\pi }{2},[/латекс] или 90° |
| Косинус | 1 | [латекс]\frac{\sqrt[\leftroot{1}\uproot{2} ]{3}}{2}[/latex] | [латекс]\frac{\sqrt[\leftroot{1}\uproot{2} ]{2}}{2}[/latex] | [латекс]\фракция{1}{2}[/латекс] | 0 |
| Синус | 0 | [латекс]\фракция{1}{2}[/латекс] | [латекс]\frac{\sqrt[\leftroot{1}\uproot{2} ]{2}}{2}[/latex] | [латекс]\frac{\sqrt[\leftroot{1}\uproot{2} ]{3}}{2}[/latex] | 1 |
Рис.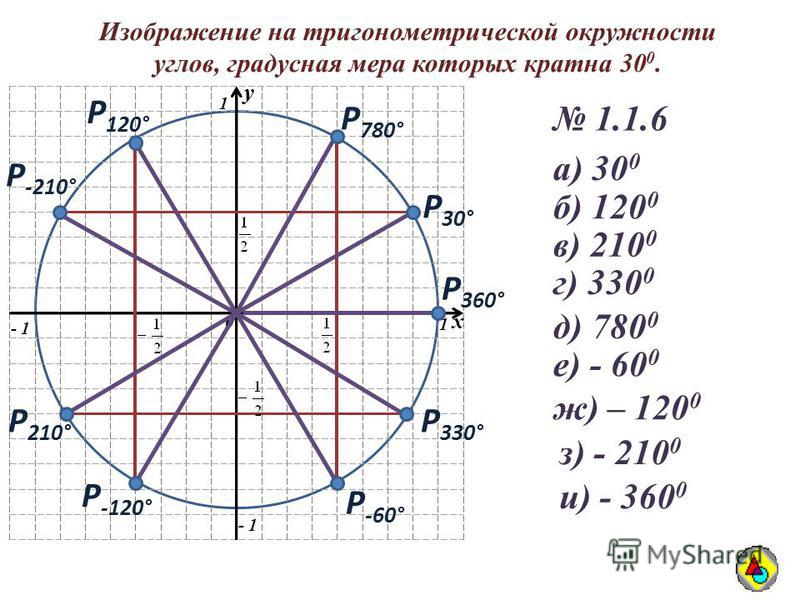 9: График четверти окружности с углами 0, 30, 45, 60 и 90 градусов вписано. Показана эквивалентность углов в радианах.
9: График четверти окружности с углами 0, 30, 45, 60 и 90 градусов вписано. Показана эквивалентность углов в радианах.
Использование калькулятора для нахождения синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов, мы обратимся к компьютеру или калькулятору. Имейте в виду : Большинство калькуляторов можно установить в режим «градусы» или «радианы», которые сообщают калькулятору единицы измерения для входного значения. Когда мы оцениваем [латекс]\mathrm{cos}\left(30\right)[/latex] на нашем калькуляторе, он оценивает его как косинус 30 градусов, если калькулятор находится в режиме градусов, или как косинус 30 радиан если калькулятор находится в радианном режиме.
How To
Зная угол в радианах, используйте графический калькулятор, чтобы найти косинус.
- Если в калькуляторе есть режимы в градусах и в радианах, установите его в режим в радианах.
- Нажмите клавишу COS.

- Введите значение угла в радианах и нажмите клавишу закрытия скобок «)».
- Нажмите ВВОД.
Пример 4. Использование графического калькулятора для нахождения синуса и косинуса
Вычислить [латекс]\mathrm{cos}\left(5.1\right)[/latex] с помощью графического калькулятора или компьютера.
Показать решение
Попробуйте #4
Оценить [латекс]\mathrm{sin}\left(2.3\right).[/latex]
Показать решение
Опорные углы
Для любого заданного угла в первом квадранте существует угол во втором квадранте с таким же значением y и, следовательно, с таким же значением синуса. Поскольку значением синуса является координата y на единичной окружности, другой угол с таким же синусом будет иметь такое же значение y , но будет иметь противоположное значение 9.0025 x -значение. Следовательно, его значение косинуса будет противоположно значению косинуса первого угла.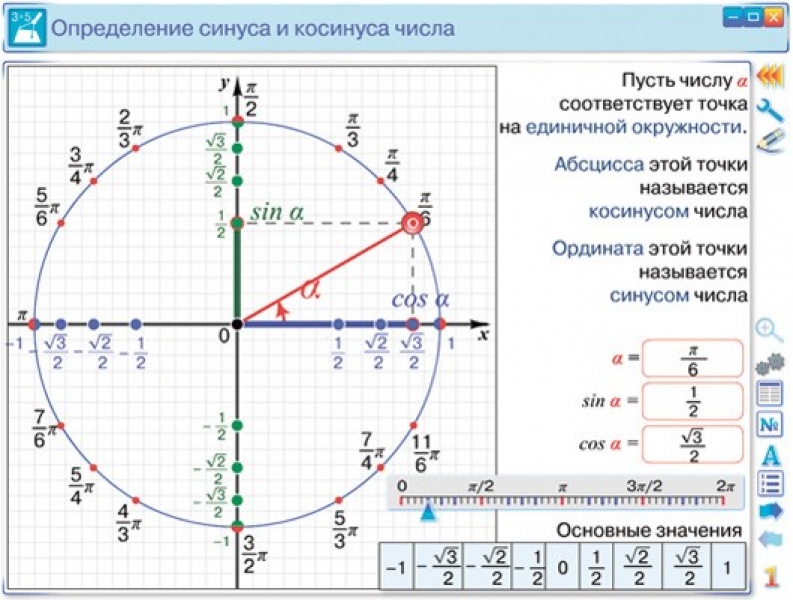
Аналогично, в четвертом квадранте будет угол с тем же значением x и, следовательно, с тем же косинусом, что и исходный угол в первом квадранте. Угол с тем же косинусом будет иметь то же значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположно значению синуса исходного угла.
Как показано на рисунке 11, угол [латекс]\альфа [/латекс] имеет то же значение синуса, что и угол [латекс]t;[/латекс] значения косинуса противоположны. Угол [латекс]\бета [/латекс] имеет то же значение косинуса, что и угол [латекс]t;[/латекс] значения синуса противоположны.
[латекс]\begin{array}{lll}\mathrm{sin}\left(t\right)=\text{ }\mathrm{sin}\left(\alpha \right)\text{ }\hfill & \text{and}\hfill & \mathrm{cos}\left(t\right)=-\mathrm{cos}\left(\alpha \right)\hfill \\ \mathrm{sin}\left(t\right) )=-\mathrm{sin}\left(\beta\right)\hfill & \text{and}\hfill & \mathrm{cos}\left(t\right)=\text{ }\mathrm{cos}\ left(\beta \right)\hfill \end{array}[/latex]
Рисунок 11
Нахождение опорных углов
Опорный угол угла 9{\circ}[/latex], как показано на рисунке 13.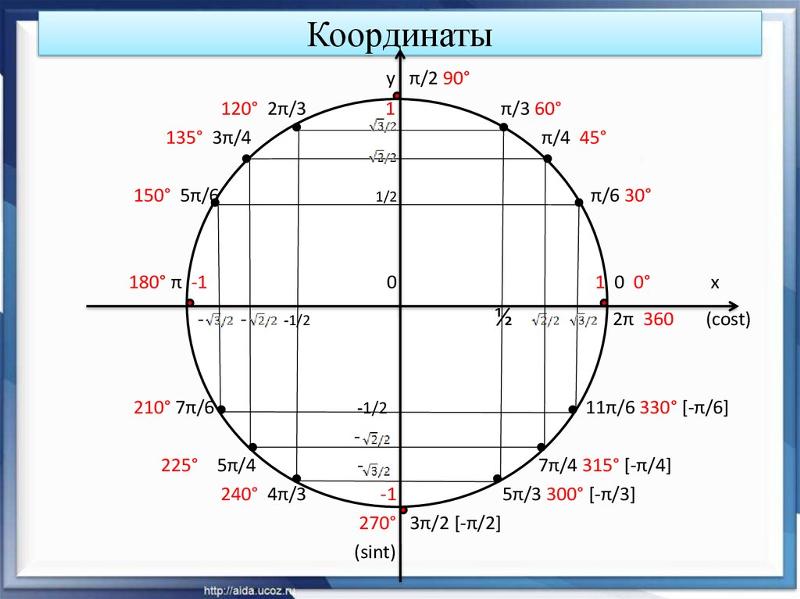
Рисунок 13: График окружности с вписанным углом 225 градусов.
Показать решение
Попробуйте # 5
Найдите опорный угол [латекс]\frac{5\pi }{3}.[/latex]
Показать решение
Использование опорных углов для нахождения точных значений косинуса и синуса
Мы можем найти косинус и синус любого угла в любом квадранте, если знаем косинус или синус его опорного угла. Абсолютные значения косинуса и синуса угла такие же, как у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака числа 9.0025 x — значения в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений и в этом квадранте.
Для угла, который имеет специальный угол в качестве опорного угла ([латекс]\frac{\pi}{6}, \frac{\pi}{4},[/latex] или [латекс]\frac{\ pi}{3},[/latex]) мы можем получить точные выходные значения для синуса и косинуса.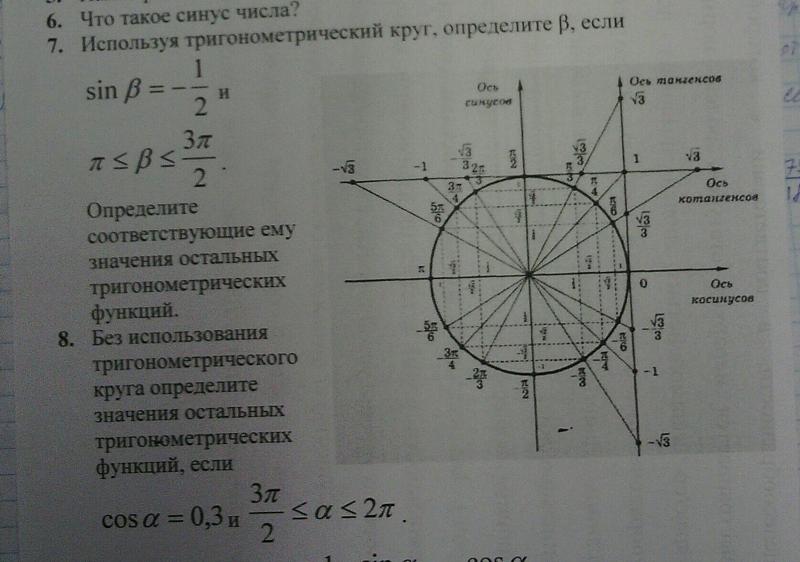
Как сделать
Зная угол в стандартном положении, найдите опорный угол, а также косинус и синус исходного угла.
- Измерьте угол между конечной стороной заданного угла и горизонтальной осью. Это опорный угол.
- Определить значения косинуса и синуса опорного угла.
- Присвойте косинусу тот же знак, что и значениям x в квадранте исходного угла.
- Присвойте синусу тот же знак, что и y -значения в квадранте исходного угла.
Пример 6. Использование опорных углов для нахождения синуса и косинуса 9{\circ}\right).[/латекс]
Показать раствор
Пример 7. Использование опорных углов для нахождения синуса и косинуса
- Используя опорный угол, найдите точные значения [латекс]\mathrm{cos}\left(\frac{5\pi}{4}\ right)[/latex] и [latex]\mathrm{sin}\left(\frac{5\pi}{4}\right).[/latex]
- Найдите углы между [латекс]0\текст{ и }2\пи[/латекс], которые имеют те же самые значения, что и [латекс]\mathrm{cos}\left(\frac{5\pi}{4}\right )[/латекс] и [латекс]\mathrm{sin}\left(\frac{5\pi}{4}\right).
 [/latex]
[/latex]
Показать раствор
Попробуйте # 7
- Используйте опорный угол [латекс]-\frac{\pi }{6}[/латекс], чтобы найти точные значения [латекс]\mathrm{cos}\left( -\frac{\pi}{6}\right)[/latex] и [латекс]\mathrm{sin}\left(-\frac{\pi}{6}\right).[/latex]
- Найдите углы между [латекс]0\текст{ и }2\пи[/латекс], которые имеют те же самые значения, что и [латекс]\mathrm{cos}\left(-\frac{\pi}{6}\right )[/латекс] и [латекс]\mathrm{sin}\left(-\frac{\pi}{6}\right).[/latex]
Показать раствор
Использование опорных углов для нахождения координат
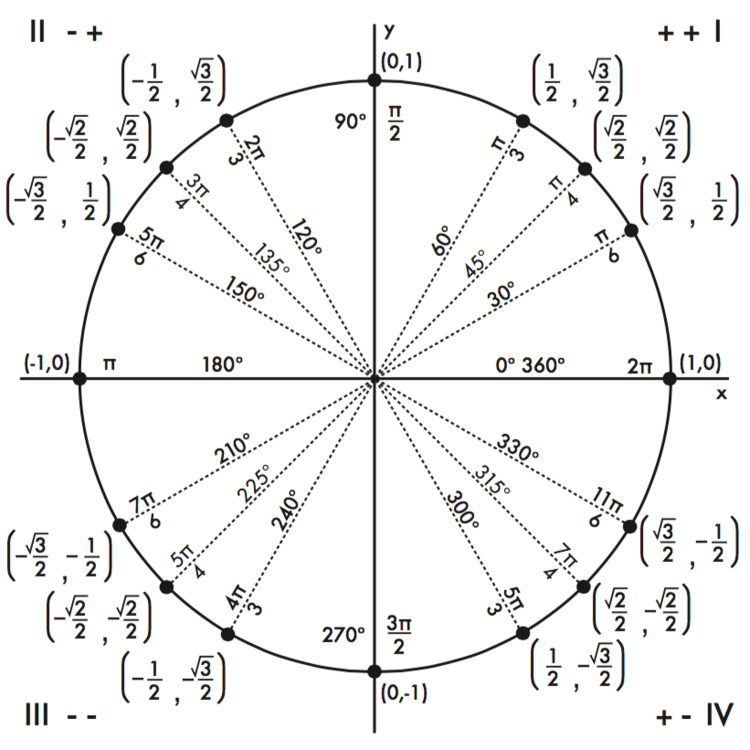
Теперь, когда мы научились находить значения косинуса и синуса для углов, опорными углами которых являются острые специальные углы, можно определить остальные специальные углы на единичной окружности. Они показаны на рис. 14. Найдите время, чтобы узнать координаты [латекс]\влево(х,у\вправо)[/латекс] всех основных углов в первом квадранте.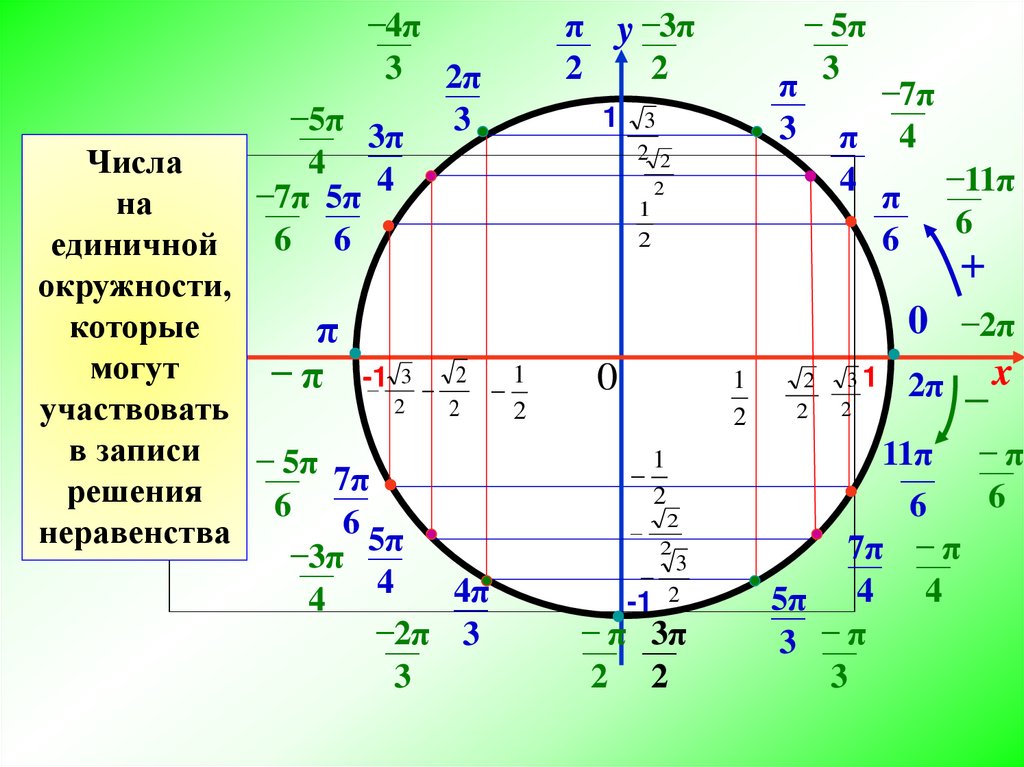
Рисунок 14: Особые углы и координаты соответствующих точек на единичной окружности
Помимо изучения значений специальных углов, мы можем использовать эталонные углы для нахождения [латексных]\левых(х,у\правых)[/латексных] координат любой точки на единичной окружности, используя то, что мы знаем об эталонных углы вместе с тождествами
[латекс]\begin{align*}x&=\mathrm{cos}\left(t\right) \\ y&=\mathrm{sin}\left(t\right).\end{ align*}[/latex][latex]\\[/latex]
Сначала мы находим опорный угол, соответствующий заданному углу. Затем мы берем значения синуса и косинуса опорного угла и присваиваем им знаки, соответствующие y – и x – значения квадранта.
Как сделать
Зная угол точки на единичной окружности, найдите [латекс]\влево(х,у\вправо)[/латекс] координаты точки.
- Найдите опорный угол, измерив наименьший угол относительно оси x .
- Найдите косинус и синус опорного угла.

- Определите соответствующие знаки для [латекс]x[/латекс] и [латекс]у[/латекс] в заданном квадранте.
Пример 8. Использование единичного круга для поиска координат
Найдите координаты точки на единичном круге под углом [latex]\frac{7\pi }{6}.[/latex]
Показать решение
Попробуйте # 8
Найдите координаты точки на единичной окружности под углом [latex]\frac{5\pi }{3}.[/latex]
Показать решение
Окружности с радиусом, отличным от 1
Предположим, у нас есть окружность с центром в начале координат, отличном от единичной окружности. Как найти координаты точки, в которой конечная сторона угла в стандартном положении пересекает окружность? Из раздела 3.1 мы знаем, что значения синуса и косинуса острого угла не меняются независимо от размера треугольника. Это означает, что [латекс]\mathrm{cos}\left(t\right)[/latex] будет одинаковым, независимо от того, находится ли [latex]t[/latex] в треугольнике с маленькими или большими сторонами.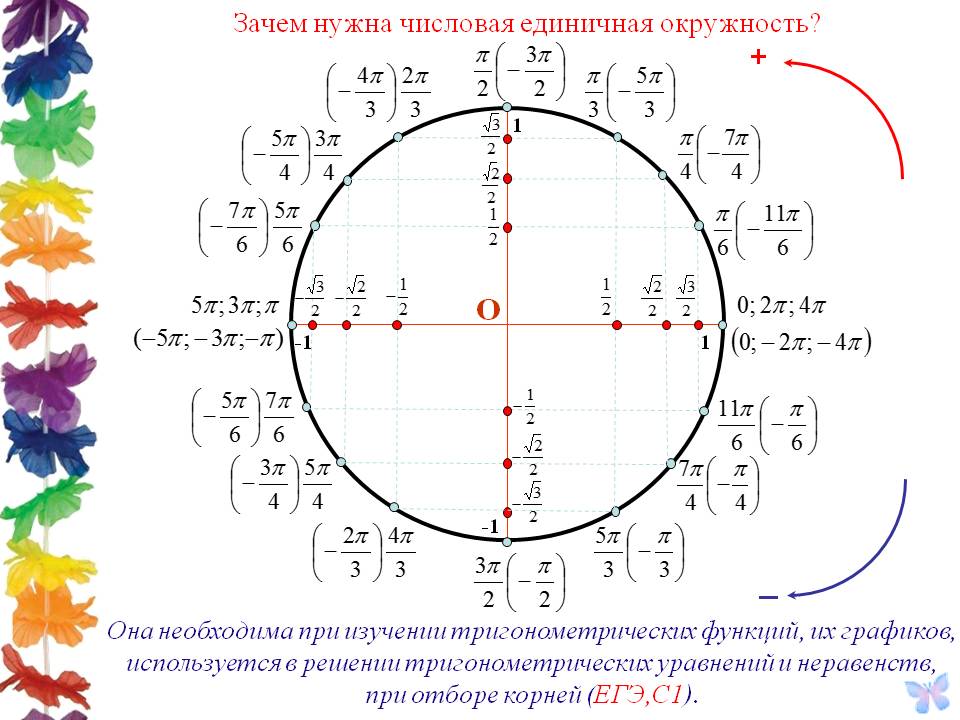 Однако ясно, что координаты точки пересечения торцевой стороны с окружностью радиуса r не будут совпадать с координатами точки на единичной окружности.
Однако ясно, что координаты точки пересечения торцевой стороны с окружностью радиуса r не будут совпадать с координатами точки на единичной окружности.
Мы можем применить аналогичные рассуждения к рассмотрению значений синуса и косинуса на окружности, которая не является единичной окружностью, как мы делали ранее в этом разделе. Проведя угол в стандартном положении в квадранте 1, мы можем опустить перпендикуляр из точки пересечения конечной стороны с окружностью, центр которой находится в начале координат, на ось x. Если точка на окружности равна (x, y), то стороны прямоугольного треугольника, образованного опусканием перпендикуляра, также будут равны [latex]x\text{ и }y.[/latex] Теперь вместо радиуса 1, у нас будет радиус [латекс]r.[/латекс] Таким образом, [латекс]\mathrm{cos}\left(t\right)=\frac{x}{r}\text{ и }\mathrm {sin}\left(t\right)=\frac{y}{r}.[/latex] Это означает, что [latex]x=r\mathrm{cos}\left(t\right)\text{ и } y=r\mathrm{sin}\left(t\right).[/latex]
Определение
Точка [латекс]\влево(х,у\вправо)[/латекс] на окружности с центром в начале координат и радиусом [латекс]r[/латекс] соответствует
[латекс]\ begin{align*}x&=r\mathrm{cos}\left(t\right)\text{ и }\\y&=r\mathrm{sin}\left(t\right)\end{align*}[/ латекс][латекс]\\[/латекс]
где [латекс]t[/латекс] — угол в стандартном положении.
Пример 9. Нахождение координат на окружности с радиусом [latex]r[/latex]
Нахождение координат точки на окружности с радиусом 5 под углом [latex]\frac{7\pi}{6 }.[/латекс]
Показать решение
Попробуйте # 9
Найдите координаты точки на окружности радиусом 7 под углом [latex]\frac{5\pi }{3}.[/latex]
Показать решение
Четные и нечетные функции
Чтобы иметь возможность свободно использовать наши функции синуса и косинуса как с положительными, так и с отрицательными входными значениями угла, мы должны изучить, как каждая функция обрабатывает отрицательный вход. Как оказалось, между функциями в этом отношении есть важное различие.
Напомним, что:
- Четная функция — это функция, в которой [латекс]f\left(-x\right)=f\left(x\right).[/latex]
- Нечетная функция — это функция, в которой [латекс]f\left(-x\right)=-f\left(x\right).[/latex]
Мы можем проверить, является ли тригонометрическая функция четной или нечетной, нарисовав единичный круг с положительным и отрицательным углами, как показано на рис. 15. Синус положительного угла равен [латекс]у.[/латекс] Синус отрицательный угол равен [латекс]-y.[/латекс] Функция синуса, таким образом, является нечетной функцией. Косинус положительного угла равен [латекс]х[/латекс], как и косинус отрицательного угла. Следовательно, функция косинуса является четной функцией. 9Рисунок 15 right)\\ \mathrm{cos}\left(-x\right)&=\mathrm{cos}\left(x\right)\end{align*}[/latex]
15. Синус положительного угла равен [латекс]у.[/латекс] Синус отрицательный угол равен [латекс]-y.[/латекс] Функция синуса, таким образом, является нечетной функцией. Косинус положительного угла равен [латекс]х[/латекс], как и косинус отрицательного угла. Следовательно, функция косинуса является четной функцией. 9Рисунок 15 right)\\ \mathrm{cos}\left(-x\right)&=\mathrm{cos}\left(x\right)\end{align*}[/latex]
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и потренируйтесь с функциями синуса и косинуса.
- Тригонометрические функции с использованием единичной окружности
- Синус и косинус единичной окружности
- Синус и косинус единичной окружности и числа Пи, деленные на шесть 9{2}\влево(т\вправо)=1[/латекс]
Ключевые понятия
- Нахождение значений функций для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом 1 единица.
- Используя единичную окружность, синус угла [latex]t[/latex] равен y -значению конечной точки единичной окружности дуги длины [latex]t[/latex], тогда как косинус угла угол [latex]t[/latex] равен x -значению конечной точки.

- Когда синус или косинус известны, мы можем использовать тождество Пифагора, чтобы найти другое. Тождество Пифагора также полезно для определения синусов и косинусов специальных углов.
- Калькуляторы и программы для построения графиков полезны для нахождения синусов и косинусов, если известна правильная процедура ввода информации.
- Областью определения функций синуса и косинуса являются все действительные числа.
- Диапазон функций синуса и косинуса: [латекс]\влево[-1,1\вправо].[/латекс]
- Синус и косинус угла имеют то же абсолютное значение, что и синус и косинус исходного угла.
- Знаки синуса и косинуса определяются из значений x и y в квадранте исходного угла.
- Опорный угол угла представляет собой размерный угол, [латекс]t,[/латекс], образованный конечной стороной угла [латекс]t[/латекс] и горизонтальной осью.
- Опорные углы можно использовать для нахождения синуса и косинуса исходного угла.

- Опорные углы также можно использовать для нахождения координат точки на единичной окружности.
- Если радиус окружности с центром в начале координат не равен 1, мы можем найти координаты точки на окружности, умножив синус и косинус угла на [latex]r.[/latex]
Глоссарий
- Функция косинуса
- x -значение точки на единичной окружности, соответствующей заданному углу
- Пифагорейская идентичность
- следствие теоремы Пифагора, утверждающее, что квадрат косинуса данного угла плюс квадрат синуса этого угла равен 1
- функция синуса
- y -значение точки на единичной окружности, соответствующей заданному углу
- единичный круг
- круг с центром в точке [латекс]\влево(0,0\вправо)[/латекс] и радиусом 1.
тригонометрия — Как в единичном круге получаются значения синуса и косинуса для точек на нем?
$\begingroup$
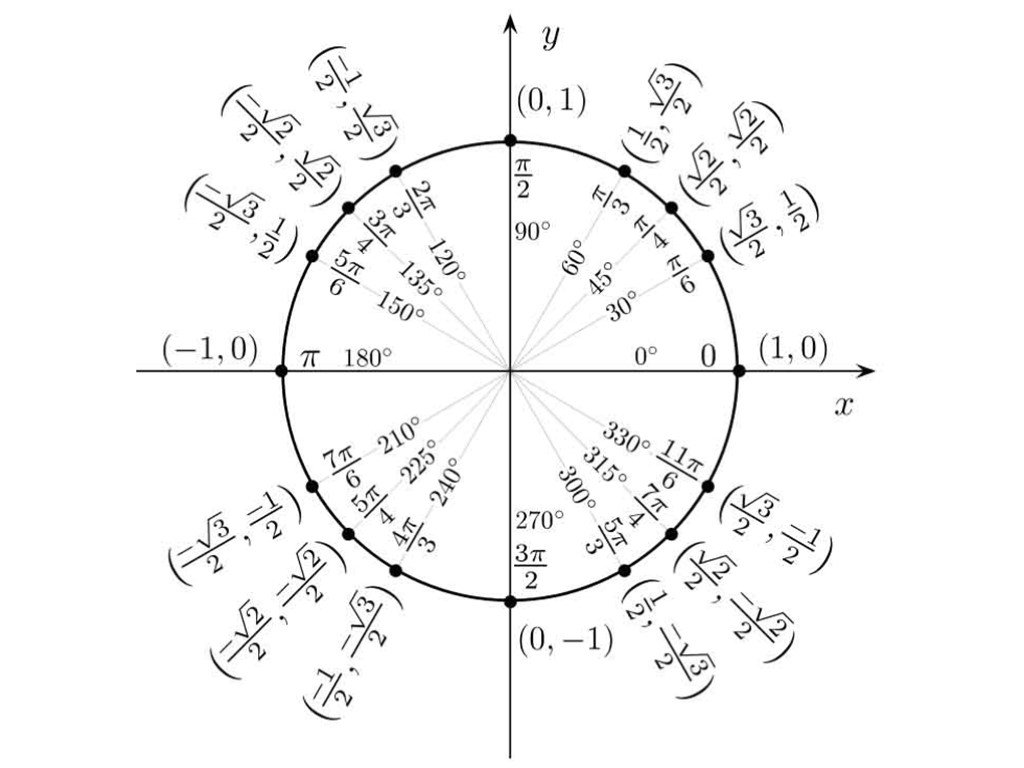
Как видно здесь, в этом единичном кружке (вроде этого: http://www.
 coolmath.com/sites/cmat/files/images/28-trigonometry-03.gif) и в таблице, которую я ссылка на Википедию ниже, есть несколько точек на единичной окружности, в которых можно использовать радикал, разделенный на значение (для синуса и косинуса, о чем я спрашиваю, это значение равно 2), чтобы получить точное значение для синуса или косинус угла. Например, для $\frac{\pi}{3}$ радиан, где синус этого угла равен $\frac{\sqrt 3}{2}$.
coolmath.com/sites/cmat/files/images/28-trigonometry-03.gif) и в таблице, которую я ссылка на Википедию ниже, есть несколько точек на единичной окружности, в которых можно использовать радикал, разделенный на значение (для синуса и косинуса, о чем я спрашиваю, это значение равно 2), чтобы получить точное значение для синуса или косинус угла. Например, для $\frac{\pi}{3}$ радиан, где синус этого угла равен $\frac{\sqrt 3}{2}$.Чего я не понимаю, так это откуда пришла идея использовать квадратный корень из 3, а также откуда пришла идея разделить значение на 2. Я понимаю, что радиус единичного круга равен 1, а стороны треугольников внутри него должны соответствовать теореме Пифагора (отсюда и эти значения с радикалами, для точности), но это все, что я понимаю.
Как узнать, что синус радианов $\frac{\pi}{3}$ равен $\frac{\sqrt 3}{2}$? Это мне непонятно.
https://en.wikipedia.org/wiki/Trigonometric_constants_expressed_in_real_radicals#Table_of_some_common_angles
- тригонометрия
- круги
- угол
$\endgroup$
4
$\begingroup$
Начнем с рисунка 1 со всеми данными, как показано.


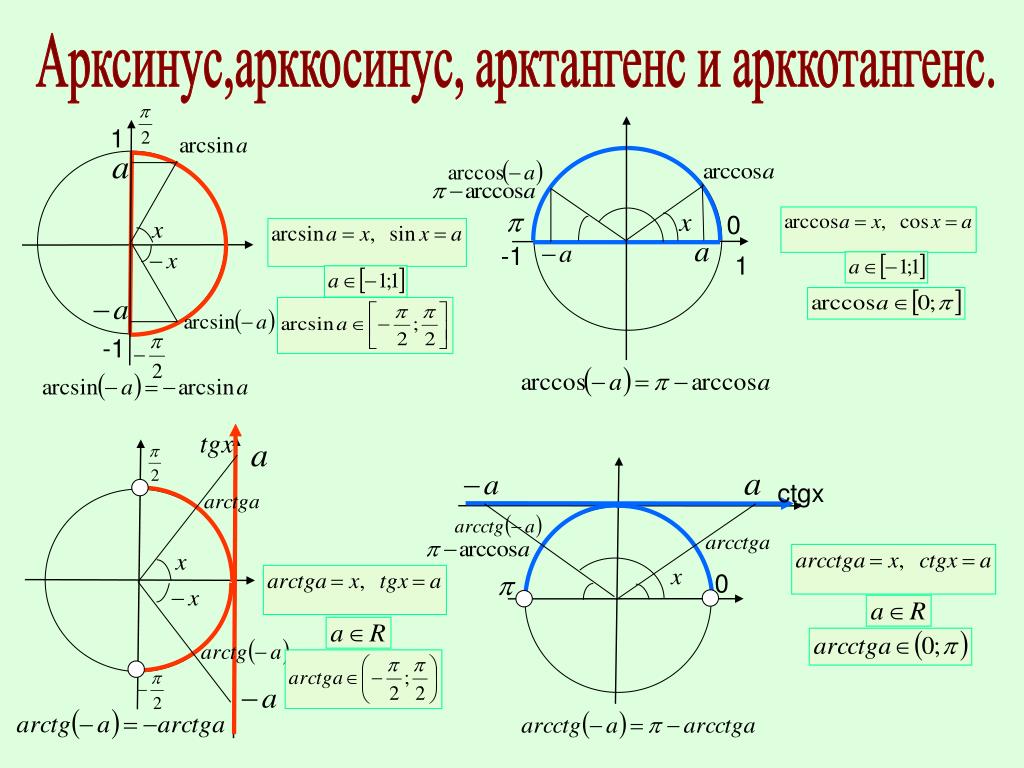 2 Kb.
2 Kb.
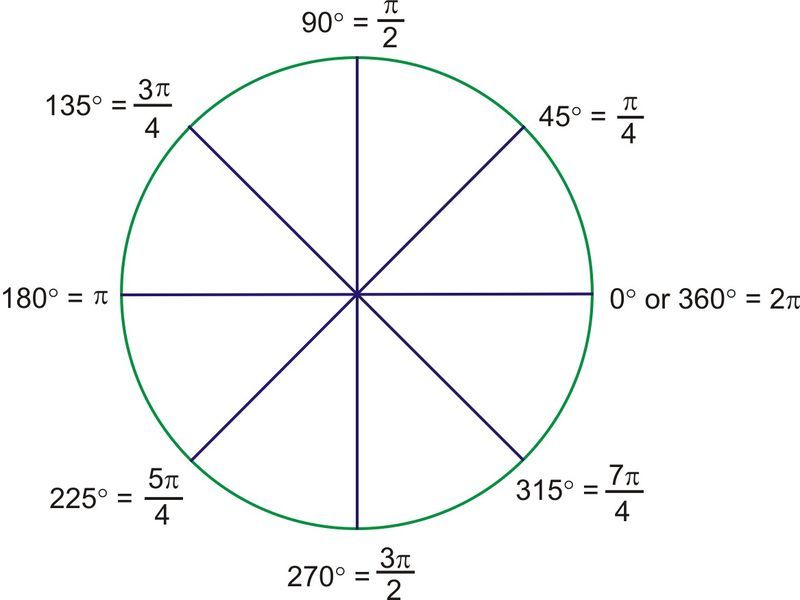
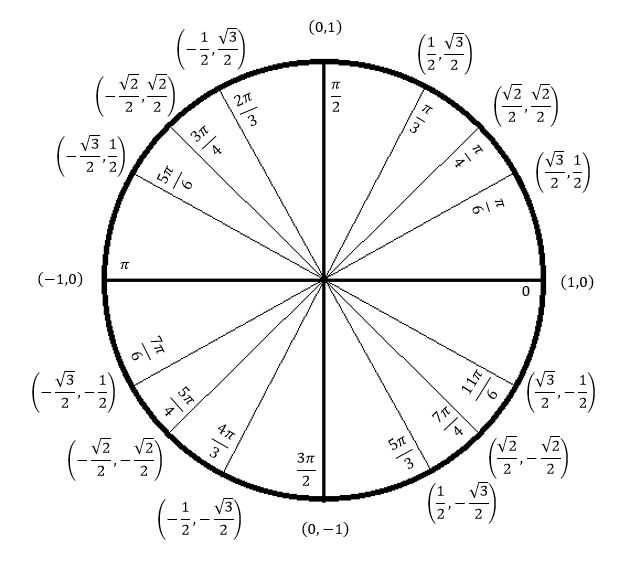 Располагаем треугольник, чтобы угол альфа лежал слева. И тогда:
Располагаем треугольник, чтобы угол альфа лежал слева. И тогда: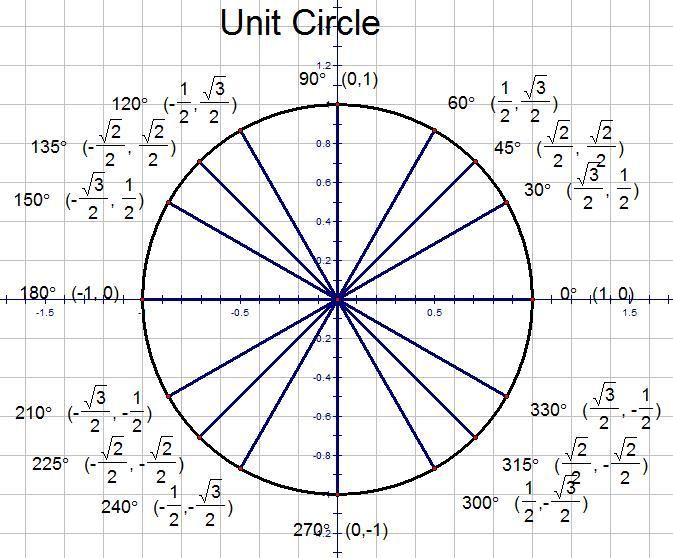
 [/latex]
[/latex]
 coolmath.com/sites/cmat/files/images/28-trigonometry-03.gif) и в таблице, которую я ссылка на Википедию ниже, есть несколько точек на единичной окружности, в которых можно использовать радикал, разделенный на значение (для синуса и косинуса, о чем я спрашиваю, это значение равно 2), чтобы получить точное значение для синуса или косинус угла. Например, для $\frac{\pi}{3}$ радиан, где синус этого угла равен $\frac{\sqrt 3}{2}$.
coolmath.com/sites/cmat/files/images/28-trigonometry-03.gif) и в таблице, которую я ссылка на Википедию ниже, есть несколько точек на единичной окружности, в которых можно использовать радикал, разделенный на значение (для синуса и косинуса, о чем я спрашиваю, это значение равно 2), чтобы получить точное значение для синуса или косинус угла. Например, для $\frac{\pi}{3}$ радиан, где синус этого угла равен $\frac{\sqrt 3}{2}$.