Как косинус выразить через синус: Формулы синуса и косинуса суммы и разности аргументов — урок. Алгебра, 10 класс.

ГДЗ Выразив синус…Упр 714 параграф 40 Алимов Алгебра 10-11 класс – Рамблер/класс

ГДЗ Выразив синус…Упр 714 параграф 40 Алимов Алгебра 10-11 класс – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Привет всем) Поможете? Нужно:
Выразив синус через косинус по формулам приведения, сравнить числа

ответы

Привет! лови:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

9 класс

11 класс

Химия

похожие вопросы 5

Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство

Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)

ГДЗАлгебраАлимов Ш.А.Школа9 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло.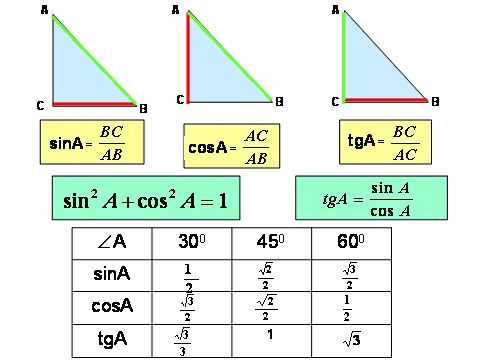 В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

тригонометрических тождеств | bartleby

Что такое тригонометрические тождества?

Тригонометрия в математике имеет дело с углами и сторонами прямоугольного треугольника. Под тригонометрическими тождествами мы подразумеваем тождества, которые мы используем всякий раз, когда нам нужно выразить различные тригонометрические функции в терминах уравнения.

Почему мы используем тригонометрические тождества?

Тригонометрические тождества помогают нам обозначать и связывать различные стороны и углы прямоугольного треугольника. Понятие тригонометрических тождеств пришло из теоремы Пифагора. Он гласит, что квадрат гипотенузы, которая является самой длинной стороной прямоугольного треугольника, равен сумме квадратов двух других сторон. Каждое тригонометрическое тождество было разработано с помощью гипотенузы и двух других сторон. Создавая уравнения, которые можно выразить через эти стороны и угол, образованный между ними, мы можем прийти к тождествам в тригонометрии.

Эти тождества верны как для равенств, так и для неравенств. В этих тождествах задействовано множество аспектов и функций. Когда нам нужно описать сторону или угол треугольника, мы используем различные соотношения, существующие между тригонометрическими функциями. Однако только прямоугольные треугольники могут быть выражены по их сторонам и углам с помощью тригонометрических тождеств.

Что мы подразумеваем под личностью?

Каждое уравнение не может быть тождеством. Только когда уравнение выполняется для каждого возможного случая, мы можем назвать его тождеством. В случае тригонометрического уравнения, только когда уравнение выполняется для всех входящих в него угловых значений, мы называем его тригонометрическим тождеством. Личность может быть установлена ​​многими методами. Наиболее распространенным является сокращение любой одной или обеих частей уравнений, чтобы можно было получить требуемую модифицированную форму.

Важно понимать тригонометрические или тригонометрические тождества для решения тригонометрических выражений или уравнений. Однако, чтобы правильно понять тождества, мы должны знать и о соотношениях, которые существуют и в триггерах.

Что мы подразумеваем под тригонометрическими отношениями?

Теперь обсудим тригонометрические отношения. В тригонометрии мы используем шесть основных соотношений. Они:

• Синус (sin)
• Косинус (cos)
• Тангенс (tan)
• Косеканс (косек)
• Секанс (сек)
• Котангенс (кот)

Если мы рассмотрим прямоугольный треугольник, то можно описать все шесть основных тригонометрических соотношений. Обычно мы используем отношения сторон треугольника, таких как гипотенуза, противолежащие и смежные стороны, чтобы выразить эти тригонометрические отношения. Каждое отдельное тригонометрическое тождество образовано из тригонометрических соотношений. Следовательно, очень важно также понимать соотношение триггеров.

Как выразить тригонометрические отношения?

Обычно тригонометрические отношения выражаются с помощью углов. В общих случаях используется угол «θ» или тета. Мы используем шесть основных тригонометрических соотношений с помощью θ следующим образом:

• Sin θ — это отношение противоположной стороны θ к гипотенузе.
• Cos θ — отношение прилежащей стороны θ к гипотенузе.
• Tan θ — это отношение противоположной стороны θ к соседней стороне θ. Можно также сказать, что это отношение sin θ и cos θ.
• Cot θ — это отношение примыкающей стороны θ к противоположной стороне θ. Можно также сказать, что это отношение 1 к тангенсу θ.
• Сек θ — это отношение гипотенузы к прилежащей стороне θ. Он также выражается как отношение 1 к cos θ.
• Cosec θ — это отношение гипотенузы к стороне, противоположной θ. Альтернативно это выражается как отношение 1 и sin θ.

В прямоугольном треугольнике прилежащая сторона θ является основанием треугольника, а противоположная сторона является перпендикуляром. Сторона, соединяющая эти две стороны, известна как гипотенуза, и это также самая длинная сторона в треугольнике.

Формула

Теперь опишем различные тригонометрические тождества и их формулы. Важно знать об этих тождествах, поскольку они могут помочь в решении различных тригонометрических задач.

Все основные тождества тригонометрии приведены ниже.

Что такое взаимные тождества?

Под взаимными тождествами мы подразумеваем тригонометрические функции, которые связаны друг с другом посредством взаимного действия. Они следующие-

Sin θ = 1Cosec θ=>Cosec θ = 1Sin θCos θ=1Sec θ=>Secθ=1Cos θTan θ=1Cot θ=>Cot θ=1Tan θ

Здесь мы видим, что синус и косеканс, косинус и секанс, а тангенс и котангенс обратны друг другу.

Что такое пифагорейские тождества?

Под тождествами Пифагора мы понимаем тригонометрические функции, связанные между собой теоремой Пифагора. Они следующие:

sin2θ+cos2θ=11+tan2θ=sec2θcosec2θ=1+cot2θ

Каковы соотношения тождеств?

Под тождествами соотношений мы понимаем тригонометрические функции, которые связаны друг с другом в виде отношения. Они следующие:

tan θ = sin θcos θcot θ = cos θsin θ

У нас есть только tan и cot как тождества правильного соотношения.

Что такое тождества с противоположными углами?

Под тождествами противоположных углов мы понимаем тригонометрические функции, которые связаны друг с другом в виде своих противоположных углов. Здесь косинус и секанс являются четными функциями. Синус, тангенс, котангенс и косеканс являются нечетными функциями. Они следующие-

sin -θ = — sin θcos -θ = cos θtan -θ = — tan θcot -θ = — cot θsec -θ = sec θcosec -θ = — cosec θ

Что такое дополнительные углы?

Под тождествами дополнительных углов мы подразумеваем тригонометрические тождества, которые могут быть выражены в виде их дополнительных углов. Они следующие:

sin 90 — θ = cos θcos 90 — θ = sin θtan 90 — θ = cot θcot 90 — θ = tan θsec 90 — θ = cosec θcosec 90 — θ = sec θ

и различия тождеств?

Тригонометрические тождества, которые могут быть выражены суммой и разностью двух углов, известны как тождества суммы углов и тождества разности углов.

Если мы рассмотрим два угла как «A» и «B», то тождества будут такими: .sin Bcos A+B = cos A + tan B1 — sin A.sin Bcos A-B = cos A.cos B + sin A.sin Btan A+B = tan A + tan B1 — tan A.tan Btan A-B = tan A — tan B1 + tan A.tan B

Однако существуют тригонометрические тождества и для трех углов. Если мы рассмотрим любые три угла как A, B и C соответственно, то мы получим следующие тождества:0005

sin A+B+C = sin A.cos B.cos C + cos A.sin B.cos C + cos A.cos B.sin C — sin A.sin B.sin Ccos A+B+C = cos A.cos B.cos C — cos A.sin B.sin C — sin A.cos B.sin C — sin A.sin B.cos Ctan A+B+C = tan A + tan B + tan C — tan A.tan B.tan C1 — tan A.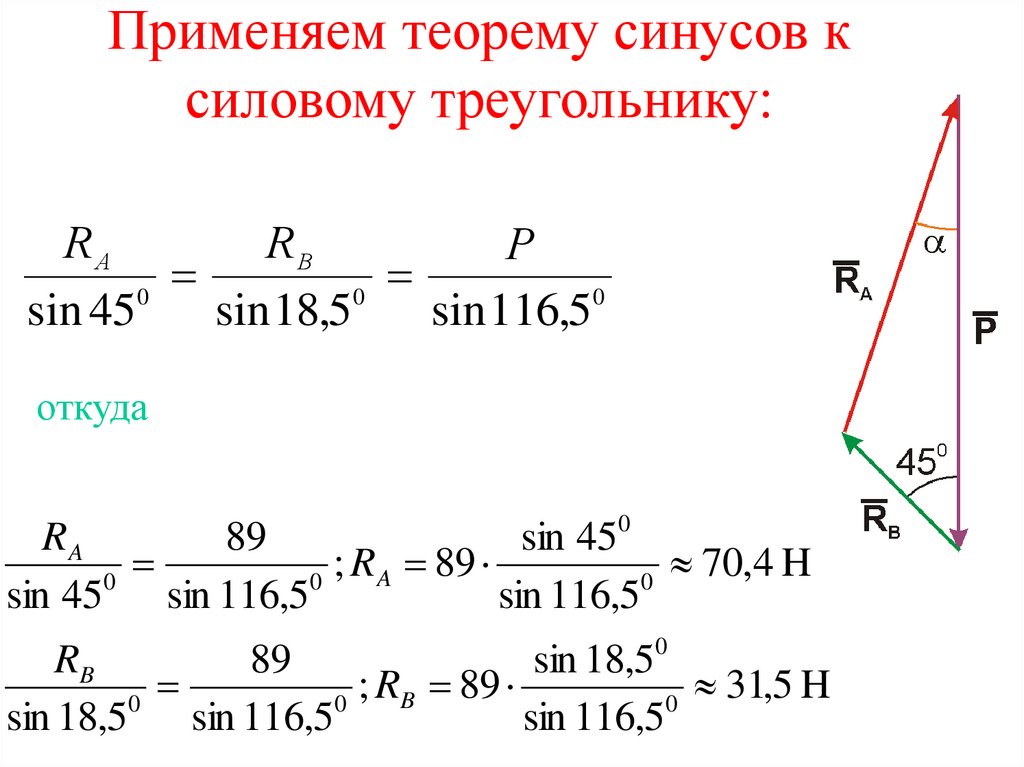 tan B — tan B.tan C — tan A.tan Ccot A+B+C = cot A.cot B.cot C — кроватка A — кроватка B — кроватка Ccot A .cot B + cot B.cot C + cot A.cot C

Если углы A, B и C являются тремя углами одного и того же треугольника, то выполняются следующие тождества:

sin A.cos B.cos C + cos A.sin B.cos C + cos A.cos B.sin C = sin A.sin B.sin Ccos A.sin B.sin C + sin A.cos B. sin C + sin A.sin B.cos C = 1 + cos A.cos B.cos Ctan A + tan B + tan C = tan A.tan B.tan Ccot B. cot C + cot C.cot A + cot A.cot B = 1tan B2.tan C2 + tan C2.tan A2 + tan A2.tan B2 = 1cot A2 + cot B2 + cot C2 = cot A2.cot B2.cot C2sin 2A + sin 2B + sin 2C = 4 sin A.sin B.sin Ccos 2A + cos 2B + cos 2C = -1 — 4 cos A.cos B.cos Ccos 2A + cos 2B + cos 2C = 1 — 2 cos A.cos B.cos Csin A + sin B + sin C = 4 cos A2.cos B2.cos C2cos A + cos B + cos C = 1 + 4 sin A2.sin B2.sin C2

Существуют специальные формулы половинного угла, формулы двойного угла и формулы тройного угла, которые помогают решать тригонометрические функции, производные и интегрирование.

Обратите внимание, что вышеприведенные тригонометрические тождества являются модифицированными версиями тождеств, существующих для любых трех углов. Только когда углы A, B и C являются частями одного и того же треугольника или если мы можем написать A + B + C = π, только тогда можно использовать эти модифицированные тригонометрические тождества.

Законы синусов

Указывает отношение между сторонами треугольника и синусом его угла. Если a, b и c являются сторонами косого треугольника, а ∠A, ∠B и ∠Care углы, противоположные сторонам a, b и c соответственно, то закон синусов может быть задан как:

sinAa= sinBb=sinCc

Практическая задача

1. Если Sin θ = 0,5, то найти значение cos θ.

⇒ Мы знаем, sin ² θ + cos ² θ = 1.

     Если Sin θ = 0,5, то мы можем решить задачу следующим образом:

sin2θ+cos2θ = 1 m порядки 0,52+cos2θ = 1 m Аведельника = 1-1-0,52 m Аведельниковой

2. Запишите формулу двойного угла для tan x.

tan2x=2tanx1−tan2x

Контекст и приложения

Тригонометрические тождества составляют основу тригонометрии и являются важной частью математики. Для таких экзаменов, как CSIR, NEET, GATE, IITJEE, ISI, CMI и вступительных экзаменов для выпускников, «тригонометрические тождества» являются очень важной темой.

• Bachelor of Science in Mathematics
• Master of Science in Mathematics

find-the-trigonometric-ratio-maze-answer-key — Google Suche

AlleBilderVideosNewsMapsShoppingBücher

Suchoptionen

Bilder

Alle anzeigen

Alle anzeigen

[PDF] Key

mathschmidt.weebly.com › uploads › trigonometry_practice_2019_key

Для чисел 1–6 используйте приведенные цифры, чтобы найти каждое тригонометрическое отношение. Выразите ответы в виде дроби и упростите! … Лабиринт углов тригонометрии!

Тригонометрические соотношения (прямоугольные треугольники): Лабиринт — TPT

www. teacherspayteachers.com › Продукт › Trigono…

1,50 $

Этот лабиринт позволяет учащимся находить тригонометрические соотношения. … Нахождение каждой тригонометрической пропорции приведет … … Ключ ответа прилагается!

тригонометрические отношения лабиринт ответ ключ … — Документы в формате PDF

pdfprof.com › PDF_Documents_Doc › q=6PDF263…

[PDF] [PDF] Таблица тригонометрических отношений ответы с работой. На этом уроке учащиеся узнают названия тригонометрических соотношений, которые они использовали в …

Лабиринт с коэффициентом триггера — YouTube

www.youtube.com › смотреть

02.05.2019 · Лабиринт с коэффициентом триггера. Смотреть позже. Делиться. Копировать ссылку. Информация. Покупка. Нажмите, чтобы включить звук. Если воспроизведение не…
Dauer: 4:27
Прислан: 02.05.2019

Ähnliche Fragen

Как легко запомнить тригонометрические отношения?

Как ответить на 6 тригонометрических соотношений?

Что такое мнемонический прием для запоминания 6 тригонометрических соотношений?

Тригонометрические лабиринты PDF | PDF | Тригонометрические функции — Scribd

www. scribd.com › document › Trigonometry-Maze…

Bewertung 4,0

(4)

Тригонометрические отношения (A) Лабиринт! Направления: Начните в верхнем левом углу. Следуй инструкциям. Используйте свои решения, чтобы пройти через

Тригонометрические соотношения (синус, косинус и тангенс) Лабиринт — Решение для …

www.pinterest.com › Исследовать › Образование

Нахождение неизвестных мер в подобных треугольниках Рабочий лист — Лабиринт. Моим ученикам 7-го класса по математике понравилось это задание с использованием подобных треугольников. The …

TrigonometricRatiosRightTriangl…

www.coursehero.com › файл › TrigonometricRatiosRi…

View TrigonometricRatiosRightTrianglesMaze-1.pdf из MATH 2 в Topsail High. Информация: Это лабиринт, который позволяет учащимся находить тригонометрические отношения.

Тригонометрические лабиринты.pdf — Курс Hero

www.