Помогите решить / разобраться (М)
| gogoshik |
| ||
11/12/16 |
| ||
| |||
| teleglaz |
| ||
16/08/17 |
| ||
| |||
| gogoshik |
| ||
11/12/16 |
| ||
| |||
| Mikhail_K |
| |||
26/01/14 |
| |||
| ||||
| Someone |
| ||
23/07/05 | |||
| |||
| gogoshik |
| ||
11/12/16 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| gogoshik |
| ||
11/12/16 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| vpb |
| |||
18/01/15 |
| |||
| ||||
| gogoshik |
| ||
11/12/16 |
| ||
| |||
| Otta |
| |||
09/05/13 |
| |||
| ||||
| kernel1983 |
| ||
10/11/15 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 14 ] |
Модераторы: Модераторы Математики, Супермодераторы
ЛЕКЦИЯ N1
назад | содержание | вперед
ЛЕКЦИЯ N1.
Элементы теории множеств.
1.Множества и основные операции над ними.
2.Отображения. Разбиения на классы.
1.Множества и основные операции над ними.
Понятие множества и элемента множества относятся к понятиям неопределимым явно, таким, как, например, точка и прямая. Эти понятия являются исходными, служат теми «кирпичиками», из которых складывается общая теория. Мы определяем только, как соотносятся эти исходные понятия, не говоря о природе рассматриваемых объектов.
Под множеством М понимается совокупность некоторых объектов, которые будут называться элементами множества М. Тот факт, что x является элементом множества М, будем обозначать через xÎM, в противном случае xÏM.
Элементы множества могут
сами являться множествами. Множество можно задать перечислением принадлежащих
ему элементов (то есть писать M={x1, x2,…, xn}) или указанием свойств, которым элементы
множества должны удовлетворять, то есть, если имеется свойство P, которым могут обладать элементы некоторого множества A, то будем обозначать {xÎA | x обладает свойством P} или {x | P(x)}, если из контекста ясно, о
каком множестве А идет речь.
Множество N или w — множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество вещественных чисел, C – множество комплексных чисел.
Множество А называется подмножеством множества В (обозначается АÍВ), если все элементы множества А принадлежат В:
ABÛ»x (xÎAÞ xÎB).
Если АÍВ, то будем также говорить, что множество А содержится в В, или имеется включение множества А в В. Множества А и В называются равными или совпадающими (обозначается А=В), если они состоят из одних и тех же элементов, то есть, если АÍВ и ВÍА. Таким образом, чтобы доказать равенство множеств, требуется установить два включения.
Пример
1: Справедливы следующие включения: NÍZ, ZÍQ, QÍR, RÍC.
Пример 2: Покажем, что множества М1={x | sin x=1} и M2={x | x=p/2+2kp, kÎZ} совпадают.
Если xÎM1, то x можно представить в виде x=p/2+2kp и поэтому xÎM2. Таким образом, M1ÍM2. Если же xÎM2, то есть x=p/2+2kp, то sin x=1, то есть M2ÍM1. Следовательно, M1=M2.
Запись АÌВ означает, что АÍВ и А¹В (А не равно В), и в этом случае будем говорить, что А строго включено в В, или является собственным подмножеством В.
Так, включения из примера 1 являются строгими.
Заметим, что XÍZ; если XÍY и YÍZ, то XÍZ; если XÍY и YÍX, то X=Y.
Не
следует смешивать отношение принадлежности Î и отношение включения Í. Хотя 0Î{0} и {0}Î{{0}}, неверно, что 0Î{{0}}, поскольку единственным элементом
множества {{0}} является {0}.
Хотя 0Î{0} и {0}Î{{0}}, неверно, что 0Î{{0}}, поскольку единственным элементом
множества {{0}} является {0}.
Совокупность всех подмножеств множества А называется его булеаном или множеством-степенью и обозначается через Р(А) или 2А. Таким образом, Р(А)={B | BÍA}.
Мы будем предполагать, что существует множество, не содержащее ни одного элемента, которое называется пустым и обозначается через Æ. Ясно, что ÆÍА для любого множества А.
Пример 3. Если А={1; 2; 3}, то Р(А)={Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, A}.
Множество, содержащее все элементы, находящиеся в рассмотрении, называется универсальным или универсумом и обозначается через U. Рассмотрим операции на булеане P(U). Если А, ВÎР(U), то пересечение АВ и объединение АВ множеств А и В определяются равенствами АВ={ x | xÎA и xÎB}, АВ={x | xÎA или xÎB}. Пересечение множеств А и В называется также их произведением и обозначается А×B, а объединение – суммой: А+В. Множество А\В=А-В={x | xÎA и xB} называется разностью множеств А и В, множество АВ=(А\В)(В\А) – кольцевой суммой или симметрической разностью множеств А и В, множество =U\А – дополнением множества А в U (см. рис., на котором изображены так называемые диаграммы Эйлера-Венна, наглядно поясняющие соотношения между
множествами).
Пересечение множеств А и В называется также их произведением и обозначается А×B, а объединение – суммой: А+В. Множество А\В=А-В={x | xÎA и xB} называется разностью множеств А и В, множество АВ=(А\В)(В\А) – кольцевой суммой или симметрической разностью множеств А и В, множество =U\А – дополнением множества А в U (см. рис., на котором изображены так называемые диаграммы Эйлера-Венна, наглядно поясняющие соотношения между
множествами).
Пример 4. Докажем, что А\В=А.
Сначала установим, что А\ВÍА. Пусть x – произвольный элемент А\В. Тогда по определению
разности множеств имеем xÎA и xÏB, отсюда xÎA и xÎ, значит, xÎA. Теперь
покажем, что AÍA\B. Если xÎA, то xÎA и xÎ, поэтому xÎA и xÏB, значит, xÎA\B. На основании включений A\BÍA и AÍA\B делаем вывод, что A\B=A.
На основании включений A\BÍA и AÍA\B делаем вывод, что A\B=A.
Аналогично примеру 4 устанавливаются следующие основные свойства операций пересечения, объединения и дополнения:
1. Ассоциативность операций и :
А(ВС)=(АВ)С, А(ВС)=(АВ)С.
2. Коммутативность операций и :
АВ=ВА, АВ=ВА.
3. Законы идемпотентности:
АА=А, АА=А.
4. Законы дистрибутивности:
А(ВС)=(АВ)(АС), А (ВС)=(АВ)(АС).
5. Законы поглощения:
А(АВ)=А, А(АВ)=А.
6. Законы де Моргана:
=, =.
7. Законы нуля и единицы:положим 0ÛÆ, 1ÛU, тогда
А0=А, А0=0, А1=А, А1=А, А=1, А=0.
8. Законы двойного отрицания:
=А.
Пересечение и объединение могут быть определены для любого
множества множеств Ai, где индексы i пробегают множество I. Пересечение {Ai | iÎI} и объединение {Ai | iÎI} задаются равенствами:
Пересечение {Ai | iÎI} и объединение {Ai | iÎI} задаются равенствами:
{Ai | iÎI} = {x | xÎAi для всех iÎI},
{Ai | iÎI} = {x | xÎAi для некоторого iÎI}.
Вместо {Ai | iÎI} и {Ai | iÎI} часто пишут соответственно Ai и Ai, а иногда просто Ai, Ai, если из контекста ясно, какое множество I имеется в виду. Если
I={1, 2,…, n}, то используются записи A1A2An и A1A2An, а также Ai и Ai.
Множество {Ai |
iÎI} непустых подмножеств множества А называется покрытием множества А, если А=Ai.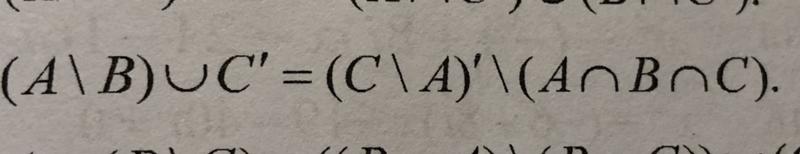 Покрытие
называется разбиением, если AiAj=Æ при i¹j.
Другими словами, множество {Ai | iÎI} непустых подмножеств множества А является его
разбиением, если каждый элемент xÎА принадлежит в точности
одному из подмножеств Ai, каждое из
которых не является пустым.
Покрытие
называется разбиением, если AiAj=Æ при i¹j.
Другими словами, множество {Ai | iÎI} непустых подмножеств множества А является его
разбиением, если каждый элемент xÎА принадлежит в точности
одному из подмножеств Ai, каждое из
которых не является пустым.
Упорядоченную последовательность из n элементов x1, x2,…, xn будем обозначать через (x1, x2,…, xn) или áx1, x2,…, xnñ. Здесь круглые или угловые скобки используются для того, чтобы указать на порядок, в котором записаны элементы. Будем называть такую последовательность упорядоченным набором длины n, кортежем длины n или просто n-кой. Элемент xiназывается i-ой координатой кортежа áx1, x2,…, xnñ.
Декартовым (прямым) произведением множеств A1, A2,…, An называется множество
{(x1, x2,…, xn) | x1ÎA1, x2ÎA2,…, xnÎAn}, обозначаемое через или .
Если A1=A2=…=An=A, то множество называется n-й декартовой степенью множества А и обозначается Аn. Положим по определению A0 = {Æ}.
Пример 5. Пусть А={1, 2}, B={3, 4}. Тогда ={(1, 3), (1, 4), (2, 3), (2, 4)},
={(3, 1), (3, 2), (4, 1), (4, 2)}, ={(1, 1), (1, 2), (2, 1), (2, 2)}.
2.Отображения. Разбиения на классы.
Отображение множеств. Общее понятие функции.
В анализе понятие функции вводится следующим образом.
Пусть X – некоторое множество на числовой прямой.
Говорят, что на этом множестве определена функция f, если каждому числу xÎX поставлено в соответствие определенное число y=f(x). При этом X называется областью определения данной функции, а Y – совокупность всех значений, принимаемых этой
функцией, — ее областью значений.
Если же вместо числовых рассматривать множества какой угодно природы, то мы придем к самому общему понятию функции. Пусть M и N – два произвольных множества. Говорят, что на М определена функция f, принимающая значения из N, если каждому элементу xÎM поставлен в соответствие один и только один элемент y из N. Для множеств произвольной природы (как, впрочем, и в случае числовых множеств) вместо термина «функция» часто пользуются термином «отображение», говоря об отображении одного множества в другое. При специализации природы множеств M и N возникают специальные типы функций, которые носят особые названия «вектор-функция», «мера», «функционал», «оператор» и так далее. Мы столкнемся с ними в дальнейшем.
Для обозначения функции (отображения) из М в N мы будем часто пользоваться записью f: M®N.
Если а – элемент из M, то отвечающий ему элемент b=f(a) из N называется его образом (при отображении f). Совокупность всех тех элементов а из M, образом которых является данный элемент bÎN, называется прообразом (или, точнее полным прообразом) элемента b и обозначается f-–1(b).
Совокупность всех тех элементов а из M, образом которых является данный элемент bÎN, называется прообразом (или, точнее полным прообразом) элемента b и обозначается f-–1(b).
Пусть А – некоторое множество из М; совокупность {f(a) | aÎA} всех элементов вида f(a), где aÎA, называется образом А и обозначается f(A). В свою очередь для каждого множества В из N определяется его (полный) прообраз f–1(B), а именно: f-–1(B) есть совокупность всех тех элементов из М, образы которых принадлежат В. Может оказаться, что ни один элемент b из В не имеет непустого прообраза, тогда и прообраз f-–1(B) будет пустым множеством.
Здесь мы ограничимся рассмотрением самых общих свойств отображений.
Введем следующую терминологию. Мы будем говорить, что f есть отображение множества М «на»
множество N, если f(M)=N;
такое отображение называют также сюръекцией. Будем писать f: MN. (В общем случае, то есть, когда f(M)ÌN, говорят, что f есть отображение М «в» N.)
Будем писать f: MN. (В общем случае, то есть, когда f(M)ÌN, говорят, что f есть отображение М «в» N.)
Если для любых двух различных элементов x1 и x2 из М их образы y1=f(x1) и y2=f(x2) также различны, то f называется инъекцией (будем писать f: MN). Отображение f: MN, которое одновременно является сюръекцией и инъекцией называется биекцией или взаимно однозначным соответствием между M и N, будем писать f: M«N.
Пример. Рассмотрим три функции fi: R®R, i=1, 2, 3:
1) функция f1(x)=ex инъективна, но не сюръективна;
2) функция f2(x)=x×sin x сюръективна, но не инъективна;
3) функция f3(x)=2x-1 биективна.
Установим основные свойства отображений.
Теорема 1. Прообраз суммы двух множеств равен сумме
их прообразов:
Прообраз суммы двух множеств равен сумме
их прообразов:
f–1(AB)=f–1(A)f-–1(B).
Теорема 2. Прообраз пересечения двух множеств равен пересечению их прообразов:
f-–1(AB)=f-–1(A)f-–1(B).
Теорема 3. Образ суммы двух множеств равен сумме их образов: f(AB)=f(A)f(B).
Заметим, что образ пересечения двух множеств, вообще говоря, не совпадает с пересечением их образов. Например, пусть рассматриваемое отображение представляет собой проектирование плоскости на ось x. Тогда отрезки 0£x£1, y=0; 0£x£1; y=1 не пересекаются, а в то же время их образы совпадают.
элементарная теория множеств — Доказательство равенства множеств
Задавать вопрос
спросил
Изменено 6 лет, 1 месяц назад
Просмотрено 3к раз
$\begingroup$
Как мне доказать следующие уравнения (я новичок в статистике и не знаю, с чего начать, даже после попытки выяснить это):
(a) $A — B = A — A \cap B = A \cup B — B$
(b) $A \mathbin{\Delta} B = A \cup B — A \cap B$
- элементарная теория множеств
- логика
$\endgroup$
2
$\begingroup$
Сначала убедитесь, что вы точно знаете, что означают соответствующие символы. Затем можно доказать равенство двух множеств $S$ и $T$, показав $S \subseteq T$ и $T \subseteq S$.
Затем можно доказать равенство двух множеств $S$ и $T$, показав $S \subseteq T$ и $T \subseteq S$.
В первом примере вы должны показать, что $A — B = A — A \cap B$. Первый шаг — доказать, что $A — B \subseteq A — A \cap B$. Для этого возьмем произвольный элемент $x \in A — B$. По определению разности множеств мы знаем, что $x \in A$ и $x \notin B$. Поскольку $x \notin B$, мы также имеем $x \notin A \cap B$. Следовательно, $x \in A — A \cap B$. Так как $x$ был произвольным элементом $A — B$, мы можем заключить, что $A — B \subseteq A — A \cap B$. Затем аналогично докажите, что $A — A \cap B \subseteq A — B$.
$\endgroup$
$\begingroup$
Доказательство $_1$: $A\setminus(B\cap C)=(A\setminus B) \cup (A\setminus C)$ \begin{align*} x\in A\setminus(B\cap C) &\leftrightarrow x \in A \wedge x \notin (B \cap C)\\ &\leftrightarrow x \in A \wedge (x \ notin B \vee x \notin C)\\ &\leftrightarrow (x \in A \wedge x \notin B) \vee (x \in A \wedge x \notin C) \\ &\leftrightarrow x \in (A \setminus B) \vee x \in (A\setminus C) \\ &\leftrightarrow x \in (A\setminus B) \cup (B\setminus C) \end{align*} поэтому Доказательство $_{1_1}$: $A \setminus (A \cap B)=(A\setminus A)\cup (A\setminus B)=\emptyset \cup (A\setminus B)=A\setminus
бразильских доллараДоказательство $_2$: $(A \cup B)\setminus B=A \setminus B$ \begin{align*} x \in(A \cup B)\setminus B &\leftrightarrow x \in (A\cup B) \wedge x \notin B \\ &\leftrightarrow (x \in A \vee x \ in B)\клин x \notin B\\ &\leftrightarrow (x \in A \wedge x \notin B) \vee (x \in B \wedge x \notin B) \\ &\leftrightarrow x \in (A \setminus B) \vee x \in (B\setminus B) \\ &\leftrightarrow x \in ((A\setminus B) \cup \emptyset )\\ &\leftrightarrow x \in (A\setminus B) \ конец{выравнивание*}
Доказательство $_3$: $(A \cup B) \setminus (A \cap B)=(A \setminus B) \cup (B\setminus A) =: A \bigtriangleup B$ \begin{align*} (A \cup B)\setminus (A\cap B) &= ((A \cup B) \setminus A) \cup ((A \cup B) \setminus B) \text{ ( по Доказательству} _1)\\ &=(B \cup A) \setminus A) \cup ((A \cup B) \setminus B) \\ &= (B \setminus A) \cup (A \setminus B) \text{ (по Proof} _2)\\ &=(A \setminus B) \cup (B\setminus A) \end{align*}
$\endgroup$
дискретная математика — Как доказать равенство множеств?
спросил
Изменено 5 лет, 9 месяцев назад
Просмотрено 1к раз
$\begingroup$
Докажите, что $[x \in \mathbb{Z}:6|x] = [x \in \mathbb{Z}:2|x]\cap[x\in\mathbb{Z}:3|x] . $
$
Я понимаю, что мне нужно доказать это с разных точек зрения, но я впервые работаю с доказательствами, используя наборы. Как мне подойти к решению такой проблемы?
Будем признательны за любой отзыв!
- дискретная математика
- теория элементарных множеств
- корректура
$\endgroup$
1
$\begingroup$
Докажите, что каждое множество является подмножеством другого. То есть возьмем $x \in \{ x \in \mathbb{Z} : 2 \mid x \} \cap \{ x \in \mathbb{Z} : 3 \mid x \}$. Тогда, поскольку 2 и 3 взаимно просты, мы имеем $6 \mid x$, так что $x \in \{ x \in \mathbb{Z} : 6 \mid x \}$. Это означает $\{ x \in \mathbb{Z} : 2 \mid x \} \cap \{ x \in \mathbb{Z} : 3 \mid x \} \subset \{ x \in \mathbb{Z } : 6 \mid x \}$. Обратное аналогично.
$\endgroup$
2
$\begingroup$
Требование подтверждения.
 Чтобы показать, что два множества $A$ и $B$ равны, мы можем показать, что два
множества являются подмножествами друг друга, т. е. $A \subseteq B$ и $B \subseteq
$. В частности, мы можем показать, что если $y \in A$, то $y \in B$ и
и наоборот, если $y \in B$, то $y \in A$. Мы можем думать об этом как
примерно аналогично показу «обеих сторон» тогда и только тогда, когда
операторы $(\iff)$.
Чтобы показать, что два множества $A$ и $B$ равны, мы можем показать, что два
множества являются подмножествами друг друга, т. е. $A \subseteq B$ и $B \subseteq
$. В частности, мы можем показать, что если $y \in A$, то $y \in B$ и
и наоборот, если $y \in B$, то $y \in A$. Мы можем думать об этом как
примерно аналогично показу «обеих сторон» тогда и только тогда, когда
операторы $(\iff)$.Доказательство. Поскольку наборы, которые мы здесь имеем, имеют хорошие алгебраические представления, мы покажем, что если число $y$ может быть представлен как кратный $6$, он также может быть представлен как кратно 3$ и кратно 2$, и наоборот.
Предположим, что $y \in \{x \in \mathbb Z : x|6\}$. Тогда $6$ делит $y$, это означает, что существует $z \in \mathbb Z$, такой что $y$ может быть записывается как $y = 6z$. Но тогда $y = 3\cdot(2z)$ и $y = 2 \cdot(3z)$ и, конечно же, $2z$ и $3z$ также являются целыми числами. Следовательно, $3$ делит $y$, а $2$ делит $y$, так что $y \in \{x \in \mathbb Z : x |3\} \cap \{x \in \mathbb Z : x|2\} $.



 12.2017, 18:28
12.2017, 18:28  Напишите подробно, откуда Вы это получили.
Напишите подробно, откуда Вы это получили.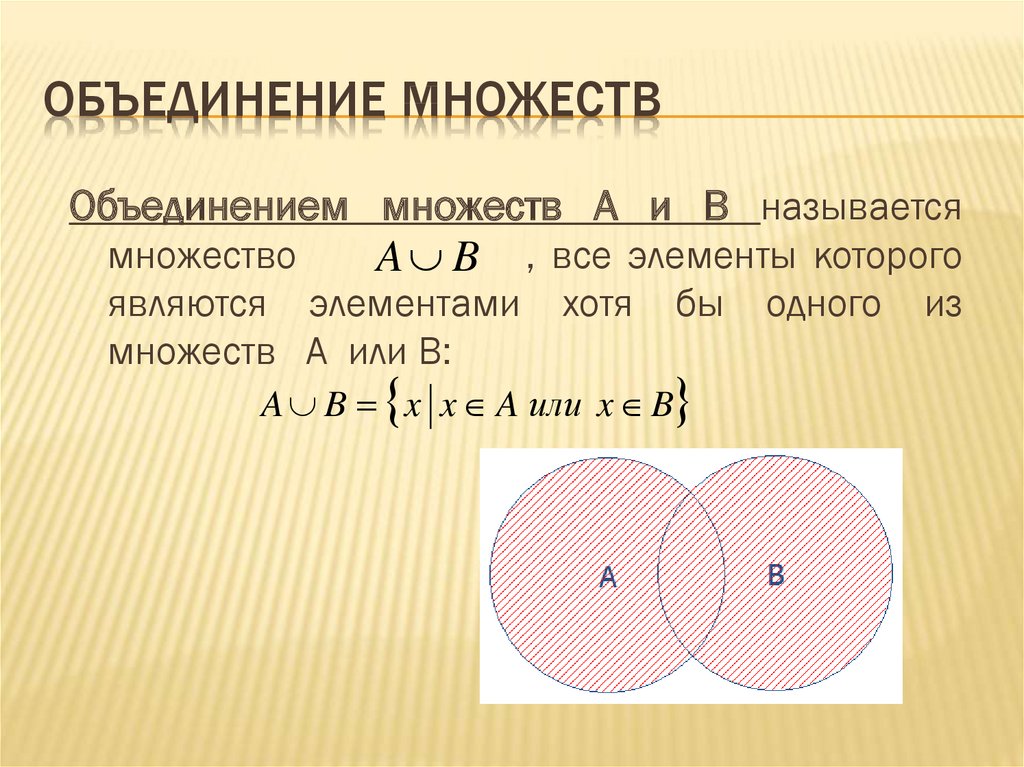 12.2017, 00:03
12.2017, 00:03  12.2017, 01:22
12.2017, 01:22  12.2017, 14:30
12.2017, 14:30  12.2017, 15:26
12.2017, 15:26  12.2017, 16:08
12.2017, 16:08 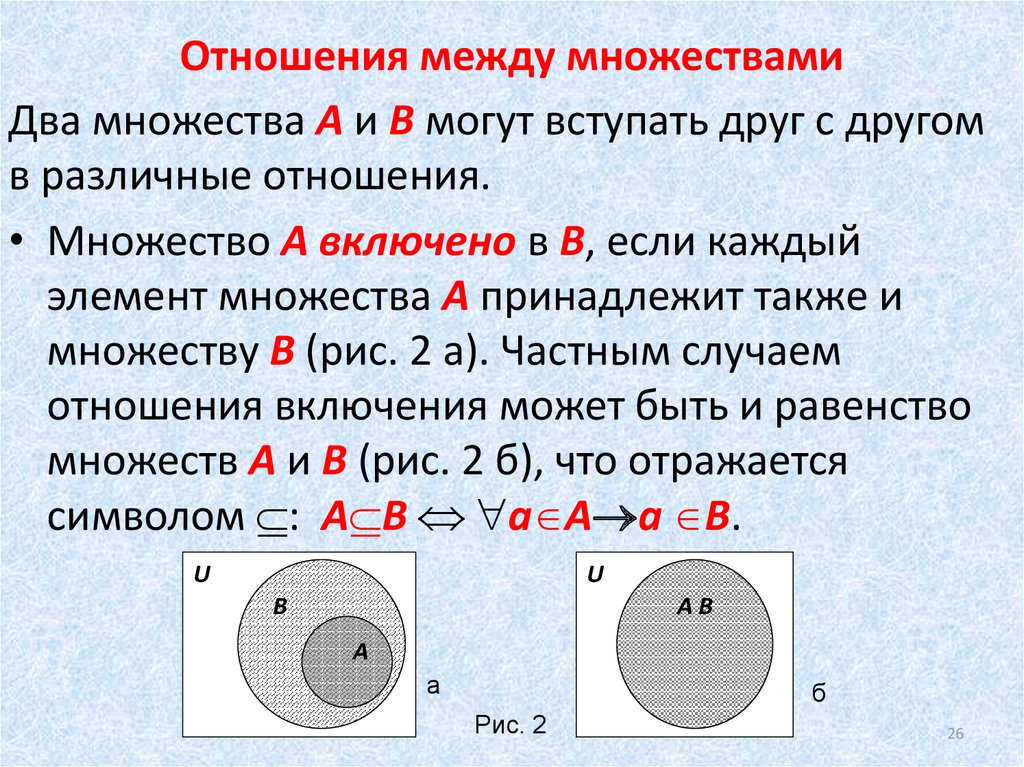 е. лежит в пересечении . С другой стороны, любой элемент из лежит в . Значит, множества и состоят из одних и тех же элементов, т.е. . Обратно, допустим, что . Поскольку для любых множеств и пересечение — подмножество в , то ввиду равенства получаем, что . Итак, соотношения и эквивалентны.»
е. лежит в пересечении . С другой стороны, любой элемент из лежит в . Значит, множества и состоят из одних и тех же элементов, т.е. . Обратно, допустим, что . Поскольку для любых множеств и пересечение — подмножество в , то ввиду равенства получаем, что . Итак, соотношения и эквивалентны.» 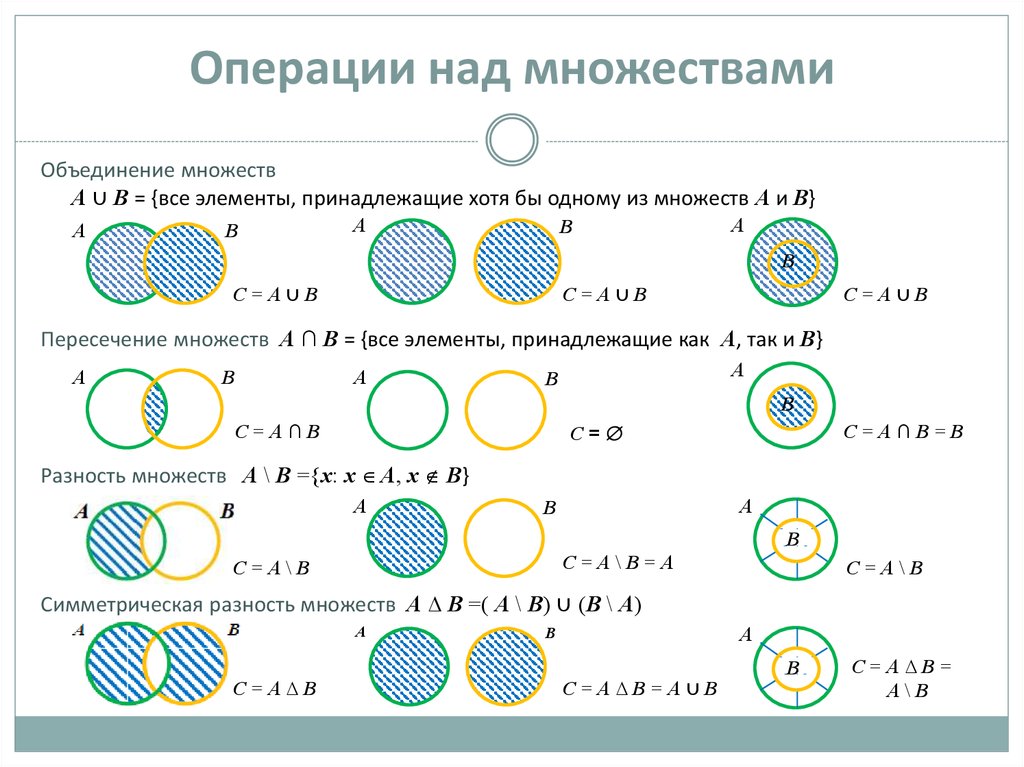 12.2017, 16:23
12.2017, 16:23  12.2017, 16:31
12.2017, 16:31  Гораздо прозрачнее, имхо.
Гораздо прозрачнее, имхо.

 Чтобы показать, что два множества $A$ и $B$ равны, мы можем показать, что два
множества являются подмножествами друг друга, т. е. $A \subseteq B$ и $B \subseteq
$. В частности, мы можем показать, что если $y \in A$, то $y \in B$ и
и наоборот, если $y \in B$, то $y \in A$. Мы можем думать об этом как
примерно аналогично показу «обеих сторон» тогда и только тогда, когда
операторы $(\iff)$.
Чтобы показать, что два множества $A$ и $B$ равны, мы можем показать, что два
множества являются подмножествами друг друга, т. е. $A \subseteq B$ и $B \subseteq
$. В частности, мы можем показать, что если $y \in A$, то $y \in B$ и
и наоборот, если $y \in B$, то $y \in A$. Мы можем думать об этом как
примерно аналогично показу «обеих сторон» тогда и только тогда, когда
операторы $(\iff)$.